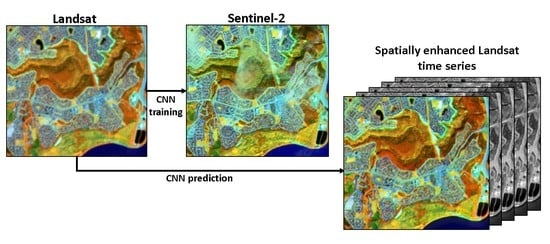
Landsat Super-Resolution Enhancement Using Convolution Neural Networks and Sentinel-2 for Training
Abstract
:1. Introduction
- Assesses the effectiveness of a shallow and deep CNN for super-resolution enhancement of Landsat trained from Sentinel-2 data for characteristic landscape environments in Canada including boreal forest, tundra, and cropland/woodland landscapes.
- Evaluate the potential for spatial extension over short distances of less than 100 km and temporal extension of a trained CNN model.
2. Materials and Methods
2.1. Landsat and Sentinel-2 Datasets
2.2. Sampling and Assessment
2.2.1. Hold-Out and Spatial Extension
2.2.2. Temporal Extension
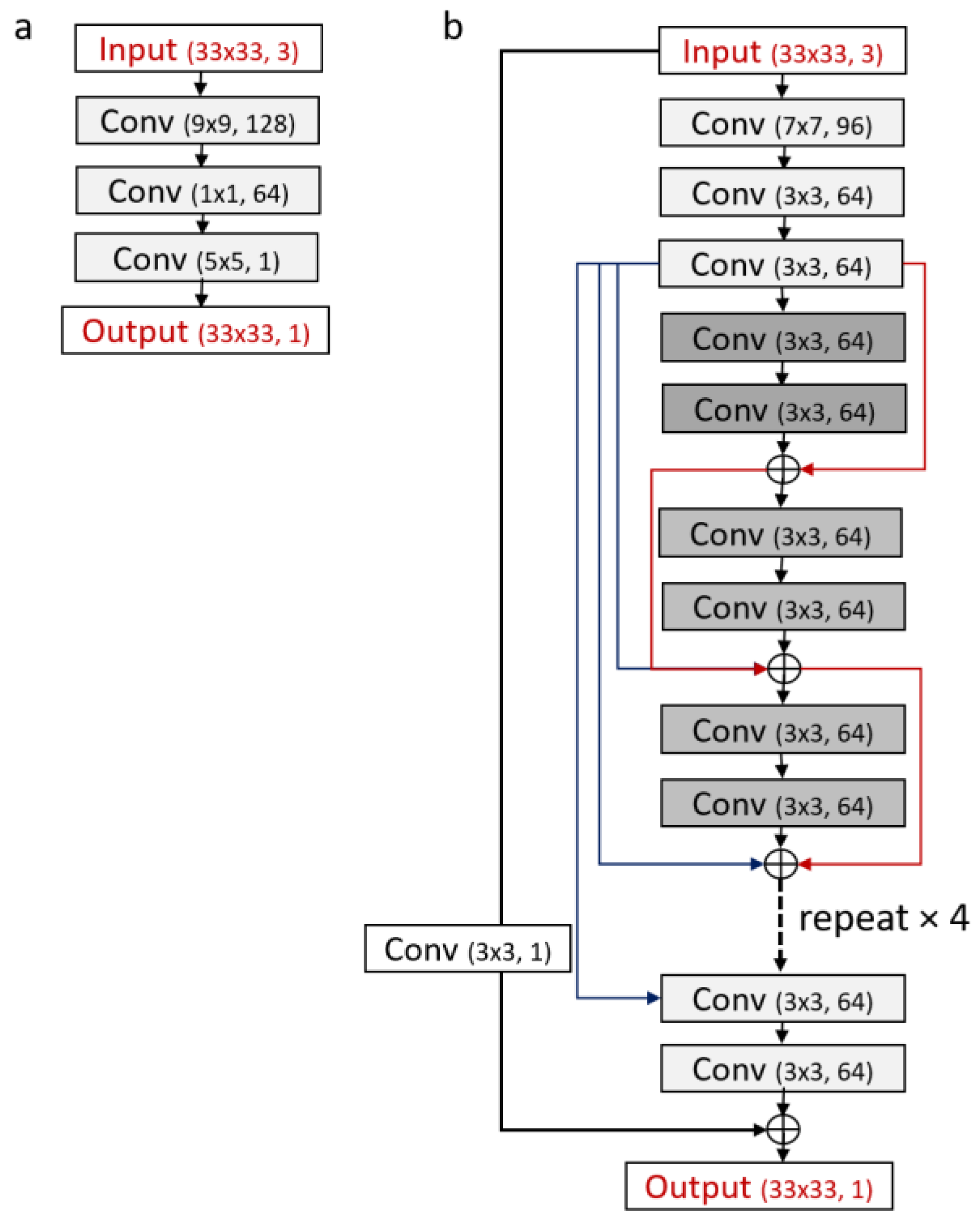
2.3. CNN Super-Resolution Models
3. Results
3.1. Hold-Out Accuracy
3.2. Spatial Extension Accuracy
3.3. Temporal Extension Accuracy
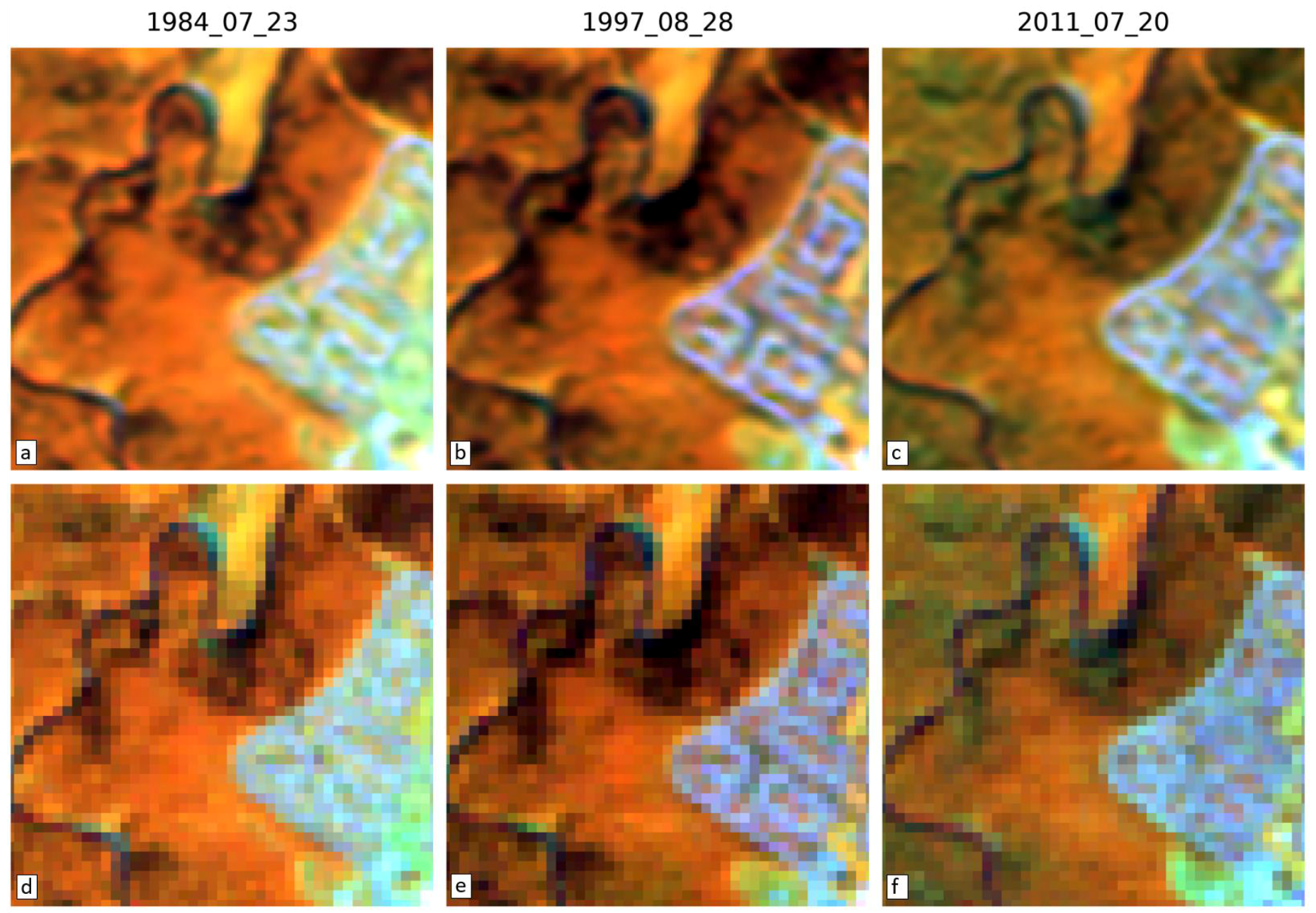
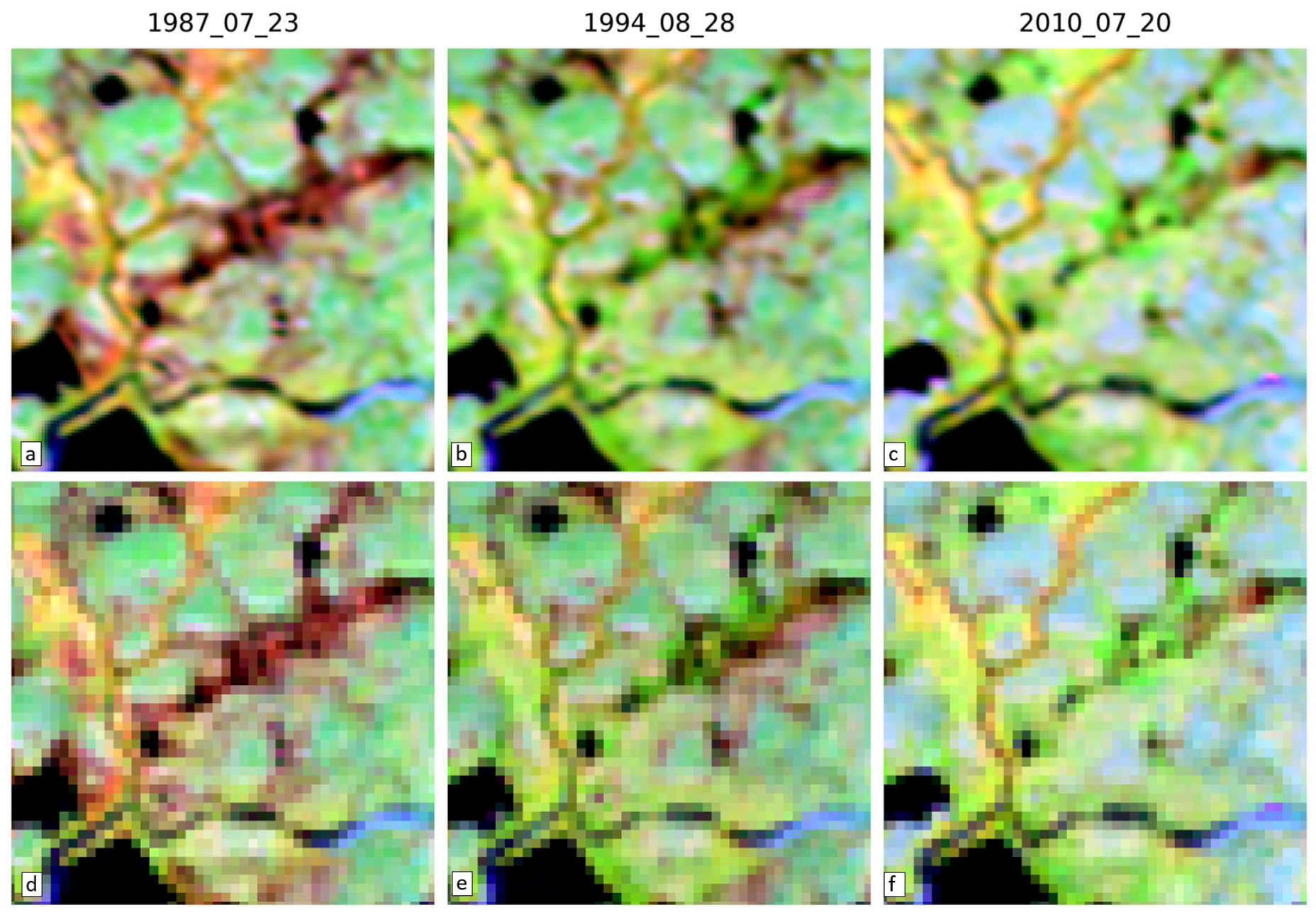
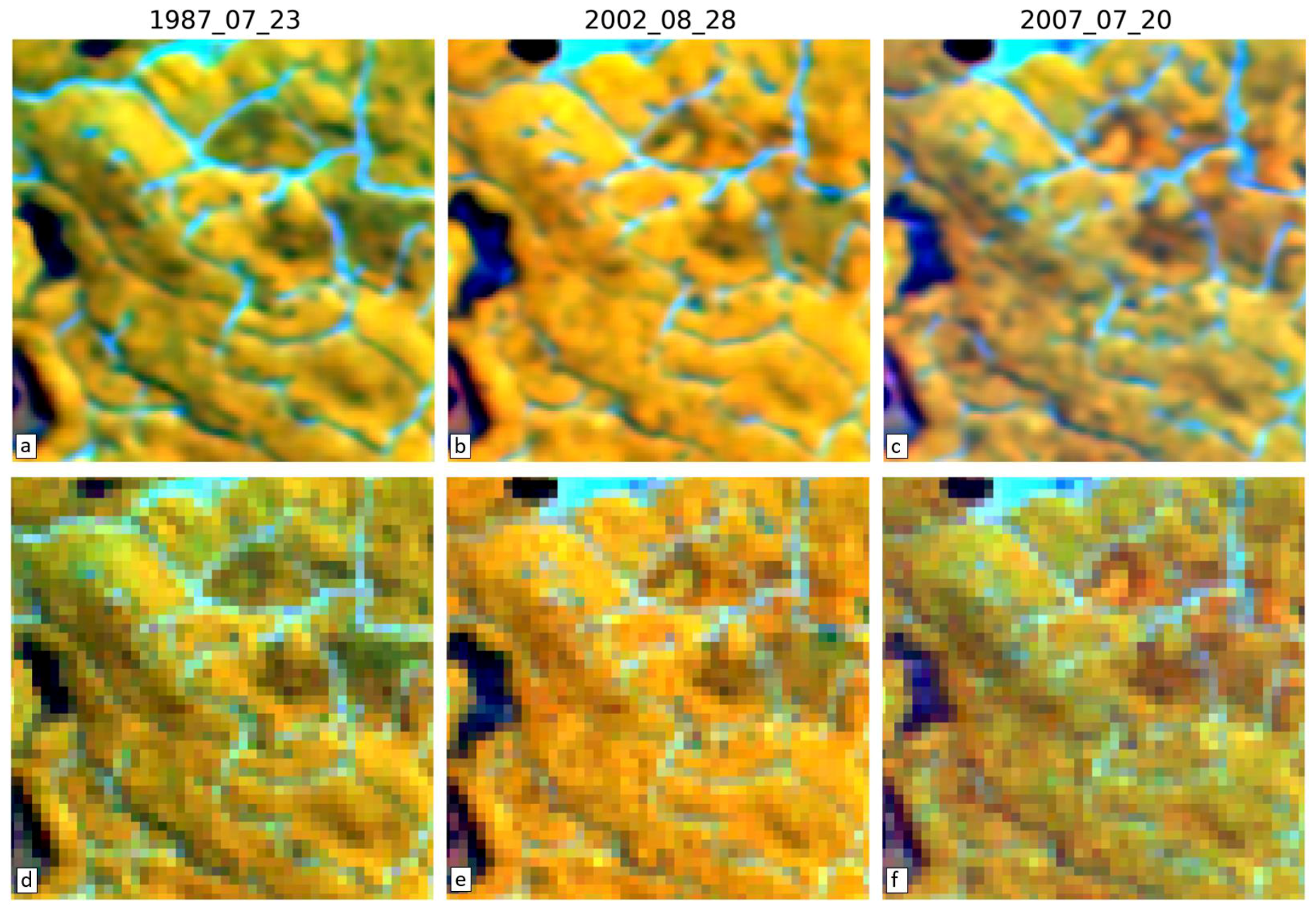
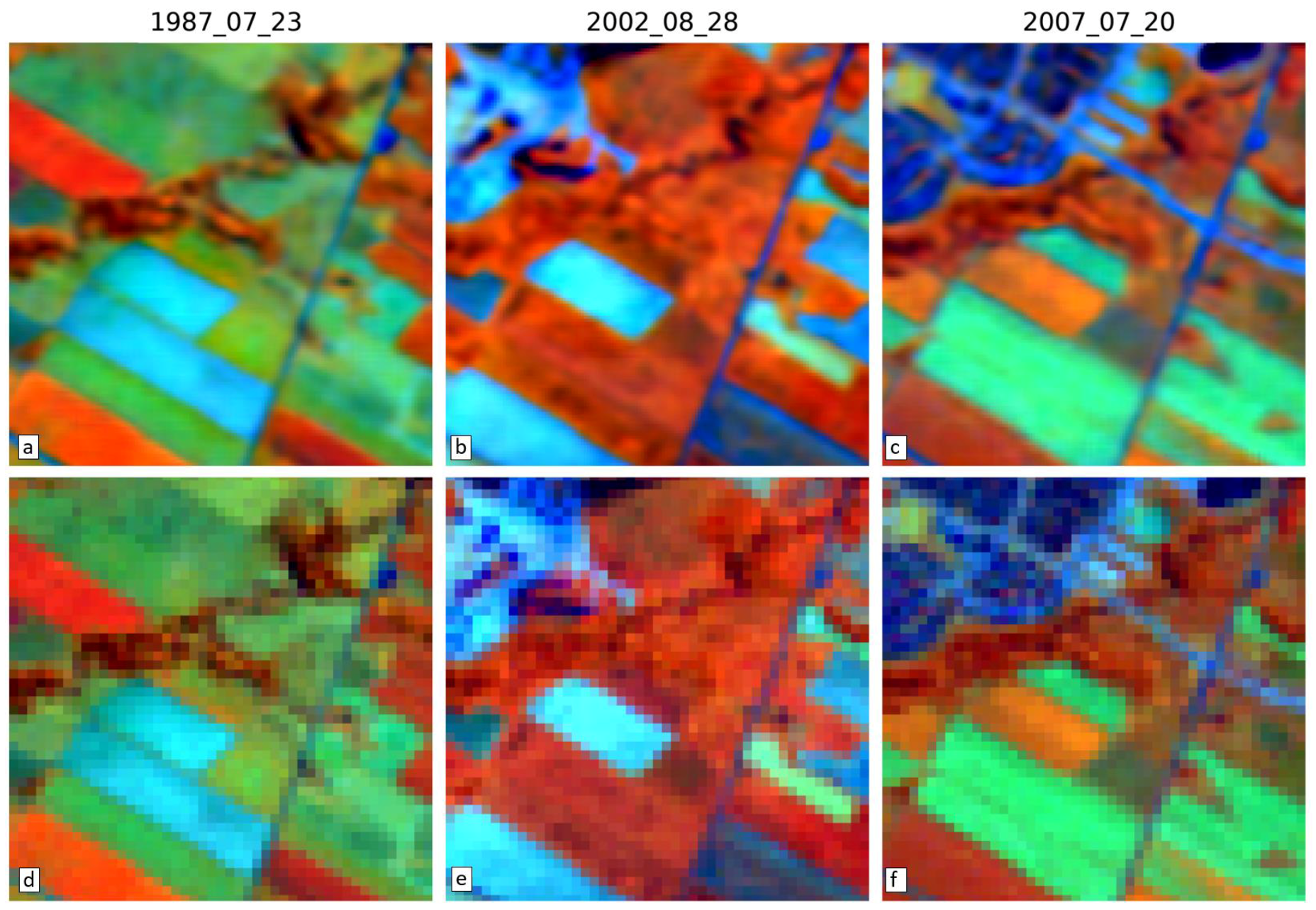
3.4. Visual Assessment
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhu, Z.; Woodcock, C.E.; Olofsson, P. Continuous monitoring of forest disturbance using all available Landsat imagery. Remote Sens. Environ. 2012, 122, 75–91. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Pouliot, D.; Latifovic, R. Reconstruction of Landsat time series in the presence of irregular and sparse observations: Development and assessment in north-eastern Alberta, Canada. Remote Sens. Environ. 2017. [Google Scholar] [CrossRef]
- Song, H.; Huang, B.; Liu, Q.; Zhang, K. Improving the Spatial Resolution of Landsat TM/ETM+ Through Fusion with SPOT5. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1195–1204. [Google Scholar] [CrossRef]
- Grochala, A.; Kedzierski, M. A method of panchromatic image modification for satellite imagery data fusion. Remote Sens. 2017, 9, 639. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, K.H.; Roy, P.D.; Yan, L.; Huang, H.; Li, J. Landsat 15-m Panchromatic-Assisted Downscaling (LPAD) of the 30-m Reflective Wavelength Bands to Sentinel-2 20-m Resolution. Remote Sens. 2017, 9, 755. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Gilbertson, J.K.; Kemp, J.; van Niekerk, A. Effect of pan-sharpening multi-temporal Landsat 8 imagery for crop type differentiation using different classification techniques. Comput. Electron. Agric. 2017, 134, 151–159. [Google Scholar] [CrossRef]
- Joshi, N.; Baumann, M.; Ehammer, A.; Fensholt, R.; Grogan, K.; Hostert, P.; Jepsen, M.R.; Kuemmerle, T.; Meyfroidt, P.; Mitchard, E.T.A.; et al. A review of the application of optical and radar remote sensing data fusion to land use mapping and monitoring. Remote Sens. 2016, 8, 70. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning deep convolutional networks for image super resolution. In Proceedings of the European Conference on Computer Vision, Athens, Greece, 11–13 November 2015. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 1–9. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.-S.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images; University of Toronto: Toronto, ON, Canada, 2009; pp. 1–60. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-Recursive Convolutional Network for Image Super-Resolution. arXiv, 2015; arXiv:1511.04491. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. arXiv, 2016; arXiv:1511.04587. [Google Scholar]
- Svoboda, P.; Hradis, M.; Barina, D.; Zemcik, P. Compression Artifacts Removal Using Convolutional Neural Networks. arXiv, 2016; arXiv:1605.00366. [Google Scholar]
- Mao, X.-J.; Shen, C.; Yang, Y.-B. Image Restoration using very Deep Convolutional Encoder-Decoder Networks with Symmetric Skip Connections. arXiv, 2016; arXiv:1603.09056. [Google Scholar]
- Wang, L.; Huang, Z.; Gong, Y.; Pan, C. Ensemble based deep networks for image super-resolution. Pattern Recognit. 2017, 68, 191–198. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. arXiv, 2016; arXiv:1609.05158. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X. Image Super-Resolution via Deep Recursive Residual Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3147–3155. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv, 2015; arXiv:1512.03385. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide Residual Networks. arXiv, 2016; arXiv:1605.07146. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated Residual Transformations for Deep Neural Networks. arXiv, 2017; arXiv:1611.05431. [Google Scholar]
- Collins, C.B.; Beck, J.M.; Bridges, S.M.; Rushing, J.A.; Graves, S.J. Deep Learning for Multisensor Image Resolution Enhancement. In Proceedings of the 1st Workshop on Artificial Intelligence and Deep Learning for Geographic Knowledge Discovery, Redondo Beach, CA, USA, 7 November 2017; pp. 37–44. [Google Scholar] [CrossRef]
- Latifovic, R.; Pouliot, D.; Olthof, I. Circa 2010 Land Cover of Canada: Local Optimization Methodology and Product Development. Remote Sens. 2017, 9, 1098. [Google Scholar] [CrossRef]
- Mueller-Wilm, U.M. S2 MPC Sen2Cor Configuration and User Manual; European Space Agency: Paris, France, 2017. [Google Scholar]
- Storey, J.; Roy, D.P.; Masek, J.; Gascon, F.; Dwyer, J.; Choate, M. A note on the temporary misregistration of Landsat-8 Operational Land Imager (OLI) and Sentinel-2 Multi Spectral Instrument (MSI) imagery. Remote Sens. Environ. 2016, 186, 121–122. [Google Scholar] [CrossRef]
- Storey, J.; Choate, M.; Rengarajan, R.; Lubke, M. Landsat-8/Sentinel-2 Registration Accuracy and Improvement Status; United States Geological Survey: Reston, VA, USA, 2017.
- Latifovic, R.; Pouliot, D.; Sun, L.; Schwarz, J.; Parkinson, W. Moderate Resolution Time Series Data Management and Analysis: Automated Large Area Mosaicking and Quality Control; Natural Resources Canada: Ottawa, ON, Canada, 2015. [Google Scholar] [CrossRef]
- United States Geological Survey. USGS Product Guide Landsat 8 Surface Reflectance Code (LaSRC) Product; United States Geological Survey: Reston, VA, USA, 2017; pp. 1–38.
- Lambin, E.F.; Strahlers, A.H. Change-vector analysis in multitemporal space: A tool to detect and categorize land-cover change processes using high temporal-resolution satellite data. Remote Sens. Environ. 1994, 48, 231–244. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, R.; Leblanc, S.G. Parametric (modified least squares) and non-parametric (Theil-Sen) linear regressions for predicting biophysical parameters in the presence of measurement errors. Remote Sens. Environ. 2005, 95, 303–316. [Google Scholar] [CrossRef]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv, 2016; arXiv:1609.04747. [Google Scholar]
- Goodwin, L.D.; Leech, N.L. Understanding correlation: Factors that affect the size of r. J. Exp. Educ. 2006, 74, 249–266. [Google Scholar] [CrossRef]
- Liang, Y.; Yang, Z.; Zhang, K.; He, Y.; Wang, J.; Zheng, N. Single Image Super-resolution with a Parameter Economic Residual-like Convolutional Neural Network. In Proceedings of the International Conference on Multimedia Modeling, Reykjavik, Iceland, 4–6 January 2017. [Google Scholar]
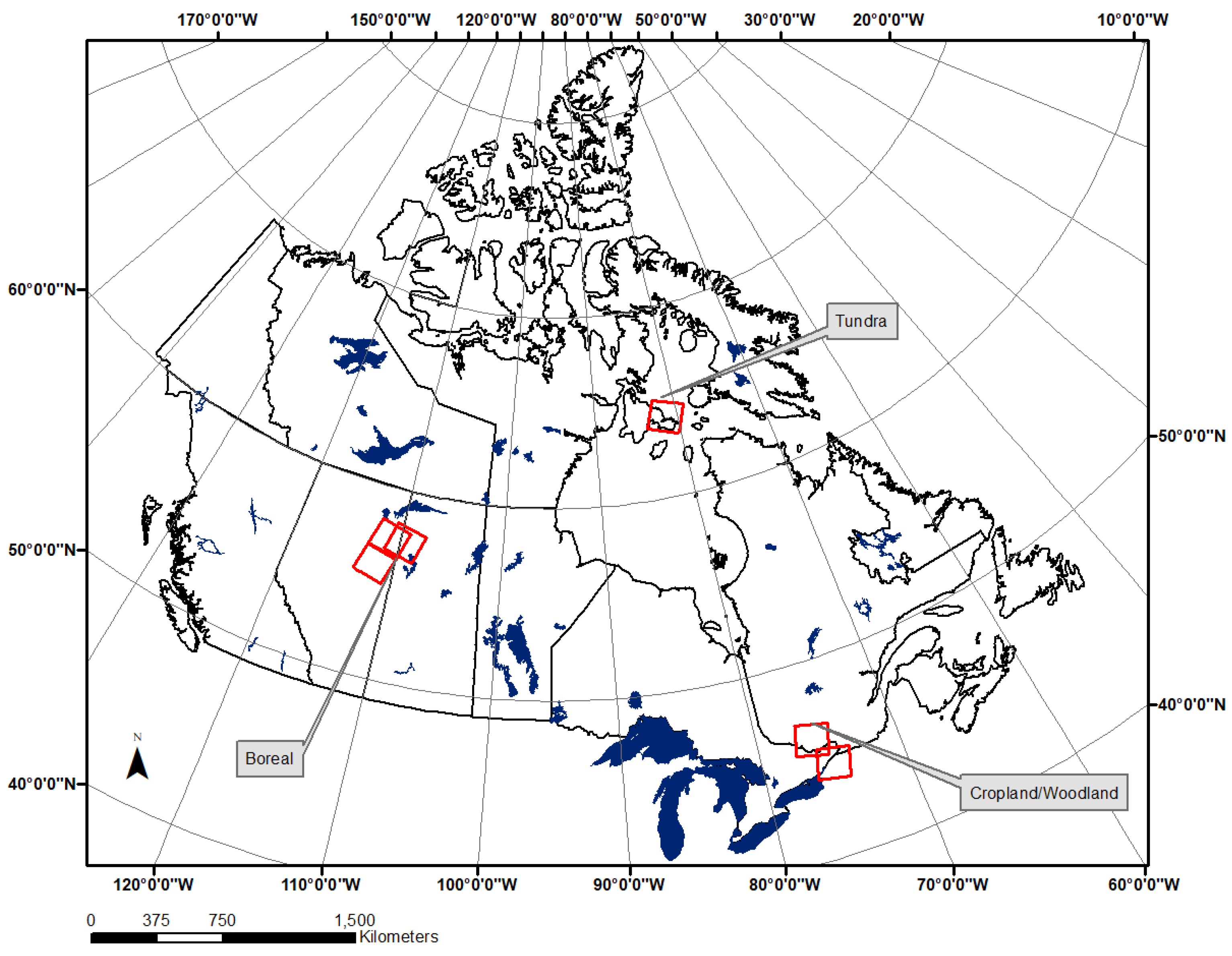


| Region | Sentinel-2 | Landsat-8 | Landsat-5 | |||
|---|---|---|---|---|---|---|
| Tile Reference | Date | Tile Reference | Date | Tile Reference | Date | |
| Boreal | T12VWH 8 | 7/19/2016 | 40_20 | 7/17/2016 | 42_20 | 7/31/1984 |
| T12VVH 8 | 8/30/2016 | 42_20 | 7/15/2016 | 42_20 | 8/28/1997 | |
| T12VVJ 5 | 7/9/2017 | 42_21 | 8/30/2015 | 42_20 | 7/20/2011 | |
| Tundra | T17VML 5,8 | 8/14/2016 | 26_15 | 8/16/2016 | 26_15 | 8/1/1987 |
| T17WMM 5,8 | 8/13/2016 | 26_15 | 8/4/1994 | |||
| T17WMM 5,8 | 8/13/2016 | 26_15 | 7/15/2010 | |||
| Cropland/Woodland | T18TVR 5,8 | 7/20/2016 | 15_29 | 8/19/2016 | 16_28 | 8/11/1987 |
| T18TWR 5,8 | 7/20/2016 | 16_28 | 8/26/2016 | 16_28 | 7/3/2002 | |
| 16_28 | 8/26/2016 | 16_28 | 8/2/2007 | |||
| Region | Method | Band | MEAN | STD | ME | MAE | STDE | P5E | P95E | SSIMm | SSIMs | CORm | CORs |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Boreal forest | No Transform | Red | 323 | 166 | −0.88 | 36.50 | 63.14 | −77.00 | 76.00 | 0.965 | 0.037 | 0.746 | 0.139 |
| Boreal forest | No Transform | NIR | 2050 | 720 | −1.40 | 201.79 | 292.76 | −450.00 | 469.00 | 0.827 | 0.085 | 0.803 | 0.110 |
| Boreal forest | No Transform | SWIR | 1247 | 428 | −0.66 | 96.45 | 152.28 | −225.00 | 219.00 | 0.915 | 0.075 | 0.852 | 0.122 |
| Boreal forest | SRCNN | Red | 323 | 166 | −0.84 | 31.45 | 54.02 | −62.03 | 67.86 | 0.973 | 0.029 | 0.794 | 0.139 |
| Boreal forest | SRCNN | NIR | 2050 | 720 | 4.76 | 167.19 | 240.25 | −365.91 | 384.17 | 0.875 | 0.078 | 0.853 | 0.104 |
| Boreal forest | SRCNN | SWIR | 1247 | 428 | −3.73 | 72.95 | 107.91 | −160.51 | 166.31 | 0.942 | 0.063 | 0.895 | 0.118 |
| Boreal forest | DCR_SRCNN | Red | 323 | 166 | 3.95 | 28.36 | 42.50 | −54.50 | 65.81 | 0.978 | 0.017 | 0.811 | 0.131 |
| Boreal forest | DCR_SRCNN | NIR | 2050 | 720 | −8.66 | 141.01 | 195.48 | −322.54 | 301.10 | 0.904 | 0.059 | 0.881 | 0.085 |
| Boreal forest | DCR_SRCNN | SWIR | 1247 | 428 | 5.72 | 49.00 | 69.94 | −98.04 | 116.91 | 0.967 | 0.033 | 0.931 | 0.084 |
| Tundra | No Transform | Red | 1013 | 720 | 0.49 | 110.46 | 190.91 | −240.00 | 263.00 | 0.875 | 0.069 | 0.784 | 0.098 |
| Tundra | No Transform | NIR | 1948 | 909 | −0.66 | 163.53 | 258.55 | −379.00 | 373.00 | 0.845 | 0.065 | 0.804 | 0.090 |
| Tundra | No Transform | SWIR | 2363 | 1449 | 2.58 | 184.42 | 314.71 | −445.00 | 447.00 | 0.893 | 0.056 | 0.864 | 0.082 |
| Tundra | SRCNN | Red | 1013 | 718 | −2.18 | 72.42 | 116.81 | −161.39 | 160.70 | 0.943 | 0.037 | 0.885 | 0.078 |
| Tundra | SRCNN | NIR | 1948 | 908 | 8.23 | 103.97 | 151.04 | −222.45 | 242.11 | 0.934 | 0.041 | 0.912 | 0.066 |
| Tundra | SRCNN | SWIR | 2363 | 1446 | −0.34 | 99.10 | 154.68 | −229.38 | 234.23 | 0.961 | 0.042 | 0.948 | 0.075 |
| Tundra | DCR_SRCNN | Red | 1013 | 718 | 9.23 | 62.935 | 93.99 | −123.38 | 158.16 | 0.954 | 0.027 | 0.900 | 0.072 |
| Tundra | DCR_SRCNN | NIR | 1948 | 908 | −5.24 | 85.713 | 118.71 | −196.30 | 185.54 | 0.950 | 0.032 | 0.931 | 0.058 |
| Tundra | DCR_SRCNN | SWIR | 2363 | 1447 | 6.45 | 59.619 | 85.33 | −129.24 | 142.42 | 0.980 | 0.022 | 0.969 | 0.060 |
| Cropland/Woodland | No Transform | Red | 318 | 253 | −1.16 | 61.43 | 123.19 | −149.00 | 170.00 | 0.899 | 0.107 | 0.644 | 0.177 |
| Cropland/Woodland | No Transform | NIR | 3325 | 1256 | −12.73 | 319.87 | 441.58 | −714.00 | 684.00 | 0.741 | 0.126 | 0.755 | 0.173 |
| Cropland/Woodland | No Transform | SWIR | 1582 | 605 | −4.43 | 123.88 | 187.29 | −291.00 | 278.00 | 0.869 | 0.112 | 0.773 | 0.118 |
| Cropland/Woodland | SRCNN | Red | 318 | 253 | −0.41 | 52.65 | 101.73 | −129.22 | 142.18 | 0.928 | 0.083 | 0.719 | 0.181 |
| Cropland/Woodland | SRCNN | NIR | 3325 | 1256 | 0.24 | 258.85 | 351.04 | −563.76 | 569.60 | 0.830 | 0.112 | 0.819 | 0.160 |
| Cropland/Woodland | SRCNN | SWIR | 1582 | 605 | −0.79 | 89.03 | 134.10 | −194.72 | 207.90 | 0.913 | 0.099 | 0.874 | 0.172 |
| Cropland/Woodland | DCR_SRCNN | Red | 318 | 253 | 4.09 | 45.465 | 82.76 | −103.66 | 123.95 | 0.945 | 0.057 | 0.748 | 0.173 |
| Cropland/Woodland | DCR_SRCNN | NIR | 3325 | 1256 | 28.70 | 232.460 | 312.05 | −475.67 | 541.73 | 0.860 | 0.089 | 0.845 | 0.142 |
| Cropland/Woodland | DCR_SRCNN | SWIR | 1582 | 605 | 13.58 | 66.388 | 93.63 | −127.05 | 164.15 | 0.948 | 0.052 | 0.909 | 0.134 |
| Region | Method | Band | MEAN | STD | ME | MAE | STDE | P5E | P95E | SSIMm | SSIMs | CORm | CORs |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Boreal forest | No Transform | Red | 336 | 114 | −0.53 | 26.17 | 41.53 | −54.00 | 55.00 | 0.977 | 0.024 | 0.775 | 0.142 |
| Boreal forest | No Transform | NIR | 2084 | 921 | −0.69 | 143.96 | 211.10 | −317.00 | 332.00 | 0.876 | 0.059 | 0.820 | 0.161 |
| Boreal forest | No Transform | SWIR | 1420 | 524 | −1.10 | 49.94 | 77.52 | −116.00 | 114.00 | 0.955 | 0.024 | 0.880 | 0.166 |
| Boreal forest | SRCNN | Red | 336 | 114 | 4.48 | 24.73 | 39.58 | −46.10 | 56.61 | 0.979 | 0.025 | 0.791 | 0.162 |
| Boreal forest | SRCNN | NIR | 2084 | 921 | −3.57 | 126.70 | 182.72 | −277.60 | 289.22 | 0.903 | 0.053 | 0.847 | 0.173 |
| Boreal forest | SRCNN | SWIR | 1420 | 524 | −12.31 | 50.14 | 73.00 | −111.35 | 110.59 | 0.969 | 0.025 | 0.902 | 0.177 |
| Boreal forest | DCR_SRCNN | Red | 336 | 114 | −0.37 | 24.23 | 37.80 | −42.17 | 57.03 | 0.981 | 0.020 | 0.807 | 0.152 |
| Boreal forest | DCR_SRCNN | NIR | 2084 | 921 | 1.20 | 122.82 | 176.15 | −280.86 | 268.82 | 0.910 | 0.051 | 0.853 | 0.166 |
| Boreal forest | DCR_SRCNN | SWIR | 1420 | 524 | −0.47 | 51.35 | 82.06 | −116.80 | 129.43 | 0.961 | 0.029 | 0.885 | 0.176 |
| Tundra | No Transform | Red | 1500 | 962 | 1.74 | 148.04 | 256.00 | −346.00 | 353.00 | 0.865 | 0.112 | 0.820 | 0.120 |
| Tundra | No Transform | NIR | 2275 | 1132 | 1.06 | 170.06 | 283.40 | −389.00 | 380.00 | 0.870 | 0.075 | 0.840 | 0.101 |
| Tundra | No Transform | SWIR | 3101 | 1701 | 0.37 | 223.58 | 413.35 | −554.00 | 566.00 | 0.896 | 0.099 | 0.872 | 0.104 |
| Tundra | SRCNN | Red | 1500 | 962 | −3.17 | 97.18 | 180.10 | −205.83 | 208.11 | 0.936 | 0.106 | 0.909 | 0.110 |
| Tundra | SRCNN | NIR | 2275 | 1132 | −3.57 | 101.92 | 158.59 | −228.87 | 215.30 | 0.949 | 0.057 | 0.934 | 0.076 |
| Tundra | SRCNN | SWIR | 3101 | 1701 | −8.22 | 129.31 | 251.22 | −291.85 | 297.05 | 0.951 | 0.094 | 0.941 | 0.100 |
| Tundra | DCR_SRCNN | Red | 1500 | 962 | 12.78 | 92.82 | 176.46 | −170.22 | 220.73 | 0.941 | 0.106 | 0.914 | 0.110 |
| Tundra | DCR_SRCNN | NIR | 2275 | 1132 | −3.47 | 97.39 | 154.86 | −218.60 | 209.26 | 0.952 | 0.056 | 0.937 | 0.073 |
| Tundra | DCR_SRCNN | SWIR | 3101 | 1701 | 5.69 | 138.25 | 271.00 | −311.06 | 347.59 | 0.945 | 0.094 | 0.933 | 0.099 |
| Cropland/Woodland | No Transform | Red | 328 | 300 | 0.43 | 79.90 | 159.20 | −184.00 | 231.00 | 0.864 | 0.109 | 0.640 | 0.176 |
| Cropland/Woodland | No Transform | NIR | 3632 | 1250 | −10.51 | 354.13 | 490.97 | −810.00 | 772.00 | 0.721 | 0.125 | 0.720 | 0.181 |
| Cropland/Woodland | No Transform | SWIR | 1628 | 543 | −1.61 | 132.12 | 203.57 | −299.00 | 303.00 | 0.848 | 0.118 | 0.770 | 0.200 |
| Cropland/Woodland | SRCNN | Red | 328 | 300 | −2.44 | 69.22 | 135.09 | −169.95 | 186.18 | 0.902 | 0.086 | 0.721 | 0.176 |
| Cropland/Woodland | SRCNN | NIR | 3632 | 1250 | −6.12 | 304.61 | 419.01 | −678.00 | 672.29 | 0.807 | 0.111 | 0.789 | 0.166 |
| Cropland/Woodland | SRCNN | SWIR | 1628 | 543 | −1.43 | 104.11 | 157.00 | −222.85 | 242.84 | 0.896 | 0.104 | 0.844 | 0.193 |
| Cropland/Woodland | DCR_SRCNN | Red | 328 | 300 | 4.41 | 69.81 | 139.20 | −163.35 | 195.46 | 0.902 | 0.084 | 0.720 | 0.170 |
| Cropland/Woodland | DCR_SRCNN | NIR | 3632 | 1250 | 26.46 | 300.29 | 412.67 | −630.31 | 695.18 | 0.816 | 0.110 | 0.797 | 0.161 |
| Cropland/Woodland | DCR_SRCNN | SWIR | 1628 | 543 | 14.42 | 89.49 | 141.21 | −174.24 | 227.41 | 0.909 | 0.101 | 0.856 | 0.191 |
| Region | Date | Band | No Transform | SRCNN | DCDR_SRCNN | No Transform | SRCNN | DCDR_SRCNN | No Transform | SRCNN | DCDR_SRCNN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | STDE | MAE | STDE | MAE | STDE | CORm | CORs | CORm | CORs | CORm | CORs | SSIMm | SSIMs | SSIMm | SSIMs | SSIMm | SSIMs | |||
| Boreal forest | 1984_07_23 | Red | 43 | 65 | 39 | 61 | 36 | 59 | 0.406 | 0.267 | 0.443 | 0.279 | 0.454 | 0.277 | 0.925 | 0.096 | 0.934 | 0.098 | 0.936 | 0.097 |
| Boreal forest | 1984_07_23 | NIR | 275 | 374 | 272 | 373 | 273 | 374 | 0.515 | 0.251 | 0.548 | 0.247 | 0.559 | 0.246 | 0.575 | 0.199 | 0.609 | 0.205 | 0.620 | 0.206 |
| Boreal forest | 1984_07_23 | SWIR | 136 | 186 | 134 | 183 | 129 | 179 | 0.488 | 0.288 | 0.527 | 0.295 | 0.538 | 0.298 | 0.702 | 0.179 | 0.721 | 0.184 | 0.726 | 0.184 |
| Boreal forest | 1997_08_28 | Red | 42 | 65 | 36 | 59 | 34 | 58 | 0.507 | 0.223 | 0.563 | 0.238 | 0.576 | 0.239 | 0.932 | 0.087 | 0.942 | 0.090 | 0.945 | 0.089 |
| Boreal forest | 1997_08_28 | NIR | 269 | 370 | 261 | 363 | 259 | 360 | 0.572 | 0.221 | 0.628 | 0.212 | 0.643 | 0.207 | 0.618 | 0.188 | 0.669 | 0.185 | 0.682 | 0.180 |
| Boreal forest | 1997_08_28 | SWIR | 120 | 169 | 116 | 164 | 111 | 160 | 0.644 | 0.233 | 0.686 | 0.240 | 0.695 | 0.241 | 0.779 | 0.156 | 0.801 | 0.160 | 0.807 | 0.160 |
| Boreal forest | 2011_07_20 | Red | 33 | 52 | 28 | 47 | 27 | 46 | 0.674 | 0.122 | 0.738 | 0.114 | 0.752 | 0.107 | 0.959 | 0.042 | 0.966 | 0.046 | 0.968 | 0.044 |
| Boreal forest | 2011_07_20 | NIR | 199 | 273 | 174 | 241 | 169 | 235 | 0.798 | 0.080 | 0.839 | 0.072 | 0.848 | 0.071 | 0.784 | 0.077 | 0.845 | 0.066 | 0.860 | 0.064 |
| Boreal forest | 2011_07_20 | SWIR | 80 | 114 | 75 | 107 | 64 | 92 | 0.855 | 0.061 | 0.899 | 0.057 | 0.913 | 0.057 | 0.907 | 0.049 | 0.932 | 0.048 | 0.940 | 0.048 |
| Cropland/Woodland | 1987_08_11 | Red | 65 | 121 | 64 | 126 | 69 | 127 | 0.527 | 0.229 | 0.576 | 0.236 | 0.582 | 0.243 | 0.866 | 0.125 | 0.870 | 0.124 | 0.870 | 0.122 |
| Cropland/Woodland | 1987_08_11 | NIR | 459 | 606 | 415 | 556 | 400 | 541 | 0.679 | 0.233 | 0.722 | 0.214 | 0.732 | 0.217 | 0.632 | 0.203 | 0.724 | 0.198 | 0.737 | 0.202 |
| Cropland/Woodland | 1987_08_11 | SWIR | 176 | 241 | 167 | 225 | 146 | 207 | 0.750 | 0.222 | 0.781 | 0.224 | 0.787 | 0.228 | 0.785 | 0.149 | 0.820 | 0.157 | 0.828 | 0.162 |
| Cropland/Woodland | 2002_07_30 | Red | 57 | 107 | 55 | 109 | 58 | 107 | 0.611 | 0.192 | 0.655 | 0.198 | 0.663 | 0.200 | 0.891 | 0.102 | 0.897 | 0.103 | 0.900 | 0.098 |
| Cropland/Woodland | 2002_07_30 | NIR | 414 | 551 | 374 | 505 | 364 | 499 | 0.763 | 0.166 | 0.796 | 0.160 | 0.805 | 0.159 | 0.725 | 0.152 | 0.799 | 0.150 | 0.807 | 0.152 |
| Cropland/Woodland | 2002_07_30 | SWIR | 149 | 206 | 143 | 189 | 119 | 184 | 0.819 | 0.158 | 0.846 | 0.171 | 0.853 | 0.172 | 0.841 | 0.105 | 0.872 | 0.121 | 0.880 | 0.123 |
| Cropland/Woodland | 2007_08_20 | Red | 57 | 105 | 47 | 88 | 46 | 86 | 0.638 | 0.149 | 0.723 | 0.132 | 0.745 | 0.128 | 0.897 | 0.094 | 0.926 | 0.065 | 0.931 | 0.061 |
| Cropland/Woodland | 2007_08_20 | NIR | 433 | 574 | 317 | 420 | 300 | 404 | 0.805 | 0.115 | 0.848 | 0.100 | 0.857 | 0.100 | 0.684 | 0.110 | 0.835 | 0.098 | 0.853 | 0.100 |
| Cropland/Woodland | 2007_08_20 | SWIR | 135 | 188 | 105 | 148 | 93 | 131 | 0.875 | 0.077 | 0.915 | 0.069 | 0.924 | 0.069 | 0.880 | 0.050 | 0.925 | 0.055 | 0.936 | 0.054 |
| Tundra | 1987_08_01 | Red | 91 | 136 | 79 | 114 | 78 | 111 | 0.749 | 0.142 | 0.804 | 0.134 | 0.806 | 0.135 | 0.877 | 0.067 | 0.906 | 0.061 | 0.908 | 0.061 |
| Tundra | 1987_08_01 | NIR | 155 | 230 | 126 | 180 | 127 | 183 | 0.813 | 0.100 | 0.878 | 0.088 | 0.878 | 0.090 | 0.853 | 0.067 | 0.907 | 0.057 | 0.907 | 0.058 |
| Tundra | 1987_08_01 | SWIR | 207 | 312 | 154 | 226 | 131 | 190 | 0.851 | 0.092 | 0.907 | 0.083 | 0.915 | 0.080 | 0.870 | 0.075 | 0.918 | 0.066 | 0.925 | 0.067 |
| Tundra | 1994_08_04 | Red | 91 | 135 | 78 | 111 | 77 | 110 | 0.757 | 0.142 | 0.810 | 0.135 | 0.811 | 0.137 | 0.875 | 0.067 | 0.907 | 0.060 | 0.907 | 0.060 |
| Tundra | 1994_08_04 | NIR | 157 | 230 | 121 | 172 | 119 | 171 | 0.816 | 0.107 | 0.881 | 0.097 | 0.882 | 0.095 | 0.846 | 0.078 | 0.906 | 0.067 | 0.908 | 0.065 |
| Tundra | 1994_08_04 | SWIR | 190 | 294 | 142 | 211 | 119 | 176 | 0.847 | 0.117 | 0.907 | 0.103 | 0.916 | 0.099 | 0.872 | 0.092 | 0.921 | 0.081 | 0.928 | 0.078 |
| Tundra | 2010_07_15 | Red | 83 | 139 | 65 | 98 | 64 | 94 | 0.801 | 0.103 | 0.876 | 0.080 | 0.881 | 0.078 | 0.895 | 0.076 | 0.939 | 0.045 | 0.942 | 0.041 |
| Tundra | 2010_07_15 | NIR | 150 | 226 | 106 | 150 | 103 | 148 | 0.829 | 0.085 | 0.910 | 0.063 | 0.913 | 0.061 | 0.859 | 0.063 | 0.930 | 0.042 | 0.934 | 0.040 |
| Tundra | 2010_07_15 | SWIR | 190 | 292 | 133 | 195 | 104 | 152 | 0.861 | 0.082 | 0.929 | 0.059 | 0.941 | 0.054 | 0.883 | 0.063 | 0.939 | 0.046 | 0.950 | 0.043 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pouliot, D.; Latifovic, R.; Pasher, J.; Duffe, J. Landsat Super-Resolution Enhancement Using Convolution Neural Networks and Sentinel-2 for Training. Remote Sens. 2018, 10, 394. https://doi.org/10.3390/rs10030394
Pouliot D, Latifovic R, Pasher J, Duffe J. Landsat Super-Resolution Enhancement Using Convolution Neural Networks and Sentinel-2 for Training. Remote Sensing. 2018; 10(3):394. https://doi.org/10.3390/rs10030394
Chicago/Turabian StylePouliot, Darren, Rasim Latifovic, Jon Pasher, and Jason Duffe. 2018. "Landsat Super-Resolution Enhancement Using Convolution Neural Networks and Sentinel-2 for Training" Remote Sensing 10, no. 3: 394. https://doi.org/10.3390/rs10030394