Figure 1.
Spatial locations of meteorological stations (left) and relative pixel sizes of the rain data products (right).
Figure 1.
Spatial locations of meteorological stations (left) and relative pixel sizes of the rain data products (right).
Figure 2.
Distribution of the average accumulated precipitation estimated from Eta, TRMM, and CHIRPS and observed at fourteen INMET meteorological stations between July 2009 to June 2015, for the south-southeast region of Minas, MG.
Figure 2.
Distribution of the average accumulated precipitation estimated from Eta, TRMM, and CHIRPS and observed at fourteen INMET meteorological stations between July 2009 to June 2015, for the south-southeast region of Minas, MG.
Figure 3.
Precipitation (mm) from INMET versus the precipitation estimates from Eta, TRMM, and CHIRPS, per crop year.
Figure 3.
Precipitation (mm) from INMET versus the precipitation estimates from Eta, TRMM, and CHIRPS, per crop year.
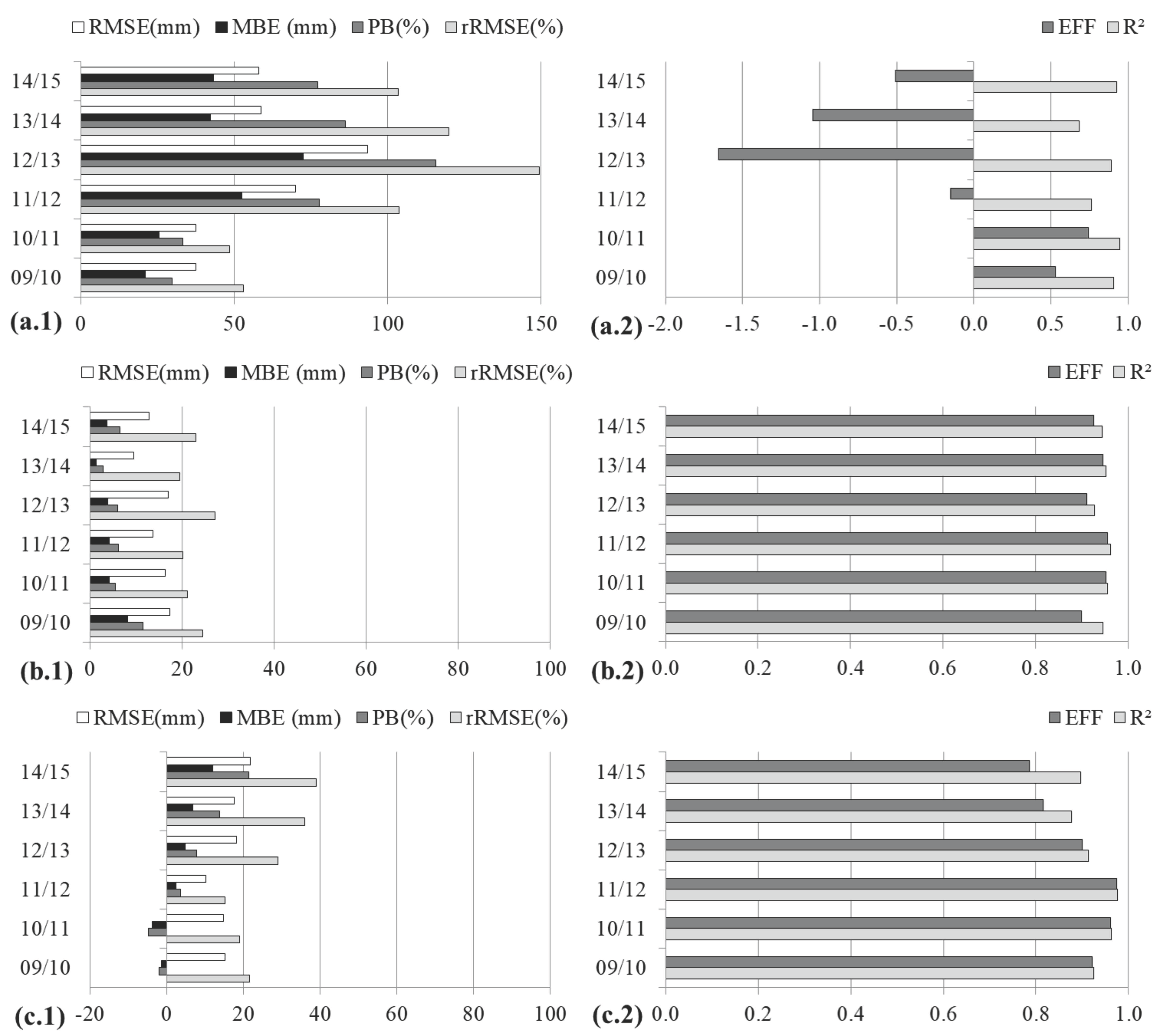
Figure 4.
(a.1, b.1, c.1) Root mean squared error (RMSE), average of errors (MBE), relative root mean squared error (rRSME; %), and percent average of errors (PB; %); (a.2, b.2, c.2) Nash-Sutcliffe efficiency coefficient (EFF) and coefficient of determination (R2) between the precipitation (PREC) data from the meteorological stations and estimates from (a) Eta, (b) TRMM, and (c) CHIRPS.
Figure 4.
(a.1, b.1, c.1) Root mean squared error (RMSE), average of errors (MBE), relative root mean squared error (rRSME; %), and percent average of errors (PB; %); (a.2, b.2, c.2) Nash-Sutcliffe efficiency coefficient (EFF) and coefficient of determination (R2) between the precipitation (PREC) data from the meteorological stations and estimates from (a) Eta, (b) TRMM, and (c) CHIRPS.
Figure 5.
Seasonal variations in (a.1, b.1, c.1) PB and rRMSE, and in (a.2, b.2, c.2) EFF and R2, for the periods (DJF, SON, JJA, and MAM), for the precipitation at meteorological stations and precipitation estimated by (a) Eta, (b) TRMM, and (c) CHIRPS.
Figure 5.
Seasonal variations in (a.1, b.1, c.1) PB and rRMSE, and in (a.2, b.2, c.2) EFF and R2, for the periods (DJF, SON, JJA, and MAM), for the precipitation at meteorological stations and precipitation estimated by (a) Eta, (b) TRMM, and (c) CHIRPS.
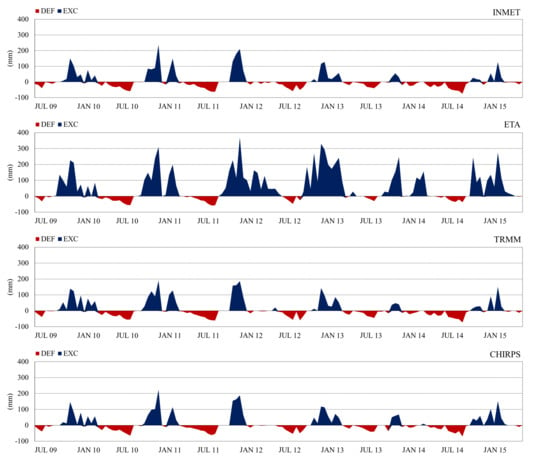
Figure 6.
Average values of water deficit (DEF) and water surplus (EXC) estimated through the sequential water balance, with use of the observed data of INMET meteorological stations and the Eta, TRMM, and CHIRPS data for the period July 2009 to June 2015.
Figure 6.
Average values of water deficit (DEF) and water surplus (EXC) estimated through the sequential water balance, with use of the observed data of INMET meteorological stations and the Eta, TRMM, and CHIRPS data for the period July 2009 to June 2015.
Figure 7.
Average values of evapotranspiration (ETR) estimated through the sequential water balance, using INMET, Eta, TRMM, and CHIRPS data, for the period July 2009 to June 2015.
Figure 7.
Average values of evapotranspiration (ETR) estimated through the sequential water balance, using INMET, Eta, TRMM, and CHIRPS data, for the period July 2009 to June 2015.
Figure 8.
(a.1, b.1, c.1) Nash-Sutcliffe efficiency coefficient (EFF) and (a.2, b.2, c.2) average of errors (MBE), for the periods (DJF, MAN, JJA, and SON), determined for (a) water deficit, (b) water surplus, and (c) evapotranspiration.
Figure 8.
(a.1, b.1, c.1) Nash-Sutcliffe efficiency coefficient (EFF) and (a.2, b.2, c.2) average of errors (MBE), for the periods (DJF, MAN, JJA, and SON), determined for (a) water deficit, (b) water surplus, and (c) evapotranspiration.
Table 1.
Location of the meteorological stations. Availability of data is indicated by (✓).
Table 1.
Location of the meteorological stations. Availability of data is indicated by (✓).
| N° | Station | State 1 | Latitude (°) | Longitude (°) | Altitude (m) | Precipitation | WB 2 |
|---|
| 1 | São Lourenço | MG | −22.13 | −45.04 | 930.65 | ✓ | ✓ |
| 2 | Poços de Caldas | MG | −21.92 | −46.38 | 1077.08 | ✓ | |
| 3 | Lavras | MG | −21.23 | −44.98 | 916.19 | ✓ | ✓ |
| 4 | Machado | MG | −21.68 | −45.94 | 892.44 | ✓ | ✓ |
| 5 | Bambuí | MG | −20.03 | −46.01 | 684.43 | ✓ | ✓ |
| 6 | Barbacena | MG | −21.24 | −43.78 | 1128.08 | ✓ | |
| 7 | Juiz de Fora | MG | −21.77 | −43.36 | 936.88 | ✓ | ✓ |
| 8 | Divinópolis | MG | −20.17 | −44.87 | 787.42 | ✓ | ✓ |
| 9 | Araxá | MG | −19.61 | −46.95 | 1018.32 | ✓ | ✓ |
| 10 | Bom Despacho | MG | −19.72 | −45.37 | 659.46 | ✓ | ✓ |
| 11 | São Simão | SP | −21.48 | −47.55 | 617.39 | ✓ | |
| 12 | Franca | SP | −20.58 | −47.37 | 1026.20 | ✓ | ✓ |
| 13 | Campos do Jordão | SP | −22.75 | −45.60 | 1642.00 | ✓ | |
| 14 | Resende | RJ | −22.45 | −44.44 | 439.89 | ✓ | |
Table 2.
Formulas of performance measures coefficient of determination (R2), average of errors (MBE), root mean squared error (RMSE), relative root mean squared error (rRMSE), percent average of errors (PB), and Nash-Sutcliffe efficiency (EFF).
Table 2.
Formulas of performance measures coefficient of determination (R2), average of errors (MBE), root mean squared error (RMSE), relative root mean squared error (rRMSE), percent average of errors (PB), and Nash-Sutcliffe efficiency (EFF).
| Name | Formula |
|---|
| Coefficient of determination | |
| Average of errors (Bias) | |
| Root mean squared error | |
| Relative root mean squared error | |
| Percent Bias | |
| Nash-Sutcliffe efficiency coefficient | |
| where: = estimated variable; = variable observed at meteorological station; and = average of the values observed at meteorological stations; N = total number of observations. |
Table 3.
Formulas for performance measurements based on Probability of Detection (POD), False Alarm Ratio (FAR), Critical Success Index (CSI) and Probability of false detection (POFD).
Table 3.
Formulas for performance measurements based on Probability of Detection (POD), False Alarm Ratio (FAR), Critical Success Index (CSI) and Probability of false detection (POFD).
| Name | Formula |
|---|
| Probability of Detection | |
| False Alarm Ratio | |
| Critical Success Index | |
| Probability of false detection | |
Table 4.
Coefficients of correlation (R), of determination (R2), and of Nash-Sutcliffe efficiency (EFF), average of errors (MBE), root mean squared error (RMSE), relative root mean squared error (rRMSE), and percent bias (PB) for precipitation during the period from July 2009 to June 2015.
Table 4.
Coefficients of correlation (R), of determination (R2), and of Nash-Sutcliffe efficiency (EFF), average of errors (MBE), root mean squared error (RMSE), relative root mean squared error (rRMSE), and percent bias (PB) for precipitation during the period from July 2009 to June 2015.
| Dataset | R | R2 | EFF | MBE | RSME | rRMSE | PB |
|---|
| (mm) | (mm) | (%) | (%) |
|---|
| Eta | 0.90 | 0.80 | 0.42 | 42.81 | 62.24 | 97.57 | 67.11 |
| TRMM | 0.97 | 0.95 | 0.97 | 4.21 | 14.70 | 23.05 | 6.60 |
| CHIRPS | 0.96 | 0.92 | 0.96 | 3.45 | 16.68 | 26.14 | 5.42 |
Table 5.
Probability of Detection (POD), False Alarm Ratio (FAR), Critical Success Index (CSI), and Probability of false detection (POFD) for precipitation during the period from July 2009 to June 2015.
Table 5.
Probability of Detection (POD), False Alarm Ratio (FAR), Critical Success Index (CSI), and Probability of false detection (POFD) for precipitation during the period from July 2009 to June 2015.
| Dataset | POD | FAR | CSI | POFD |
|---|
| Eta | 1.00 | 0.08 | 0.92 | 0.69 |
| TRMM | 0.94 | 0.01 | 0.94 | 0.06 |
| CHIRPS | 0.95 | 0.03 | 0.93 | 0.18 |
Table 6.
Coefficients of correlation (R), determination (R2) and Nash-Sutcliffe efficiency (EFF), Average of errors (MBE), root mean squared error (RMSE), relative root mean squared error (rRMSE), and percent bias (PB) for the water deficit (DEF), and water surplus (EXC) in the period from July 2009 to June 2015.
Table 6.
Coefficients of correlation (R), determination (R2) and Nash-Sutcliffe efficiency (EFF), Average of errors (MBE), root mean squared error (RMSE), relative root mean squared error (rRMSE), and percent bias (PB) for the water deficit (DEF), and water surplus (EXC) in the period from July 2009 to June 2015.
| Dataset | R | R2 | EFF | MBE | RMSE | rRMSE | PB |
|---|
| (mm) | (mm) | (%) | (%) |
|---|
| WATER DEFICIT |
| Eta | 0.88 | 0.77 | 0.64 | −6.15 | 10.80 | 83.27 | −47.38 |
| TRMM | 0.98 | 0.95 | 0.95 | −0.80 | 3.97 | 30.63 | −6.14 |
| CHIRPS | 0.95 | 0.90 | 0.89 | −1.56 | 5.87 | 45.28 | −12.03 |
| WATER SURPLUS |
| Eta | 0.74 | 0.55 | −2.02 | 42.63 | 75.62 | 399.15 | 225.01 |
| TRMM | 0.96 | 0.92 | 0.92 | 2.40 | 12.69 | 66.99 | 12.65 |
| CHIRPS | 0.96 | 0.93 | 0.93 | 2.15 | 11.88 | 62.72 | 11.34 |
Table 7.
Coefficients of correlation (R), determination (R2) and Nash-Sutcliffe efficiency (EFF), average of errors (MBE), root mean squared error (RMSE), relative root mean squared error (rRMSE), and percent bias (PB) for evapotranspiration in the period from July 2009 to June 2015.
Table 7.
Coefficients of correlation (R), determination (R2) and Nash-Sutcliffe efficiency (EFF), average of errors (MBE), root mean squared error (RMSE), relative root mean squared error (rRMSE), and percent bias (PB) for evapotranspiration in the period from July 2009 to June 2015.
| Dataset | R | R2 | EFF | MBE | RMSE | rRMSE | PB |
|---|
| (mm·period−1) | (mm·period−1) | (%) | (%) |
|---|
| Eta | 0.92 | 0.84 | 0.76 | 6.15 | 10.80 | 24.72 | 14.06 |
| TRMM | 0.98 | 0.97 | 0.97 | 0.80 | 3.97 | 9.09 | 1.82 |
| CHIRPS | 0.97 | 0.94 | 0.93 | 1.56 | 5.87 | 13.44 | 3.57 |