Evaluating the Performance of the SCOPE Model in Simulating Canopy Solar-Induced Chlorophyll Fluorescence
Abstract
1. Introduction
2. Materials and Methods
2.1. SCOPE (Soil Canopy Observation of Photochemistry and Energy Fluxes)
2.1.1. SCOPE Model Description
2.1.2. SCOPE Model Inputs
2.2. In Situ Measurements
2.2.1. Measurements of Vegetation Parameters
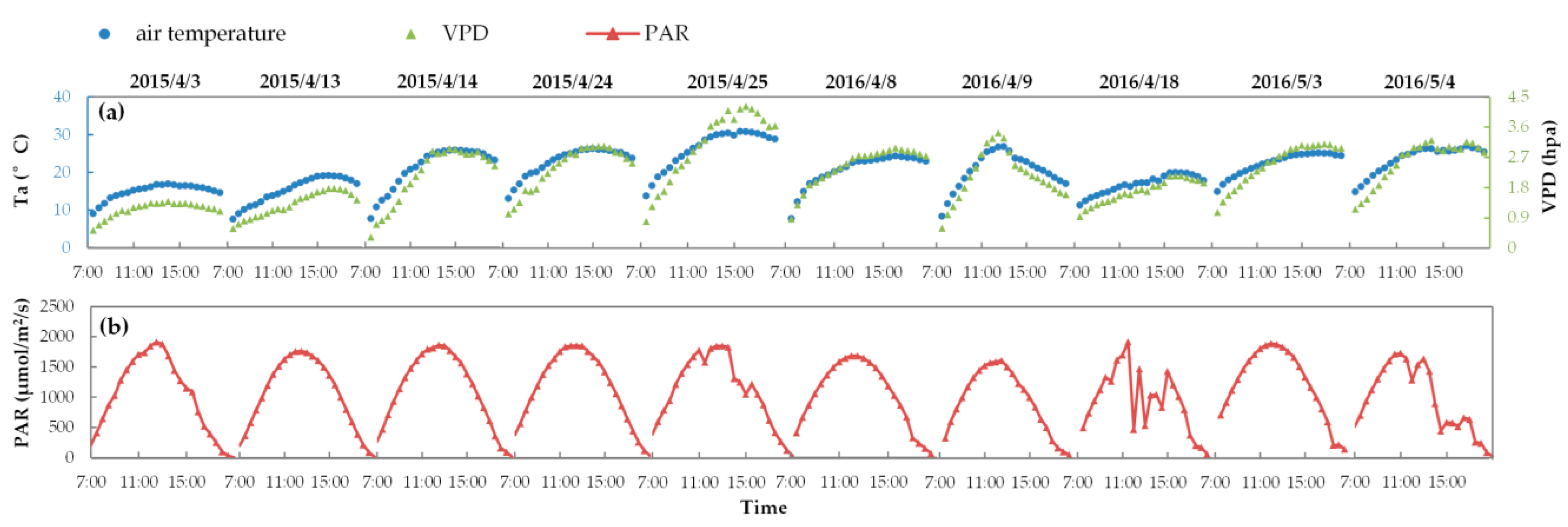
2.2.2. Diurnal Flux and Meteorological Observations
2.2.3. Diurnal Spectral Measurements
2.2.4. SIF Retrievals from the Spectral Measurements
2.3. Inversion of LIDFa and Vcmo from In Situ Measurements
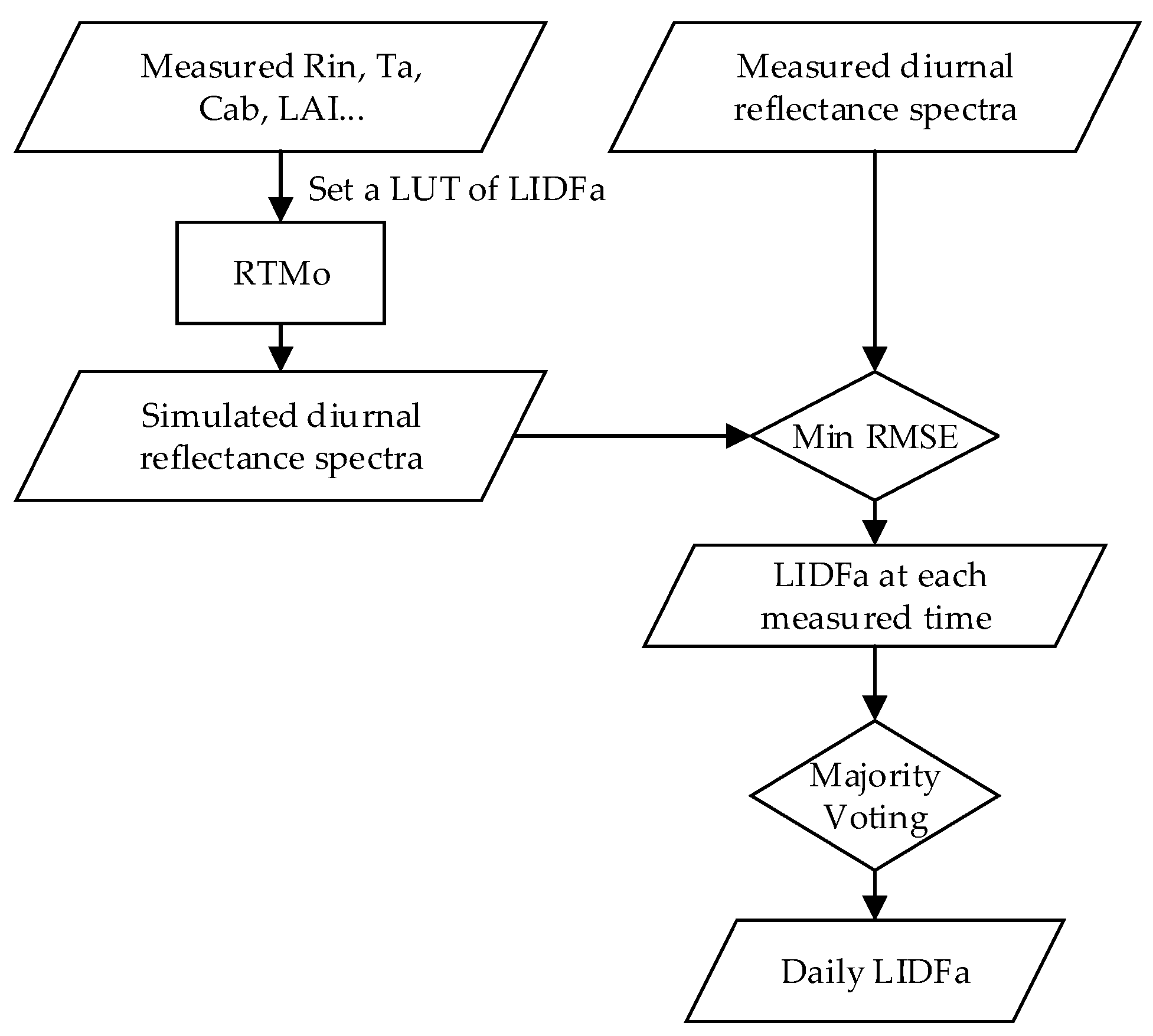
2.3.1. LIDFa Inversion from the Diurnal Canopy Reflectance Spectra
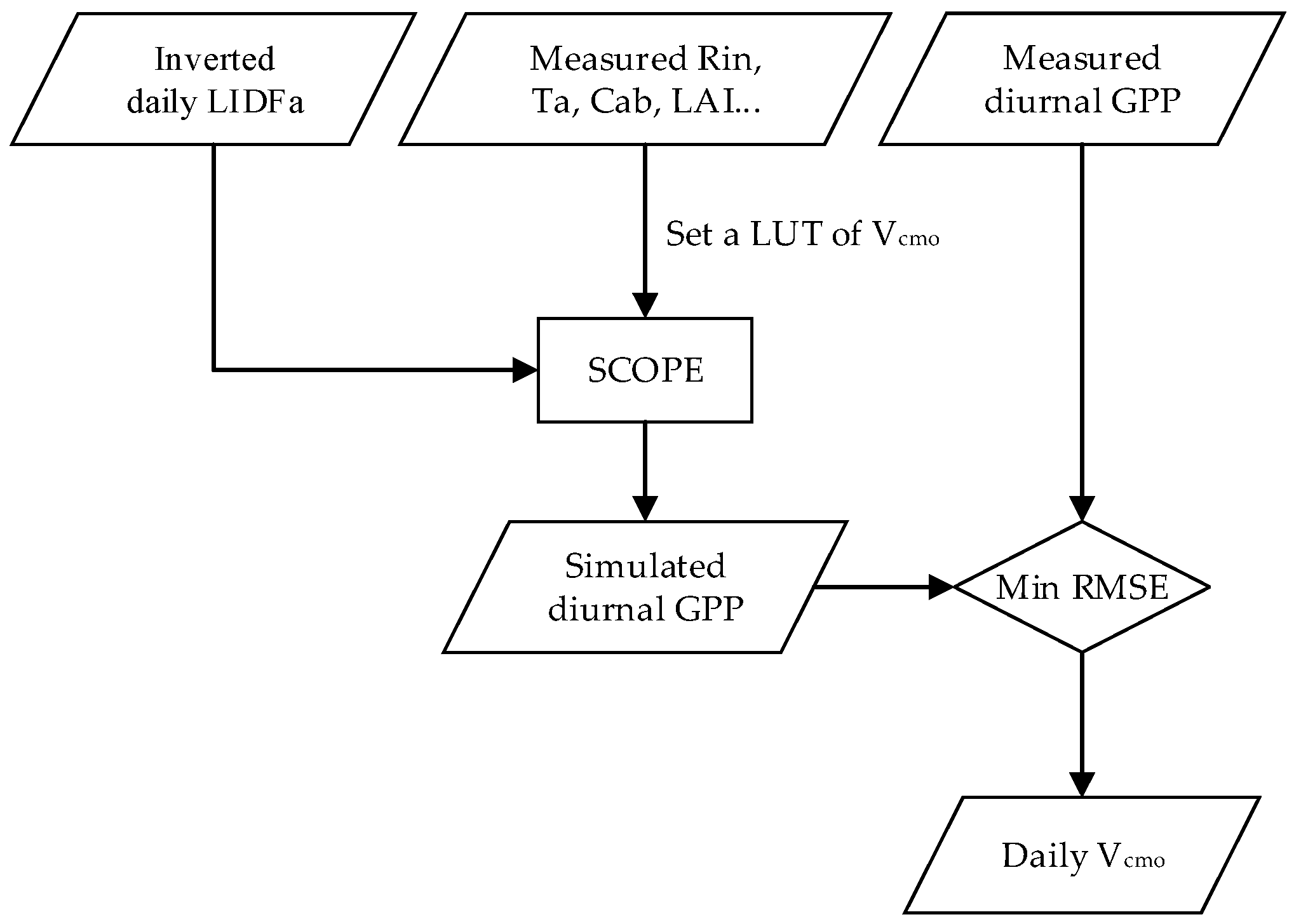
2.3.2. Vcmo Inversion from Diurnal GPP Observations
2.4. Settings of FQE Values
- (1)
- Fixed FQE, simulations with fixed FQE values as the literature suggested values: 0.01 for fqe2 and 0.2 for fqe1/fqe2.
- (2)
- Variable FQE, simulations with variable FQE values, which were estimated by fitting the SIF simulations to the observed SIF data and minimizing the systematic deviations in SIFA and SIFB simulations with the LUT of changing values of FQE.
2.5. Experimental Process
3. Results
3.1. LIDFa and Vcmo Retrieved from In Situ Measurements
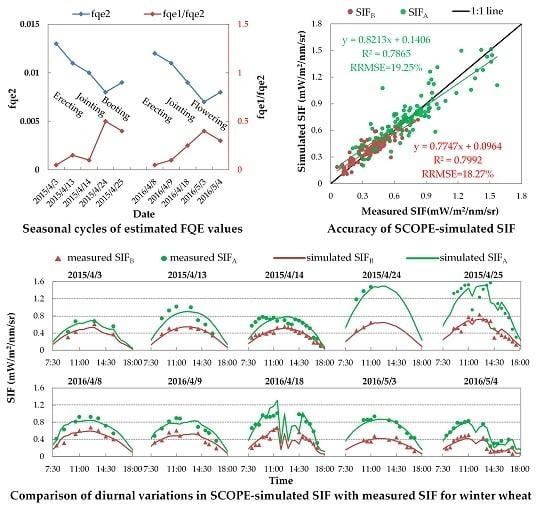
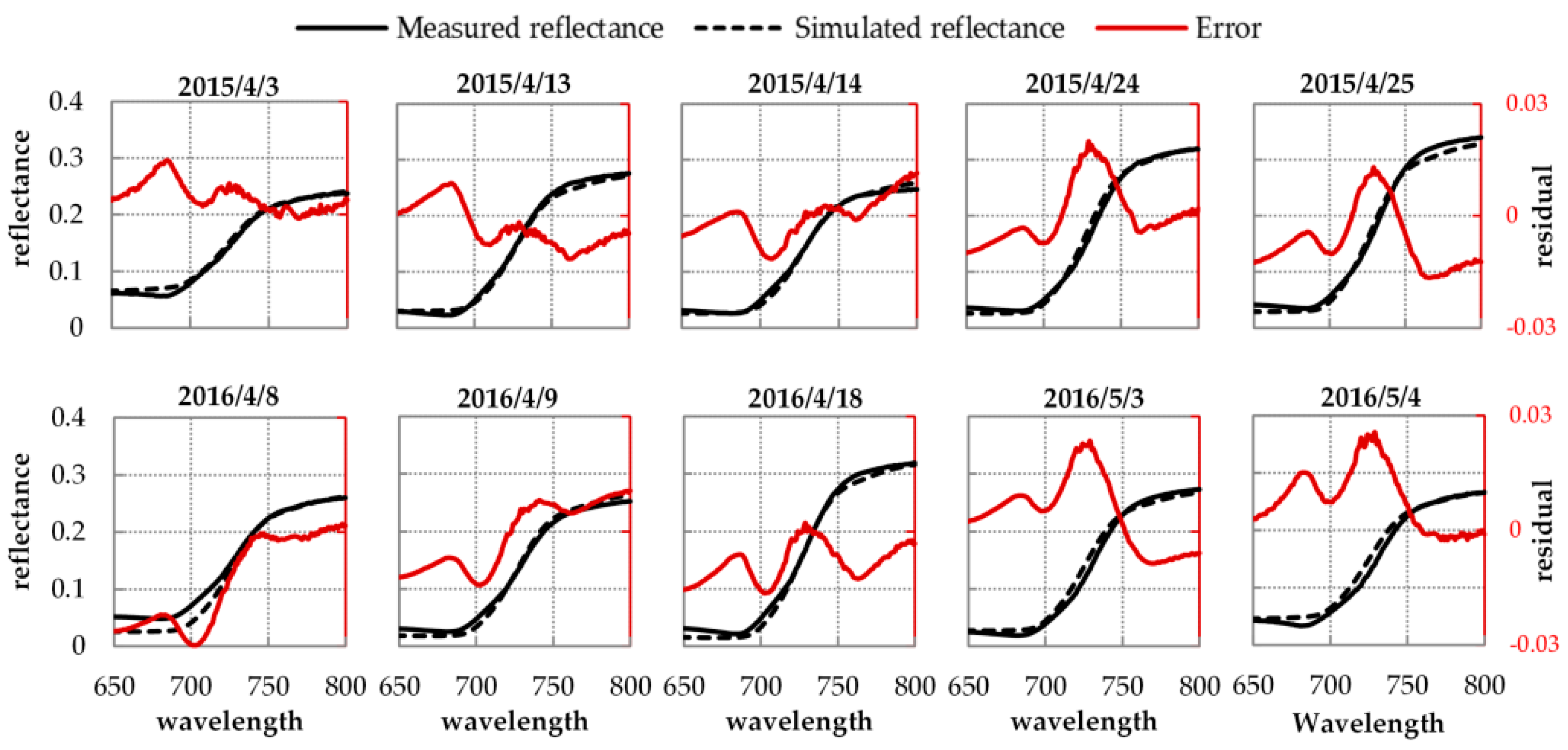
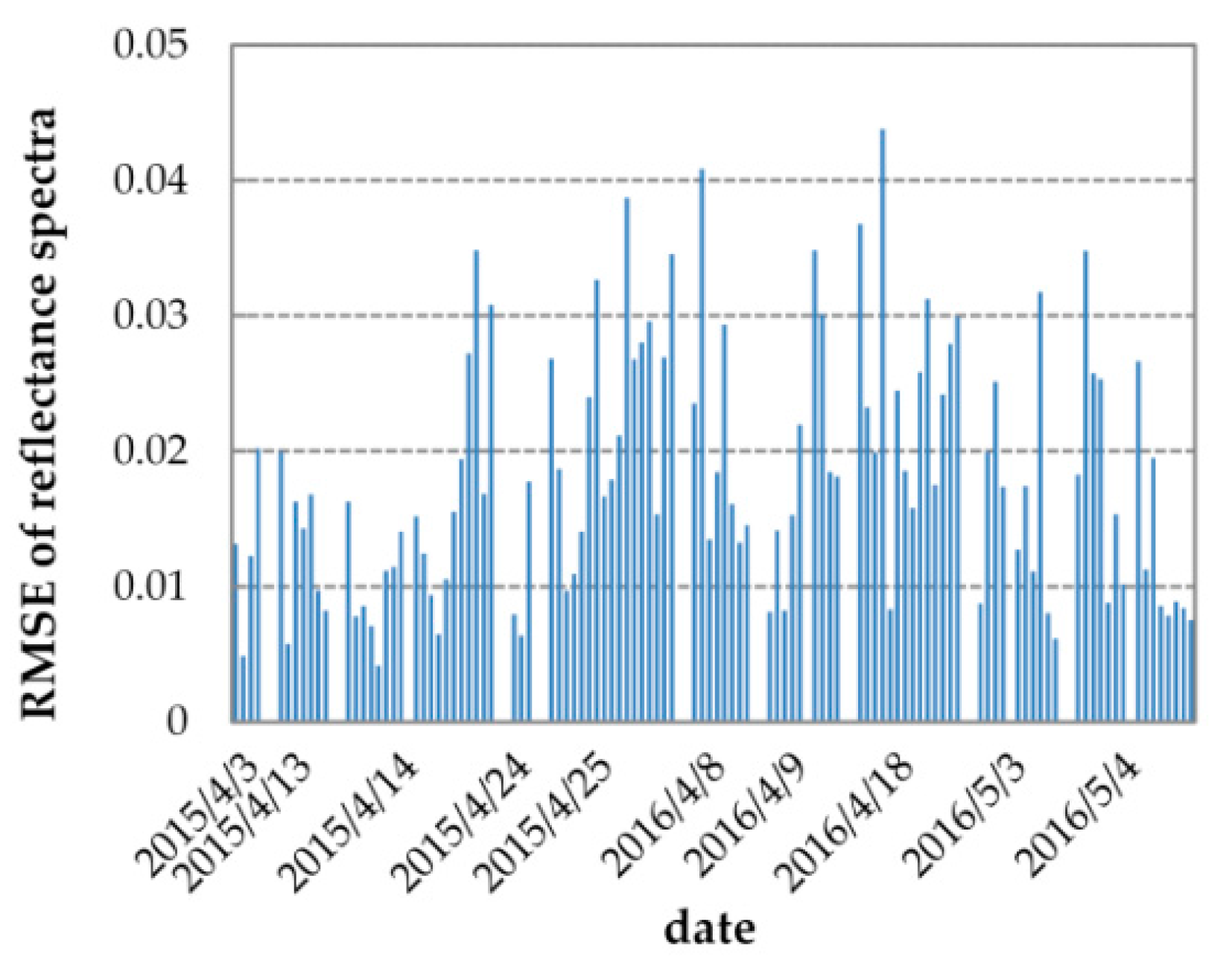
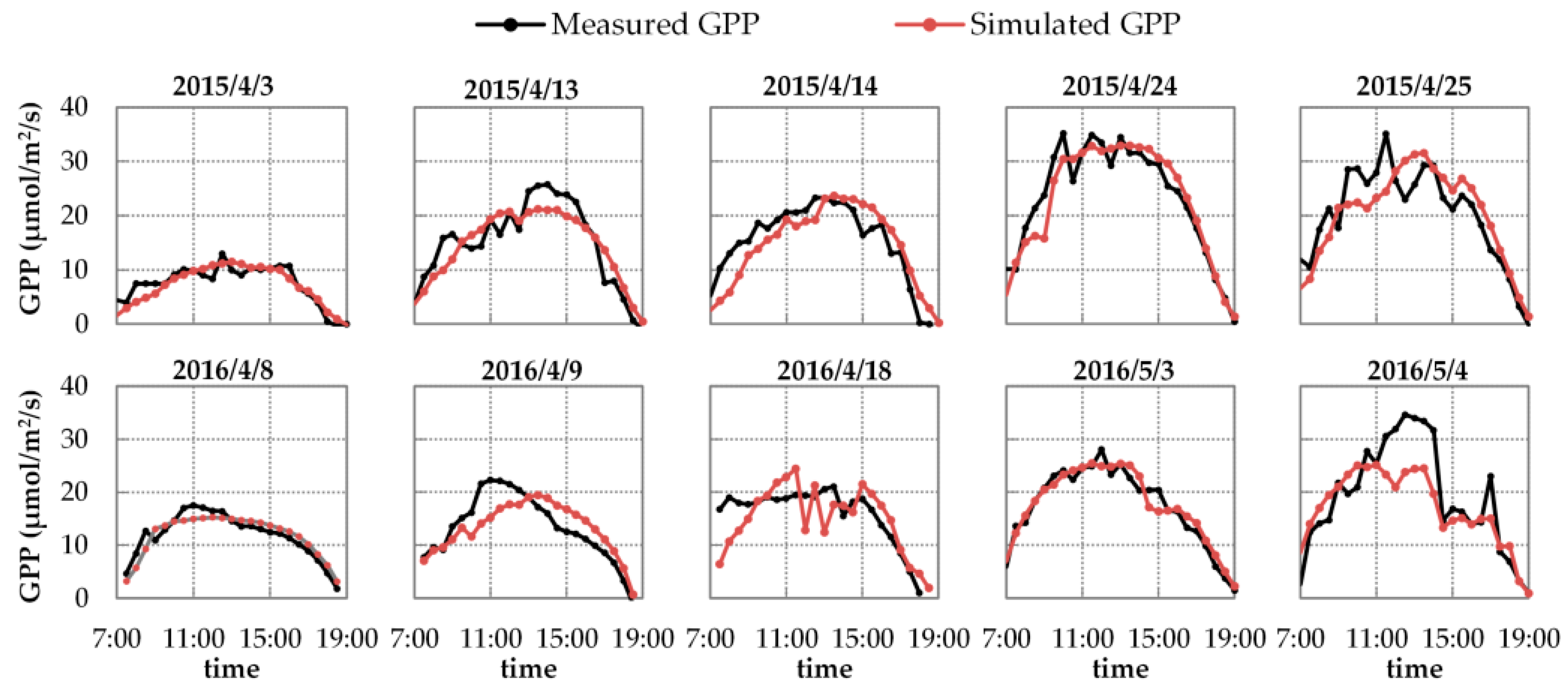
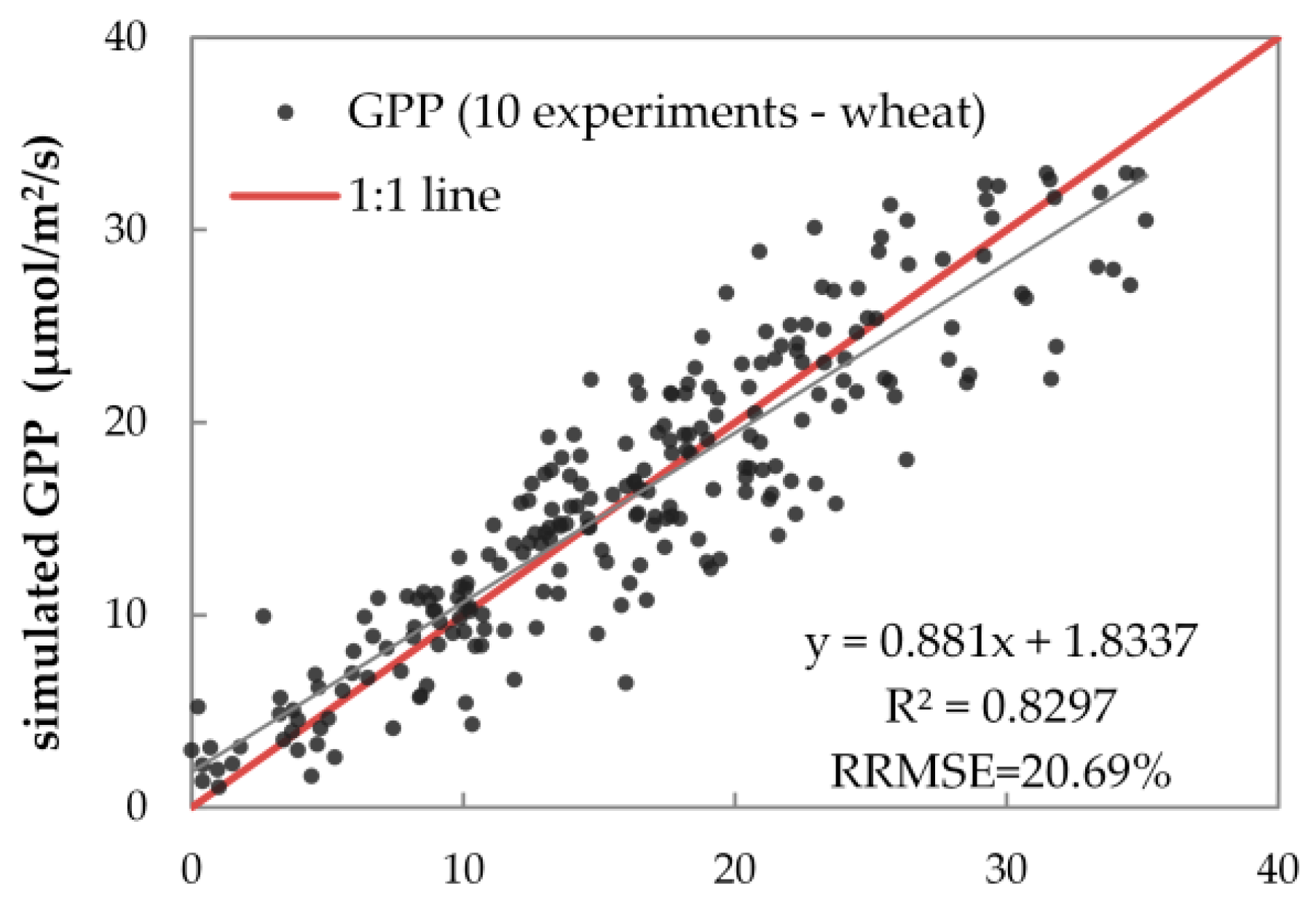
3.2. Results of Reflectance and GPP Simulations
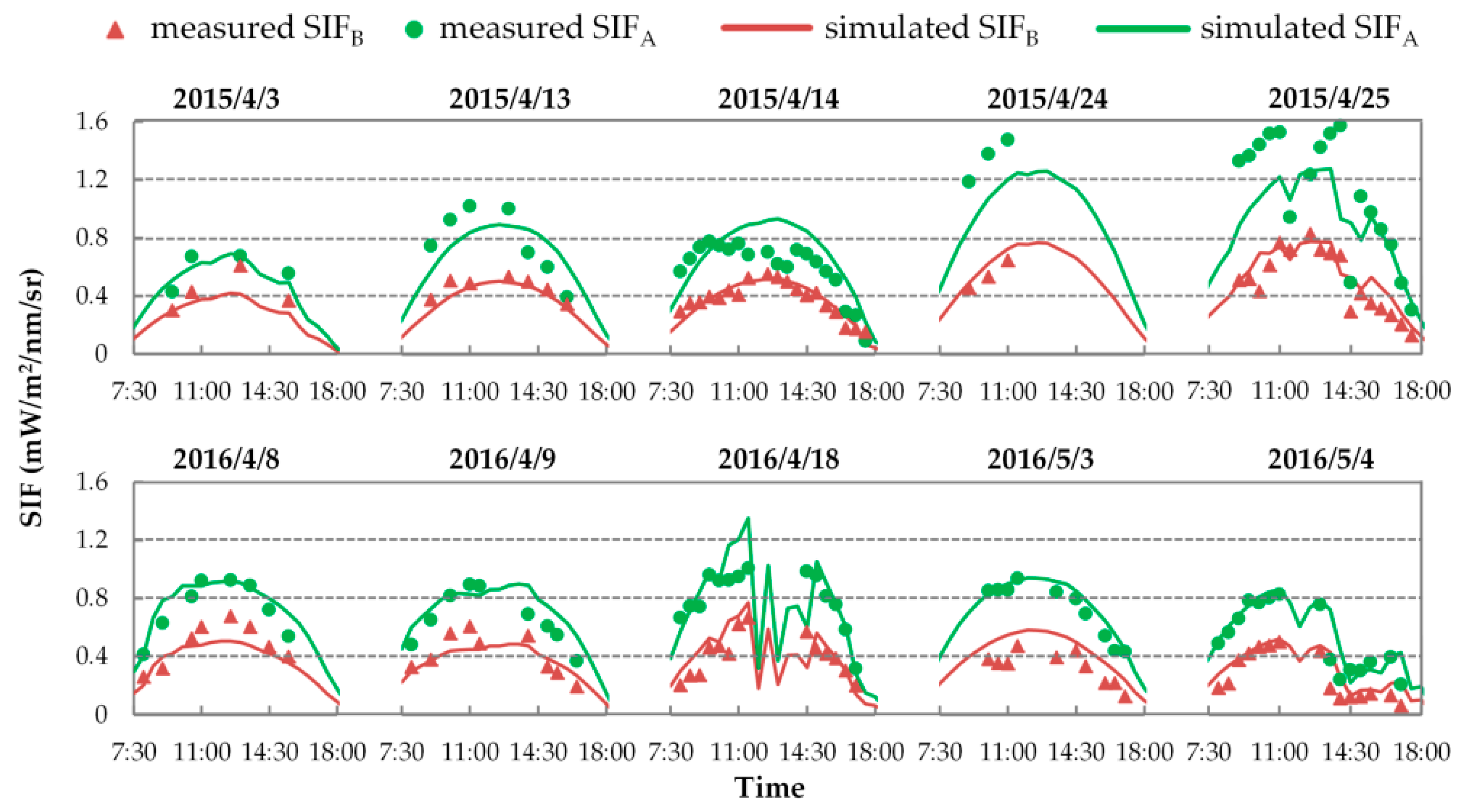
3.3. Evaluation of SIF Simulations
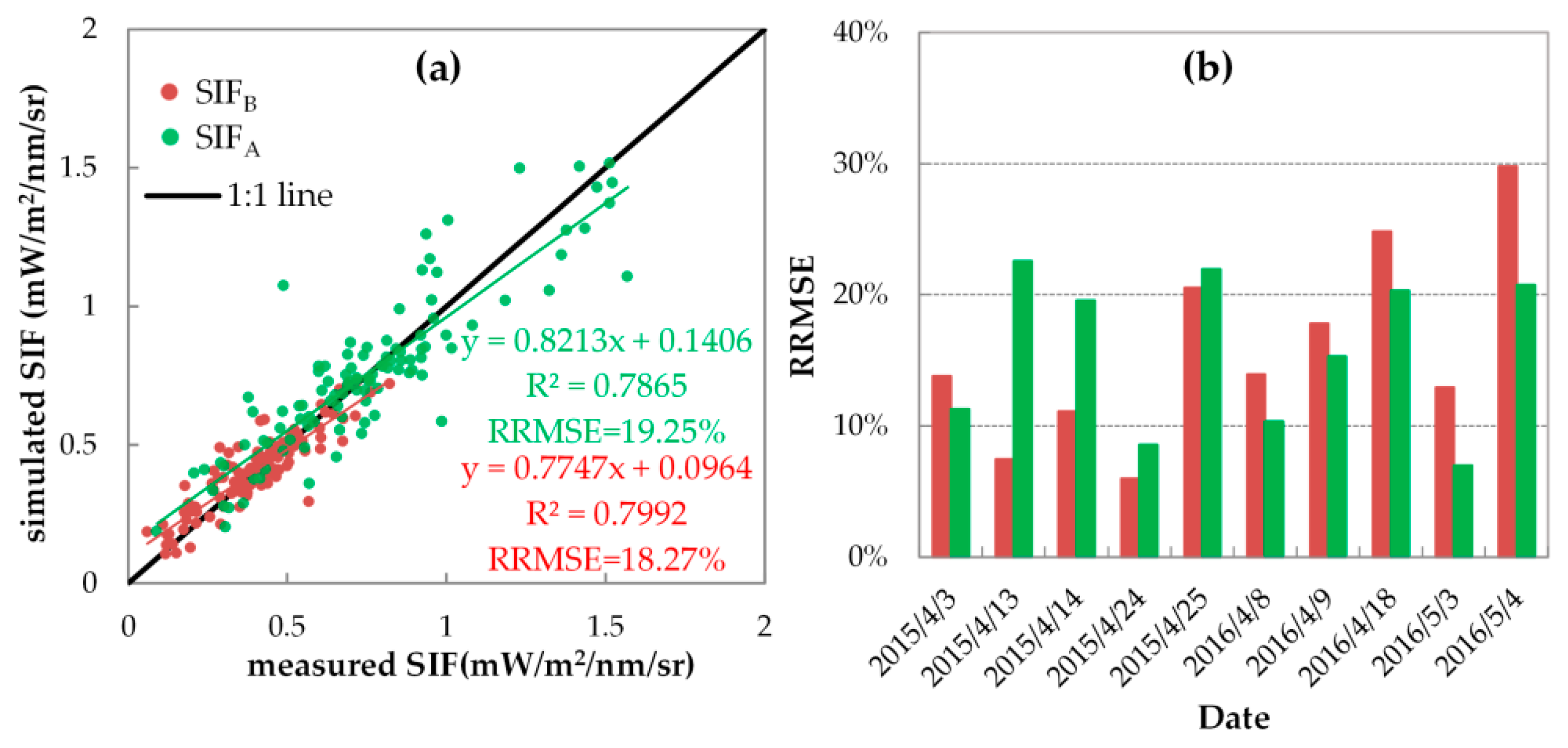
3.3.1. Evaluation of SIF Simulations with Fixed FQE
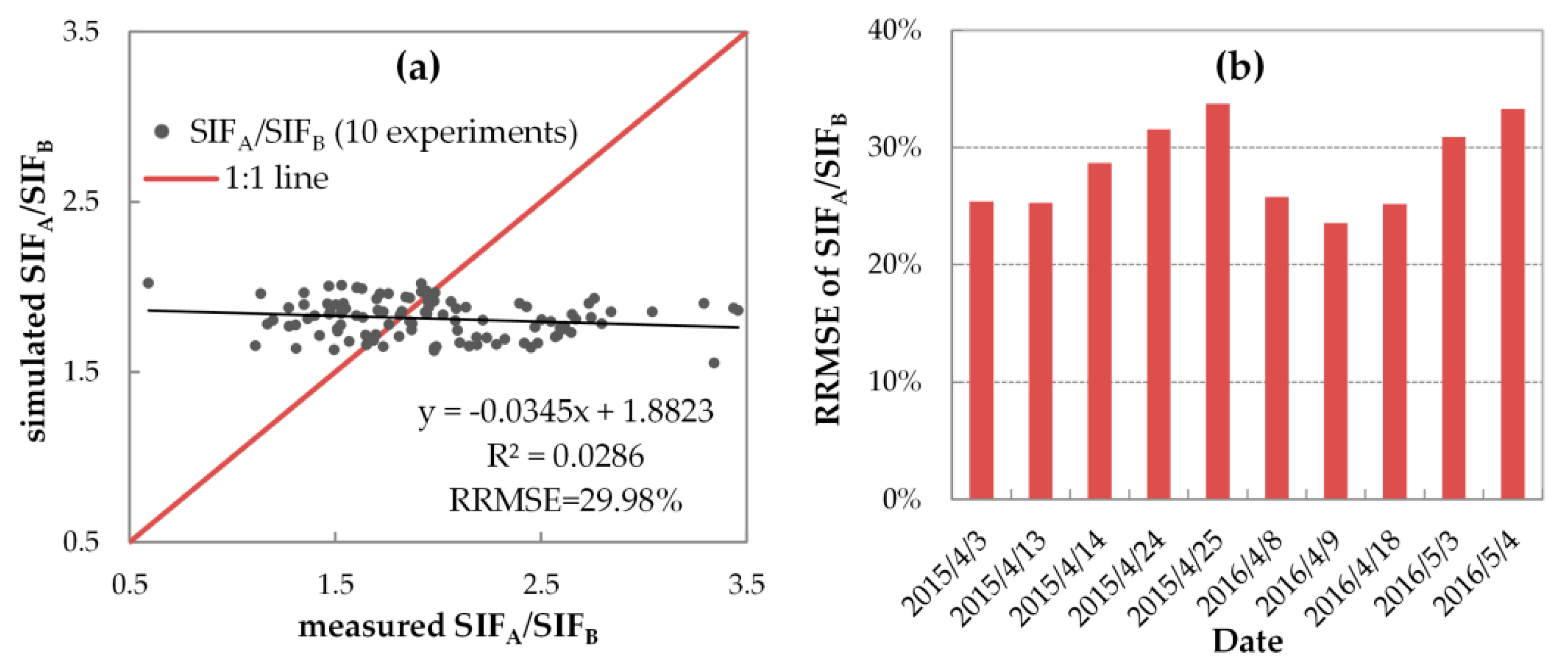
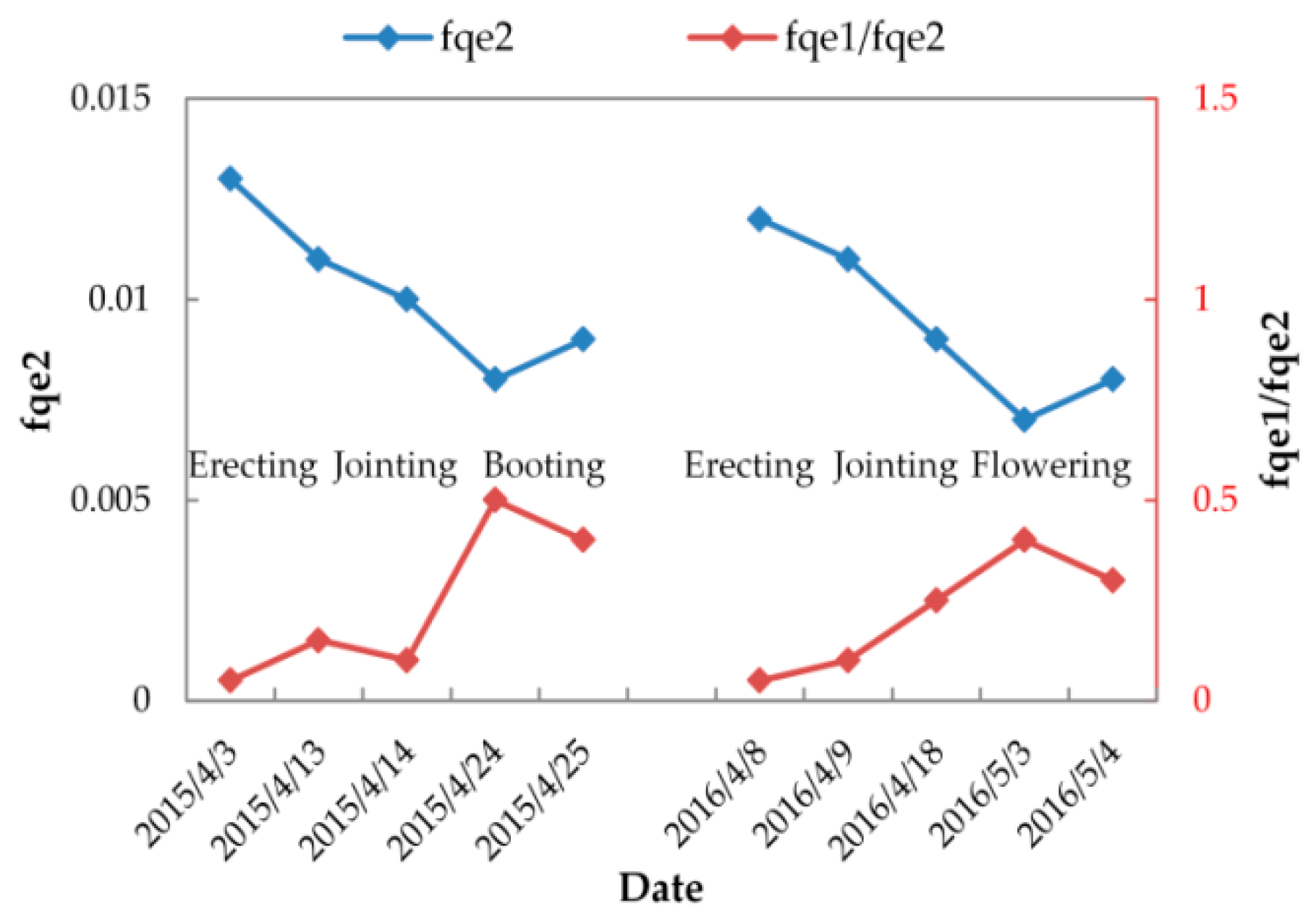
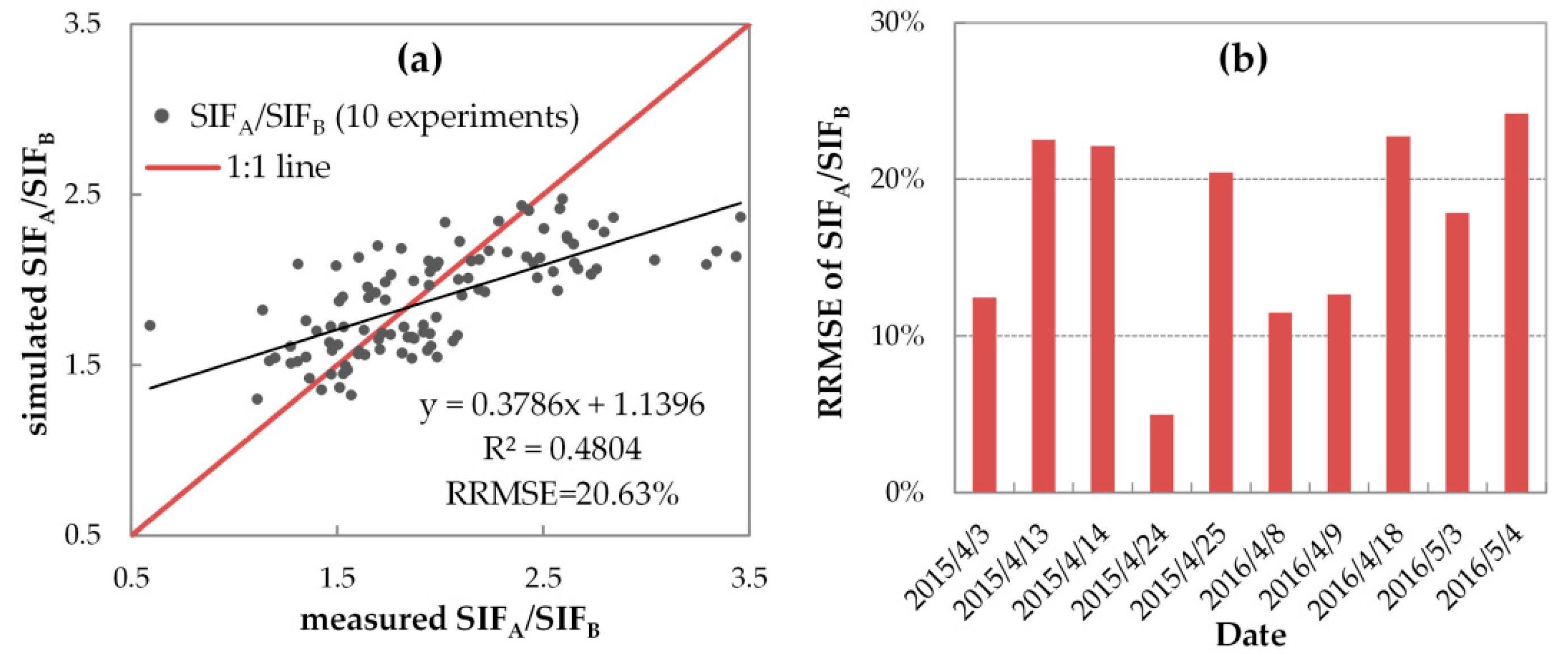
3.3.2. Variable FQE Estimated from SIF Observations
3.3.3. Evaluation of SIF Simulations with Variable FQE
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pedrós, R.; Moya, I.; Goulas, Y.; Jacquemoud, S. Chlorophyll fluorescence emission spectrum inside a leaf. Photochem. Photobiol. Sci. 2008, 7, 498–502. [Google Scholar] [CrossRef] [PubMed]
- Zarco-Tejada, P.J. Hyperspectral Remote Sensing of Closed Forest Canopies: Estimation of Chlorophyll Fluorescence and Pigment Content. Ph.D. Thesis, York University Toronto, Toronto, ON, Canada, December 2000. [Google Scholar]
- Pfündel, E. Estimating the contribution of photosystem i to total leaf chlorophyll fluorescence. Photosynth. Res. 1998, 56, 185–195. [Google Scholar] [CrossRef]
- Krause, G.H.; Weis, E. Chlorophyll fluorescence and photosynthesis—The basics. Ann. Rev. Plant Biol. 1991, 42, 313–349. [Google Scholar] [CrossRef]
- Porcar-Castell, A.; Tyystjärvi, E.; Atherton, J.; van der Tol, C.; Flexas, J.; Pfündel, E.E.; Moreno, J.; Frankenberg, C.; Berry, J.A. Linking chlorophyll a fluorescence to photosynthesis for remote sensing applications: Mechanisms and challenges. J. Exp. Bot. 2014, 65, 4065–4095. [Google Scholar] [CrossRef] [PubMed]
- Lichtenthaler, H.K.; Rinderle, U. The role of chlorophyll fluorescence in the detection of stress conditions in plants. CRC Crit. Rev. Anal. Chem. 1988, 19, S29–S85. [Google Scholar] [CrossRef]
- Damm, A.; Elbers, J.A.N.; Erler, A.; Gioli, B.; Hamdi, K.; Hutjes, R.; Kosvancova, M.; Meroni, M.; Miglietta, F.; Moersch, A.; et al. Remote sensing of sun-induced fluorescence to improve modeling of diurnal courses of gross primary production (GPP). Glob. Chang. Biol. 2010, 16, 171–186. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Paul-Limoges, E.; van der Tol, C.; Hueni, A.; Buchmann, N.; Eugster, W.; Ammann, C.; Schaepman, M.E. Far-red sun-induced chlorophyll fluorescence shows ecosystem-specific relationships to gross primary production: An assessment based on observational and modeling approaches. Remote Sens. Environ. 2015, 166, 91–105. [Google Scholar] [CrossRef]
- Guanter, L.; Zhang, Y.; Jung, M.; Joiner, J.; Voigt, M.; Berry, J.A.; Frankenberg, C.; Huete, A.R.; Zarco-Tejada, P.; Lee, J.-E. Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence. Proc. Natl. Acad. Sci. USA 2014, 111, 1327–1333. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Guan, L.; Liu, X. Directly estimating diurnal changes in GPP for C3 and C4 crops using far-red sun-induced chlorophyll fluorescence. Agric. For. Meteorol. 2017, 232, 1–9. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.; Mustard, J.F.; Lee, J.E.; Rossini, M.; Joiner, J.; Munger, J.W.; Kornfeld, A.; Richardson, A.D. Solar-induced chlorophyll fluorescence that correlates with canopy photosynthesis on diurnal and seasonal scales in a temperate deciduous forest. Geophys. Res. Lett. 2015, 42, 2977–2987. [Google Scholar] [CrossRef]
- Plascyk, J.A. The MK II fraunhofer line discriminator (FLD-II) for airborne and orbital remote sensing of solar-stimulated luminescence. Opt. Eng. 1975, 14, 339–346. [Google Scholar] [CrossRef]
- Meroni, M.; Rossini, M.; Guanter, L.; Alonso, L.; Rascher, U.; Colombo, R.; Moreno, J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sens. Environ. 2009, 113, 2037–2051. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A.; et al. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011, 38, 351–365. [Google Scholar] [CrossRef]
- Frankenberg, C.; O’Dell, C.; Berry, J.; Guanter, L.; Joiner, J.; Köhler, P.; Pollock, R.; Taylor, T.E. Prospects for chlorophyll fluorescence remote sensing from the orbiting carbon observatory-2. Remote Sens. Environ. 2014, 147, 1–12. [Google Scholar] [CrossRef]
- Guanter, L.; Frankenberg, C.; Dudhia, A.; Lewis, P.E.; Gómez-Dans, J.; Kuze, A.; Suto, H.; Grainger, R.G. Retrieval and global assessment of terrestrial chlorophyll fluorescence from gosat space measurements. Remote Sens. Environ. 2012, 121, 236–251. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Vasilkov, A.P.; Corp, L.A.; Middleton, E.M. First observations of global and seasonal terrestrial chlorophyll fluorescence from space. Biogeosciences 2011, 8, 637–651. [Google Scholar] [CrossRef]
- Joiner, J.; Guanter, L.; Lindstrot, R.; Voigt, M.; Vasilkov, A.P.; Middleton, E.M.; Huemmrich, K.F.; Yoshida, Y.; Frankenberg, C. Global monitoring of terrestrial chlorophyll fluorescence from moderate spectral resolution near-infrared satellite measurements: Methodology, simulations, and application to gome-2. Atmos. Meas. Tech. 2013, 6, 2803–2823. [Google Scholar] [CrossRef]
- Guan, K.; Berry, J.A.; Zhang, Y.; Joiner, J.; Guanter, L.; Badgley, G.; Lobell, D.B. Improving the monitoring of crop productivity using spaceborne solar-induced fluorescence. Glob. Chang. Biol. 2016, 22, 716–726. [Google Scholar] [CrossRef] [PubMed]
- Van der Tol, C.; Verhoef, W.; Timmermans, J.; Verhoef, A.; Su, Z. An integrated model of soil-canopy spectral radiances, photosynthesis, fluorescence, temperature and energy balance. Biogeosciences 2009, 6, 3109–3129. [Google Scholar] [CrossRef]
- Liu, X.; Liu, L. Improving chlorophyll fluorescence retrieval using reflectance reconstruction based on principal components analysis. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1645–1649. [Google Scholar]
- Liu, X.; Liu, L.; Zhang, S.; Zhou, X. New spectral fitting method for full-spectrum solar-induced chlorophyll fluorescence retrieval based on principal components analysis. Remote Sens. 2015, 7, 10626–10645. [Google Scholar] [CrossRef]
- Zhang, Y.; Guanter, L.; Berry, J.A.; Joiner, J.; van der Tol, C.; Huete, A.; Gitelson, A.; Voigt, M.; Kohler, P. Estimation of vegetation photosynthetic capacity from space-based measurements of chlorophyll fluorescence for terrestrial biosphere models. Glob. Chang. Biol. 2014, 20, 3727–3742. [Google Scholar] [CrossRef] [PubMed]
- Verrelst, J.; van der Tol, C.; Magnani, F.; Sabater, N.; Rivera, J.P.; Mohammed, G.; Moreno, J. Evaluating the predictive power of sun-induced chlorophyll fluorescence to estimate net photosynthesis of vegetation canopies: A scope modeling study. Remote Sens. Environ. 2016, 176, 139–151. [Google Scholar] [CrossRef]
- Van der Tol, C.; Berry, J.; Campbell, P.; Rascher, U. Models of fluorescence and photosynthesis for interpreting measurements of solar-induced chlorophyll fluorescence. J. Geophys. Res. Biogeosci. 2014, 119, 2312–2327. [Google Scholar] [CrossRef] [PubMed]
- Koffi, E.; Rayner, P.; Norton, A.; Frankenberg, C.; Scholze, M. Investigating the usefulness of satellite derived fluorescence data in inferring gross primary productivity within the carbon cycle data assimilation system. Biogeosci. Discuss. 2015, 12, 707–749. [Google Scholar] [CrossRef]
- Lee, J.E.; Berry, J.A.; Tol, C.; Yang, X.; Guanter, L.; Damm, A.; Baker, I.; Frankenberg, C. Simulations of chlorophyll fluorescence incorporated into the Community Land Model version 4. Glob. Chang Biol. 2015, 21, 3469–3477. [Google Scholar] [CrossRef] [PubMed]
- Van der Tol, C.; Rossini, M.; Cogliati, S.; Verhoef, W.; Colombo, R.; Rascher, U.; Mohammed, G. A model and measurement comparison of diurnal cycles of sun-induced chlorophyll fluorescence of crops. Remote Sens. Environ. 2016, 186, 663–677. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; van der Tol, C.; Magnani, F.; Mohammed, G.; Moreno, J. Global sensitivity analysis of the scope model: What drives simulated canopy-leaving sun-induced fluorescence? Remote Sens. Environ. 2015, 166, 8–21. [Google Scholar] [CrossRef]
- Agati, G.; Mazzinghi, P.; Fusi, F.; Ambrosini, I. The F685/F730 chlorophyll fluorescence ratio as a tool in plant physiology: Response to physiological and environmental factors. J. Plant Physiol. 1995, 145, 228–238. [Google Scholar] [CrossRef]
- Cheng, Y.-B.; Middleton, E.; Zhang, Q.; Huemmrich, K.; Campbell, P.; Corp, L.; Cook, B.; Kustas, W.; Daughtry, C. Integrating solar induced fluorescence and the photochemical reflectance index for estimating gross primary production in a cornfield. Remote Sens. 2013, 5, 6857–6879. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Buschmann, C.; Lichtenthaler, H.K. Leaf chlorophyll fluorescence corrected for re-absorption by means of absorption and reflectance measurements. J. Plant Physiol. 1998, 152, 283–296. [Google Scholar] [CrossRef]
- Genty, B.; Briantais, J.M.; Baker, N.R. The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence. BBA—Gen. Subj. 1989, 990, 87–92. [Google Scholar] [CrossRef]
- Lazár, D. Chlorophyll a fluorescence induction. Biochim. Biophys. Acta 1999, 1412, 1–28. [Google Scholar] [CrossRef]
- Lazár, D. Chlorophyll a fluorescence rise induced by high light illumination of dark-adapted plant tissue studied by means of a model of photosystem II and considering photosystem II heterogeneity. J. Theor. Biol. 2003, 220, 469–503. [Google Scholar] [CrossRef] [PubMed]
- Lazár, D. Parameters of photosynthetic energy partitioning. J. Plant Physiol. 2015, 175, 131–147. [Google Scholar] [CrossRef] [PubMed]
- Trissl, H.W.; Gao, Y.; Wulf, K. Theoretical fluorescence induction curves derived from coupled differential equations describing the primary photochemistry of photosystem II by an exciton-radical pair equilibrium. Biophys. J. 1993, 64, 974–988. [Google Scholar] [CrossRef]
- Björkman, O.; Barbara, D. Photon yield of O2 evolution and chlorophyll fluorescence characteristics at 77 K among vascular plants of diverse origins. Planta 1987, 170, 489–504. [Google Scholar] [CrossRef] [PubMed]
- Lazár, D. Simulations show that a small part of variable chlorophyll a, fluorescence originates in photosystem I and contributes to overall fluorescence rise. J. Theor. Biol. 2013, 335, 249–264. [Google Scholar] [CrossRef] [PubMed]
- Weis, E.; Berry, J.A. Quantum efficiency of photosystem II in relation to energy-dependent quenching of chlorophyll fluorescence. Biochim. Biophys. Acta (BBA)-Bioenerg. 1987, 894, 198–208. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Farquhar, G.D.; von Caemmerer, S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Von Caemmerer, S. Steady-state models of photosynthesis. Plant Cell Environ. 2013, 36, 1617–1630. [Google Scholar] [CrossRef] [PubMed]
- Collatz, G.J.; Ball, J.T.; Grivet, C.; Berry, J.A. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. For. Meteorol. 1991, 54, 107–136. [Google Scholar] [CrossRef]
- Collatz, G.J.; Ribas-Carbo, M.; Berry, J.A. Coupled photosynthesis–stomatal conductance model for leaves of C4 plants. Aust. J. Plant Physiol. 1992, 19, 519–538. [Google Scholar] [CrossRef]
- Magnani, F.; Olioso, A.; Demarty, J.; Germain, V.; Verhoef, W.; Moya, I.; Van der Tol, C. Assessment of Vegetation Photosynthesis through Observation of Solar Induced Fluorescence from Space. In Final Report for the European Space Agency under ESTEC Contract No. 20678/07/NL/HE; ESA: Paris, France, 2009. [Google Scholar]
- Porcar-Castell, A. A high-resolution portrait of the annual dynamics of photochemical and non-photochemical quenching in needles of Pinus sylvestris. Physiol. Plant. 2011, 143, 139–153. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Baldocchi, D.D. Seasonal trends in photosynthetic parameters and stomatal conductance of blue oak (Quercus douglasii) under prolonged summer drought and high temperature. Tree Physiol. 2003, 23, 865–877. [Google Scholar] [CrossRef] [PubMed]
- Goel, N.S.; Strebel, D.E. Simple beta distribution representation of leaf orientation in vegetation canopies. Agron. J. 1984, 76, 800–802. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Bao, Y.; Huang, W.; Ma, Z.; Zhao, C. Predicting winter wheat condition, grain yield and protein content using multi-temporal EnviSat-ASAR and Landsat TM satellite images. Int. J. Remote Sens. 2006, 27, 737–753. [Google Scholar] [CrossRef]
- Ergun, E.; Demirata, B.; Gumus, G.; Apak, R. Simultaneous determination of chlorophyll a and chlorophyll b by derivative spectrophotometry. Anal. Bioanal. Chem. 2004, 379, 803–811. [Google Scholar] [CrossRef] [PubMed]
- Falge, E.; Baldocchi, D.; Olson, R.; Anthoni, P.; Aubinet, M.; Bernhofer, C.; Burba, G.; Ceulemans, R.; Clement, R.; Dolman, H. Gap filling strategies for defensible annual sums of net ecosystem exchange. Agric. For. Meteorol. 2001, 107, 43–69. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Plascyk, J.A.; Gabriel, F.C. Fraunhofer line discriminator MK II—Airborne instrument for precise and standardized ecological luminescence measurement. IEEE Trans. Instrum. Meas. 1975, 24, 306–313. [Google Scholar] [CrossRef]
- Liu, L.; Liu, X.; Hu, J. Effects of spectral resolution and SNR on the vegetation solar-induced fluorescence retrieval using FLD-based methods at canopy level. Eur. J. Remote Sens. 2015, 48, 743–762. [Google Scholar] [CrossRef]
- Liu, L.; Liu, X.; Hu, J.; Guan, L. Assessing the wavelength-dependent ability of solar-induced chlorophyll fluorescence to estimate the GPP of winter wheat at the canopy level. Int. J. Remote Sens. 2017, 38, 4396–4417. [Google Scholar] [CrossRef]
- Maier, S.W.; Günther, K.P.; Stellmes, M. Sun-induced fluorescence: A new tool for precision farming. In Digital Imaging and Spectral Techniques: Applications to Precision Agriculture and Crop Physiology; Kral, D.M., Barbarick, K.A., Volenec, J.J., Dick, W.A., Eds.; American Society of Agronomy Special Publication: Madison, WI, USA, 2003; pp. 209–222. [Google Scholar]
- Wullschleger, S.D. Biochemical Limitations to Carbon Assimilation in C3 Plants—A Retrospective Analysis of the A/Ci Curves from 109 Species. J. Exp. Bot. 1993, 44, 907–920. [Google Scholar] [CrossRef]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Kattge, J.; Knorr, W.; Raddatz, T.; Wirth, C. Quantifying photosynthetic capacity and its relationship to leaf nitrogen content for global scale terrestrial biosphere models. Glob. Chang. Biol. 2009, 15, 976–991. [Google Scholar] [CrossRef]
- Mäkelä, A.; Hari, P.; Berninger, F.; Hänninen, H.; Nikinmaa, E. Acclimation of photosynthetic capacity in Scots pine to the annual cycle of temperature. Tree Physiol. 2004, 24, 369–376. [Google Scholar] [CrossRef] [PubMed]
- Wolf, A.; Akshalov, K.; Saliendra, N.; Johnson, D.A.; Laca, E.A. Inverse estimation of Vcmax, leaf area index, and the Ball-Berry parameter from carbon and energy fluxes. J. Geophys. Res. Atmos. 2006, 111, 1003–1019. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Wang, J.; Zhao, C. Detecting solar-induced chlorophyll fluorescence from field radiance spectra based on the fraunhofer line principle. IEEE Trans. Geosci. Remote Sens. 2005, 43, 827–832. [Google Scholar]
- Poolman, M.G.; Fell, D.A.; Thomas, S. Modelling photosynthesis and its control. J. Exp. Bot. 2000, 51, 319–328. [Google Scholar] [CrossRef] [PubMed]
- Poolman, M.G.; Olçer, H.; Lloyd, J.C.; Raines, C.A.; Fell, D.A. Computer modelling and experimental evidence for two steady states in the photosynthetic Calvin cycle. Eur. J. Biochem. 2001, 268, 2810–2816. [Google Scholar] [CrossRef] [PubMed]
- Ainsworth, E.A.; Serbin, S.P.; Skoneczka, J.A.; Townsend, P.A. Using leaf optical properties to detect ozone effects on foliar biochemistry. Photosynth. Res. 2014, 119, 65–76. [Google Scholar] [CrossRef] [PubMed]
- Kothavala, Z.; Arain, M.A.; Black, T.A.; Verseghy, D. The simulation of energy, water vapor and carbon dioxide fluxes over common crops by the Canadian Land Surface Scheme (CLASS). Agric. For. Meteorol. 2005, 133, 89–108. [Google Scholar] [CrossRef]
- Lokupitiya, E.; Denning, S.; Paustian, K.; Baker, I.; Schaefer, K.; Verma, S.B.; Meyers, T.; Bernacchi, C.J.; Suyker, A.E.; Fischer, M. Incorporation of crop phenology in Simple Biosphere model (SiBcrop) to improve land-atmosphere carbon exchanges from croplands. Biogeosciences 2009, 6, 969–986. [Google Scholar] [CrossRef]
- Wilson, K.B.; Baldocchi, D.D.; Hanson, P.J. Spatial and seasonal variability of photosynthetic parameters and their relationship to leaf nitrogen in a deciduous forest. Tree Physiol. 2000, 20, 565–578. [Google Scholar] [CrossRef] [PubMed]
- Morales, F.; Abadía, A.; Abadía, J. Chlorophyll Fluorescence and Photon Yield of Oxygen Evolution in Iron-Deficient Sugar Beet (Beta vulgaris L.) Leaves. Plant Physiol. 1991, 97, 886–893. [Google Scholar] [CrossRef] [PubMed]
- Hussain, M.I.; Reigosa, M.J. A chlorophyll fluorescence analysis of photosynthetic efficiency, quantum yield and photon energy dissipation in PSII antennae of Lactuca sativa L. leaves exposed to cinnamic acid. Plant Physiol. Biochem. 2011, 49, 1290–1298. [Google Scholar] [CrossRef] [PubMed]
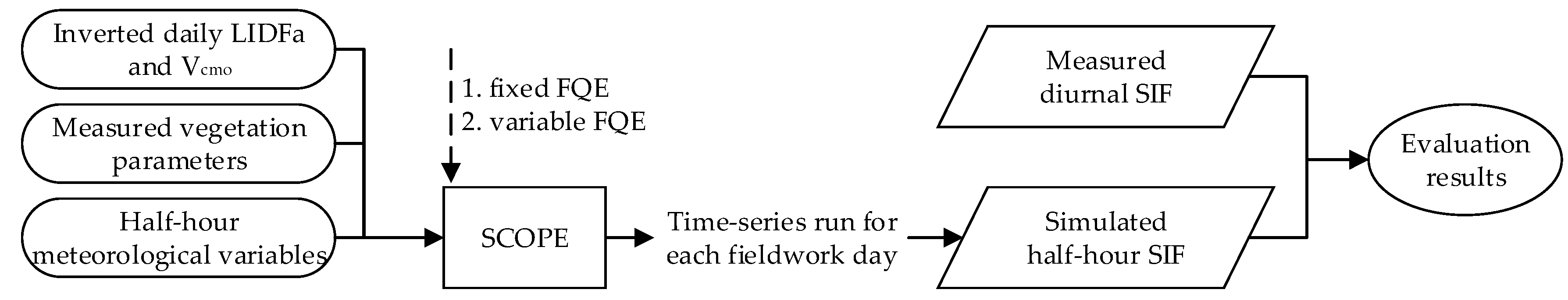
| Parameters | Definition | Unit | Value/Source |
|---|---|---|---|
| Leaf biochemistry | |||
| Vcmo | Maximum carboxylation capacity at 25 °C | μmol m−2 s−1 | Inversion |
| m | Ball-berry stomatal conductance parameter | — | 9 |
| Rdparam | Parameter for dark respiration (Rd = Rdparam × Vcmo) | — | 0 |
| Leaf optical | |||
| Cab | Chlorophyll content density | μg/cm2 | Measurement |
| Cw | Leaf equivalent water thickness | cm | Measurement |
| Cdm | Dry matter content | g/cm2 | Measurement |
| N | Leaf thickness parameters | — | 1.4 |
| Canopy | |||
| LAI | Leaf area index | m2/m2 | Measurement |
| LIDFa | LIDF parameter a, which controls the average leaf scope | — | Inversion |
| LIDFb | LIDF parameter b, which controls the distribution’s bimodality | — | −0.15 |
| Fluorescence | |||
| fqe2 | Fluorescence efficiency for PSII in dark-adapted condition | — | 0.01 or adjusted |
| fqe1/fqe2 | Ratio of fqe1 to fqe2 | — | 0.2 or adjusted |
| Meteorology | |||
| Rin | Broadband incoming shortwave radiation (0.4–2.5 μm) | W/m2 | Measurement |
| Ta | Air temperature | T | Measurement |
| p | Air pressure | hPa | Measurement |
| ea | Atmospheric vapor pressure | hPa | Measurement |
| u | Wind speed at measurement height | m/s | Measurement |
| Ca | Atmospheric CO2 concentration | ppm | Measurement |
| Geometry | |||
| LAT | Latitude | degree | Measurement |
| LON | Longitude | degree | Measurement |
| VZA | Observation zenith angle | degree | 0 |
| 2015 | 2016 | |||||
|---|---|---|---|---|---|---|
| April 3 | April 13 & 14 | April 24 & 25 | April 8 & 9 | April 18 | May 3 & 4 | |
| Growth stage | Erecting | Jointing | Booting | Erecting | Jointing | Flowering |
| LAI | 1.5 | 2.1 | 2.4 | 2.5 | 2.9 | 1.9 |
| Cab (μg/cm2) | 59.2 | 62.2 | 61.3 | 55.3 | 53.7 | 57.3 |
| Cw (cm) | 0.0138 | 0.0126 | 0.0158 | 0.0163 | 0.0199 | 0.0177 |
| Cdm (g/cm2) | 0.0042 | 0.0040 | 0.0045 | 0.0048 | 0.0049 | 0.0043 |
| 2015 | 2016 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| April 3 | April 13 | April 14 | April 24 | April 25 | April 8 | April 9 | April 18 | May 3 | May 4 | |
| LIDFa | −0.975 | −0.875 | −0.875 | −0.625 | −0.625 | −0.875 | −0.875 | −0.75 | −0.85 | −0.85 |
| Vcmo | 50 | 80 | 80 | 110 | 110 | 45 | 55 | 65 | 95 | 100 |
| Year | Date | O2-B | O2-A | ||
|---|---|---|---|---|---|
| RRMSE | bias | RRMSE | bias | ||
| 2015 | April 3 | 25.97% | −20.35% | 11.14% | −1.74% |
| April 13 | 12.47% | −10.78% | 22.64% | −1.96% | |
| April 14 | 12.13% | 0.71% | 28.30% | 18.29% | |
| April 24 | 13.43% | 12.62% | 22.30% | −22.24% | |
| April 25 | 24.54% | 13.47% | 26.43% | −13.85% | |
| 2016 | April 8 | 20.23% | −13.70% | 12.07% | 6.93% |
| April 9 | 19.53% | −5.83% | 18.77% | 12.43% | |
| April 18 | 29.54% | 12.99% | 21.69% | 5.58% | |
| May 3 | 40.13% | 38.16% | 8.94% | 6.43% | |
| May 4 | 38.67% | 27.79% | 23.51% | 10.84% | |
| all ten days | 24.35% | — | 23.67% | — | |
| 2015 | 2016 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| April 3 | April 13 | April 14 | April 24 | April 25 | April 8 | April 9 | April 18 | May 3 | May 4 | |
| simulated | 1.690 | 1.853 | 1.857 | 1.705 | 1.698 | 1.885 | 1.916 | 1.859 | 1.705 | 1.732 |
| measured | 1.370 | 1.686 | 1.590 | 2.470 | 2.237 | 1.522 | 1.605 | 1.990 | 2.213 | 1.997 |
| RE | 23.37% | 9.88% | 16.80% | −30.95% | −24.08% | 23.90% | 19.39% | −6.56% | −22.97% | −13.26% |
| 2015 | 2016 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| April 3 | April 13 | April 14 | April 24 | April 25 | April 8 | April 9 | April 18 | May 3 | May 4 | |
| fqe2 | 0.013 | 0.011 | 0.01 | 0.008 | 0.009 | 0.012 | 0.011 | 0.009 | 0.007 | 0.008 |
| fqe1/fqe2 | 0.05 | 0.15 | 0.1 | 0.5 | 0.4 | 0.05 | 0.1 | 0.25 | 0.4 | 0.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Liu, X.; Liu, L.; Guan, L. Evaluating the Performance of the SCOPE Model in Simulating Canopy Solar-Induced Chlorophyll Fluorescence. Remote Sens. 2018, 10, 250. https://doi.org/10.3390/rs10020250
Hu J, Liu X, Liu L, Guan L. Evaluating the Performance of the SCOPE Model in Simulating Canopy Solar-Induced Chlorophyll Fluorescence. Remote Sensing. 2018; 10(2):250. https://doi.org/10.3390/rs10020250
Chicago/Turabian StyleHu, Jiaochan, Xinjie Liu, Liangyun Liu, and Linlin Guan. 2018. "Evaluating the Performance of the SCOPE Model in Simulating Canopy Solar-Induced Chlorophyll Fluorescence" Remote Sensing 10, no. 2: 250. https://doi.org/10.3390/rs10020250
APA StyleHu, J., Liu, X., Liu, L., & Guan, L. (2018). Evaluating the Performance of the SCOPE Model in Simulating Canopy Solar-Induced Chlorophyll Fluorescence. Remote Sensing, 10(2), 250. https://doi.org/10.3390/rs10020250