1. Introduction
Unmanned Aerial Vehicle (UAV)-borne imaging and orthorectification are currently trivial tasks, allowing almost anyone to acquire visually stunning aerial imagery. Numerous commercial companies now also offer multi- and hyperspectral sensors to be used with drones. This seemingly makes acquisition of advanced radiometric data trivial, but unfortunately, solutions for the proper calibration and processing of the data are not standardized [
1] and not as readily available as the hardware. For example, most manufacturers of even high-end sensors usually provide means only to produce images of radiance or digital number (DN) level. The numeric values in such images are always affected by the varying illumination conditions, making it impossible to compare data acquired at different times, or to use it for quantitative analysis.
To solve this, the radiance images need to be converted to reflectance factors and thus made invariant of the intensity of illumination i.e., irradiance. The reflectance factor conversion is done by normalizing the pixel radiance values (
) by irradiance of illumination (
) that was present at the target during the image exposure (
) [
2,
3]. In an idealized case, this is enough to characterize and normalize the illumination received by the target. In studies requiring the highest accuracy, e.g., reflectance anisotropy or bidirectional reflectance factor (BRF) analysis [
4,
5,
6], the solar zenith angle and angular distribution (diffuse vs. direct) of illumination should also be known. However, usually this is not necessary and is left out, being too complicated to take into account.
The current standard methods for the reflectance factor conversion can be distributed into roughly four categories:
(1) The “atmospheric model”—methods where the irradiances are calculated using simulation or modeling of the atmosphere. These methods are the standard method for satellite applications [
7,
8], and are also used commonly in airplane or high-altitude UAV-based remote sensing [
9,
10]. Unfortunately, these methods work accurately only in stable blue-sky conditions and fail completely in the presence of broken clouds. In addition, in practice, too often the real atmospheric parameters are not used, but the simulation is based just on the generic atmospheric parameters for the applicable climate.
(2) The “reflectance reference target”—methods, where object(s) with known reflectance factor present in the image, are used for image calibration. For the highest accuracy, the target’s BRF should also be known to correctly take the view and illumination angle into account [
11,
12]. These targets can be either purpose-prepared reference panels e.g., in references [
13,
14,
15,
16] or other targets present in images [
17,
18,
19], for which the reflectance factor has been measured. The empirical line method is a variation of this method, where more than one reference target is used [
20]. If done properly, and imaging is done in perfectly stable illumination conditions, this can be considered one of the most accurate ways to perform the reflectance factor conversion, as many of the errors in the camera calibration and atmospheric transmission are canceled out in the mathematics. The downside of these methods is that they are not capable of handling varying illumination conditions during the flight campaign, since they work only locally near the reference panels, and thus also require the presence of a ground team to place targets in the area of interest. This is typically not a big problem in the visual line of sight (VLOS) UAV flights but makes these methods less practical for satellite, airplane, and beyond visual line of sight (BVLOS) UAV operations. This method is also compromised in areas such as forests, where it is not easy to avoid placing the targets far from the reflections and shadows from the objects.
(3) The “on-ground irradiance sensor”—method uses a device on the ground to measure the irradiance. This method has been used e.g., in reference [
21]. Most commonly the irradiance measurements are synchronized to the camera exposures by GPS time tags in a post-processing phase. Similar to the reflectance reference target method, this method can be very accurate, but again it works only locally, requires the presence of a ground team, and has challenges in e.g., forested areas.
(4) The “on-board irradiance sensor”—method takes a similar sensor as previously but places it onboard a UAV. This method has been used by the authors in references [
3,
22,
23]. In a way, this is the ideal method as it can provide the irradiance measured in the camera location in real time. As the irradiance reading is highly tilt-sensitive, in practice on UAVs, the sensor must be placed on a stabilized gimbal or be otherwise corrected for effects of tilt.
Radiometric block adjustment is an image-based approach to model and compensates for various radiometric disturbances in image DNs to calculate reflectance images. A model between the object reflectance and image DNs is selected and its parameters are solved using optimization techniques. The model implemented in the RadBA software of the FGI [
6] includes BRF parameters, a relative multiplicative parameter for irradiance differences, and a linear model for transforming image DNs to reflectance factors. The model parameters are determined on the basis of radiometric tie points, and optional “on-ground” [
24] or “on-board” [
25] irradiance observations and reflectance reference observations. The outputs of the process are the parameters of the radiometric model, which are used in the following processes to produce radiometrically corrected image products, such as reflectance mosaics, reflectance point clouds, or reflectance observations of objects of interest. Several studies in different environments and illumination conditions have shown that the methods have significantly compensated for radiometric disturbances in images and improved subsequent interpretation processes [
24,
25,
26,
27,
28].
As the irradiance is a spectral quantity, and its spectral shape varies in natural illumination, the irradiance should be known on the same spectral bands as the camera uses. Datawise, a spectrometer, is the most versatile instrument for irradiance measurement as it allows mathematical resampling of data to any virtual spectral band within its spectral range and resolution. Unfortunately, spectrometers are also usually larger, heavier, and more expensive than photodiodes. Thus, for RGB and multispectral sensors, photodiodes with filters can provide an excellent solution for irradiance reference. Additionally, as the spectral shape of natural illumination is predictable [
29], a combination of just a few photodiodes with well-selected spectral filters could possibly provide practically the same information content as a full spectrometer does.
The exact definition of irradiance is the radiant power received by a surface per unit area [
2]. In the application of calibrating remote sensing images to reflectance factors, most commonly the surface is usually a horizontal plane located above the target and all its surroundings, i.e., top-of-canopy irradiance is used for the irradiance. To estimate this irradiance on target, by using a measurement on-board the UAV, includes some challenges. Firstly, the irradiance at UAV locations is not always the same as illumination in all parts of the image area. This is clearly visible near the edges of broken clouds, where it is common to have a full shadow at the UAV, while there is full sunshine at the ground target. This problem cannot be circumvented completely, but especially in low-altitude UAV images, it is often possible to flag and filter out most of the serious cases of variably illuminated images by detecting changes in the illumination. Secondly, the UAV irradiance sensor might not be perfectly horizontal as required by the reference. This has a large effect, especially in direct sunshine on a low elevation angle, where the error in reading can be many percent per degree tilted (see
Section 3.1). As the small multirotor and fixed wing UAVs typically experience tilts of 5–10° in random directions, depending on flight maneuvers and wind gusts, an unstabilized irradiance sensor can observe errors in the order of tens of percents. Part of this error cannot be averaged out, as flight direction and wind cause systematic tilts to the UAV.
Current state-of-the-art methods for improving quality of on-board irradiance measurements are to either use a stabilizing gimbal [
30], to filter out the tilted data, or to apply a mathematical solar zenith angle correction to the tilted value. The solar zenith angle correction requires a knowledge of the direct and diffuse portions of the irradiance [
31] as only the direct component should be corrected. Thus using this correction requires measurements of both a fully lit and shadowed components of the irradiance. In on-ground measurements using pyranometer stations, such direct and diffuse measurements are done routinely using moving shaders, but on-board unstable platforms such arrangements become tricky. Long et al. [
31] presented in 2010, a method for measuring broadband shortwave irradiance onboard moving platforms using an “SPN1 Sunshine Pyranometer” (Delta-T Devices Ltd., London, UK). The SPN1 houses a set of seven thermopile irradiance sensors installed under a static shader that always fully shadows at least one of the sensors and fully exposes another one for direct sunlight. This setup allowed them to measure the direct and diffuse components onboard an airplane and correct the tilt effects using the tilt information in aircraft navigation data.
In addition to the irradiance data, processing of aerial images is supported by the image positions and orientations measured by an integrated global navigation satellite system (GNSS) and an inertial measurement unit (IMU). Although with photogrammetric processing techniques, the image georeferencing can often be done using only the image data and ground control points (GCPs), the process gets more efficient and accurate if initial image positions and orientations are known. Although the highest georeferencing accuracy is usually reached with the help of GCPs, using them is not mandatory in all remote sensing applications if high-accuracy, real-time kinematic (RTK), or post-processed kinematic (PPK) camera positions are available. Avoiding the GCPs simplifies the processing as it removes one of the only manual steps and allows fully automated, real-time processing of the data.
In this study, our objective was to develop a UAV-borne instrument that is able to provide an accurate irradiance spectrum, image position, and image orientation for our remote sensing sensors in real time. As including a gimbal for stabilizing the irradiance spectrometer was found not to be preferable, we developed a novel irradiance sensor tilt correction method based on three (or more) tilted photodiode irradiance sensors. The operating principle of our method is different from that of Long et al. [
31], as ours is based on the usage of tilted irradiance sensors instead of the measurement of direct and diffuse components of the irradiance. In this paper, we present the novel tilt correction method, present the FGI
Aerial Image Reference System (FGI AIRS) developed at the Finnish Geospatial Research Institute (FGI) employing it, and demonstrate the performance on a typical UAV remote sensing mission.
2. Materials and Methods
2.1. FGI AIRS Hardware
In designing the FGI AIRS, the following design goals were set:
Full irradiance spectrum in 350–1000 nm spectral range with in-flight stability better than ±1% and absolute accuracy better than ±5%
Image position with RTK accuracy
System orientation (roll, pitch, heading) with as high accuracy as feasible for small Inertial Navigation System (INS)
Synchronization to camera exposures with better than 1ms accuracy.
Capability to trigger external cameras
Real-time processing and output of the data to a serial output, to a cloud service, and to a USB flash drive.
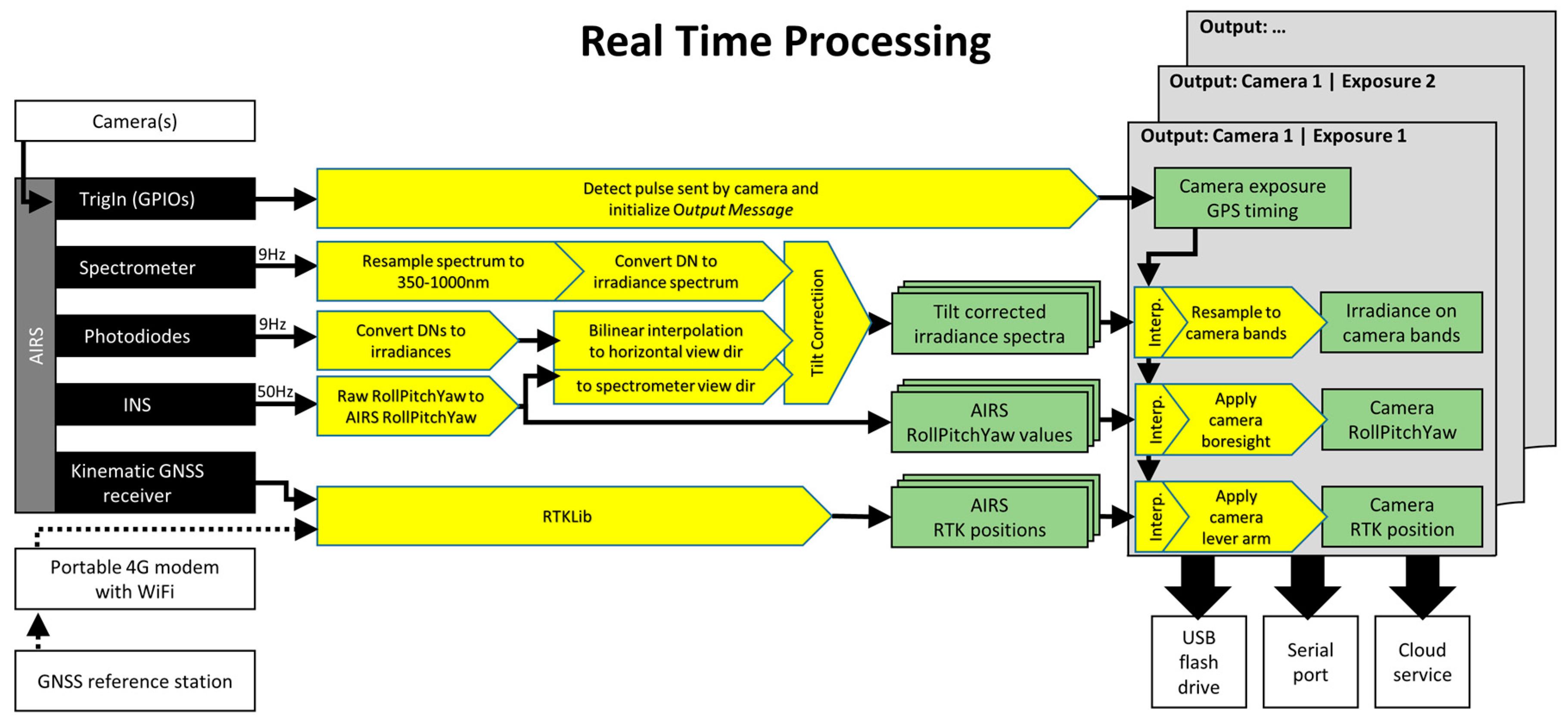
To meet the design goals, the FGI AIRS (
Figure 1) was selected to consist of the components listed in
Table 1. Firstly, a miniature spectrometer was included to measure the irradiance spectrum. The spectrometer was attached behind the diffuser optics to provide a near-Lambertian field of view, and the system was calibrated against ASD FieldSpec Pro to output irradiance in absolute units. Secondly, to measure irradiance on varying tilt angles, three RGB+Pan photodiodes were installed on the frame—each tilted 10° from zenith to opposite directions. Similarly, as with the spectrometer, the photodiodes were mounted behind diffusers and calibrated for irradiance outputs. Thirdly, a GNSS INS was added to measure tilt and position of the system. Fourth, as the INS did not have accurate enough positioning, a single band kinematic GNSS receiver was added for RTK/PPK positioning. Fifth, a miniature computer with Wi-Fi connectivity was added to handle the data acquisition and real-time processing. All the components were mounted into a custom-designed frame that was SLS 3D printed (selective laser sintering) in nylon and painted in black. The system has dimensions of 132 × 86 × 98 mm and weighs 650 g.
The FGI AIRS has versatile options for connections. It has a USB port for connecting flash memory. This memory is used both to input the camera configuration file and to store the acquired data. The AIRS allow simultaneous connection of up to five cameras. When connected, each camera gets one general-purpose input/output (GPIO) pin as input to send camera exposure synchronization pulses to the AIRS and one output pin so that the AIRS optionally can trigger the camera at desired intervals. The AIRS also supports real-time output of the processed data. This data can be sent to a local or cloud-based processing unit over Wi-Fi/internet or shared locally over a three-wire TTL serial cable. A cloud-based web page user interface has also been developed to visualize the data in real time.
The AIRS provides timing of the camera exposures as GPS time, based on the trigger pulses sent to the GPIO pin. The GPIO pulse arrival is timed using the Raspberry Pi’s internal microsecond clock, which has a practical resolution of a few microseconds. The microsecond clock is continuously synchronized to the GPS time provided by the INS unit using the GPS pulse-per-second (PPS) signal with approximately the same accuracy. Thus, the GPS time of camera synchronization pulses can be determined with an accuracy better than 10 µs. This can be considered better than sufficient as the remote sensing cameras typically use 1–10 ms exposures, and there is rarely any need for better than 1 ms timing accuracy.
2.2. Irradiance Tilt Correction Using Multi View Angle Observations
The novel aspect in AIRS irradiance measurement (
Figure 1) is the method to mathematically correct for the tilt of the irradiance measurement using three (or more) tilted photodiode irradiance sensors. However, this method is not limited to exact hardware choices made for the FGI AIRS unit but can be also employed in other suitable configurations. For the irradiance tilt correction, the critical AIRS components are the upward looking spectrometer, the three photodiodes, each tilted 10° from zenith in opposite directions (
Figure 1), and the IMU.
Firstly, the system tilt angles from IMU and the readings of the three photodiodes are used to calculate readings for virtual photodiodes in desired angles. By applying the boresight angle of each photodiode to the IMU roll and pitch angles of the whole system, the pointing direction of each photodiode in global coordinates can be calculated. These photodiodes provide 3 samples of an irradiance sensor reading at different known tilt angles. This data can be used to interpolate a reading of a virtual photodiode pointing to any direction within the real photodiode pointing directions. In our implementation, we chose to use bilinear interpolation, as it is the simplest type of interpolation and sets the least assumptions on the angular distribution of the illumination. This, however, assumes linear development of the irradiance sensor reading within the tilt angles of the photodiodes. In our testing, this was found to be sufficiently accurate, and no need was found for more advanced interpolation or irradiance modeling strategies.
This interpolation is then used to calculate irradiance readings for a virtual photodiode pointing to zenith (
) and another virtual photodiode pointing to the view direction of the spectrometer (
). Using this information, the spectrometer irradiance spectrum (
) can be converted to tilt corrected irradiance spectrum (
):
The equation above uses only a single-band photodiode for the correction of the whole spectrum. As, in blue sky conditions, the angular distribution of irradiance is strongly wavelength dependent, taking advantage of the photodiode RGB bands can be useful. This can be done by fitting a linear model (parameters
and
) that uses a known blue-sky irradiance spectrum (
) to the RGB irradiance values:
This model can then be used to calculate the spectral equivalents of and , which can be placed directly in the Equation (1) for wavelength-wise tilt correction.
2.3. FGI AIRS Processing Chain and Calibration
The FGI AIRS real-time processing is built on two software modules running on Raspberry Pi. The real-time module is programmed in C-language and handles the time-critical, low-level hardware communications and RTKLib processing. The high-level module is programmed in Python (version 3.6), and it handles processing and storing of the data and communications to the cloud and serial clients. The two modules transfer data between each other over an internal TCP socket.
The AIRS installation geometry, the definition of attached camera systems, and types of real-time outputs are configured using an INI-file placed on the USB flash drive. Each output message is triggered by a pulse received on one of the input GPIO pins. Once the real-time processing code receives the trigger pulse, it will start calculating a dataset for the trigger event (
Figure 2). First, the exact time of the exposure is calculated by converting the internal CPU time of the trigger pulse to GPS time and applying the pulse-to-exposure delay parameter. Second, the tilt corrected irradiance spectra are calculated by using the spectrometer, photodiode, and INS data (Equation (1)). Then, irradiance on each configured camera band is calculated by interpolating the irradiance spectrum at the time of the exposure and resampling it to match the spectral sensitivities of the camera bands. Third, the camera view direction is calculated by interpolating the INS data to the time of the exposure and by applying boresight parameters of the camera installation. Fourth, the camera GNSS position is calculated by interpolating the RTK data to the time of the exposure and by applying the camera lever arm offsets. This data is then combined to a single data message, which is stored to the USB drive and, optionally, sent to the cloud over WiFi/mobile data modem and to the local image processing unit over a serial cable.
If AIRS data is needed after the mission, a post-processing algorithm can be used to reprocess the data. The post processing allows a higher quality of positioning by using two-directional PPK processing, usage of kinematic GNSS ground station data instead of RTK, and averaging irradiance readings in longer time-windows, but otherwise follows the same processing method as the real-time algorithm.
2.4. Ground Experiment on Irradiance Sensor Tilt Response
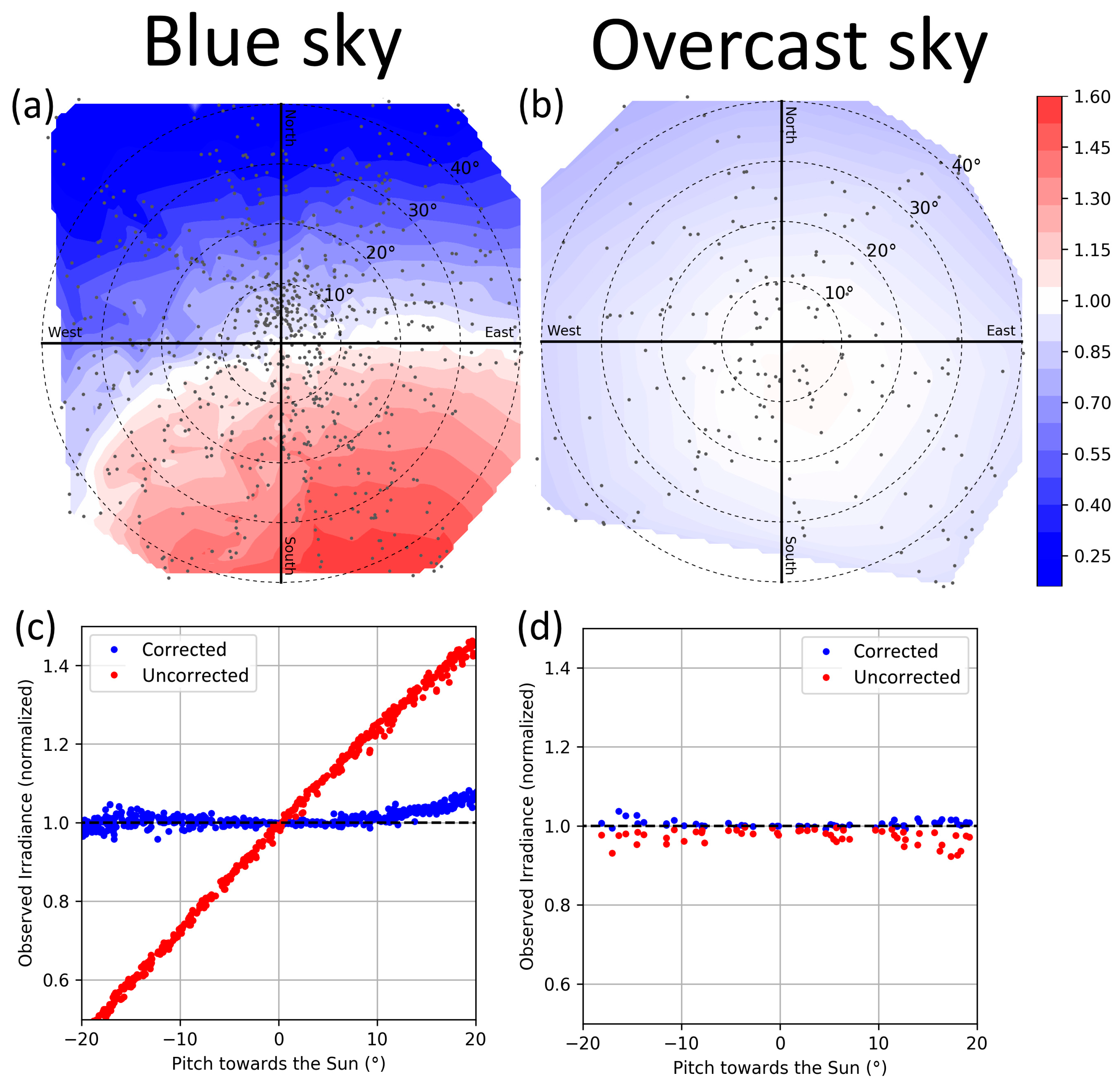
The accuracy of the AIRS irradiance tilt correction was evaluated by performing a series of tilt movements outdoors during stable illumination conditions. The test was performed both in blue-sky conditions with direct sunshine (solar zenith angle 57.5°) and in fully clouded diffuse illumination conditions. In the test, the AIRS was tilted well beyond the normal tilt angles to all heading directions in an attempt to catch the full range of tilt angles experienced in typical UAV flights.
2.5. UAV Mapping Experiment
For the UAV mapping flight test of this study, the AIRS was integrated to a Gryphon Dynamics QX1400V quadcopter (GD1400) with a FPI2012b hyperspectral camera (VTT Technical Research Centre of Finland, Espoo, Finland) [
28], and a Sony A7R (Sony Corporation, Minato, Tokyo, Japan) RGB consumer camera (
Figure 3). GD1400 is a mid-size, multirotor UAV capable of carrying a 4.5 kg payload for a flight time up to 24 min. The FPI2012b is a hyperspectral frame camera based on a piezo-adjusted Fabry-Pérot filter, allowing sequential acquisition of 1024x648 pixel snapshot images on selected spectral bands in a range of 500–900 nm. The Sony A7R is a consumer RGB camera with a 36.4-megapixel, full-frame CMOS sensor. In the installation, exposures of both cameras were synchronized to the AIRS with trigger cables. The AIRS was attached directly to the top of the UAV frame. The irradiance sensors had mostly clear hemispherical fields-of-view to the sky, with only minor obstructions from motors and propellers at the extreme low angles. The camera system was mounted under the UAV on a vibration-dampened rig.
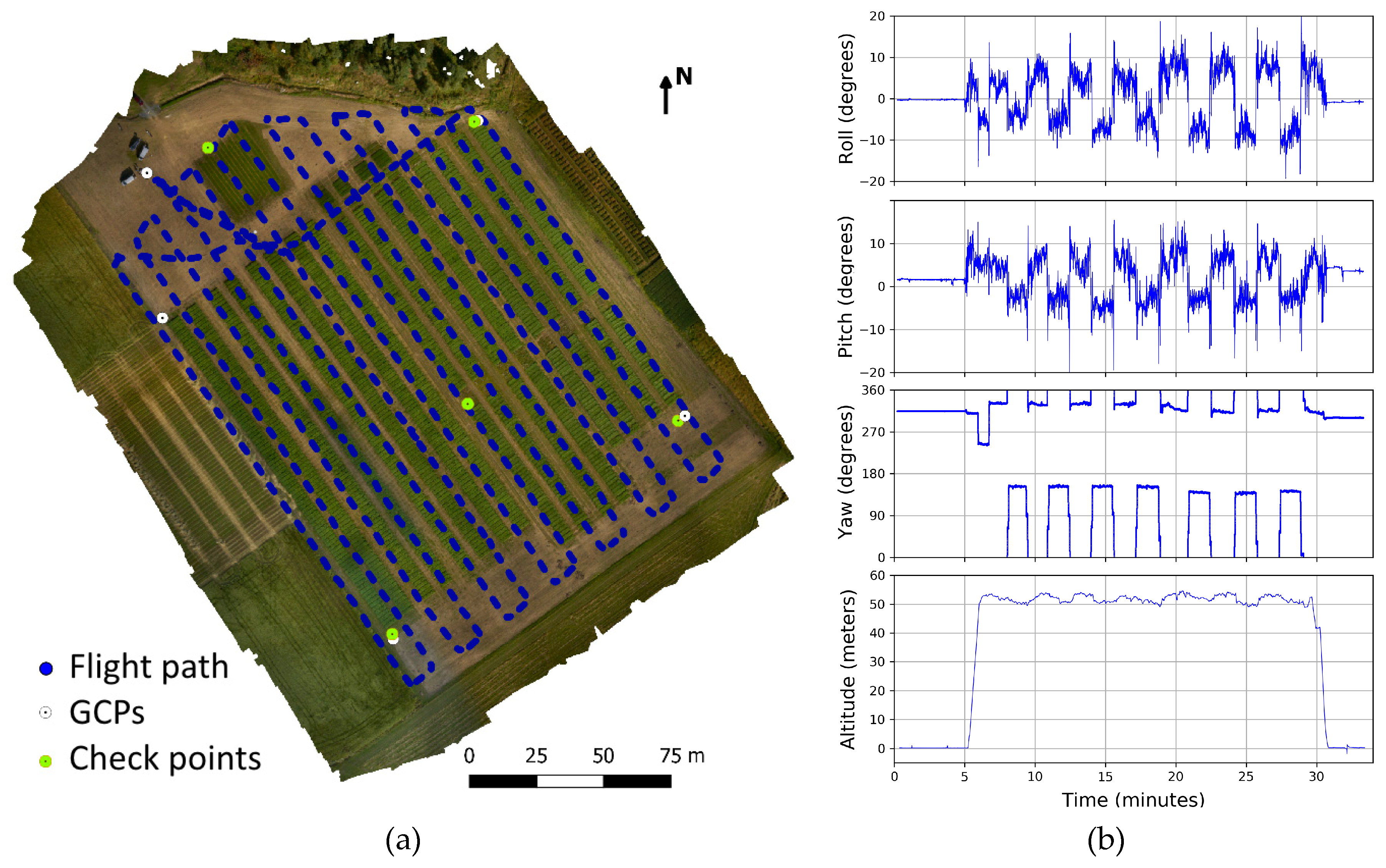
Experimental testing of the AIRS in realistic usage conditions was carried out at a grass experiment site located in Jokioinen, in southern Finland, (60.82°N, 23.50°E) on 5 September 2017 around 11:30 at local time (
Figure 4). The experimental field was set up to study variations and detectability of grass growth, but in this article, we did not do analysis the actual grass data. The sun had a zenith angle of 58° and an azimuth angle of 145°. The area was mapped using a camera system described in
Section 2.4.
The size of the mapped area was approximately 250 m by 300 m. The flight consisted of 14 flight lines in approximately SE-NW directions with the nose of the UAV always pointing towards the direction of propagation. The flight produced 720 RGB images and 382 hyperspectral datacubes. In this analysis, hyperspectral images only on the 844-nm spectral band were used. The image overlaps were 80% along the path and 75% between flight lines. The images were acquired from altitudes between 50 m and 57 m above ground level, resulting in an average ground sampling distance of 5.7 cm for the hyperspectral data and better than 1 cm for the RGB data.
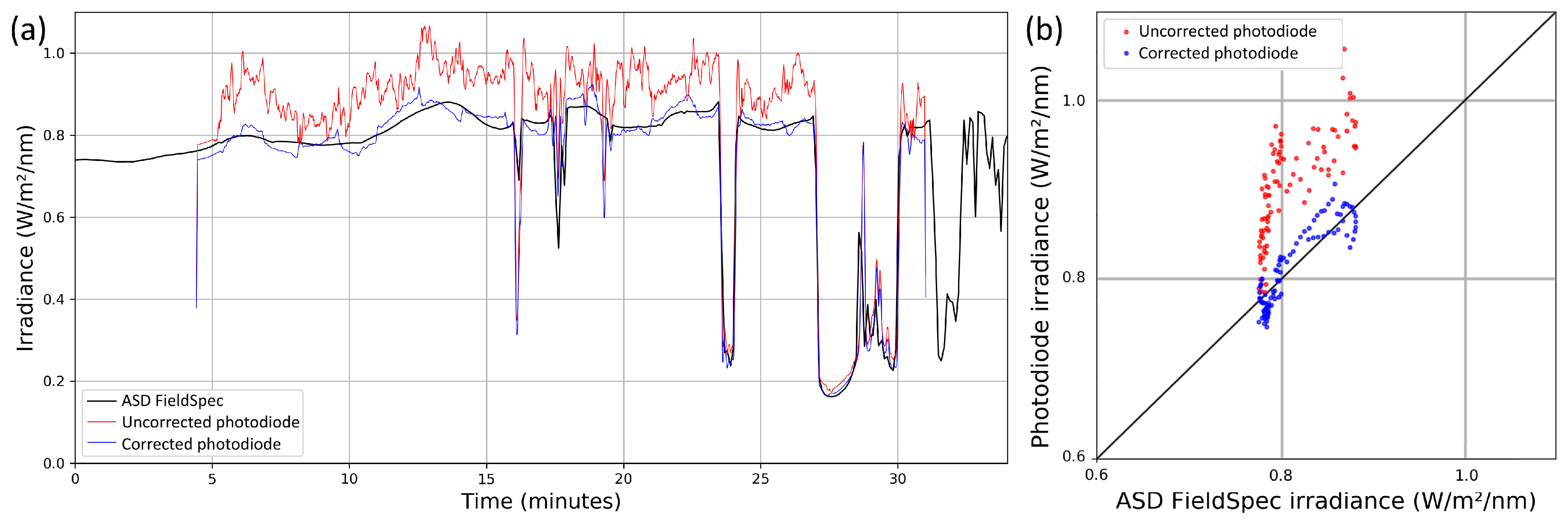
In addition, additional on-ground measurements were performed. Firstly, an ASD FieldSpec Pro spectrometer (Analytical Spectral Devices Inc., Boulder, CO, USA) with cosine corrector was used to measure the irradiance continuously during the flight. The spectrometer was placed on the ground inside the mapped area with a distance of approximately 200 m from the furthest corner. Secondly, ten GCPs were placed around the target area, and their positions were measured with Trimble R10 RTK DGNSS (Trimble, Sunnyvale, CA, USA) with 0.03 m horizontal and 0.04 m vertical accuracy.
During the flight, the atmospheric and illumination conditions represented typical suboptimal UAV mapping conditions. The atmospheric conditions were mostly blue sky with thin upper clouds and with some fast-moving broken Cumulus clouds at the lower altitude. The upper clouds caused continuous slow variations in illumination, while the Cumulus clouds passing over the area casted strong shadows over the imaged area on at least four clearly detectable occasions over the 27 min of the data acquisition. During the whole flight, there was a moderate wind blowing from the south-west. As the UAV had to lean against the wind, the on-board irradiance sensor had an average tilt of 4.6° towards the sun over the whole flight.
To evaluate the performance of AIRS orientation and position data, both the RTK and PPK coordinates were calculated. The RTK solution was processed using differential GNSS correction data from the FinnREF service, while the PPK was processed relative to a local GNSS ground station (uBlox NEO-M8P, Thalwil, Switzerland). To produce reference data to these GNSS positions, a photogrammetric image orientation process was performed on the RGB and hyperspectral images using the PhotoScan Pro (v1.2.5; AgiSoft LLC, St. Petersburg, Russia) software. The processing was done separately using both RTK and PPK positions as initial image orientations. The GCPs were marked manually. The position accuracy of GCPs was set to 5 mm, while for initial camera positions this was set to 1m, to ensure that the positions were mostly derived from GCPs. The RGB images and three bands of the hyperspectral datacubes as individual images were extracted and processed simultaneously in PhotoScan. The camera exterior orientation parameters (EOPs) were estimated using the “Align”-method with “high” quality. The tie point outlier removal step was performed using the automatic tools based on re-projection residuals and the standard deviations of the tie point 3D coordinates. Some outlier tie points were further removed manually. The camera geometric calibration was performed with image orientation (self-calibration). Once images were aligned, the image EOPs were exported out of PhotoScan for analysis.
To evaluate the performance of AIRS irradiance data in image processing, three traditional reflectance factor conversion methods were tested against the AIRS method. Firstly, reflectance reference panels of a size of 1 m by 1 m, with nominal reflectance of 0.03, 0.1, and 0.5, were placed on-ground near the take-off position and imaged from the air at the beginning of the flight. Secondly, the irradiance spectra acquired by the ASD FieldSpec Pro spectrometer was used in conversion. Thirdly, the raw AIRS spectrometer data was used as an unstabilized irradiance sensor on-board UAV. Each irradiance determination method was used separately to convert the hyperspectral raw radiance images to reflectance factor images. With the on-board AIRS data and on-ground FieldSpec data, it was possible to detect and filter out images which were taken temporally near cloud edge events potentially having varying illumination within the image. The reflectance reference panel did not have any irradiance data available and the unstabilized onboard irradiance data had natively larger variations too great that such automated filtering was not feasible for those. Manual filtering was deemed too subjective for this study; thus, no filtering was applied to the images of these two methods. The usable images of each method were then processed in Photoscan to produce the orthomosaics. For each ground pixel on the mosaic, the source image with view angle closest to nadir was used without border blending.
4. Discussion
4.1. Accuracy of AIRS Irradiances
The absolute accuracy of irradiance readings produced by AIRS is too complicated to estimate accurately. The results presented in
Section 3.2.2 showed that, with tilt correction, the stability and linearity of the measurement within one flight were better than ±2.5%. The experiments performed for this article do not allow exact numerical evaluation of the absolute accuracy of AIRS irradiances, however, based on the experiments and knowledge of the calibration process we can give our estimates on contributions of different error sources: First, the spectrometer has an accuracy of 1% (or better) due to its stability and linearity. Second, in normal use, the spectrometer diffuser optics are exposed to dust, dirt, and scratching. This can easily cause errors up to 5% before being noticed and cleaned. Third, the diffuser optics do not provide perfect Lambertian field-of-view; thus, the illumination with angular distributions other than which was used in calibration may not produce consistent readings. Fourth, the spectrometer and optics assembly were calibrated by transferring the radiometric calibration of an ASD FieldSpec Pro irradiance probe to it. The FieldSpec is calibrated by the manufacturer at NIST-traceable (National Institute of Standards and Technology, USA) accuracy of 2.5–3.5%, and we estimate that our transfer was done at an accuracy of approximately 3%. Fifth, in a controlled test, the AIRS tilt correction method was shown to work with an accuracy of 0.8% (RRMSE) in tilts up to the tilt angle of the photodiodes (10°), and an accuracy of 1.2° in tilts up to 15° (
Section 3.1). In the flight test, the on-board measurement correlated with the on-ground measurement with an accuracy of ±2.5%, even if these measurements were taken in different locations. Based on the propagation of error from these error sources, we estimate the overall absolute accuracy of the AIRS irradiances in operational conditions is to be in the order of ±5%.
The stability and linearity of our method was found to be roughly equivalent to the accuracy demonstrated by Long et al. [
31]. Their method is based on measuring diffuse and direct components of the irradiance and correcting tilt in the direct component mathematically based on solar direction. With their solution, they were able to correct 90% of their flight data on tilts up to 10° to within 10
of the reference value. As the total irradiance in their experiments varied between 350 and 1100
, this means their relative accuracy was between 0.9% and 2.9%. Their technical solution is based on broadband thermopile sensors, which are not directly suitable for determining the spectrum of the irradiance and thus not directly usable in the processing of optical remote sensing data. However, the principle of their measurement could also be implemented with optical irradiance sensors, which could allow the production of similar data as our method. As the technical requirements of our and their method are quite similar (require multiple irradiance sensors, and an IMU unit to measure the tilt of the system) and also the reported accuracies are in the same range, it is not possible yet to make definite conclusions on the superiority of either method. To make a direct comparison of the two methods, an optical version of their sensor should be prepared and evaluated against our method in similar conditions.
The mathematics of AIRS tilt correction assumes that the irradiance changes linearly with the tilt angle. The results presented in
Section 3.1 and
Section 3.2 show that the irradiance tilt response is sufficiently linear at least in the tested cases. In AIRS, the photodiodes are installed at a 10° tilt, as this was considered to be the maximum UAV tilt angle that needs to be well covered. If for other applications, the photodiode angle was to be increased, it is possible that the linearity of the sensor tilt response might not be as good anymore, especially in all atmospheric conditions and with all solar elevations. In such a case, selection of a more advanced interpolation method using empirical or modeled tilt response shapes should be considered.
The flight test also revealed some imperfections in the FGI AIRS calibration. Firstly, the tilt corrected irradiance data showed (
Figure 6a) up to 3% outliers from trend occurring during fast flight maneuvers, where the UAV changed orientation rapidly. This could indicate some issues in accurate synchronization and handling of the almost instantaneous IMU measurements and up to 100 ms photodiode exposures. The tilt corrected data also showed still approximately ±2% shifts relative to the on-ground reference occurring at the times where the attitude of the UAV changed. This indicates that the relative radiometric calibration of the photodiodes should still be improved. However, even with these issues identified in the system calibration, the method was shown to significantly improve the stability of the on-board measurement.
In future studies, in order to facilitate accurate direct reflectance measurements of the full spectra, we will perform further calibration and cross-calibration of the imaging and irradiance sensors.
4.2. Accuracy of AIRS Image Position and Orientation
The accuracy of the single-band kinematic GNSS positioning was found to be in the order of 26 cm for RTK and in the order of 10 cm for PPK processing. After the boresight adjustment, the image orientation angles were determined with an absolute accuracy of ±0.5° for roll and pitch. This uncertainty is comparable to the accuracy specified by the INS manufacturer and can be considered good, as the cameras were mounted on an anti-vibration mount separate from the AIRS unit. However, the Yaw/Heading accuracy of ±7.5° is almost 4x greater than the specification. This error was not just an offset that could be corrected by the static boresight parameter, but the INS solution was drifting during the flight, possibly due to magnetic fields caused by the UAV. In future work, a proper calibration flight will be performed, aiding the system in geometric calibration and evaluation.
The combination of IMU and GNSS measurements can also improve the obtained accuracy. The heading measurement from two GNSS antennas is more accurate than the magnetometers data [
33,
34]. For example, Eling et al. [
35] achieved an accuracy of 5 cm in position and 0.5° in attitude using a baseline between a dual-frequency and a single-frequency GPS receiver for the heading estimation. A low-cost IMU was also integrated for other attitude angles estimation and the dual-frequency GPS was also used for the RTK-GNSS positioning. However, the accuracy of the estimation depends on the baseline length between the antennas, which is not always feasible for a small UAV structure.
Low-cost positioning equipment used on board UAVs are not as precise as high-grade geodetic GNSS and IMU. Furthermore, a multipath signal due to the environment and/or poor GPS space segment geometry can compromise the GNSS quality. In these cases, the UAV position estimation can be enhanced by integrating a visual navigation method [
36]. This will be a topic for our future studies.
One of the goals for designing AIRS was to enable fully automatic, real-time geoprocessing of aerial images without GCPs. In our test case, the real-time image position accuracy was found to have an accuracy of 26 cm, which, when combined with photogrammetric processing, can provide good enough georeferencing accuracy for many coarse resolution applications and especially for data preview purposes. However, with the miniature INS and single-band GNSS of the AIRS, the accuracy is not good enough to perform direct georeferencing of images without photogrammetry, except for the coarsest preview purposes.
4.3. Hardware Selections
In AIRS hardware, we decided to include a spectrometer for irradiance measurement, because we use the system with hyperspectral sensors. However, this would not be necessary in all use cases. In applications using, for example, RGB cameras or simple multispectral sensors, the RGB photodiodes could already provide sufficient spectral information on irradiance. In addition, even if the full irradiance spectrum is needed in mathematics, the RGB photodiodes might contain enough spectral information to reconstruct the full spectrum. The spectral shapes present in natural illumination are usually predictable; thus, it might be possible to convert the RGB irradiances to full spectra using look-up-tables. In future sensors based on the AIRS concept, the inclusion of a spectrometer should be debated, as it is the largest and one of the most expensive components in the build. Leaving it out would allow crafting of a significantly more lightweight, compact, and affordable system.
The AIRS includes separately a kinematic GNSS receiver and a GNSS-INS unit both with their own antennas. This inclusion of two GNSS devices is not a desirable feature but was purely due to the low position accuracy of the previously available GNSS-INS device. New INS systems are becoming available with better accuracy and reasonable prices. Thus, for new designs, we recommend usage of only a single INS unit with kinematic GNSS, which can simplify the integration of the sensors. If the system should be used also for real time direct georeferencing processing (without photogrammetry), we would recommend upgrading the GNSS/INS to a higher grade unit and preferably also including a separate IMU installed directly on the camera mount.
4.4. Comparison of Reflectance Factor Conversion Methods
The orthomosaics produced using different methods do not allow true numerical analysis of the performance of each method but depict clearly the varying types and magnitudes of errors associated with them. Firstly, the orthomosaic with reflectance reference panel method (
Figure 7a) shows the problems typically present in UAV data acquired in varying cloud conditions. This method was not able to fix variations in the illumination and thus the parts of the area mapped during clouds show up as dark patches. Based on ASD FieldSpec irradiance data (
Figure 6), it can be estimated that even the seemingly uniform areas experience errors of approximately ±5% due to variations in illumination. Secondly, the orthomosaic with unstabilized on-board sensor (
Figure 7b) was able to mostly fix the clouded areas but suffers from other problems. As the data is noisy due to UAV tilt effects, the orthomosaic continuously shows both overly dark and overly bright patches, especially in cloud-free areas. In addition, as the automated filtering of partially clouded images was not feasible, and manual filtering was considered too subjective for this study, these areas of change show large errors to both positive and negative directions. Thirdly, the orthomosaic with an on-ground spectrometer (
Figure 7c) shows visually consistent results. Due to the fact that the spectrometer was not located in the same place as the observed targets, the spectrometer irradiance readings have a temporal offset growing with distance along the direction of cloud movement and uncorrelation growing with distance in cross-wind direction. However, as the mapped area was quite small and the cloud-edge images were filtered out, this was not causing visible problems in this dataset. Fourth, the orthomosaic with AIRS method (
Figure 7d) also shows visually consistent results. The mosaic is very similar to the on-ground spectrometer mosaic with only minor variations in the filtering of the partially clouded images.
The AIRS-approach can be valuable especially in forest applications when it is difficult to find open places for the panels (see e.g., [
25]). In addition, it is useful in real-time applications, as the irradiances collected by AIRS can be used directly to transform the image radiances to reflectance factors. AIRS data could also be used as the input to the radiometric block adjustment method [
6]; the advantage of this approach is that it could compensate for the remaining uncertainties. Furthermore, the BRF model calculation could be integrated into the same process to generate uniform mosaics.
5. Conclusions
The concept of FGI AIRS was shown to work well and to be a valuable accessory in UAV-based remote sensing by providing timing, orientation, position, and irradiance metadata for the aerial images. The real-time image positioning accuracy of the AIRS (26 cm) was found good enough for real-time georeferencing of the images using photogrammetric processing without GCPs in coarse resolution applications and for data preview purposes. For high resolution applications or for processing using only direct georeferencing, an upgrade on the GNSS/INS would be necessary.
The AIRS irradiance sensor tilt correction method was shown to perform well and be a good alternative for using a stabilized gimbal. Thus, we recommend implementation of this method in all future UAV irradiance sensors if they are not to be installed on a stabilized gimbal. To implement the method on an irradiance sensor, only three photodiodes and an IMU must be included. For 1% (RRMSE) accuracy in typical low-solar elevations, the roll and pitch accuracy of the IMU should be better than 0.5°, but preferably in the order of 0.1°.
In this study, we also tested different aerial image reflectance factor conversion methods. In our experiment with broken cloud conditions, the methods using irradiance from the on-ground spectrometer and from AIRS gave the best results, being both scientifically sensible and visually pleasing. In this weather, the reflectance reference panel method failed to produce good orthomosaic, as it was not able to correct for fast variations in illumination at all, leaving parts of the mosaic visibly dark and whole mosaics numerically unreliable. The simple on-board irradiance sensor without stabilization also failed miserably in producing good orthomosaic. Although the method was able to correct most of the shadowed areas to visibly pleasing images, the random tilting of the UAV caused irradiance data to be so noisy that the sunlit areas of the mosaic were visibly patchy and numerically unreliable.
For UAV mapping flights covering only small areas (some hundreds of meters in range), we recommend usage of an on-ground spectrometer, the AIRS method, or a stabilized on-board irradiance sensor. If the atmospheric conditions are (near-)perfect, then the reflectance reference panel method can also be recommended. For mapping flights covering larger areas, the local methods using on-ground spectrometer or panels are no longer suitable, and the only recommendable options are to use the AIRS method or a stabilized on-board irradiance sensor. Alternatively, the radiometric block adjustment method is capable of compensating for the radiometric differences due to the varying illumination conditions and can be used either with reflectance panels or an irradiance spectrometer. Usage of an unstabilized on-board irradiance sensor is not recommended for all use cases.