Estimation of the Motion-Induced Horizontal-Wind-Speed Standard Deviation in an Offshore Doppler Lidar
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. The Velocity–Azimuth-Display Motion Simulator
2.3. Motion-Induced HWS Error Variance
2.4. Roll/Pitch Correlation Hypothesis
2.5. Wind Direction Exclusion
3. Results and Discussion
3.1. Binning
3.2. Variance of the Sum of Partially Correlated Variables
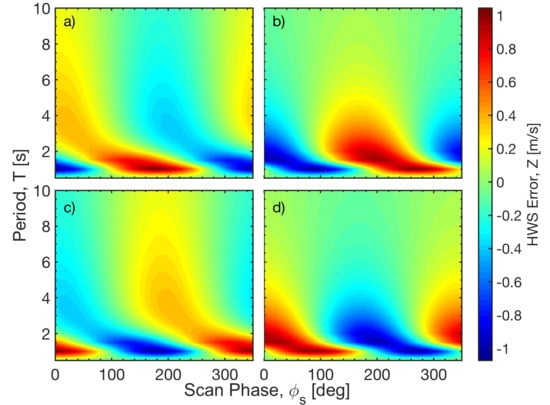
3.3. Analysis of Particular Cases
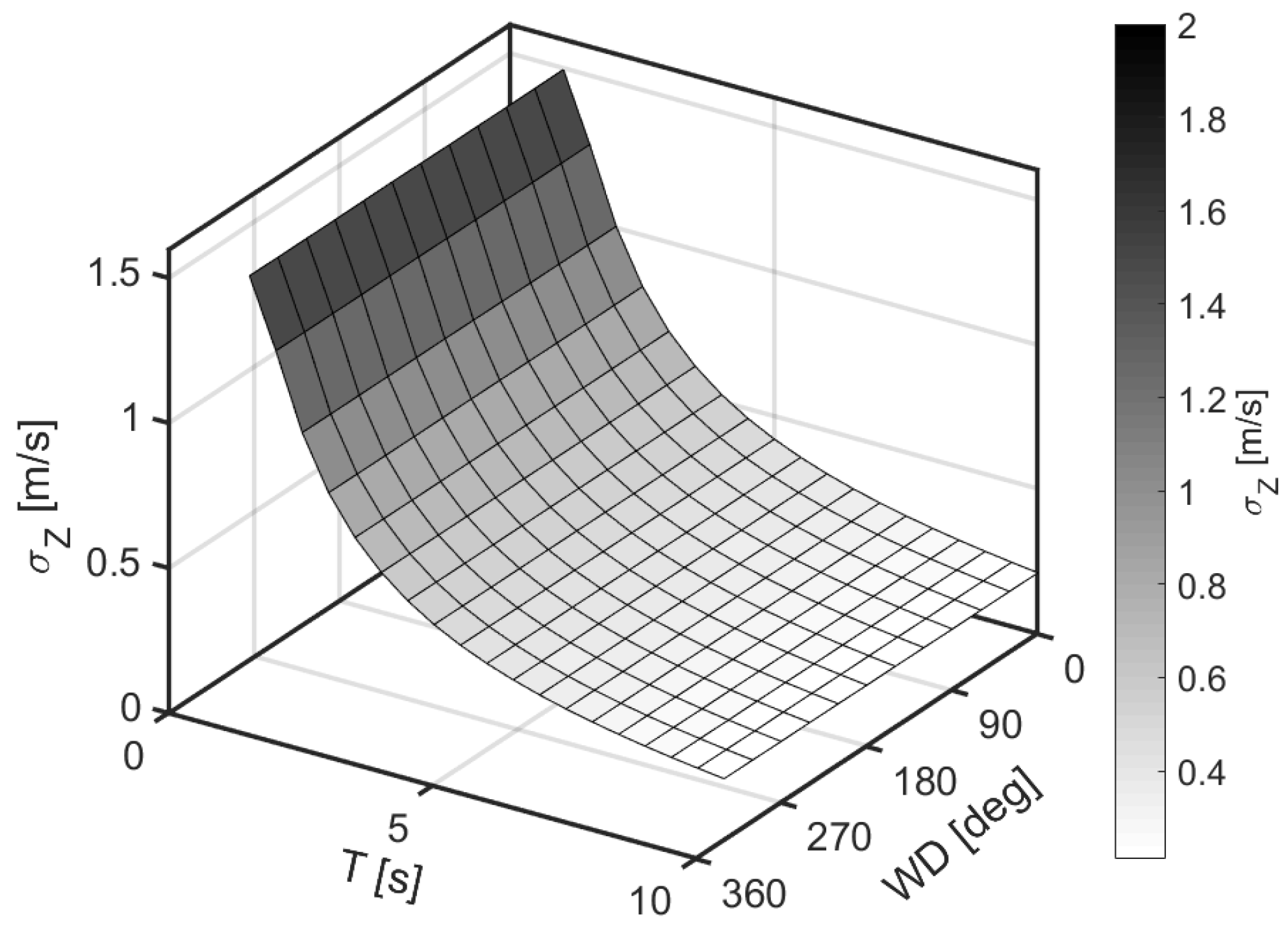
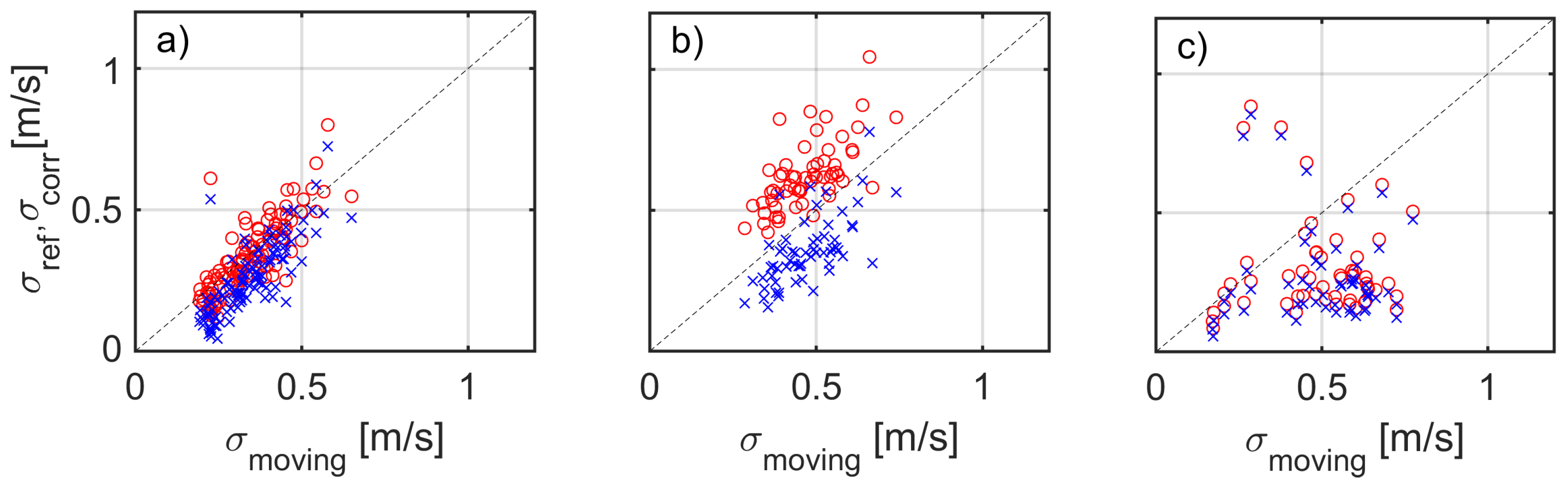
3.4. Analysis of the Whole Campaign
3.5. Turbulence Intensity
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| HWS | Horizontal Wind Speed |
| LAT | Lowest Astronomical Tide |
| MD | Mean Difference |
| SV | Spatial Variation |
| RMSE | Root Mean Square Error |
| TI | Turbulence Intensity |
| VAD | Velocity–Azimuth Display |
| WD | Wind Direction |
References
- Global Wind Energy Council. Global Wind Energy Outlook 2016; Technical Report; Global Wind Energy Council: Brussels, Belgium, 2016. [Google Scholar]
- Global Wind Energy Council. Global Wind Energy Rerport 2016: Annual Market Update; Technical Report; Global Wind Energy Council: Brussels, Belgium, 2017. [Google Scholar]
- Roland Berger. Offshore Wind toward 2020: On the Pathway to Cost Competitiveness; Technical Report; Roland Berger: Munich, Germany, 2013. [Google Scholar]
- Barthelmie, R.; Pryor, S. Can Satellite Sampling of Offshore Wind Speeds Realistically Represent Wind Speed Distributions? J. Appl. Meteorol. 2003, 42, 83–94. [Google Scholar] [CrossRef]
- Chang, R.; Zhu, R.; Badger, M.; Hasager, C.B.; Zhou, R.; Ye, D.; Zhang, X. Applicability of Synthetic Aperture Radar wind retrievals on offshore wind resources assessment in Hangzhou Bay, China. Energies 2014, 7, 3339–3354. [Google Scholar] [CrossRef]
- Hirth, B.D.; Schroeder, J.L.; Gunter, W.S.; Guynes, J.G. Measuring a utility-scale turbine wake using the TTUKa mobile research radars. J. Atmos. Ocean. Technol. 2012, 29, 765–771. [Google Scholar] [CrossRef]
- Barthelmie, R.; Folkerts, L.; Ormel, F.; Sanderhoff, P.; Eecen, P.; Stobbe, O.; Nielsen, N. Offshore wind turbine wakes measured by SODAR. J. Atmos. Ocean. Technol. 2003, 20, 466–477. [Google Scholar] [CrossRef]
- Vogt, S.; Thomas, P. SODAR—A useful remote sounder to measure wind and turbulence. J. Wind Eng. Ind. Aerodyn. 1995, 54, 163–172. [Google Scholar] [CrossRef]
- Lang, S.; McKeogh, E. LIDAR and SODAR Measurements of Wind Speed and Direction in Upland Terrain for Wind Energy Purposes. Remote Sens. 2011, 3, 1871–1901. [Google Scholar] [CrossRef]
- International Energy Association. State of the Art of Remote Wind Speed Sensing Techniques Using Sodar, Lidar and Satellites; Technical Report; International Energy Association: Paris, France, 2007. [Google Scholar]
- Sempreviva, A.M.; Barthelmie, R.J.; Pryor, S.C. Review of Methodologies for Offshore Wind Resource Assessment in European Seas. Surv. Geophys. 2008, 29, 471–497. [Google Scholar] [CrossRef]
- Scholbrock, A.; Fleming, P.; Schlipf, D.; Wright, A.; Johnson, K.; Wang, N. Lidar-Enhanced Wind Turbine Control: Past, Present, and Future. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 1399–1406. [Google Scholar]
- Rodrigo, J.S. State-of-the-Art of Wind Resource Assessment. Deliverable D7, CENER. 2010. Available online: https://cordis.europa.eu/project/rcn/93290_en.html (accessed on 14 December 2012).
- Clifton, A.; Courtney, M. 15. Ground-Based Vertically Profiling Remote Sensing for Wind Reource Assessment; Technical Report; IEA Wind Expert Group Study on Recommended Practices; IEA: Paris, France, 2013. [Google Scholar]
- Li, J.; Yu, X.B. LiDAR technology for wind energy potential assessment: Demonstration and validation at a site around Lake Erie. Energy Convers. Manag. 2017, 144, 252–261. [Google Scholar] [CrossRef]
- Trabucchi, D.; Trujillo, J.J.; Kühn, M. Nacelle-based Lidar Measurements for the Calibration of a Wake Model at Different Offshore Operating Conditions. Energy Procedia 2017, 137, 77–88. [Google Scholar] [CrossRef]
- Krishnamurthy, R.; Reuder, J.; Svardal, B.; Fernando, H.; Jakobsen, J. Offshore Wind Turbine Wake characteristics using Scanning Doppler Lidar. Energy Procedia 2017, 137, 428–442. [Google Scholar] [CrossRef]
- van Dooren, M.; Trabucchi, D.; Kühn, M. A Methodology for the Reconstruction of 2D Horizontal Wind Fields of Wind Turbine Wakes Based on Dual-Doppler Lidar Measurements. Remote Sens. 2016, 8, 809. [Google Scholar] [CrossRef]
- International Electrotechnical Commission. IEC 61400-12 Wind Turbine Power Performance Testing; Technical Report; International Electrotechnical Commission: Geneva, Switzerland, 1998. [Google Scholar]
- Williams, B.M. New Applications of Remote Sensing Technology for Offshore Wind Powert. Master’s Thesis, University Delawre, Newark, DE, USA, 2013. [Google Scholar]
- Pichugina, Y.L.; Banta, R.M.; Brewer, W.A.; Sandberg, S.P.; Hardesty, R.M. Doppler Lidar–Based Wind-Profile Measurement System for Offshore Wind-Energy and Other Marine Boundary Layer Applications. J. Appl. Meteorol. Climatol. 2011, 51, 327–349. [Google Scholar] [CrossRef]
- Courtney, M.S.; Hasager, C.B. Remote sensing technologies for measuring offshore wind. In Offshore Wind Farms; Elsevier: Amsterdam, The Netherlands, 2016; Chapter 4; pp. 59–82. [Google Scholar]
- Antoniou, I.; Jorgensen, H.E.; Mikkelsen, T.; Frandsen, S.; Barthelmie, R.; Perstrup, C.; Hurtig, M. Offshore wind profile measurements from remote sensing instruments. In Proceedings of the European Wind Energy Association Conference & Exhibition, Athens, Greece, 27 February–2 March 2006. [Google Scholar]
- Carbon Trust. Carbon Trust Offshore Wind Accelerator Roadmap for the Commercial Acceptance of Floating LIDAR Technology; Technical Report; Carbon Trust: London, UK, 2013. [Google Scholar]
- Clifton, A.; Clive, P.; Gottschall, J.; Schlipf, D.; Simley, E.; Simmons, L.; Stein, D.; Trabucchi, D.; Vasiljevic, N.; Würth, I. IEA Wind Task 32: Wind Lidar Identifying and Mitigating Barriers to the Adoption of Wind Lidar. Remote Sens. 2018, 10, 406. [Google Scholar] [CrossRef]
- Bischoff, O.; Wurth, I.; Gottschall, J.; Gribben, B.; Hughes, J.; Stein, D.; Verhoef, H. Recommended Practices for Floating Lidar Systems; Technical Report; IEA Wind Task 32; IEA: Paris, France, 2016. [Google Scholar]
- Gottschall, J.; Wolken-Möhlmann, G.; Viergutz, T.; Lange, B. Results and conclusions of a floating-lidar offshore test. Energy Procedia 2014, 53, 156–161. [Google Scholar] [CrossRef]
- Schuon, F.; González, D.; Rocadenbosch, F.; Bischoff, O.; Jané, R. KIC InnoEnergy Project Neptune: Development of a Floating LiDAR Buoy for Wind, Wave and Current Measurements. In Proceedings of the DEWEK 2012 German Wind Energy Conference, Bremen, Germany, 7–8 November 2012. [Google Scholar]
- Sospedra, J.; Cateura, J.; Puigdefàbregas, J. Novel multipurpose buoy for offshore wind profile measurements EOLOS platform faces validation at ijmuiden offshore metmast. Sea Technol. 2015, 56, 25–28. [Google Scholar]
- Mathisen, J.P. Measurement of wind profile with a buoy mounted lidar. Energy Procedia 2013, 30, 12. [Google Scholar]
- Kyriazis, T. Low cost and flexible offshore wind measurements using a floating lidar solution (FLIDAR™). In Proceedings of the EWEA Conference, Vienna, Austria, 4–7 February 2013. [Google Scholar]
- Hung, J.B.; Hsu, W.Y.; Chang, P.C.; Yang, R.Y.; Lin, T.H. The performance validation and operation of nearshore wind measurements using the floating lidar. Coast. Eng. Proc. 2014, 1, 11. [Google Scholar] [CrossRef]
- Hsuan, C.Y.; Tasi, Y.S.; Ke, J.H.; Prahmana, R.A.; Chen, K.J.; Lin, T.H. Validation and Measurements of Floating LiDAR for Nearshore Wind Resource Assessment Application. Energy Procedia 2014, 61, 1699–1702. [Google Scholar] [CrossRef]
- Gottschall, J.; Gribben, B.; Stein, D.; Würth, I. Floating lidar as an advanced offshore wind speed measurement technique: Current technology status and gap analysis in regard to full maturity. Wiley Interdiscip. Rev. Energy Environ. 2017, 6. [Google Scholar] [CrossRef]
- Gottschall, J.; Wolken-Möhlmann, G.; Lange, B. About offshore resource assessment with floating lidars with special respect to turbulence and extreme events. J. Phys. Conf. Ser. 2014, 555, 012043. [Google Scholar] [CrossRef]
- Mangat, M.; des Roziers, E.B.; Medley, J.; Pitter, M.; Barker, W.; Harris, M. The impact of tilt and inflow angle on ground based lidar wind measurements. In Proceedings of the EWEA 2014, Barcelona, Spain, 10–13 March 2014. [Google Scholar]
- Pitter, M.; Burin des Roziers, E.; Medley, J.; Mangat, M.; Slinger, C.; Harris, M. Performance Stability of Zephir in High Motion Enviroments: Floating and Turbine Mounted. Available online: https://bit.ly/2EuDY5i (accessed on 14 December 2018).
- Wolken-Möhlmann, G.; Lilov, H.; Lange, B. Simulation of motion induced measurement errors for wind measurements using LIDAR on floating platforms. Fraunhofer IWES Am Seedeich 2011, 45, 27572. [Google Scholar]
- Bischoff, O.; Würth, I.; Cheng, P.; Tiana-Alsina, J.; Gutiérrez, M. Motion effects on lidar wind measurement data of the EOLOS buoy. In Proceedings of the First International Conference on Renewable Energies Offshore, Lisbon, Portugal, 24–26 November 2014. [Google Scholar]
- Tiana-Alsina, J.; Rocadenbosch, F.; Gutierrez-Antunano, M.A. Vertical Azimuth Display simulator for wind-Doppler lidar error assessment. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar] [CrossRef]
- Nicholls-Lee, R. A low motion floating platform for offshore wind resource assessment using Lidars. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Tiana-Alsina, J.; Gutiérrez, M.A.; Würth, I.; Puigdefàbregas, J.; Rocadenbosch, F. Motion compensation study for a floating Doppler wind lidar. In Proceedings of the Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015. [Google Scholar]
- Bischoff, O.; Schlipf, D.; Würth, I.; Cheng, P. Dynamic Motion Effects and Compensation Methods of a Floating Lidar Buoy. In Proceedings of the EERA DeepWind 2015 Deep Sea Offshore Wind Conference, Trondheim, Norway, 4–6 February 2015. [Google Scholar]
- Gottschall, J.; Lilov, H.; Wolken-Möhlmann, G.; Lange, B. Lidars on floating offshore platforms; about the correction of motion-induced lidar measurement errors. In Proceedings of the EWEA 2012, Copenhagen, Denmark, 16–19 April 2012. [Google Scholar]
- International Electrotechnical Commission. IEC 61400-1 2005 Wind Turbine Power Performance Testing; Technical Report; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; Number Book, Whole; Wiley: Chichester, UK, 2009. [Google Scholar]
- Hansen, K.S.; Barthelmie, R.J.; Jensen, L.E.; Sommer, A. The impact of turbulence intensity and atmospheric stability on power deficits due to wind turbine wakes at Horns Rev wind farm. Wind Energy 2012, 15, 183–196. [Google Scholar] [CrossRef]
- Sathe, A.; Mann, J.; Gottschall, J.; Courtney, M. Can wind lidars measure turbulence? J. Atmos. Ocean. Technol. 2011, 28, 853–868. [Google Scholar] [CrossRef]
- Sathe, A. Influence of Wind Conditions on Wind Turbine Loads and Measurements of Turbulence Using Lidars. Ph.D. Thesis, Delft University, Delft, The Netherlands, 2012. [Google Scholar]
- Sathe, A.; Banta, R.; Pauscher, L.; Vogstad, K.; Schilpf, D.; Wylie, S. Estimating Turbulence Statistics and Parameters from Ground- and Nacelle-Based Lidar Measurements; Technical Report; Technical University of Denmark: Lyngby, Denmark, 2015. [Google Scholar]
- Wagner, R.; Mikkelsen, T.; Courtney, M. Investigation of Turbulence Measurements With a Continuous Wave, Conically Scanning LiDAR; Technical Report; DTU: Lyngby, Denmark, 2009. [Google Scholar]
- Henderson, S.W.; Gatt, P.; Rees, D.; Huffaker, M. Wind LIDAR. In Laser Remote Sensing; Optical Science and Engineering; CRC Press: Boca Raton, FL, USA, 2005; Chapter 7. [Google Scholar]
- Gutierrez-Antunano, M.A.; Tiana-Alsina, J.; Rocadenbosch, F.; Sospedra, J.; Aghabi, R.; Gonzalez-Marco, D. A wind-lidar buoy for offshore wind measurements: First commissioning test-phase results. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar] [CrossRef]
- Werkhoven, E.J.; Verhoef, J.P. Offshore Meteorological Mast Ijmuiden Abstract of Instrumentation Report. Available online: https://bit.ly/2PCjjxg (accessed on 14 December 2018).
- Poveda, J.; Wouters, D.; Nederland, S.E.C. Wind Measurements at Meteorological Mast Ijmuiden. Available online: https://bit.ly/2QYbqHj (accessed on 14 December 2018).
- Clifford, S.F.; Kaimal, J.C.; Lataitis, R.J.; Strauch, R.G. Ground-based remote profiling in atmospheric studies: An overview. Proc. IEEE 1994, 82, 313–355. [Google Scholar] [CrossRef]
- Barlow, R.J. Statistics: A Guide to the Use of Statistical Methods in the Physical Sciences; Manchester Physics Series; Wiley: Chichester, UK, 1989. [Google Scholar]
- Papoulis, A. Probability, Random Variables, and Stochastic Processes; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Gutiérrez-Antuñano, M.A.; Tiana-Alsina, J.; Rocadenbosch, F. Performance evaluation of a floating lidar buoy in nearshore conditions. Wind Energy 2017, 20, 1711–1726. [Google Scholar] [CrossRef]

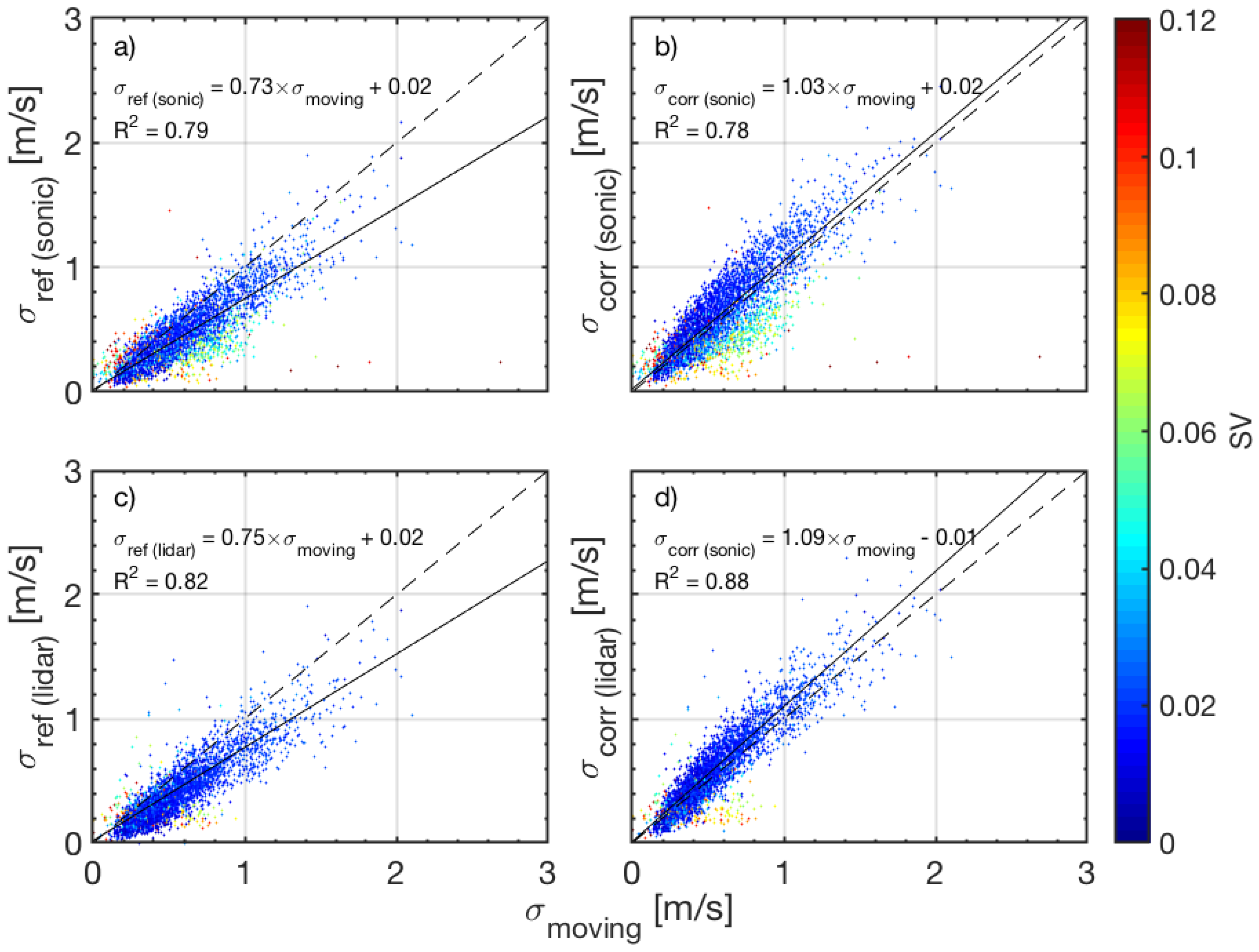
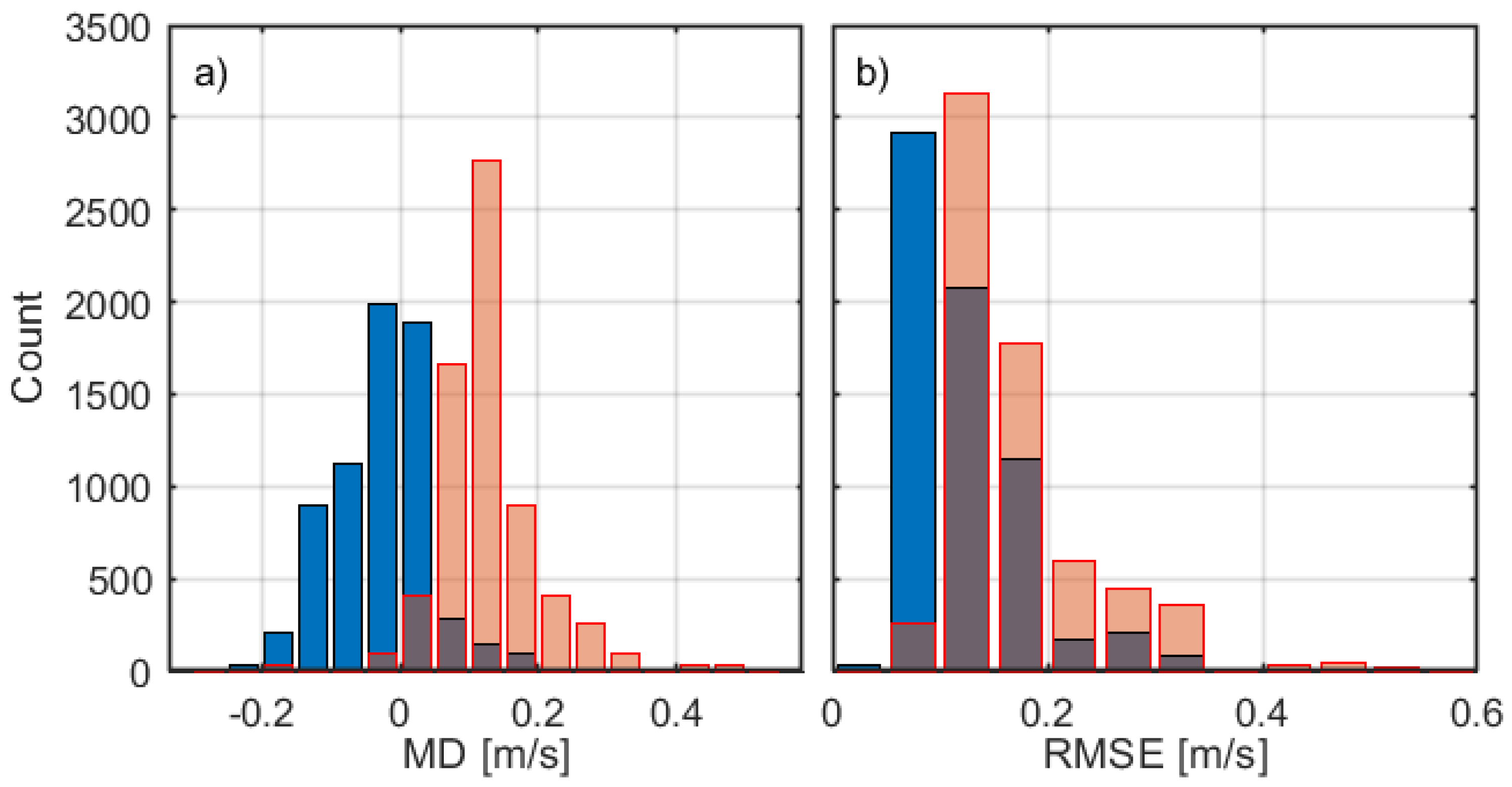
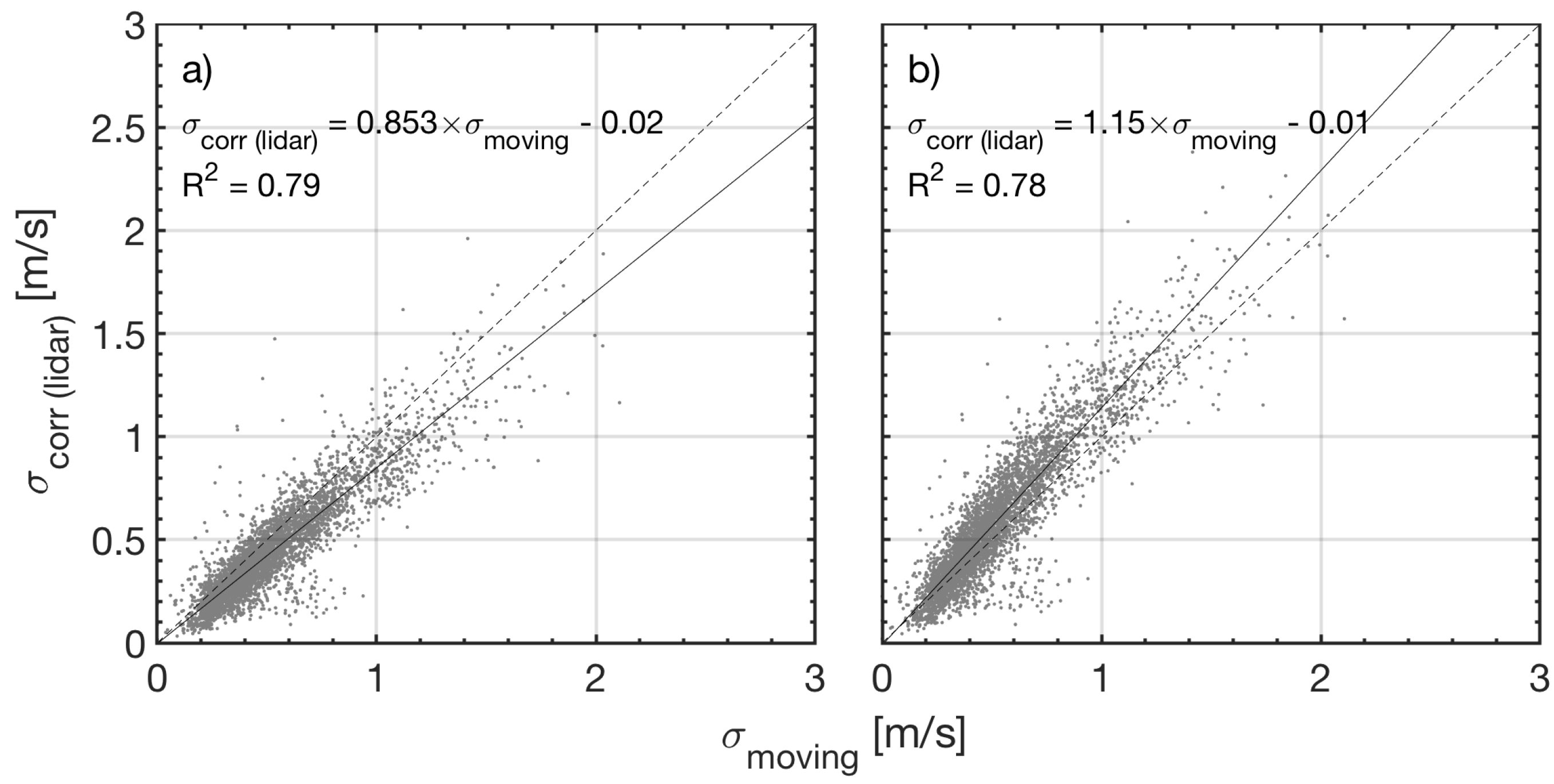

| Case No. | HWS (m/s) | AA (deg) | T (s) | Count No. | (m/s) |
|---|---|---|---|---|---|
| 1 | 8 | 3 | 4 | 288 | 0.18 |
| 2 | 5 | 2 | 4 | 247 | 0.07 |
| 3 | 9 | 3 | 4 | 237 | 0.20 |
| 4 | 7 | 2 | 4 | 208 | 0.10 |
| 5 | 6 | 2 | 4 | 198 | 0.09 |
| 6 | 7 | 3 | 4 | 196 | 0.16 |
| 7 | 6 | 3 | 4 | 182 | 0.13 |
| 8 | 6 | 2 | 3 | 180 | 0.12 |
| 9 | 3 | 2 | 4 | 175 | 0.04 |
| 10 | 7 | 2 | 3 | 174 | 0.14 |
| 11 | 10 | 3 | 4 | 169 | 0.22 |
| 12 | 5 | 2 | 3 | 166 | 0.10 |
| 13 | 4 | 2 | 4 | 164 | 0.06 |
| 14 | 8 | 2 | 4 | 157 | 0.12 |
| 15 | 8 | 2 | 3 | 133 | 0.16 |
| 16 | 11 | 3 | 4 | 130 | 0.25 |
| 17 | 5 | 3 | 4 | 130 | 0.11 |
| 18 | 9 | 3 | 3 | 112 | 0.27 |
| 19 | 8 | 3 | 3 | 108 | 0.24 |
| 20 | 7 | 3 | 3 | 106 | 0.21 |
| 21 | 12 | 3 | 4 | 100 | 0.27 |
| 22 | 11 | 4 | 4 | 95 | 0.33 |
| 23 | 2 | 1 | 3 | 91 | 0.02 |
| 24 | 4 | 2 | 3 | 86 | 0.08 |
| 25 | 3 | 1 | 3 | 80 | 0.03 |
| Case No. | Count No. | Reference Sonic | Reference Lidar | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Corrected | Uncorrected | Corrected | Uncorrected | ||||||
| MD | RMSE | MD | RMSE | MD | RMSE | MD | RMSE | ||
| 2 | 247 | 0.08 | 0.15 | 0.14 | 0.19 | 0.02 | 0.08 | 0.08 | 0.11 |
| 18 | 112 | −0.10 | 0.18 | 0.14 | 0.21 | −0.12 | 0.15 | 0.12 | 0.15 |
| 25 | 80 | 0.20 | 0.26 | 0.22 | 0.28 | 0.20 | 0.31 | 0.22 | 0.33 |
| Variance-Combination Law for | Uncorrected, | |||||||
|---|---|---|---|---|---|---|---|---|
| (C) Equation (17) | (PC) Equation (15) | (U) Equation (16) | ||||||
| Sonic | Lidar | Sonic | Lidar | Sonic | Lidar | Sonic | Lidar | |
| MD | −0.06 | −0.05 | −0.03 | −0.03 | 0.08 | 0.08 | 0.12 | 0.13 |
| RMSE | 0.17 | 0.13 | 0.16 | 0.12 | 0.15 | 0.13 | 0.18 | 0.17 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez-Antuñano, M.A.; Tiana-Alsina, J.; Salcedo, A.; Rocadenbosch, F. Estimation of the Motion-Induced Horizontal-Wind-Speed Standard Deviation in an Offshore Doppler Lidar. Remote Sens. 2018, 10, 2037. https://doi.org/10.3390/rs10122037
Gutiérrez-Antuñano MA, Tiana-Alsina J, Salcedo A, Rocadenbosch F. Estimation of the Motion-Induced Horizontal-Wind-Speed Standard Deviation in an Offshore Doppler Lidar. Remote Sensing. 2018; 10(12):2037. https://doi.org/10.3390/rs10122037
Chicago/Turabian StyleGutiérrez-Antuñano, Miguel A., Jordi Tiana-Alsina, Andreu Salcedo, and Francesc Rocadenbosch. 2018. "Estimation of the Motion-Induced Horizontal-Wind-Speed Standard Deviation in an Offshore Doppler Lidar" Remote Sensing 10, no. 12: 2037. https://doi.org/10.3390/rs10122037
APA StyleGutiérrez-Antuñano, M. A., Tiana-Alsina, J., Salcedo, A., & Rocadenbosch, F. (2018). Estimation of the Motion-Induced Horizontal-Wind-Speed Standard Deviation in an Offshore Doppler Lidar. Remote Sensing, 10(12), 2037. https://doi.org/10.3390/rs10122037