Abstract
The efficient use of nitrogen fertilizer is a crucial problem in modern agriculture. Fertilization has to be minimized to reduce environmental impacts but done so optimally without negatively affecting yield. In June 2017, a controlled experiment with eight different nitrogen treatments was applied to winter wheat plants and investigated with the UAV-based hyperspectral pushbroom camera Resonon Pika-L (400–1000 nm). The system, in combination with an accurate inertial measurement unit (IMU) and precise gimbal, was very stable and capable of acquiring hyperspectral imagery of high spectral and spatial quality. Additionally, in situ measurements of 48 samples (leaf area index (LAI), chlorophyll (CHL), and reflectance spectra) were taken in the field, which were equally distributed across the different nitrogen treatments. These measurements were used to predict grain yield, since the parameter itself had no direct effect on the spectral reflection of plants. Therefore, we present an indirect approach based on LAI and chlorophyll estimations from the acquired hyperspectral image data using partial least-squares regression (PLSR). The resulting models showed a reliable predictability for these parameters (R2LAI = 0.79, RMSELAI [m2m−2] = 0.18, R2CHL = 0.77, RMSECHL [µg cm−2] = 7.02). The LAI and CHL predictions were used afterwards to calibrate a multiple linear regression model to estimate grain yield (R2yield = 0.88, RMSEyield [dt ha−1] = 4.18). With this model, a pixel-wise prediction of the hyperspectral image was performed. The resulting yield estimates were validated and opposed to the different nitrogen treatments, which revealed that, above a certain amount of applied nitrogen, further fertilization does not necessarily lead to larger yield.
1. Introduction
Efficient food production requires a balance between the minimization of environmental damage and the maximization of yield [1]. Extensive use of nitrogen (N) for fertilization is one of the key problems in today’s agriculture. Unused N leaches into groundwater and therefore endangers the quality of drinking water. Furthermore, polluted groundwater drains into rivers and lakes, contributing to the eutrophication of these water bodies [2].
From the farmer’s perspective, the most important economic parameter is achieved yields. An overdose of N fertilizer, within the legal limits, results higher costs without adding value in terms of additional yield. Further possible regulations for the application of fertilizers should only have a limited negative impact on yields. With controlled experiments, directly comparing the harvested yield resulting from different N applications, one can identify the effects of reduced fertilization. Moreover, new concepts of monitoring these effects during vegetative growth enables the development of precision farming applications, especially created for efficient N fertilization [3].
Remote sensing technology at various scales has often proved to be a suitable tool for agricultural crop monitoring [4]. In particular, UAV-supported remote sensing enables very precise monitoring of individual areas through lower flight altitudes and high-resolution data [5]. In recent years, the development of UAV-based hyperspectral recording systems has made rapid progress [6]. In comparison to manned aircraft based systems, the sensors are smaller, lighter, and less costly during acquisition and processing [7]. The great potential of this technology has been demonstrated [8].
Hyperspectral snapshot camera systems are frequently used, as they are easier to handle in comparison to pushbroom cameras, especially when mosaicking images [6]. Another problem is the orthorectification of the lines of a pushbroom camera during preprocessing, as the quality of the raw data highly depends on the measurement accuracy of the inertial measurement unit (IMU), the overall stability of the gimbal, and wind conditions [6]. Many studies have already shown the capabilities and constraints of these datasets [9,10,11,12,13]. Once these obstacles have been overcome, pushbroom scanner systems are able to record substantially less noise-affected spectra with higher resolution (spatial and spectral) than snapshot systems due to their narrower line-shaped camera aperture and higher sensor resolution [6].
Since grain yield has no direct influence on the reflectance of crops, it should be derived indirectly by estimating other biophysical parameters [14]. Although [15,16,17,18] could show that an estimation of grain yield directly from reflection spectra is statistically possible, it was finally determined that this relationship can only be explained indirectly by biophysical and biochemical properties. Among other plant properties, chlorophyll content (CHL) and leaf area index (LAI) correlated with grain yield [19], which can be estimated reliably from remote sensing data of different scales and platforms [4]. Furthermore, soil mineral nitrogen naturally has strong effects on plant development and thus on the production of chlorophyll and leaf area, and therefore, these parameters can also be taken as indicators for plant uptake of nitrogen [20].
LAI is one of the most important parameters to describe plant conditions in agriculture. It can be used, for example, to derive information on biomass, nutrient supply, growth stage, and yield estimation [21]. The possibilities of hyperspectral remote sensing data for the assessment of LAI have already been carried out in various studies on different scales. By using hyperspectral field spectrometers [22,23,24,25], could determine the good predictability of LAI. Airborne hyperspectral imagers have also been successfully used to predict LAI [25,26,27]. Many recent publications using UAV-supported systems have frequently relied on multispectral sensors to derive LAI. However, the use of UAV-based hyperspectral sensors has only been efficiently possible for a couple of years, which is why only a few studies are available that estimate LAI from such data. Reference [28] used a hyperspectral snapshot camera (450–950 nm) on a UAV to estimate the winter wheat LAI across different growth phases. For this purpose, various indices were calculated from the spectra combined with height information, and the LAI was estimated with the help of partial least-squares regression (PLSR) or random forest regression, leading to mediocre results (R2 = 0.59). Another study from [29] compared different regression and sampling techniques to predict the LAI of soybeans with data from the same hyperspectral snapshot camera. They obtained similar robust results (R2 = ~0.70) for all methods, using measurements gained throughout the whole phenology. On the contrary, working with data taken only once during growth phase, significantly weaker models were produced.
CHL concentration is an extremely important biochemical parameter, since it is a direct indicator for plant health, availability of nutrients, and plant stress [30]. This parameter has been extensively investigated with hyperspectral remote sensing on the field [22,27,28,31,32] and airplane level [25,27,30], while derivation of CHL from UAV-based hyperspectral data is relatively rare due to it being fairly new technology. Reference [33] acquired hyperspectral snapshot data from spring wheat and predicted chlorophyll contents with a least-squares regression approach, resulting in models of medium quality. They also compared these results with predictions from regular RGB imagery and could not find a large advantage for the use of hyperspectral data.
As the derivation of both parameters, to our knowledge, has so far only been investigated to a limited extent applying a high-resolution UAV-based hyperspectral pushbroom scanner, the aim of this study was to investigate the potential of such data for the estimation of CHL and LAI of winter wheat. Hence, we studied whether the aforementioned obstacles could be overcome with UAV-based hyperspectral pushbroom scanners and what data quality could be expected from this technology. Furthermore, the indirect derivation of grain yield was reliably possible from estimated CHL and LAI. Finally, the effect of different N fertilization on these estimations and on grain yield within the study site was examined.
2. Materials and Methods
2.1. Study Area and Crop Management
The field data for winter wheat were collected within an existing field trial (small area around 830 m2) of Osnabrück University of Applied Sciences in Belm (52.31°N, 8.11°E), northwestern Germany. The initial aim of the trial was to evaluate the impact of different N-fertilization strategies on drinking water quality. The terrain is very flat, ranging from around 110 m above sea level (m.a.s.l.) in the northeast to 109 m.a.s.l. in the southeast. Climate conditions are temperate oceanic (Cfb) [34] with a mean annual precipitation of 883 mm and a mean annual air temperature of 9.4 °C [35]. Table 1 summarizes the main crop management operations.

Table 1.
Crop management experimental season 2016/2017. DAS: days after sowing.
The experimental setup comprised eight treatments with a total of six N fertilization levels in three replications (Table 2, Figure 1). The optimal treatment (“opt”) followed the official regional recommendations by the Chamber of Agriculture [36], whereas the reduced optimal treatment (“opt–“) reflected the fertilizer limitation for groundwater protection (Table 2, Figure 1). All other N fertilization levels were chosen equidistantly between 0 and 150 kg ha−1.

Table 2.
Split fertilizer application rates in kg ha−1 N according to different treatments. m: mineral fertilization (calcium ammonium nitrate, 27% N), o: organic fertilization (pig manure, 4.52% N), opt: optimal N fertilizer rate calculated following official recommendations; opt–: opt reduced by 10%.
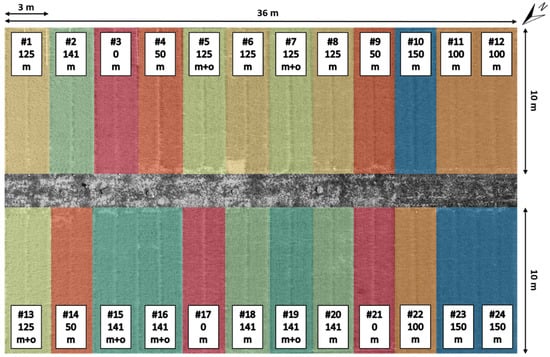
Figure 1.
Overview of the study site; each plot colorized by treatment, numbered, and labeled with applied N amounts and N types. m: mineral, o: organic.
2.2. Data and Preprocessing
2.2.1. Field Data
During a field campaign on 20 June 2017 (252 DAS), 48 CHL and LAI measurements were taken, two from each plot of the field experiment (Figure 1). Therefore, 10 equally distributed CHL and 5 equally distributed LAI measurements within a 0.25-m2 area were averaged on each location. The CHL measurements were conducted with a SPAD-502 Plus chlorophyll meter from Konica Minolta. The SPAD measurements were done at 10 fully developed uppermost leaves in each plot. Afterwards, the SPAD values were converted into µg cm−2 CHL according to Markwell [37]. LAI measurements were taken with a LAI-2200C plant canopy analyzer from Li-Cor. Furthermore, each plot was observed with the field spectrometer SVC HR-1024i mounted on a tripod.
For fresh biomass determination, the 24 plots were harvested at physiological maturity by hand cutting of whole plants in four randomly selected 0.25 m2 areas within each plot. These areas did not match with the locations of the previously mentioned sampling locations. Harvest of the core plots (14.7 m2) was done with a Hege experimental combine. Grain yield data is presented at 86% dry matter.
2.2.2. Hyperspectral UAV Image Data
In this study, a radiance calibrated Resonon Pika-L hyperspectral pushbroom scanner was used. The sensor has 900 spatial pixels each with 281 spectral channels covering a spectral range from 400 to 1000 nm. The maximum spectral resolution is 2.1 nm. The equipped objective lens has a field of view of 17.6°. The camera was mounted on a DJI S1000+ octocopter with a three-axis gimbal and the Ellipse-N IMU from SBG Systems with an accuracy of 0.1° for roll and pitch and 0.5° for heading (Figure 2). The complete UAV system weighed 11.2 kg and allowed an overall flight time of about 7 min.

Figure 2.
Octocopter with mounted camera (a) and close up of the three-axis gimbal with camera system and inertial measurement unit (IMU) (b).
The image data acquisition was conducted on 19 June 2017 under cloudless weather conditions. Three 0.25m2 reference panels with different brightness (95% white, 40% grey, and 5% black) were placed within the study area for postprocessing and measured with the field spectrometer SVC HR-1024i. With a flight height of 100 m, a ground swath of 31 m was achieved. This resulted in an initial spatial resolution of roughly 3 cm, which was reduced to 10 cm during orthorectification. The image was then georeferenced using in-field targets. All preprocessing steps are illustrated in Figure 3. Since the camera system in combination with the three-axis gimbal proved to be very reliable and stable, the image geometry of the raw data was already close to the real situation (Figure 4).
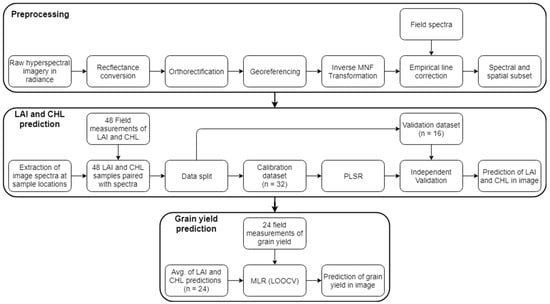
Figure 3.
Overview of each performed step during preprocessing and analysis.

Figure 4.
Raw geometry of imagery (a) and orthorectified imagery (b).
The spectral quality of the hyperspectral imagery was evaluated by calculating the mean distances between field and image spectra of the observed 0.25-m2 plots. Initially, the white reference panel was used to convert the radiance data into reflection. Comparing image and field spectra showed relatively high differences between 400 and 450 nm and beyond 900 nm (Figure 5a) due to noise in the image data. This indicated the necessity of excluding certain bands of the image data at the beginning and end of the observed spectral range and a radiometric correction. Furthermore, for radiometric correction, an empirical line correction [38] was performed using the image and field spectra of the reference panels and wheat measurements. To reduce noise, the spectral data was limited to a spectral range from 450 to 900 nm and binned to 106 spectral channels each with 4 nm. Since the spectra were still affected by some noise, a minimum noise fraction transformation (MNF) [39] was performed and inverted with the first 14 MNF bands. These performed steps resulted in a less noisy and smaller deviations from field spectra (Figure 5b, please consider the different scaling of the Y-axis compared to Figure 5a). Spatially, the image data were reduced to the true extent of the study area (Figure 1), excluding the walkway in the middle and protective wheat plants around the experiment. Also, one line of pixels from the borders of the investigated plots was excluded for the further analysis to avoid spectrally mixed pixels.
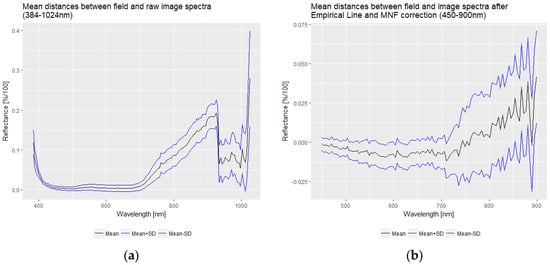
Figure 5.
Mean distances between field and raw image spectra for each band (a) and mean distances between field and noise-reduced image spectra for each spectral band (b).
2.3. Methodology
In the first step, the spectra from the 0.25-m2 sampled areas from each of the 48 plots were extracted from the image using the coordinates from LAI measurements. These spectra were averaged, leading to a set of 48 image spectra corresponding to the LAI and CHL measurements.
Two PLSR models [40] were calibrated using the extracted spectra with LAI and CHL measurements, respectively. Since each nitrogen treatment was applied on three plots, one of these plots was excluded from model calibration and used for an independent validation. The validation plot was always the one with the largest spatial distance to the other two. This resulted in 32 samples for calibration and 16 for validation. A maximum of 10 latent variables was included into the models, using R2 and root-mean-square error (RMSE) as quality measures. The resulting best performing models with the lowest RMSE were afterwards verified with the validation samples. The residuals were tested on normal distribution and significance with a one-sample t-test. To receive estimations for the complete study site, the models were used to predict CHL content and LAI for the complete image.
Since the grain yield information was only available as a single value for each plot, the LAI and CHL estimations from image data were averaged for each of these. After that, a multiple linear regression (MLR) [41] was performed predicting the grain yield from LAI and CHL. In this case, leave-one-out cross validation (LOOCV) was used to validate the model, since the number of samples (n = 24) was too small for independent validation. LOOCV excludes each sample once from the PLSR model calibration (n-1) and is instead predicted from the model as a quality measure [42]. The model was applied on every individual pixel of the image data to predict the grain yield for each pixel in the image. All described steps were performed using the R statistical environment [43]. A stepwise illustration of the methodology is shown in Figure 3.
3. Results
3.1. Data Analysis
The investigated 48 wheat plots showed relatively low LAI ranging from 1.13 to 2.70 with a mean of 2.17 and a standard deviations (SD) of 0.42. CHL had a larger variety from 19.82 to 77.18 µg cm−2. On average, the CHL content was 46.02 and with an SD of 15.59 µg cm−2. The 24 grain yield samples ranged from around 18.61 to 62.71 dt ha−1 with a mean of 46.94 dt ha−1 and an SD of 12.30 dt ha−1. The variety of grain yield was significantly influenced by the amount of applied nitrogen fertilizer (Figure 6). Both measurements for CHL and LAI showed high positive correlations with the measured grain yields (CHL/yield = 0.79, LAI/yield = 0.90). Therefore, both parameters were considered to be highly suitable for yield prediction.
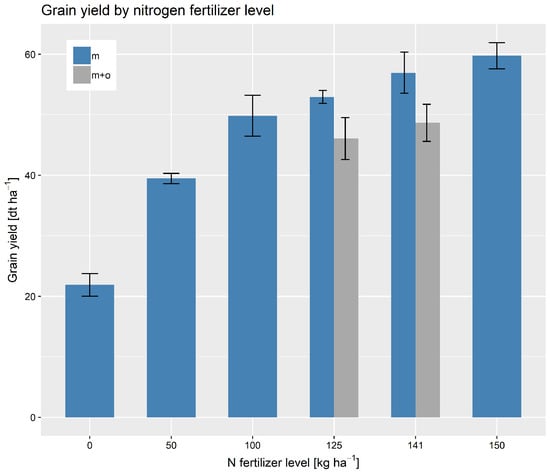
Figure 6.
Mean harvest results (three samples each) for six N levels with grain yield at 86% dry matter. Error bars indicate standard error of the mean.
3.2. PLSR and MLR
The independently validated PLSR model for LAI resulted in a R2 = 0.79 with an RMSE of 0.182 (Figure 7). The regression line was close to the 1:1 line with a slope close to 1. Residuals were normally distributed (pLAI = 0.41) and t-tests on the residuals showed no significant difference from zero (pLAI = 0.26). Over- and underestimations amounted to a maximum of around 0.5. The LAI measurements of the plots without any fertilization were far below the remaining measurements and therefore had a considerable influence on the model quality. However, one of the plots showed an LAI close to 2. Plots with higher fertilization had relatively similar LAI values between 2 and 2.5. According to the PLSR loadings, the most relevant wavelengths ranges were located at the red edge between 710 and 760 nm (loadings at ~0.2). The infrared plateau (760–900 nm) was also considered as an important wavelength range from the model (loadings at ~0.15). The visual part of the spectrum contributed less relevantly to the resulted model (loadings at ~0.05).
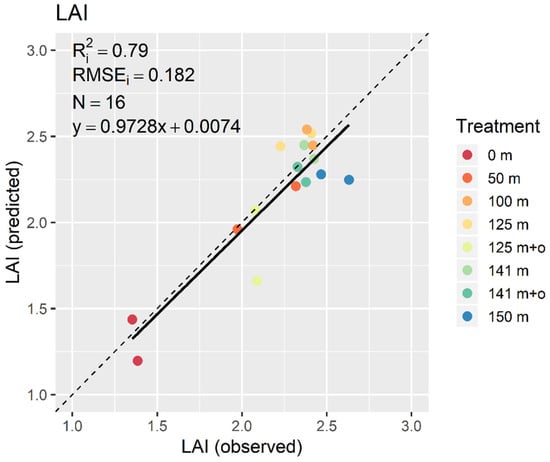
Figure 7.
Scatterplot of independently validated partial least-squares regression (PLSR) models for leaf area index (LAI) with the regression line (continuous) and the 1:1 line (dashed).
The model for CHL was calibrated with an R2 of 0.77 and a RMSE of 7.016 µg cm−2 (Figure 8). The CHL observations were spread equally across the observed data range. Over- and underestimations were at a maximum of around 20 µg cm−2. A slope of 0.87 and an offset of 8.77 indicated an overestimation of lower values, while higher CHL values above of 70 µg cm−2 tended to be underestimated. A normal distribution of the residuals (pCHL = 0.96) was given and the t-test on the residuals also showed no significant difference from zero (pCHL = 0.08). The PLSR loadings showed significant wavelengths in blue (450 nm) and red (660 nm) parts of the electromagnetic spectrum. Both areas showed loadings at around 0.18. The green area (550 nm) was not relevant for the model. The red-edge and infrared plateau also had no significant relevance and showed noisy oscillation below and above loadings of 0.
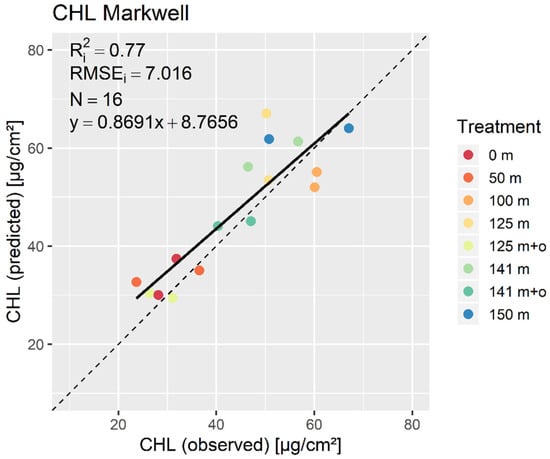
Figure 8.
Scatterplot of independently validated PLSR models for chlorophyll (CHL) with the regression line (continuous) and the 1:1 line (dashed).
The prediction for LAI across the entire study area (Figure 9) showed replicable results. Very low LAI values close to zero mostly occurred on the narrow lanes between the plots and areas where no wheat plants pullulated. Due to the influence of the neighboring pixels for these lanes, LAI values still slightly greater than zero were estimated. LAI estimations lower than one were located in the areas with no additional fertilization (plot nos. 3, 17, and 21). Values between one and two predominantly occurred at the plots with 50 kg ha−1 of applied N fertilizer (plot nos. 4, 9, and 14). Most of the other plots had an LAI between two and three. Plots with 125 and 141 kg ha−1 mineral and organic fertilizer mixtures (plot nos. 5, 7, 13, 15, 16, and 19) had lower LAI values than pure minerally fertilized plots with similar amounts. In general, LAI estimations tended to increase with larger amounts of applied fertilizer. LAI estimations higher than three were located in plots with mineral fertilizer applications from 125 to 150 kg ha−1, slightly increasing with larger amounts. Overall, even under the controlled conditions of this experiment, some plots were noticeably heterogeneous (for example, plot no. 16). There was also a slight difference in LAI predictions between the western and the eastern half of the study site, even within the same treatment classes. For example, plot number 22 with 100 kg ha−1 showed higher LAI estimations then plot numbers 11 and 12 with identical nitrogen treatment.
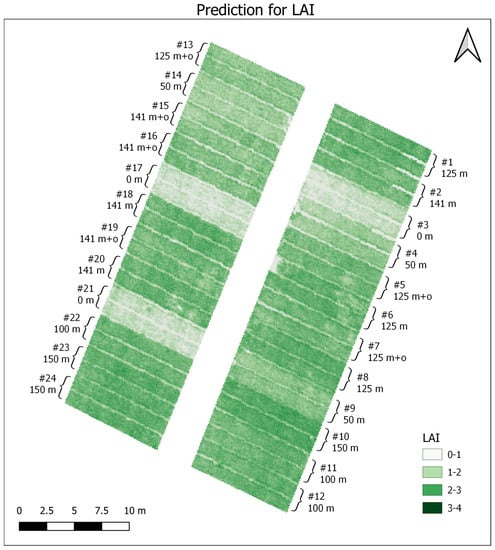
Figure 9.
Spatial prediction for LAI based on PLSR model.
The predictions of CHL (Figure 10) for the different plots were overall more distinctive than for LAI and showed a noticeable heterogeneity within the plots of the same treatment. The lowest CHL predictions (0–20 µg cm−2) were located at the walkways between the plots. Values greater zero were caused by mixed spectra from the neighboring pixels. Values roughly between 20 and 40 µg cm−2 were mostly present in the plots with no additional fertilization (plot nos. 3, 17, and 21) and plots with 50 kg ha−1 applied fertilizer. Higher CHL (40–60 µg cm−2) was predicted at the 141 kg ha−1 mineral and organic mixture treatments (plot nos. 2, 18, and 20). The plots with the 125 kg ha−1 combined mineral and organic fertilizer showed lower CHL (plot nos. 5, 7, and 13) than those with the same amount of solely mineral fertilizer (plot nos. 1, 6, and 8). The highest CHL (>80 µg cm−2) was predicted within the plots with 125, 141, and 150 kg ha−1 treatments, distinguishably increasing in that order. Again, some plots with the same treatment showed differences according to their location within the experimental setup (for example, plot nos. 11 and 12 vs. 22).
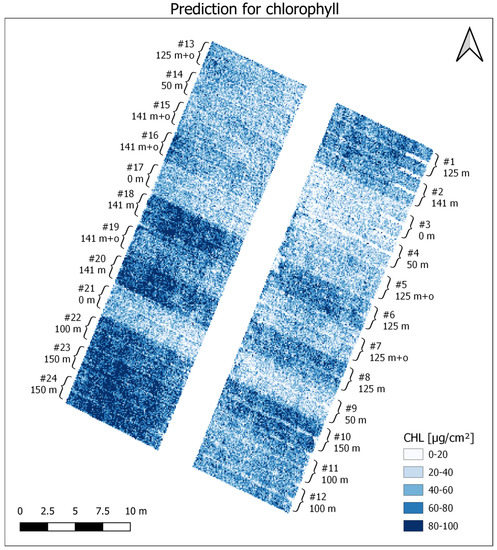
Figure 10.
Spatial prediction for CHL based on PLSR model.
The leave-one-out cross-validated MLR model with 24 samples (just one for each plot) indicated a significant predictability of grain yield predicted from LAI and CHL and grain yield determined by harvesting (R2 = 0.88) (Figure 11). The RMSE error of roughly four dt ha−1 proved the good predictability of grain yield with these two predictor variables. The regression line was very close to the 1:1 line with a slope close to one and a negligible offset of −0.10 dt ha−1. Over- and underestimations were equally distributed across the observed data range. The residuals were normally distributed (p = 0.18) and the t-test showed no significant difference from zero (p = 0.96).
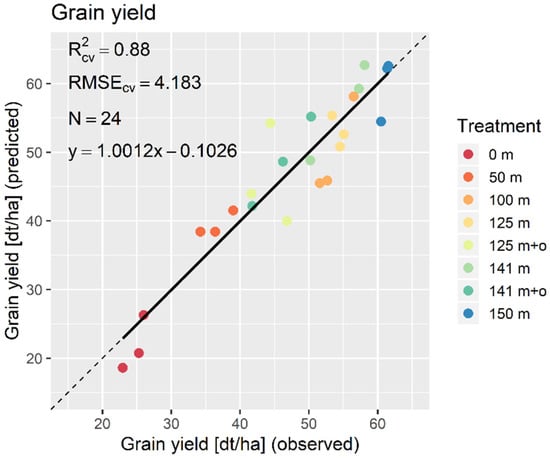
Figure 11.
Scatterplot of leave-one-out cross-validated multiple linear regression (MLR) models for grain yield with the regression line (continuous) and the 1:1 line (dashed).
The application of the MLR model for grain yield prediction to the image resulted in a comprehensible estimation. The inner plot variability for the grain yield prediction was very distinctive. The increase of grain yield with higher fertilizer treatment (Figure 12) was visible in this prediction. Without any treatment at all, the crops delivered the lowest grain yield, with about 20 dt ha−1 (plot nos. 3, 17, and 21). Slightly higher yields (up to 40 dt ha−1) occurred at 50 kg ha−1 fertilizer treatments (plot nos. 4, 9, and 14). Plots with 100 kg ha−1 applied fertilizer provided grain yields around 60 dt ha−1. Similar treatments, such as 125 kg ha−1 mineral (plot nos. 1, 6, and 8) and 125 kg ha−1 mineral plus organic (plot nos. 5, 7, and 13), showed clear differences in estimated grain yield. This effect was also noticeable within the 141-kg ha−1 treatments but with a higher overall grain yield. Highest grain yields were estimated at the 150-kg ha−1 treatments with up to 80 dt ha−1 (plot nos. 10, 23, and 24), with a few higher estimations larger 80 dt ha−1 at single pixels in plots 23 and 24.
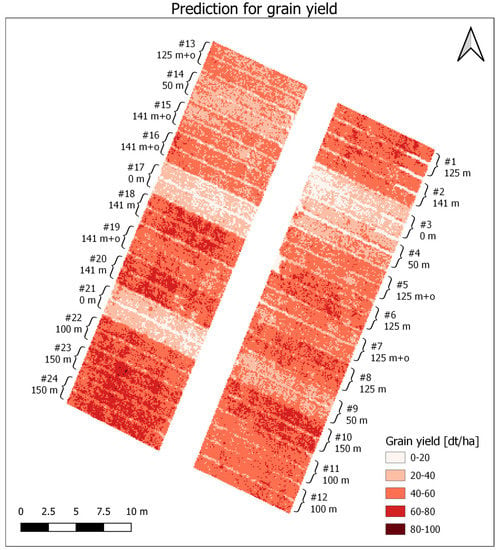
Figure 12.
Spatial prediction for grain yield based on MLR model.
4. Discussion
This small-scale field trial, with well documented spatial differentiation of six different N-levels, enabled a case study for yield estimations based on CHL and LAI predictions from UAV-based hyperspectral pushbroom scanner data. In comparison to other studies using similar technical equipment [9,10,11,12,13], the acquired imagery was geometrically very stable even before the orthorectification via IMU data. This was mostly achieved by the very stable and accurate three-axis gimbal and the good flight properties of the UAV platform. Even though that the pitch axis was theoretically obsolete in an all-time nadir adjusted camera setup, the gimbal corrections for this axis prevented the camera from picking up platform vibrations and therefore reduced disturbances within the data.
The relatively low LAI measurements were reasonable on the investigated day after sowing (252), with a Zadoks’ state at around 77 [44]. Reference [45] measured similar LAI at this growth stage on winter wheat plants under different nitrogen treatments. LAI and CHL increased with ascending fertilization. These correlations were well in line with findings from [46,47]. When opposing the achieved grain yield (Figure 7) at each fertilization stage, on average, there was only a slight yield benefit beyond an applied amount of 125 kg ha−1, at least considering the mineral fertilized plots. The CHL of the nonfertilized plots were the lowest values observed, but they were not as remarkably lower than the LAI values of these plots. This can be explained, since these plants, even though they were undernourished, had healthy but fewer leaves, which resulted in low LAI measurements. In addition, the rather sparse plant population in these plots may have led to earlier maturation of the lower leaf levels, which may have resulted in an overall reduction of leaf area.
The observed LAI measurements were correlated with the extracted corresponding image spectra from the same location using PLSR regression. The model achieved for LAI turned out to be quite robust. It has already been shown by many studies that LAI prediction from hyperspectral data is possible on different scales [19,20,21,22,23,24,25]. The most relevant wavelengths were located at the red-edge and infrared plateau, which is well in line with findings from [48,49]. Since there were a few lower LAI measurements (located in the nonfertilized plots), the prediction of these values had a strong influence on the model quality. The small variance of LAI predictions at the plots with higher N treatments (125, 141, and 150 kg ha−1) indicated that the higher amounts of plant-available N did not increase leaf growth significantly. Consequently, LAI alone was not capable of predicting yields for the different N-treated plots, since the additional nutrients were obviously mainly used to develop other plant parameters. Therefore, on behalf of a more reliable differentiation, CHL modelling was performed as well to be included in the later yield estimation.
The PLSR model for CHL was also of high quality, which is well in line with findings from [25,30] working on other scales. The relevant wavelengths were identified mainly at around 450 and 650 nm, which was expected due to the known absorption features from CHL within these areas [50]. Lower CHL values tended to be slightly overestimated by the model. However, compared to the LAI, the measurement data of the CHL were much more evenly distributed. In particular, the stronger differentiation between mineral plus organic and purely mineral-fertilized plots can be an important component with regard to yield estimation.
The spatial prediction of the LAI allowed a very precise distinguishing between the different fertilizer treatments and the predicted values were reasonable. As expected, the LAI for each plot in the predicted image increased with ascending fertilization analogous to the developed PLSR model. Overall, a separation between the fertilization groups was possible in most cases. However, plots with very similar fertilization (for example, 125 and 141 kg ha−1 plots) were impossible to distinguish without any additional information. This can be explained by the very similar LAI field measurements for these treatments, indicating that no strong increase of the LAI can be expected from a fertilizer quantity of more than 125 kg ha−1. The investigation of the inner plot variability showed the strength of the proposed results. Some plots with the same treatment differed depending on their location, visualizing that, even under very controlled conditions and on a small scale, unintended variability occurred. The differences between the plots with 100 kg ha−1 might be an effect of the terrain. Since there was a slight slope to the southeast at the two neighboring equivalent plots 11 and 12, small amounts of nutrients might have been washed out, reducing their availability in comparison to plot 22 and affecting the development of plants.
The spatial prediction of the CHL pointed out different structures and relations, therefore enabling a differentiation of the plots from another perspective. Plots with similar fertilization, which showed low variance in the LAI, such as the ones with 125 m kg ha−1 and 125 m + o kg ha−1, were easier to distinguish when investigating CHL. On the contrary, plots with no fertilization were harder to separate with relatively similar prediction, as for the 50 kg ha−1 plots. Plots with partly organic fertilization had less CHL than plots with full mineral fertilization. What was noticeable was the very low CHL of the combined mineral and organically fertilized areas (125 m + o, 141 m + o). The differences to the purely mineral fertilized plots of the same amount were much more pronounced than with LAI. Considering that organic nitrogen is not instantly fully available and has to be mineralized beforehand, these plants were less developed than the plants with mineral treatments [51]. In contrast, plots 3 and 4 showed similar CHL but differing LAI. CHL also seemed to be smaller at the inner sides of the plots, since at this side, the experimental plots had no protective unobserved area. Partly, the center of plots 18–24 had very high CHL in two linear structures ranging across the plots. The same structures became visible at plots 1 and 2 but were less distinct. This might have been caused by small inaccuracies during fertilization.
To benefit from both of the distinct estimations for LAI and CHL, the average values of each parameter for each plot were used to calibrate an MLR to predict the measured grain yields. This model turned out to be of high quality. This result supports the findings from [19], indicating the predictability of grain yield from LAI and CHL. The model follows the trend shown in Figure 7, that stronger fertilization also tends to lead to higher yields, with a less steep increase at higher N rates. The highest uncertainties existed for the areas fertilized with 125 m + o kg ha−1, which were clearly over- or underestimated in two out of three cases. This effect can be explained by the fact that the PLSR model for LAI already strongly underestimated one of the 125 m + o kg ha−1 plots. Furthermore, the plot taken out for validation might have had effects that could not be modelled with the help of the two plots used for calibration. Thus, this could have been caused solely by the choice of validation strategy. Due to the small sample size and the strong influence of the very low grain yields, these results have to be handled with some caution.
The spatial grain yield prediction enabled a very good distinguishability between all treatments. Plots which had similar LAI values but differing CHL values (plot nos. 5, 6, 7, and 8) and vice versa showed clear differences in grain yield. This showed that by combining the estimates for CHL and LAI, a reliable spatial estimation of yields was possible. Variability of yield within the individual plots also became clear at this point. Especially in the southwestern part of the study area, the yields in the middle of the plots were significantly higher. These effects might have been caused by the protective effect of the surrounding plants as well as by the already-mentioned possibility of slightly uneven application of the fertilizer. At the beginning of the experiment, the remaining N in the soil was measured with 49 kg ha−1. This value was assumed to be true for the complete study area, while in reality, the amounts were probably not evenly distributed and could therefore have induced variations in plant development as well.
The visual comparison of the prediction maps for LAI (Figure 9), CHL (Figure 10), and grain yield (Figure 12), as well as the RGB representation of the hyperspectral data set (Figure 4), showed clear structural similarities. These were probably biophysically based. Dark green regions in the image data had higher LAI and CHL values than brighter areas. This is due to the fact that denser and multilayered foliage (higher LAI) absorbed more light than less densely vegetated parts. These regions consequently had higher CHL contents as well. These aspects too were finally reflected in the yield estimation.
5. Conclusions
The main insights and relevant results presented in this study are threefold. Firstly, we presented a UAV-based hyperspectral pushbroom scanner system that is capable of recording high-resolution data of high spectral and spatial quality. The system is extremely suitable for investigations, especially on smaller areas, like single fields in precision farming. With the presented hardware combination, we were able to show that the aforementioned obstacles could be overcome when using hyperspectral pushbroom cameras on a UAV. In addition, the strengths compared to snapshot camera systems could be used effectively. The Resonon Pika-L camera was able to record high-quality spectral signals between 450 and 900 nm. However, beyond 900 nm, the signal was noisy and therefore not used for this study. It was also shown that radiometric correction applying empirical line correction significantly improved signal quality. The collection of field spectra is therefore necessary for every flight. When working with hyperspectral pushbroom scanners on UAVs, it is recommended to pay special attention to the additional hardware components. This was especially critical for the used gimbal. A high-precision three-axis stabilization is important in order to reduce the movements of the camera to a minimum and to absorb vibrations from the UAV. In addition, the IMU should be attached directly to the camera within the gimbal. This allows a very accurate recording of the camera orientation, which is completely independent from UAV movement. Secondly, we showed that LAI and CHL predictions from UAV-based hyperspectral data with high spatial resolution were promising. Distinguishing plots with different treatments, even though they were partly similar, was always possible with either the LAI or the CHL prediction. With this approach, it is possible for phenotyping and precision farming applications to spatially predict plant parameters reliably. This information could be used prior to fertilization to calculate the optimal amount of nitrogen required and to apply it in a precise manner and therefore reduce environmental damages without yield loss. Thirdly, a promising grain yield prediction was realized using the benefits from both the LAI and the CHL predictions, which showed a strong correlation to different treatments. For future research, the approach can be used to investigate the most suitable point in phenology for grain yield predictions by acquiring dense time series. The methodology presented here was carried out on the basis of CHL and LAI measurements with relatively high variability due to different N treatments. This variability may not occur in this form under real field conditions. Therefore, it is important for the future to test the presented method on other, more homogeneous data and to adapt it if necessary. Furthermore, the used UAV and camera technology must be checked with regard to its applicability to larger areas.
Author Contributions
Conceptualization, methodology, formal analysis and main writing was done by M.K., I.K. contributed to writing and formal analysis. Field data was acquired by M.K. and I.K. Text editing was performed by I.K., D.T., and T.J., D.T. and T.J. supervised the study.
Funding
This work was funded by the German Aerospace Center (DLR), using the financial resources of the Federal Ministry of Economics and Technology on the basis of a decision by the German Parliament, under grant number 50EE1014.
Acknowledgments
First of all, we would like to thank Timo Otte-Vinke for the help with setup and testing of the UAV, as well as for the excellent work as a pilot. We also thank Lucas Wittstruck, Lars Hoppius, and Alexander Schubert for their assistance in the field. Further thanks to Maik Kohlbrecher and Maria Vergara Hernandez for the advices and help in the field.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tilman, D. Global environmental impacts of agricultural expansion: The need for sustainable and efficient practices. Proc. Natl. Acad. Sci. USA 1999, 96, 5995–6000. [Google Scholar] [CrossRef] [PubMed]
- Rütting, T.; Aronsson, H.; Delin, S. Efficient use of nitrogen in agriculture. Nutr. Cycl. Agroecosyst. 2018, 110, 1–5. [Google Scholar] [CrossRef]
- Diacono, M.; Rubino, P.; Montemurro, F. Precision nitrogen management of wheat. A review. Agron. Sustain. Dev. 2013, 33, 219–241. [Google Scholar] [CrossRef]
- Gitelson, A. Remote sensing estimation of crop biophysical characteristics at various scales. In Hyperspectral Remote Sensing of Vegetation; Thenkabail, P.S., Lyon, J.G., Huete, A., Eds.; CRC Press: Boca Raton, FL, USA, 2012; ISBN 978-1-4398-4537-0. [Google Scholar]
- Hunt, E.R.; Daughtry, C.S.T. What good are unmanned aircraft systems for agricultural remote sensing and precision agriculture? Int. J. Remote Sens. 2017, 39, 1–32. [Google Scholar] [CrossRef]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative remote sensing at ultra-high resolution with UAV spectroscopy: A review of sensor technology, measurement procedures, and data correctionworkflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Madrigal, V.P.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the use of unmanned aerial systems for environmental monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Lucieer, A. HyperUAS—Imaging Spectroscopy from a Multirotor Unmanned Aircraft System. J. F. Robot. 2014, 31, 571–590. [Google Scholar] [CrossRef]
- Hruska, R.; Mitchell, J.; Anderson, M.; Glenn, N.F. Radiometric and geometric analysis of hyperspectral imagery acquired from an unmanned aerial vehicle. Remote Sens. 2012, 4, 2736–2752. [Google Scholar] [CrossRef]
- Jaud, M.; Le Dantec, N.; Ammann, J.; Grandjean, P.; Constantin, D.; Akhtman, Y.; Barbieux, K.; Allemand, P.; Delacourt, C.; Merminod, B. Direct georeferencing of a pushbroom, lightweight hyperspectral system for mini-UAV applications. Remote Sens. 2018, 10, 204. [Google Scholar] [CrossRef]
- Calderón, R.; Navas-Cortés, J.A.; Lucena, C.; Zarco-Tejada, P.J. High-resolution airborne hyperspectral and thermal imagery for early detection of Verticillium wilt of olive using fluorescence, temperature and narrow-band spectral indices. Remote Sens. Environ. 2013, 139, 231–245. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; McCabe, M.; Parkes, S.; Clarke, I. Pushbroom hyperspectral imaging from an Unmanned Aircraft System (UAS)—Geometric processing workflow and accuracy assessment. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2017, 42, 379–384. [Google Scholar] [CrossRef]
- Singh, R. Crop Yield Estimation and Forecasting Using Remote Sensing; Indian Agricultural Statistics Research Institute: New Delhi, India, 2012. [Google Scholar]
- Oøvergaard, S.I.; Isaksson, T.; Kvaalc, K.; Korsaeth, A. Comparisons of two hand-held, multispectral field radiometers and a hyperspectral airborne imager in terms of predicting spring wheat grain yield and quality by means of powered partial least squares regression. J. Near Infrared Spectrosc. 2010, 18, 247–261. [Google Scholar] [CrossRef]
- Herrmann, I.; Vosberg, S.K.; Ravindran, P.; Singh, A.; Chang, H.X.; Chilvers, M.I.; Conley, S.P.; Townsend, P.A. Leaf and canopy level detection of Fusarium virguliforme (sudden death syndrome) in soybean. Remote Sens. 2018, 10, 426. [Google Scholar] [CrossRef]
- Ma, B.L.; Dwyer, L.M.; Costa, C.; Cober, E.R.; Morrison, M.J. Early prediction of soybean yield from canopy reflectance measurements. Agron. J. 2001, 93, 1227–1234. [Google Scholar] [CrossRef]
- Weber, V.S.; Araus, J.L.; Cairns, J.E.; Sanchez, C.; Melchinger, A.E.; Orsini, E. Prediction of grain yield using reflectance spectra of canopy and leaves in maize plants grown under different water regimes. F. Crop. Res. 2012, 128, 82–90. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, K.; Zhang, Z.; Cao, Q.; Lv, Z.; Yuan, Z.; Tian, Y.; Cao, W.; Zhu, Y. Canopy chlorophyll density based index for estimating nitrogen status and predicting grain yield in rice. Front. Plant Sci. 2017, 8, 1–12. [Google Scholar] [CrossRef]
- Muñoz-Huerta, R.F.; Guevara-Gonzalez, R.G.; Contreras-Medina, L.M.; Torres-Pacheco, I.; Prado-Olivarez, J.; Ocampo-Velazquez, R.V. A review of methods for sensing the nitrogen status in plants: Advantages, disadvantages and recent advances. Sensors 2013, 13, 10823–10843. [Google Scholar] [CrossRef]
- Herrmann, I.; Pimstein, A.; Karnieli, A.; Cohen, Y.; Alchanatis, V.; Bonfil, D.J. LAI assessment of wheat and potato crops by VENμS and Sentinel-2 bands. Remote Sens. Environ. 2011, 115, 2141–2151. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Siegmann, B.; Jarmer, T. Comparison of different regression models and validation techniques for the assessment of wheat leaf area index from hyperspectral data. Int. J. Remote Sens. 2015, 36, 4519–4534. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimation for a heterogeneous grassland using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
- Goel, P.K.; Prasher, S.O.; Patel, R.M.; Viau, A.A.; Miller, J.R. Estimation of crop biophysical parameters through airborne and field hyperspectral remote sensing. Trans. ASAE 2003, 46, 1235–1246. [Google Scholar]
- Atzberger, C.; Darvishzadeh, R.; Immitzer, M.; Schlerf, M.; Skidmore, A.; le Maire, G. Comparative analysis of different retrieval methods for mapping grassland leaf area index using airborne imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 19–31. [Google Scholar] [CrossRef]
- Jarmer, T. Spectroscopy and hyperspectral imagery for monitoring summer barley. Int. J. Remote Sens. 2013, 34, 6067–6078. [Google Scholar] [CrossRef]
- Yue, J.; Feng, H.; Jin, X.; Yuan, H.; Li, Z.; Zhou, C.; Yang, G.; Tian, Q. A comparison of crop parameters estimation using images from UAV-mounted snapshot hyperspectral sensor and high-definition digital camera. Remote Sens. 2018, 10, 1138. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving soybean leaf area index from unmanned aerial vehicle hyperspectral remote sensing: Analysis of RF, ANN, and SVM regression models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Morales, A.; Berjón, A.; Agüera, J. Hyperspectral indices and model simulation for chlorophyll estimation in open-canopy tree crops. Remote Sens. Environ. 2004, 90, 463–476. [Google Scholar] [CrossRef]
- Atzberger, C.; Guérif, M.; Baret, F.; Werner, W. Comparative analysis of three chemometric techniques for the spectroradiometric assessment of canopy chlorophyll content in winter wheat. Comput. Electron. Agric. 2010, 73, 165–173. [Google Scholar] [CrossRef]
- Blackburn, G.A. Quantifying chlorophylls and caroteniods at leaf and canopy scales. Remote Sens. Environ. 1998, 66, 273–285. [Google Scholar] [CrossRef]
- Mozgeris, G.; Jonikavičius, D.; Jovarauskas, D.; Zinkevičius, R.; Petkevičius, S.; Steponavičius, D. Imaging from manned ultra-light and unmanned aerial vehicles for estimating properties of spring wheat. Precis. Agric. 2018, 19, 876–894. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Deutscher Wetterdienst (DWD) Climate Dataset—Archive Data Station 342 Belm. Available online: http://www.dwd.de (accessed on 5 October 2017).
- LWK-NDS: Chamber of Agriculture Lower Saxony Plant Production and Plant Protection—Recommendations; Landwirtschaftskammer Niedersachsen: Hannover, Gernany, 2016.
- Markwell, J.; Osterman, J.C.; Mitchell, J.L. Calibration of the Minolta SPAD-502 leaf chlorophyll meter. Photosynth. Res. 1995, 46, 467–472. [Google Scholar] [CrossRef] [PubMed]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A Transformation for Ordering Multispectral Data in Terms of Image Quality with Implications for Noise Removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: Q tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Hocking, A.R.R. The Analysis and Selection of Variables in Linear Regression. Biometrics 1976, 32, 1–49. [Google Scholar] [CrossRef]
- Otto, M. Chemometrics: Statistics and Computer Application in Analytical chemistry, 3rd ed.; John Wiley & Sons: Weinheim, Germany, 2016. [Google Scholar]
- R Core Team R: A Language and Environment for Statistical Computing. Available online: https://www.r-project.org (accessed on 10 December 2018).
- Zadoks, J.; Chang, T.; Konzak, C. A decimal growth code for the growth stages of cereals. Weed Res. 1974, 14, 415–421. [Google Scholar] [CrossRef]
- Lazauskas, S.; Povilaitis, V.; Antanaitis, S.; Sakalauskaitė, J.; Sakalauskienė, S.; Pšibišauskienė, G.; Auškalnienė, O.; Raudonius, S.; Duchovskis, P. Winter wheat leaf area index under low and moderate input management and climate change. J. Food Agric. Environ. 2012, 10, 588–593. [Google Scholar]
- Skudra, I.; Ruza, A. Effect of nitrogen and sulphur fertilization on chlorophyll content in winter wheat. Rural Sustain. Res. 2017, 37. [Google Scholar] [CrossRef]
- Serrano, L.; Filella, I.; Peñuelas, J. Remote sensing of biomass and yield of winter wheat under different nitrogen supplies. Crop Sci. 2000, 40, 723. [Google Scholar] [CrossRef]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red edge of plant leaf reflectance. Int. J. Remote Sens. 1983, 4, 273–288. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
- Curran, P.J. Remote Sensing of Foliar Chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Haynes, R. Mineral Nitrogen in the Plant-Soil System; Academic Press: New York, NY, USA, 2012. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).