Abstract
The Global Navigation Satellite System (GNSS) is commonly recognized by its all-weather capability. However, observations depend on atmospheric conditions which requires the induced tropospheric delay to be estimated as an unknown parameter. In the following study, we investigate the impact of intense weather events on GNSS estimates. GNSS slant total delays (STD) in Precise Point Positioning technique (PPP) strategy were calculated for stations in southwest Poland in a 56 days period covering several heavy precipitation cases. The corresponding delays retrieved from Weather Research and Forecasting (WRF) model by a ray-tracing technique considered only gaseous parts of the atmosphere. The discrepancies are correlated with rain rates and cloud type products from remote sensing platforms. Positive correlation is found as well as GNSS estimates tend to be systematically larger than modeled delays. Mean differences mapped to the zenith direction are showed to vary between 10 mm and 30 mm. The magnitude of discrepancies follows the intensity of phenomena, especially for severe weather events. Results suggest that effects induced by commonly neglected liquid and solid water terms in the troposphere modeling should be considered in precise GNSS applications for the atmosphere monitoring. The state-of-art functional model applied in GNSS processing strategies shows certain deficits. Estimated tropospheric delays with gradients and post-fit residuals could be replaced by a loosely constrained solution without loss of quality.
1. Introduction
Weather monitoring and particularly nowcasting is currently based on two major data sources: rapid update weather forecast [1,2] and weather radars [3,4], providing information about current weather and short term forecasts. However, weather radars are very expensive and observations may be affected by several errors such as echo lines, topography, canopy and building shadowing effects as well as rain bands reduction [5]. For over two decades, ground-based GNSS networks have been used for operational positioning and collecting data time series in order to better understand interference on transmitted radio waves. The dependency on tropospheric conditions revealed the remote sensing application of GNSS signals [6,7]. The total tropospheric delay is usually expressed in zenith direction, hence it is called zenith total delay (ZTD). Its conversion into Integrated Water Vapor (IWV) has become a routine in nowadays GNSS data processing within Network of European Meteorological Services (EUMETNET) EIG GNSS Water Vapour Programme (E-GVAP, egvap.dmi.dk) and activities of ESSEM COST Action ES1206 “Advanced Global Navigation Satellite Systems tropospheric products for monitoring severe weather events and climate (GNSS4SWEC)” (gnss4swec.knmi.nl). Assimilation of GNSS ZTD into Numerical Weather Prediction (NWP) models [8,9,10] has helped to reduce forecast uncertainty. The delay in the direction to the satellite, i.e., the slant total delay (STD) contains full information of the troposphere along the propagation path. Currently, improvement of weather models based on GNSS STDs stands a challenge in variational assimilation [11,12].
Ray-tracing has become a common technique to provide independent values of tropospheric delays [13,14]. Contrary to ground-based GNSS delays that rely on clocks, orbits and associated pseudoranges [15], ray-tracing uses NWP model variables. Thus, it serves as a forward observation operator in variational assimilation which allows converting model data into geodetic observations [16]. With ray-tracing we are able to compute tropospheric delays for ground station in the specified elevation angle and azimuth associated with satellite position as long as the weather model is available. The precision of ray-traced delays with respect to GNSS estimates is reported to be at the 1-cm level in terms of standard deviation of ZTD [17].
In the neutral atmosphere, the major contribution to the tropospheric delay comes from gaseous constituents that form hydrostatic and wet components of the delay. The hydrostatic delay is proportional to air pressure, whereas the wet part is related to temperature and water vapor content. As the GNSS signals sit in the L band of the microwave spectrum, they are almost insensitive to the hydrometeors. Hence, the effect of liquid and solid particles suspended in the air is usually neglected in the tropospheric delays since the impact is a few orders of magnitude smaller than other air constituents [18].
The significance of hydrometeors becomes important during weather phenomena that produce heavy rainfalls or snow, fog and dust storms which are usually connected with the large amount of clouds. Various particles are expected to induce 3% of the delay compared to that caused by dry air and water vapor [18]. Douša et al. [19] reported that the difference between maximum and minimum slant delay mapped to the zenith direction due to the presence of hydrometeors is on the level of 1 cm. Number of studies attempted to characterize local atmospheric structures using GNSS products and associated variables as an indicator. De Haan et al. [20] analyzed tropospheric delays during cold front passage and demonstrated azimuth-elevation anisotropy visible in the wet delay component. Brenot et al. [21] simulated and observed ZTDs during extreme weather event to quantify the impact of hydrometeors, they attained maximum 30 mm delay. The Saastamoinen formulation of hydrostatic delay [22] applied in the presence of high hydrometeor contribution is expected to overestimate the total delay. Application of ZTD and horizontal gradients in the study of Brenot et al. [23] allowed to point out convection cells during heavy rainfall event, where wet gradients appeared to increase towards its direction. Shoji et al. [24] used similar methodology to indicate severe weather based on estimated precipitable water vapor gradient calculated from ZTD and mapped STD. In the recent study, Masoumi et al. [25] presented effects of improper modeling in GNSS data processing induced by horizontal gradients [26] which may affect estimated tropospheric delays in particular weather conditions.
In this paper, we use GNSS observations and ray-tracing technique to find a potential correlation between rain, clouds and tropospheric delays. We use cases with intense rainfalls observed over Poland during the period of GNSS4SWEC Benchmark campaign [19]. In our approach, we model ray-traced STDs using Weather Research and Forecasting (WRF) model assuming that the signal propagates in the atmosphere that is a pure gas. Thus, it theoretically depends only on pressure, temperature and water vapor pressure, but it also reflects the model accuracy. On the other hand, the GNSS observations provide slant delays with total atmospheric contribution. Hence, the influence of neglected liquid and solid particles should be visible in calculated GNSS estimates reduced by ray-traced delays. In severe atmospheric conditions, these residuals should surpass the uncertainty level of estimated tropospheric delays. Both GNSS and ray-traced delays need to be provided with superior accuracy in order to properly distinguish troposphere-induced effects from other systematic effects. In the normal equation system GNSS STDs cannot be estimated directly as the number of unknown parameters exceeds number of observations. Thus, GNSS retrievals will absorb part of the uncertainty introduced by assumptions and constraints such as mapping functions and phase ambiguity. The other data source of ray-traced retrievals is affected by uncertainty of meteorological background and assumptions for the propagation of electromagnetic field. The paper provides a detailed analysis of data uncertainties and a comprehensive error propagation for tropospheric estimates to reveal effects of atmospheric liquid and solid water absorbed in GNSS signal.
The novel approach in this study is the application of GNSS STDs to assess the potential to retrieve impact of hydrometeors on independent ray-traced retrievals. The saturation of air with liquid and solid particles is indicated based on cloud type remote sensing measurements and rain rate satellite observations. For easier interpretation of residual magnitudes, the computed differences in tropospheric delays are mapped to the zenith direction. The paper is organized as follows: in Section 2 we present our approach to ray-trace the GNSS signal from ground station to satellite. Section 3 shows the applied GNSS STD estimation strategy. In the next chapter, we introduce meteorological observations used in our study. In Section 5 and Section 6, an overview of the data quality is presented and discussed. Section 7 presents statistics for GNSS stations involved in the analysis to demonstrate the impact of hydrometeors on GNSS tropospheric delays. The paper is closed with a conclusion.
2. Ray-Path Model
The ray-tracing technique is used to calculate tropospheric delays in WRF model. We follow similar methodology to Böhm et al. [27] which has been operationally applied to provide forecast Vienna Mapping Functions (VMF1). Wilgan et al. [28] showed that application of our ray-tracer to derive WRF-based mapping function results in comparable performance to VMF1-FC Böhm et al. [29] in terms of position and can help to improve convergence time in real-time PPP. The ray-tracing algorithm is based on the geometrical optics approximation and assumes the signal to propagate within the plane of a constant azimuth. Since horizontal gradients in the troposphere are generally much lower than vertical gradients [30], the perpendicular contribution to the ray-path is neglected which makes the trajectory two-dimensional (no out-of-plane components). The signal delay is considered to be a phase excess introduced by the atmospheric refraction n along the ray-path trajectory. It causes the path length to differ from its geometric straight-line distance S [31] according to the equation
Here, we separate the signal path into finite number of linear ray-pieces along the bent ray-path. The refractive index n or alternatively refractivity N describes the medium properties and its impact on radio propagation. The fundamental variables necessary to express atmospheric state in terms of gaseous properties are: the air pressure (hPa), the air temperature T (K) and the water vapor partial pressure (hPa) that form the equation valid for GNSS frequencies according to Davis et al. [7]
with being atmospheric density that can be described as a relation
where and are molar masses of dry and wet air respectively and is the universal gas constant. The values , and denote empirically derived refractivity coefficients with with J/K/kg and J/K/kg being gas constants for dry and wet air, respectively. In this study, we adopt coefficients of Bevis et al. [32] which equal K/hPa, K/hPa and = 373,900 K/hPa.
Refractivity fields for the gaseous part of the delay are taken from WRF model [33]. We assume WRF spherical latitudes to be WGS84 latitudes. Discrepancies introduced by inconsistency between geographic and geodetic coordinates have a minor effect on ray-traced tropospheric delays [13], but can significantly reduce the computational efficiency. A peculiar feature of WRF model is that the geopotential height, which serve as a standard vertical coordinate, are determined on staggered vertical grid which are usually known as full-eta levels. Processing of meteorological parameters requires to make all model variables collocate vertically so that they share common layers. The geopotential heights are unstaggered in a simple arithmetic average to create half-eta levels. This procedure allows stating reference layers for interpolation in order to obtain finer resolution of meteorological variables. The numerical implementation of the ray-path model to derive tropospheric delays from WRF refractivity field is described in detail in Appendix A. To provide approximations of rain effect and liquid cloud water, a theoretical model described in Appendix B is adopted for calculations of respective tropospheric delays.
3. GNSS Slant Delays Estimation
GNSS data processed with Bernese GNSS Software v.5.2 [34] are based on Precise Point Positioning (PPP) strategy [35]. The procedure uses two different settings to test products sensitivity on hydrometeors, both with the same input data: GNSS observations, CODE final products—satellites orbits in 15 min interval, clocks information in 30 s interval, monthly differential code biases (DCBs) and daily Earth Rotation Parameters (ERPs) [36]. Applied ocean and atmospheric tidal loadings use finite element solution (FES) model FES2004 [37] and model of Ray and Ponte [38] respectively.
The STD reconstruction procedure is achieved in two ways: with and without using the ZTD gradients in order to account for the possibility of weak representation of troposphere anisotropy by horizontal gradients. GNSS delays are estimated based on corrections to the VMF1 model prepared at Vienna University of Technology (http://ggosatm.hg.tuwien.ac.at/DELAY/GRID/VMFG/) [27]. The tropospheric refraction is divided into hydrostatic (ZHD) and “wet” (ZWD) parts of zenith delay with being a priori zenith hydrostatic delay from VMF1 model. The is the estimated unknown, and are ZTD horizontal gradients that depend on elevation () and azimuth (A). The hydrostatic and wet mapping functions for conversion to slant delays are derived from a continued fraction [39] using VMF1 coefficients [27]. The gradient mapping function is calculated according to Chen and Herring [26].
The STD estimation procedure follows the standard Bernese GNSS Software PPP scenario, where the coordinates and receiver clock corrections are estimated together with ZWD and ZTD horizontal gradients. L3 post-fit phase residuals are computed for all stations to assess the site-dependent phase multipath effect and subtract it from the STD. The final for each of GNSS observation i is calculated using Equation (4) following the procedure and for the same period of time as presented in Kačmařík et al. [17]
where is averaged from all L3 residuals within equal-area bins of the sky with 1° elevation height boundaries :
The azimuthal width boundaries (, ) [40] are calculated as . No constraint is applied to the coordinate estimation (free solution). The ZWD is estimated in 5 min intervals, and relatively constrained to 1 mm within the next 10 min. ZTD gradients are relatively constrained to 0.1 mm within 30 min. The slant delays are reconstructed as well every 5 min. For later comparison purpose, we choose the slant delays from the full hour epochs without any averaging.
4. Meteorological Observations
The meteorological data presented in this study are collected for validation purposes only. Following data types are considered:
- SYNOP observations,
- radiosonde observations,
- Multisensor Precipitation Estimate (MPE) from European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT),
- Cloud Type (CT) product from Satellite Application Facility on support to Nowcasting (SAFNWC).
The temperature, relative humidity, wind speed and rain rate measurements are available every hour at 66 SYNOP stations, evenly distributed over the area of Poland, operated by the Institute of Meteorology and Water Management—National Research Institute. Radiosonde data are collected from three Polish stations with following WMO identifiers: 12120 (LEBA), 12374 (LEGIONOWO) and 12425 (WROCLAW). Coordinates of the radiosonde stations are listed in Table A1 in Appendix C. Meteorological parameters used in the study consist of the air pressure, the air temperature and the dew point temperature, which is converted to water vapor partial pressure. Observations are collected at mandatory pressure levels and significant with respect to temperature and can consist of 40–80 different height levels in total. The number of levels varies between observations on a daily basis with weather conditions and radiosonde performance. Data for measurements taken twice a day at 0.00 and 12.00 UTC are retrieved from the National Oceanic and Atmospheric Administration’s Earth System Research Laboratory (NOAA/ESRL) Radiosonde Database available under https://ruc.noaa.gov/raobs/.
Remote sensing information linked with precipitation locations and rain rates are retrieved from EUMETSAT. The data comprise of MPE product [41] that is a mixture of high-temporal (30 min), relatively high resolution infrared geostationary observations combined with high quality microwave rain rates from polar orbiting satellites [42]. The temporal and spatial matching of both data types is performed on a basis of rain rates adjusted to the brightness temperature. In our study, we use the MPE product with 15 min resolution, cropped to cover the study area of Poland. Data collected within the radius of 45 km with respect to each station are then subtracted from raster and median values are taken. Only observations at full hours are considered to follow WRF resolution. The choice of 45 km radius aligns with the standard field of view for GNSS station. The data are used as a rain intensity indicator for all considered GNSS stations.
Another source of remotely sensed observations is CT retrieval from SAFNWC software [43]. The CT multi-mission product contains information on cloud structure and its vertical extent, which includes but is not limited to fractional clouds, semitransparent clouds, high, medium and low clouds. The algorithm is based on the brightness temperature retrieval and reflectance of cloudy pixels, which vary substantially depending on the cloud height (low, medium and height), amount (semi-transparent or opaque) and water phase (liquid or ice). The estimates are provided from the combination of Spinning Enhanced Visible and Infrared Imager (SEVIRI) channels that allow for separation of clouds with different characteristics, taking into account atmospheric conditions and sun/satellite geometry [44].
Temporal resolution of CT is 6 hours. Typically, 21 pixel classes are distinguished to define cloud types. However, for the purpose of our analysis, we reclassify pixels into 7 classes from no impact on GNSS signal to the most significant impact. The classification in Table 1 was consulted with Andreas Wirth from ZAMG (personal communication). A single CT value per GNSS station is retained from 45 km pixel radius. A station-specific CT is taken as a median of all pixels within the radius of interest.

Table 1.
Classification of CT product for the analysis of hydrometeors’ contributions to GNSS tropospheric delays. The data samples correspond to number of observations collected during the study period at 13 GNSS stations for specified classes.
5. WRF Model
We used WRF model version 3.6.1 [45] that was configured using two nested domains, with spatial resolution of km and km. In this study, only meteorological data from the km nested domain are used. The nested domain dimensions are 238 grids in west-east direction and 220 grids in south-north direction and 48 layers in vertical. The model was run using default static data fields (e.g., elevation or land-use), and the input files were generated using the WRF Preprocessing Software (WPS). The USGS 24-classes land-use was used in this study. The model was run using the GFS-FNL data as meteorological initial and boundary conditions. The simulations were initialized each day at 00 UTC, and the forecasts were calculated for the next 24 h. Detailed model configuration in terms of physics is summarized in Table 2.

Table 2.
Physics options used in WRF model configuration. Please see the WRF model user guide for further details.
The model performance for air temperature, relative humidity and wind speed was summarized using four statistics:
- Mean Error (ME)—describing the tendency of the model for over (ME ) or underestimation of the given meteorological variable. ME is calculated as a mean difference between the modeled and observed values for all the stations (domain wide statistics). The units are the same as for the analyzed meteorological variable.
- Root Mean Squared Error (RMSE)—calculated as a root of the squared differences between the modeled and observed values for all stations. The units are the same as for the analyzed meteorological variable.
- Pearson correlation coefficient (cor)—takes the values from −1 to +1 and the expected value is 1. Cor is unitless.
- Index of Agreement (IOA; [52]) is a standardized measure of the degree of model prediction error. IOA is unitless, and values vary between 0 and 1 (1 indicates a perfect match).
Model performance for rainfall was done using the binary evaluation and presented with the performance diagram [53]. The rainfall events were treated separately regarding to the rainfall intensity and analyzed for five different thresholds. Additionally, at one radiosonde location, central with respect to the area of interest, radiosonde minus WRF refracitivity fields were calculated for whole study period. Resampled differences in model space were used as an input for uncertainty propagation with ray-tracing.
6. WRF Model Evaluation
The model performance for the entire study period is summarized in Table 3. The model underestimates observed air temperature and relative humidity at 2 m. Correlation coefficient exceeds 0.8 for air temperature, which suggests good temporal agreement between the model and observations. Cor is lower for relative humidity and wind speed.

Table 3.
WRF model performance for surface air temperature (T2), relative humidity (RH2) and wind speed (WSPD) for entire period and all SYNOP stations.
The changes in model performance during the study period is summarized for air temperature in Figure 1 and relative humidity in Figure 2. For air temperature, the model tends to underestimate the observed values during the entire period except the days from 152 to 162 DOY. For this period, the median values of the model-observation are significantly above zero. For the same period relative humidity is underestimated.
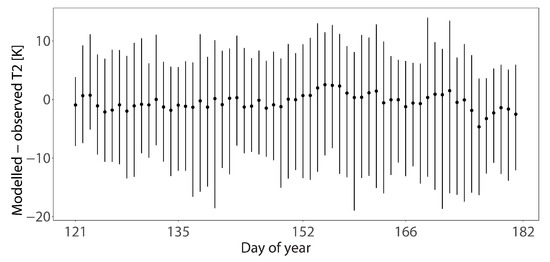
Figure 1.
Min, max and median values (black dots) for modeled—observed hourly T2, summarized for each day and all stations.

Figure 2.
Min, max and median values (black dots) for modeled—observed hourly RH2, summarized for each day and all stations.
The model performance for rainfall is summarized in Figure 3 using the binary evaluation. The model skills in forecasting rainfall decrease with observed rainfall intensity. This is partly because of the fact that the high intensity rainfall episodes are of convective origin and cover only small areas and are short in time. This, combined with high spatial and temporal resolution of the data (even relatively small shift in modeled rainfall location/time will lead to errors in binary evaluation) and small number of the episodes with high intensity of rainfall leads to poor performance of the model for the thresholds >2.5 mm/h.

Figure 3.
Model performance for hourly rainfall for entire study period and all stations.
The model performance for rainfall was also analyzed for each day of the study period. For each day the mean daily rainfall intensity was calculated from hourly measurements gathered at all stations and from corresponding WRF model grid cells (Figure 4). The correlation between the modeled and measured values is high and close to 0.7. The model underpredicts the mean daily rainfall intensity for the peak days, but still, for the majority of days, shows increased values for the days with high measured intensity.

Figure 4.
Mean daily rainfall intensities from observations (gray bars) and WRF model (cyan bars) calculated from hourly measurements gathered at all stations.
7. Cross-Validation of Ray-Traced and GNSS Slant Delays
We analyze the quality of tropospheric delays based on representative sample of thirteen ground GNSS stations in southwest Poland that vary in altitude and location. Stations with following IDs of ASG-EUPOS network are considered: GLOG, GNIE, JLGR, KALI, KLDZ, LESZ, OPLE, WLBR, ZARY, ZIGR including three EUREF Permanent Network (EPN) stations: BOR1, GWWL, WROC. Figure 5 displays the distribution of the station network. Table with listed GNSS stations and their coordinates is provided in Appendix C. Collected GNSS observations cover a benchmark period of COST ES1206 GNSS4SWEC Action [19] between 5th May and 30th June of 2013, which corresponds to 125 and 181 day of year (DOY). Selected stations belong to the PL0 cluster.
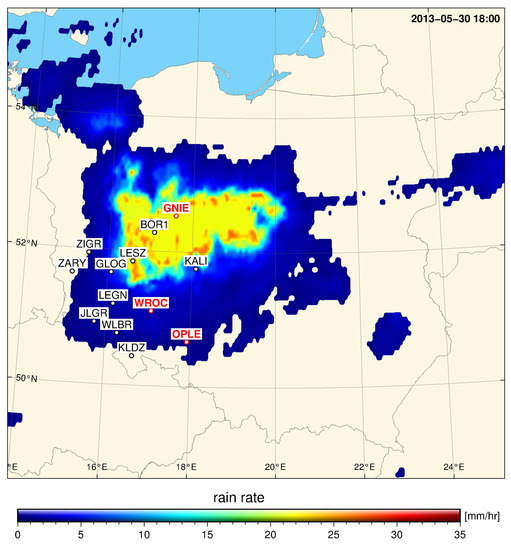
Figure 5.
Distribution of GNSS stations used in the analysis on the background of a frontal case (DOY 150) represented by MPE product.
Slant delays down to three degree of elevation angle are taken into account to calculate residuals as GNSS minus ray-traced values in 1-h temporal resolution. A clear dependence on the elevation angle is displayed in Figure 6a. The mean statistics respective for STD differences are calculated in 5-degree bins of elevation angle starting from 5 degrees up to 90 degrees. Slant delays below 5 degrees are not analyzed in terms of mean bias and standard deviation due to relatively low number of observations. Therefore, Figure 6a shows that their residuals can reach up to 600 mm for 3 degree elevation angle. The results suggest no considerable differences in estimated STDs as an effect of applied GNSS processing scenario. The inconsistencies in terms of standard deviation due to neglected horizontal gradients equals only 3 mm. Although the reconstruction with horizontal gradients leads to more biased STDs towards smaller values, estimates at the lowest elevation angles are mostly affected. Additional 8 mm negative bias is observed below elevation angle of 5 degree. However, estimates at such low elevation angle are not used in the statistical assessment of hydrometeors’ contributions to tropospheric delays.

Figure 6.
Differences calculated as GNSS minus ray-traced delays in terms of (a) slant total delay and (b) converted to zenith direction with mapping functions. Red and green lines show mean bias and standard deviation respectively, averaged in 5 degree intervals.
Since ray-traced and GNSS-based slant delays are calculated together with their respective mapping functions separated on hydrostatic and wet part, it is possible to express residuals in the zenith direction. ZTD discrepancies are presented in Figure 6b. The differences generally do not exceed 50 mm, which is a valid residual distribution for STD differences at high elevation angles. No distinctive systematic effects with respect to the elevation angle are observed in ZTD residuals. The delays are affected by mean bias of around −2.5 mm and have 14 mm or 14.4 mm standard deviation, respectively for solution including and excluding post-fit residuals.
The results show that the quality of ray-traced delays with respect to GNSS estimates is comparable to the study of Kačmařík et al. [17]. There is no statistically significant difference induced by a treatment of post-fit residuals in GNSS solution nor the horizontal gradients affect STD and ZTD values considerably. Therefore, the interpretation of results in the following study will be independent on the applied GNSS processing scenario.
8. Uncertainties of Tropospheric Delays
The quality of derived tropospheric delays can be affected by number of factors which originate from input data uncertainties used in calculations as well as assumptions applied in the processing. The error sources in GNSS estimation procedure and ray-tracing have been carefully accounted for in order to correctly identify hydrometeor effect in estimated tropospheric delays.
8.1. Uncertainties of Ray-Traced Delays
The errors in ray-traced delays arise from uncertainties related to (1) simplifications in the mathematical algorithm and (2) the uncertainty of background meteorological fields. According to Zus et al. [14], the uncertainty introduced by quality of NWP variables significantly exceed uncertainty due to assumptions in the ray-path model. Hobiger et al. [13] attribute the root mean square error of 16 mm from GNSS and ray-tracing cross-validation to inconsistencies in NWP model when 3-D Eikonal solver is used for the signal propagation. The simplified assumption with no out-of-plane components (2-D) yields nearly identical results. Nafisi et al. [54] prove a high agreement between 3-D and 2-D approaches in ray-tracing solutions and suggest induced inconsistencies to arise mostly from the performance of a weather model in terms of a forecast skill.
The relatively high, km spatial resolution of WRF model to derive ray-traced delays in the following study is expected to introduce uncertainties of background fields due to horizontal re-sampling, vertical refinement and mismodeling of meteorological variables. Since the tropospheric delay depends on the atmospheric refractivity, we estimate its uncertainty based on radiosonde observations.
Reports from weather balloons are collected at radiosonde station close to the GNSS station WROC. However, both stations differ in position in terms of latitude, longitude and altitude. In order to avoid the effect of inconsistent coordinates, the quality of WRF background is analyzed at the radiosonde location. For each radiosonde retrieval, refractivity profiles were extracted based on mandatory and significant levels with respect to temperature. Using whole Benchmark period of 56 days, radiosonde minus WRF refractivity differences were calculated to assess uncertainty of WRF refractivity field. A gap in radiosonde data on 128 DOY was filled by neighboring retrievals to provided consistent time-series. The assessed residuals were then re-sampled to common altitudes to calculate statistics in terms of mean bias and standard deviation up to top WRF layer at around 20 km. The results in terms of relative and fractional error are presented in Figure 7. The highest differences are observed in the lower troposphere with mean standard deviation of 10% and mean negative bias of 3%. There is around 1% positive refractivity bias at the altitude of 11 km with 2% standard deviation which both systematically decrease and become stable above 14 km, resulting in uncertainty of 1%. We assume the uncertainty to be consistent for altitudes exceeding uppermost WRF layer which corresponds to about 0.2 unit in refractivity. The overall quality achieved for ray-traced delays in terms of uncertainty of refractivity fields agrees well with empirical values provided by Zus et al. [14] and analysis based on error covariance matrix from HIRLAM limited-area NWP system [12]. The results are also supported by analysis of WRF fields conducted by Wilgan et al. [55].
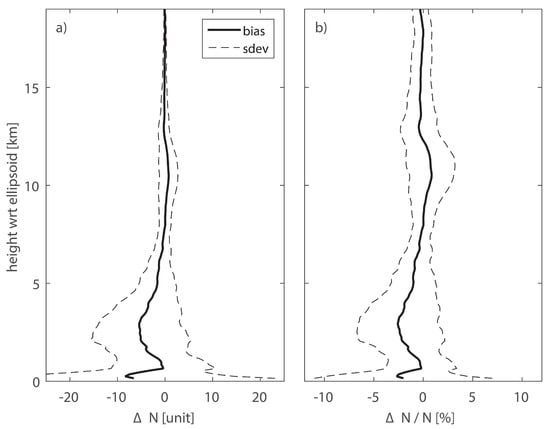
Figure 7.
Mean bias (solid line) and standard deviation (dashed line) for refractivity differences between radiosonde and WRF model calculated in terms of (a) units of refractivity and (b) fractional errors in percentage.
To perform validation with radiosondes, the delays corresponding to WRF retrievals need to be modeled. The vertical atmospheric soundings allow for the reference modeling only in terms of zenith delays, which are computed at weather balloons’ release times. Figure 8 presents ZTD time-series for radiosonde, WRF and GNSS observations. The delays computed at the radiosonde site are expected to be larger than at the neighboring GNSS station due to a difference in the altitude. The GNSS station is located 30 m higher than the radiosonde site that causes the GNSS hydrostatic delay to be systematically underestimated due to smaller portion of the atmosphere above the station. Hence, the GNSS observations in Figure 8 are used only to show data variability in time. A higher agreement with WRF delays is expected once GNSS delays are estimated at radiosonde station. Negligible differences are introduced by horizontal variability of meteorological parameters (12 km distance mis-match).

Figure 8.
Zenith delays at the location of radiosonde station 12425 retrieved from: radiosonde profile (red solid line), WRF model (dash-dot green line) and GNSS observations (dashed black line). Note the GNSS delays correspond to the altitude of WROC station and are systematically underestimated.
Having the uncertainties of WRF refractivity fields at the epochs of radiosonde reports, we assume their distribution to be spherically symmetric to perform error propagation and derive the uncertainty of ray-traced delays. Their relative differences are calculated after mapping WRF delays to zenith direction with a temporal resolution consistent with delays derived from radiosonde (12-hourly). Figure 9 presents the magnitude of uncertainties at GNSS station WROC as a function of time and elevation angle.

Figure 9.
Uncertainties of ray-traced delays due to uncertainty of refractivity: (a) for slant delays mapped to zenith by sine of elevation angle with respect to time, (b) for slant delays with respect to elevation angle.
As slant total delays become larger together with decreasing the elevation angle, the highest uncertainties are observed at 3 degrees with magnitude varying from around 20 to 90 mm. The uncertainties expressed in the zenith direction after conversion by sine of elevation angle do not generally exceed 6 mm, except the period from 162 DOY at 12:00 UTC to 165 DOY at 12:00 UTC, which was expected to introduce mismodeling of meteorological variables already visible in the time-series of WRF-based ZTD in Figure 9. Very low uncertainties below 2 mm are observed for DOYs 132, 150 and 178.
8.2. GNSS Delays Errors
The error propagation for GNSS delays is performed based on the assumption that the parameters of STD in Equation (4) have the normal distribution and are unbiased. Hence, we may propagate their covariances into the variance of STD estimates following the law of variance propagation:
where J is the Jacobian operator of the STD function:
and the STD function parameters matrix contains the parameter variances:
We assume the following mean errors of function parameters:
- mean error of in VMF1 model mm [56],
- mean error of hydrostatic mapping function VMF1 [27],
- mean error of wet mapping function VMF1 [27].
Mean error of in VMF1 model (), following the Kouba, J. [56] study, was performed on 11 stations located worldwide and for one year of observations. The 4 mm value expresses the maximum standard deviation of gridded VMF1 with respect to site-specific VMF1 obtained within January–December 2005 period [56]. The mean errors of (), () and () are taken from the Bernese GNSS Software [34] estimated from PPP least-square solution. Mean errors of hydrostatic and wet VMF1 mapping functions follow from Böhm et al. [27], and were evaluated as the maximum possible uncertainties in mapping function coefficients at the 5 degree elevation angle following the assumed 10 hPa uncertainty in ECMWF used in VMF1. Mean errors of the gradient mapping function [26] were calculated following the same procedure [27] as the difference between the gradient mapping function at given satellite elevation angle and the same mapping function including the mean error of parameter C equals [26]. The STD mean error estimates are then used to calculate the mean errors of STD differences (GNSS minus ray-traced) mapped to zenith direction (). The ZTD gradient estimates () and errors () as well as their mapping function coefficients () are neglected for slant delay estimation without gradients. Study [17] shows that there is no significant discrepancy between slants estimated with different software and strategies, moreover the processing strategy adopted in this manuscript is found to provide one of the best estimates among tested ones.
The combined ZTD uncertainties including both GNSS errors and uncertainty of WRF refractivity field relative to radiosoundings are presented in Figure 10. To account for the time resolution difference between radiosonde (12 h) and WRF (1 h), ZTD errors from ray-tracing are assumed to be constant within ±6 h with respect to the radiosonde launch time, thus yielding hourly resolution of uncertainties. The mean uncertainty averaged over full time-series at GNSS station WROC equals 5.2 mm. The dZTD observations exceeding the mean error are removed from the observations to ensure accurate tropospheric estimates. These are marked with gray circles in Figure 10. Number of observations remaining after filtering is reduced from 1430 to 832. Epochs with lower accuracy of dZTD identified at station WROC were removed from the data for all other stations.

Figure 10.
(a) ZTD differences between GNSS and ray-tracing. (b) Total combined uncertainties of ZTDs based on uncertainty of WRF refractivity field and GNSS formal errors. Black circles show observations within uncertainty threshold, whereas epochs that correspond to gray dots have been removed from the analysis.
9. Applications in Weather Monitoring
As stated in Kačmařík et al. [17] and Solheim et al. [18] the presence of hydrometeors should be visible in estimated GNSS tropospheric delays. In our initial study, we use ray-tracing to attribute the induced delay to the gaseous part of the troposphere by Equation (2). Hence, the GNSS observations should differ from WRF delays by the neglected hydrometeors contribution assuming properly modeled atmospheric conditions. Part of the impact is expected to be introduced by small uncertainties originating from NWP model. However, this effect is kept to minimum by quality verification procedure using the error propagation and filtering of analyzed time-series. The theoretical impact of liquid water and rain rate on zenith delays is illustrated and described in Appendix B.
The analysis of hydrometeors impact on GNSS signal propagation in terms of dependency of ZTD residuals on CT product is presented in Figure 11. GNSS STDs estimated under specific cloudy conditions were selected from observations in 6-hourly temporal resolution, as provided by CT data. Corresponding ray-traced delays modeled in a cloud-free atmosphere were subtracted from GNSS observations to estimate potential cloud contributions. The differences calculated at 13 GNSS stations were mapped to the zenith to make troposphere delays independent on the elevation angle. Cloud type estimates from 15 pixels around each GNSS stations are subtracted from the MPE product and median value is calculated for each observation epoch (6 hours in case of CT). Mean dZTDs for each cloud class for all stations and epochs are calculated and displayed in Figure 11. The CT ranges follow from Table 1.
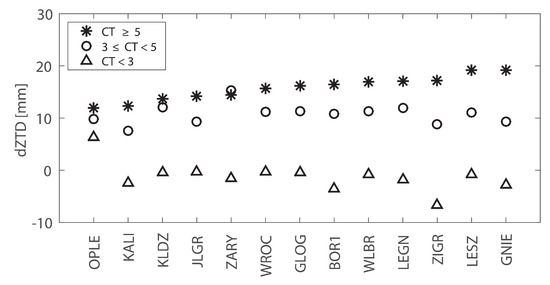
Figure 11.
dZTD averaged in 56 days at 13 GNSS stations with respect to CT product. Stars represent highest concentration of cloud water (CT ≥ 5), circles show moderate cloud impact (3 ≤ CT < 5) whereas triangles refer to low cloud content (CT < 3).
Results show that, on average for epochs with high content of clouds expressed by CT above 5, dZTD is consistently biased from 10 mm at station KALI up to 20 mm at station GNIE. Moreover, for the moderate cloud content, the magnitude of dZTD bias is lower, but still clearly pronounced. The variability from 6 to 12 mm is observed on the example of stations ZIGR and ZARY, respectively. Atmospheric conditions described by low CT values introduce either no bias or slight negative bias of −5 mm, with an exception of station OPLE where positive bias of 4 mm applies. For stations ZIGR, JLGR, BOR1, GLOG, LESZ, LEGN, GNIE, there is a clear, around 10 mm separation between cloud classes. The respective separation for stations KALI, OPLE, KLDZ, ZARY, WRIC, WLBR is lower by 3 mm, especially between class with high or moderate cloud content. It has to be noted however that for each CT class the spread of dZTDs measured as a standard deviation varies between 16 mm for CT below 3 to 20 mm for CT above 5.
Similar analysis is performed for rain rate intensity and its effect on GNSS tropospheric estimates. The dependency of ZTD differences on MPE product results is summarized in Figure 12. ZTD differences are grouped into three classes for respective MPE: (1) affected by rain intensity under 0.01 mm/h; (2) light rain between 0.01 mm/h and 2.5 mm/h; (3) significant precipitation over 2.5 mm/h. Similar pattern, as for CT product, could be observed. The localized rain events are however less frequent than analyzed cloudy conditions. The number of observations within each class varies and cases of minor precipitation under 0.01 mm/h are the most frequent, resulting in over 700 observations. Light rain affected 50 observations, whereas for the significant rain only up to 15 cases at each station were found. Hence, respective data samples are not equally representative.
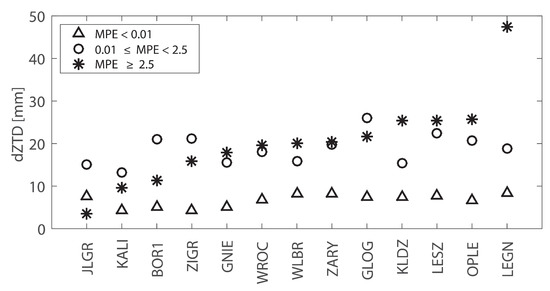
Figure 12.
dZTD averaged in 56 days at 13 GNSS stations with respect to MPE parameter. Stars correspond to high precipitation events (MPE ≥ 2.5 mm/h), circles show moderate rain intensity (0.01 ≤ MPE < 2.5 mm/h) and triangles refer to negligible precipitation (MPE < 0.01 mm/h).
Recent study on the MPE quality [57] based on ground-based rain gauges shows that for light rain with intensity below 5 mm/day the MPE retrieval might not agree well with the rain gauge data (0% events detected). Better performance is provided for the medium rain rates (5–20 mm/day) with only 31% events undetected. High detection rate applies to extreme events with precipitation above 20 mm/day with only 10% undetected. Therefore, the emphasis is put on analysis of tropospheric delays in cases of heavy precipitation. The results presented in Figure 12 prove that tropospheric delays affected by low precipitation events introduce significantly smaller bias than rainfalls of medium or high intensity. Station JLGR is the only example that does not follow this rule. The dZTD bias for low rain class varies between 4 mm and 8 mm and is always positive. 7 out of 13 stations investigated have greater dZTD bias for intensive rain events, where precipitation varies from 2.6 mm/h to 22.9 mm/h, than for medium rain from 0.1 mm/h to 2.5 mm/h. According to Figure 12, the separation between rain and no-rain events expressed as a mean ZTD difference is between 12 and 18 mm. It has to be however noted that for each MPE class the spread of dZTDs measured as a standard deviation is between 20 mm for no rain class to 16 mm for highest rain intensity.
The analysis of hydrometeors impact on discrepancies in tropospheric delays from GNSS and ray-tracing is summarized in Table 4 by correlation coefficients with respect to CT and MPE products. The correlation between CT and ZTD differences is always positive and reaches up to 0.43 at station JLGR. This suggests that the cloud coverage could affect GNSS observations. The average correlation for CT is at the order of 0.38. Therefore, larger CT parameter introduces increments in ZTD discrepancies between GNSS and ray-tracing. The correlation coefficients for MPE product indicate similar relationship of ZTD differences as for CT product. The increase of MPE at 8 out of 13 stations (OPLE, KALI, WROC, GNIE, KLDZ, ZIGR, BOR1, LEGN) is related to the significant increase of correlation coefficients. If MPE > 0.01 mm/h is considered, the average correlation is 0.10. For MPE > 2.50 mm/h the increment in the correlation coefficient yields 0.28. However, negative correlation coefficients with respect to MPE can be also identified in Table 4. One of factors that might contribute to such incidences is a non-uniform representation of ZTD differences within MPE ranges for concerned stations. The coefficients can be also affected by sampling errors arising from uneven data series, though cannot entirely explain such large uncorrelation. Particularly, the lack of correlation coefficient for JLGR is due to the low number of observations with MPE > 2.50 in the vicinity of the station.

Table 4.
Correlation coefficients between ZTD differences and CT and MPE products at 13 GNSS stations.
The applied approach within this study disables a direct separation of hydrometeors on the rain-induced (MPE product) and cloud cover (CT product) contributions to GNSS tropospheric delays. However, the impact of typically negligible terms of atmospheric refraction is observed in the statistical sense. The larger contributions to the delays are expected due to a significant cloud cover rather than those induced by precipitation events. This suggests that severe weather events could be considered in the analysis of GNSS data time-series as a source of larger tropospheric delays. The ability to isolate the impact of weather events demonstrated by the analysis of GNSS and ray-traced data can be further studied based on GNSS observations co-located with water vapor radiometers, radars and in-situ rain gauges to support presented results.
10. Discussion
The number of research papers that deal with the impact of intense weather events on GNSS tropospheric delays is still low. One of the first attempts to assess effects of hydrometeors on GNSS signal was a paper of Solheim et al. [18]. The authors estimated delays due to permittivity of ice and water droplets sustained in clouds to 8 mm/km, which contributes with 40 mm to the delay if we assume 5 km constant liquid and ice concentration in the zenith direction. The propagation delay due to scattering induced by rain can reach 6 mm, assuming the signal travels through 3 km in the presence of rain with 20 mm/h rate. Such semi-empirical estimates agrees with the results of our study showing biases up to 45 mm (Figure 10). Moreover, stations with large amount of water and ice in the clouds (above class 5) or rain detected by MPE algorithm show consistent mean positive bias through the whole Benchmark campaign period with average biases of up to 25 mm as indicated in Figure 11 and Figure 12. This bias, however only slightly exceeds the standard deviation of collected dZTD, which varies between 16 mm and 20 mm, and hence more data in each class are required in further studies. Also comparing the RH in Figure 2 and rain intensity in Figure 4 between day 135 and 166, one can see that more rain (quite well captured by the model), leads to increased negative bias of RH, which means that the model underestimates the water vapour. It may result in increased difference between GNSS and the model. The initial physics-based retrieval of liquid and rain rate induced delay illustrated in Figure A2 suggests that hydrometeors do not introduce delay exceeding 5 mm. However, these calculations are based on forecast variables and MPE rain rates that depend on the performance of individual background data, which might require further verification.
De Haan et al. [20] presented azimuthal anisotropy of the atmosphere from GNSS and NWP data during a cold front passage. The SWD gradient varied by 40 mm and helped to indicate boundary of investigated event. The variability is also demonstrated in the following study as there are differences between stations in mountain valleys (JLGR) and low-lands (WROC). Brenot et al. [21] tested sensitivity of GNSS observations collected during weather event that brought an intense precipitation. GNSS ZTDs were compared with corresponding delays from NWP model that attained sporadic hydrometeor contributions up to 70 mm. Kačmařík et al. [17] and Douša et al. [19] estimated maximum hydrometeor contribution of 17 mm in zenith direction during extreme weather events, whereas observations in this paper showed mean ZTD discrepancies at the order of 10 to 30 mm.
Currently, there are no tools available in widely used Bernese GNSS Software [34] to improve the GNSS tropospheric delay estimation under unusual weather conditions. Thus, no sophisticated processing strategies are applied for GNSS products retrieval under intense weather events [19] which are mostly limited to data constraining. In most geodetic applications, the atmosphere is assumed to be calm [28,58]. Due to the magnitude of the liquid and ice water that is relatively small, their impact is also considered to be negligible when applying ray-tracing methods [13,14,27]. The mismodeling effect of conventional gradient model [26] in GNSS processing has been already indicated by [25] and proves that major change in the functional model for troposphere estimation is required. The estimation procedure could be also improved by adding satellite-grade clock to the receiver to remove one estimation parameter. Another approach is to observe the same satellite with at least three collocated receivers (three degrees of freedom more). Certainly, the application of new method for gradients, as reported by [25], is a step forward.
Further verification of impact of hydrometeors in a case-by-case study requires high quality NWP data an input for ray-tracer. Data from instruments that can directly derive the liquid and ice water content along line-of-sight between a satellite and a receiver are essential source for the purpose of validations. Microwave radiometers and other devices to measure cloud base height e.g., ceilometer should be considered. An effort should be made towards inter-comparisons of GNSS and ray-traced slant delays with included hydrometeors, which would influence the current level of inconsistency and help to improve predictions of rain- and cloud-related variables in NWP models. The residual time-series should be carefully analyzed in order to distinguish between the noise and potential systematic effects associated with atmospheric conditions. The application of multi-GNSS data [59] is likely to lower uncertainty of final solution, hence providing better estimates of tropospheric delays. Since the higher the intensity of weather events, the higher contributions of the liquid and ice water on GNSS signal is expected. Thus, it is recommended to use examples of tropical cyclones and mesoscale convective systems for case studies.
11. Conclusions
GNSS observations are commonly recognized by all-weather capability, thus allowing to continuously monitor weather conditions. The troposphere-induced delays are highly dependent on atmospheric conditions and their magnitudes can be used to express intensity of weather phenomena. The presented study focuses on higher order terms of tropospheric refractivity and their contribution to GNSS estimates. Based on the observations collected during intense rainfalls and cloudy conditions, the effect of associated liquid and solid water terms is expected to affect tropospheric delays. The assessment of such dependency is performed based on retrievals of STD from GNSS observations and ray-tracing technique. The ray-traced delays contain contribution of NWP-based gaseous constituents. The GNSS signal propagates through the real atmosphere and contains contribution from all atmosphere constituents. The difference was assumed to give the rain and cloud impact. To avoid and account for NWP-induced errors, the uncertainty analysis was performed for NWP refractivity field with respect to radiosonde observations and for GNSS slant delay estimation process. Epochs with combined uncertainty of ZTD larger than the mean error of 5.2 mm were removed from further investigations to ensure robust interpretation of the results.
By comparing GNSS and ray-traced tropospheric delays, we were able to estimate the tropospheric delay precision. In the zenith direction, delays agree to within −2.5 mm in terms of bias and 14 mm in terms of standard deviation. Various processing strategies of GNSS observations were applied in order to account for signatures induced by clouds and rainfalls. Results, however, presented only negligible differences in terms of bias and standard deviation for analyzed processing scenarios when compared to ray-traced delays. Treatment of post-fit residuals and application of horizontal gradients from GNSS solution is showed to play a minor role in the estimation procedure. This suggests that ZTD estimation algorithms, with one correction for all satellites, only two gradients and residuals, are not fully representing slant delays.
In the analysis of hydrometeors impact on tropospheric delays, over 131,000 slant delays were considered at 13 stations. The data sample was composed of GNSS observations in cloudy and rain conditions expressed by CT and MPE remote sensing products, respectively. Positive ZTD residuals were indicated for observations that propagated through thick clouds and intense rain. The introduced systematic effect varies between 10 to 30 mm, whereas standard deviation for obtained values varies between 16 and 20 mm. The differences are correlated with intensities of phenomena since more significant clouds and precipitation rates lead to increments in correlation coefficients. ZTD discrepancies are lower for CT parameter than for MPE product. However, separation of GNSS observations characterized by different magnitude of precipitation is less pronounced for precipitation rates. This might be due to more localized rainfall events relative to cloud, which tend to form more extensive fractions.
The initial model-based liquid water and MPE rain rates retrieval shows maximum impact of hydrometeors to be on the level of 5 mm. However, to further advance this research, ray-tracing algorithms should be augmented with liquid water contributions associated with severe weather events to independently assess their magnitude. NWP models need to be carefully validated against radar, radiometer or satellite observations in order to establish comparable data-set, distinguish the effect of hydrometeors and to investigate the impact of estimation procedure on the inhomogeneity studies. The emphasis should be placed on better recognition of azimuthal anisotropy so that weather events could be robustly localized based on differences in tropospheric delays.
Author Contributions
P.H., W.R. and J.K. conceived and designed the experiments. P.H. developed the ray-path model and computed ray-traced delays with uncertainties, performed cross-validation with GNSS data, processed and analyzed radiosonde data. J.K. conceived and performed the calculation of STD from GNSS data, their error estimates and multipath effect for STD reduction with the contribution of own analysis tools. W.R. processed MPE and CT products and conducted the analysis with tropospheric delays. M.K. performed WRF products verification, he also routinely provides WRF forecasts.
Funding
This work has been supported by National Science Centre, Poland Project No. 2013/11/D/ST10/03473.
Acknowledgments
The study has been carried out under COST Action ES1206 GNSS4SWEC (gnss4swec.knmi.nl). Comments by anonymous reviewers on earlier versions improved this paper considerably. We would like to thank Wroclaw Municipal Water and Sewage Company for providing rain gauges data. Department of Climatology and Atmosphere Protection is acknowledged for WRF forecasts and rain rate measurements. We also thank EUMETSAT and NWCSAF for remote sensing data and the Wroclaw Center of Networking and Supercomputing (www.wcss.wroc.pl): computational grant using MATLAB Software License No: 101979.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CODE | Center for Orbit Determination in Europe |
| COST | European Cooperation in Science and Technology (organization) |
| CT | Cloud Type |
| DCB | Differential Code Biases |
| DOY | Day Of Year |
| GNSS | Global Navigation Satellite System |
| GNSS4SWEC | Advanced Global Navigation Satellite Systems tropospheric products for monitoring severe weather events and climate |
| EGM | Earth Gravitational Model |
| EIG EUMETNET | European Meteorological Services Network |
| ERP | Earth Rotation Parameters |
| EUMETSAT | European Organization for the Exploitation of Meteorological Satellites |
| ESRL | Earth System Research Laboratory |
| E-GVAP | The EUMETNET EIG GNSS Water Vapour Programme |
| ESSEM | Earth System Science and Environmental Management |
| FES | Finite Element Solution |
| HIRLAM | High Resolution Limited Area Model |
| IWV | Integrated Water Vapor |
| MPE | Multisensor Precipitation Estimate |
| NOAA | National Oceanic and Atmospheric Administration |
| NWP | Numerical Weather Prediction |
| PPP | Precise Point Positioning |
| SAFNWC | Satellite Application Facility on Support to Nowcasting |
| STD | Slant Total Delay (of GNSS signal towards satellite, in neutral atmosphere) |
| UTC | Coordinated Universal Time |
| VMF | Vienna Mapping Functions |
| WGS | World Geodetic System |
| WMO | World Meteorologic Organization |
| WRF | Weather Research and Forecasting (model) |
| ZAMG | Zentralanstalt für Meteorologie und Geodynamik |
| ZHD | Zenith Hydrostatic Delay (of GNSS signal in neutral atmosphere) |
| ZTD | Zenith Total Delay (of GNSS signal in neutral atmosphere) |
| ZWD | Zenith Wet Delay (of GNSS signal in neutral atmosphere) |
Appendix A. Computation of Tropospheric Delays from the Ray-Path Model
The ray-tracer determines position according to Snell’s law based on two main geometric variables: the geocentric angle and the global elevation angle . The geocentric angle is easily found by the spherical trigonometry whereas can be calculated according to the Equation [13]
where is the refractional radius for the ray which tangent radius is at given refractive index . The refractive index needs to be updated for each step following height-dependent increments [60] with the vertical spacing: 10 m, 20 m, 50 m, 100 m, 500 m respectively for geometric altitudes between 0–2 km, 2–6 km, 6–16 km, 16–36 km and above 36 km in the NWP model domain. The radius of the Earth’s curvature at the reference ellipsoid is derived from the Euler formula
where A is the ray-path azimuth between a receiver and a satellite, and are radii of curvature along a meridian and a prime vertical, respectively. For the series of radii computed accordingly to predefined vertical spacing, we can calculate a chord length s to subsequent points using global elevation angle
The associated ray coordinates are determined iteratively together with the refractive index. The total electromagnetic delay in a direction to a satellite () is a sum of partial delays between two consecutive ray points, which is evaluated as
where the total refractive index can be separated into hydrostatic and non-hydrostatic parts to compute respective delays individually. The geometric bending effect , which constitutes a part of the delay, is calculated accordingly
where describes an outgoing elevation angle at the model’s uppermost level. The piece length can be replaced by the corresponding vertical distance to calculate the ZTD
In case of zenith delays, the term related to signal bending equals zero, thus vanishing from the equation. The associated mapping functions used to project slant delays to the zenith direction for given elevation angle are calculated as follows, including the geometric bending contribution to the hydrostatic part:
The initial global elevation angle needs to be corrected in order to calculate the observed angle. This correction is required due to the atmospheric density in the vicinity of the ground station causing a signal bending. In the exact solution, the ray-tracing should be performed iteratively until the outgoing elevation angle at the uppermost model level agrees with the vacuum one. Since it is inefficient in terms of computational speed and the actual number of iterations cannot be known in advance, we apply approximate approach for the initial elevation angle [61] based on the refractive index at the ground station altitude
where is the vacuum elevation angle and is presented in Figure A1. We repeatedly compute slant delays using a half-difference between the vacuum and the outgoing elevation angle as a correction step until they mutually agree. Usually, the angles converge after four iterations for observations at 3-degree elevation angle.
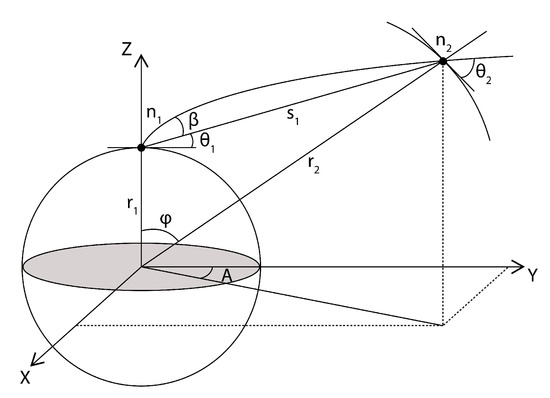
Figure A1.
Illustration of ray-path model. The geometric variables are: geocentric angle , ray-path azimuth A, global elevation angle , initial bending , radius r and geometric distance S between two consecutive ray points. Refractive index along ray-path is described by n. For details see Appendix A.
Before the geometric components of ray-tracing are calculated, both geodetic and meteorological variables need to be expressed in a homogeneous coordinate system. The height system needs to be coherent, hence geopotential meters are derived simply by dividing geopotential (m/s) by World Meteorological Organization (WMO) standard gravity m/s prior to transformation to the ellipsoidal height. The geopotential height Z is converted to the geometric altitude h by the following formula
where is effective Earth radius for the ellipsoid defined as
where a is semi-major axis of WGS84 ellipsoid, e is the ellipsoid eccentricity and is a gravity ratio. The acceleration due to gravity g for given node’s latitude is calculated on the reference ellipsoid according to Somigliana [62]
where is equatorial gravity in m/s. While geopotential strictly refers to the geoid and the geometric altitude is calculated relative to the ellipsoid, it is required to include the geoid undulation after conversion using e.g., Earth Gravitational Model 1996 (EGM96) [63].
Appendix B. Modeling of Cloud and Rain Effect on Tropospheric Delays
The refractivity considered to be a function of non-dispersive atmospheric properties is defined as a real and positive part and consists of the following terms:
where and are respectively dry and water vapor terms of gaseous characteristics combined in Equation (2), refers to suspended liquid water droplets and is rain approximation.
The contribution of water droplets to the refractivity is modeled from WRF model variables. The water content introduced by clouds is considered to be of liquid phase. No solid fractions (or to a insignificant extent) were found in mixed-phase ( T ) and ice-phase ( T) clouds. The Rayleigh approximation of Mie scattering theory is applied to formulate the non-dispersive liquid water refractivity based on Debye model [64]
where is liquid water content in grams per cubic meter, g/cm is density of liquid water, is static permittivity of liquid water with reciprocal temperature variable in Kelvin. The liquid water content equals
where is liquid water mixing ratio.
The total amount of atmospheric water in single column in units of kg/m is expressed in terms of liquid water path (LWP). The integrand to derive LWP is defined as a function of liquid water mixing ratio and total density of air at mean geometric heights between consecutive model levels with vertical distance
To express scattering of rain in terms of zenith delays, the non-dispersive refractivity term is derived from point rainfall rate R in mm/h, viz
where in GHz. The applied approximation for the rain effect is a generalization of Mie scattering theory and does not require drop shape or size distributions [64,65]. MPE rain rates serve as an input parameter for modeling of rain effect. The radio signals are assumed to propagate through 3 km of given rain rate following [18] to yield respective path delays.
The theoretical impact of cloud liquid water and rain rate on zenith delays is demonstrated for the station WROC in Figure A2. The contributions are expressed in terms of Zenith Hydrometeor Delay (). Cloud fractions accumulated in LWP variable are shown to be in proportionality to the induced path delays and the overall impact does not exceed 1.5 mm. The magnitude of the effect suggests that the vertical extent of clouds is small and the structures are typically single-layered. Several significant overcasts have been identified based on CT observations. However, the WRF model performance in terms of forecast skill for rainfalls is suspected to affect the representation of associated cloud fractions, which might be underestimated.
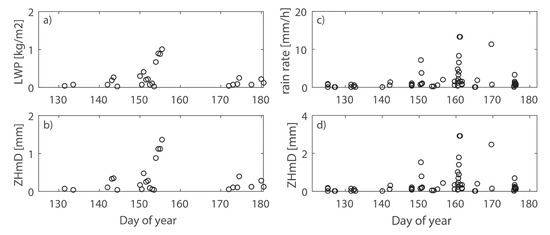
Figure A2.
Hydrometeors’ content induced by (a) liquid water expressed in terms of LWP and (c) MPE rain rate with their respective contributions to zenith delays (b,d).
The most significant rain episode is observed on 160 DOY, as indicated by MPE data in Figure A2c. This however goes against LWP values in Figure A2a as no cloud fractions can be identified in DOYs between 160 and 170. The exclusion of WRF dataset within specified period, as shown in Figure 10, thus confirms large uncertainties in background fields. The observed rain effect with intensity of 16 mm/h corresponds to 3.5 mm of additional path delay. Thus, the overall combined contribution of modeled hydrometeors to zenith delays does not exceed 5 mm. However, the majority of precipitation events is below 10 mm/h of rain rate. Given MPE precipitation rates adopted in the following study as median values, the contribution to tropospheric delays is expected to be underestimated and should be considered as an average. Moreover, the station-specific rain rates collected at the vicinity of WROC do not represent the upper-most intensity observed in the temporal framework of the study. An example of precipitation rate with a magnitude up to 35 mm/h is displayed in Figure 5 during a frontal case and rate rates reaching 60 mm/h have been also identified (not shown). Therefore, zenith delays due to rain presented in Figure A2 have a potential to vastly increase and exceed 10 mm. Application of ray-tracint to investigate the potential effect due to neglected refractivity terms, which include liquid and ice water contents as well as rain rates from ground-based observations, in addition to the gaseous part is recommended for further studies.
Appendix C. List of GNSS and Radiosonde Stations

Table A1.
Coordinates of GNSS and radiosonde stations used in the analysis. The altitude corresponds to the geometric height above the geoid.
Table A1.
Coordinates of GNSS and radiosonde stations used in the analysis. The altitude corresponds to the geometric height above the geoid.
| ID | Latitude [deg] | Longitude [deg] | Altitude [m] | |
|---|---|---|---|---|
| GNSS Stations | ||||
| BOR1 | 52.2769547 | 17.0734520 | 88.855 | |
| GLOG | 51.6652565 | 16.0742817 | 104.529 | |
| GNIE | 52.5329437 | 17.5838547 | 138.839 | |
| JLGR | 50.9194603 | 15.7332487 | 365.712 | |
| KALI | 51.7538757 | 18.0951633 | 111.766 | |
| KLDZ | 50.4355774 | 16.6518860 | 316.457 | |
| LEGN | 51.2000084 | 16.1549683 | 140.163 | |
| LESZ | 51.8403893 | 16.5784855 | 111.106 | |
| OPLE | 50.6676140 | 17.9193401 | 185.575 | |
| WLBR | 50.7679672 | 16.2800694 | 467.014 | |
| WROC | 51.1132584 | 17.0620365 | 140.565 | |
| ZARY | 51.6399193 | 15.1461058 | 163.124 | |
| ZIGR | 51.9403114 | 15.5142927 | 186.068 | |
| Radiosonde Stations | ||||
| 12120 | 54.75 | 17.53 | 6.0 | |
| 12374 | 52.40 | 20.97 | 96.0 | |
| 12425 | 51.13 | 16.98 | 116.0 | |
References
- Brewster, K.; Thomas, K.W.; Gao, J.; Brotzge, J.; Xue, M.; Wang, Y. A nowcasting system using full physics numerical weather prediction initialized with CASA and NEXRAD radar data. In Proceedings of the 25th Conference on Severe Local Storms, Denver, CO, USA, 11–14 October 2010. [Google Scholar]
- Stanešić, A.; Brewster, K.A. Impact of Radar Data Assimilation on the Numerical Simulation of a Severe Storm in Croatia. Meteorol. Z. 2016, 25, 37–53. [Google Scholar] [CrossRef]
- Novak, P. The Czech Hydrometeorological Institute’s severe storm nowcasting system. Atmos. Res. 2007, 83, 450–457. [Google Scholar] [CrossRef]
- Ruzanski, E.; Chandrasekar, V.; Wang, Y. The CASA nowcasting system. J. Atmos. Ocean. Technol. 2011, 28, 640–655. [Google Scholar] [CrossRef]
- Meischner, P. Weather Radar: Principles and Advanced Applications; Springer: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-662-05202-0. [Google Scholar]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Davis, J.; Herring, T.; Shapiro, I.; Rogers, A.; Elgered, G. Geodesy by radio interferometry: Effects of atmosphere modeling errors on estimates of baseline lenghts. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Bennitt, G.V.; Jupp, A. Operational assimilation of GPS zenith total delay observations into the Met Office numerical weather prediction models. Mon. Weather Rev. 2012, 140, 2706–2719. [Google Scholar] [CrossRef]
- Karabatić, A.; Weber, R.; Haiden, T. Near real-time estimation of tropospheric water vapour content from ground based GNSS data and its potential contribution to weather now-casting in Austria. Adv. Space Res. 2011, 47, 1691–1703. [Google Scholar] [CrossRef]
- Vedel, H.; Huang, X.-Y. Impact of ground based GPS data on numerical weather prediction. J. Meteorol. Soc. Jpn. Ser. II 2004, 82, 459–472. [Google Scholar] [CrossRef]
- Bender, M.; Dick, G.; Ge, M.; Deng, Z.; Wickert, J.; Kahle, H.-G.; Raabe, A.; Tetzlaff, G. Development of a GNSS water vapour tomography system using algebraic reconstruction techniques. Adv. Space Res. 2011, 47, 1704–1720. [Google Scholar] [CrossRef]
- Järvinen, H.; Eresmaa, R.; Vedel, H.; Salonen, K.; Niemelä, S.; de Vries, J. A variational data assimilation system for ground-based GPS slant delays. Q. J. R. Meteorol. Soc. 2007, 133, 969–980. [Google Scholar] [CrossRef]
- Hobiger, T.; Ichikawa, R.; Koyama, Y.; Kondo, T. Fast and accurate ray-tracing algorithms for real-time space geodetic applications using numerical weather models. J. Geophys. Res. Atmos. 2008, 113, 1–14. [Google Scholar] [CrossRef]
- Zus, F.; Bender, M.; Deng, Z.; Dick, G.; Heise, S.; Shang-Guan, M.; Wickert, J. A methodology to compute GPS slant total delays in a numerical weather model. Radio Sci. 2012, 47, 1–15. [Google Scholar] [CrossRef]
- Bosy, J.; Kaplon, J.; Rohm, W.; Sierny, J.; Hadas, T. Near real-time estimation of water vapour in the troposphere using ground GNSS and the meteorological data. Ann. Geophys. 2012, 30, 1379–1391. [Google Scholar] [CrossRef]
- Eresmaa, R.; Järvinen, H. An observation operator for ground-based GPS slant delays. Tellus A Dyn. Meteorol. Oceanogr. 2006, 58, 131–140. [Google Scholar] [CrossRef]
- Kačmařík, M.; Douša, J.; Dick, G.; Zus, F.; Brenot, H.; Möller, G.; Pottiaux, E.; Kapłon, J.; Hordyniec, P.; Václavovic, P.; et al. Inter-technique validation of tropospheric slant total delays. Atmos. Meas. Tech. 2017, 10, 2183–2208. [Google Scholar] [CrossRef]
- Solheim, F.S.; Vivekanandan, J.; Ware, R.H.; Rocken, C. Propagation delays induced in GPS signals by dry air, water vapor, hydrometeors, and other particulates. J. Geophys. Res. 1999, 104, 9663–9670. [Google Scholar] [CrossRef]
- Douša, J.; Dick, G.; Kačmařík, M.; Brožková, R.; Zus, F.; Brenot, H.; Stoycheva, A.; Möller, G.; Kaplon, J. Benchmark campaign and case study episode in central Europe for development and assessment of advanced GNSS tropospheric models and products. Atmos. Meas. Tech. 2016, 9, 2989–3008. [Google Scholar] [CrossRef]
- De Haan, S.; Van Der Marel, H.; Barlag, S. Comparison of GPS slant delay measurements to a numerical model: case study of a cold front passage. Phys. Chem. Earth Parts A/B/C 2002, 27, 317–322. [Google Scholar] [CrossRef]
- Brenot, H.; Ducrocq, V.; Walpersdorf, A.; Champollion, C.; Caumont, O. GPS zenith delay sensitivity evaluated from high-resolution numerical weather prediction simulations of the 8–9 September 2002 flash flood overnsoutheastern France. J. Geophys. Res. Atmos. 2006, 111, 1–20. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction. Bull. Géodésique (1946–1975) 1973, 107, 13–34. [Google Scholar] [CrossRef]
- Brenot, H.; Neméghaire, J.; Delobbe, L.; Clerbaux, N.; De Meutter, P.; Deckmyn, A.; Delcloo, A.; Frappez, L.; Van Roozendael, M. Preliminary signs of the initiation of deep convection by GNSS. Atmos. Chem. Phys. 2013, 13, 5425. [Google Scholar] [CrossRef]
- Shoji, Y.; Yamauchi, H.; Mashiko, W.; Sato, E. Estimation of local-scale precipitable water vapor distribution around each GNSS station using slant path delay. SOLA 2014, 10, 29–33. [Google Scholar] [CrossRef]
- Masoumi, S.; McClusky, S.; Koulali, A.; Tregoning, P. A directional model of tropospheric horizontal gradients in Global Positioning System and its application for particular weather scenarios. J. Geophys. Res. Atmos. 2017, 122, 4401–4425. [Google Scholar] [CrossRef]
- Chen, G.; Herring, T.A. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophys. Res. 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Böhm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. Solid Earth 2006, 111, 1–9. [Google Scholar] [CrossRef]
- Wilgan, K.; Hadas, T.; Hordyniec, P.; Bosy, J. Real-time precise point positioning augmented with high-resolution numerical weather prediction model. GPS Solut. 2017, 21, 1341–1353. [Google Scholar] [CrossRef]
- Böhm, J.; Kouba, J.; Schuh, H. Forecast Vienna Mapping Functions 1 for real-time analysis of space geodetic observations. J. Geod. 2009, 83, 397–401. [Google Scholar] [CrossRef]
- Norman, R.; Le Marshall, J.; Rohm, W.; Carter, B.; Kirchengast, G.; Alexander, S.; Liu, C.; Zhang, K. Simulating the impact of refractive transverse gradients resulting from a severe troposphere weather event on GPS signal propagation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 418–424. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-211-73017-1. [Google Scholar]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Kryza, M.; Werner, M.; Wałszek, K.; Dore, A.J. Application and evaluation of the WRF model for high-resolution forecasting of rainfall—A case study of SW Poland. Meteorol. Z. 2013, 22, 595–601. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Bernese GNSS Software Version 5.2. User Manual; Astronomical Institute, Universtiy of Bern, Bern Open Publishing: Bern, Switzerland, 2015; ISBN 978-3-906813-05-9. [Google Scholar]
- Zumberge, J.; Heflin, M.; Jefferson, D.; Watkins, M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Dach, R.; Schaer, S.; Arnold, D.; Prange, L.; Sidorov, D.; Susnik, A.; Villiger, A.; Jaeggi, A. CODE Final Product Series for the IGS; Astronomical Institute, University of Bern: Bern, Switzerland, 2017. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Ray, R.D.; Ponte, R.M. Barometric tides from ECMWF operational analyses. Ann. Geophys. 2003, 21, 1897–1910. [Google Scholar] [CrossRef]
- Marini, J.W. Correction of satellite tracking data for an arbitrary tropospheric profile. Radio Sci. 1972, 7, 223–231. [Google Scholar] [CrossRef]
- Huisman, L.; van der Marel, H.; Teunissen, P. CORS local-site finger-printing using undifferenced least squares GNSS phase residuals. In Proceedings of the International Global Navigation Satellite Systems Society IGNSS Symposium 2009, Brisbane, Australia, 1–3 December 2009. [Google Scholar]
- Heinemann, T.; Latanzio, A.; Roveda, F. The Eumetsat multi-sensor precipitation estimate (MPE). In Proceedings of the Second International Precipitation Working group (IPWG) Meeting, Madrid, Spain, 23–27 September 2002. [Google Scholar]
- Levizzani, V.; Schmetz, J.; Lutz, H.; Kerkmann, J.; Alberoni, P.; Cervino, M.; Turk, F. Precipitation estimates using METEOSAT second generation (MSG): New perspectives from geostationary orbit. In Proceedings of the EUMETSAT Meteorological Satellite Data User’s Conference, Copenhagen, Denmark, 6–10 September 1999; pp. 121–128. [Google Scholar]
- Derrien, M.; Gléau, H. Product User Manual For “cloud Products” (cma-pge01 v3. 2, ct-pge02 v2. 2, ctth-pge03 v2. 2). 2014. Available online: http://www.nwcsaf.org/AemetWebContents/ScientificDocumentation/Documentation/MSG/SAF-NWC-CDOP2-MFL-SCI-PUM-01_v3.2.3.pdf (accessed on 30 November 2018).
- Gléau, H. Algorithm Theoretical Basis Document for the Cloud Product Processors of the NWC/GEO. 2016. Available online: http://www.nwcsaf.org/documents/20182/30662/NWC-CDOP2-GEO-MFL-SCI-ATBD-Cloud_v1.1.pdf/a5bb6eca-871b-4707-9c76-e0be09915d94 (accessed on 30 November 2018).
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR/TN-475+STR NCAR Technical NOTE; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, 1–8. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Jimenez, P.A.; Dudhia, J.; Gonzalez-Rouco, J.F.; Navarro, J.; Montavez, J.P.; Garcia-Bustamante, E. A revised scheme for the WRF surface layer formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Niu, G.-Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; Tewari, M.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the Evaluation and Comparison of Models. J. Geophys. Res. 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
- Roebber, P.J. Visualizing multiple measures of forecast quality. Weather Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef]
- Nafisi, V.; Urquhart, L.; Santos, M.C.; Nievinski, F.G.; Bohm, J.; Wijaya, D.D.; Schuh, H.; Ardalan, A.A.; Hobiger, T.; Ichikawa, R.; et al. Comparison of ray-tracing packages for troposphere delays. IEEE Trans. Geosci. Remote Sens. 2012, 50, 469–481. [Google Scholar] [CrossRef]
- Wilgan, K.; Hurter, F.; Geiger, A.; Rohm, W.; Bosy, J. Tropospheric refractivity and zenith path delays from least-squares collocation of meteorological and GNSS data. J. Geod. 2017, 91, 117–134. [Google Scholar] [CrossRef]
- Kouba, J. Implementation and testing of the gridded Vienna Mapping Function 1 (VMF1). J. Geod. 2008, 82, 193–205. [Google Scholar] [CrossRef]
- Dhib, S.; Mannaerts, C.M.; Bargaoui, Z.; Retsios, V.; Maathuis, B.H. Evaluating the MSG satellite Multi-Sensor Precipitation Estimate for extreme rainfall monitoring over northern Tunisia. Weather Clim. Extrem. 2017, 16, 14–22. [Google Scholar] [CrossRef]
- Hadas, T.; Bosy, J. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef]
- Kazmierski, K.; Hadas, T.; Sośnica, K. Weighting of multi-GNSS observations in real-time precise point positioning. Remote Sens. 2018, 10, 84. [Google Scholar] [CrossRef]
- Rocken, C.; Sokolovskiy, S.; Johnson, J.M.; Hunt, D. Improved mapping of tropospheric delays. J. Atmos. Ocean. Technol. 2001, 18, 1205–1213. [Google Scholar] [CrossRef]
- Davis, J.L.; Elgered, G.; Niell, A.E.; Kuehn, C.E. Ground-based measurement of gradients in the “wet” radio refractivity of air. Radio Sci. 1993, 28, 1003–1018. [Google Scholar] [CrossRef]
- Somigliana, C. Teoria generale del campo gravitazionale dell’ellissoide di rotazione. Mem. Soc. Astron. Ital. 1929, 4, 425. [Google Scholar]
- Lemoine, F.G.; Kenyon, S.C.; Factor, J.K.; Trimmer, R.G.; Pavlis, N.K.; Chinn, D.S.; Cox, C.M.; Klosko, S.M.; Luthcke, S.B.; Torrence, M.H.; et al. The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) Geopotential Model EGM96; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1998. [Google Scholar]
- Liebe, H.J. MPM-An atmospheric millimeter-wave propagation model. Int. J. Infrared Millim. Waves 1989, 10, 631–650. [Google Scholar] [CrossRef]
- Oguchi, T. Electromagnetic wave propagation and scattering in rain and other hydrometeors. Proc. IEEE 1983, 71, 1029–1078. [Google Scholar] [CrossRef]
Sample Availability: The data used are listed in the references and repository at URL: http://156.17.181.89:8080/share.cgi?ssid=0lPU69Q. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).