Assessing Hydrological Modelling Driven by Different Precipitation Datasets via the SMAP Soil Moisture Product and Gauged Streamflow Data
Abstract
:1. Introduction
2. Data
2.1. Study Area and Study Period
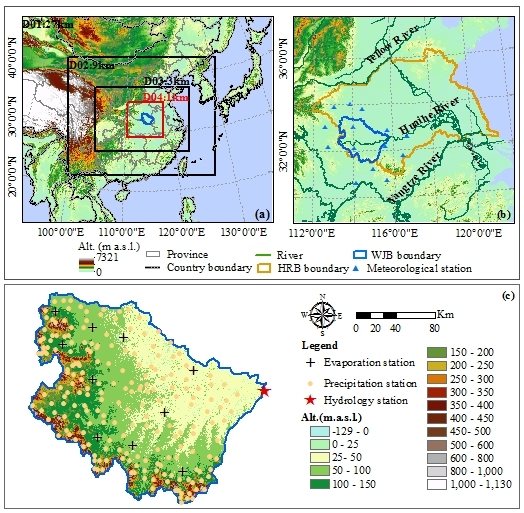
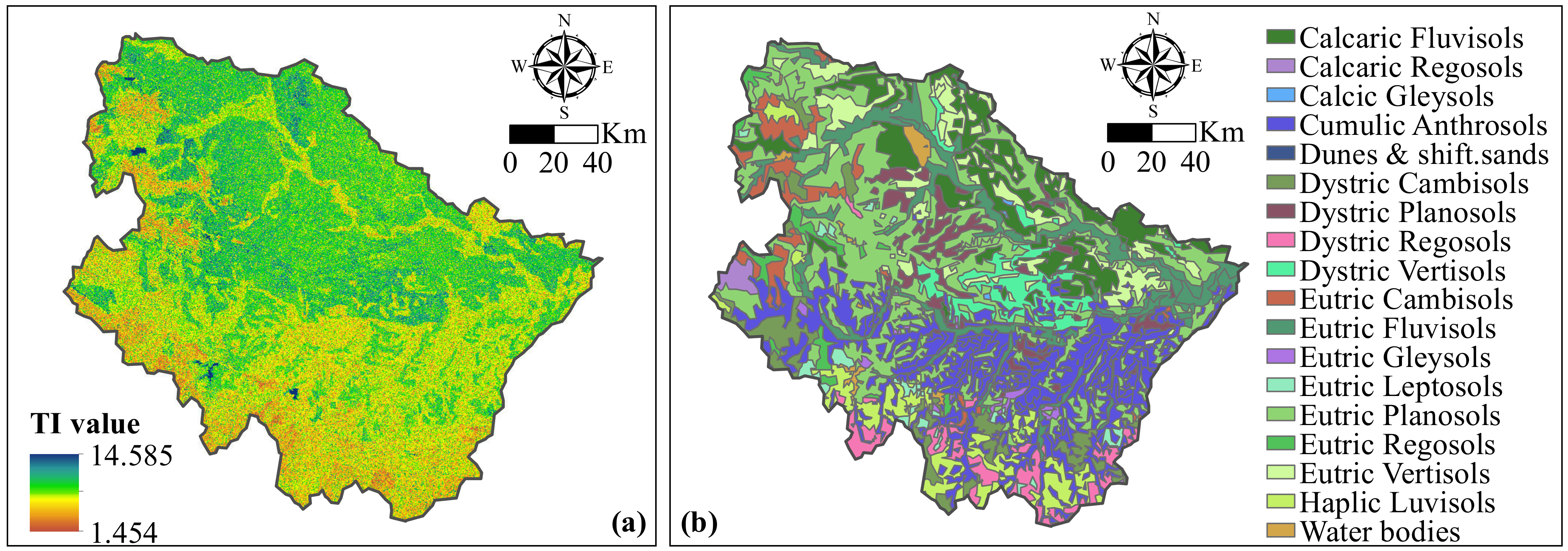
2.1.1. Study Area
2.1.2. Study Period
2.2. Study Data
2.2.1. In Situ Observed Precipitation
2.2.2. Remotely Sensed Precipitation
2.2.3. NWP-Predicted Precipitation
2.2.4. Soil Moisture and Outlet Discharge
3. Methods
3.1. Hydrological Model
3.2. Experimental Design
3.3. Evaluation of Precipitation, Soil Moisture and Outlet Discharge
4. Results
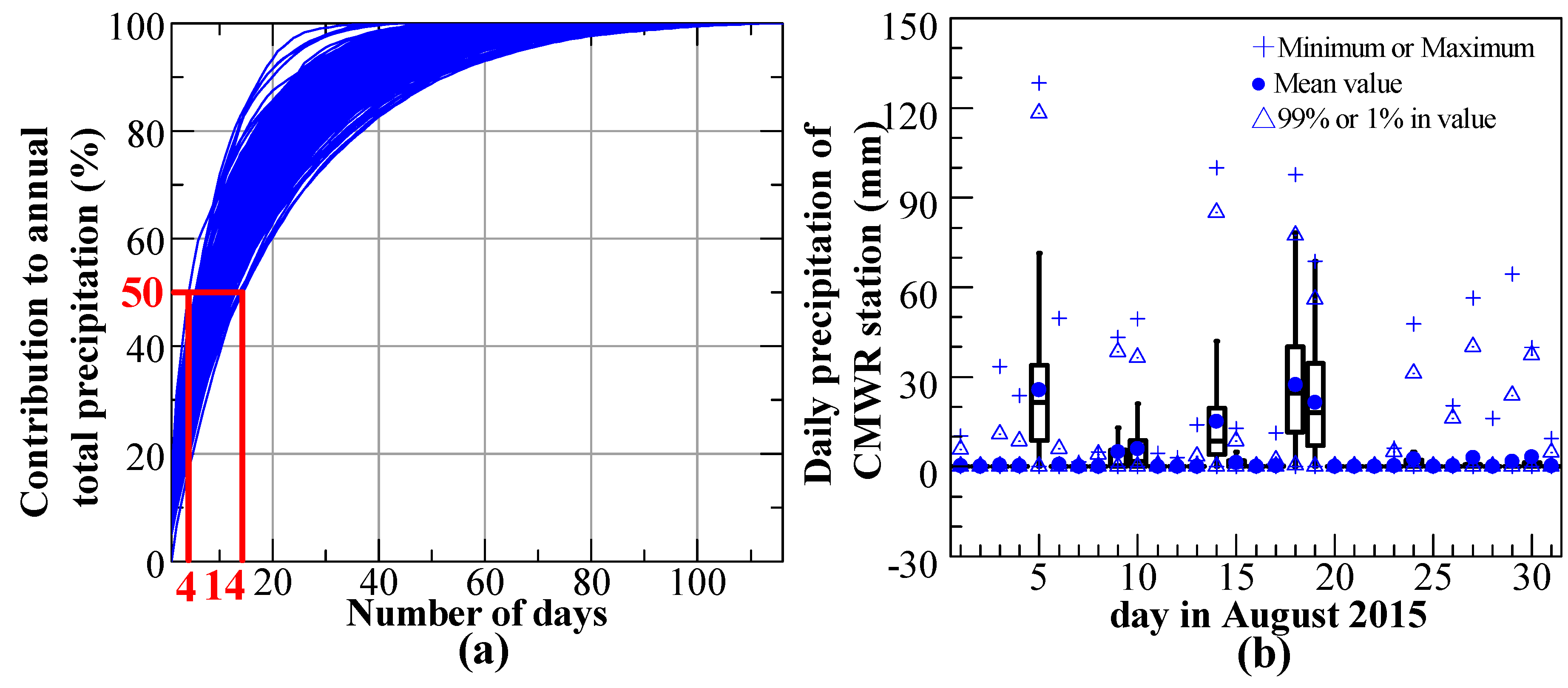
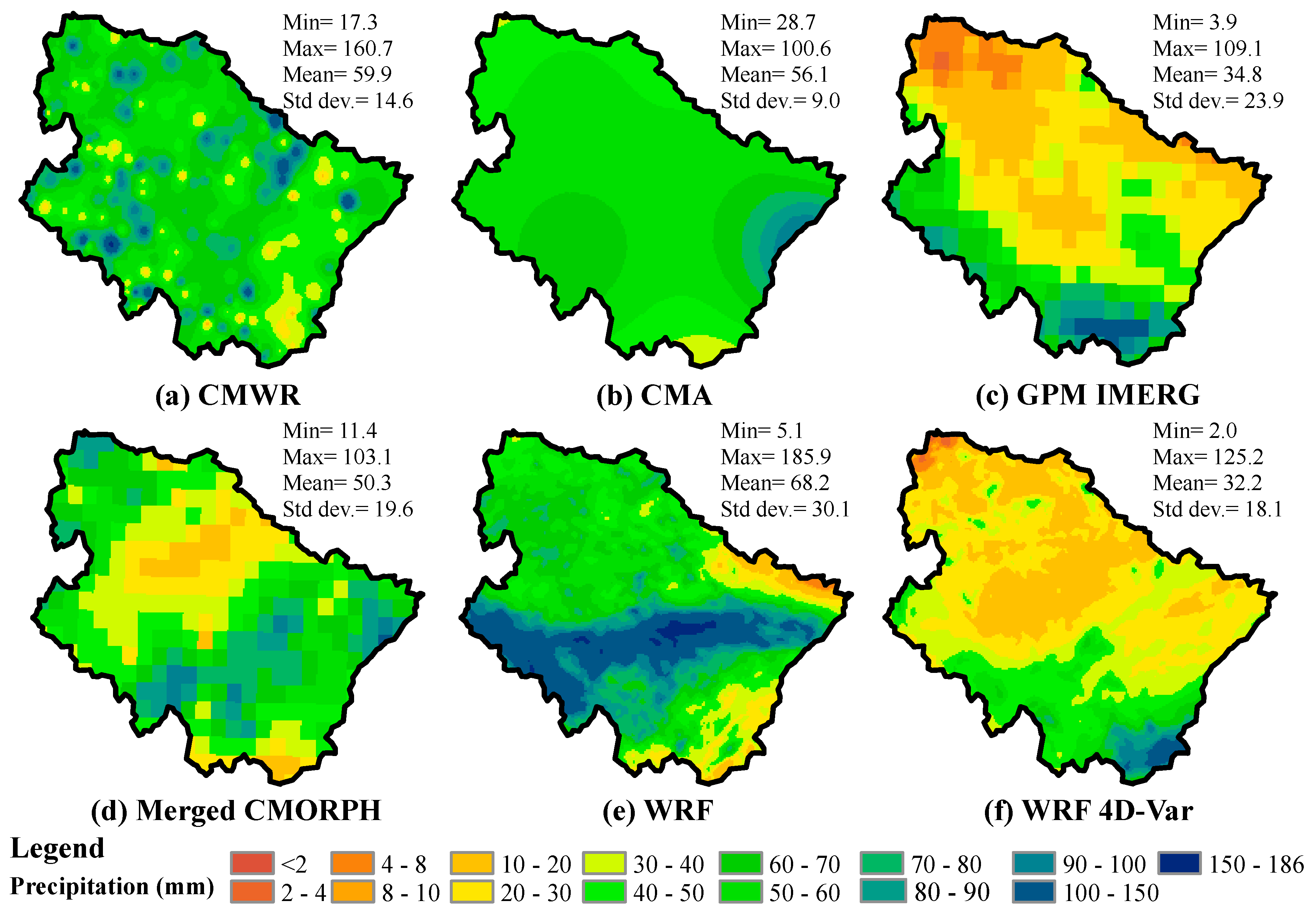
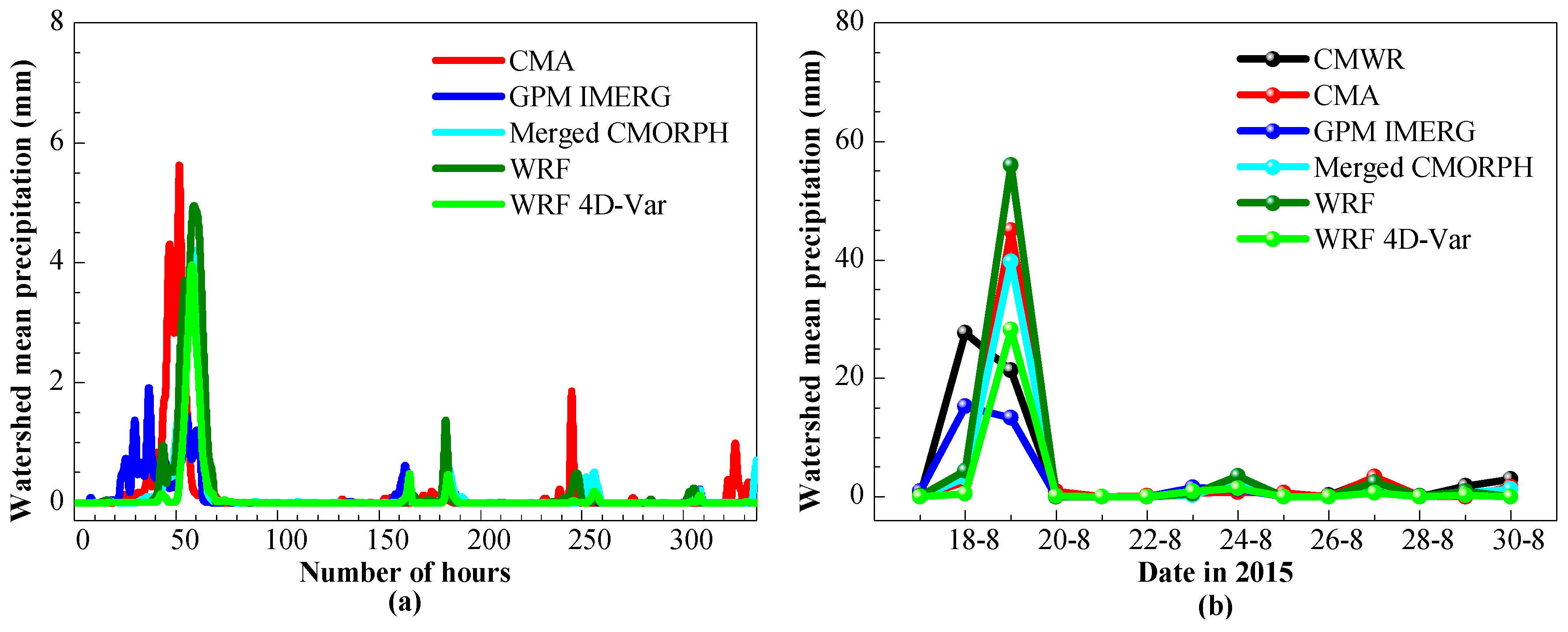
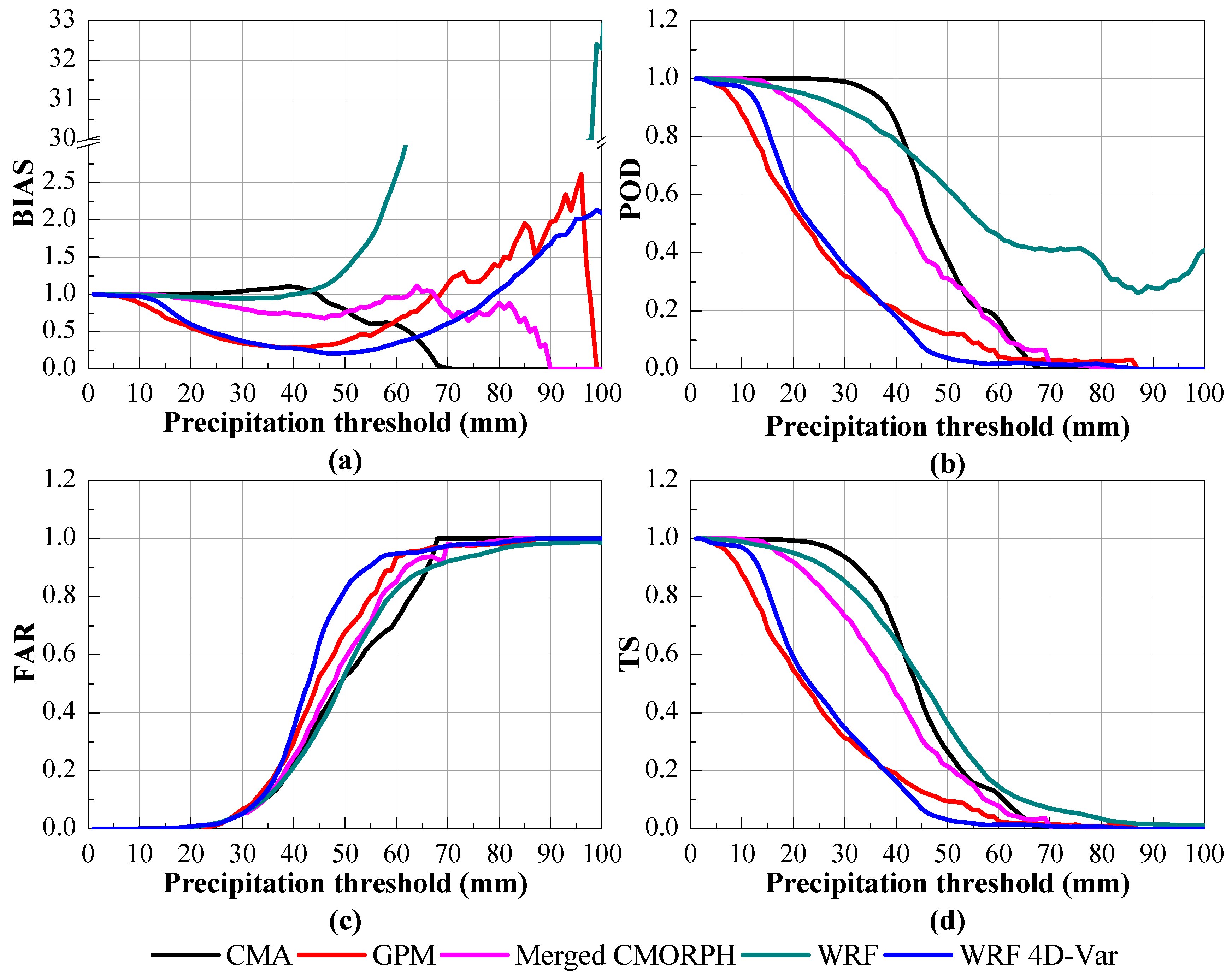
4.1. 1-km Grid Data of Different Precipitation Datasets
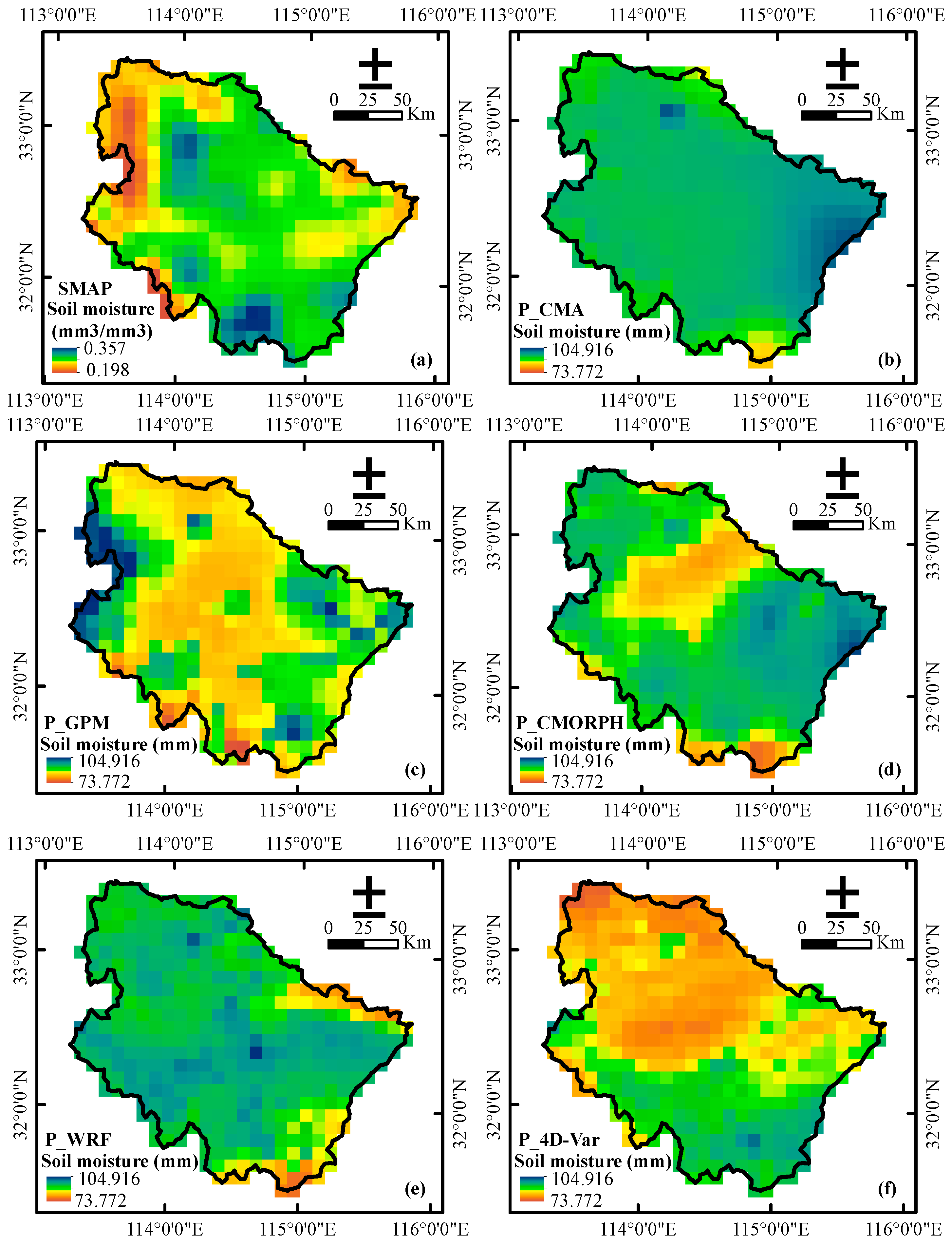
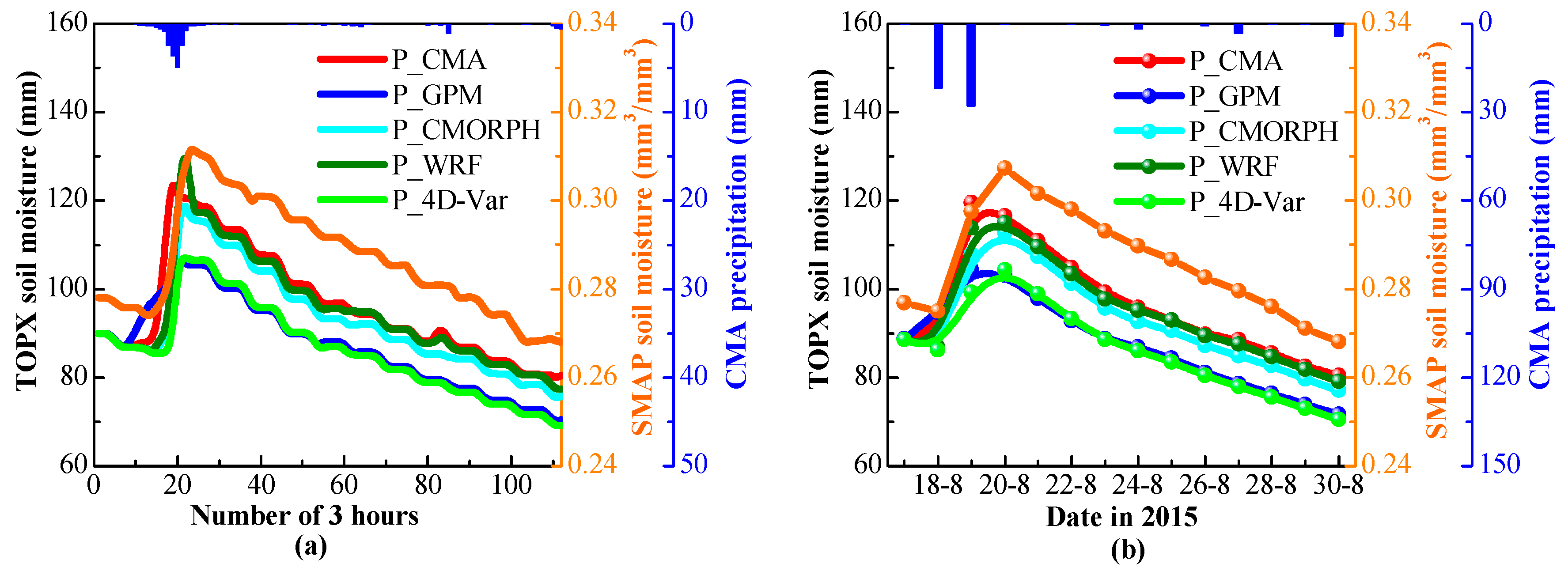
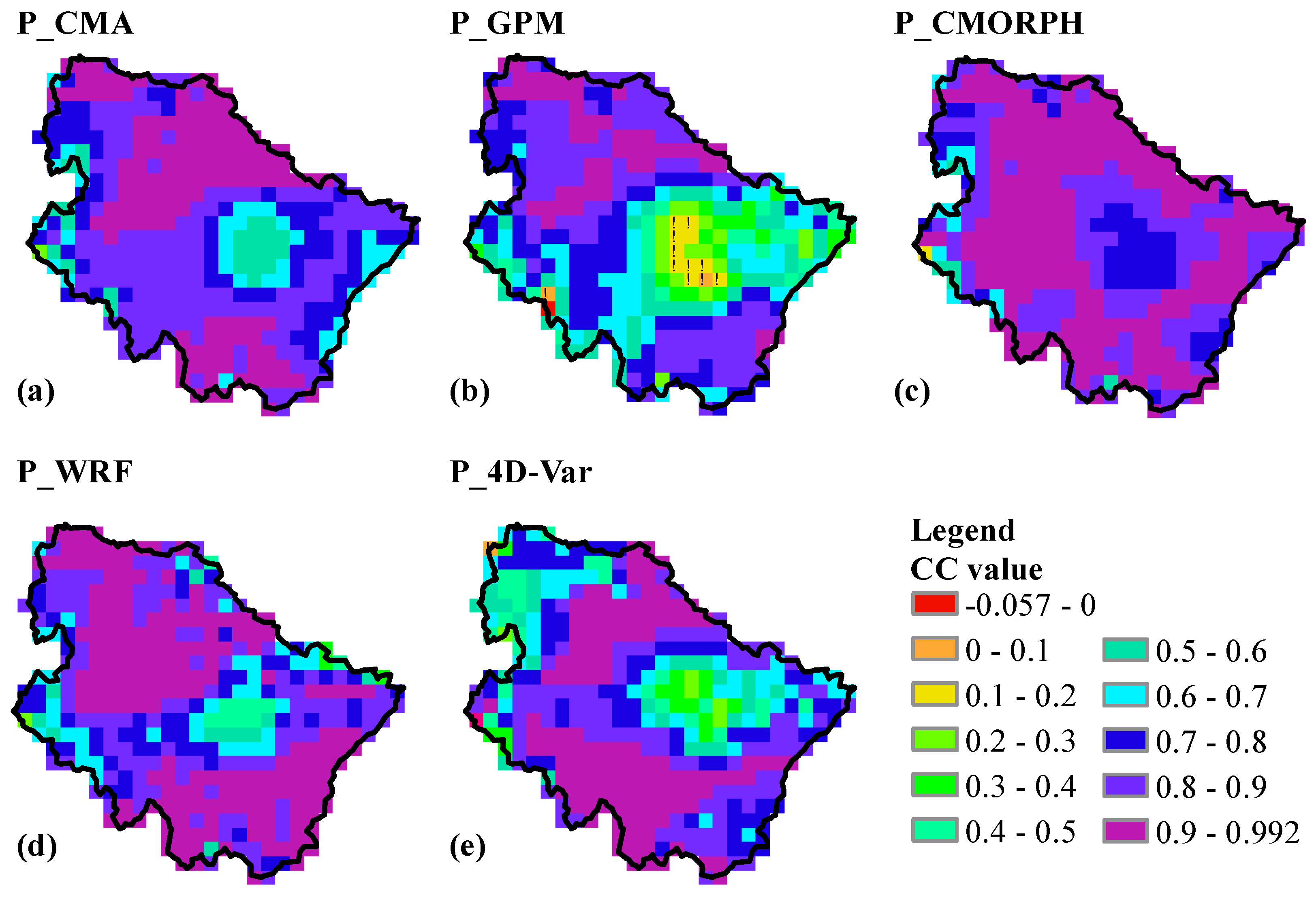
4.2. The Simulated Soil Moisture
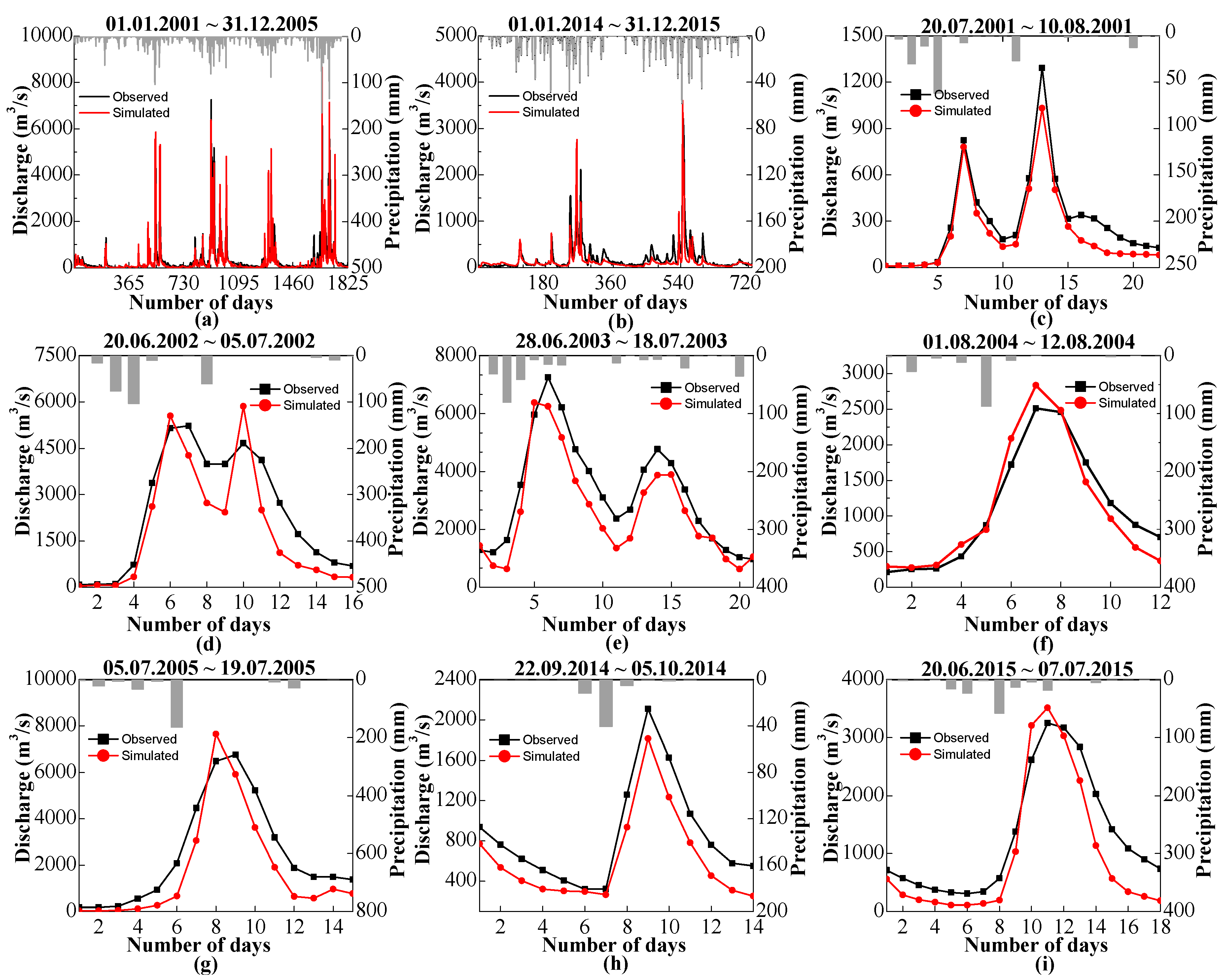
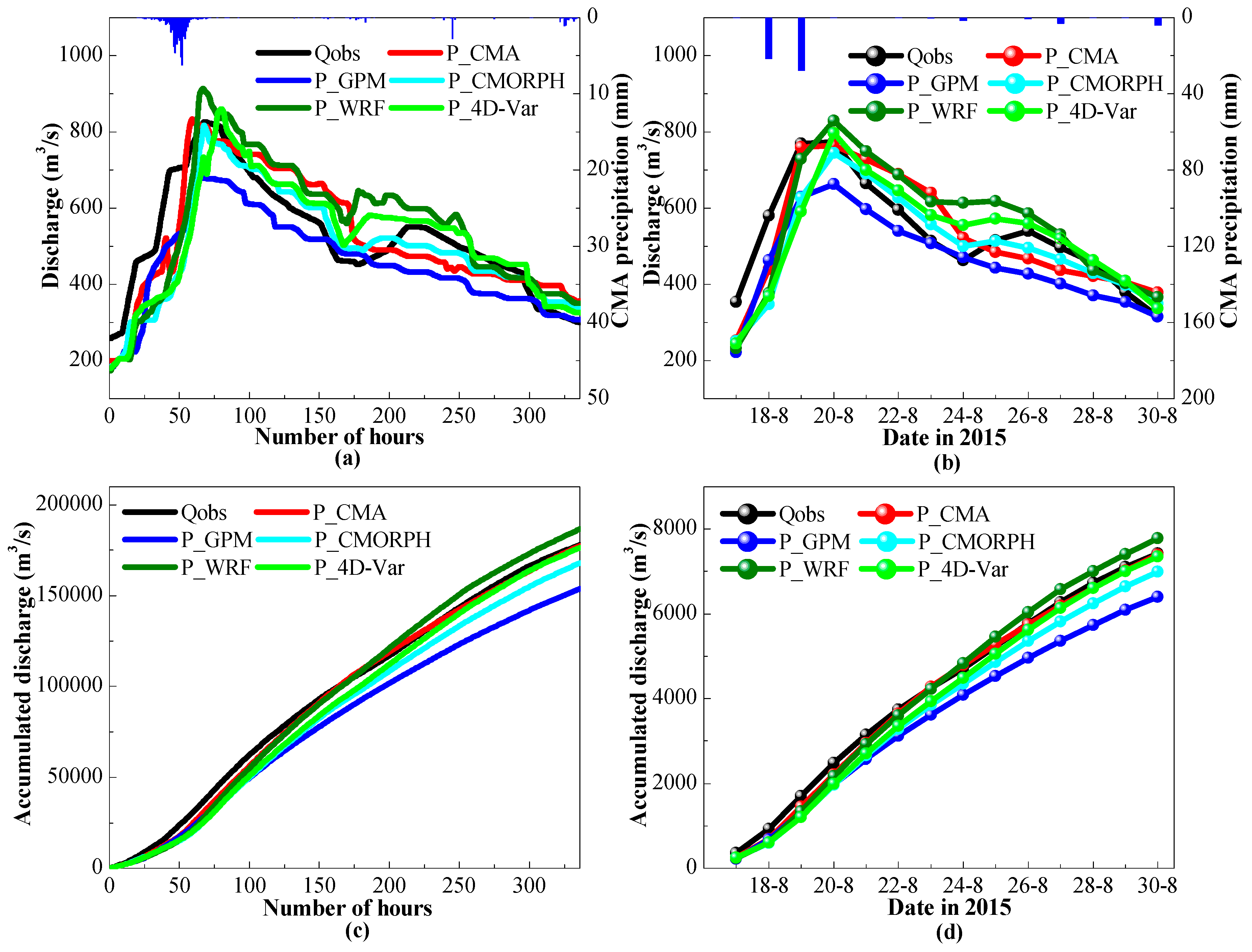
4.3. The Simulaed Outlet Discharge
5. Discussion
5.1. Evaluation of the Different Precipitation Datasets
5.2. Evaluation of the Simulated Soil Moisture
5.3. Evaluation of the Simulated Outlet Discharge
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Essou, G.R.C.; Sabarly, F.; Lucas-Picher, P.; Brissette, F.; Poulin, A. Can precipitation and temperature from meteorological reanalyses be used for hydrological modeling? J. Hydrometeorol. 2016, 17, 1929–1950. [Google Scholar] [CrossRef]
- Valeriano, O.C.S.; Koike, T.; Yang, K.; Graf, T.; Li, X.; Wang, L.; Han, X.J. Decision support for dam release during floods using a distributed biosphere hydrological model driven by quantitative precipitation forecasts. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Duethmann, D.; Zimmer, J.; Gafurov, A.; Guntner, A.; Kriegel, D.; Merz, B.; Vorogushyn, S. Evaluation of areal precipitation estimates based on downscaled reanalysis and station data by hydrological modelling. Hydrol. Earth Syst. Sci. 2013, 17, 2415–2434. [Google Scholar] [CrossRef] [Green Version]
- Yan, D.H.; Liu, S.H.; Qin, T.L.; Weng, B.S.; Li, C.Z.; Lu, Y.J.; Liu, J.J. Evaluation of TRMM precipitation and its application to distributed hydrological model in Naqu River Basin of the Tibetan Plateau. Hydrol. Res. 2017, 48, 822–839. [Google Scholar] [CrossRef]
- Delpla, I.; Baures, E.; Jung, A.V.; Thomas, O. Impacts of rainfall events on runoff water quality in an agricultural environment in temperate areas. Sci. Total Environ. 2011, 409, 1683–1688. [Google Scholar] [CrossRef] [PubMed]
- Mei, Y.W.; Nikolopoulos, E.I.; Anagnostou, E.N.; Zoccatelli, D.; Borga, M. Error analysis of satellite precipitation-driven modeling of flood events in complex Alpine terrain. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Shah, H.L.; Mishra, V. Uncertainty and bias in satellite-based precipitation estimates over Indian subcontinental basins: Implications for real-time streamflow simulation and flood prediction. J. Hydrometeorol. 2016, 17, 615–636. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Hossain, F. Understanding the dependence of satellite rainfall uncertainty on topography and climate for hydrologic model simulation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 704–718. [Google Scholar] [CrossRef]
- Nourani, V.; Fard, A.F.; Gupta, H.V.; Goodrich, D.C.; Niazi, F. Hydrological model parameterization using NDVI values to account for the effects of land cover change on the rainfall-runoff response. Hydrol. Res. 2017, 48, 1455–1473. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Knudsen, J. Operational validation and intercomparison of different types of hydrological models. Water Resour. Res. 1996, 32, 2189–2202. [Google Scholar] [CrossRef]
- Yang, D.; Herath, S.; Musiake, K. Comparison of different distributed hydrological models for characterization of catchment spatial variability. Hydrol. Process. 2000, 14, 403–416. [Google Scholar] [CrossRef]
- Demirel, M.C.; Booij, M.J.; Hoekstra, A.Y. The skill of seasonal ensemble low-flow forecasts in the Moselle River for three different hydrological models. Hydrol. Earth Syst. Sci. 2015, 19, 275–291. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Brissette, F.P. Hydrological modelling using proxies for gauged precipitation and temperature. Hydrol. Process. 2017, 31, 3881–3897. [Google Scholar] [CrossRef]
- Baymani-Nezhad, M.; Han, D. Hydrological modeling using Effective Rainfall routed by the Muskingum method (ERM). J. Hydroinform. 2013, 15, 1437–1455. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Gebremichael, M. Using self-organizing maps and wavelet transforms for space-time pre-processing of satellite precipitation and runoff data in neural network based rainfall-runoff modeling. J. Hydrol. 2013, 476, 228–243. [Google Scholar] [CrossRef]
- Mei, Y.; Anagnostou, E.N.; Shen, X.; Nikolopoulos, E.I. Decomposing the satellite precipitation error propagation through the rainfall-runoff processes. Adv. Water Resour. 2017, 109, 253–266. [Google Scholar] [CrossRef]
- Qi, W.; Liu, J.G.; Yang, H.; Sweetapple, C. An ensemble-based dynamic Bayesian averaging approach for discharge simulations using multiple global precipitation products and hydrological models. J. Hydrol. 2018, 558, 405–420. [Google Scholar] [CrossRef]
- Yi, L.; Zhang, W.C.; Wang, K. Evaluation of heavy precipitations dynamically downscaled by WRF 4D-Var data assimilation system with TRMM 3B42 and GPM IMERG over the Huaihe River Basin, China. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Chen, Y.J.; Ebert, E.; Walsh, K.E.; Davidson, N. Evaluation of TRMM 3B42 precipitation estimates of tropical cyclone rainfall using PACRAIN data. J. Geophys. Res.-Atmos. 2013, 118, 2184–2196. [Google Scholar] [CrossRef] [Green Version]
- McCabe, M.F.; Rodell, M.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.C.; Franz, T.E.; et al. The future of earth observation in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3879–3914. [Google Scholar] [CrossRef] [PubMed]
- Steiner, M.; Smith, J.A.; Burges, S.J.; Alonso, C.V.; Darden, R.W. Effect of bias adjustment and rain gauge data quality control on radar rainfall estimation. Water Resour. Res. 1999, 35, 2487–2503. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, C.; Kunstmann, H. The hydrological cycle in three state-of-the-art reanalyses: Intercomparison and performance analysis. J. Hydrometeorol. 2012, 13, 1397–1420. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; McNab, A.; Rudolf, B.; Schneider, U. The Global Precipitation Climatology Project (GPCP) combined precipitation dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P.P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Garstang, M.; Kummerow, C.D. The joanne simpson special issue on the Tropical Rainfall Measuring Mission (TRMM). J. Appl. Meteorol. 2000, 39, 1961. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Zhou, X.; Luo, Y.L.; Guo, X.L. Application of a CMORPH-a WS merged hourly gridded precipitation product in analyzing charateristics of short-duration heavy rainfall over southern China. J. Trop. Meteorol. 2015, 31, 333–344. [Google Scholar]
- Gaona, M.F.R.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. First-year evaluation of GPM rainfall over the netherlands: IMERG Day 1 final run (VO3D). J. Hydrometeorol. 2016, 17, 2799–2814. [Google Scholar] [CrossRef]
- Schmidli, J.; Goodess, C.M.; Frei, C.; Haylock, M.R.; Hundecha, Y.; Ribalaygua, J.; Schmith, T. Statistical and dynamical downscaling of precipitation: An evaluation and comparison of scenarios for the European Alps. J. Geophys. Res.-Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.X.; Anagnostou, E.; Frediani, M.; Solomos, S.; Kallos, G. Using NWP simulations in satellite rainfall estimation of heavy precipitation events over mountainous areas. J. Hydrometeorol. 2013, 14, 1844–1858. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Koizumi, K.; Ishikawa, Y.; Tsuyuki, T. Assimilation of precipitation data to the JMA mesoscale model with a four-dimensional variational method and its impact on precipitation forecasts. Sola 2005, 1, 45–48. [Google Scholar] [CrossRef]
- Mazrooei, A.; Sinha, T.; Sankarasubramanian, A.; Kumar, S.; Peters-Lidard, C.D. Decomposition of sources of errors in seasonal streamflow forecasting over the US Sunbelt. J. Geophys. Res.-Atmos. 2015, 120. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Performance and uncertainty evaluation of empirical downscaling methods in quantifying the climate change impacts on hydrology over two North American river basins. J. Hydrol. 2013, 479, 200–214. [Google Scholar] [CrossRef]
- Bardossy, A.; Pegram, G. Downscaling precipitation using regional climate models and circulation patterns toward hydrology. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Huang, X.Y.; Xiao, Q.N.; Barker, D.M.; Zhang, X.; Michalakes, J.; Huang, W.; Henderson, T.; Bray, J.; Chen, Y.S.; Ma, Z.Z.; et al. Four-dimensional variational data assimilation for WRF: Formulation and preliminary results. Mon. Weather Rev. 2009, 137, 299–314. [Google Scholar] [CrossRef]
- Lei, L.; Stauffer, D.R.; Deng, A. A hybrid nudging-ensemble Kalman filter approach to data assimilation in WRF/DART. Q. J. R. Meteorol. Soc. 2012, 138, 2066–2078. [Google Scholar] [CrossRef]
- Lorenc, A.C.; Bowler, N.E.; Clayton, A.M.; Pring, S.R.; Fairbairn, D. Comparison of hybrid-4DEnVar and hybrid-4DVar data assimilation methods for global NWP. Mon. Weather Rev. 2015, 143, 212–229. [Google Scholar] [CrossRef]
- Buehner, M.; Houtekamer, P.L.; Charette, C.; Mitchell, H.L.; He, B. Intercomparison of variational data assimilation and the ensemble Kalman filter for global deterministic NWP. Part II: One-month experiments with real observations. Mon. Weather Rev. 2010, 138, 1567–1586. [Google Scholar] [CrossRef]
- Buehner, M.; Houtekamer, P.L.; Charette, C.; Mitchell, H.L.; He, B. Intercomparison of variational data assimilation and the ensemble Kalman filter for global deterministic NWP. Part I: Description and single-observation experiments. Mon. Weather Rev. 2010, 138, 1550–1566. [Google Scholar] [CrossRef]
- Black, T.L. The new NMC mesoscale ETA model–description and forecast examples. Weather Forecast. 1994, 9, 265–278. [Google Scholar] [CrossRef]
- Dudhia, J.; Klemp, J.; Skamarock, W.; Dempsey, D.; Janjic, Z.; Benjamin, S.; Brown, J. A collaborative effort towards a future community mesoscale model (WRF). In Proceedings of the 12th Conference on Numerical Weather Prediction, Phoenix, AZ, USA, 11–16 January 1998; pp. 242–243. [Google Scholar]
- Saito, K.; Fujita, T.; Yamada, Y.; Ishida, J.I.; Kumagai, Y.; Aranami, K.; Ohmori, S.; Nagasawa, R.; Kumagai, S.; Muroi, C.; et al. The operational JMA nonhydrostatic mesoscale model. Mon. Weather Rev. 2006, 134, 1266–1298. [Google Scholar] [CrossRef]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF ensemble prediction system: Methodology and validation. Q. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Zubieta, R.; Getirana, A.; Espinoza, J.C.; Lavado-Casimiro, W.; Aragon, L. Hydrological modeling of the Peruvian-Ecuadorian Amazon Basin using GPM-IMERG satellite-based precipitation dataset. Hydrol. Earth Syst. Sci. 2017, 21. [Google Scholar] [CrossRef]
- Xu, H.L.; Xu, C.Y.; Saelthun, N.R.; Zhou, B.; Xu, Y.P. Evaluation of reanalysis and satellite-based precipitation datasets in driving hydrological models in a humid region of Southern China. Stoch. Environ. Res. Risk Assess. 2015, 29, 2003–2020. [Google Scholar] [CrossRef]
- Wu, H.; Adler, R.F.; Tian, Y.D.; Gu, G.J.; Huffman, G.J. Evaluation of quantitative precipitation estimations through hydrological modeling in IFloodS River basins. J. Hydrometeorol. 2017, 18, 529–553. [Google Scholar] [CrossRef]
- Rasmussen, S.H.; Christensen, J.H.; Drews, M.; Gochis, D.J.; Refsgaard, J.C. Spatial-scale characteristics of precipitation simulated by regional climate models and the implications for hydrological modeling. J. Hydrometeorol. 2012, 13, 1817–1835. [Google Scholar] [CrossRef]
- Parkes, B.L.; Wetterhall, F.; Pappenberger, F.; He, Y.; Malamud, B.D.; Cloke, H.L. Assessment of a 1-h gridded precipitation dataset to drive a hydrological model: A case study of the summer 2007 floods in the Upper Severn, UK. Hydrol. Res. 2013, 44, 89–105. [Google Scholar] [CrossRef]
- Lin, C.A.; Wen, L.; Lu, G.H.; Wu, Z.Y.; Zhang, J.Y.; Yang, Y.; Zhu, Y.F.; Tong, L.Y. Atmospheric-hydrological modeling of severe precipitation and floods in the Huaihe River Basin, China. J. Hydrol. 2006, 330, 249–259. [Google Scholar] [CrossRef]
- Liechti, T.C.; Matos, J.P.; Boillat, J.L.; Schleiss, A.J. Comparison and evaluation of satellite derived precipitation products for hydrological modeling of the Zambezi River Basin. Hydrol. Earth Syst. Sci. 2012, 16, 489–500. [Google Scholar] [CrossRef] [Green Version]
- Lauri, H.; Rasanen, T.A.; Kummu, M. Using reanalysis and remotely sensed temperature and precipitation data for hydrological modeling in monsoon climate: Mekong river aase study. J. Hydrometeorol. 2014, 15, 1532–1545. [Google Scholar] [CrossRef]
- Georgakakos, K.P.; Kavvas, M.L. Precipitation analysis, modeling, and prediction in hydrology. Rev. Geophys. 1987, 25, 163–178. [Google Scholar] [CrossRef]
- Nguyen, T.H.M.; Masih, I.; Mohamed, Y.A.; van der Zaag, P. Validating rainfall-runoff modelling using satellite-based and reanalysis precipitation products in the Sre Pok catchment, the Mekong river basin. Geosciences 2018, 8, 164. [Google Scholar] [CrossRef]
- Ottle, C.; Vidalmadjar, D. Assimilation of soil-moisture inferred from infrared remote-sensing in a hydrological model over the HAPEX-MOBILHY region. J. Hydrol. 1994, 158, 241–264. [Google Scholar] [CrossRef]
- Western, A.W.; Grayson, R.B.; Green, T.R. The Tarrawarra project: High resolution spatial measurement, modelling and analysis of soil moisture and hydrological response. Hydrol. Process. 1999, 13, 633–652. [Google Scholar] [CrossRef]
- Wanders, N.; Bierkens, M.F.P.; de Jong, S.M.; de Roo, A.; Karssenberg, D. The benefits of using remotely sensed soil moisture in parameter identification of large-scale hydrological models. Water Resour. Res. 2014, 50, 6874–6891. [Google Scholar] [CrossRef] [Green Version]
- Draper, C.; Mahfouf, J.F.; Calvet, J.C.; Martin, E.; Wagner, W. Assimilation of ASCAT near- surface soil moisture into the SIM hydrological model over France. Hydrol. Earth Syst. Sci. 2011, 15, 3829–3841. [Google Scholar] [CrossRef] [Green Version]
- Lopez, P.L.; Wanders, N.; Schellekens, J.; Renzullo, L.J.; Sutanudjaja, E.H.; Bierkens, M.F.P. Improved large-scale hydrological modelling through the assimilation of streamflow and downscaled satellite soil moisture observations. Hydrol. Earth Syst. Sci. 2016, 20, 3059–3076. [Google Scholar] [CrossRef]
- Baguis, P.; Roulin, E. Soil Moisture Data Assimilation in a Hydrological Model: A Case Study in Belgium Using Large-Scale Satellite Data. Remote Sens. 2017, 9, 820. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pettinato, S.; Notarnicola, C.; Pasolli, L.; Pistocchi, A. Comparison between SAR Soil Moisture Estimates and Hydrological Model Simulations over the Scrivia Test Site. Remote Sens. 2013, 5, 4961–4976. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Mo, X.; Zhao, W.; Naeimi, V.; Dai, D.; Shu, C.; Mao, L. Temporal variation of soil moisture over the Wuding River basin assessed with an eco-hydrological model, in-situ observations and remote sensing. Hydrol. Earth Syst. Sci. 2009, 13, 1375–1398. [Google Scholar] [CrossRef] [Green Version]
- Bertoldi, G.; Della Chiesa, S.; Notarnicola, C.; Pasolli, L.; Niedrist, G.; Tappeiner, U. Estimation of soil moisture patterns in mountain grasslands by means of SAR RADARSAT2 images and hydrological modeling. J. Hydrol. 2014, 516, 245–257. [Google Scholar] [CrossRef]
- Trudel, M.; Leconte, R.; Paniconi, C. Analysis of the hydrological response of a distributed physically-based model using post-assimilation (EnKF) diagnostics of streamflow and in situ soil moisture observations. J. Hydrol. 2014, 514, 192–201. [Google Scholar] [CrossRef]
- Koch, J.; Cornelissen, T.; Fang, Z.F.; Bogena, H.; Diekkruger, B.; Kollet, S.; Stisen, S. Inter-comparison of three distributed hydrological models with respect to seasonal variability of soil moisture patterns at a small forested catchment. J. Hydrol. 2016, 533, 234–249. [Google Scholar] [CrossRef]
- Iacobellis, V.; Gioia, A.; Milella, P.; Satalino, G.; Balenzano, A.; Mattia, F. Inter-comparison of hydrological model simulations with time series of SAR-derived soil moisture maps. Eur. J. Remote Sens. 2013, 46, 739–757. [Google Scholar] [CrossRef]
- Xiong, L.H.; Yang, H.; Zeng, L.; Xu, C.Y. Evaluating Consistency between the Remotely Sensed Soil Moisture and the Hydrological Model-Simulated Soil Moisture in the Qujiang Catchment of China. Water 2018, 10, 291. [Google Scholar] [CrossRef]
- Khan, U.; Ajami, H.; Tuteja, N.K.; Sharma, A.; Kim, S. Catchment scale simulations of soil moisture dynamics using an equivalent cross-section based hydrological modelling approach. J. Hydrol. 2018, 564, 944–966. [Google Scholar] [CrossRef]
- Tang, G.Q.; Ma, Y.Z.; Long, D.; Zhong, L.Z.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Pombo, S.; de Oliveira, R.P.; Mendes, A. Validation of remote-sensing precipitation products for Angola. Meteorol. Appl. 2015, 22, 395–409. [Google Scholar] [CrossRef]
- Pan, X.D.; Li, X.; Cheng, G.D.; Hong, Y. Effects of 4D-Var data assimilation using remote sensing precipitation products in a WRF model over the complex terrain of an arid region river basin. Remote Sens. 2017, 9, 963. [Google Scholar] [CrossRef]
- Lin, L.F.; Ebtehaj, A.M.; Bras, R.L.; Flores, A.N.; Wang, J.F. Dynamical precipitation downscaling for hydrologic applications using WRF 4D-Var data assimilation: Implications for GPM era. J. Hydrometeorol. 2015, 16, 811–829. [Google Scholar] [CrossRef]
- Rogelis, M.C.; Werner, M. Streamflow forecasts from WRF precipitation for flood early warning in mountain tropical areas. Hydrol. Earth Syst. Sci. 2018, 22, 853–870. [Google Scholar] [CrossRef] [Green Version]
- Pennelly, C.; Reuter, G.; Flesch, T. Verification of the WRF model for simulating heavy precipitation in Alberta. Atmos. Res. 2014, 135, 172–192. [Google Scholar] [CrossRef]
- Bukovsky, M.S.; Karoly, D.J. Precipitation simulations using WRF as a nested regional climate model. J. Appl. Meteorol. Climatol. 2009, 48, 2152–2159. [Google Scholar] [CrossRef]
- Yuan, Z.; Yang, Z.Y.; Zheng, X.D.; Yuan, Y. Spatial and temporal variations of precipitation in Huaihe river basin in recent 50 years. South-to-North Water Divers. Water Sci. Technol. 2012, 10. [Google Scholar] [CrossRef]
- Xia, J.; She, D.X.; Zhang, Y.Y.; Du, H. Spatio-temporal trend and statistical distribution of extreme precipitation events in Huaihe River Basin during 1960–2009. J. Geogr. Sci. 2012, 22, 195–208. [Google Scholar] [CrossRef] [Green Version]
- Kleczek, M.A.; Steeneveld, G.J.; Holtslag, A.A.M. Evaluation of the Weather Research and Forecasting mesoscale model for GABLS3: Impact of boundary-layer schemes, boundary conditions and spin-up. Bound.-Layer Meteor. 2014, 152, 213–243. [Google Scholar] [CrossRef]
- Srinivas, D.; Rao, D.V.B. Implications of vortex initialization and model spin-up in tropical cyclone prediction using Advanced Research Weather Research and Forecasting Model. Nat. Hazards 2014, 73, 1043–1062. [Google Scholar] [CrossRef]
- Veerse, F.; Thepaut, J.N. Multiple-truncation incremental approach for four-dimensional variational data assimilation. Q. J. R. Meteorol. Soc. 1998, 124, 1889–1908. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and Other Precipitation Products against Gauge Data under Different Topographic and Climatic Conditions in Iran: Preliminary Results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Yong, B.; Hong, Y.; Yang, X.; Yuan, F. Evaluation of latest TMPA and CMORPH precipitation products with independent rain gauge observation networks over high-latitude and low-latitude basins in China. Chin. Geogr. Sci. 2016, 26, 439–455. [Google Scholar] [CrossRef]
- Asong, Z.E.; Razavi, S.; Wheater, H.S.; Wong, J.S. Evaluation of Integrated Multisatellite Retrievals for GPM (IMERG) over Southern Canada against Ground Precipitation Observations: A Preliminary Assessment. J. Hydrometeorol. 2017, 18, 1033–1050. [Google Scholar] [CrossRef]
- Liu, Y.B.; Wu, G.P.; Ke, C.Q. Hydrological Remote Sensing; Science Press: Beijing, China, 2016; ISBN 978-7-03-049302-6. [Google Scholar]
- Wang, Z.L.; Zhong, R.D.; Lai, C.G.; Chen, J.C. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Liu, Z. Comparison of Integrated Multisatellite Retrievals for GPM (IMERG) and TRMM Multisatellite Precipitation Analysis (TMPA) Monthly Precipitation Products: Initial Results. J. Hydrometeorol. 2016, 17, 777–790. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- Zhang, X.Z.; Xiong, Z.; Zheng, J.Y.; Ge, Q.S. High-resolution precipitation data derived from dynamical downscaling using the WRF model for the Heihe River Basin, northwest China. Theor. Appl. Climatol. 2018, 131, 1249–1259. [Google Scholar] [CrossRef]
- Pieri, A.B.; von Hardenberg, J.; Parodi, A.; Provenzale, A. Sensitivity of Precipitation Statistics to Resolution, Microphysics, and Convective Parameterization: A Case Study with the High-Resolution WRF Climate Model over Europe. J. Hydrometeorol. 2015, 16, 1857–1872. [Google Scholar] [CrossRef]
- Cardoso, R.M.; Soares, P.M.M.; Miranda, P.M.A.; Belo-Pereira, M. WRF high resolution simulation of Iberian mean and extreme precipitation climate. Int. J. Climatol. 2013, 33, 2591–2608. [Google Scholar] [CrossRef]
- Lim, K.S.S.; Hong, S.Y. Development of an effective double-moment cloud microphysics scheme with prognostic Cloud Condensation Nuclei (CCN) for weather and climate models. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res.-Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Grell, G.A.; Devenyi, D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Barker, D.; Huang, X.Y.; Liu, Z.Q.; Auligne, T.; Zhang, X.; Rugg, S.; Ajjaji, R.; Bourgeois, A.; Bray, J.; Chen, Y.S.; et al. The Weather Research and Forecasting model’s community variational/ensemble data assimilation system WRFDA. Bull. Am. Meteorol. Soc. 2012, 93, 831–843. [Google Scholar] [CrossRef]
- Barker, D.M.; Huang, W.; Guo, Y.R.; Bourgeois, A.J.; Xiao, Q.N. A three-dimensional variational data assimilation system for MM5: Implementation and initial results. Mon. Weather Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef]
- Courtier, P.; Thepaut, J.N.; Hollingsworth, A. A strategy for operational imlementation of 4D-Var, using an incremental approach. Q. J. R. Meteorol. Soc. 1994, 120, 1367–1387. [Google Scholar] [CrossRef]
- Lorenc, A.C. Modelling of error covariances by 4D-Var data assimilation. Q. J. R. Meteorol. Soc. 2003, 129, 3167–3182. [Google Scholar] [CrossRef] [Green Version]
- Parrish, D.F.; Derber, J.C. The national-meteorological-centers spectral statistical-interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Reichle, R.H.; De Lannoy, G.J.M.; Liu, Q.; Ardizzone, J.V.; Colliander, A.; Conaty, A.; Crow, W.; Jackson, T.J.; Jones, L.A.; Kimball, J.S.; et al. Assessment of the SMAP level-4 surface and root-zone soil moisture product using in situ measurements. J. Hydrometeorol. 2017, 18, 2621–2645. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Dickinson, R.E.; Gulden, L.E. A simple TOPMODEL-based runoff parameterization (SIMTOP) for use in global climate models. J. Geophys. Res.-Atmos. 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Yi, L.; Zhang, W.C.; Yan, C.A. A modified topographic index that incorporates the hydraulic and physical properties of soil. Hydrol. Res. 2017, 48, 370–383. [Google Scholar] [CrossRef]
- Yong, B. Development of a land-Surface Hydrological Model TOPX and Its Coupling Study with Regional Climate Model RIEMS; Nanjing University: Nanjing, China, 2007. [Google Scholar]
- Wu, Z.Y. Study on Quantitative Rainfall and Real Time Flood Forecasting. Ph.D. Thesis, Hohai University, Nanjing, China, 2007. [Google Scholar]
- Zhao, R.J. Watershed Hydrological Simulation-Xin’anjiang Model and Shanbei Model; Water Resources and Electric Power Press: Beijing, China, 1984. [Google Scholar]
- Lu, G.H.; Wu, Z.Y.; He, H. Hydrologic Cycle Process and Quantitative Prediction; Science Press: Beijing, China, 2010; ISBN 978-7-03-026608-8. [Google Scholar]
- Nash, L.L.; Gleick, P.H. Sensitivity of streamflow in the Colorado basin to climatic changes. J. Hydrol. 1991, 125, 221–241. [Google Scholar] [CrossRef]
- Taylan, E.D.; Damcayiri, D. The Prediction of Precipitations of Isparta Region By Using IDW and Kriging. Teknik Dergi 2016, 27, 7551–7559. [Google Scholar]
- Accadia, C.; Mariani, S.; Casaioli, M.; Lavagnini, A.; Speranza, A. Sensitivity of precipitation forecast skill scores to bilinear interpolation and a simple nearest-neighbor average method on high-resolution verification grids. Weather Forecast. 2003, 18, 918–932. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2006; Volume 91, p. 627. ISBN 978-0-12-751996-1. [Google Scholar]
- Cui, C.Y.; Xu, J.; Zeng, J.Y.; Chen, K.S.; Bai, X.J.; Lu, H.; Chen, Q.; Zhao, T.J. Soil moisture mapping from satellites: An intercomparison of SMAP, SMOS, FY3B, AMSR2, and ESA CCI over two dense network regions at different spatial scales. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Huang, T.N.; Zheng, Y.F.; Duan, C.C.; Yin, J.F.; Wu, R.J. Comparative analysis of soil moisture retrieval by satellites in China. Remote Sens. Inf. 2017, 32, 25–33. [Google Scholar] [CrossRef]
- Albergel, C.; Zakharova, E.; Calvet, J.C.; Zribi, M.; Parde, M.; Wigneron, J.P.; Novello, N.; Kerr, Y.; Mialon, A.; Fritz, N.E.D. A first assessment of the SMOS data in southwestern France using in situ and airborne soil moisture estimates: The CAROLS airborne campaign. Remote Sens. Environ. 2011, 115, 2718–2728. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Chen, Q.; Duan, Z.; Zhang, J.; Mo, K.; Li, Z.; Tang, G. Multiscale Comparative Evaluation of the GPM IMERG v5 and TRMM 3B42 v7 Precipitation Products from 2015 to 2017 over a Climate Transition Area of China. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Kumar, S.; Godrej, A.N.; Grizzard, T.J. Watershed size effects on applicability of regression-based methods for fluvial loads estimation. Water Resour. Res. 2013, 49, 7698–7710. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.T.; Huang, J.-K. Influence of storm magnitude and watershed size on runoff nonlinearity. J. Earth Syst. Sci. 2016, 125, 777–794. [Google Scholar] [CrossRef]
- Black, P.E.; Cronn, J.W. Hydrograph responses to watershed model size and similitude relations. J. Hydrol. 1975, 26, 255–266. [Google Scholar] [CrossRef]
- Zhou, S.M.; Lei, T.W.; Warrington, D.N.; Lei, Q.X.; Zhang, M.L. Does watershed size affect simple mathematical relationships between flow velocity and discharge rate at watershed outlets on the Loess Plateau of China. J. Hydrol. 2012, 444, 1–9. [Google Scholar] [CrossRef]
| Map and Grids | |
|---|---|
| Map projection | Lambert conformal |
| Centre point of domain | 35.8°N, 114°E |
| Number of vertical layers | 27 |
| Horizontal grid spacing | 27 km, 9 km, 3 km, 1 km |
| Grids | 180 × 155, 322 × 271, 604 × 433, 700 × 700 |
| Static geographical fields | Standard dataset at 30″ resolution from the United States Geological Survey (USGS) |
| Time step | 150 s, 50 s, 17 s, 6 s |
| Physical Parameterization Schemes | |
| Cloud microphysics | WRF double-moment 6 scheme [93] |
| Long-wave radiation | Rapid radiative transfer model (RRTM) [94] |
| Short-wave radiation | Dudhia scheme [95] |
| Land-surface model | Noah land-surface model (LSM) [96] |
| Planetary boundary layer | Yonsei University scheme [97] |
| Cumulus parameterization | New Grell-Devenyi 3 scheme [98] (only in D01) |
| Simulation Time | NS | CC | RE | ||
|---|---|---|---|---|---|
| Long-term | Calibration | 1 January 2001~31 December 2005 | 0.787 | 0.898 | −0.292 |
| Validation | 1 January 2014~31 December 2015 | 0.700 | 0.857 | −0.248 | |
| Short-term | Calibration | 20 July 2001~10 August 2001 | 0.894 | 0.982 | −0.241 |
| 20 June 2002~05 July 2002 | 0.747 | 0.921 | −0.236 | ||
| 28 June 2003~18 July 2003 | 0.815 | 0.967 | −0.194 | ||
| 01 August 2004~12 August 2004 | 0.919 | 0.968 | −0.012 | ||
| 05 July 2005~19 July 2005 | 0.806 | 0.954 | −0.281 | ||
| Validation | 22 September 2014~05 October 2014 | 0.755 | 0.985 | −0.266 | |
| 20 June 2015~07 July 2015 | 0.772 | 0.953 | −0.251 | ||
| Parameter | Value |
|---|---|
| Decay factor (f, m−1) | 160 |
| Evapotranspiration coefficient (E) | 0.95 |
| Initial soil moisture content (W, mm) | 90 |
| Impact factor of vegetation root (C) | 0.12 |
| Maximum subsurface runoff (Rsb,max, mm) | 80 |
| No. | Experiment Label | Precipitation Category | Precipitation Data | Resolution of Precipitation Data |
|---|---|---|---|---|
| 1 | P_CMA | In situ observation | CMA data | Point scale, hourly |
| 2 | P_GPM | Remote sensing estimation | GPM IMERG | 0.1°, 30-min |
| 3 | P_CMORPH | Merged CMORPH | 0.1°, hourly | |
| 4 | P_WRF | NWP simulation | WRF output | 1 km, 6-s |
| 5 | P_4D-Var | WRF 4D-Var output | 1 km, 6-s |
| Statistical Metric | Equation | Perfect Value |
|---|---|---|
| Mean error (ME, mm) | 0 | |
| Relative error (RE) | 0 | |
| Root mean square error (RMSE, mm) | 0 | |
| Correlation coefficient (CC) | 1 | |
| Bias score (BIAS) | 1 | |
| False alarm ratio (FAR) | 0 | |
| Probability of detection (POD) | 1 | |
| Threat score (TS) | 1 | |
| Nash-Sutcliffe coefficient (NS) | 1 |
| Error Score | Precipitation Data | ||||
|---|---|---|---|---|---|
| CMA | GPM IMERG | Merged CMORPH | WRF Output | WRF 4D-Var Output | |
| ME | −0.424 | −1.489 | −0.805 | 0.159 | −1.868 |
| RE | −0.099 | −0.347 | −0.188 | 0.037 | −0.436 |
| RMSE | 11.719 | 10.112 | 11.577 | 13.411 | 11.946 |
| CC | 0.459 | 0.493 | 0.433 | 0.343 | 0.444 |
| No. | Experiment | Minimum 3 h/Daily | Maximum 3 h/Daily | Mean Value 3 h/Daily | Standard Deviation 3 h/Daily |
|---|---|---|---|---|---|
| 1 | P_CMA | 0.256/0.504 | 0.963/0.986 | 0.825/0.858 | 0.111/0.114 |
| 2 | P_GPM | −0.020/−0.096 | 0.967/0.986 | 0.695/0.705 | 0.208/0.235 |
| 3 | P_CMORPH | 0.197/0.477 | 0.992/0.996 | 0.885/0.891 | 0.091/0.093 |
| 4 | P_WRF | 0.259/0.186 | 0.986/0.992 | 0.841/0.852 | 0.132/0.136 |
| 5 | P_4D-Var | −0.057/0.067 | 0.983/0.993 | 0.774/0.780 | 0.183/0.194 |
| No. | Experiment | Hourly | Daily | ||||
|---|---|---|---|---|---|---|---|
| NS | CC | RE | NS | CC | RE | ||
| 1 | P_CMA | 0.658 | 0.855 | −0.003 | 0.694 | 0.876 | −0.003 |
| 2 | P_GPM | 0.576 | 0.919 | −0.137 | 0.582 | 0.935 | −0.137 |
| 3 | P_CMORPH | 0.596 | 0.823 | −0.057 | 0.621 | 0.837 | −0.057 |
| 4 | P_WRF | 0.464 | 0.816 | 0.048 | 0.499 | 0.832 | 0.048 |
| 5 | P_4D-Var | 0.547 | 0.787 | −0.010 | 0.560 | 0.796 | −0.010 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, L.; Zhang, W.; Li, X. Assessing Hydrological Modelling Driven by Different Precipitation Datasets via the SMAP Soil Moisture Product and Gauged Streamflow Data. Remote Sens. 2018, 10, 1872. https://doi.org/10.3390/rs10121872
Yi L, Zhang W, Li X. Assessing Hydrological Modelling Driven by Different Precipitation Datasets via the SMAP Soil Moisture Product and Gauged Streamflow Data. Remote Sensing. 2018; 10(12):1872. https://doi.org/10.3390/rs10121872
Chicago/Turabian StyleYi, Lu, Wanchang Zhang, and Xiangyang Li. 2018. "Assessing Hydrological Modelling Driven by Different Precipitation Datasets via the SMAP Soil Moisture Product and Gauged Streamflow Data" Remote Sensing 10, no. 12: 1872. https://doi.org/10.3390/rs10121872
APA StyleYi, L., Zhang, W., & Li, X. (2018). Assessing Hydrological Modelling Driven by Different Precipitation Datasets via the SMAP Soil Moisture Product and Gauged Streamflow Data. Remote Sensing, 10(12), 1872. https://doi.org/10.3390/rs10121872