An Interplay between Photons, Canopy Structure, and Recollision Probability: A Review of the Spectral Invariants Theory of 3D Canopy Radiative Transfer Processes

Abstract

Earth observations collected by remote sensors provide unique information to our ever-growing knowledge of the terrestrial biosphere. Yet, retrieving information from remote sensing data requires sophisticated processing and demands a better understanding of the underlying physics. This paper reviews research efforts that lead to the developments of the stochastic radiative transfer equation (RTE) and the spectral invariants theory. The former simplifies the characteristics of canopy structures with a pair-correlation function so that the 3D information can be succinctly packed into a 1D equation. The latter indicates that the interactions between photons and canopy elements converge to certain invariant patterns quantifiable by a few wavelength independent parameters, which satisfy the law of energy conservation. By revealing the connections between plant structural characteristics and photon recollision probability, these developments significantly advance our understanding of the transportation of radiation within vegetation canopies. They enable a novel physically-based algorithm to simulate the “hot-spot” phenomenon of canopy bidirectional reflectance while conserving energy, a challenge known to the classic radiative transfer models. Therefore, these theoretical developments have a far-reaching influence in optical remote sensing of the biosphere.

1. Introduction

The past a few decades have seen rapid development in scientific research and applications that monitor and/or simulate terrestrial ecosystems with the help of remote sensing data [1]. Thanks to advances in technology, we have sensors that operate across a broad spectral range, at high spatial, temporal, and spectral resolutions, and with passive or active modes. For instance, on sun-synchronous orbits the classic MODIS (Moderate Resolution Imaging Spectroradiometer) and SUOMI NPP (National Polar-Orbiting Partnership) VIIRS (Visible Infrared Imaging Radiometer Suite) are now joined by Landsat 8/OLI (Operational Land Imager) [2,3], Copernicus Sentinel-2 [4], and JPSS (Joint Polar Satellite System) VIIRS [5]. On geostationary orbits we now have advanced multi-band imagers on Himawari-8/9 [6], GOES-16/17 [7,8], FengYun-4 [9] and the forthcoming sensors from Korea Meteorological Administration and European Organization for the Exploitation of Meteorological Satellites (EUMETSAT). On the International Space Station there is ECOSTRESS (Ecosystem Spaceborne Thermal Radiometer Experiment on Space Station), which will be soon joined by GEDI (Global Ecosystem Dynamics Investigation) [10]. A plethora of remote sensing products have been derived that reflect various characteristics of the terrestrial biosphere, including vegetation spectral indices, land cover types, canopy structural parameters, and many others. As remote sensing data uniquely provide consistent coverage over large spatial scales, it is rare nowadays that a global change study does not use such information.

Remote sensing data are not uncertainty-free but come with caveats. In optical remote sensing, for example, photons that reach the sensor have gone through complicated interactions with the atmosphere-vegetation-soil medium [11]. A series of processing must be conducted to calibrate and correct the top-of-atmosphere signals before information about the surface can be extracted from them. As remote sensors cannot directly measure the surface biophysical characteristics of interest, models are used to transform the measurements into estimates of the desirable vegetation canopy variables (e.g., Leaf Area Index), a process methodologically called “inversion.” The inverse problems encountered in remote sensing are often under-determined and “ill-posed” [12], thus a priori information, additional constraints on potential solution space, and regularization techniques are often applied to make the problem solvable [13,14,15,16,17]. Given these challenges, a better understanding of the methodological backgrounds of remote sensing products can be beneficial for users of these datasets.

Interactions between photons and the atmosphere-vegetation-soil medium are succinctly quantified by the radiative transfer equation (RTE) and the associated boundary conditions [18]. The theory of radiative transfer was originally developed to study the scattering and absorption of sunlight in the atmosphere and later to simulate the transport of neutrons in nuclear reactors [19]. The theory was applied to model the radiation regime in vegetation canopy in the second half of the last century [20,21,22]. A range of models have been developed to describe the radiation regime in vegetation canopies as well as their interactions with the atmosphere and the soil. Some of the representative models, for instance, include Raytran [23], DART (Discrete Anisotropic Radiative Transfer) [24,25], SAIL (Scattering by Arbitrary Inclined Leaves) [26,27,28], PROSPECT [29], GORT (Geometric Optical-Radiative Transfer) [30,31], and PARAS [32]. A recent review of the canopy radiative transfer models can be found in Reference [18].

Compared with turbid media or nuclear reactors, vegetation canopy has its own structural and optical characteristics. On one hand, leaves have finite sizes and therefore cast shadows [33], which violates the assumptions of Beer’s law [34,35]. For instance, the mutual shadowing effects of the canopy elements are mainly responsive for a sharp peak of the canopy reflectance in the retro-illumination direction. This phenomenon is often called the “hot-spot” effect, which is difficult to simulate with the classic RTE [33,36]. On the other side, the sizes of leaves (and twigs, branches, etc.) are often much larger than the spectral wavelengths considered in optical remote sensing. The total extinction coefficient (or cross-section) of photons in vegetation canopies is thus determined by the structural distribution of the leaves (and other phytoelements) rather than the wavelengths of photons [37]. Such characteristics of the vegetation medium present both challenges and opportunities to research efforts on the radiative transfer theory in vegetation canopies.

This paper intends to contribute a review of the theoretical advancements in modeling radiative transfer processes in 3D vegetation canopies. It particularly focuses on the developments of the stochastic radiative equation and the spectral invariant theory, which have been widely applied in retrieving vegetation structural information from remote sensors like MODIS and MISR (Multi-Angle Imaging Spectroradiometer) to the recent EPIC (Earth Polychromatic Imaging Camera) on the DSCOVR (Deep Space Climate Observatory) platform and the latest geostationary sensors like AHI (Advanced Himawari Imager; on Himawari-8/9) and ABI (Advanced Baseline Imager; on GOES-16/17). However, a detailed account of such theoretical progresses is somewhat scarce in recent review papers [38,39,40,41,42,43,44,45] or textbooks [46] on remote sensing sciences and applications, which becomes a main motivation for this paper.

A question may rise: Why should we care so much about the theoretical properties of the radiative transfer processes in a time of big data, artificial intelligence and machine learning? It is true that in general the RTE has to be solved numerically [47]. In many applications we rely on statistical or empirical methods to solve the problem at hand [43]. Artificial intelligence and machine learning tools have also been introduced into remote sensing applications since their early stages and are gaining increasing popularity with rapid developments in the technology [48]. However, as mentioned earlier, the task of remote sensing is essentially ill-posed. The solution to the inverse problem often is not unique [43] and may not even be physical [35]. For instance, though the spectroscopy of a single leaf may be accurately measured in a laboratory, those measured for a forest stand by remote sensors convolute signals from the phytoelements (e.g., leaves, twigs, branches, trunks), the land surface, the atmosphere in between, as well as the interactions among them [22]. It is far from straightforward to establish a robust quantitative link between satellite measurements and leaf-level biogeochemical or biogeophysical traits. Without a clear understanding of the underlying processes, we may misinterpret empirically identified correlations from the data [49]. Furthermore, physically-based radiative transfer models (RTM) usually assume many parameters, which make them difficult to invert in practice [43]. The success of an RTM in remote sensing applications thus requires a balance between the simplicity of the model formulation and the fidelity of physics it preserves. Such a task can only be achieved with a deep understanding of the radiative transfer processes. As we will discuss later, the stochastic RTE and the spectral invariant theory represent elegant advancements with this modeling aspect regarded.

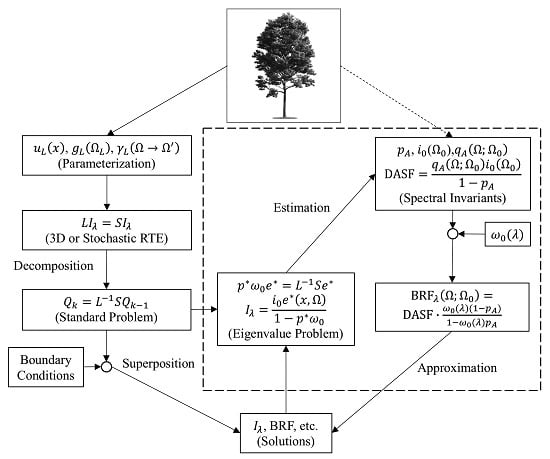
The rest of the paper is organized as follows. We begin by introducing the radiative transfer equation formulated for 3D vegetation canopies. We then focus on four particular topics in the main text, including the decomposition of RTE into the black-soil (“BS”) and the soil (“S”) problems, the development of the stochastic RTE that efficiently packs 3D canopy features into a 1D form, the spectral invariants theory that links the solutions of the RTE at different wavelengths by a few key canopy structural parameters, and the latest effort to address the “hot-spot” problem in vegetation remote sensing. We conclude the paper with a brief summary of the key ideas reviewed in these topics.

We would like to emphasize that, although the concepts of the spectral invariants and stochastic canopy geometrical properties may appear abstract, they have concrete physical interpretations and are measurable from ground and remote observations. Additionally, the basic ideas behind these theoretical developments are actually simple. Their derivations repeatedly make use of the ideas of decomposition and superposition, convergence and invariants, and the law of energy conservation. Therefore, we invite the readers to pay more attention to these ideas rather than the mathematical details of the theory, if the latter appears to be a bit complicated at the first look.

2. Radiative Transfer Equation for Vegetation Canopy

The classic RTE theory assumes that the radiative transfer properties of a vegetation canopy are largely determined by how the leaves are distributed in space, how they are oriented, and the fashions in which photons interact with the leaves [11,22,37,50]. These three aspects are mathematically described by the leaf area density distribution function $u_L\left(x\right)$, the leaf normal distribution function $g_L\left(x,{\mathsf{\Omega }}_L\right)/2\pi$, and the leaf element scattering phase function ${\gamma }_L\left(\lambda ,x,\mathsf{\Omega }\to \mathsf{\Omega }\prime ,{\mathsf{\Omega }}_L\right)$, respectively (Figure 1). Here, ${\mathsf{\Omega }}_L$ represents the direction of the leaf normal, $\mathsf{\Omega }$ is the incident direction, and $\mathsf{\Omega }\prime$ is the direction in which photons are scattered into. Note that the scattering phase function ${\gamma }_L$ explicitly depends on both $\mathsf{\Omega }$ and $\mathsf{\Omega }\prime$ but not only the scattering angle ${\cos }^{-1}\left(\mathsf{\Omega }·{\mathsf{\Omega }}^{-1}\right)$, which is a key difference between vegetation canopies and gaseous media [37].

From these functions we can derive a few key parameters to be used in RTE, including the single scattering albedo ${\omega }_0\left(\lambda \right)$, the total extinction cross-section $\mathsf{\sigma }\left(\mathsf{\Omega }\right)$, and the differential scattering cross-section ${\mathsf{\sigma }}_S\left(\mathsf{\Omega }\to \mathsf{\Omega }\prime \right)$. Here we have assumed that ${\omega }_0$ is a variable of only spectral wavelength and that $\mathsf{\sigma }\left(\mathsf{\Omega }\right)$ and ${\mathsf{\sigma }}_S\left(\mathsf{\Omega }\to \mathsf{\Omega }\prime \right)$ do not depend on locations ($x$) or spectral wavelengths ($x$). The detailed definitions of these variables and their relationships are given in the Appendix A. Note that although the single scattering albedo is generally understood as the averaged leaf albedo, its definition actually depends on the spatial scales of the elementary scatters considered in the equation [51]. As will be discussed later, this parameter is related to the canopy scattering coefficients by the associated scaling rules [45].

Denoting $I_{\lambda }\left(x,\mathsf{\Omega }\right)$ as the monochromatic radiation intensity (radiance), we use the operator notations [52] to describe the radiative transfer processes in vegetation canopies (for readers who are not familiar with linear differential/integral operators, you may think them as matrices with infinite dimensions). In particular, the streaming-collision operator (L) describes the spatial/directional change of the radiation intensity and the extinction of radiance due to collisions between photons and phytoelements (Reference [52]; the same for Equations (2)–(5)),

$$L{I}_{\lambda }\equiv \mathsf{\Omega }·\nabla I_{\lambda }\left(x,\mathsf{\Omega }\right)+\mathsf{\sigma }\left(x,\mathsf{\Omega }\right)I_{\lambda }\left(x,\mathsf{\Omega }\right)$$

(1)

The scattering operator ($S_{\lambda }$) describes the addition of radiance by photons scattered in from other directions,

$$S_{\lambda }{I}_{\lambda }\equiv \underset{4\pi }{\overset{}{\int }}{\omega }_0\left(\lambda \right){\mathsf{\sigma }}_S\left(x,\mathsf{\Omega }\prime \to \mathsf{\Omega }\right)I_{\lambda }\left(x,\mathsf{\Omega }\prime \right)d\mathsf{\Omega }\prime$$

(2)

The steady state RTE is thus

$$L{I}_{\lambda }=S_{\lambda }{I}_{\lambda },$$

(3)

with the boundary conditions specified by

$$I_{\lambda }\left(x_T,\mathsf{\Omega }\right)=\delta \left(\mathsf{\Omega }-{\mathsf{\Omega }}_0\right),\hspace{1em}{n}_T·\mathsf{\Omega }<0$$

(4)

and

$$I_{\lambda }\left(x_B,\mathsf{\Omega }\right)=\frac{1}{\pi }\underset{n_B·\mathsf{\Omega }\prime >0}{\overset{}{\int }}{\rho }_{\lambda }\left(x_B,\mathsf{\Omega }\prime \to \mathsf{\Omega }\right)I_{\lambda }\left(x_B,\mathsf{\Omega }\prime \right)\left|n_B·\mathsf{\Omega }\prime \right|d\mathsf{\Omega }\prime ,\hspace{1em}{n}_B·\mathsf{\Omega }<0$$

(5)

where $x_T$ and $x_B\in \partial V$, $n_T$ and $n_B$ and the outward normal of the boundary, ${\rho }_{\lambda }$ is the bidirectional reflectance factor (BRF) of the lower boundary (i.e., soil surface). In remote sensing applications the influence of lateral boundaries is considered small and thus neglected [35,37]. For simplicity we also only consider the direct solar illumination but neglect the diffuse radiation. This corresponds to the case where the influences of path radiances are removed through atmospheric corrections.

The RTE of Equation (3) describes photon-canopy interactions in three spatial dimensions (i.e., x) and two directional dimensions ($\mathsf{\Omega }$ and $\mathsf{\Omega }\prime$). As the phase function ${\gamma }_L$ is not rotational invariant, we cannot decompose the solution in spherical harmonics to simplify the calculation [37]. Direct numerical schemes to solve the equation thus have to perform 5-dimensional integration at every iteration, which is complicated and prone to numerical errors. Therefore, we seek to simplify the problem based on its mathematical/physical properties, which is discussed in the following sections.

3. Black-Soil and Soil Problems

A key property of the RTE is its linearity with regard to $I_{\lambda }$, which allows the problem to be decomposed into a set of sub-problems that are easier to solve. The classic MODIS algorithm [35] decomposes the RTE problem according to its boundary conditions. The easiest boundary condition is represented by the black-soil (“BS”) problem, which is formulated for a vegetation canopy illuminated from above by a mono-directional sun beam and otherwise bounded by purely absorbing (i.e., “black”) surface from below. In contrast, the soil (“S”) problem is formulated for the same canopy but illuminated from below by anisotropic sources and bounded by absorbing surfaces everywhere else. Such a decomposition scheme separates the influence of illumination conditions from those of soils. The two sub-problems are solved independently but their solutions can be flexibly superposed to render the full solution of the original problem (Figure 1).

To solve the black-soil problem, we further decompose the radiation field into the un-collided component, $Q_0$,

$$Q_0\left(x_T,\mathsf{\Omega }\right)=\delta \left(\mathsf{\Omega }-{\mathsf{\Omega }}_0\right),n_T·\mathsf{\Omega }<0$$

(6)

and the collided (or diffuse) components, $I_{dif}$, which satisfies the so-called standard problem with zero boundary conditions where no photon entering the canopy from above or below [53],

$$L_0{I}_{dif}=S_{\lambda }{I}_{dif}+S_{\lambda }{Q}_0.$$

(7)

As L is an ordinary differential operator, the solution of $Q_0$ can be relatively easily obtained. By introducing the integral operator $T=L_0^{-1}{S}_{\lambda }$, we write the diffuse component, $I_{dif}$, symbolically as

$$I_{dif}=T{I}_{dif}+T{Q}_0.$$

(8)

We should explain the physical meaning of the T operator later in Section 5. For now, note that we can solve for $I_{dif}$ as

$$I_{dif}=\frac{T{Q}_0}{E-T},$$

(9)

where “E” is the identity operator (i.e., $E{I}_{dif}=I_{dif}$). Adding $Q_0$ to both sides, we obtain the solution of the black-soil problem as

$$\begin{gathered} I_{bs}=I_{dif}+Q_0=\frac{Q_0}{E-T} \\ =\left(E+T+T^2+\cdots +T^k+\cdots \right)Q_0. \end{gathered}$$

(10)

The last line of Equation (10) is the expansion of the operator ${\left(E-T\right)}^{-1}$ in Neumann series, which is analogous to geometrical series of numbers. Physically it indicates that $I_{BS}$ is the superposition of photons that are un-collided, once-collided, twice-collided, and so on. The condition that the series converge is provided by the law of energy conservation because the system is dissipative. This superposition scheme, generally referred to as “successive-order scattering approximation” (SOSA; Reference [54]), also bridges the black-soil problem solution to a few key concepts in the radiative transfer theory in vegetation canopies.

The soil (“S”) problem is formulated as follows:

$$\begin{gathered} L{I}_s=S_{\lambda }{I}_s, \\ {I}_s\left(x_B,\mathsf{\Omega }\right)=d_B\left(x_B,\mathsf{\Omega }\right),n_B·\mathsf{\Omega }<0, \end{gathered}$$

(11)

where $d_B\left(x_B,\mathsf{\Omega }\right)$ is an anisotropic source normalized to have its hemispherical integral (i.e., irradiance) to be unit. Note that the soil problem also assumes purely absorbing boundaries and the only difference is that the canopy is illuminated from below by a diffuse source. It can be solved with the same approach as the black-soil problem.

We now explain how to use the solutions of the black-soil and the soil problems to model interactions between the canopy and the underlying soil surface. First, the anisotropic source in the S-problem is initialized by radiation that passes through the canopy and reflected by the soil surface. If the spatial distribution pattern of the downward radiation (as which is regulated by the structure of the canopy) does not change significantly, we may assume that the anisotropy is determined by the soil surface but independent on the incoming radiation field [35].

Let the spatial mean effective ground bi-hemispherical reflectance (BHR) of the soil surface to be ${\overline{\rho }}_{eff}$ and the mean radiation flux (irradiance) from the downward radiance generated by the black-soil problem to be ${\overline{F}}_{bs}$. As the system is linear, the radiation field that generated by the first interaction of the canopy and the soil surface is (approximately) ${\overline{\rho }}_{eff}{\overline{F}}_{bs}{I}_s$. A part of the photons will be scattered back by the canopy to interact with the soil surface again. Denote the mean BHR of the canopy illuminated by the anisotropic source $d_B\left(x_B,\mathsf{\Omega }\right)$ to be ${\overline{R}}_s$, and the radiation field generated by the second interaction between the canopy and the soil surface is thus ${\left({\overline{\rho }}_{eff}\right)}^2{\overline{R}}_s{\overline{F}}_{bs}{I}_s$. As this process iterates, we arrive at the total radiation generated by the interactions between the canopy and the soil surface

$$I_{rest}\left(x,\mathsf{\Omega }\right)=\frac{{\overline{\rho }}_{eff}{\overline{F}}_{bs}}{1-{\overline{\rho }}_{eff}{\overline{R}}_s}{I}_s\left(x,\mathsf{\Omega }\right)$$

(12)

and the solution to the full RTE problem is therefore

$$I_{\lambda }\left(x,\mathsf{\Omega }\right)=I_{bs}\left(x,\mathsf{\Omega }\right)+\frac{{\overline{\rho }}_{eff}{\overline{F}}_{bs}}{1-{\overline{\rho }}_{eff}{\overline{R}}_s}{I}_s\left(x,\mathsf{\Omega }\right).$$

(13)

The above derivation of Equation (13) is slightly different from Reference [35] but shares the same the idea. Ultimately, these decomposition schemes can be derived from the concept of Green’s function of the RTE [53]. The assumption about the constancy of canopy BHR (${\overline{R}}_s$) and the anisotropy $d_B\left(x_B,\mathsf{\Omega }\right)$ is reasonable. This is because the diffused radiation field within the canopy tend to converge toward certain spatial distributions that are independent on external illumination conditions (see below).

4. Stochastic Radiative Transfer Equation

In remote sensing applications we are generally more interested in the statistical mean of the radiation fields than individual solutions [35]. An apparent way to achieve this goal is to generate an ensemble of representative canopy realizations, solve the RTE for them separately, and then calculate the mean in the end. However, this approach costs time and computation resources. Alternatively, we can also calculate the statistical mean canopy first before solving for the RTE. The second approach is the main idea behind the development of the Stochastic RTE, which turns out to be more efficient in addressing the question [55]. As the ensemble mean is usually equivalent to the average of the 3D radiation field over the horizontal space (i.e., the ergodicity assumption), the central task of Stochastic RTE is the same as to efficiently pack a 3D radiative regime into a 1D form.

To illustrate, recall that $\mathsf{\Omega }·\nabla I\left(x,\mathsf{\Omega }\right)$ is a directional derivative, i.e.,

$$\mathsf{\Omega }·\nabla I\left(x,\mathsf{\Omega }\right)=\frac{\mathrm{d}I\left(x_B+\xi \mathsf{\Omega },\mathsf{\Omega }\right)}{\mathrm{d}\xi }=\frac{\mathrm{d}I\left(x_B+\left(z-z_B\right)/\mu \mathsf{\Omega },\mathsf{\Omega }\right)}{1/\mu \mathrm{d}z}.$$

(14)

Integrating the RTE over the vertical dimension from the top ($z=0$) or the bottom ($z=1$) of the canopy leads to

$$\begin{array}{l}I\left(x,\mathsf{\Omega }\right)+\frac{1}{\mu }{\int }_Z^{}{u}_L\left(x^{\prime }\right)\mathsf{\sigma }\left(\mathsf{\Omega }\right)I\left(x^{\prime },\mathsf{\Omega }\right)d{z}^{\prime }\\ =\frac{1}{\mu }{\int }_Z^{}{\omega }_0{u}_L\left(x^{\prime }\right)d{z}^{\prime }\underset{4\pi }{\overset{}{\int }}{\mathsf{\sigma }}_s\left(\mathsf{\Omega }\prime \to \mathsf{\Omega }\right)I\left(x^{\prime },\mathsf{\Omega }\prime \right)d\mathsf{\Omega }\prime +I\left(x_B,\mathsf{\Omega }\right)\end{array}$$

(15)

where $x^{\prime }=x+\left(z^{\prime }-z\right)/\mu \mathsf{\Omega }$ and Z represents appropriate integration intervals. The subscript “B” denotes general boundaries, which may be “top” or “bottom” according to the direction of the integration [55]. Let $\langle ·\rangle$ denote the horizontal average. Apply the operator to both sides of the equation and we obtain,

$$\begin{array}{l}\overline{I}\left(x,\mathsf{\Omega }\right)+\frac{1}{\mu }{\int }_Z^{}\mathsf{\sigma }\left(\mathsf{\Omega }\right)\langle u_L\left(x^{\prime }\right)I\left(x^{\prime },\mathsf{\Omega }\right)\rangle d{z}^{\prime }\\ =\frac{1}{\mu }{\int }_Z^{}{\omega }_{0}d{z}^{\prime }\underset{4\pi }{\overset{}{\int }}{\mathsf{\sigma }}_s\left(\mathsf{\Omega }\prime \to \mathsf{\Omega }\right)\langle u_L\left(x^{\prime }\right)I\left(x^{\prime },\mathsf{\Omega }\prime \right)\rangle d\mathsf{\Omega }\prime +\overline{I}\left(x_B,\mathsf{\Omega }\right)\end{array}$$

(16)

where $\overline{I}\left(x,\mathsf{\Omega }\right)=\langle I\left(x,\mathsf{\Omega }\right)\rangle$. Therefore, the original RTE becomes a 1D equation with regard to the vertical (“z”) dimension.

Note that in Equation (16) $\overline{I}\left(x,\mathsf{\Omega }\right)$ is the mean radiation intensity (at the vertical level z) averaged over the whole horizontal domain while the “second-moment” variable $\langle u_L\left(x\right)I\left(x,\mathsf{\Omega }\right)\rangle$ is the mean intensity averaged only at locations where a leaf element presents. These two variables are generally different from each other except for special cases. In order to evaluate $\langle u_L\left(x\right)I(x,\mathsf{\Omega }\rangle )$, we multiply both sides of the RTE by $u_L\left(x\right)$ and integrate over the horizontal scale to get

$$\begin{array}{l}\langle u_L\left(x\right)I\left(x,\mathsf{\Omega }\right)\rangle +\frac{1}{\mu }\mathsf{\sigma }\left(\mathsf{\Omega }\right){\int }_Z^{}\langle u_L\left(x\right)u_L\left(x^{\prime }\right)I\left(x^{\prime },\mathsf{\Omega }\right)\rangle d{z}^{\prime }\\ =\frac{1}{\mu }{\int }_Z^{}{\omega }_{0}d{z}^{\prime }\underset{4\pi }{\overset{}{\int }}{\mathsf{\sigma }}_s\left(\mathsf{\Omega }\prime \to \mathsf{\Omega }\right)\langle u_L\left(x\right)u_L\left(x^{\prime }\right)I\left(x^{\prime },\mathsf{\Omega }\prime \right)\rangle d\mathsf{\Omega }\prime +\langle u_L\left(x_B\right)I\left(x,\mathsf{\Omega }\right)\rangle \end{array}$$

(17)

Now another new (the “third-moment”) variable, $\langle u_L\left(x\right)u_L\left(r^{\prime }\right)I\left(r^{\prime },\mathsf{\Omega }\prime \right)\rangle$, appears in the equation! The procedure can go on and on, but every time we try to solve for a lower-moment variable, we end up introducing a new higher-order unknown into the equation. The process is conceptually analogous to the “Reynolds Averaging” technique in fluid dynamics. A parameterization scheme thus must be introduced to “close” the Stochastic RTE [56].

The scheme adopted in the current literature is derived based on the binary-medium assumption, under which the leaf density function $u_L\left(x\right)$ is represented by an indicator function $\chi \left(x\right)$ that specifies the presence ($\chi =1$) or absence ($\chi =0$) of a unit leaf element ($d_L$), i.e., $u_L\left(x\right)=d_L\chi \left(x\right)$. Note that for a random variable like $\chi \left(x\right)$ its spatial averaging (〈$·$〉) is essentially the same as its spatial expectation. As $\chi \left(x\right)=\chi {\left(x\right)}^2$, by the standard formula of statistical covariance of two variables, we see that

$$\begin{array}{l}\langle \chi \left(x\right)\chi \left(x^{\prime }\right)I\left(x^{\prime },\mathsf{\Omega }\prime \right)\rangle =\langle \chi \left(x\right)\chi {\left(x^{\prime }\right)}^{2}I\left(x^{\prime },\mathsf{\Omega }\prime \right)\rangle \\ \hspace{1em}\hspace{1em}\hspace{1em}=\langle \chi \left(x\right)\chi \left(x^{\prime }\right)\rangle \langle \chi \left(x^{\prime }\right)I\left(x^{\prime },\mathsf{\Omega }\prime \right)\rangle +\mathrm{cov}\left(\chi \left(x\right)\chi \left(x^{\prime }\right),\chi \left(x^{\prime }\right)I\left(x^{\prime },\mathsf{\Omega }\prime \right)\right).\end{array}$$

(18)

The first term in Equation (18) represents the “global mean” of $\chi \left(x\right)\chi \left(x^{\prime }\right)$ and $\chi \left(x^{\prime }\right)I\left(x^{\prime },\mathsf{\Omega }\prime \right)$, respectively, whose meaning will be explained below. The second (the covariance) term represents their “local chaotisity”, which is assumed negligible [57]. We thus arrive at

$$\langle \chi \left(x\right)\chi \left(x^{\prime }\right)I\left(x^{\prime },\mathsf{\Omega }\prime \right)\rangle \approx \langle \chi \left(x\right)\chi \left(x^{\prime }\right)\rangle \langle \chi \left(x^{\prime }\right)I\left(x^{\prime },\mathsf{\Omega }\prime \right)\rangle .$$

(19)

By the common notation of the literature [55,58], we define

$$\begin{gathered} p_c\left(z\right)=\langle \chi \left(x\right)\rangle , \\ {q}_c\left(z,z^{\prime },\mathsf{\Omega }\right)=\langle \chi \left(x\right)\chi \left(x^{\prime }\right)\rangle , \\ K\left(z,z^{\prime },\mathsf{\Omega }\right)=q_c\left(z,z,\mathsf{\Omega }\right)/p_c\left(z\right), \\ U\left(z,\mathsf{\Omega }\right)=\langle \chi \left(x\right)I\left(x,\mathsf{\Omega }\right)\rangle /p_c\left(z\right), \end{gathered}$$

(20)

where $p_c\left(z\right)$ is the probability of finding leaf elements at locations z. $q_c\left(z,z^{\prime },\mathsf{\Omega }\right)$ and $K\left(z,z^{\prime },\mathsf{\Omega }\right)$ are the joint and the conditional probability (or pair correlation functions) of finding leaf elements at locations z and $z^{\prime }$ along the direction $\mathsf{\Omega }$ simultaneously. $U\left(z,\mathsf{\Omega }\right)$ is the mean radiation intensity averaged over vegetation occupied horizontal space (i.e., with gaps excluded). The stochastic RTE is then fully specified as [55,58]

$$\begin{array}{l}\overline{I}\left(z,\mathsf{\Omega }\right)+\frac{1}{\mu }{\int }_Z^{}\mathsf{\sigma }\left(\mathsf{\Omega }\right)p_c\left(z^{\prime }\right)U\left(z^{\prime },\mathsf{\Omega }\right)d{z}^{\prime }\\ =\frac{1}{\mu }{\int }_Z^{}{\omega }_{0}d{z}^{\prime }\underset{4\pi }{\overset{}{\int }}{p}_c\left(z^{\prime }\right)U\left(z^{\prime },\mathsf{\Omega }\prime \right){\mathsf{\sigma }}_s\left(\mathsf{\Omega }\prime \to \mathsf{\Omega }\right)d\mathsf{\Omega }\prime +\overline{I}\left(z_B,\mathsf{\Omega }\right)\end{array}$$

(21)

and

$$\begin{array}{l}U\left(z,\mathsf{\Omega }\right)+\frac{1}{\mu }\mathsf{\sigma }\left(\mathsf{\Omega }\right){\int }_Z^{}K\left(z,z^{\prime },\mathsf{\Omega }\right)U\left(z^{\prime },\mathsf{\Omega }\right)d{z}^{\prime }\\ =\frac{1}{\mu }{\int }_Z^{}{\omega }_{0}d{z}^{\prime }\underset{4\pi }{\overset{}{\int }}{\mathsf{\sigma }}_s\left(\mathsf{\Omega }\prime \to \mathsf{\Omega }\right)K\left(z,z^{\prime },\mathsf{\Omega }\prime \right)U\left(z^{\prime },\mathsf{\Omega }\prime \right)d\mathsf{\Omega }\prime +U\left(x_B,\mathsf{\Omega }\right)\end{array}$$

(22)

with corresponding boundary conditions adapted for $\overline{I}\left(x_B,\mathsf{\Omega }\right)$ and $U\left(x_B,\mathsf{\Omega }\right)$, respectively. In general, we must evaluate $U\left(z,\mathsf{\Omega }\right)$ first by Equation (22) before solving Equation (21) for $\overline{I}\left(z,\mathsf{\Omega }\right)$. Note that because $K\left(z,z^{\prime },\mathsf{\Omega }\prime \right)$ is a function of both $z^{\prime }$ and $z$, Equation (22) is a Volterra integral equation.

The stochastic RTE was initially developed to solve the mean radiation intensity in the medium of broken clouds [57,59,60]. It was first applied to the vegetation canopy by Reference [61]. The current form of the Stochastic RTE in vegetation canopy was introduced in Reference [55], who also detailed a SOSA procedure to solve the Volterra integral equation.

The most important feature of the Stochastic RTE is the incorporation of the pair correlation function $K\left(z,z^{\prime },\mathsf{\Omega }\prime \right)$. The function succinctly characterizes the structural and the spatial distribution properties such as heterogeneity and anisotropy of the 3D canopies. It encompasses information presented by traditional metrics like forest gap fractions and clumping indices. Indeed, the introduction of $K\left(z,z^{\prime },\mathsf{\Omega }\prime \right)$ allows the 1D RTE to resolve the differences between $U\left(x_B,\mathsf{\Omega }\right)$ and $\overline{I}\left(x_B,\mathsf{\Omega }\right)$, which can be used to retrieve canopy gap fractions [62]. The first set of realistic pair-correlation functions was derived by Reference [58] using stochastic geometry models [63]. The approach is to idealize individual tree crowns as regular geometrical objects (e.g., spheres, cylinders, cones, etc.) and assume their locations follow certain spatial patterns (e.g., Poisson’s distribution). The pair-correlation functions then can be computed analytically or statistically. Reference [58] presents detailed examples of the pair correlation functions for different crown shapes and canopy distribution patterns. As a special case, when the leaf elements are spatially not correlated, $K\left(z,z^{\prime },\mathsf{\Omega }\prime \right)$ reduces to $p_c\left(z\right)$, Equation (22) reduces to a classic 1D RTE, and $U\left(z,\mathsf{\Omega }\right)$ becomes the same as $\overline{I}\left(z,\mathsf{\Omega }\right)$. Reference [58] also systematically compared the simulation results of the stochastic RTE with those of the classic 1D RTE as well as field measurements, showing that the Stochastic RTE is able to capture the 3D radiation effects previously reported in the literature and therefore the pair-correlation function provides a “most natural and physically meaningful” [58] measure to 3D canopy structural properties over a range of scales.

There are a couple of more facts about the Stochastic RTE that need attention. First, the pair correlation function is not a merely theoretical concept but can be evaluated from observations for real-world applications. With the development of terrestrial lidar scanning (TLS) instruments, now we can measure the 3D structure of forest stands with relative ease and the pair correlation function of the canopy can be accurately computed with such measurements. The function can also be estimated from high-resolution satellite imageries and air-/space-born lidar data over larger spatial scales. Second, as the pair correlation function encapsulates purely the structural or geometrical characteristics of the canopy, it has a close connection with the school of geometrical optical (GO) models in remote sensing [30,31,64,65]. Indeed, the stochastic geometry models used in deriving the theoretical pair correlation functions in Reference [58] are essentially the same as those used in References [64,65]. However, the two schools are different in the specific approaches to use the canopy geometric information. In GO models, the information is used to derive “kernels” of the bidirectional reflectance distribution function (BRDF), which allow the model to fit with observations in a semi-empirical fashion. In contrast, the Stochastic RTE tries to preserve the law of energy conservation and rigorously follows the radiative transfer formulation. As a cost, the Stochastic RTE inherits the limitations of the 3D RTE and cannot resolve, at least to certain spatial scales, the “hot-spot” effects of the canopy radiation regime [33]. We shall return to this topic in Section 6.

5. Canopy Spectral Invariants

The preceding sections have described the traditional algorithms to solve the RTE at a specific wavelength ($\lambda$). In remote sensing applications we often need to obtain solutions at many wavelengths to sample the (multiple or hyperspectral) bandwidth of the sensors. Do we have to iterate the process for $I_{\lambda }\left(x,\mathsf{\Omega }\right)$ at every wavelength? This question is the main concern of the spectral invariant theory (Figure 1).

The idea underlying the spectral invariant theory is simple: The single albedo ${\omega }_0\left(\lambda \right)$ is the only parameter in the RTE of Equation (1) that depends on wavelengths, while all the other parameters are determined by the structures of the canopy [52]. Therefore, we seek a formula to separate the influence of ${\omega }_0\left(\lambda \right)$ on the solutions of $I_{\lambda }\left(x,\mathsf{\Omega }\right)$ at different wavelengths. There are multiple ways in the literature [35,52,66] to derive the spectral invariants theory. Below we follow the SOSA approach described in Reference [66], which represents the most general case and is the easiest to understand. We will use the black-soil problem as the example, though the same methods can be applied to the “S” problem as well [67].

Recall that the black-soil problem can be decomposed to successively collided problems, each of which satisfies the Law of Energy Conservation. For instance, integrating the first-collision problem over the spatial domain and the solid angles eventually leads to (Appendix A)

$$\underset{\delta V}{\overset{}{\int }}\mathrm{d}{x}_B\underset{\mathsf{\Omega }·\mathrm{n}\left(x_B\right)>0}{\overset{}{\int }}{Q}_1\left|\mathsf{\Omega }·\mathrm{n}\left(x_B\right)\right|\mathrm{d}\mathsf{\Omega }+\underset{4\pi \times V}{\overset{}{\int }}\sigma Q_1\mathrm{d}\mathsf{\Omega }\mathrm{d}x={\omega }_0\underset{4\pi \times V}{\overset{}{\int }}\sigma Q_0\mathrm{d}\mathsf{\Omega }\mathrm{d}x$$

(23)

or, by the norm notation [66],

$$\parallel Q_1\parallel {}_{\rho }+\parallel Q_1\parallel ={\omega }_0\parallel Q_0\parallel ,$$

(24)

where “$\parallel ·\parallel$” and “$\parallel ·{\parallel }_{\rho }$” indicate the intercepted and the escaped (either being reflected or transmitted) radiation energy, respectively. Equation (24) simply indicates that the portion (i.e., ${\omega }_0$) of photons scattered from the first collision will either escape through the boundary or collide with the canopy again.

Note that the stream-collision operator ($L$ or $L_0$) depends only on canopy structural parameters, and the un-collided radiation field $Q_0$ and the initial interceptance $\parallel Q_0\parallel$ are therefore wavelength independent. The first-collided radiation field $Q_1$ (and thus $\parallel Q_1\parallel$) is regulated by ${\omega }_0\left(\lambda \right)$, but the ratios

$$\begin{gathered} p_1=\frac{\parallel Q_1\parallel }{{\omega }_0\parallel Q_0\parallel } \\ {q}_1=\frac{\parallel Q_1\parallel {}_r}{{\omega }_0\parallel Q_0\parallel } \end{gathered}$$

(25)

are also wavelength independent. Physically $p_1$ represents the recollision probability that the scattered photons will re-collide with the canopy again and $q_1$ denotes the probability that the photos will escape the canopy. Clearly $p_1+q_1=1$, satisfying the conservation of energy.

Following the same idea, we normalize the radiation fields as

$$e_k\left(x,\mathsf{\Omega }\right)=\frac{Q_k\left(x,\mathsf{\Omega }\right)}{\parallel Q_k\parallel },k=1,2,\dots$$

(26)

It is easy to see that $\parallel e_k\left(x,\mathsf{\Omega }\right)\parallel =1$ and they satisfy the standard RTE

$$p_k{\omega }_0{e}_k=T{e}_{k-1}.$$

(27)

Equations (26) and (27) have clear physical interpretations: $e_k\left(x,\mathsf{\Omega }\right)$ represents the probability density function that a photon scattered k times will arrive at x along the direction $\mathsf{\Omega }$. Therefore, the operator $T$ transforms the probability distribution of photons between successive orders of scattering and evaluates their recollision probability [66]. Note that the factor ${\omega }_0$ is separated from $e_k\left(x,\mathsf{\Omega }\right)$ so that the normalized radiation fields are indeed wavelength-independent.

Based on the above definitions we can re-write the solution of the black-soil problem as:

$$I_{\lambda }\left(x,\mathsf{\Omega }\right)=\parallel Q_0\parallel \left(\sum _{k=0}^{\infty }{T}^k\right)\frac{Q_0}{\parallel Q_0\parallel }=i_0\sum _{k=0}^{\infty }{\theta }_k^k{\omega }_0^k{e}_k\left(x,\mathsf{\Omega }\right)$$

(28)

where $i_0=\parallel Q_0\parallel ,{\theta }_k=\sqrt{p_0{p}_1{p}_2\cdots p_{k}k},$ and $p_0=1$. Note that $i_0$, ${\theta }_k$, and $e_k\left(x,\mathsf{\Omega }\right)$ are all wavelength independent.

In Equation (28) if the ${\theta }_k$’s and the $e_k$’s change little (i.e., invariant) over the order of scattering, the equation can be significantly simplified. Fortunately, this is exactly what the spectral invariants theory suggests: Based on a fundamental property established for the eigenvalues/eigenvectors of the linear RTE operator T [68], the theory indicates that the RTE has a unique dominant eigenvalue ${\gamma }^{\ast }$ (or $p^{\ast }{\omega }_0$) that corresponds to a positive (and physically feasible) eigenvector $e^{\ast }\left(x,\mathsf{\Omega }\right)$, such that

$$p^{\ast }{\omega }_0{e}^{\ast }\left(x,\mathsf{\Omega }\right)=T{e}^{\ast }\left(x,\mathsf{\Omega }\right).$$

(29)

Therefore, if $e_0=e^{\ast }\left(x,\mathsf{\Omega }\right)$, we will subsequently have $e_k=e^{\ast }\left(x,\mathsf{\Omega }\right)$ and ${\theta }_k=p^{\ast }$, so that

$$I_{\lambda }=\frac{i_0{e}^{\ast }\left(x,\mathsf{\Omega }\right)}{1-{\gamma }^{\ast }}=\frac{i_0{e}^{\ast }\left(x,\mathsf{\Omega }\right)}{1-p^{\ast }{\omega }_0\left(\lambda \right)}.$$

(30)

Although the set ($p_k{\omega }_0$, $e_k$) derived by the SOSA method are generally different from the ideal eigenvalue-eigenvector pair ($p^{\ast }{\omega }_0$, $e^{\ast }$), analyses show that they converge rapidly so that we only need a couple of ($p_k$, $e_k$) pairs to accurately represent the full solution of Equation (28). For instance, Reference [66] uses a zero-order approximation to satisfactorily estimate the recollision probability $p^{\ast }$ and the initial interceptance $i_0$ from field measured $i\left(\lambda \right)$ and ${\omega }_0\left(\lambda \right)$. A detailed analysis of the SOSA approximation can be found in Reference [66] and earlier studies [69,70,71,72]. Consistent results are also supported by simulations from Monte Carlo Ray Tracing (MCRT) models [73,74,75]. The key message is that once we have estimated a few parameters and functions ($p_k$, $e_k$, and $i_0$), the solution $I_{\lambda }\left(x,\mathsf{\Omega }\right)$ can be easily obtained with the knowledge of ${\omega }_0$ at any other wavelength (Figure 1).

The interpretation of the parameter $p^{\ast }$ as the recollision probability of photons by Reference [76] represents an important contribution to the spectral invariants theory. It helps us develop a physical intuition to the mathematical concept of the leading eigenvalue of the RTE and associate it with measurable structural properties of vegetation canopies. Once established, the interpretation sees immediate applications in scaling relevant canopy properties across different canopy hierarchies [32,74,76]. For instance, suppose $p_{sh}^{\ast }$ and $p_{cr}^{\ast }$ are the recollision probabilities of shoots and crowns, the overall $p^{\ast }$ parameter for the two-level canopy, resulting from a finite-state Markov process [67], naturally follows

$$p^{\ast }=p_{sh}^{\ast }+\left(1-p_{sh}^{\ast }\right)p_{cr}^{\ast }.$$

(31)

Similarly, the apparent single scattering albedos of two levels of canopy structures (e.g., shoots and crowns) are related by

$${\omega }_{cr}=\frac{{\omega }_{sh}\left(1-p_{sh}^{\ast }\right)}{1-p_{sh}^{\ast }{\omega }_{sh}}.$$

(32)

It can be easily verified that the canopy scattering albedo $W$ can be represented by either ${\omega }_{cr}$ or ${\omega }_{sh}$ [76]:

$$W=\frac{{\omega }_{cr}\left(1-p_{cr}^{\ast }\right)}{1-p_{cr}^{\ast }{\omega }_{cr}}=\frac{{\omega }_{sh}\left(1-p^{\ast }\right)}{1-p^{\ast }{\omega }_{sh}}.$$

(33)

Therefore, the single albedo of a higher level structure (e.g., ${\omega }_{cr}$) totally encapsulates the scattering properties of the lower level structures (e.g., ${\omega }_{sh}$). The overall scattering coefficients of the crown (or the canopy) will not change if we replace the shoots (needles) with broadleaves of the same (apparent) single albedo. This property suggests that we can use the same set of simulation results (i.e., Look-Up Tables) to retrieve effective structural parameters for both clumped and non-clumped canopies. Additionally, the scaling rules of the recollision coefficients and the scattering coefficients are often associated with changes in spatial scales. They can be used to generate consistent products from satellite sensors operating at different spatial resolutions [77,78]. A detailed review of the physical interpretation of the $p^{\ast }$ parameter, its links with measurements, and the scaling rules can be found in a recent review by Reference [45].

In practice, the recollision probability ($p^{\ast }$) of a vegetation canopy can be estimated from field measurements of canopy reflectance, absorptance, transmittance, and single-scattering albedo [66,72]. In remote sensing applications, the common measurements of the surface after atmospheric corrections are the bidirectional reflectance factor (BRF). Therefore, it is desirable to derive a relationship between BRFs and the spectral invariant parameters. Note that under the assumption that the irradiance of the incoming solar radiation is unity, the BRF is just the averaged top-of-canopy radiance (Equation (28) or Equation (30) for the ideal case) multiplied by a constant factor ($\pi$). The desired relationship is thus [52]

$${\mathrm{BRF}}_{\lambda }\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)=\frac{\pi p_A\langle e{\left(x_B,\mathsf{\Omega }\right)\rangle }_{x_B}{i}_0}{1-p_A}·\frac{{\omega }_0\left(\lambda \right)\left(1-p_A\right)}{1-{\omega }_0\left(\lambda \right)p_A},$$

(34)

where $\langle ·{\rangle }_{x_B}$ denotes spatial average over the canopy boundary $x_B$, and $p_A$ denotes the effective recollision probability. In Equation (34) we have neglected the un-collided component of the radiance, as it does not contribute to the reflectance.

In Equation (34) the first term on the right side combines the recollision probability ($p_A$), the interceptance ($i_0)$, and canopy escape probability ($q_A=\pi p_A\langle e{\left(x_B,\mathsf{\Omega }\right)\rangle }_{x_B}$), all being spectral invariant. We define this term the Directional Area Scattering Factor (DASF) [52,79],

$$\mathrm{DASF}\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)=\frac{q_A\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)i_0\left({\mathsf{\Omega }}_0\right)}{1-p_A},$$

(35)

which can be understood as the BRF for a purely reflective canopy (e.g., ${\omega }_0=1$). The second term on the right side of Equation (34) is just the canopy scattering coefficient $W$ in Equation (33). Therefore, BRF is succinctly represented by the product of DASF and the canopy single scattering albedo $W$.

An important feature of DASF is that it is measurable from both field observations and satellite remote sensing data. When ${\omega }_0\left(\lambda \right)$ is known, DASF can be easily estimated from ground measurements of spectral BRF using the inverse linear regression method [66]. In remote sensing applications where ${\omega }_0\left(\lambda \right)$ is difficult to obtain, Reference [49] developed an algorithm to retrieve DASF from BRF between 710 nm and 790 mm with an intrinsic leaf scattering spectrum ${\varpi }_0\left(\lambda \right)$, where ${\varpi }_0\left(\lambda \right)$ is computed with theoretical models. A key component of the algorithm is to use the scaling rule of Equation (33) to estimate ${\omega }_0\left(\lambda \right)$ from ${\varpi }_0\left(\lambda \right)$ with a within-leaf recollision probability $p_L$, an intermediate variable that is later cancelled from the calculation. The algorithm is recently used in Reference [80] to derive a global DASF map from the GOME-2 (Global Ozone Monitoring Experiment-2) data.

Of the above spectral invariant parameters, only $p^{\ast }$ is an intrinsic property of the canopy while the others ($i_0$, $p_A$, $q_A$ and DASF) are influenced by the external illumination conditions. The values of these parameters generally change with the direction of the incident beam (${\mathsf{\Omega }}_0$). Indeed, the directional illumination has an important effect on the angular signature of canopy BRF (and DASF), which we review in the next section.

6. The “Hot-Spot” Problem

In optical remote sensing, the term “hot spot” refers to the phenomenon that the canopy reflectance has a sharp peak in the retro-illumination direction. The main physical mechanism of the phenomenon is the mutual shadowing of the canopy elements. This is because shadows are invisible from the backscattering direction but become increasingly visible when the view and the illumination angles deviate away from each other [33,36].

It is known that the classic RTE has difficulties simulating the hot-spot effects. This is because the stream-collision operator, which follows the Beer’s law, is essentially formulated for gaseous media where the spatial distribution of the scatters is statistically independent at all spatial scales [34]. On the contrary, leaves have finite sizes and their spatial distributions are intrinsically correlated at a certain level. To illustrate the difference between the two cases, we consider a conceptual experiment that a purely absorptive (${\omega }_0$ = 0) canopy bounded below by a perfect mirror (${\rho }_{\lambda }$ = 1) that is positioned to reflect the nadir incident photons back along the same paths they come from (i.e., the retro-illumination direction). Let the optical depth of the canopy be $\sigma$ and the intensity of the radiation beam be 1. Under the gaseous media assumption, the intensity of the reflected radiation beam at the top of the canopy will be $\exp \left(-2\mathsf{\sigma }\right)$, attenuated by the same fashion on the incident and the return paths. For finite-sized leaves, the intensity of the reflected radiation will be $\exp \left(-\mathsf{\sigma }\right)$, for all the photons that reach the lower surface (i.e., mirror) are guaranteed a free path to travel through the canopy on the way back.

The above example suggests that, due to the effects of mutual shadowing, the canopy extinction cross section in the backscattering direction $\mathsf{\sigma }\left(x,-{\mathsf{\Omega }}_0\right)$ appears to be smaller than those of other directions. Therefore, previous efforts to model the hot-spot phenomenon focused on developing a function $H(x,\mathsf{\Omega },{\mathsf{\Omega }}_0$) to regulate the cross section $\mathsf{\sigma }\left(x,\mathsf{\Omega }\right)$, especially for the first collision component [33,81,82,83]. However, the incorporation of $H(x,\mathsf{\Omega },{\mathsf{\Omega }}_0$) in the RTE is equivalent to the introduction of an additional source term in the equation. As a result, the solution no longer satisfies the law of energy conservation [35].

Recently, Reference [79] developed a new algorithm that uses the spectral invariant theory to model the spectral BRF of vegetation canopies in the hot-spot region. A key idea of the algorithm is to decompose the canopy into sun-lit and sun-shaded leaf area, where the former is referred to as the “stochastic reflecting boundary” and the latter as the “interior” of the canopy. Photons escaping from the sun-shaded leaf area must have gone through multiple scattering. Thus, their escape probability approximately converges to a certain value, $q_{iso}\left(\mathsf{\Omega }\right)$. Photons reflected from the sun-lit leaf area that is visible from the direction $\mathsf{\Omega }$ can escape with a unit probability. Thus, their conditional escape probability, $q_{lit}\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)$, is expected to be higher than $q_{iso}\left(\mathsf{\Omega }\right)$. Therefore, we need to evaluate their contribution to the canopy directional escape probability $q_A\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)$ separately. Let $h\left({\mathsf{\Omega }}_0,\mathsf{\Omega }\right)$ represent the correlation between the sun-lit and the visible leaf areas. The probability $q_A\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)$ is therefore composed of two components that is weighted by $h\left({\mathsf{\Omega }}_0,\mathsf{\Omega }\right)$ as

$$q_A\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)=\left[1-h\left({\mathsf{\Omega }}_0;\mathsf{\Omega }\right)\right]q_{iso}\left(\mathsf{\Omega }\right)+h\left({\mathsf{\Omega }}_0;\mathsf{\Omega }\right)q_{lit}\left({\mathsf{\Omega }}_0;\mathsf{\Omega }\right).$$

(36)

Similarly, we can decompose DASF and BRF by contributions from the interior leaves and the stochastic boundary separately [79].

In the above equation $q_{lit}\left({\mathsf{\Omega }}_0;\mathsf{\Omega }\right)$ can be evaluated from canopy structural properties and $q_{iso}$ can be estimated with the classic RTE [79]. Therefore, if the correlation function $h$ is known, we can estimate $q_A$. Conversely, if $q_A$ is known, we can estimate the correlation function $h$ as [79]

$$h\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)=\frac{q_A\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)-q_{iso}\left(\mathsf{\Omega }\right)}{q_{lit}\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)-q_{iso}\left(\mathsf{\Omega }\right)}.$$

(37)

The current algorithm of Reference [79] uses the latter approach to evaluate correlation coefficient $h\left({\mathsf{\Omega }}_0;\mathsf{\Omega }\right)$ with a stochastic RTE (Section 3) that is modified to incorporate an additional hot-spot parameter $c_{HS}$ [36]. The stochastic RTE needs to run twice, with an actual $c_{HS}$ and with a zero value, respectively, in order to evaluate $q_A\left(\mathsf{\Omega };{\mathsf{\Omega }}_0\right)$ and $q_{iso}\left(\mathsf{\Omega }\right)$ [79].

The algorithm of Reference [79] has two main benefits. First, some of the intermediate results are easy to verify with field measurements. For instance, the visible fraction of leaf area (VFLA) can be estimated with below canopy measurements of transmittance $t_0\left(\mathsf{\Omega }\right)$ as [79]

$$VFLA\left(\mathsf{\Omega }\right)=\frac{1-t_0\left(\mathsf{\Omega }\right)}{\left|\ln \left(t_0\left(\mathsf{\Omega }\right)\right)\right|}=\frac{i_0\left(\mathsf{\Omega }\right)}{\left|\ln \left(t_0\left(\mathsf{\Omega }\right)\right)\right|},$$

(38)

and the canopy DASF under isotropic illumination conditions (an approximation for the interior canopy component) can be estimated as [79]

$$\frac{q_{iso}\left(\mathsf{\Omega }\right)i_0\left({\mathsf{\Omega }}_0\right)}{1-p_{iso}}\approx \frac{i_0\left(\mathsf{\Omega }\right)i_0\left({\mathsf{\Omega }}_0\right)}{2·i_{dif}},$$

(39)

where $i_{dif}$ is the canopy interceptance under the isotropic sky radiation [84]. These relationships provide a set of convenient tools to validate the solutions.

Second and more importantly, the spectral invariants relationships do not necessarily depend on the formulation of the classic RTE but are supported by both observations and the simulation results of MCRT models, whose formulation does not require Beer’s law at all [85]. Therefore, the spectral invariants relationships may conserve energy and capture the hot-spot phenomenon at the same time. Reference [79] illustrates this potential with a simple stochastic Monte Carlo model. Though the algorithm is still subjected to further examinations and refinements in the future, it introduces a new and promising perspective to address the old challenge.

7. Summary

This paper reviews developments of the radiative transfer theory in optical remote sensing of terrestrial vegetation, including the decomposition of the black-soil (BS) and the soil (S) problems, the development of the stochastic RTE, the theory of spectral invariants, and the latest effort to address the “hot-spot” challenge. The first three topics are centered around the idea as how to simplify the solutions of the RTE under different boundary conditions (e.g., soil reflective properties), over full 3-dimensional spatial domains, and with regard to radiation at different wavelengths. The last topic is intended to highlight the advantage of the spectral invariants theory in remote sensing applications.

As the RTE is linear as regard to $I_{\lambda }$, a fundamental strategy to solve the equation is decomposition and superposition. The separation of the black-soil and the soil problems, the expansion of Neumann’s series, and the method of successive orders of scattering approximation discussed in Section 3 are all demonstrations of this strategy. The concept of invariants, the convergence of the radiation field to a certain distribution that does not change (except for the magnitude) over subsequent scattering, is also a natural result that follows the line of thinking. The existence of such a unique intrinsic solution is backed by the mathematical theories of eigenvalues/eigenvectors of the RTE and the physical law of energy conservation.

Another important thread of developments in the Stochastic RTE and the spectral invariants theory is to efficiently represent the canopy structural or geometrical information in the equation. The stochastic RTE introduces a pair-correlation function $K\left(z,z^{\prime },\mathsf{\Omega }\right)$, which describes the probability of simultaneously finding leaves at two locations $\left(z,z^{\prime }\right)$ along the direction $\mathsf{\Omega }$. It characterizes the heterogeneity and anisotropy characteristics of the canopies and regulate the corresponding cross sections ($\sigma$ and ${\sigma }_s$). Therefore, the function provides a natural and physically meaningful measure of 3D canopy structural properties over a range of scales.

The spectral invariants theory further simplifies the representation of canopy structural characteristics to a single wavelength-independent parameter $p^{\ast }$, which defines the recollision probability that a scattered photon will interact with the canopy again. Once $p^{\ast }$ (and the corresponding escape probability function) is estimated, we can accurately approximate the solution (radiance or BRF) of the RTE at any other wavelength with the knowledge of ${\mathsf{\omega }}_0\left(\mathsf{\lambda }\right)$, which imbues the wavelength-dependent influence on the radiation field. As $p^{\ast }$ represents recollision probability, it can be used to scale canopy properties (e.g., scattering coefficients) across various canopy hierarchies or spatial scales.

Although the pair-correlation function $K\left(z,z^{\prime },\mathsf{\Omega }\right)$, the photon recollision probability $p^{\ast }$, and the other spectral invariants functions/parameters such as DASF appear to be “abstract,” they all can be estimated from field measurements or remote sensing data. For instance, the pair-correlation function can be derived from high-resolution satellite images and lidar data. The recollision probability of a vegetation canopy can be determined from field measurements of canopy reflectance, absorptance, transmittance, and single-scattering albedo with simple linear correlations. DASF can also be retrieved directly from ground measurements or hyperspectral remote sensing data between 710 nm and 790 mm for dense vegetation in a similar fashion. These concepts, backed by rigorous mathematical analysis and physical principles, thus represent our current best understanding of the empirical relationships identified from observations.

The spectral invariants theory also provides a promising approach to solve the “hot-spot” problem known to the classic RTE models. This challenge has its roots in the formulation of the equation based on the turbid medium assumption and Beer’s law. On the contrary, leaves are finite sized and their spatial correlations cannot be neglected. Previous efforts to address this problem usually introduce a semi-empirical factor to regulate the extinction cross section in the equation, which however violate the law of energy conservation. A new algorithm was recently developed to address the challenge based on the spectral invariants theory. The algorithm decomposes the canopy into a reflective boundary and interior points and models the escape probability (and DASF) for the two components separately. The directional escape probability from the reflective boundary is assumed to be unity, a feature that cannot be simulated by the classic RTE. As such, the new approach does not depend on the Beer’s law formulation in the RTE but satisfies the law of energy conservation. This example further demonstrates the spectral invariants theory as a powerful tool in optical remote sensing applications.