Abstract
Generally, the characterization of land surface roughness is obtained from the analysis of height variations observed along transects (e.g., root mean square (RMS) height, correlation length, and autocorrelation function). These surface roughness measurements are then used as inputs for surface dynamics modeling, e.g., for soil erosion modeling, runoff estimation, and microwave remote sensing scattering modeling and calibration. In the past, researchers have suggested various methods for estimating roughness parameters based on ground measurements, e.g., using a pin profilometer, but these methods require physical contact with the land and can be time-consuming to conduct. The target of this research is to develop a technique for deriving surface roughness characteristics from digital camera images by applying photogrammetric and geographical information systems (GIS) analysis techniques. First, ground photos acquired by a digital camera in the field were used to create a point cloud and 3D digital terrain model (DTM). Then, the DTM was imported to a GIS environment to calculate the surface roughness parameter for each field site. The results of the roughness derivation can be integrated with soil moisture for backscattering simulation, e.g., for inversion modeling to retrieve the backscattering coefficient. The results show that the proposed method has a high potential for retrieving surface roughness parameters in a time- and cost-efficient manner. The selection of homogeneous fields and the increased spatial distribution of sites in the study area will show a better result for microwave backscattering modeling.
1. Introduction
Surface roughness plays a key role in microwave remote sensing backscattering and modeling and is an important parameter for studies on soil moisture, soil erosion, and hydrological processes. Microwave remote sensing images are commonly used for large-area soil moisture retrieval and mapping from space, but despite much research, accurate soil moisture estimation is still challenging due to the inherent dependency of the backscattered microwave radiation on both the geometric and dielectric properties of the land surface [1,2,3,4,5]. The dielectric constant of natural surfaces (e.g., soil or water) can be measured directly, but the land or water surface roughness conditions adversely affect most remote measurements of this parameter closely related to soil water content [5,6,7,8]. Soil surface roughness can be considered as a stochastic height variation of the soil surface towards a reference surface. Generally, the characterization of surface roughness is obtained from the analysis of height variations observed along transects, from which the RMS height, correlation length, and autocorrelation function are commonly calculated as the input(s) to backscatter models [4,6,9]. Although in recent years some methods have been developed for inverting both soil moisture and soil surface roughness separately using multi-temporal synthetic aperture radar (SAR) images and/or multi-frequency, multi-polarized SAR data, their performance has mainly been evaluated at relatively small scales, and their suitability for large-area operational usage is therefore uncertain [10,11,12].
Researchers have suggested several methods for estimating surface roughness parameters to allow for the more accurate retrieval of dielectric properties. These methods can be divided into two groups: those using instruments which make physical contact with the soil surface (i.e., contact instrument methods), and those using instruments which do not make physical contact with the surface (i.e., noncontact instrument methods) [7]. The contact instrument group comprises, e.g., meshboards and pin profilometers, while the noncontact group includes laser profilers, image photogrammetry, acoustic backscatter, infrared, and ultrasonic techniques [10]. Meshboards and needle profilers are still the most common instruments used for measuring soil surface roughness [11]. The main disadvantage of pin profilers and meshboards is that they are contact instruments which may modify the surface profile being measured. Because all these methods provide only 2D measurements, they are poorly suitable for roughness characterization over agricultural soils, which often present some degree of anisotropy due to tillage operations [10]. Because microwave scattering is the result of the interaction of the incident electromagnetic wave with the soil surface, 3D measurements are preferable.
In recent years, various researchers have used laser profilers [13,14] or 3D photogrammetric approaches [15,16]. The main downside of laser scanners with millimeter accuracy over extended areas is their cost. Photogrammetry might be more affordable but has other limitations. Several authors have related the first hurdle to a poor characterization of surface roughness over natural soils due to the limited capabilities of current in situ roughness measurement methods. The parameterization of soil surface roughness and its description in the available backscatter model are the main reason for this insufficiency [10,17].
A number of studies have involved experimentation at fine scales for the retrieval of soil surface roughness, but few have used photogrammetric approaches to computing the roughness index. These studies using photogrammetric approaches have mainly utilized images from unmanned aerial vehicle (UAV)-borne sensors, while only two studies we are aware of have utilized images from hand-held cameras. [4,6,18]. Photogrammetry is a science of surveying and mapping measurements, often from photographs [19]. In recent years, due to the widespread availability of cameras in smartphone devices, as well as the possibility of acquiring very high spatial resolution aerial imagery from drones, photogrammetric techniques have become an effective and cost-efficient method to easily create the digital surface and 3D models [20,21]. This new camera technology can help researchers to extend the usages of photogrammetry to study various environmental processes by studying and modeling land surface change dynamics. In previous research, photogrammetric techniques have been used for land surface modeling and characterization to derive micro-scale soil roughness. In most recent approaches, researchers have tried to estimate soil moisture without roughness, input the other environmental factors in backward modeling, and extract the roughness from a digital elevation model (DEM), but this method is challenging due to various problems including the unavailability of the environmental factors in the field, and it requires very precise measurements of in situ soil moisture. Baghdadi et al. applied the inverse model using Sentinel-1 data to estimate the surface roughness (Hrms) over agriculture fields, however the results showed the overestimation of roughness parameterization [22]. On the other hand, for inverse backscatter modeling the accurate in situ soil moisture is required, which is difficult and costly to obtain. Recently, working with cameras that are not particularly designed for the requirements of photogrammetry has become common in close-range applications [23,24,25]. However, we proposed to introduce this method to calculate the microwave remote sensing surface roughness parameter.
The main goal of this research is to use and analyze common camera photos to derive the surface roughness parameter for microwave remote sensing backscatter modeling in agricultural areas. In this study, we measure and evaluate the parameterization of surface roughness in an agricultural field by the acquisition of images from a hand-held camera to support the SAR soil moisture retrieval.
2. Material and Methodology
2.1. Image Acquisition and Processing
The proposed surface roughness measurement process consists of four main parts: (1) reference area setup; (2) photographic image acquisition; (3) image processing with Agisoft Photoscan; and (4) computation. The first step involves conducting fieldwork and collecting SAR data. In this study, we used test plots containing 36 different agricultural plots toward the soil moisture retrieval in the Garmsar region, northern Iran [7,9]. This manuscript will only present the image acquisition of the agricultural field in the mechanized furrow of the harvested wheat field within the varied field types of this study. For the photographic image acquisition step, a commercial camera (specifications in Table 1) was used to take images of field plots approximately 3 × 2 m in size. Reference targets were included in each plot to make multi-angle and scheme acquisitions of the same soil surface possible and to allow for scaling the final generated 3D model to create the DEM.

Table 1.
Specifications of the camera.
Two sets of images were taken in each plot at a height of about 1 m, with a total of 50 images taken to cover each plot. These images were used to capture small ground surface roughness features. These features can be captured without detailed images of the soil and it is sampled over a reduced surface area with close-range images; thus, we used the close range image to reduce the soil detailed. For reaching the goal of this work, it should acquisition the photos in aligning the plot of study which the photos must overlap by at least 30% although there are different scenarios for photography (Figure 1).
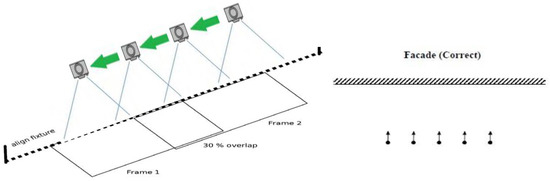
Figure 1.
Acquisition scheme for the sampling of roughness measurements with a single reference frame by photography capturing scenarios.
The third step, image processing with Agisoft PhotoScan, can perform countenance image alignment without any further information, but the implementation of initial estimates of camera positions is supported as well. Figure 2 shows the general workflow of the image processing chain in Agisoft PhotoScan (Figure 2). The camera orientations are calculated by image matching with common points, and the resulting digital terrain model (DTM) is defined based on the identified camera positions and the images [26]. The software can work with a minimum of two photos for 2D surface mapping, while for 3D mapping at least 10 aligned photos with 30–60% overlap are required (Figure 3 and Figure 4). Consequently, we captured the more than 50 photos aligned in each plot in the study area. Firstly, the image resolution was decreased from 2592 × 1728 pixels to 1728 × 1152 pixels, and then a set of images was inputted and the corresponding point cloud was generated, which was finally scaled using the reference points.
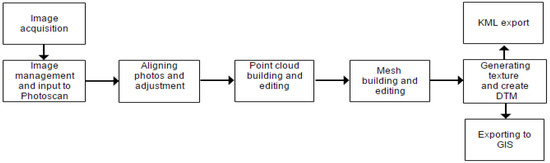
Figure 2.
The processing chain of image processing toward DTM in Agisoft.
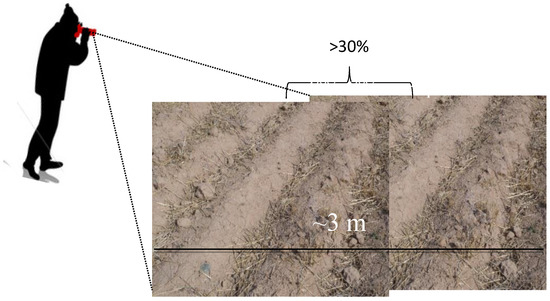
Figure 3.
Acquisition of reference frames by photography capturing in the field.

Figure 4.
The perspective model of DTM in Agisoft (a) and the export DEM (b).
It should be considered that for most DTM software, at least four ground control points (GCPs) are required in each plot; otherwise, generating a DTM would be impossible. Thus, a total of four reference points are spaced within each of the two imaged patches and used the four points marker in each plot and used the camera’s GPS device for referencing of each photo in the Agisoft for preprocessing.
2.2. Soil Surface Roughness Parameterization
The last step of the methodology is to compute the soil surface roughness, which can be characterized by a vertical and a horizontal component including root mean square (RMS) height and correlation length. Most radar backscattering models account for surface roughness with three parameters: RMS height, autocorrelation function, R, and correlation length [3,4,5,7,10]. The RMS describes the random surface characteristics, while the correlation length and correlation function describe the periodicity of the surface. In terms of the mean surface height () and the second moment (), the rms height to quantify the vertical component is represented by:
where z is the surface height in cm, which can be calculated by two difference height of two DEM of each plot. Then, the calculation of the rms height can be simplified to:
where s is the rms height in cm and Z is the height value in cm. Therefore, the Zi is computed by each point cloud in profile and the Ż is the average height of point clouds in each plot.
The horizontal roughness component is described by the autocorrelation length, l. For an efficient estimation of l, a variogram analysis is used. The inversion of the autocorrelation function (ACF) from a calculated theoretical directional variogram (γ(hj)) where l is defined as the distance (h) at which the ACF falls below e−1 [3].
Additionally, the rms height parallel and perpendicular to the tillage direction could be calculated separately to quantify the non-isotropic behavior of the sampled surface. The mean rms height parallel to the tillage direction is then defined as:
While the average RMS height perpendicular to the tillage direction is defined as:
As a consequence, the ratio / is a measure for the directionality of the surface roughness, where for a value of 1 the surface is an absolute isotropic scatter.
As roughness is a function of wavelength, its appearance changes with different wavelengths. Using lower frequencies, the illuminated target appears much smoother than at higher frequencies. To compensate for this effect, the RMS Height has to be scaled to the actual wavelength using the wavenumber, k, within the following equation:
where ks is the RMS height normalized to the wavenumber k and λ is the wavelength (which at the used L-band in the case of PALSAR data is 23.05 cm). As demonstrated by different authors, roughness parameters often change with the length of the profile over which they are estimated [3,10].
ks = s × k = s × 2π/λ
A photogrammetric approach was chosen for measuring soil surface roughness due to its 3D output and highly accurate estimates. Additional advantages for choosing a photogrammetric approach are its efficiency with regard to a decoupled acquisition and analysis compared to similar accurate acquisition setups.
3. Result and Discussion
This research mainly focused on categorizing soil roughness for developing microwave remote sensing backscattering models in areas containing mechanized agricultural land cover. Hand-held digital camera images were processed in Agisoft to create a 3D model and DEM (Figure 4a,b). Four referenced points were used for calibration of the plot images for georeferencing and to calculate the measurement errors, which are the difference in horizontal errors between x and y and comes from the acquisition process shown in Table 2. The RMS error in the z-direction (RMSEZ) of the sample plots is shown in Table 2. A high accuracy was observed in the generated DTMs compared to the reference frame in the result. The two examples of the generated DEM and 3D model are presented in the agricultural field of soil surface roughness in Figure 4 and Figure 5.

Table 2.
Average error for the 3D position of four control points.
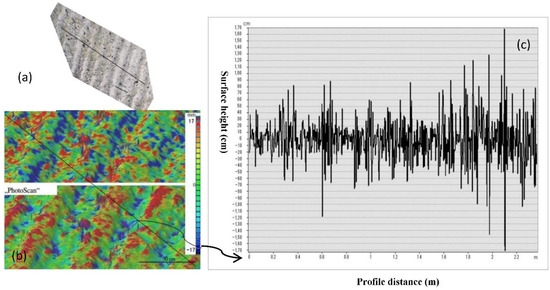
Figure 5.
The original photograph (a) and DEM (b) with a profile line (2.5 m) horizontal profile in ArcGIS 3D toolbox (c) surface height changes in the profile.
Figure 4 shows the exported DTM in tiff format, and Table 3 shows the characteristic of the computed The DTM was imported in a GIS software and the “3D Analyst” toolbox was used to make the profile stack and line features (Figure 5). This toolbox also allowed the computation of the height of each point along a line transect by deciding the interval and making graph of the profile, which is very useful for understanding the surface trend (Figure 5).

Table 3.
Characteristics of DEM.
The graph showed along the ~2-m profile which has a different height between −17 to 17 mm. By distinguishing the standard deviation of the RMS height of profiles in different plots, the soil surface roughness could be categorized into three groups: <2.5 cm (smooth roughness) in disk tilling field; 2.5–4 cm (moderate roughness) in plowed and tillage field; and >4 cm (rough) soil surface of furrow and mechanized cultivating field (Table 4).

Table 4.
The classification of the roughness types in the test site with real ground photos.
Currently, new methods such as laser scanner and photogrammetry techniques can produce DTMs with a maximum accuracy of a few millimeters. A higher accuracy can be expected from 3D measurements because of the larger number of measurement points available in the photogrammetry method. Although photogrammetry is becoming more accessible, special care needs to be taken for the setup (camera calibration, accuracy of external orientation with radar beam direction) and post-processing still requires knowledge of photogrammetry. That said, photogrammetry techniques represent a potentially robust, systematic, and accessible method to measure surface roughness.
4. Conclusions
In this paper, we proposed a simple approach for the measurement of land surface roughness using a hand-held digital camera and photogrammetry techniques. The derived surface roughness measurements can be used to improve microwave remote sensing backscatter modeling. Most recently, researchers have tried to use the inverse model for backscattering without parametrizing the surface roughness, however this method requires soil moisture measurement in situ and is often not applicable in the forward model because of the lack of in situ soil moisture data, and because it is very costly to set up the soil moisture measurement network.
The accuracy of our approach was acceptable compared with direct field surveying techniques (e.g., pin profile meter) for the purpose of supporting microwave remote sensing. Other new methods, such as the independent roughness model, showed the overestimation of the roughness parameter, and laser scanners still have thehurdle of being difficult to setup and very costly. This research only focused on the perpendicular direction assessment of surface roughness in the furrowed agricultural field, contrary to previous research which applied a multidimensional approach in microwave remote sensing. We found that photogrammetric techniques using stereo imagery can successfully generate the surface roughness in the agricultural land cover from smooth to rough surfaces. This method provides a very economical approach to support microwave remote sensing applications, e.g., backscattering, and soil moisture measurement. The difficulties are the short focal range of the handheld camera, which is a limitation for applying the methodology at larger scales than that of field plots. The investigation of surface roughness depends on the size of the image and close or far range of image acquisition; this means the scale of roughness index has a direct relationship, therefore for the small scale of roughness from the close range of an image can work better than far range. On the other hand, close range image acquisition can support only small plot areas and generate limited sized DEMs. Future studies should consider the different range of image acquisitions over time. Additionally, the anisotropy of images should be investigated because the backscattering characteristic is dependent on the direction of surface roughness.
Finally, this research initially confirmed that one of the benefits of photogrammetry is that common photographs can be utilized to recreate 3D DTMs for surface roughness measurements in a cost-effective way compared with, e.g., the pin-profile meter, laser scanners, or other equipment which have been used in the past for surface roughness microwave remote sensing.
Author Contributions
S.G. did the data processing and writing. R.T. and B.A.J. advised the methodology and revised the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schuler, D.L.; Lee, J.-S.; Kasilingam, D.; Nesti, G. Surface roughness and slope measurements using polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 687–698. [Google Scholar] [CrossRef]
- Gharechelou, S.; Tateishi, R.; Sharma, R.C.; Johnson, B.A. Soil Moisture Mapping in an Arid Area Using a Land Unit Area (LUA) Sampling Approach and Geostatistical Interpolation Techniques. ISPRS Int. J. Geo-Inf. 2016, 5, 35. [Google Scholar] [CrossRef]
- Marzahn, P.; Rieke-Zapp, D.; Ludwig, R. Assessment of soil surface roughness statistics for microwave remote sensing applications using a simple photogrammetric acquisition system. ISPRS J. Photogramm. Remote Sens. 2012, 72, 80–89. [Google Scholar] [CrossRef]
- Snapir, B.; Hobbs, S.; Waine, T. Roughness measurements over an agricultural soil surface with structure from motion. J. Photogramm. Remote Sens. 2014, 96, 210–223. [Google Scholar] [CrossRef]
- Marzahn, P.; Ludwig, R. On the Derivation of Soil Surface Roughness from MultiParametric PolSAR Data and its Potential for Hydrological Modeling. Hydrol. Earth Syst. Sci. 2009, 13, 381–394. [Google Scholar] [CrossRef]
- Marzahn, P.; Seidel, M.; Ludwig, R. Decomposing Dual-Scale Soil Surface Roughness for Microwave Remote Sensing Applications. Remote Sens. 2012, 4, 2016–2032. [Google Scholar] [CrossRef]
- Gharechelou, S.; Tateishi, R.; Sumantyo, J. Interrelationship Analysis of L-Band Backscattering Intensity and Soil Dielectric Constant for Soil Moisture Retrieval Using PALSAR Data. Adv. Remote Sens. 2015, 4, 15–24. [Google Scholar] [CrossRef]
- Oh, Y.; Kay, Y.C. Condition for precise measurement of soil surface roughness. IEEE Trans. Geosci. Remote Sens. 1998, 36, 691–695. [Google Scholar]
- Gharechelou, S.; Tateishi, R.; Sumantyo, J. Comparison of Simulated Backscattering Signal and ALOS PALSAR Backscattering over Arid Environment Using Experimental Measurement. Adv. Remote Sens. 2015, 4, 224–233. [Google Scholar] [CrossRef]
- Verhoest, N.E.C.; Lievens, H.; Wagner, W.; Mozos, J.Ã.; Moran, M.S.; Mattia, F. On the soil roughness parameterization problem in soil moisture retrieval of bare surfaces from synthetic aperture radar. Sensors 2008, 8, 4213–4248. [Google Scholar] [CrossRef] [PubMed]
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of surface parameters from polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 727–744. [Google Scholar] [CrossRef]
- Loew, A.; Hajnsek, I.; Schoen, H.; Jagdhuber, T.; Hoekman, D. Exploiting Longer Wavelength SAR Data for the Improvement of Surface Modelling; Tech. Rep. ESA Contract No. 19569/06/NL/HE; ESA: Paris, France, 2008. [Google Scholar]
- Alvarez-Mozos, J.; Verhoest, N.; Larranaga, A.; Casalf, J.; Gonzlez-Audfcana, M. Influence of surface roughness spatial variability and temporal dynamics on the retrieval of soil moisture from SAR observations. Sensors 2009, 9, 463–489. [Google Scholar] [CrossRef] [PubMed]
- Davidson, M.W.J.; Toan, T.L.; Mattia, F.; Satalino, C.; Manninen, T.; Borgeaud, M. On the characterization of agricultural soil roughness for radar remote sensing studies. IEEE Trans. Geosci. Remote Sens. 2000, 38, 630–640. [Google Scholar] [CrossRef]
- Blaes, X.; Defourny, P. Characterizing bidimensional roughness of agricultural soil surfaces for SAR modeling. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4050–4061. [Google Scholar] [CrossRef]
- Milenković, M.; Pfeifer, N.; Glira, P. Applying Terrestrial Laser Scanning for Soil Surface Roughness Assessment. Remote Sens. 2015, 7, 2007–2045. [Google Scholar] [CrossRef]
- Lievens, H.; Vernieuwe, H.; Alvarez-Mozos, J.; De Baets, B.; Verhoest, N. Error in radar-derived soil moisture due to roughness parameterization: an analysis based on synthetical surface profiles. Sensors 2009, 9, 1067–1093. [Google Scholar] [CrossRef] [PubMed]
- Kaźmierowski, C.; Jasiewicz, J.; Zwoliński, Z.; Mitasova, H.; Hengl, T. Soil surface roughness quantification using DEM obtained from UAV photogrammetry. In Geomorphometry for Geosciences, Adam Mickiewicz University in Poznań–Institute of Geoecology and Geoinformation; International Society for Geomorphometry: Tokyo, Japan, 2015. [Google Scholar]
- Rau, J.-Y.; Cheng, C.-K. A cost-effective strategy for multi-scale photo-realistic building modeling and web-based 3-D GIS applications in real estate. Comput. Environ. Urban Syst. 2013, 38, 35–44. [Google Scholar] [CrossRef]
- Jeong, H.H.; Park, J.W.; Kim, J.S.; Choi, C.U. Assessing the Accuracy of Ortho-image using Photogrammetric Unmanned Aerial System. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B1, 867–872. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Ahn, H.; Seo, D.; Park, S.; Choi, C. Feasibility of employing a smartphone as the payload in a photogrammetric UAV system. ISPRS J. Photogramm. Remote Sens. 2013, 79, 1–18. [Google Scholar] [CrossRef]
- Baghdadi, N.; El Hajj, M.; Choker, M.; Zribi, M.; Bazzi, H.; Vaudour, E.; Gilliot, J.-M.; Ebengo, D.M. Potential of Sentinel-1 Images for Estimating the Soil Roughness over Bare Agricultural Soils. Water 2018, 10, 131. [Google Scholar] [CrossRef]
- Rieke-Zapp, D.; Tecklenburg, W.; Peipe, J.; Hastedt, H.; Haig, C. Evaluation of the geometric stability and the accuracy potential of digital cameras comparing mechanical stabilisation versus parameterisation. ISPRS J. Photogramm. Remote Sens. 2009, 64, 248–258. [Google Scholar] [CrossRef]
- Rieke-Zapp, D.H. A digital medium-format camera for metric applications—Alpa 12 metric. Photogramm. Rec. 2010, 25, 283–298. [Google Scholar] [CrossRef]
- Barber, M.E.; Grings, F.M.; Álvarez-Mozos, J.; Piscitelli, M.; Perna, P.A.; Karszenbaum, H. Effects of Spatial Sampling Interval on Roughness Parameters and Microwave Backscatter over Agricultural Soil Surfaces. Remote Sens. 2016, 8, 458. [Google Scholar] [CrossRef]
- Orthophoto & DEM Generation (with GCPs). Available online: http://www.agisoft.com/support/tutorials/beginner-level/ (accessed on 28 October 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).


