Two-Step Urban Water Index (TSUWI): A New Technique for High-Resolution Mapping of Urban Surface Water
Abstract
1. Introduction
2. Study Areas and Materials
2.1. Study Sites
2.2. GF-2 Imagery
2.3. Reference Data
2.4. Image Preprocessing
3. Methodology
3.1. Pure Pixel Selection
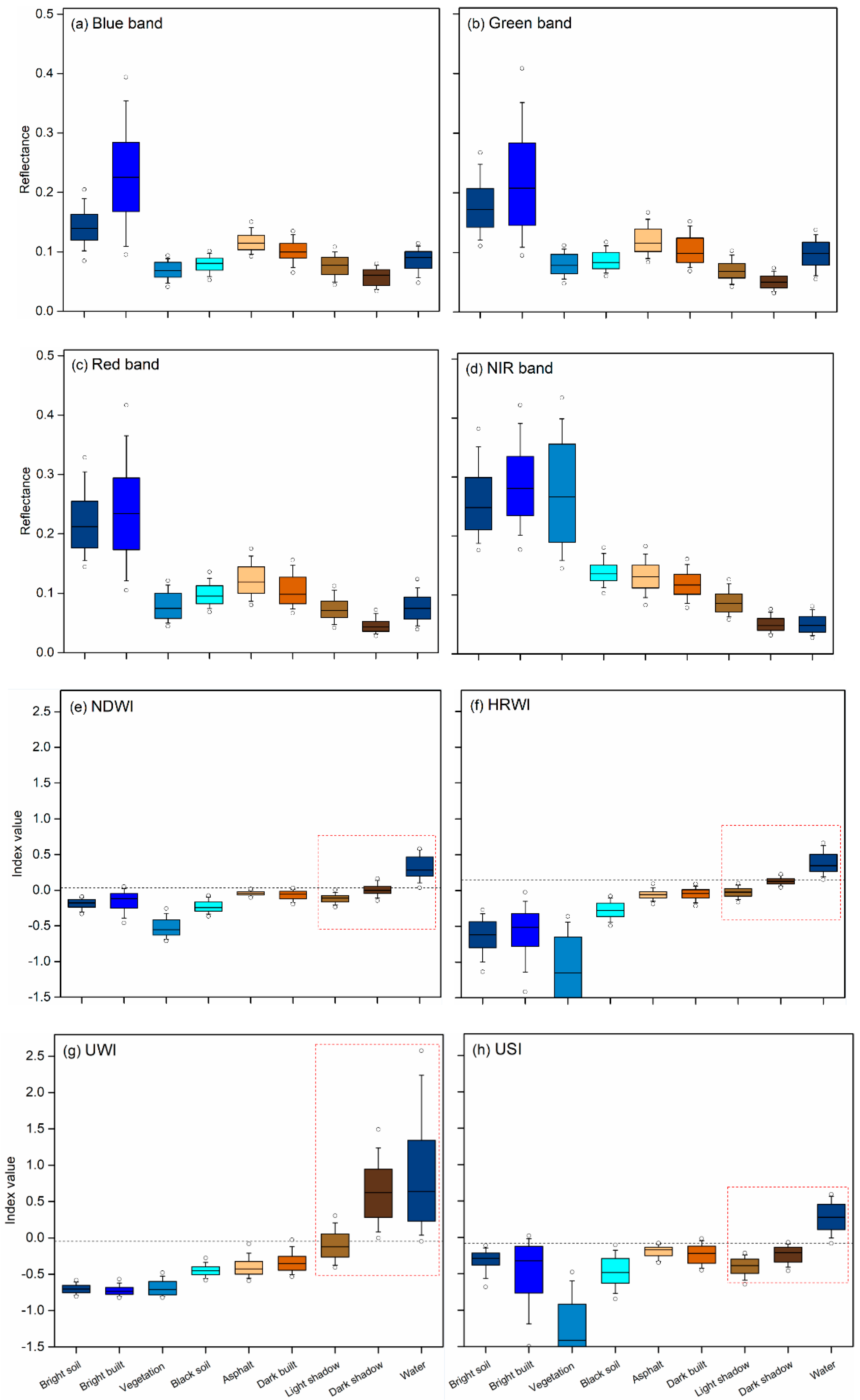
3.2. Spectral Features of Water and Non-Water Types
3.3. Constructing the Two-Step Urban Water Index
3.3.1. Linear Support Vector Machine
3.3.2. Formulation of the Urban Water Index (UWI)
3.3.3. Formulation of the Urban Shadow Index (USI)
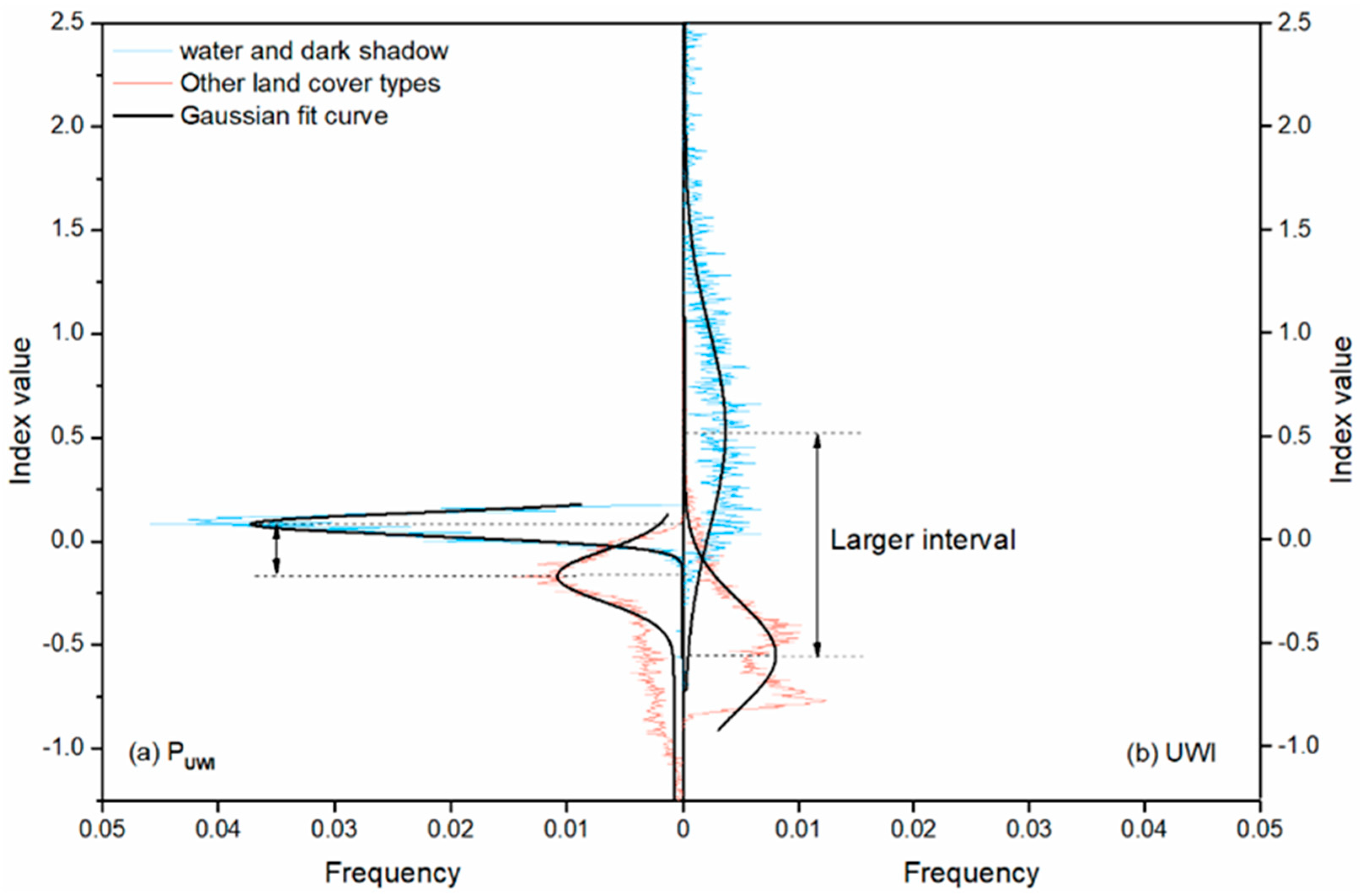
3.3.4. The Two-Step Urban Water Index
3.4. Assessment Methods
3.4.1. Accuracy Assessment
3.4.2. Threshold Stability Assessment
4. Results
4.1. Water Extraction Maps
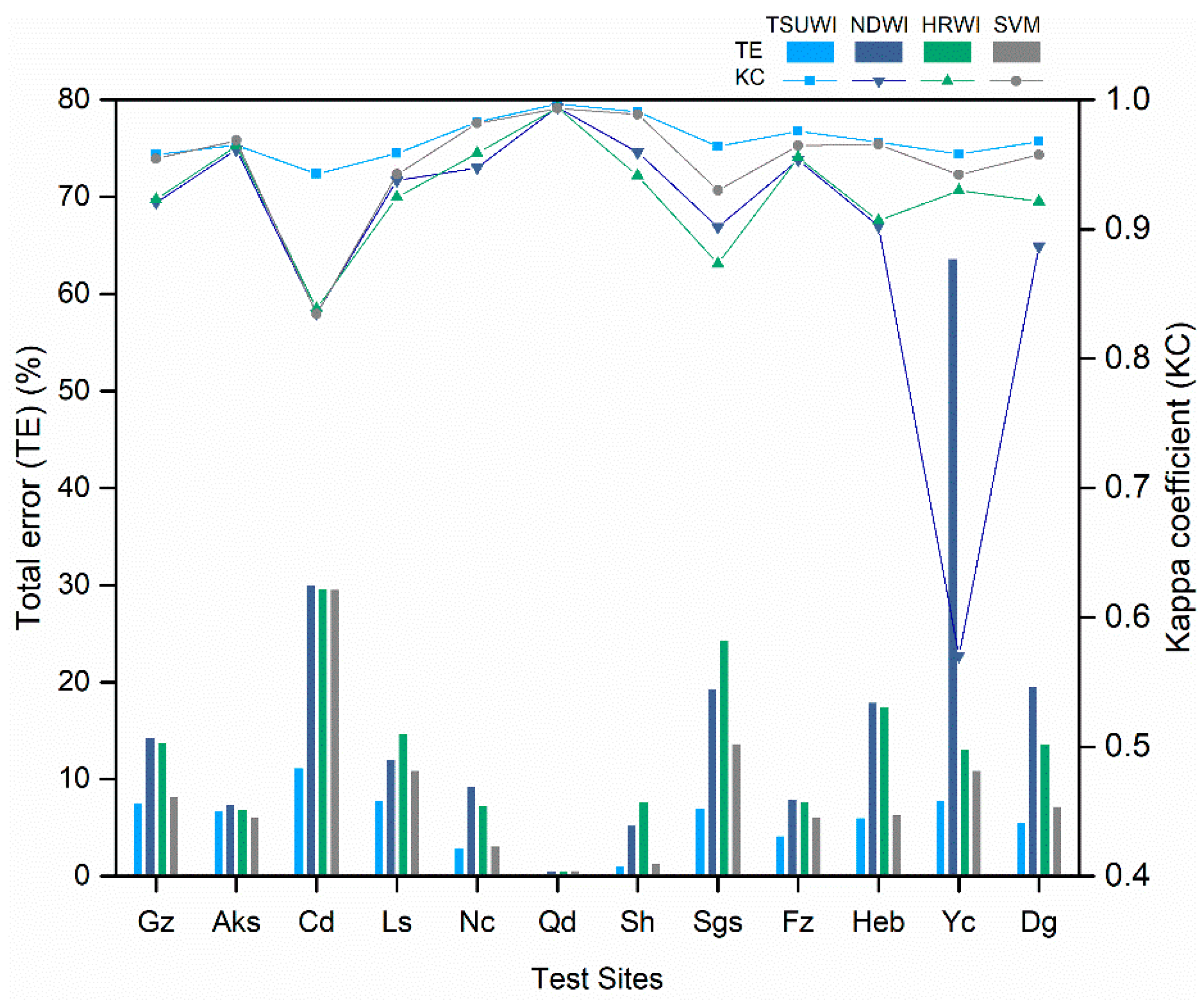
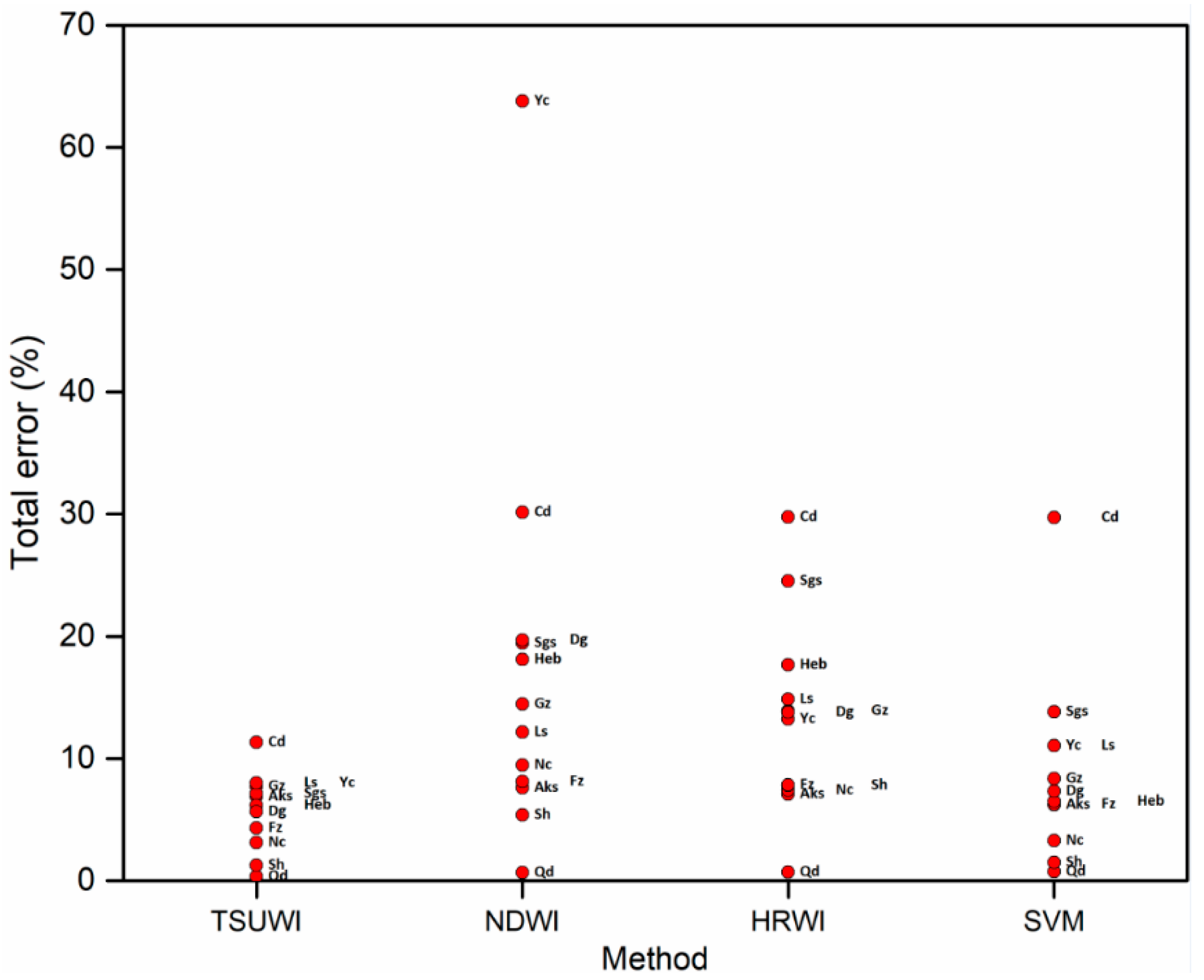
4.2. Water Extraction Accuracy
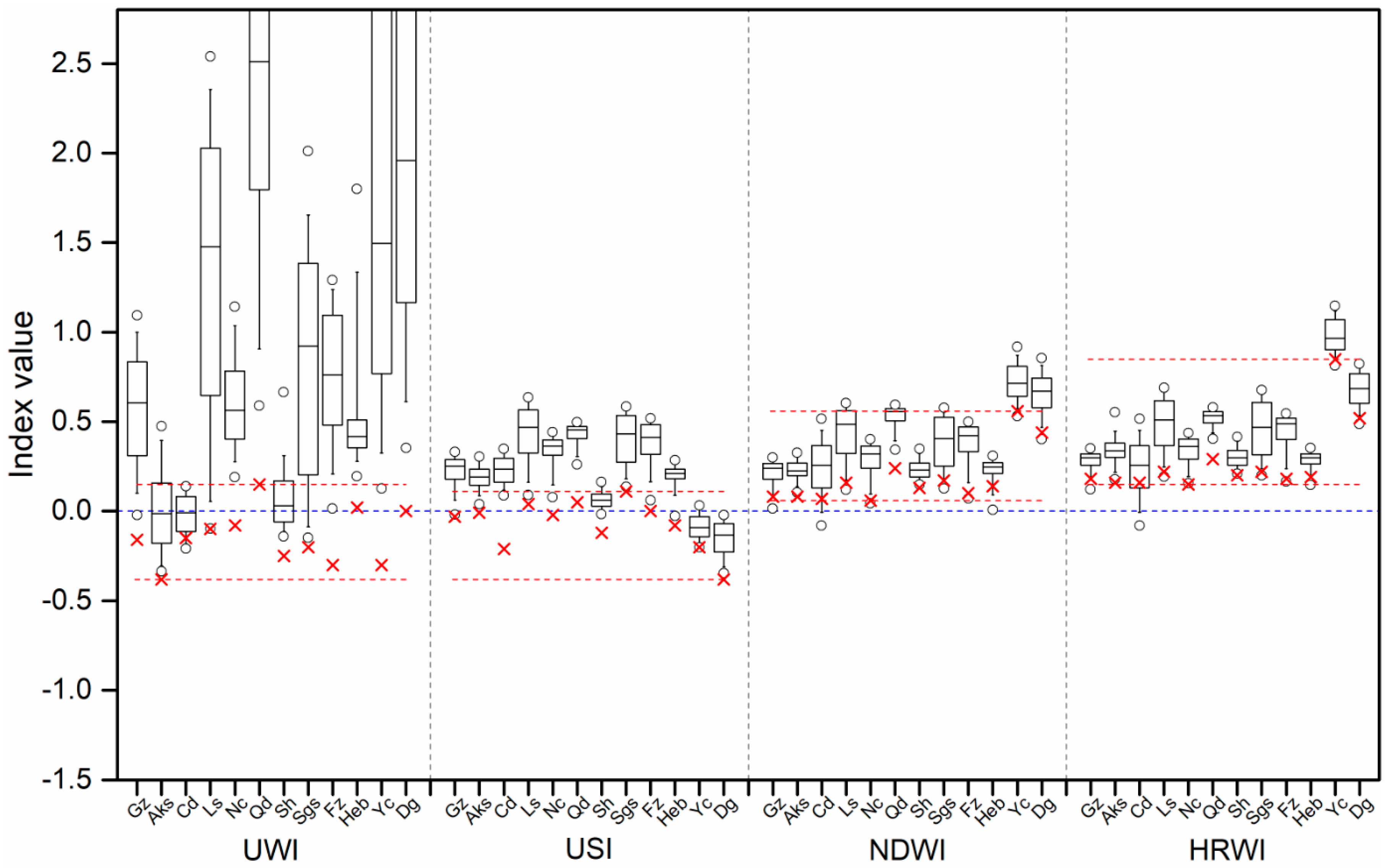
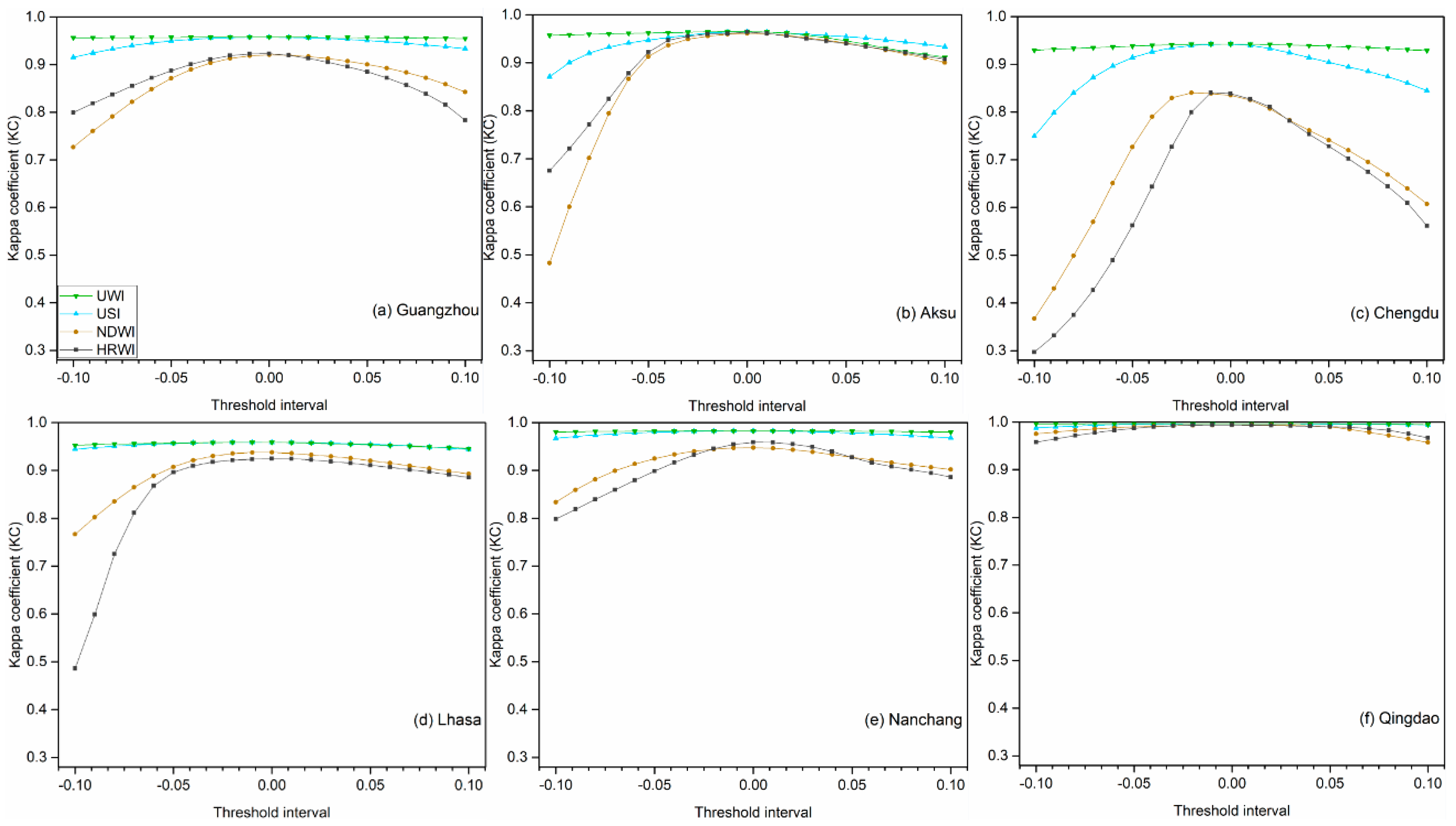
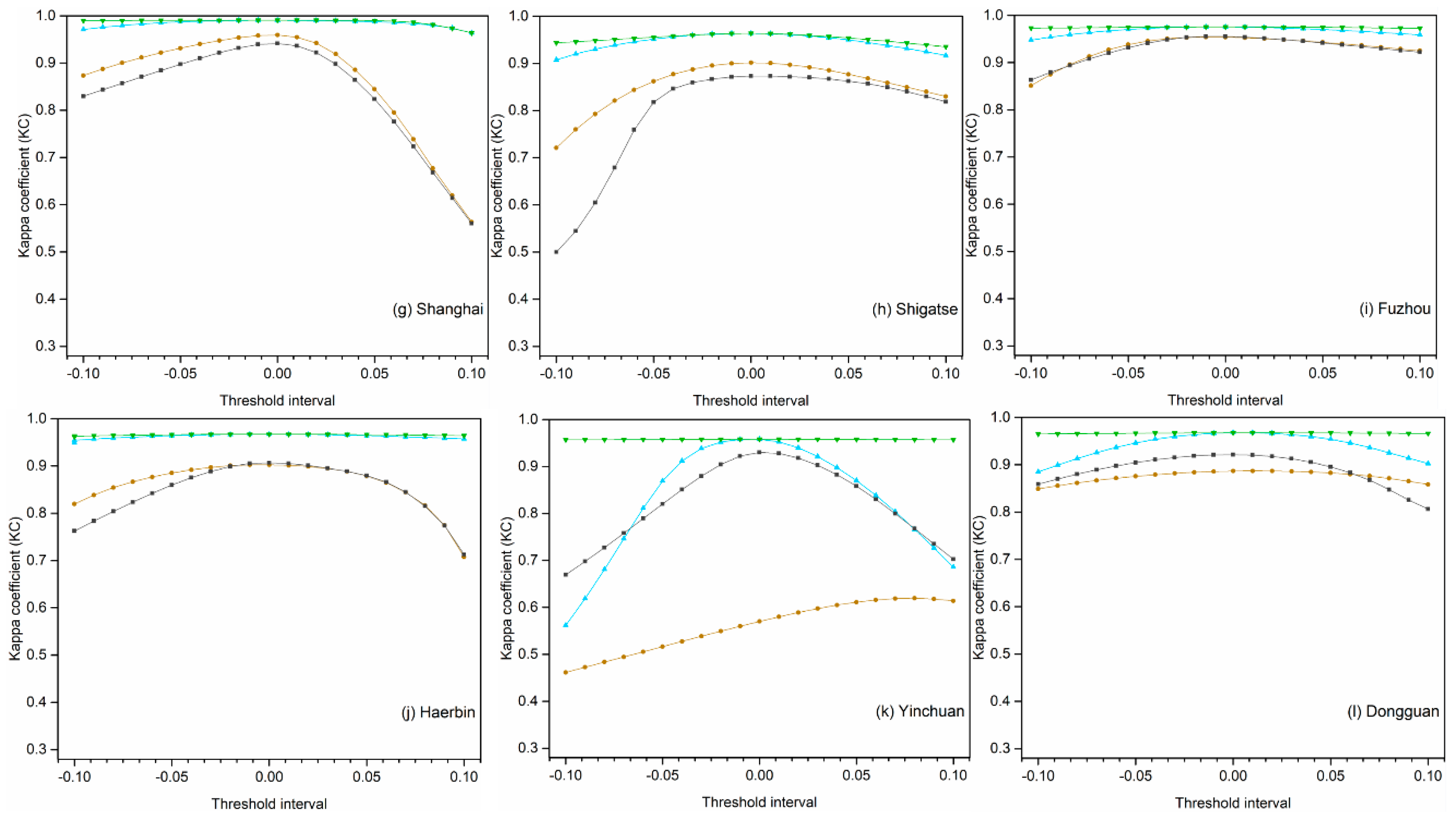
4.3. Threshold Stability Analysis
5. Discussion
5.1. Effects of Shadow Detection
5.2. Advantages of the Proposed Method
5.3. Further Improvements
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Kandulu, J.M.; Connor, J.D.; Macdonald, D.H. Ecosystem services in urban water investment. J. Environ. Manag. 2014, 145, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Robitu, M.; Musy, M.; Inard, C.; Groleau, D. Modeling the influence of vegetation and water pond on urban microclimate. Sol. Energy 2006, 80, 435–447. [Google Scholar] [CrossRef]
- Bond, N.R.; Lake, P.S.; Arthington, A.H. The impacts of drought on freshwater ecosystems: An Australian perspective. Hydrobiologia 2008, 600, 3–16. [Google Scholar] [CrossRef]
- Yao, Y.; Zhang, Y.; Liu, J.; Shen, Z.; Liu, B. Model for evaluating urban water shortage risk: A case study in Beijing. Int. J. Digit. Content Technol. Appl. 2012, 6, 68–79. [Google Scholar]
- Vermonden, K. Key Factors for Biodiversity of Urban Water Systems. Ph.D. Thesis, Radboud University, Nijmegen, The Netherlands, 2010. [Google Scholar]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Dong-Hai, L.I.; Bin, A.I.; Xia, L.I. Urban water body alleviating heat island effect based on RS and GIS: A case study of Dongguan City. Trop. Geogr. 2008, 28, 414–418. [Google Scholar]
- Jofre, J.; Blanch, A.R.; Lucena, F. Water-Borne Infectious Disease Outbreaks Associated with Water Scarcity and Rainfall Events. In Water Scarcity in the Mediterranean: Perspectives Under Global Change; Sabater, S., Barceló, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 147–159. [Google Scholar]
- Kalnay, E.; Cai, M. Impact of urbanization and land-use change on climate. Nature 2003, 423, 528–531. [Google Scholar] [CrossRef] [PubMed]
- Mckinney, M.L. Urbanization as a major cause of biotic homogenization. Biol. Conserv. 2006, 127, 247–260. [Google Scholar] [CrossRef]
- Zhang, D.L.; Shou, Y.X.; Dickerson, R.R. Upstream urbanization exacerbates urban heat island effects. Geophys. Res. Lett. 2009, 36, 88–113. [Google Scholar] [CrossRef]
- Huang, S.L.; Chen, C.W. Urbanization and socioeconomic metabolism in Taipei. J. Ind. Ecol. 2010, 13, 75–93. [Google Scholar] [CrossRef]
- Morss, R.E.; Wilhelmi, O.V.; Downton, M.W.; Gruntfest, E. Flood risk, uncertainty, and scientific information for decision making: Lessons from an interdisciplinary project. Bull. Am. Meteorol. Soc. 2005, 86, 1593–1601. [Google Scholar] [CrossRef]
- Giardino, C.; Bresciani, M.; Villa, P.; Martinelli, A. Application of remote sensing in water resource management: The case study of Lake Trasimeno, Italy. Water Resour. Manag. 2010, 24, 3885–3899. [Google Scholar] [CrossRef]
- Lira, J. Segmentation and morphology of open water bodies from multispectral images. Int. J. Remote Sens. 2006, 27, 4015–4038. [Google Scholar] [CrossRef]
- Davranche, A.; Lefebvre, G.; Poulin, B. Wetland monitoring using classification trees and SPOT-5 seasonal time series. Remote Sens. Environ. 2012, 114, 552–562. [Google Scholar] [CrossRef]
- Sethre, P.; Rundquist, B.; Todhunter, P. Remote detection of prairie pothole ponds in the devils lake basin, North Dakota. Mapp. Sci. Remote Sens. 2005, 42, 277–296. [Google Scholar] [CrossRef]
- Asis, A.M.D.; Omasa, K.; Oki, K.; Shimizu, Y. Accuracy and applicability of linear spectral unmixing in delineating potential erosion areas in tropical watersheds. Int. J. Remote Sens. 2008, 29, 4151–4171. [Google Scholar] [CrossRef]
- Xie, H.; Luo, X.; Xu, X.; Pan, H.; Tong, X. Automated subpixel surface water mapping from heterogeneous urban environments using Landsat 8 OLI imagery. Remote Sens. 2016, 8, 584. [Google Scholar] [CrossRef]
- Bryant, R.G.; Rainey, M.P. Investigation of flood inundation on playas within the zone of Chotts, using a time-series of AVHRR. Remote Sens. Environ. 2002, 82, 360–375. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, R.D.; Jain, M.K.; Lohani, A.K. Delineation of flood-prone areas using remote sensing techniques. Water Resour. Manag. 2005, 19, 333–347. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated water extraction index: A new technique for surface water mapping using landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Mcfeeters, S.K. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Tong, X. New hyperspectral difference water index for the extraction of urban water bodies by the use of airborne hyperspectral images. Int. J. Remote Sens. 2014, 8, 085098. [Google Scholar]
- Verpoorter, C.; Kutser, T.; Tranvik, L. Automated mapping of water bodies using Landsat multispectral data. Limnol. Oceanogr. Methods 2015, 10, 1037–1050. [Google Scholar] [CrossRef]
- Gessner, M.O.; Hinkelmann, R.; Nützmann, G.; Jekel, M.; Singer, G.; Lewandowski, J.; Nehls, T.; Barjenbruch, M. Urban water interfaces. J. Hydrol. 2014, 514, 226–232. [Google Scholar] [CrossRef]
- Dare, P.M. Shadow analysis in high-resolution satellite imagery of urban areas. Photogramm. Eng. Remote Sens. 2005, 71, 169–177. [Google Scholar] [CrossRef]
- Yao, F.; Wang, C.; Dong, D.; Luo, J.; Shen, Z.; Yang, K. High-resolution mapping of urban surface water using ZY-3 multi-spectral imagery. Remote Sens. 2015, 7, 12336–12355. [Google Scholar] [CrossRef]
- Exelis. Exelis Visual Information Solutions. Available online: http://www.exelisvis.com (accessed on 15 November 2017).
- ExelisHelp. Exelis Visual Information Solutions. Available online: http://www.exelisvis.com/Support/HelpArticles.aspx (accessed on 15 November 2017).
- Tachikawa, T.; Kaku, M.; Iwasaki, A.; Gesch, D.B.; Oimoen, M.J.; Zhang, Z.; Danielson, J.; Krieger, T.; Curtis, B.; Haase, J. ASTER Global Digital Elevation Model Version 2—Summary of Validation Results; NASA: Pasadena, CA, USA, 2011.
- Kaufman, Y.J.; Remer, L.A. Detection of forests using mid-IR reflectance: An application for aerosol studies. Geosci. Remote Sens. IEEE Trans. 1994, 32, 672–683. [Google Scholar] [CrossRef]
- Neto, A.M.; Rittner, L.; Leite, N.; Zampieri, D.E. Pearson’s correlation coefficient for discarding redundant information in real time autonomous navigation system. In Proceedings of the 16th IEEE International Conference on Control Applications, Singapore, 1–3 October 2007. [Google Scholar]
- Yang, F.; Guo, J.; Tan, H.; Wang, J. Automated extraction of urban water bodies from Zymulti Log Pectral imagery. Water 2017, 9, 144. [Google Scholar] [CrossRef]
- Sun, J.; Li, Q.; Lu, W.; Wang, Q. Image recognition of laser radar using linear SVM correlation filter. Chin. Opt. Lett. 2007, 5, 549–551. [Google Scholar]
- Fu, Z.; Robles-Kelly, A.; Zhou, J. Mixing linear SVMs for nonlinear classification. IEEE Trans. Neural Netw. 2010, 21, 1963–1975. [Google Scholar] [PubMed]
- Provost, F.; Kohavi, R. Guest editors’ introduction: On applied research in machine learning. Mach. Learn. 1998, 30, 127–132. [Google Scholar] [CrossRef]
- Leeuw, J.D.; Jia, H.; Yang, L.; Liu, X.; Schmidt, K.; Skidmore, A.K. Comparing accuracy assessments to infer superiority of image classification methods. Int. J. Remote Sens. 2006, 27, 223–232. [Google Scholar] [CrossRef]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the normalized difference water index. Photogramm. Eng. Remote Sens. 2009, 75, 1307–1317. [Google Scholar] [CrossRef]
- Xie, C.; Huang, X.; Zeng, W.; Fang, X. A novel water index for urban high-resolution eight-band Worldview-2 imagery. Int. J. Digit. Earth 2016, 9, 925–941. [Google Scholar] [CrossRef]
- Zhou, W.Q.; Huang, G.L.; Troy, A.; Cadenasso, M.L. Object-based land cover classification of shaded areas in high spatial resolution imagery of urban areas: A comparison study. Remote Sens. Environ. 2009, 113, 1769–1777. [Google Scholar] [CrossRef]
- Chen, Y.; Wen, D.; Jing, L.; Shi, P. Shadow information recovery in urban areas from very high resolution satellite imagery. Int. J. Remote Sens. 2007, 28, 3249–3254. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. Morphological building/shadow index for building extraction from high-resolution imagery over urban areas. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 161–172. [Google Scholar] [CrossRef]
- Tsai, V.J.D. A comparative study on shadow compensation of color aerial images in invariant color models. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1661–1671. [Google Scholar] [CrossRef]
- Arévalo, V.; González, J.; Ambrosio, G. Shadow detection in colour high-resolution satellite images. Int. J. Remote Sens. 2008, 29, 1945–1963. [Google Scholar] [CrossRef]
- Chung, K.L.; Lin, Y.R.; Huang, Y.H. Efficient shadow detection of color aerial images based on successive thresholding scheme. IEEE Trans. Geosci. Remote Sens. 2009, 47, 671–682. [Google Scholar] [CrossRef]
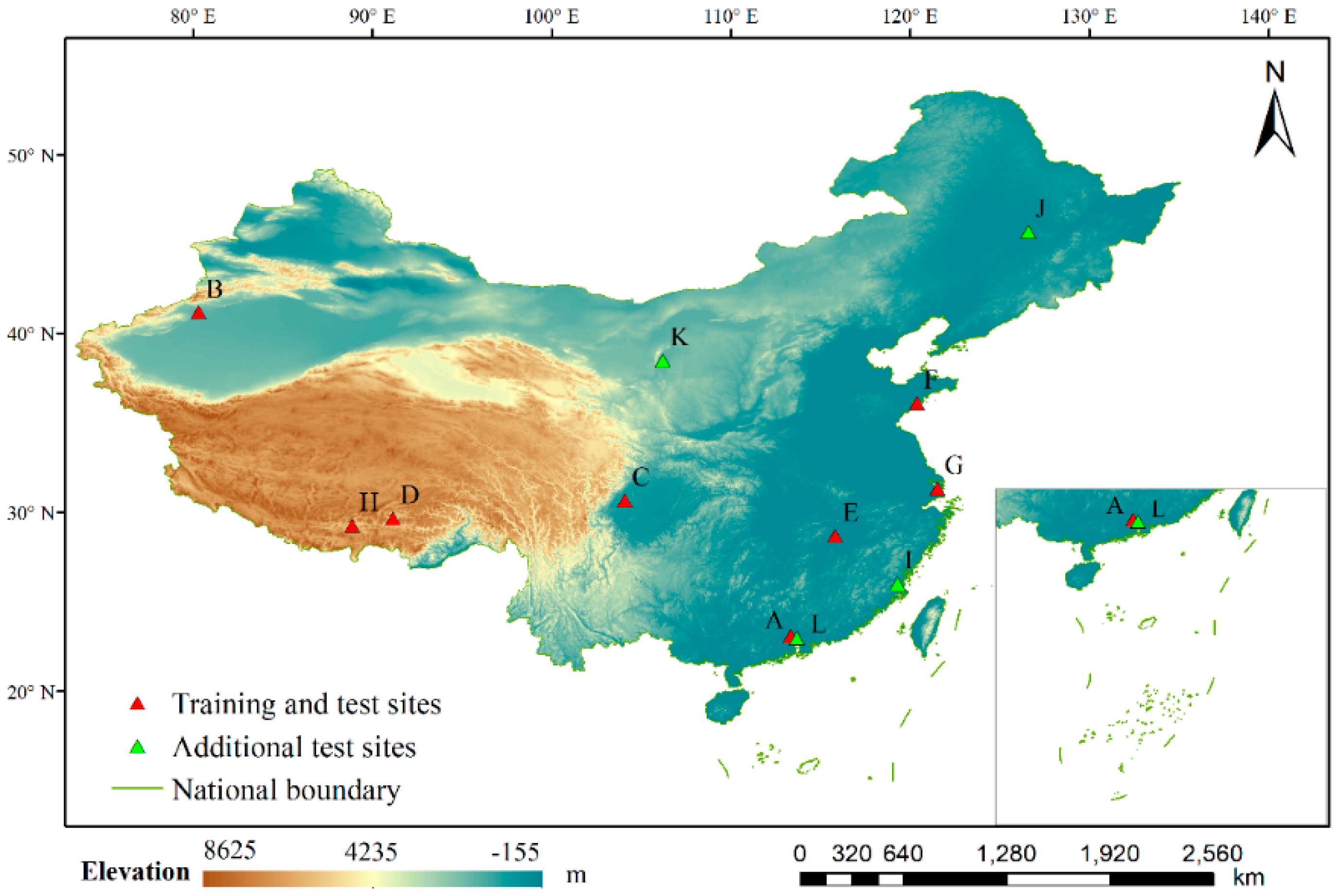

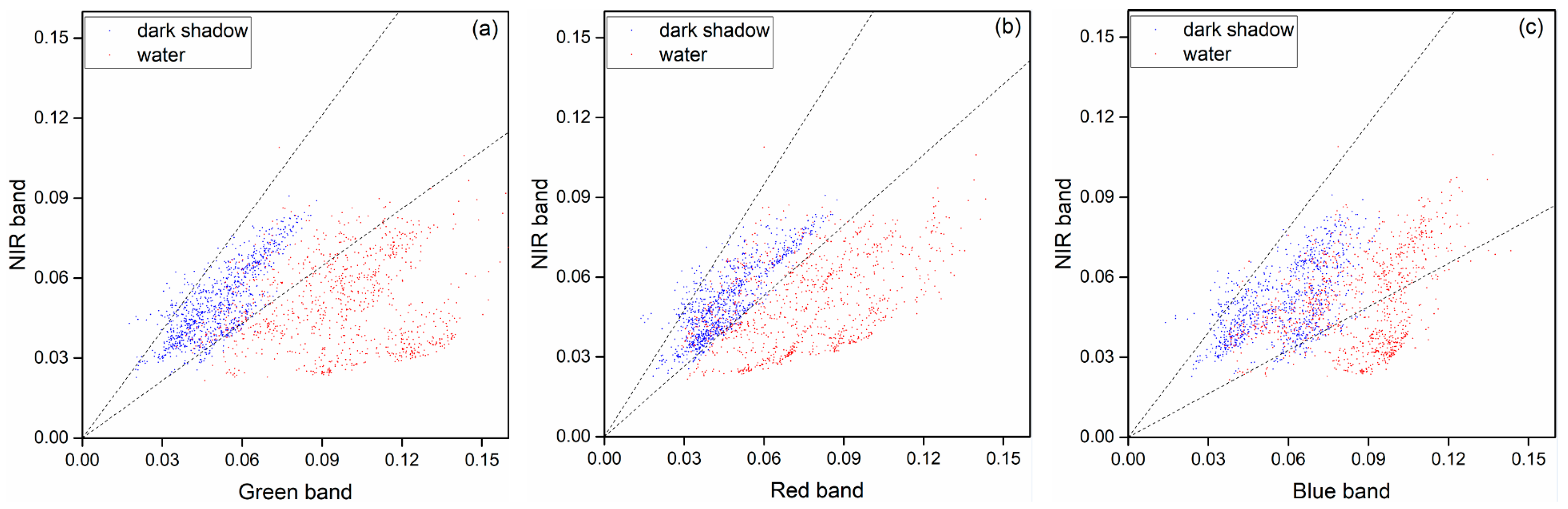
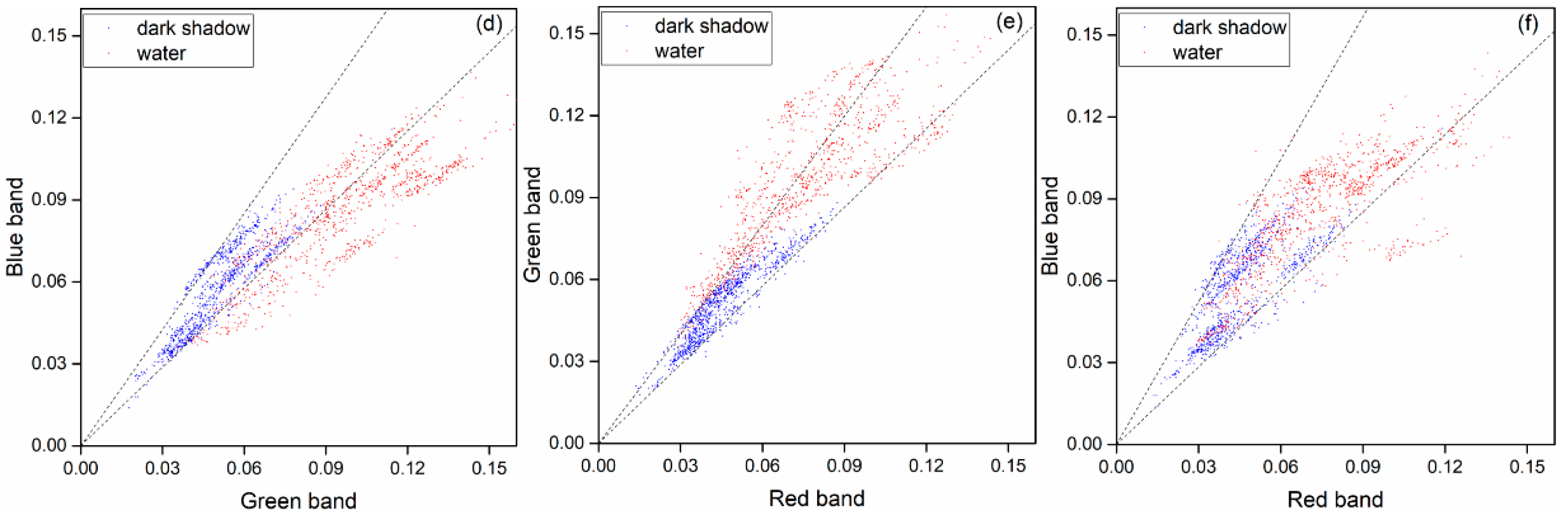
| Study Sites | Main Water Types/Features | Location | Area (km2) | Topography | Climate |
|---|---|---|---|---|---|
| Guangzhou | River c,t/lake c/pond c,t,e | 23.11°N, 113.33°E | 574.9 | Plain/hills | Subtropical oceanic monsoon |
| Aksu | River c,n/lake s,t | 41.19°N, 80.31°E | 171.7 | Basin | Temperate continental arid |
| Chengdu | River c,t,n/pond c,t/reservoir c | 30.64°N, 104.11°E | 521.9 | Plain | Subtropical humid monsoon |
| Lhasa | River c,t/pond c | 29.67°N, 91.16°E | 54.0 | Mountain/plateau | Plateau mountain |
| Nanchang | River t,w/lake c,t/pond c,t,e/reservoir c,t | 28.69°N, 115.82°E | 516.2 | Plain/hills | Subtropical humid monsoon |
| Qingdao | Sea c/tidal creek t/river n,c,t/pond c,t | 36.13°N, 120.38°E | 561.8 | Plain/hills | Warm temperate monsoon |
| Shanghai | Harbor w,t /river c,t/lake c,t/pond c,t | 31.36°N, 121.55°E | 504.9 | Plain | Subtropical oceanic monsoon |
| Shigatse | River c,t/lake c,t/pond c,t | 29.25°N, 88.89°E | 84.0 | Mountain/plateau | Plateau mountain |
| Fuzhou | River c,t,w/lake c,t/pond c,t/reservoir c | 26.01°N, 119.30°E | 522.2 | Basin/hills | Subtropical oceanic monsoon |
| Haerbin | River t,w/lake c,t,e/ponds c,t,e | 45.71°N, 126.60°E | 468.3 | Plain | Temperate monsoon |
| Yinchuan | Lake c,t/river c,n/pond c,t | 38.48°N, 106.24°E | 525.1 | Plain | Temperate continental |
| Dongguan | River c,t/lake c,t/pond c,t,e/reservoir c | 22.98°N, 113.68°E | 288.9 | Plain/hills | Subtropical oceanic monsoon |
| Spectral Bands | Wavelength (μm) | Resolution (Nadir Point) | Swath Width | Side-Swing Ability | Revisit Cycle |
|---|---|---|---|---|---|
| Panchromatic | 0.45–0.90 | 0.8 m | 45 km | ±35° | 5 days |
| Band1—Blue | 0.45–0.52 | 3.2 m | |||
| Band2—Green | 0.52–0.59 | ||||
| Band3—Red | 0.63–0.69 | ||||
| Band4—NIR | 0.77–0.89 |
| Study Sites | GF-2 Scene | Supplementary Reference Data | ||
|---|---|---|---|---|
| Acquisition Date | Path | Row | ||
| Guangzhou | 4 November 2016 | 1016 | 185 | Google Earth™ image acquired on 5 October/5 November/9 December 2016, ©Digital Globe |
| Aksu | 29 February 2016 | 102 | 135 | Google Earth™ image acquired on 17 April 2016, ©Digital Globe |
| Chengdu | 21 March 2015 | 27 | 164 | Google Earth™ image acquired on 11 February/21 March 2015, ©Digital Globe, CNES/Airbus |
| Lhasa | 3 December 2016 | 63 | 167 | Google Earth™ image acquired on 3 December 2016, ©Digital Globe |
| Nanchang | 28 November 2016 | 1013 | 170 | Google Earth™ image acquired on 24 September/1 December/31 December 2016, ©Digital Globe |
| Qingdao | 16 February 2016 | 1006 | 149 | Google Earth™ image acquired on 16 January 2016, ©Digital Globe |
| Shanghai | 2 January 2015 | 999 | 162 | Google Earth™ image acquired on 18 December 2014, and 24 January/18 February 2015, ©Digital Globe |
| Shigatse | 12 January 2017 | 69 | 168 | Google Earth™ image acquired on 21 May 2018, ©CNES/Airbus |
| Fuzhou | 7 December 2016 | 1001 | 177 | Google Earth™ image acquired on 21 January/1 March 2017, © Digital Globe, CNES/Airbus |
| Haerbin | 10 September 2015 | 997 | 122 | Google Earth™ image acquired on 19 June/9 July/16 September/24 October 2015, © Digital Globe |
| Yinchuan | 4 January 2017 | 27 | 142 | Google Earth™ image acquired on 30 October/2 November/ 13 November 2016, and 21 January 2017, ©Digital Globe |
| Dongguan | 15 February 2017 | 1015 | 186 | Google Earth™ image acquired on 12 February 2017, ©Digital Globe |
| Class Pair | M Value | |||||
|---|---|---|---|---|---|---|
| NIR/G | NIR/R | NIR/B | B/G | G/R | B/R | |
| Water vs. Dark shadows | 1.12 | 0.87 | 0.65 | 0.91 | 0.57 | 0.24 |
| Value | Band Ratio Pair | ||||||
|---|---|---|---|---|---|---|---|
| NIR/G vs. NIR/B | NIR/G vs. NIR/R | B/G vs. B/R | G/R vs. B/R | B/G vs. G/R | NIR/G vs. B/G | NIR/G vs. G/R | |
| Pearson’s r | 0.91 | 0.94 | 0.71 | 0.50 | −0.25 | 0.51 | −0.58 |
| Test Sites | Kappa Coefficient | Total Error (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| TSUWI | NDWI | HRWI | SVM | TSUWI | NDWI | HRWI | SVM | |
| Guangzhou | 0.96 | 0.92 | 0.92 | 0.95 | 7.72 | 14.46 | 13.90 | 8.35 |
| Aksu | 0.97 | 0.96 | 0.96 | 0.97 | 6.89 | 7.58 | 7.07 | 6.22 |
| Chengdu | 0.94 | 0.84 | 0.84 | 0.83 | 11.33 | 30.15 | 29.75 | 29.70 |
| Lhasa | 0.96 | 0.94 | 0.92 | 0.94 | 7.97 | 12.16 | 14.84 | 11.05 |
| Nanchang | 0.98 | 0.95 | 0.96 | 0.98 | 3.11 | 9.45 | 7.41 | 3.28 |
| Qingdao | 1.00 | 0.99 | 0.99 | 0.99 | 0.34 | 0.65 | 0.69 | 0.75 |
| Shanghai | 0.99 | 0.96 | 0.94 | 0.99 | 1.24 | 5.38 | 7.80 | 1.48 |
| Shigatse | 0.96 | 0.90 | 0.87 | 0.93 | 7.10 | 19.43 | 24.51 | 13.81 |
| Fuzhou | 0.98 | 0.95 | 0.96 | 0.96 | 4.31 | 8.10 | 7.82 | 6.25 |
| Haerbin | 0.97 | 0.90 | 0.91 | 0.97 | 6.17 | 18.09 | 17.64 | 6.50 |
| Yinchuan | 0.96 | 0.57 | 0.93 | 0.94 | 7.97 | 63.79 | 13.25 | 11.04 |
| Dongguan | 0.97 | 0.89 | 0.92 | 0.96 | 5.65 | 19.69 | 13.78 | 7.33 |
| Test Sites | TSUWI vs. NDWI | TSUWI vs. HRWI | TSUWI vs. SVM | |||
|---|---|---|---|---|---|---|
| χ2 | p-Value | χ2 | p-Value | χ2 | p-Value | |
| Guangzhou | 132,839.0 | <0.001 | 115,749.6 | <0.001 | 3154.6 | <0.001 |
| Aksu | 77.3 | <0.001 | 0.8 | 0.364 | 93.6 | <0.001 |
| Chengdu | 17,469.1 | <0.001 | 16,782.9 | <0.001 | 29,634.9 | <0.001 |
| Lhasa | 789.6 | <0.001 | 1611.7 | <0.001 | 565.7 | <0.001 |
| Nanchang | 156,460.7 | <0.001 | 90,288.0 | <0.001 | 473.3 | <0.001 |
| Qingdao | 27,076.7 | <0.001 | 29,515.0 | <0.001 | 37,705.9 | <0.001 |
| Shanghai | 365,387.6 | <0.001 | 614,546.5 | <0.001 | 5523.5 | <0.001 |
| Shigatse | 5466.0 | <0.001 | 9882.5 | <0.001 | 2461.9 | <0.001 |
| Fuzhou | 93,062.7 | <0.001 | 82,875.6 | <0.001 | 33,324.0 | <0.001 |
| Haerbin | 146,443.9 | <0.001 | 148,493.8 | <0.001 | 474.1 | <0.001 |
| Yinchuan | 1,637,618.0 | <0.001 | 41,856.2 | <0.001 | 18,304.1 | <0.001 |
| Dongguan | 242,347.7 | <0.001 | 118,820.2 | <0.001 | 10,548.3 | <0.001 |
| Test Sites | NDWI | HRWI | NDWI + USI | HRWI + USI | TSUWI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kappa | OE% | CE% | Kappa | OE% | CE% | Kappa | OE% | CE% | Kappa | OE% | CE% | Kappa | OE% | CE% | |
| Guangzhou | 0.92 | 10.22 | 4.24 | 0.92 | 10.68 | 3.22 | 0.93 | 9.08 | 3.46 | 0.95 | 5.84 | 3.48 | 0.96 | 5.37 | 2.35 |
| Aksu | 0.96 | 2.04 | 5.55 | 0.96 | 2.96 | 4.11 | 0.96 | 2.04 | 5.51 | 0.96 | 2.98 | 4.03 | 0.97 | 1.98 | 4.91 |
| Chengdu | 0.84 | 25.29 | 4.86 | 0.84 | 24.49 | 5.26 | 0.88 | 11.76 | 10.96 | 0.93 | 6.66 | 8.02 | 0.94 | 5.91 | 5.42 |
| Lhasa | 0.94 | 8.61 | 3.55 | 0.92 | 7.30 | 7.55 | 0.95 | 7.42 | 3.27 | 0.94 | 7.32 | 4.09 | 0.96 | 6.68 | 1.30 |
| Nanchang | 0.95 | 6.15 | 3.30 | 0.96 | 4.43 | 2.98 | 0.96 | 3.72 | 2.64 | 0.97 | 2.66 | 2.19 | 0.98 | 1.99 | 1.11 |
| Qingdao | 0.99 | 0.35 | 0.31 | 0.99 | 0.33 | 0.36 | 1.00 | 0.19 | 0.33 | 0.99 | 0.19 | 0.38 | 1.00 | 0.17 | 0.17 |
| Shanghai | 0.96 | 2.05 | 3.33 | 0.94 | 3.25 | 4.55 | 0.99 | 0.92 | 0.45 | 0.99 | 0.86 | 0.47 | 0.99 | 0.83 | 0.41 |
| Shigatse | 0.90 | 10.80 | 8.63 | 0.87 | 7.51 | 17.00 | 0.91 | 9.67 | 7.50 | 0.91 | 9.17 | 8.23 | 0.96 | 3.83 | 3.28 |
| Fuzhou | 0.95 | 6.64 | 1.46 | 0.96 | 6.05 | 1.77 | 0.96 | 5.93 | 1.65 | 0.97 | 3.69 | 2.01 | 0.98 | 3.05 | 1.25 |
| Haerbin | 0.90 | 13.60 | 4.49 | 0.91 | 9.67 | 7.98 | 0.91 | 11.39 | 4.49 | 0.92 | 9.55 | 4.67 | 0.97 | 4.20 | 1.97 |
| Yinchuan | 0.57 | 7.93 | 55.86 | 0.93 | 9.23 | 4.02 | 0.96 | 5.42 | 2.70 | 0.96 | 6.14 | 1.89 | 0.96 | 5.41 | 2.56 |
| Dongguan | 0.89 | 7.54 | 12.16 | 0.92 | 8.09 | 5.69 | 0.97 | 3.38 | 2.61 | 0.96 | 3.72 | 3.01 | 0.97 | 3.04 | 2.61 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Li, Q.; Zhang, Y.; Du, X.; Wang, H. Two-Step Urban Water Index (TSUWI): A New Technique for High-Resolution Mapping of Urban Surface Water. Remote Sens. 2018, 10, 1704. https://doi.org/10.3390/rs10111704
Wu W, Li Q, Zhang Y, Du X, Wang H. Two-Step Urban Water Index (TSUWI): A New Technique for High-Resolution Mapping of Urban Surface Water. Remote Sensing. 2018; 10(11):1704. https://doi.org/10.3390/rs10111704
Chicago/Turabian StyleWu, Wei, Qiangzi Li, Yuan Zhang, Xin Du, and Hongyan Wang. 2018. "Two-Step Urban Water Index (TSUWI): A New Technique for High-Resolution Mapping of Urban Surface Water" Remote Sensing 10, no. 11: 1704. https://doi.org/10.3390/rs10111704
APA StyleWu, W., Li, Q., Zhang, Y., Du, X., & Wang, H. (2018). Two-Step Urban Water Index (TSUWI): A New Technique for High-Resolution Mapping of Urban Surface Water. Remote Sensing, 10(11), 1704. https://doi.org/10.3390/rs10111704






