Effects of Sample Plot Size and GPS Location Errors on Aboveground Biomass Estimates from LiDAR in Tropical Dry Forests
Abstract
1. Introduction
2. Materials and Methods
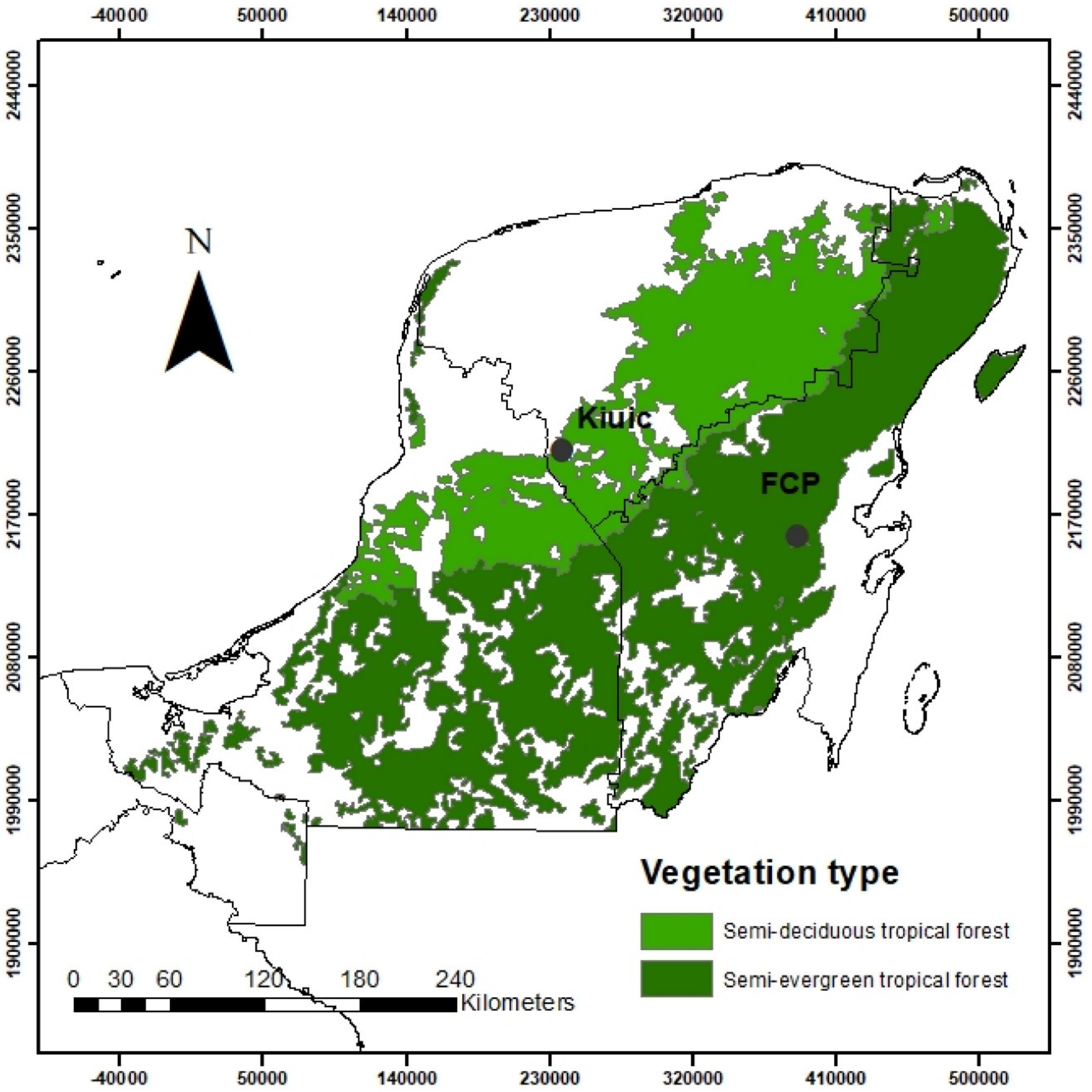
2.1. Study Area
2.2. Field Sampling and Aboveground Biomass Calculation
2.3. LiDAR Data Processing
2.4. Simulation of Position Errors
2.5. Data Analysis
3. Results
3.1. Above Ground Biomass Calculations
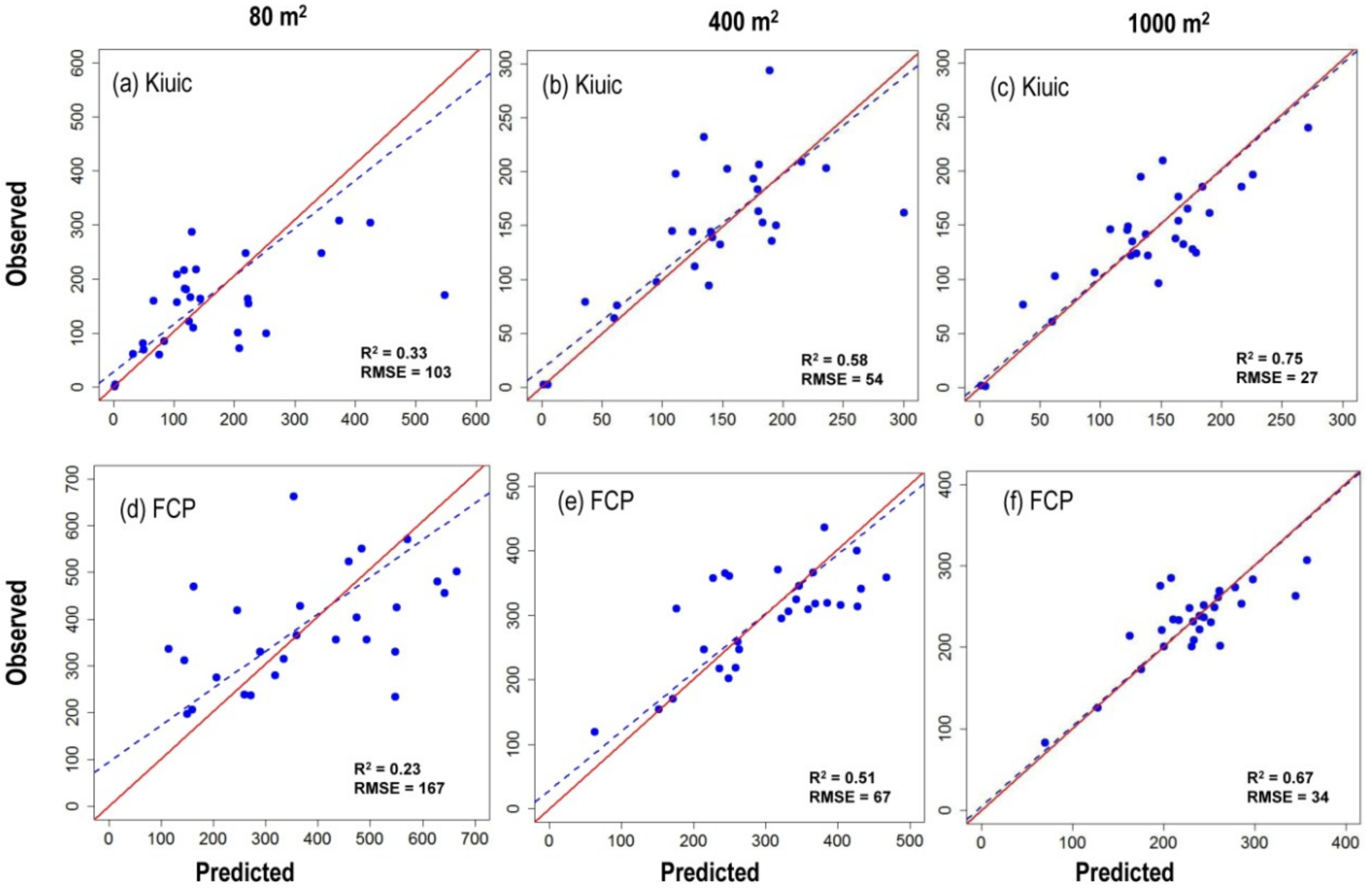
3.2. Effects of Plot Size
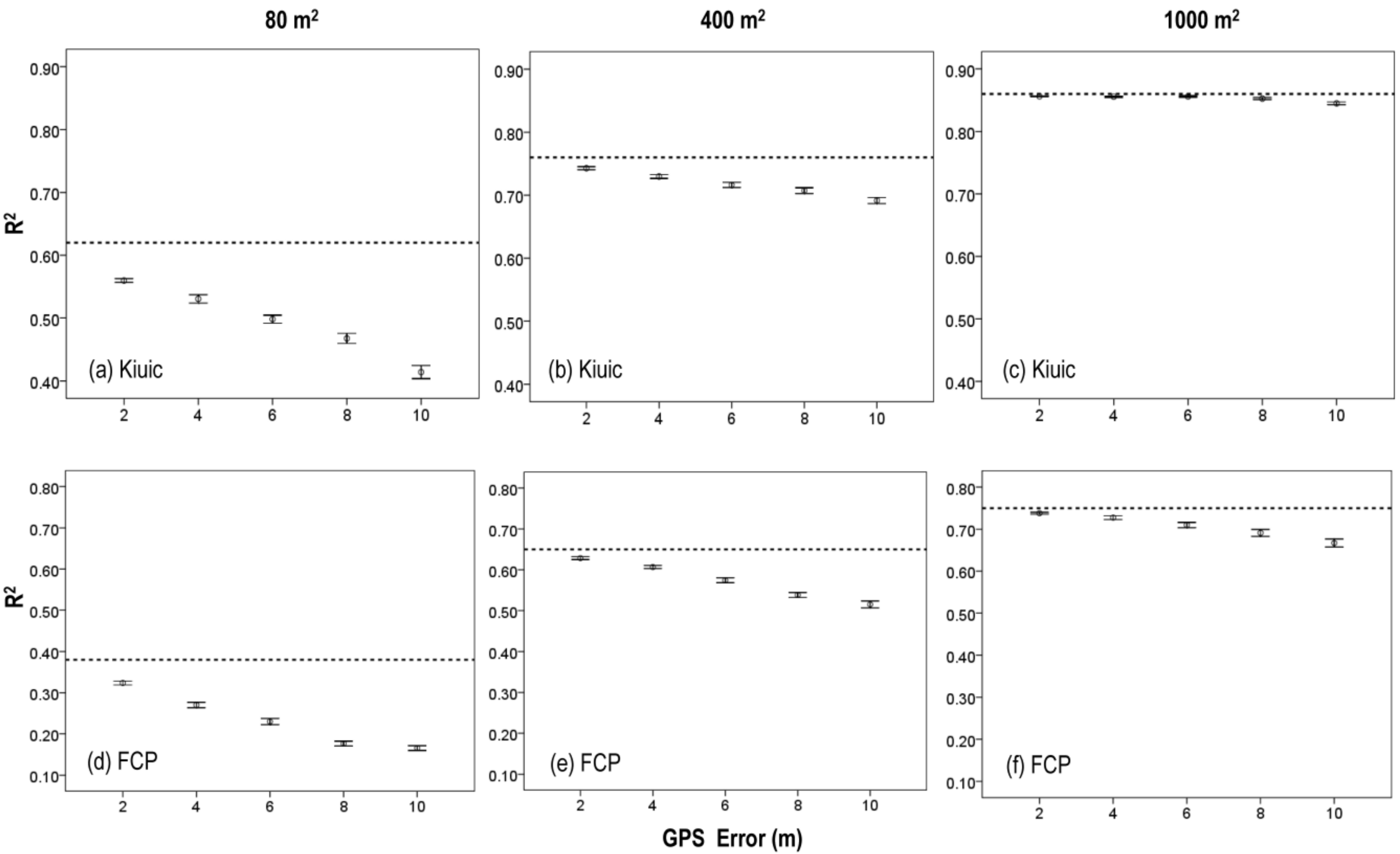
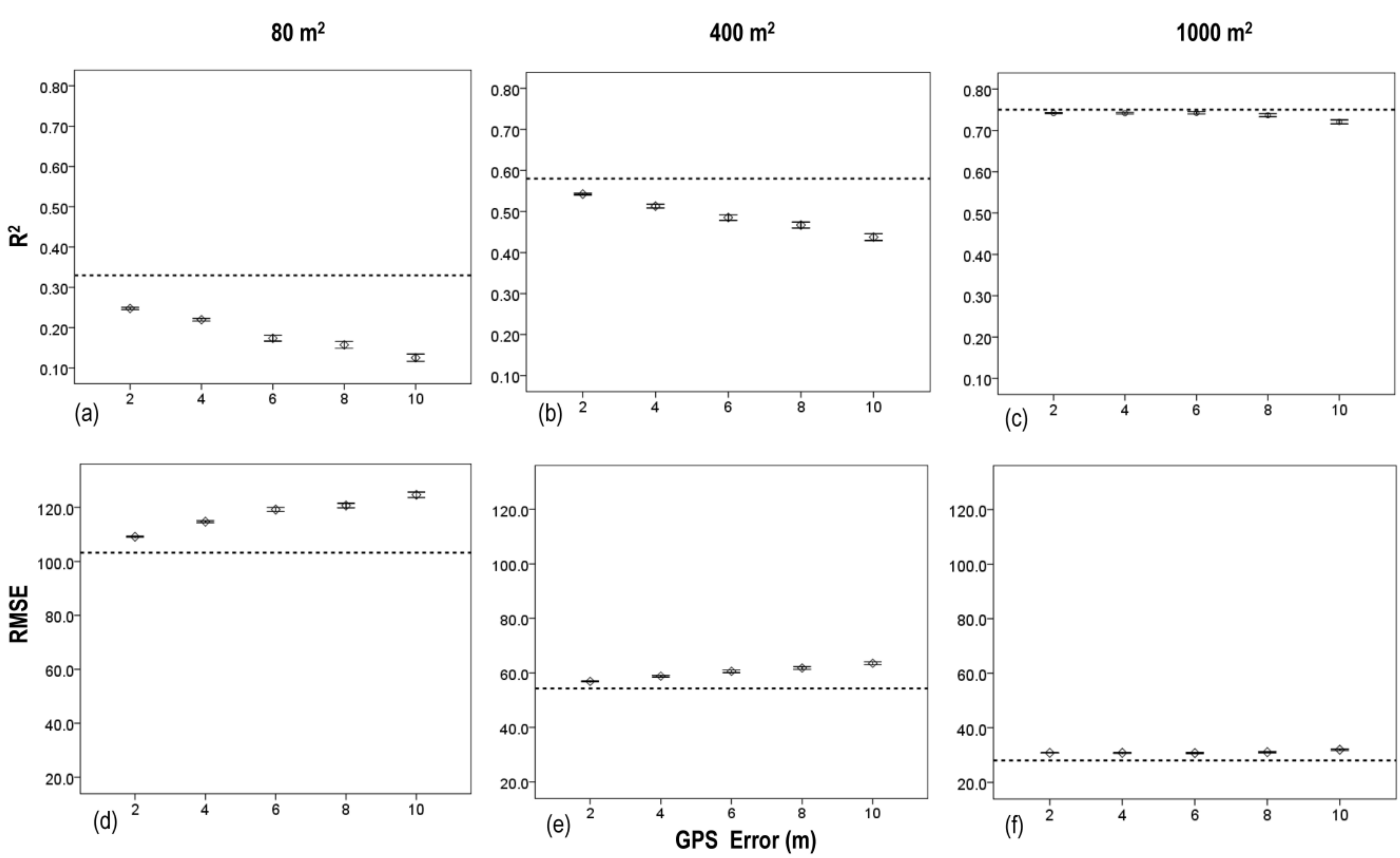
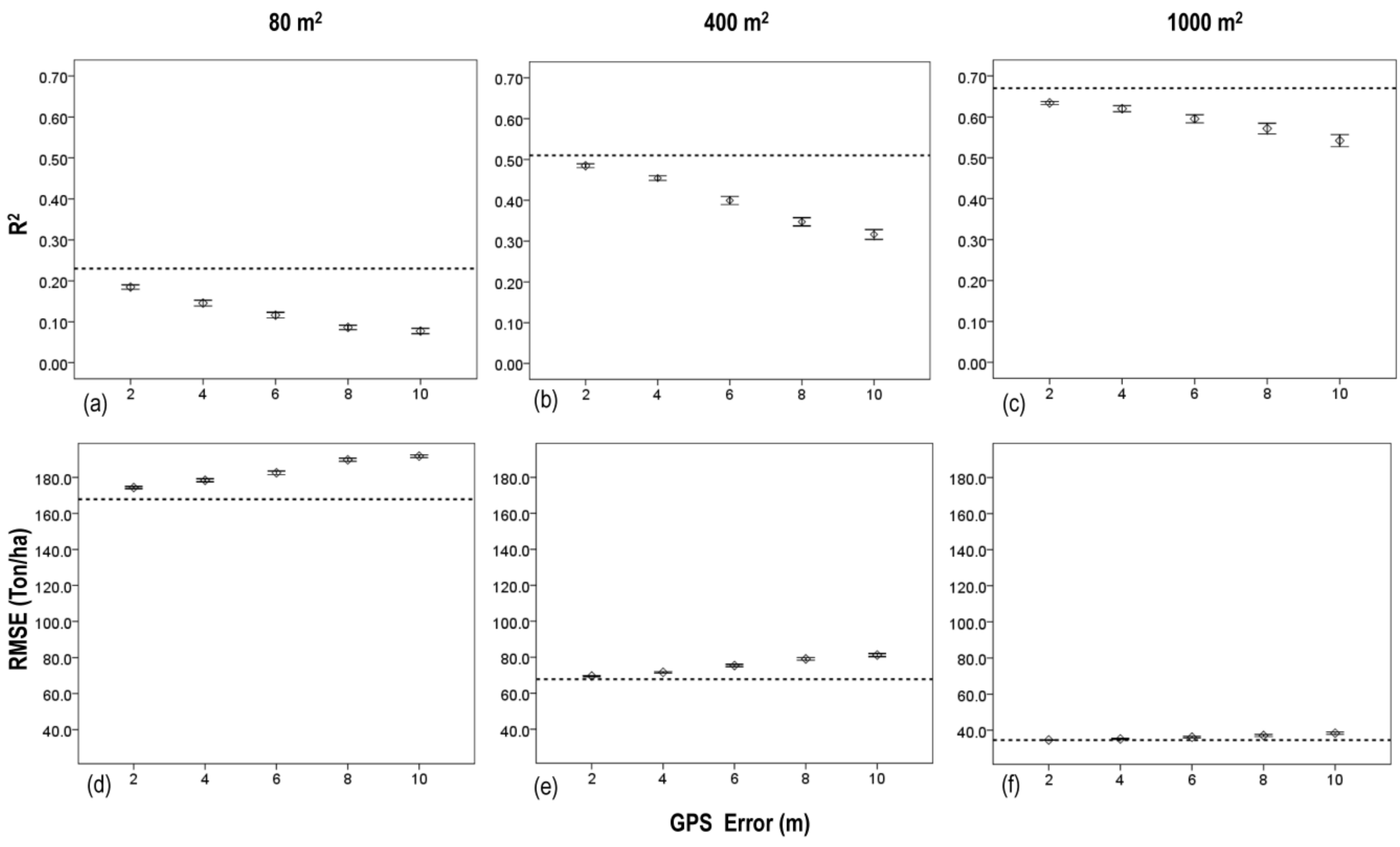
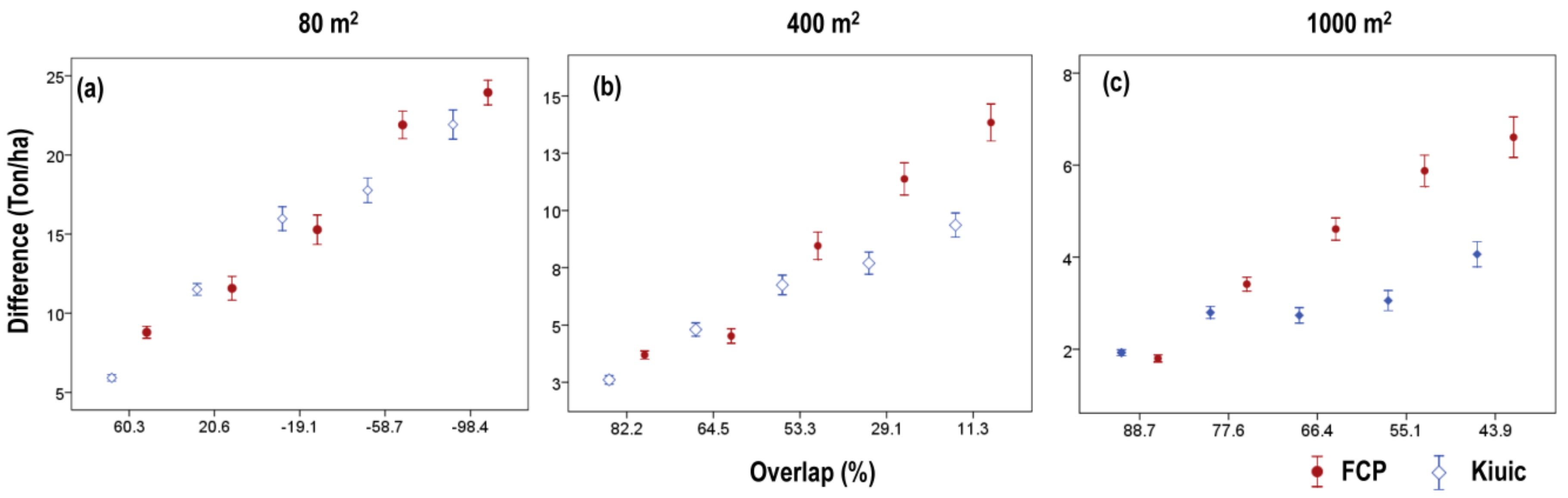
3.3. Effects of Plot Position Error and Plot Size
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thomson, A.; Calvin, K.; Chini, L.; Hurtt, G.; Edmonds, J.; Ben Bond-Lamberty, B.; Frolking, S.; Wise, M.A.; Janetos, A.C. Climate mitigation and the future of tropical landscapes. Proc. Natl. Acad. Sci. USA. 2010, 107, 19633–19638. [Google Scholar] [CrossRef] [PubMed]
- Portillo-Quintero, C.A.; Sánchez-Azofeifa, G.A. Extent and conservation of tropical dry forests in the Americas. Biol. Conserv. 2010, 143, 144–155. [Google Scholar] [CrossRef]
- Le Quéré, C.; Peters, G.P.; Andres, R.J.; Andrew, R.M.; Boden, T.; Ciais, P.; Friedlingstein, P.; Houghton, R.A.; Marland, G.; Moriarty, R.; et al. Global carbon budget 2013. Earth Syst. Sci. Data Discuss. 2013, 6, 689–760. [Google Scholar] [CrossRef]
- Miles, L.; Newton, A.; Defries, R.; Ravilious, C.; May, I.; Blyth, S.; Kapos, V.; Gordon, J. A global overview of the conservation status of tropical dry forests. J. Biogeogr. 2006, 33, 491–505. [Google Scholar] [CrossRef]
- Sanchez-Azofeifa, G.A.; Castro-Esau, K.L.; Kurz, W.A.; Joyce, A. Monitoring carbon stocks in the tropics and the remote sensing operational limitations: From local to regional projects. Ecol. Appl. 2009, 19, 480–494. [Google Scholar] [CrossRef] [PubMed]
- Foody, G.M.; Boyd, D.S.; Cutler, M.E.J. Predictive relations of tropical forest biomass from Landsat TM data and their transferability between regions. Remote Sens. Environ. 2003, 85, 463–474. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Moran, E.; Batistella, M.; Zhang, M.; Vaglio Laurin, G.; Saah, D. Aboveground forest biomass estimation with Landsat and LiDAR data and uncertainty analysis of the estimates. Int. J. For. Res. 2012, 2012, 1–16. [Google Scholar] [CrossRef]
- Carreiras, J.M.B.; Vasconcelos, M.J.; Lucas, R.M. Understanding the relationship between aboveground biomass and ALOS PALSAR data in the forests of Guinea-Bissau (West Africa). Remote Sens. Environ. 2012, 121, 426–442. [Google Scholar] [CrossRef]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef]
- Dubayah, R.O.; Sheldon, S.L.; Clark, D.B.; Hofton, M.A.; Blair, J.B.; Hurtt, G.C.; Chazdon, R.L. Estimation of tropical forest height and biomass dynamics using LIDAR remote sensing at La Selva, Costa Rica. J. Geophys. Res. Biogeosci. 2010, 115, 1–17. [Google Scholar] [CrossRef]
- Næsset, E.; Okland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve. Remote Sens. Environ. 2002, 79, 105–115. [Google Scholar] [CrossRef]
- Drake, J.B.; Knox, R.G.; Dubayah, R.O.; Clark, D.B.; Condit, R.; Blair, J.B.; Hofton, M. Above-ground biomass estimation in closed canopy Neotropical forests using Lidar remote sensing: Factors affecting the generality of relationships. Glob. Ecol. Biogeogr. 2003, 12, 147–159. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Spies, R.A. An evaluation of alternate remote sensing products for forest inventory, monitoring, and mapping of Douglas-fir forests in western Oregon. Can. J. For. Res. 2001, 31, 78–87. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Caraba-jal, C.C.; Espirito-Santo, F.D.; Hunter, M.O.; de Oliveira, R. Estimates of forest canopy height and above-ground biomass using ICESat. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Asner, G.P.; Hughes, R.F.; Varga, T.A.; Knapp, D.E.; Kennedy-Bowdoin, T. Environmental and Biotic Controls over Aboveground Biomass throughout a Tropical Rain Forest. Ecosystems 2009, 12, 261–278. [Google Scholar] [CrossRef]
- Vincent, G.; Sabatier, D.; Blanc, L.; Chave, J.; Weissenbacher, E.; Pélissier, R.; Fonty, E.; Molino, E.F.; Couteron, P. Accuracy of small footprint airborne LIDAR in its predictions of tropical moist forest stand structure. Remote Sens. Environ. 2012, 125, 23–33. [Google Scholar] [CrossRef]
- Hernández-Stefanoni, J.L.; Dupuy, J.M.; Jhonson, K.J.; Birdsey, R.; Tun-Dzul, F.; Peduzzi, A.; Camal-Sosa, J.P.; Sánchez-Santos, G.; López-Merlín, D. Improving Species Diversity and Biomass Estimates of Tropical Dry Forest Using Airbone LiDAR. Remote Sens. 2014, 6, 4741–4763. [Google Scholar] [CrossRef]
- Goldbergs, G.; Levick, S.R.; Lawes, M.; Edwards, A. Hierarchical integration of individual tree and area-based approaches for savanna biomass uncertainty estimation from airborne LiDAR. Remote Sens. Environ. 2018, 205, 141–150. [Google Scholar] [CrossRef]
- Wing, M.G.; Frank, J. An examination of five identical mapping-grade global positioning system receivers in two forest settings. West. J. Appl. For. 2011, 26, 119–125. [Google Scholar]
- Gobakken, T.; Næsset, E. Assessing effects of positioning errors and sample plot size on biophysical stand properties derived from airborne laser scanner data. Can. J. For. Res. 2009, 39, 1036–1052. [Google Scholar] [CrossRef]
- Frazer, G.W.; Magnussen, S.; Wulder, M.A.; Niemann, K.O. Simulated impact of sample plot size and co-registration error on the accuracy and uncertainty of LiDAR-derived estimates of forest stand biomass. Remote Sens. Environ. 2011, 115, 636–649. [Google Scholar] [CrossRef]
- Chave, J.; Condit, R.; Aguilar, S.; Hernandez, A.; Lao, S.; Perez, R. Error propagation and scaling for tropical forest biomass estimates. Phil. Trans. R. Soc. B. 2004, 359, 409–420. [Google Scholar] [CrossRef] [PubMed]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2012, 128, 289–298. [Google Scholar] [CrossRef]
- Brubaker, K.M.; Johnson, S.E.; Brinks, J.; Leites, L.P. Estimating canopy height of deciduous forests at a regional scale with leaf-off, low point density LIDAR. Can. J. Remote Sens. 2014, 40, 123–134. [Google Scholar]
- Hall, S.A.; Burke, I.C.; Box, D.O.; Kaufmann, M.R.; Stoker, J.M. Estimating stand structure using discrete-return lidar: An example from low density, fire prone ponderosa pine forests. For. Ecol. Manag. 2005, 208, 189–209. [Google Scholar] [CrossRef]
- Carnevali, G.; Ramírez, I.M.; González-Iturbe, J.A. Flora y vegetación de la Península de Yucatán. In Naturaleza y Sociedad en el Área Maya; Colunga GarcíaMarín, P., Larqué-Saavedra, A., Eds.; Academia Mexicana de Ciencias, Centro de Investigación Científica de Yucatán: Mérida Yucatán, México, 2003; pp. 53–68. [Google Scholar]
- Chave, J.; Andalo, C.; Brown, C.S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Lescure, J.P. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Ramírez, G.R.; Dupuy, J.M.; Ramírez, L.; Sánchez, F.J.S. Evaluación de ecuaciones alométricas de biomasa epigea en una selva mediana subcaducifolia de Yucatán. Madera y Bosques 2017, 23, 163–179. [Google Scholar] [CrossRef]
- Guyot, J. Estimation du Stock de Carbone dans la Végétation des Zones Humides de la Péninsule du Yucatan. Memoire de fin D’etudes. Bachelor’s Thesis, AgroParis Tech-El Colegio de la Frontera Sur, Chetumal Quintana Roo, México, 2011. [Google Scholar]
- Schnitzer, S.A.; DeWalt, S.J.; Chave, J. Censusing and measuring lianas: A quantitative comparison of the common methods. Biotropica 2006, 38, 581–591. [Google Scholar] [CrossRef]
- Frangi, J.L.; Lugo, A.E. Ecosystem dynamics of a sub-tropical floodplain forest. Ecol. Monogr. 1985, 55, 351–369. [Google Scholar] [CrossRef]
- CartoData. Available online: http://www.cartodata.com// (accessed on 28 August 2018).
- McGaughey, R.J. FUSION/LDV: Software for LIDAR Data Analysis and Visualization; United States Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2012; p. 154. Available online: http://forsys.cfr.washington.edu/fusion/fusion_overview.html (accessed on 28 August 2018).
- R Development Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012; ISBN 3-900051-07-0. [Google Scholar]
- Zar, J.H. Biostatistical Analysis; Prenctice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Picard, R.R.; Cook, R.D. Cross-validation of regression models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
- Miller, D.M. Reducing transformation bias in curve fitting. Am. Stat. 1984, 38, 124–126. [Google Scholar]
- Levick, S.R.; Hessenmöller, D.; Schulze, E.D. Scaling wood volume estimates from inventory plots to landscapes with airborne LiDAR in temperate deciduous forest. Carbon Balance Manag. 2016, 11, 7. [Google Scholar] [CrossRef] [PubMed]
- Mauya, E.; Hansen, E.; Gobakken, T.; Bollandsås, O.; Malimbwi, R.; Næsset, E. Effects of field plot size on prediction accuracy of aboveground biomass in airborne laser scanning-assisted inventories in tropical rainforests of Tanzania. Carbon Balance Manag. 2015, 10, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Kachamba, D.J.; Ørka, H.O.; Næsset, E.; Eid, T.; Gobakken, T. Influence of plot size on efficiency of biomass estimates in inventories of dry tropical forests assisted by photogrammetric data from an unmanned aircraft system. Remote Sens. 2017, 9, 610. [Google Scholar] [CrossRef]
- Goetz, S.; Dubayah, R. Advances in remote sensing technology and implications for measuring and monitoring forest carbon stocks and change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
- Zhang, M.; Lin, H.; Zeng, S.; Li, J.; Shi, J. Impacts of plot location errors on accuracy of mapping and scaling up aboveground forest carbon using sample plot and Landsat tm data. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1483–1487. [Google Scholar] [CrossRef]
- Gonçalves, F.; Treuhaft, R.; Law, B.; Almeida, A.; Walker, W.; Baccini, A.; Graça, P. Estimating aboveground biomass in tropical forests: Field methods and error analysis for the calibration of remote sensing observations. Remote Sens. 2017, 9, 47. [Google Scholar] [CrossRef]
- Dorigo, W.; Hollaus, M.; Wagner, W.; Schadauer, K. An application-oriented automated approach for co-registration of forest inventory and airborne laser scanning data. Int. J. Remote Sens. 2010, 31, 1133–1153. [Google Scholar] [CrossRef]
- Pascual, C.; Martín-Fernández, S.; García-Montero, L.G.; García-Abril, A. Algorithm for improving the co-registration of LiDAR-derived digital canopy height models and field data. Agroforest. Syst. 2013, 87, 967–975. [Google Scholar] [CrossRef]
- Erdody, T.L.; Moskal, L.M. Fusion of LiDAR and imagery for estimating forest canopy fuels. Remote Sens. Environ. 2010, 114, 725–737. [Google Scholar] [CrossRef]
- Knapp, N.; Fischer, R.; Huth, A. Linking lidar and forest modeling to assess biomass estimation across scales and disturbance states. Remote Sens. Environ. 2018, 205, 199–209. [Google Scholar] [CrossRef]
| Site | Number of Plots | Plot Size (m2) | Plot Radius (m) | Biomass (Mg ha−1) Mean (std Deviation) |
|---|---|---|---|---|
| Kiuic | 29 | 80 | 5.04 | 163.16 (127.16) |
| 400 | 11.28 | 155.03 (84.46) | ||
| 1000 | 17.84 | 137.06 (61.58) | ||
| FCP | 28 | 80 | 5.04 | 397.21 (193.01) |
| 400 | 11.28 | 301.21 (98.18) | ||
| 1000 | 17.84 | 232.45 (58.25) |
| Site | Plot Size (m2) | Number of Predictors | Explanatory Variables | R2 | AIC |
|---|---|---|---|---|---|
| Kiuic | 80 | 1 | Elev P75 | 0.52 | 75.0 |
| 2 | Elev P70 + All returns above mode | 0.62 | 70.0 | ||
| 3 * | Elev P70 + Elev SQRT mean SQ + All returns above mode | 0.75 | 60.0 | ||
| 400 | 1 | Percentage all returns above 4.00 | 0.72 | 46.0 | |
| 2 | Percentage all returns above 4.00 + Percentage first returns above mean | 0.76 | 43.0 | ||
| 3 * | Elev variance + Percentage all returns above 4.00 + Percentage first returns above mean | 0.80 | 40.0 | ||
| 1000 | 1 | Percentage all returns above 4.00 | 0.86 | 19.0 | |
| 2 * | Elev variance + Elev P95 | 0.87 | 17.0 | ||
| 3 * | Elev maximum + Elev variance + Elev P90 | 0.89 | 14.0 | ||
| FCP | 80 | 1 | Elev P70 | 0.17 | 87.0 |
| 2 | Percentage all returns above 4.00 + First returns above mean | 0.38 | 80.0 | ||
| 3 * | Elev P40+ Elev P50 + Elev P60 | 0.46 | 79.0 | ||
| 400 | 1 | Elev P60 | 0.60 | 38.6 | |
| 2 | Elev mode + (All returns above mode)/(Total first returns) × 100 | 0.65 | 39.0 | ||
| 3 * | Elev mode + Elev MAD median + Elev P01 | 0.70 | 36.0 | ||
| 1000 | 1 | Elev CV | 0.75 | 5.9 | |
| 2 * | Elev L3 + Percentage first returns above mean | 0.79 | 1.7 | ||
| 3 * | Elev L3 + Percentage first returns above mean + (All returns above mean)/(Total first returns) × 100 | 0.84 | −3.0 |
| Site | Plot Size (m2) | Independent Variables | β | Std Error | R2 |
|---|---|---|---|---|---|
| Kiuc | 80 | Intercept | 2.81 | 2.30 | 0.62 |
| Elev P70 | 1.49 | 0.25 | |||
| All returns above mode | 0.004 | 0.001 | |||
| 400 | Intercept | 8.60 | 3.55 | 0.76 | |
| Percentage all returns above 4.00 | 0.25 | 0.03 | |||
| Percentage first returns above mean | −0.13 | 0.06 | |||
| 1000 | Intercept | 1.20 | 0.85 | 0.86 | |
| Percentage all returns above 4.00 | 0.19 | 0.02 | |||
| FCP | 80 | Intercept | 12.43 | 4.75 | 0.38 |
| Percentage all returns above 4.00 | 0.34 | 0.09 | |||
| First returns above mean | −0.03 | 0.01 | |||
| 400 | Intercept | 1.74 | 2.98 | 0.65 | |
| Elev mode | 1.05 | 0.17 | |||
| (All returns above mode)/(Total first returns) × 100 | 0.06 | 0.02 | |||
| 1000 | Intercept | 25.76 | 1.25 | 0.75 | |
| Elev CV | −25.65 | 2.98 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Stefanoni, J.L.; Reyes-Palomeque, G.; Castillo-Santiago, M.Á.; George-Chacón, S.P.; Huechacona-Ruiz, A.H.; Tun-Dzul, F.; Rondon-Rivera, D.; Dupuy, J.M. Effects of Sample Plot Size and GPS Location Errors on Aboveground Biomass Estimates from LiDAR in Tropical Dry Forests. Remote Sens. 2018, 10, 1586. https://doi.org/10.3390/rs10101586
Hernández-Stefanoni JL, Reyes-Palomeque G, Castillo-Santiago MÁ, George-Chacón SP, Huechacona-Ruiz AH, Tun-Dzul F, Rondon-Rivera D, Dupuy JM. Effects of Sample Plot Size and GPS Location Errors on Aboveground Biomass Estimates from LiDAR in Tropical Dry Forests. Remote Sensing. 2018; 10(10):1586. https://doi.org/10.3390/rs10101586
Chicago/Turabian StyleHernández-Stefanoni, José Luis, Gabriela Reyes-Palomeque, Miguel Ángel Castillo-Santiago, Stephanie P. George-Chacón, Astrid Helena Huechacona-Ruiz, Fernando Tun-Dzul, Dinosca Rondon-Rivera, and Juan Manuel Dupuy. 2018. "Effects of Sample Plot Size and GPS Location Errors on Aboveground Biomass Estimates from LiDAR in Tropical Dry Forests" Remote Sensing 10, no. 10: 1586. https://doi.org/10.3390/rs10101586
APA StyleHernández-Stefanoni, J. L., Reyes-Palomeque, G., Castillo-Santiago, M. Á., George-Chacón, S. P., Huechacona-Ruiz, A. H., Tun-Dzul, F., Rondon-Rivera, D., & Dupuy, J. M. (2018). Effects of Sample Plot Size and GPS Location Errors on Aboveground Biomass Estimates from LiDAR in Tropical Dry Forests. Remote Sensing, 10(10), 1586. https://doi.org/10.3390/rs10101586






