Geocoding Error Correction for InSAR Point Clouds
Abstract
1. Introduction
2. InSAR Geocoding: Principle and Error Sources
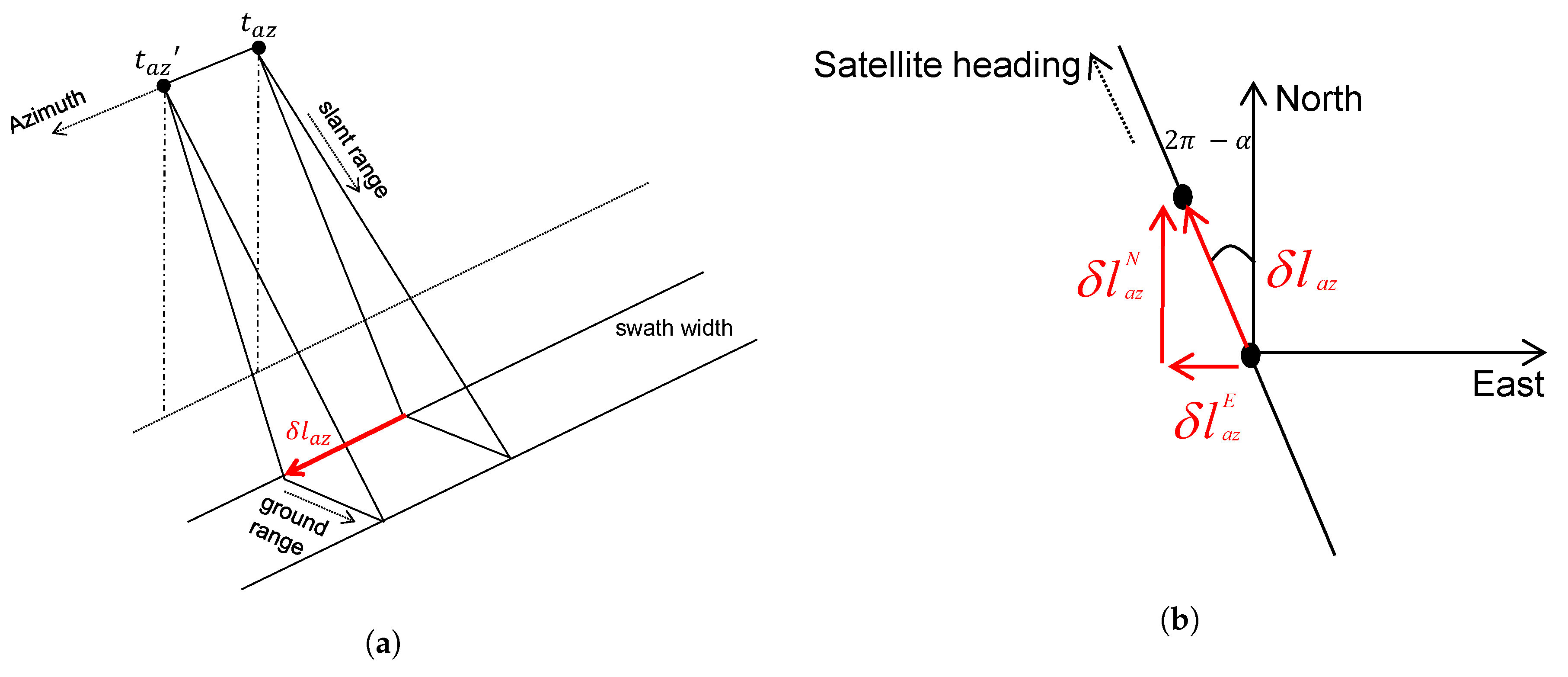
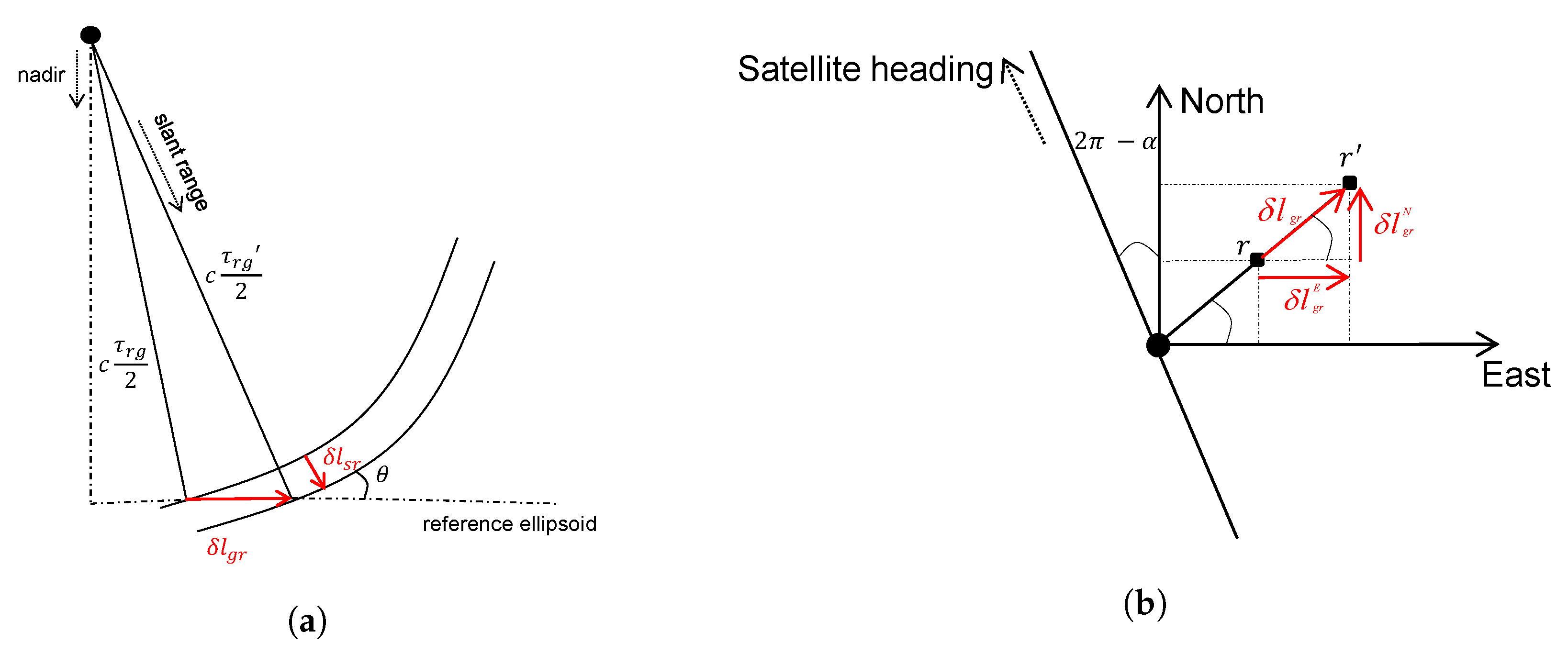
2.1. Errors in Azimuth and Range Times
- satellite dynamic effects such as incorrect annotation of in the time of radar pulse reception or incorrect annotation of due to instrument cable delays in the satellite [9].
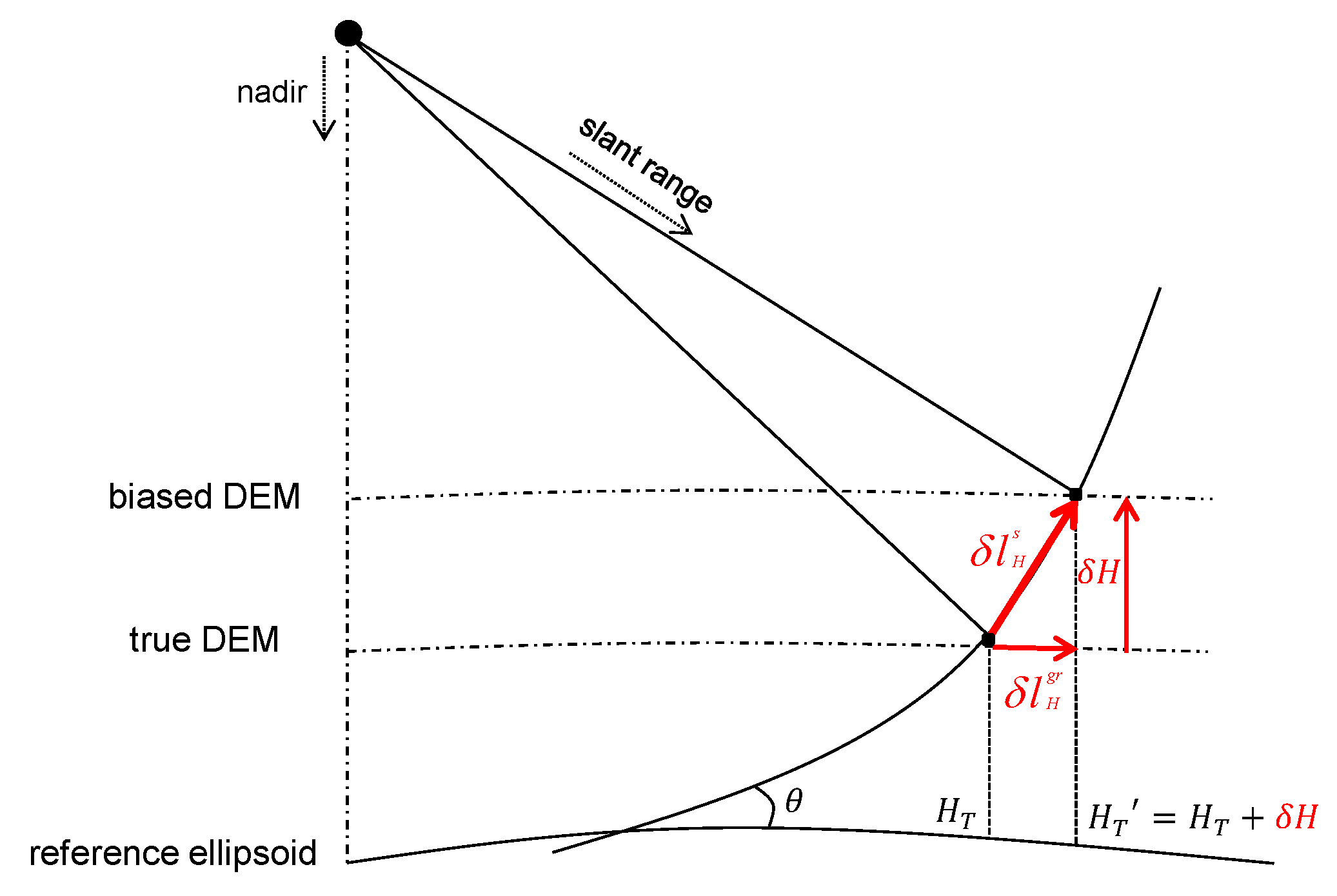
2.2. Error in the Height of PS
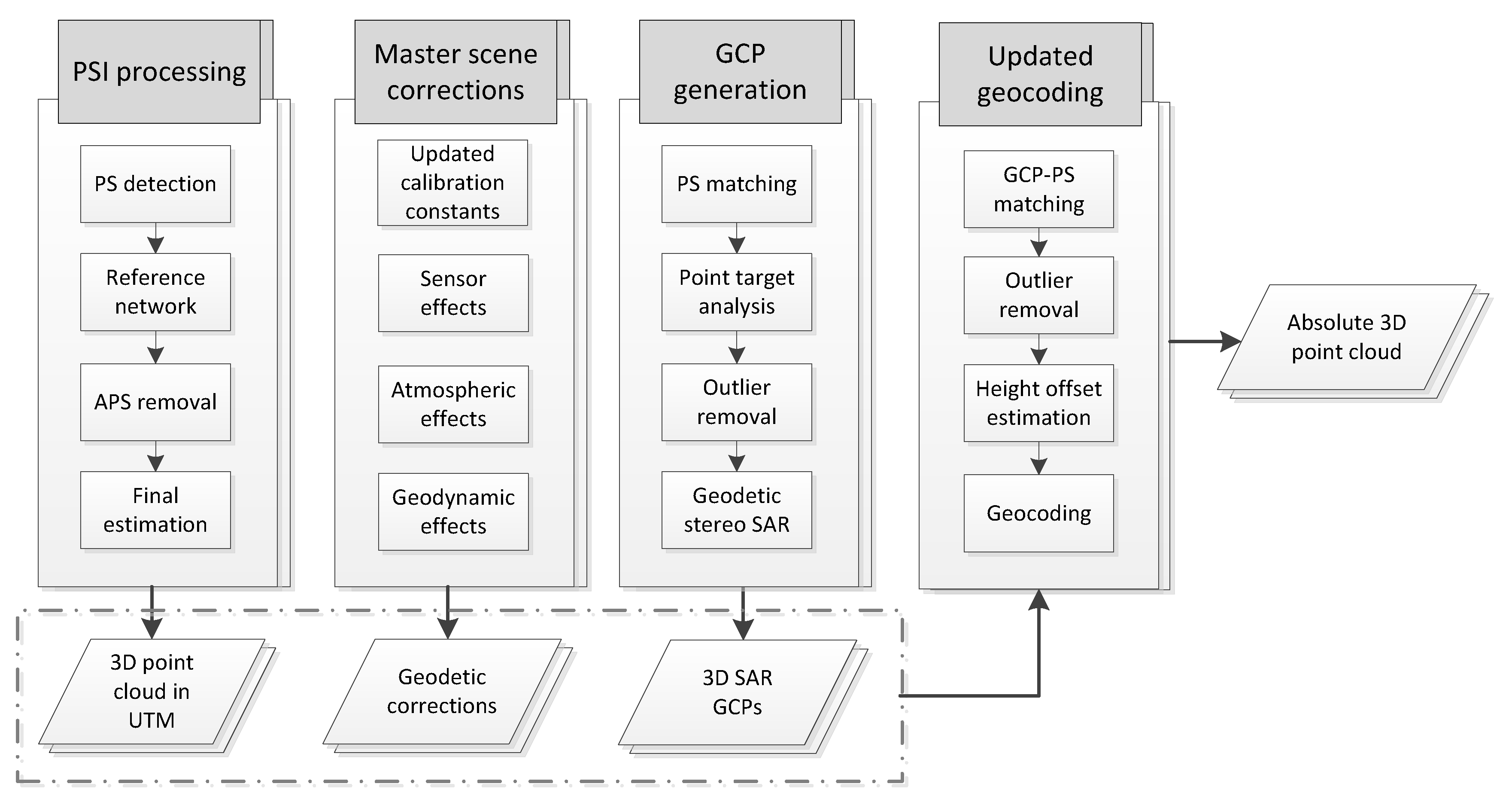
3. Methodology
3.1. PSI Processing
3.2. Master Scene Corrections
3.3. GCP Generation
3.4. Height Offset Estimation and Updated Geocoding
- Coordinate differences are calculated in range and azimuth of the GCPs and their assumed corresponding bright point in the PSI point cloud.
- Points with coordinate differences larger than two times the standard deviation of differences (2 rule) are discarded first in range and then in azimuth.
3.5. Cross-Comparison with LiDAR
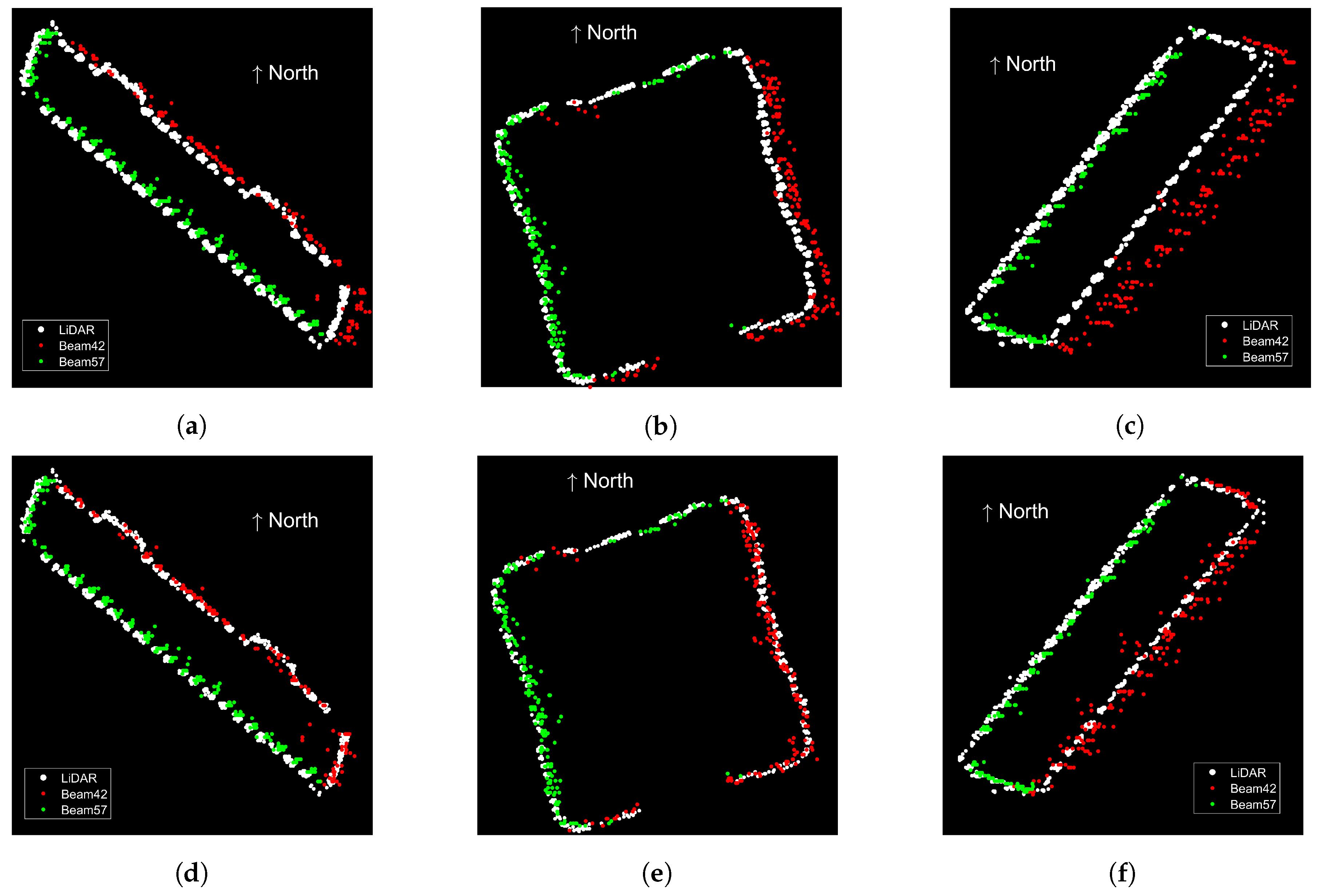
- 2D horizontal accuracy: For a number of test sites, a line is robustly fitted to each side of the building footprint in the LiDAR point cloud in the East–North plane. The mean distance of the façade PS in the PSI point clouds are evaluated with respect to the corresponding footprint line in the LiDAR data. The average of all the deviations for corrected and non-corrected PSI point clouds are separately calculated, which demonstrates the closeness of each point cloud to the reference LiDAR data.
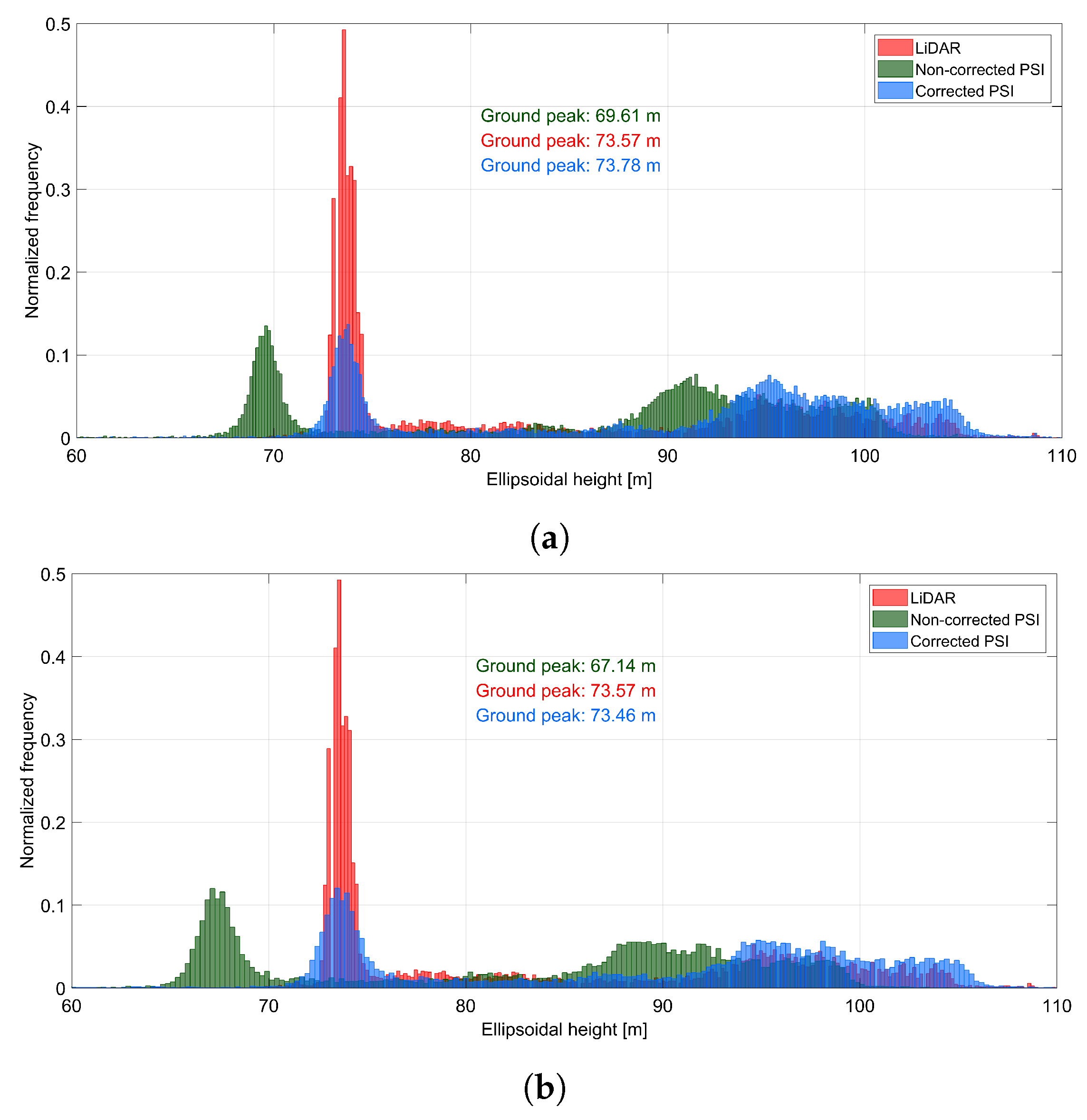
- 1D vertical accuracy: For an identical area in the LiDAR data and both corrected and non-corrected PSI point clouds, the façade points are excluded. Then for each of the three point clouds, ellipsoidal height histograms are formed containing two peaks which respectively represent ground and building roofs from the selected test site. The difference between the height values for which the ground peaks, in the PSI point cloud and in the LiDAR point cloud occur, indicates the vertical accuracy.
4. Area of Interest and Data Set
5. Results and Discussion
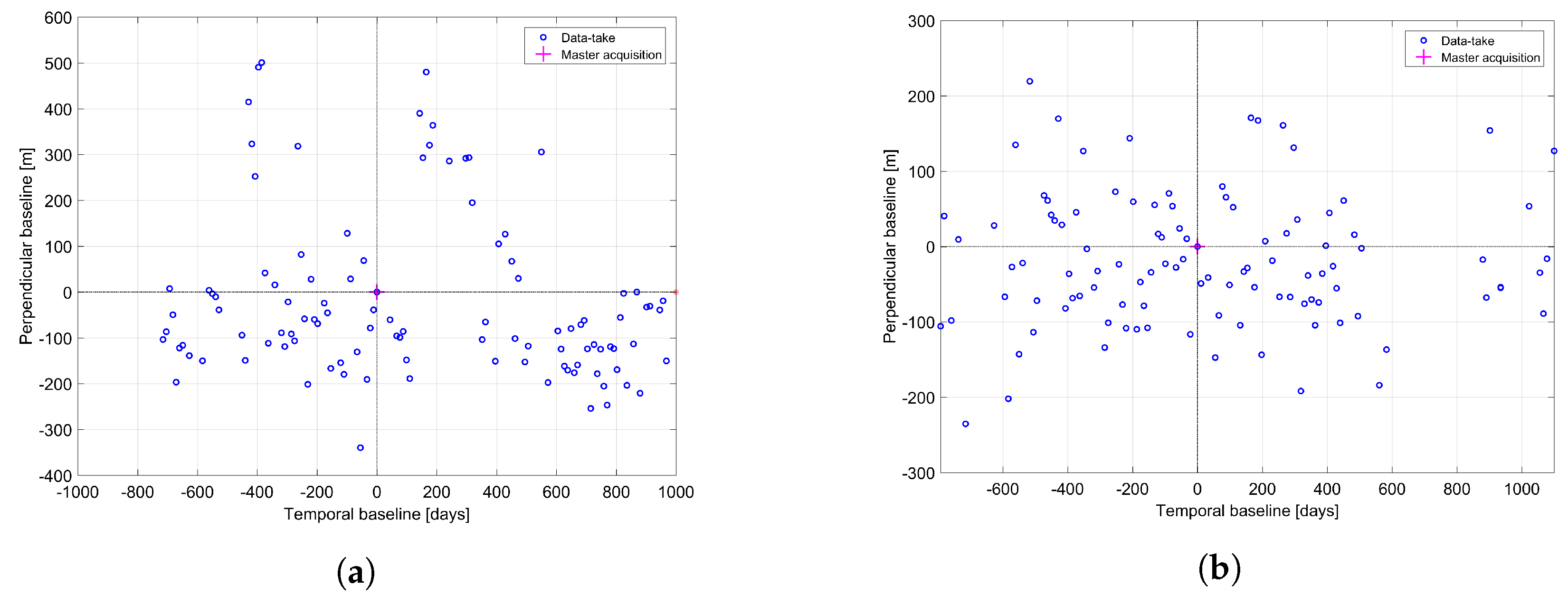
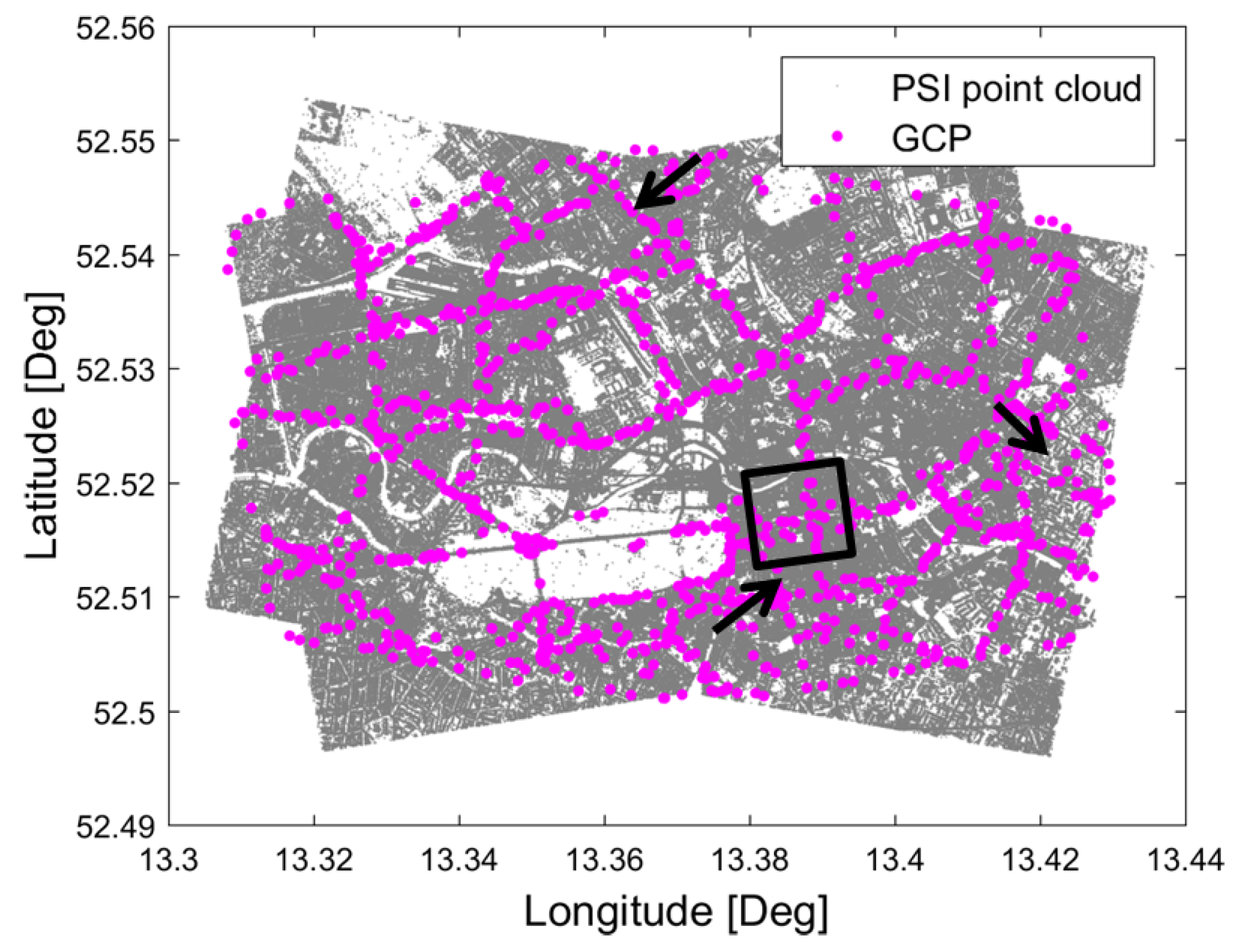
5.1. Berlin InSAR and PSI Processing
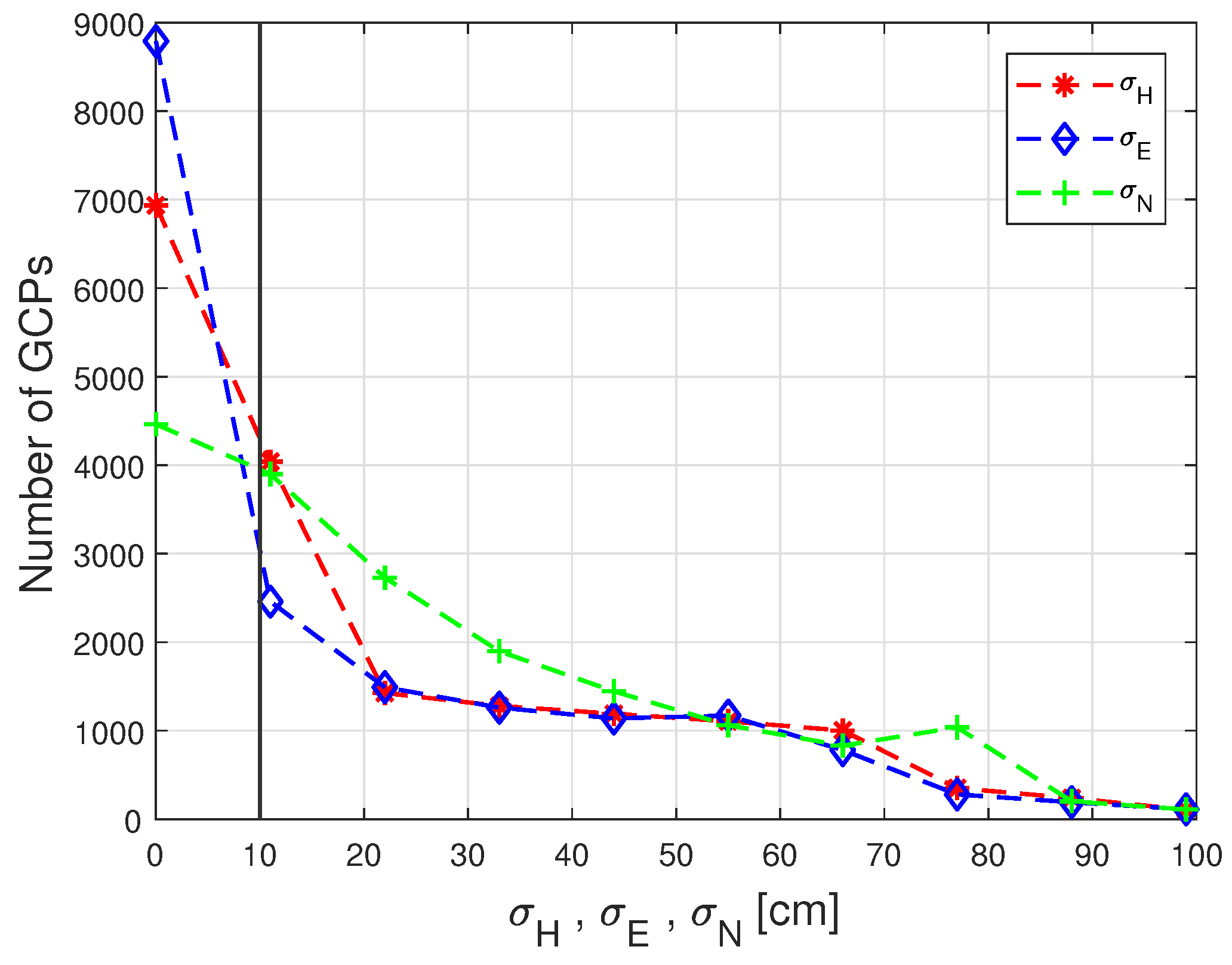
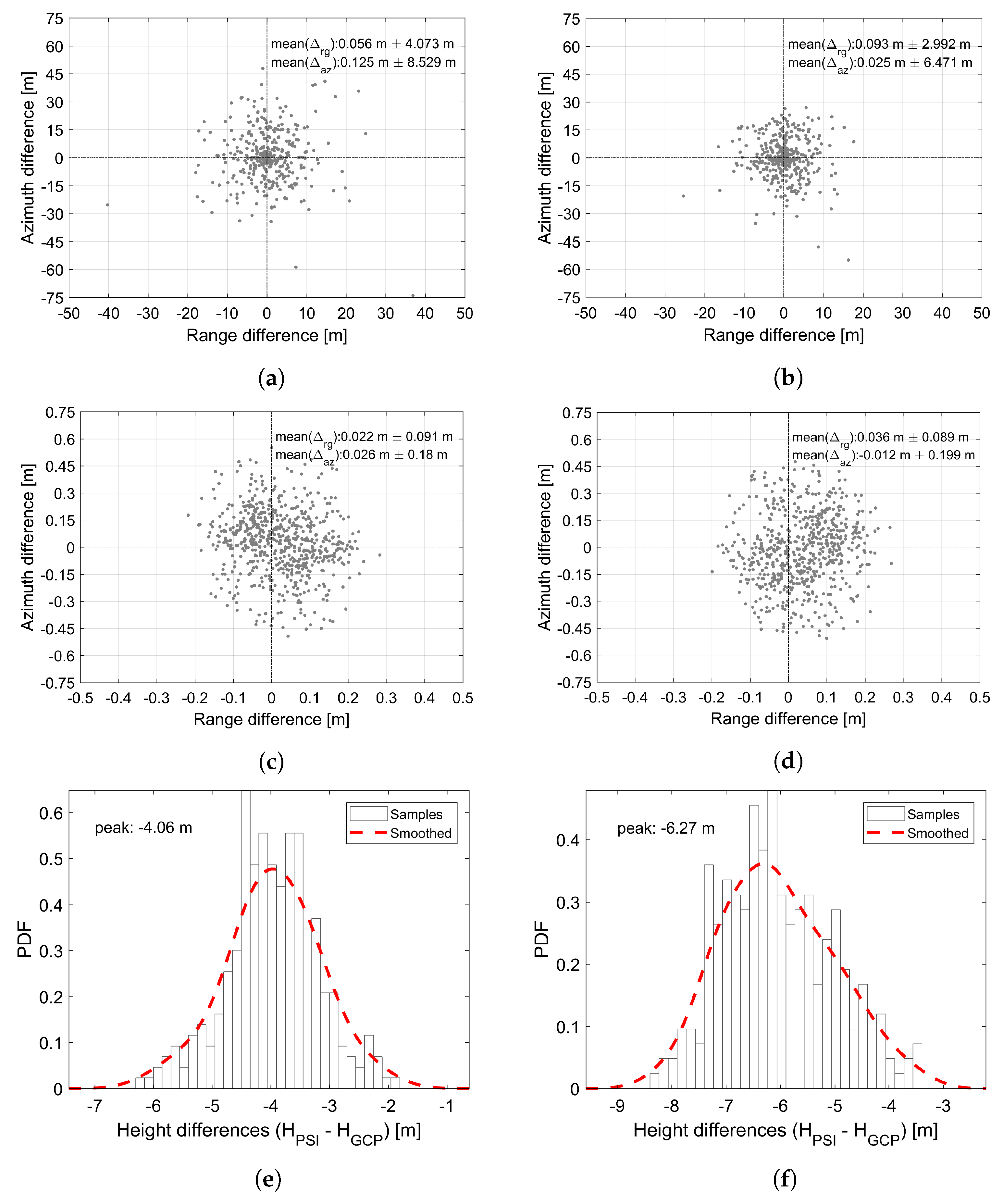
5.2. Geodetic Corrections, GCP Generation and Height Offset Estimation
5.3. Cross-Comparison with LiDAR
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADI | Amplitude Dispersion Index |
| DEM | Digital Elevation Model |
| DLR | German Aerospace Center |
| DSM | Digital Surface Model |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| GCP | Ground Control Point |
| GNSS | Global Navigation Satellite Systems |
| IERS | International Earth Rotation and Reference Systems Service |
| IGS | International GNSS Service |
| InSAR | Interferometric SAR |
| LiDAR | Light Detection and Ranging |
| MAD | Median Absolute Deviation |
| PSI | Persistent Scatterer Interferometry |
| PS | Persistent Scatterer |
| PTA | Point Target Analysis |
| SAR | Synthetic Aperture Radar |
| SCR | Signal-to-Clutter-Ratio |
| SGP | SAR Geodesy Processor |
| SLC | Single Look Complex |
| SRTM | Shuttle Radar Topography Mission |
| TEC | Total Electron Content |
| UTM | Universal Transverse Mercator |
References
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Kampes, B.M. Radar Interferometry: Persistent Scatterer Technique. In Number v. 12 in Remote Sensing and Digital Image Processing; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Zebker, H.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Gernhardt, S.; Bamler, R. Deformation monitoring of single buildings using meter-resolution SAR data in PSI. ISPRS J. Photogramm. Remote Sens. 2012, 73, 68–79. [Google Scholar] [CrossRef]
- Gernhardt, S.; Adam, N.; Eineder, M.; Bamler, R. Potential of very high resolution SAR for persistent scatterer interferometry in urban areas. Ann. GIS 2010, 16, 103–111. [Google Scholar] [CrossRef]
- Schwabisch, M. A fast and efficient technique for SAR interferogram geocoding. In Proceedings of the 1998 IEEE International Geoscience and Remote Sensing (IGARSS), Seattle, WA, USA, USA, 6–10 July 1998; Volume 2, pp. 1100–1102. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis. In Number v. 2 in Remote Sensing and Digital Image Processing; Kluwer Academic: Dordrecht, The Netherlands; Boston, MA, USA, 2001. [Google Scholar]
- Eineder, M. Efficient simulation of SAR interferograms of large areas and of rugged terrain. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1415–1427. [Google Scholar] [CrossRef]
- Eineder, M.; Minet, C.; Steigenberger, P.; Cong, X.Y.; Fritz, T. Imaging Geodesy—Toward Centimeter-Level Ranging Accuracy With TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2011, 49, 661–671. [Google Scholar] [CrossRef]
- Chang, L.; Hanssen, R.F. Detection of cavity migration and sinkhole risk using radar interferometric time series. Remote Sens. Environ. 2014, 147, 56–64. [Google Scholar] [CrossRef]
- Yang, M.; Dheenathayalan, P.; Chang, L.; Wang, J.; Lindenbergh, R.; Liao, M.; Hanssen, R. High-precision 3D geolocation of persistent scatterers with one single-Epoch GCP and LIDAR DSM data. In Proceedings of the Living Planet Symposium; European Space Agency: Paris, France, 2016; Volume 740, p. 398. [Google Scholar]
- Bateson, L.; Novali, F.; Cooksley, G. Terrafirma User Guide: A Guide to the Use and Understanding of Persistent Scatterer Interferometry in the Detection and Monitoring of Terrain-Motion; Technical Report 19366/05/I-EC; ESA: Paris, France, 2010. [Google Scholar]
- Gernhardt, S.; Cong, X.Y.; Eineder, M.; Hinz, S.; Bamler, R. Geometrical Fusion of Multitrack PS Point Clouds. IEEE Geosci. Remote Sens. Lett. 2012, 9, 38–42. [Google Scholar] [CrossRef]
- Gernhardt, S. High Precision 3D Localization and Motion Analysis of Persistent Scatterers Using Meter-Resolution Radar Satellite Data. Ph.D. Thesis, Technische Universität München, München, Germany, 2012. [Google Scholar]
- Cong, X. SAR Interferometry for Volcano Monitoring: 3D-PSI Analysis and Mitigation of Atmospheric Refractivity. Ph.D. Thesis, Technische Universität München, München, Germany, 2014. [Google Scholar]
- Besl, P.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Zhu, X.X.; Montazeri, S.; Gisinger, C.; Hanssen, R.F.; Bamler, R. Geodetic SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2016, 54, 18–35. [Google Scholar] [CrossRef]
- Gisinger, C.; Balss, U.; Pail, R.; Zhu, X.X.; Montazeri, S.; Gernhardt, S.; Eineder, M. Precise Three-Dimensional Stereo Localization of Corner Reflectors and Persistent Scatterers With TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1782–1802. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Very high resolution spaceborne SAR tomography in urban environment. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4296–4308. [Google Scholar] [CrossRef]
- Balss, U.; Runge, H.; Suchandt, S.; Cong, X.Y. Automated extraction of 3-D Ground Control Points from SAR images—An upcoming novel data product. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5023–5026. [Google Scholar] [CrossRef]
- Montazeri, S.; Gisinger, C.; Eineder, M.; Zhu, X.X. Automatic Detection and Positioning of Ground Control Points Using TerraSAR-X Multiaspect Acquisitions. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2613–2632. [Google Scholar] [CrossRef]
- Van Leijen, F. Persistent Scatterer Interferometry Based on Geodetic Estimation Theory. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar]
- Cumming, I.G.; Wong, F.H.C. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House Remote Sensing Library, Artech House: Boston, MA, USA, 2005. [Google Scholar]
- Yoon, Y.; Eineder, M.; Yague-Martinez, N.; Montenbruck, O. TerraSAR-X Precise Trajectory Estimation and Quality Assessment. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1859–1868. [Google Scholar] [CrossRef]
- Hackel, S.; Montenbruck, O.; Steigenberger, P.; Balss, U.; Gisinger, C.; Eineder, M. Model improvements and validation of TerraSAR-X precise orbit determination. J. Geod. 2017, 91, 547–562. [Google Scholar] [CrossRef]
- Cong, X.Y.; Balss, U.; Eineder, M.; Fritz, T. Imaging Geodesy—Centimeter-Level Ranging Accuracy with TerraSAR-X: An Update. IEEE Geosci. Remote Sens. Lett. 2012, 9, 948–952. [Google Scholar] [CrossRef]
- Balss, U.; Cong, X.Y.; Brcic, R.; Rexer, M.; Minet, C.; Breit, H.; Eineder, M.; Fritz, T. High precision measurement on the absolute localization accuracy of TerraSAR-X. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1625–1628. [Google Scholar] [CrossRef]
- Balss, U.; Gisinger, C.; Cong, X.Y.; Brcic, R.; Hackel, S.; Eineder, M. Precise measurements on the absolute localization accuracy of TerraSAR-X on the base of far-distributed test sites. In Proceeding of the 10th European Conference on Synthetic Aperture Radar (EUSAR), Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Balss, U.; Breit, H.; Fritz, T.; Steinbrecher, U.; Gisinger, C.; Eineder, M. Analysis of internal timings and clock rates of TerraSAR-X. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 2671–2674. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance; Misra, P., Enge, P., Eds.; Jamuna Press: Warsaw, Poland, 2006. [Google Scholar]
- Gisinger, C. Atmospheric Corrections for TerraSAR-X Derived from GNSS Observations. Master’s Thesis, Technische Universität München, München, Germany, 2012. [Google Scholar]
- Balss, U.; Gisinger, C.; Cong, X.Y.; Brcic, R.; Steigenberger, P.; Eineder, M.; Pail, R.; Hugentobler, U. High resolution geodetic earth observation with TerraSAR-X: Correction schemes and validation. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium, Melbourne, VIC, Australia, 21–26 July 2013; pp. 4499–4502. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions; IERS Technical Note No. 36; Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Balss, U.; Gisinger, C.; Eineder, M. Measurements on the Absolute 2-D and 3-D Localization Accuracy of TerraSAR-X. Remote Sens. 2018, 10, 656. [Google Scholar] [CrossRef]
- Eineder, M.; Balss, U.; Suchandt, S.; Gisinger, C.; Cong, X.; Runge, H. A definition of next-generation SAR products for geodetic applications. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium, Milan, Italy, 26–31 July 2015; pp. 1638–1641. [Google Scholar] [CrossRef]
- OpenStreetMap Contributors. Planet Dump. 2017. Available online: https://www.openstreetmap.org (accessed on 18 August 2018).
- Rousseeuw, P.J.; Hubert, M. Anomaly detection by robust statistics. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, 1–14. [Google Scholar] [CrossRef]
- Adam, N.; Kampes, B.M.; Eineder, M. The development of a scientific persistent scatterer system: Modifications for mixed ERS/ENVISAT time series. In Proceedings of the Envisat and ERS Symposium, Salzburg, Austria, 6–10 September 2004; pp. 1–9. [Google Scholar]
- Adam, N.; Gonzalez, F.R.; Parizzi, A.; Brcic, R. Wide area Persistent Scatterer Interferometry: Current developments, algorithms and examples. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium, Melbourne, VIC, Australia, 21–26 July 2013; pp. 1857–1860. [Google Scholar] [CrossRef]
- Rodriguez Gonzalez, F.; Bhutani, A.; Adam, N. L1 network inversion for robust outlier rejection in persistent Scatterer Interferometry. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 75–78. [Google Scholar] [CrossRef]
- Rodriguez Gonzalez, F.; Adam, N.; Parizzi, A.; Brcic, R. The Integrated Wide Area Processor (IWAP): A Processor for Wide Area Persistent Scatterer Interferometry. In Proceedings of the ESA Living Planet Symposium 2013; ESA: Edinburgh, UK, 2013; pp. 1–4. [Google Scholar]
- Adam, N.; Kampes, B.M.; Eineder, M.; Worawattanamateekul, J.; Kircher, M. The Development of a Scientific Permanent Scatterer System. In Proceedings of the Joint ISPRS/EARSeL Workshop on High Resolution Mapping from Space 2003, Edinburgh, UK, 9–13 September 2003. [Google Scholar]
- Montazeri, S. The Fusion of SAR Tomography and Stereo-SAR for 3D Absolute Scatterer Positioning. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar]
- Montazeri, S.; Zhu, X.X.; Eineder, M.; Bamler, R. Three-Dimensional Deformation Monitoring of Urban Infrastructure by Tomographic SAR Using Multitrack TerraSAR-X Data Stacks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6868–6878. [Google Scholar] [CrossRef]

| Beam Nr. | Center θ (Degree) | Average α (Degree) | Orbit Direction | Area (km2) | Polarization | Nr. of Images |
|---|---|---|---|---|---|---|
| 42 | 36.1 | 350.3 | descending | 40.94 | VV | 107 |
| 57 | 41.9 | 190.6 | ascending | 42.52 | VV | 107 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montazeri, S.; Rodríguez González, F.; Zhu, X.X. Geocoding Error Correction for InSAR Point Clouds. Remote Sens. 2018, 10, 1523. https://doi.org/10.3390/rs10101523
Montazeri S, Rodríguez González F, Zhu XX. Geocoding Error Correction for InSAR Point Clouds. Remote Sensing. 2018; 10(10):1523. https://doi.org/10.3390/rs10101523
Chicago/Turabian StyleMontazeri, Sina, Fernando Rodríguez González, and Xiao Xiang Zhu. 2018. "Geocoding Error Correction for InSAR Point Clouds" Remote Sensing 10, no. 10: 1523. https://doi.org/10.3390/rs10101523
APA StyleMontazeri, S., Rodríguez González, F., & Zhu, X. X. (2018). Geocoding Error Correction for InSAR Point Clouds. Remote Sensing, 10(10), 1523. https://doi.org/10.3390/rs10101523







