Spectral Invariant Provides a Practical Modeling Approach for Future Biophysical Variable Estimations
Abstract
1. Introduction
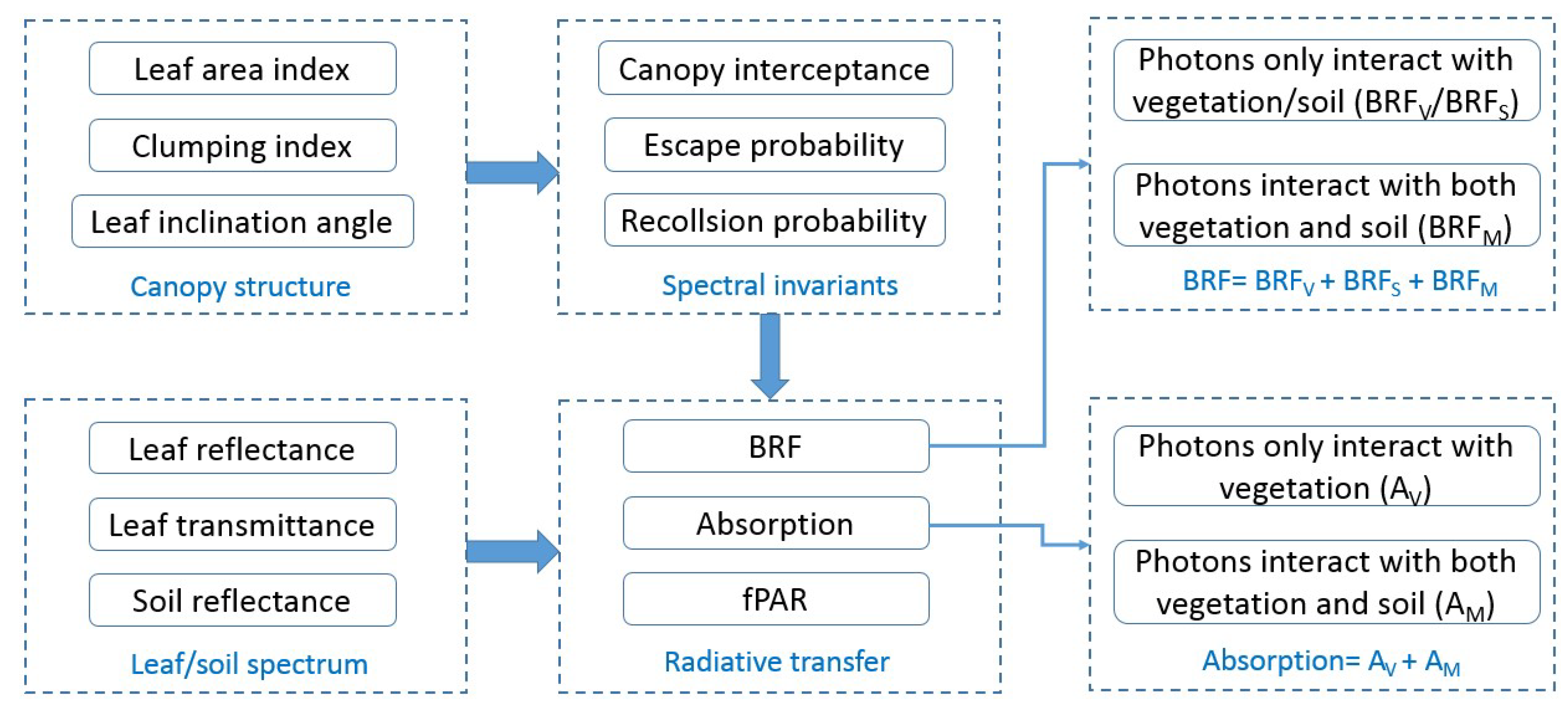
2. Model Description
2.1. BRF of the Vegetation-Soil System
2.2. Absorption of the Vegetation and fPAR
2.3. Canopy Radiation Transfer Terms by Spectral Invariant
2.4. Analytical Formula of Spectral Invariant by Canopy Structure
3. Materials and Methods
4. Results and Analysis
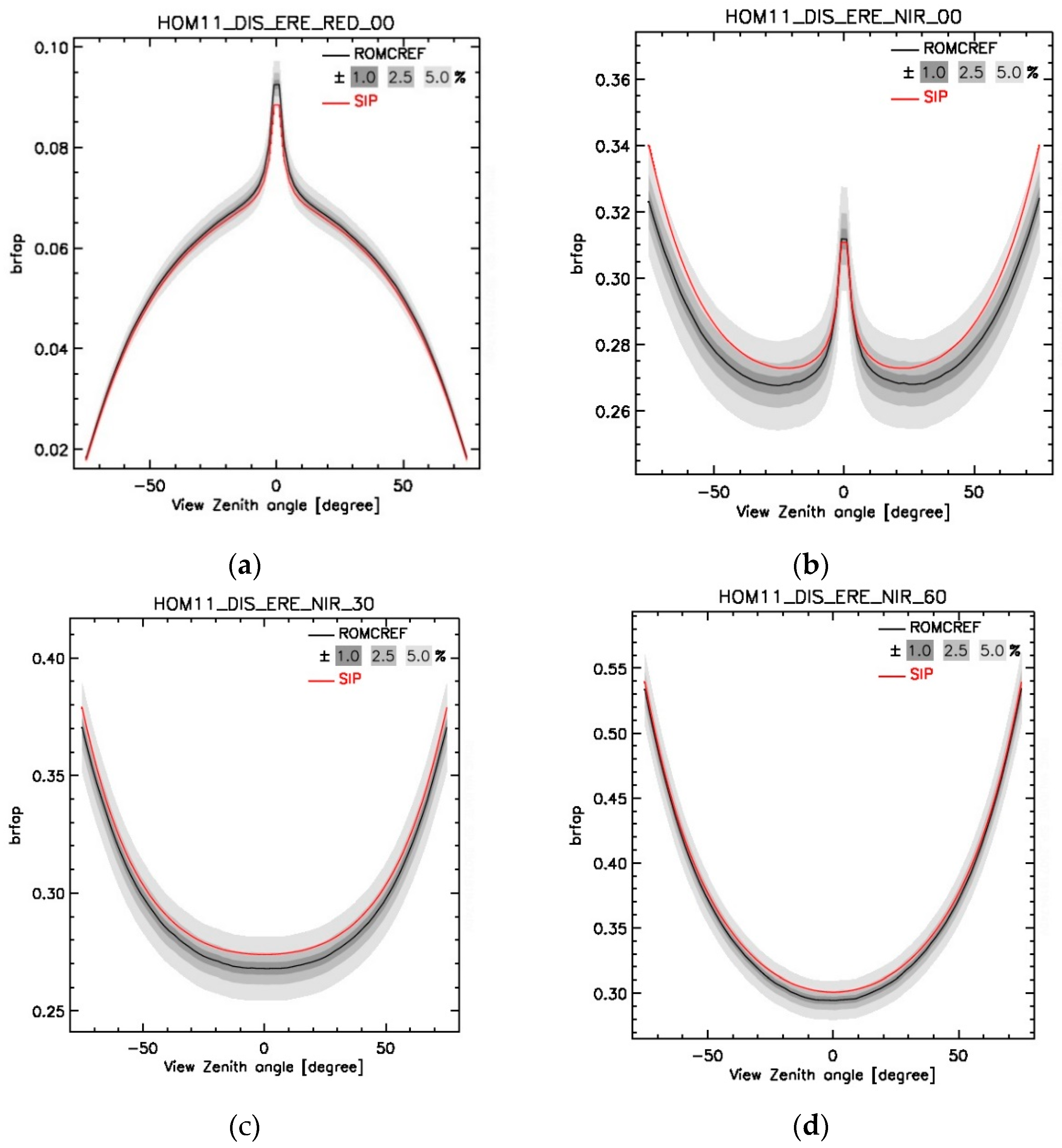
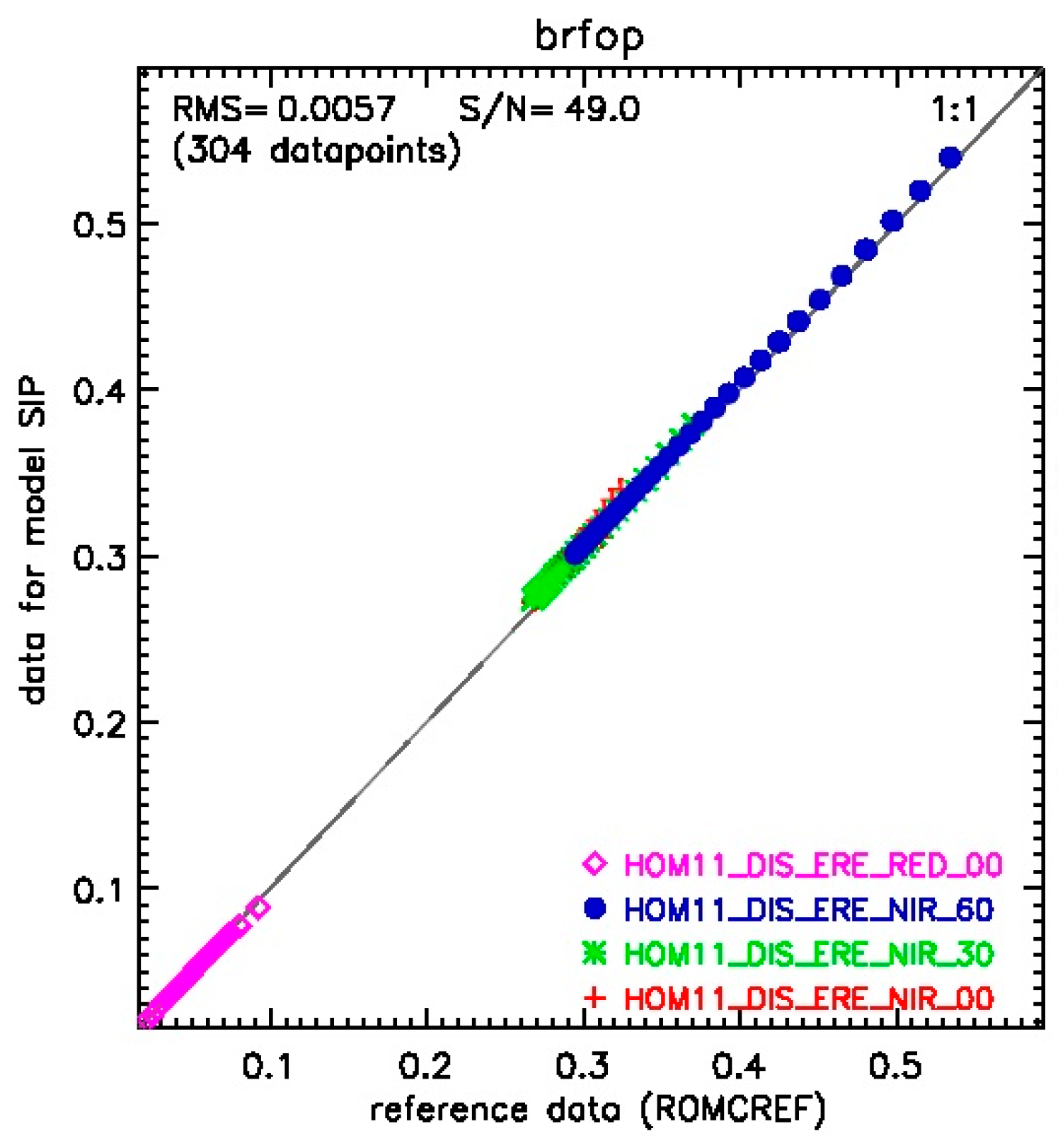
4.1. Evaluation in the RAMI Platform in Angular Space
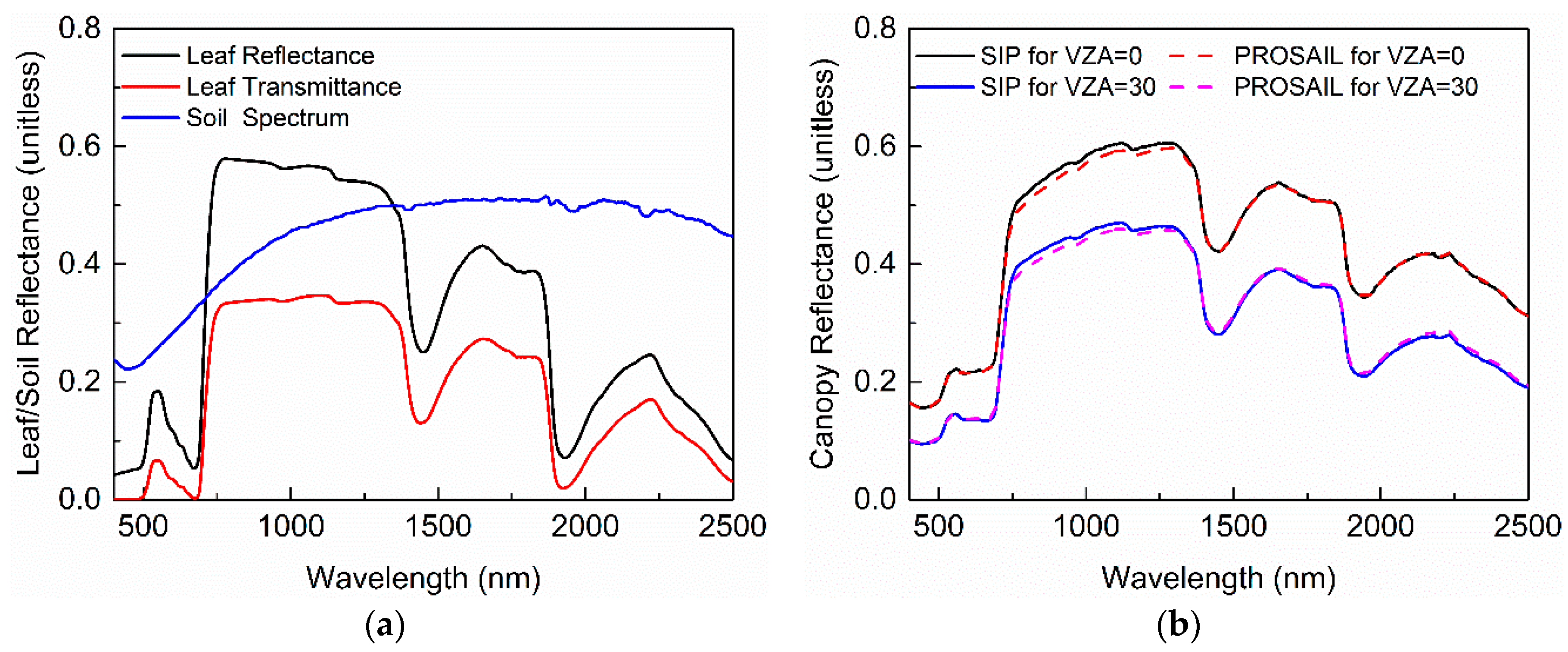
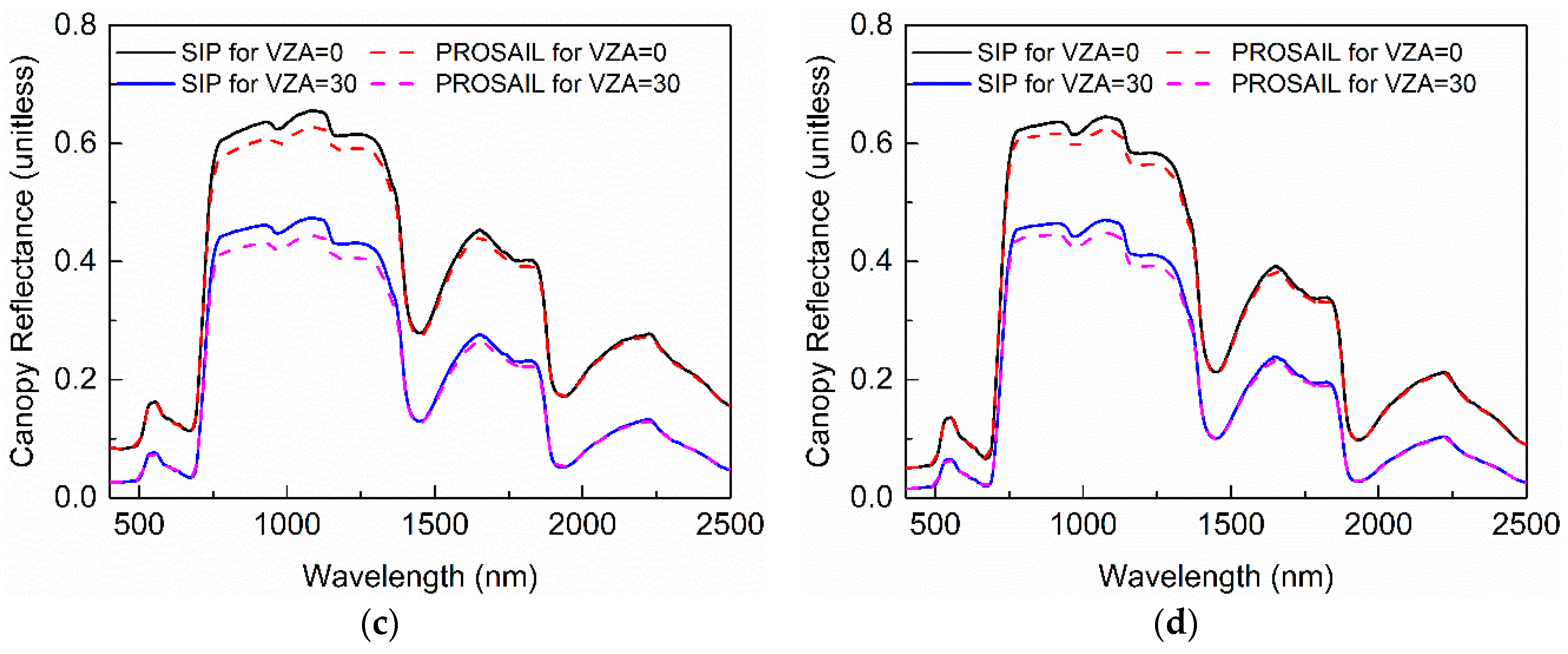
4.2. Evaluation by the PROSAIL Model in Hyperspectral Space
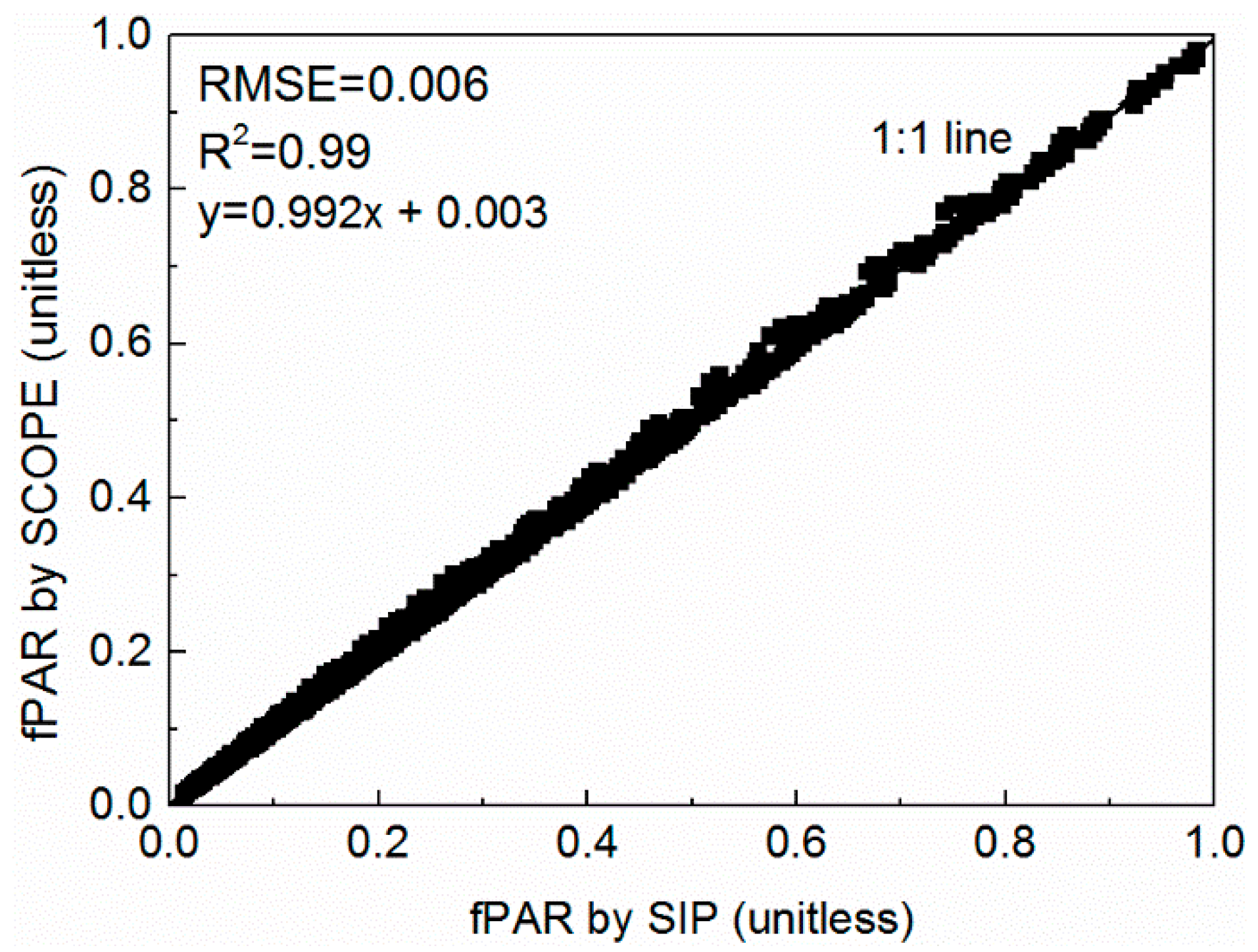
4.3. Evaluation the fPAR by the SCOPE Model
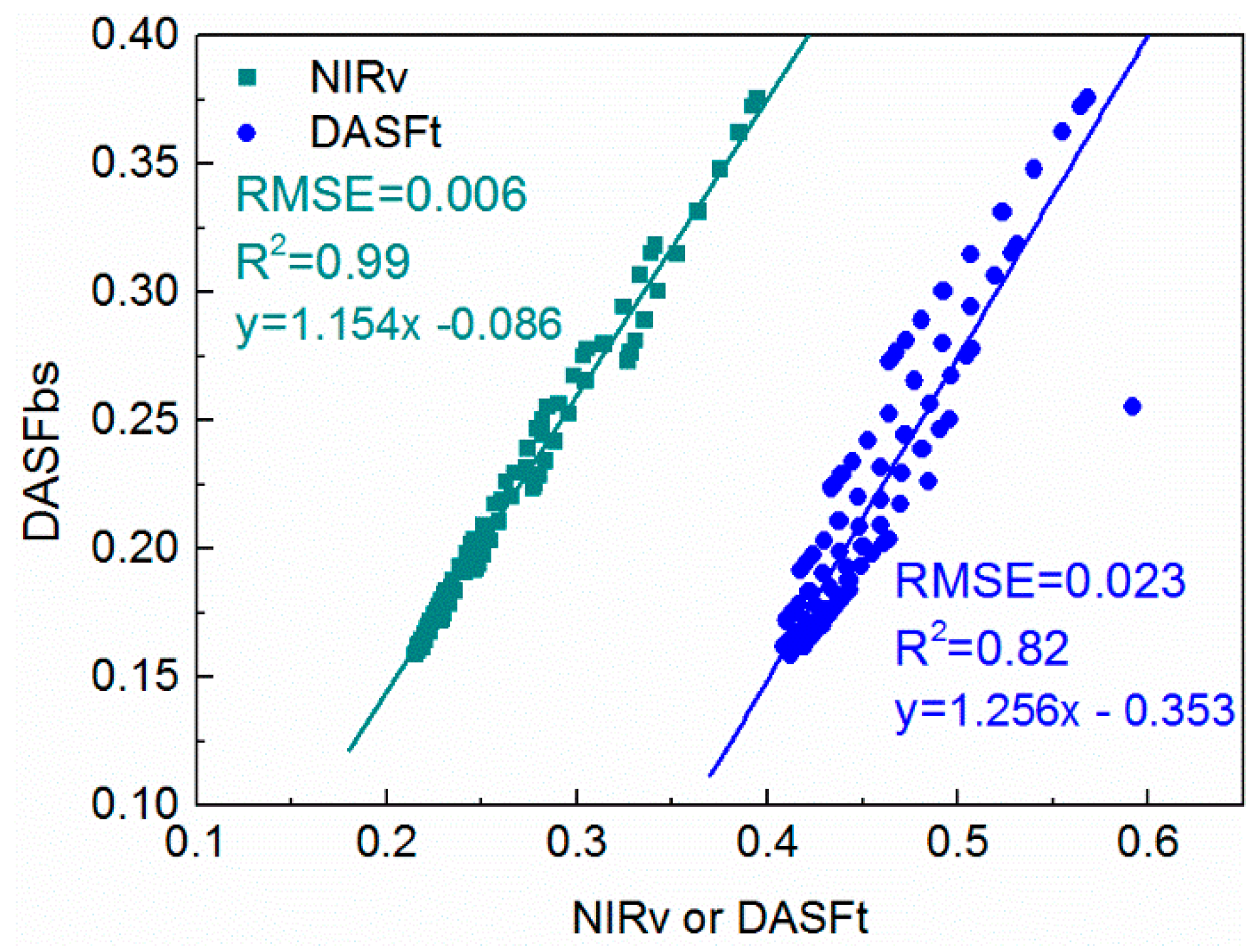
4.4. Impact of Soil Effect on DASF Calculation
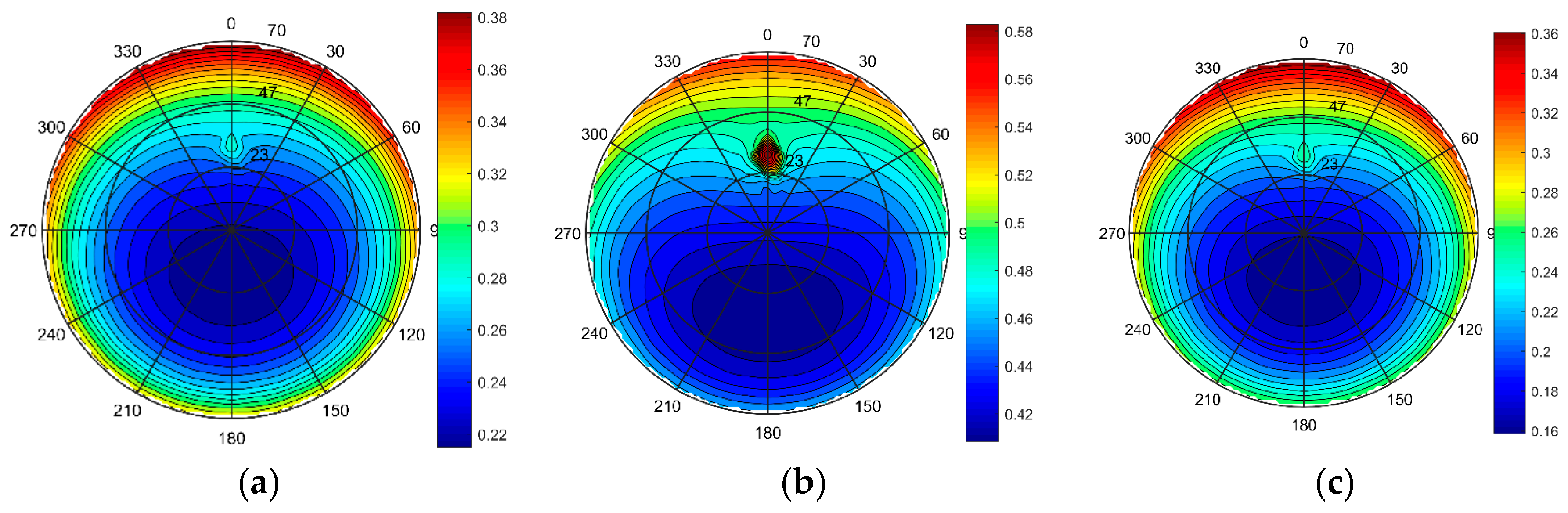
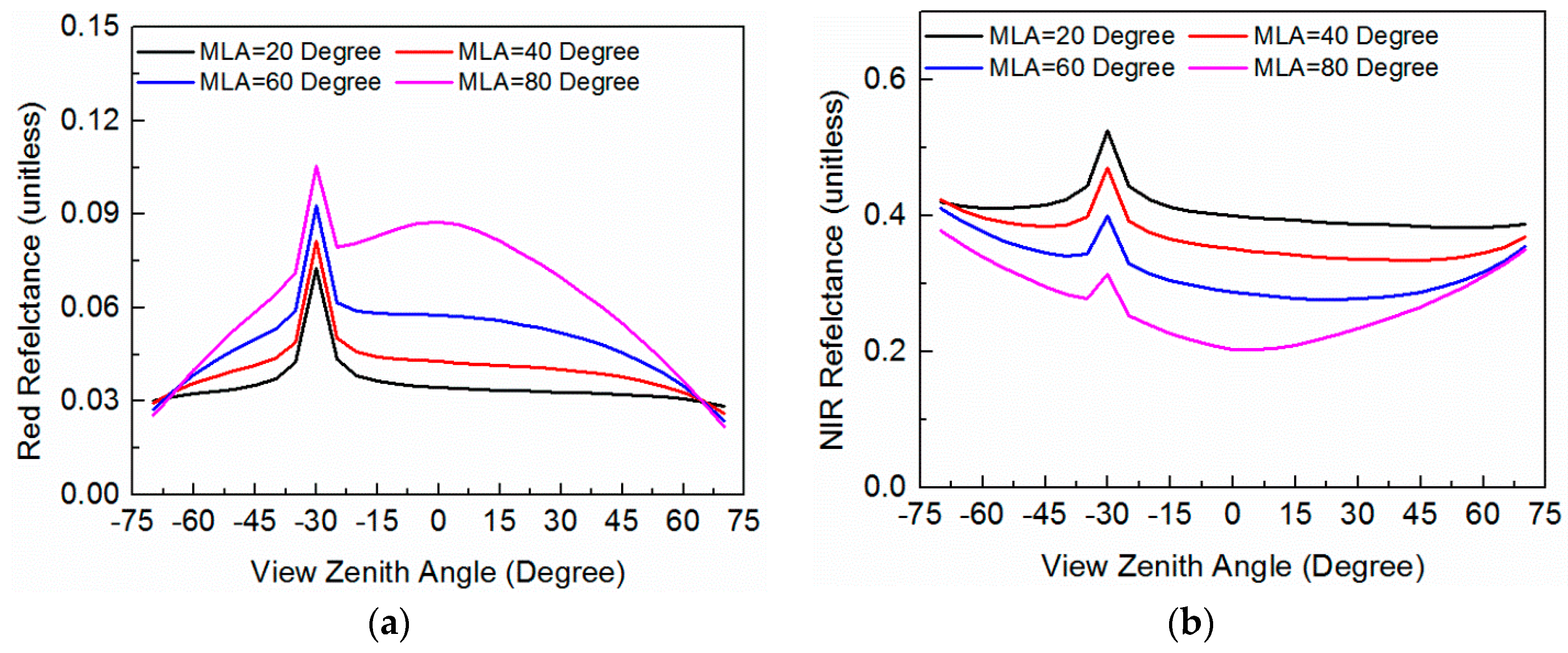
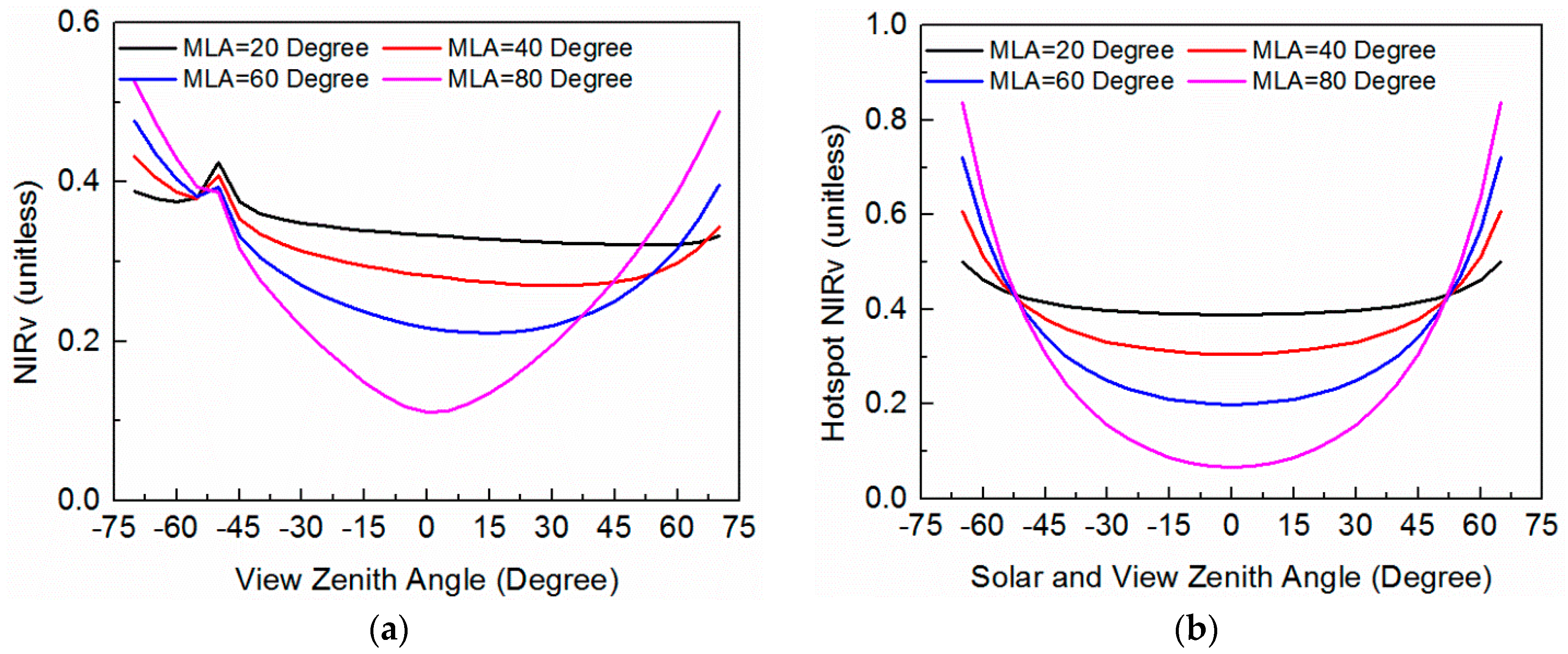
4.5. Impact of the Mean Leaf Inclination Angle on BRF and NIRv
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| bidirectional reflectance factor | |
| contribution by vegetation with no interaction with the soil background | |
| single scattering of the vegetation in BRF | |
| multiple scattering contribution of the vegetation in BRF | |
| single scattering contribution of the soil background in BRF | |
| multiple scattering contribution between the vegetation and soil in BRF | |
| leaf albedo at wavelength | |
| bidirectional scattering coefficient | |
| leaf area density | |
| canopy height | |
| directional gap fraction at the solar direction | |
| bidirectional gap fraction | |
| leaf projection function | |
| leaf inclination angle | |
| solar zenith angle | |
| view zenith angle | |
| clumping index at the zenith angle of | |
| hot spot correction function | |
| canopy directional escape probability in the upward direction of | |
| canopy directional escape probability in the downward direction of | |
| canopy hemispherical escape probability in the upward direction | |
| canopy hemispherical escape probability in the downward direction | |
| recollision probability | |
| soil reflectance | |
| the fraction of visible sunlit soil in view | |
| canopy directional interceptance in the solar direction | |
| canopy hemispherical interceptance under diffuse radiation illumination | |
| canopy zero-order transmission in the solar direction | |
| canopy zero-order transmission at the direction of under diffuse radiation | |
| canopy zero-order hemispherical transmission under diffuse radiation | |
| absorption by vegetation under isotropic diffuse illumination at bottom | |
| albedo in the downward direction under isotropic diffuse illumination at bottom | |
| canopy downwelling transmittance with black soil background | |
| canopy upward transmittance with isotropic diffuse illumination at bottom |
References
- Zhao, J.; Li, J.; Liu, Q.; Fan, W.; Zhong, B.; Wu, S.; Yang, L.; Zeng, Y.; Xu, B.; Yin, G. Leaf Area Index Retrieval Combining HJ1/CCD and Landsat8/OLI Data in the Heihe River Basin, China. Remote Sens. 2015, 7, 6862–6885. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Jin, H.; Zhao, W.; Bian, J.; Qu, Y.; Zeng, Y.; Xu, B. Derivation of temporally continuous LAI reference maps through combining the LAINet observation system with CACAO. Agric. For. Meteorol. 2017, 233, 209–221. [Google Scholar] [CrossRef]
- Mu, X.; Hu, R.; Zeng, Y.; McVicar, T.R.; Ren, H.; Song, W.; Wang, Y.; Casa, R.; Qi, J.; Xie, D. Estimating structural parameters of agricultural crops from ground-based multi-angular digital images with a fractional model of sun and shade components. Agric. For. Meteorol. 2017, 246, 162–177. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Chen, C.; Xu, B.; Song, W.; Yang, B.; Zeng, Y.; Liu, Z.; Yan, G.; Knyazikhin, Y. Generating Global Products of LAI and FPAR From SNPP-VIIRS Data: Theoretical Background and Implementation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2119–2137. [Google Scholar] [CrossRef]
- Xu, B.; Park, T.; Yan, K.; Chen, C.; Zeng, Y.; Song, W.; Yin, G.; Li, J.; Liu, Q.; Knyazikhin, Y. Analysis of Global LAI/FPAR Products from VIIRS and MODIS Sensors for Spatio-Temporal Consistency and Uncertainty from 2012–2016. Forests 2018, 9, 73. [Google Scholar] [CrossRef]
- Yin, G.; Li, J.; Liu, Q.; Fan, W.; Xu, B.; Zeng, Y.; Zhao, J. Regional Leaf Area Index Retrieval Based on Remote Sensing: The Role of Radiative Transfer Model Selection. Remote Sens. 2015, 7, 4604–4625. [Google Scholar] [CrossRef]
- Yin, G.; Li, J.; Liu, Q.; Li, L.; Zeng, Y.; Xu, B.; Yang, L.; Zhao, J. Improving Leaf Area Index Retrieval over Heterogeneous Surface by Integrating Textural and Contextual Information: A Case Study in the Heihe River Basin. IEEE Geosci. Remote Sens. Lett. 2015, 12, 359–363. [Google Scholar]
- Zeng, Y.; Li, J.; Liu, Q.; Hu, R.; Mu, X.; Fan, W.; Xu, B.; Yin, G.; Wu, S. Extracting Leaf Area Index by Sunlit Foliage Component from Downward-Looking Digital Photography under Clear-Sky Conditions. Remote Sens. 2015, 7, 13410–13435. [Google Scholar] [CrossRef]
- Kuusk, A. A two-layer canopy reflectance model. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 1–9. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Kuusk, A.; Nilson, T. A directional multispectral forest reflectance model. Remote Sens. Environ. 2000, 72, 244–252. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Huang, D.; Knyazikhin, Y.; Wang, W.; Deering, D.W.; Stenberg, P.; Shabanov, N.; Tan, B.; Myneni, R.B. Stochastic transport theory for investigating the three-dimensional canopy structure from space measurements. Remote Sens. Environ. 2008, 112, 35–50. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, J.; Liu, Q.; Yin, G.; Xu, B.; Fan, W.; Zhao, J. A canopy radiative transfer model suitable for heterogeneous Agro-Forestry scenes. In Proceedings of the IEEE International of Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3648–3651. [Google Scholar]
- Zeng, Y.; Li, J.; Liu, Q.; Huete, A.R.; Yin, G.; Xu, B.; Fan, W.; Zhao, J.; Yan, K.; Mu, X. A Radiative Transfer Model for Heterogeneous Agro-Forestry Scenarios. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4613–4628. [Google Scholar] [CrossRef]
- Marshak, A.; Knyazikhin, Y. The spectral invariant approximation within canopy radiative transfer to support the use of the EPIC/DSCOVR oxygen B-band for monitoring vegetation. J. Quant. Spectrosc. Radiat. Transf. 2017, 191, 7–12. [Google Scholar] [CrossRef] [PubMed]
- Knyazikhin, Y.; Martonchik, J.; Myneni, R.B.; Diner, D.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Mõttus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Carmona, P.L.; Kaufmann, R.K.; Lewis, P. Hyperspectral remote sensing of foliar nitrogen content. Proc. Natl. Acad. Sci. USA 2013, 110, E185–E192. [Google Scholar] [CrossRef] [PubMed]
- Stenberg, P.; Mõttus, M.; Rautiainen, M. Photon recollision probability in modelling the radiation regime of canopies—A review. Remote Sens. Environ. 2016, 183, 98–108. [Google Scholar] [CrossRef]
- Huang, D.; Knyazikhin, Y.; Dickinson, R.E.; Rautiainen, M.; Stenberg, P.; Disney, M.; Lewis, P.; Cescatti, A.; Tian, Y.; Verhoef, W. Canopy spectral invariants for remote sensing and model applications. Remote Sens. Environ. 2007, 106, 106–122. [Google Scholar] [CrossRef]
- Myneni, R.; Asrar, G.; Kanemasu, E. Light scattering in plant canopies: The method of successive orders of scattering approximations (SOSA). Agric. For. Meteorol. 1987, 39, 1–12. [Google Scholar] [CrossRef]
- Stenberg, P.; Lukeš, P.; Rautiainen, M.; Manninen, T. A new approach for simulating forest albedo based on spectral invariants. Remote Sens. Environ. 2013, 137, 12–16. [Google Scholar] [CrossRef]
- Majasalmi, T.; Rautiainen, M.; Stenberg, P. Modeled and measured fPAR in a boreal forest: Validation and application of a new model. Agric. For. Meteorol. 2014, 189, 118–124. [Google Scholar] [CrossRef]
- Yang, B.; Knyazikhin, Y.; Mõttus, M.; Rautiainen, M.; Stenberg, P.; Yan, L.; Chen, C.; Yan, K.; Choi, S.; Park, T. Estimation of leaf area index and its sunlit portion from DSCOVR EPIC data: Theoretical basis. Remote Sens. Environ. 2017, 198, 69–84. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.M. Optically-based methods for measuring seasonal variation of leaf area index in boreal conifer stands. Agric. For. Meteorol. 1996, 80, 135–163. [Google Scholar] [CrossRef]
- Mõttus, M. Photon recollision probability in discrete crown canopies. Remote Sens. Environ. 2007, 110, 176–185. [Google Scholar] [CrossRef]
- Stenberg, P. Simple analytical formula for calculating average photon recollision probability in vegetation canopies. Remote Sens. Environ. 2007, 109, 221–224. [Google Scholar] [CrossRef]
- Pisek, J.; Sonnentag, O.; Richardson, A.D.; Mõttus, M. Is the spherical leaf inclination angle distribution a valid assumption for temperate and boreal broadleaf tree species? Agric. For. Meteorol. 2013, 169, 186–194. [Google Scholar] [CrossRef]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global mapping of foliage clumping index using multi-angular satellite data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- Ryu, Y.; Sonnentag, O.; Nilson, T.; Vargas, R.; Kobayashi, H.; Wenk, R.; Baldocchi, D.D. How to quantify tree leaf area index in an open savanna ecosystem: A multi-instrument and multi-model approach. Agric. For. Meteorol. 2010, 150, 63–76. [Google Scholar] [CrossRef]
- Fang, H.; Liu, W.; Li, W.; Wei, S. Estimation of the directional and whole apparent clumping index (ACI) from indirect optical measurements. ISPRS J. Photogramm. Remote Sens. 2018, 144, 1–13. [Google Scholar] [CrossRef]
- Kucharik, C.J.; Norman, J.M.; Gower, S.T. Characterization of radiation regimes in nonrandom forest canopies: Theory, measurements, and a simplified modeling approach. Tree Physiol. 1999, 19, 695–706. [Google Scholar] [CrossRef] [PubMed]
- Marshak, A. The effect of the hot spot on the transport equation in plant canopies. J. Quant. Spectrosc. Radiat. Transf. 1989, 42, 615–630. [Google Scholar] [CrossRef]
- Rautiainen, M.; Stenberg, P. Application of photon recollision probability in coniferous canopy reflectance simulations. Remote Sens. Environ. 2005, 96, 98–107. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Robustelli, M.; Disney, M.; Gastellu-Etchegorry, J.-P.; Lavergne, T.; Lewis, P.; North, P.; Pinty, B.; Thompson, R.; Verstraete, M. The RAMI On-line Model Checker (ROMC): A web-based benchmarking facility for canopy reflectance models. Remote Sens. Environ. 2008, 112, 1144–1150. [Google Scholar] [CrossRef]
- Schull, M.A.; Knyazikhin, Y.; Xu, L.; Samanta, A.; Carmona, P.L.; Lepine, L.; Jenkins, J.; Ganguly, S.; Myneni, R.B. Canopy spectral invariants, Part 2: Application to classification of forest types from hyperspectral data. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 736–750. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef] [PubMed]
- Van der Tol, C.; Verhoef, W.; Timmermans, J.; Verhoef, A.; Su, Z. An integrated model of soil-canopy spectral radiances, photosynthesis, fluorescence, temperature and energy balance. Biogeosciences 2009, 6, 3109–3129. [Google Scholar] [CrossRef]
- Widlowski, J.L.; Mio, C.; Disney, M.; Adams, J.; Andredakis, I.; Atzberger, C.; Brennan, J.; Busetto, L.; Chelle, M.; Ceccherini, G.; et al. The fourth phase of the radiative transfer model intercomparison (RAMI) exercise: Actual canopy scenarios and conformity testing. Remote Sens. Environ. 2015, 169, 418–437. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, J.; Liu, Q.; Li, L.; Xu, B.; Yin, G.; Peng, J. A sampling strategy for remotely sensed LAI product validation over heterogeneous land surfaces. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3128–3142. [Google Scholar] [CrossRef]
- Yu, W.; Li, J.; Liu, Q.; Zeng, Y.; Zhao, J.; Xu, B.; Yin, G. Global Land Cover Heterogeneity Characteristics at Moderate Resolution for Mixed Pixel Modeling and Inversion. Remote Sens. 2018, 10, 856. [Google Scholar] [CrossRef]
- Xu, B.; Li, J.; Liu, Q.; Huete, A.R.; Yu, Q.; Zeng, Y.; Yin, G.; Zhao, J.; Yang, L. Evaluating Spatial Representativeness of Station Observations for Remotely Sensed Leaf Area Index Products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3267–3282. [Google Scholar] [CrossRef]
- Xu, B.; Li, J.; Liu, Q.; Zeng, Y.; Yin, G.; Fan, W.; Zhao, J. A method for spatial upscaling of ground LAI measurements to the remotely sensed product pixel grid. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3528–3531. [Google Scholar]
- Dou, B.; Wen, J.; Li, X.; Liu, Q.; Peng, J.; Xiao, Q.; Zhang, Z.; Tang, Y.; Wu, X.; Lin, X. Wireless sensor network of typical land surface parameters and its preliminary applications for coarse-resolution remote sensing pixel. Int. J. Distrib. Sens. Netw. 2016, 12, 9639021. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Wu, S.; Fan, W.; Zeng, Y.; Yan, K.; Xu, B.; Li, J.; Liu, Q. PLC: A simple and semi-physical topographic correction method for vegetation canopies based on path length correction. Remote Sens. Environ. 2018, 215, 184–198. [Google Scholar] [CrossRef]
- Fan, W.; Li, J.; Liu, Q.; Zhang, Q.; Yin, G.; Li, A.; Zeng, Y.; Xu, B.; Xu, X.; Zhou, G. Topographic Correction of Forest Image Data Based on the Canopy Reflectance Model for Sloping Terrains in Multiple Forward Mode. Remote Sens. 2018, 10, 717. [Google Scholar] [CrossRef]
- Yan, G.; Tong, Y.; Yan, K.; Mu, X.; Chu, Q.; Zhou, Y.; Liu, Y.; Qi, J.; Li, L.; Zeng, Y. Temporal Extrapolation of Daily Downward Shortwave Radiation Over Cloud-Free Rugged Terrains. Part 1: Analysis of Topographic Effects. IEEE Trans. Geosci. Remote Sens. 2018, PP, 1–20. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Zeng, Y.; Xu, B.; Zhao, W.; Nan, X.; Jin, H.; Bian, J. A cost-constrained sampling strategy in support of LAI product validation in mountainous areas. Remote Sens. 2016, 8, 704. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, J.; Liu, Q.; Qu, Y.; Huete, A.R.; Xu, B.; Yin, G.; Zhao, J. An Optimal Sampling Design for Observing and Validating Long-Term Leaf Area Index with Temporal Variations in Spatial Heterogeneities. Remote Sens. 2015, 7, 1300–1319. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, J.; Liu, Q.; Huete, A.R.; Xu, B.; Yin, G.; Zhao, J.; Yang, L.; Fan, W.; Wu, S. An Iterative BRDF/NDVI Inversion Algorithm Based on A Posteriori Variance Estimation of Observation Errors. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6481–6496. [Google Scholar] [CrossRef]
- Xu, B.; Li, J.; Park, T.; Liu, Q.; Zeng, Y.; Yin, G.; Zhao, J.; Fan, W.; Yang, L.; Knyazikhin, Y. An integrated method for validating long-term leaf area index products using global networks of site-based measurements. Remote Sens. Environ. 2018, 209, 134–151. [Google Scholar] [CrossRef]
| Variables | Values/Types | |
|---|---|---|
| Canopy structure | Leaf area index | 1 |
| Leaf angle distribution | Erectophile | |
| Solar-sensor geometry | Solar zenith angle | [0°, 30°, 60°] |
| View zenith angle | 0°–75° | |
| Relative azimuth angle | [0°, 90°, 180°, 270°] | |
| Leaf optics | Leaf reflectance | 0.02 (Red), 0.50 (NIR) |
| Leaf transmittance | 0.01 (Red), 0.45 (NIR) | |
| Soil background | Soil spectrum | 0.15 (Red), 0.20 (NIR) |
| Variables | Values/Types | |
|---|---|---|
| Fractional vegetation cover | [0.1–1] | |
| Canopy structure | Leaf area index | [0.5, 1, 3, 5] |
| Leaf angle distribution | Spherical, planophile, erectophile | |
| Solar geometry | Solar zenith angle | [20°, 30°, 40°, 50°, 60°] |
| Soil background | Soil spectra | Four SCOPE spectra |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Xu, B.; Yin, G.; Wu, S.; Hu, G.; Yan, K.; Yang, B.; Song, W.; Li, J. Spectral Invariant Provides a Practical Modeling Approach for Future Biophysical Variable Estimations. Remote Sens. 2018, 10, 1508. https://doi.org/10.3390/rs10101508
Zeng Y, Xu B, Yin G, Wu S, Hu G, Yan K, Yang B, Song W, Li J. Spectral Invariant Provides a Practical Modeling Approach for Future Biophysical Variable Estimations. Remote Sensing. 2018; 10(10):1508. https://doi.org/10.3390/rs10101508
Chicago/Turabian StyleZeng, Yelu, Baodong Xu, Gaofei Yin, Shengbiao Wu, Guoqing Hu, Kai Yan, Bin Yang, Wanjuan Song, and Jing Li. 2018. "Spectral Invariant Provides a Practical Modeling Approach for Future Biophysical Variable Estimations" Remote Sensing 10, no. 10: 1508. https://doi.org/10.3390/rs10101508
APA StyleZeng, Y., Xu, B., Yin, G., Wu, S., Hu, G., Yan, K., Yang, B., Song, W., & Li, J. (2018). Spectral Invariant Provides a Practical Modeling Approach for Future Biophysical Variable Estimations. Remote Sensing, 10(10), 1508. https://doi.org/10.3390/rs10101508









