Comparing Pixel- and Object-Based Approaches in Effectively Classifying Wetland-Dominated Landscapes
Abstract
1. Introduction
2. Materials and Methods
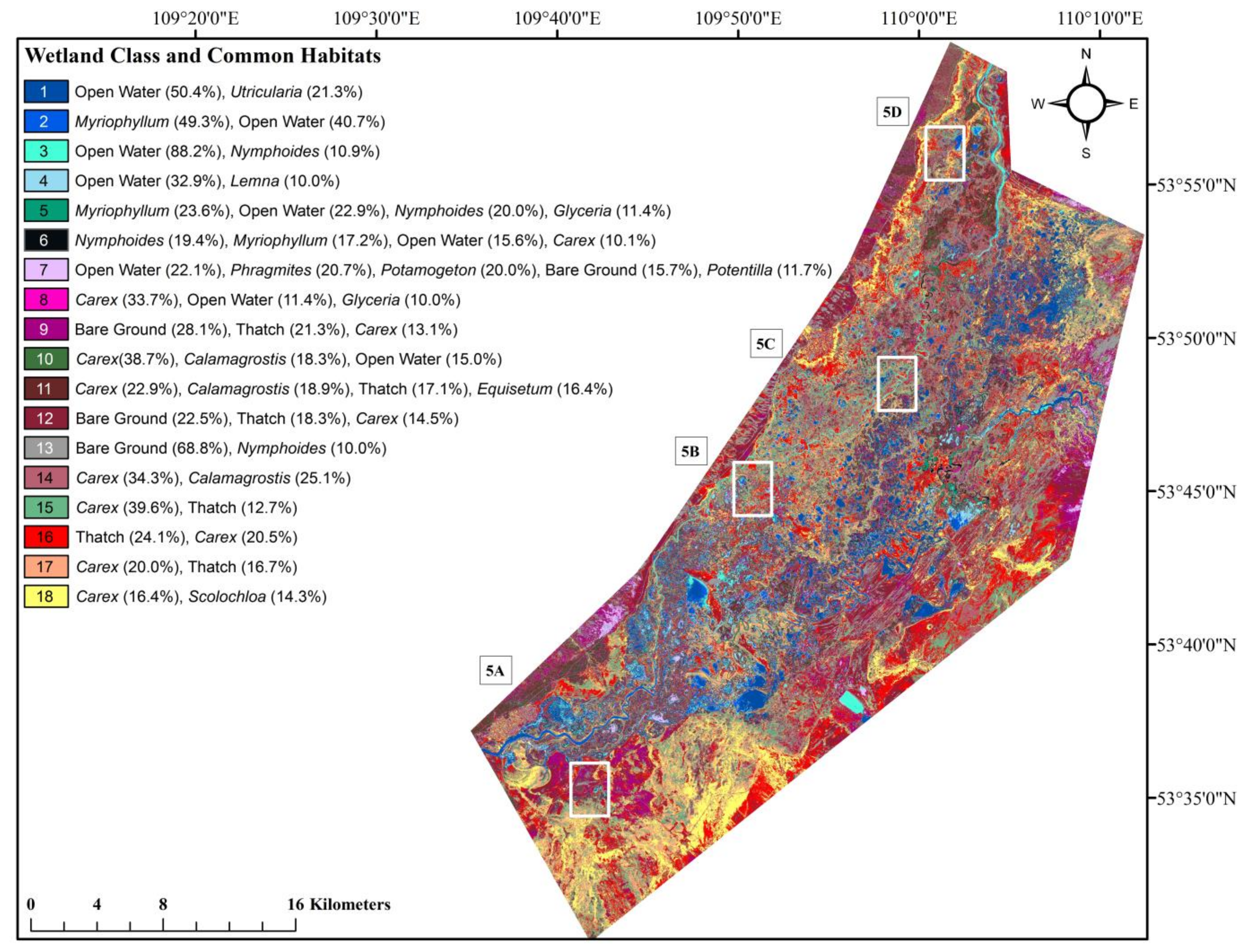
2.1. Study Area
2.2. Image Acquisition and Processing
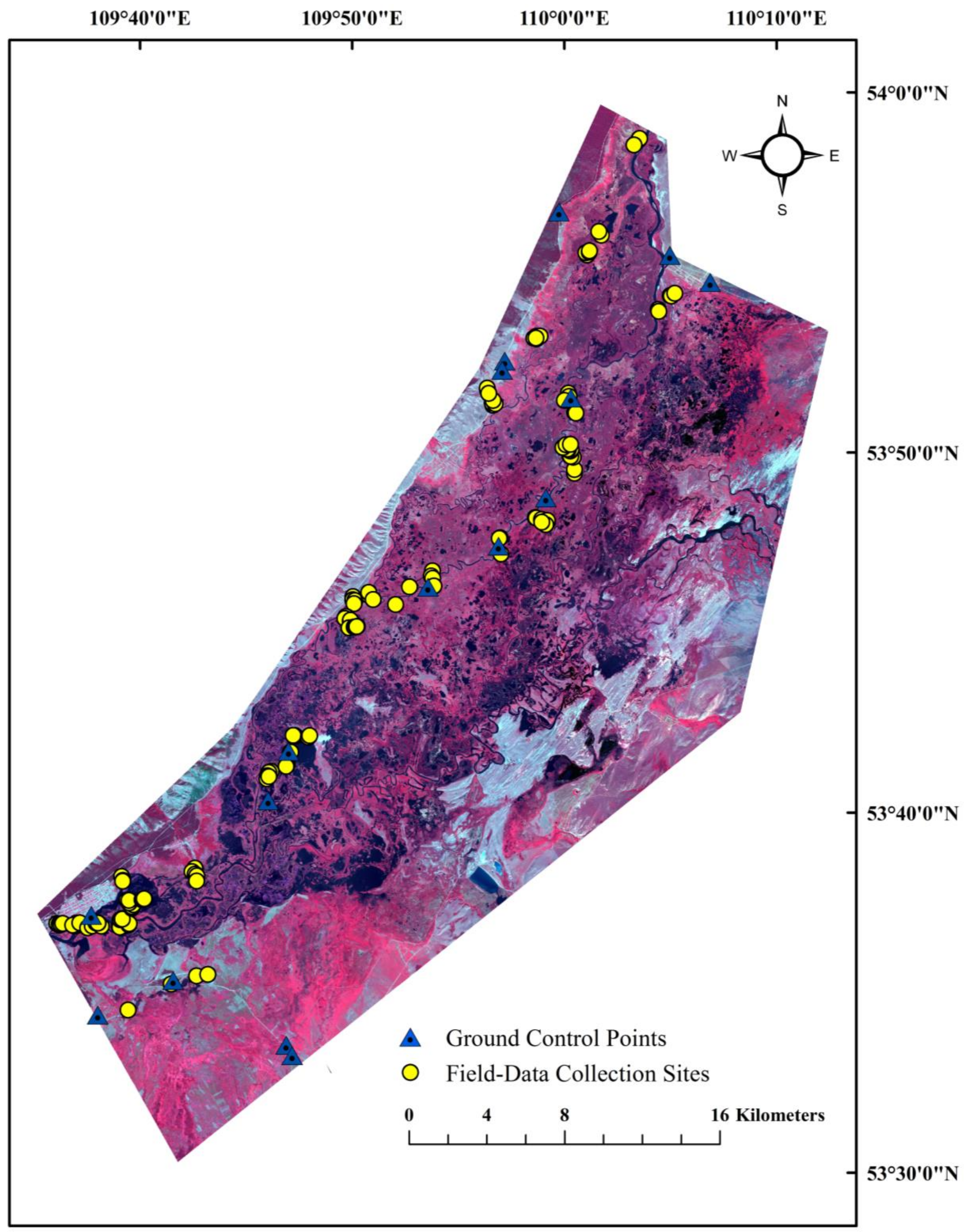
2.3. Field Data Collection
2.4. Spatial/Spectral Metrics and Geospatial Data
2.5. Supervised Image Classification
2.5.1. Pixel-Based Random Forest Classification
2.5.2. Pixel-Based Maximum Likelihood Classification
2.5.3. Object-Oriented Random Forest Classification
2.6. Classification Accuracy
3. Results
3.1. Field Data Collection
3.2. Classification Approaches
3.2.1. Pixel-Based Random Forest and Maximum Likelihood Classification
3.2.2. Object-Oriented Classification
4. Discussion
4.1. Random Forest in Wetland Classification
4.2. Variable Importance in Wetland Classification
4.3. Object-Oriented Approaches for Wetland Classification
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mitsch, W.J.; Gosselink, J.G. The value of wetlands: Importance of scale and landscape setting. Ecol. Econ. 2000, 35, 25–33. [Google Scholar] [CrossRef]
- Davidson, N.C. How much wetland has the world lost? Long-term and recent trends in global wetland area. Mar. Freshw. Res. 2014, 65, 934. [Google Scholar] [CrossRef]
- Junk, W.J.; An, S.; Finlayson, C.M.; Gopal, B.; Květ, J.; Mitchell, S.A.; Mitsch, W.J.; Robarts, R.D. Current state of knowledge regarding the world’s wetlands and their future under global climate change: A synthesis. Aquat. Sci. 2012, 75, 151–167. [Google Scholar] [CrossRef]
- Ramesh Reddy, K.; DeLaune, R. Biogeochemistry of Wetlands; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Marton, J.M.; Creed, I.F.; Lewis, D.B.; Lane, C.R.; Basu, N.B.; Cohen, M.J.; Craft, C.B. Geographically isolated wetlands are important biogeochemical reactors on the landscape. BioScience 2015, 65, 408–418. [Google Scholar] [CrossRef]
- Winter, T.C.; Rosenberry, D.O. The interaction of ground water with prairie pothole wetlands in the Cottonwood Lake area, east-central North Dakota, 1979–1990. Wetlands 1995, 15, 193–211. [Google Scholar] [CrossRef]
- Shaw, D.A.; Vanderkamp, G.; Conly, F.M.; Pietroniro, A.; Martz, L. The fill-spill hydrology of prairie wetland complexes during drought and deluge. Hydrol. Process. 2012, 26, 3147–3156. [Google Scholar] [CrossRef]
- Kirkman, L.K.; Golladay, S.W.; Laclaire, L.; Sutter, R. Biodiversity in southeastern, seasonally ponded, isolated wetlands: Management and policy perspectives for research and conservation. J. N. Am. Benthol. Soc. 1999, 18, 553–562. [Google Scholar] [CrossRef]
- Gibbons, J.W.; Winne, C.T.; Scott, D.E.; Willson, J.D.; Glaudas, X.; Andrews, K.M.; Todd, B.D.; Fedewa, L.A.; Wilkinson, L.; Tsaliagos, R.N.; et al. Remarkable amphibian biomass and abundance in an isolated wetland: Implications for wetland conservation. Conserv. Biol. 2006, 20, 1457–1465. [Google Scholar] [CrossRef] [PubMed]
- The United States Environmental Protection Agency (U.S. EPA). Connectivity of Streams and Wetlands to Downstream Waters: A Review and Synthesis of the Scientific Evidence; EPA/600/R-14/475F; U.S. EPA Office of Research and Development: Washington, DC, USA, 2015.
- Ullah, S.; Faulkner, S.P. Use of cotton gin trash to enhance denitrification in restored forested wetlands. For. Ecol. Manag. 2006, 237, 557–563. [Google Scholar] [CrossRef]
- Lane, C.; Anenkhonov, O.; Liu, H.; Autrey, B.; Chepinoga, V. Classification and inventory of freshwater wetlands and aquatic habitats in the Selenga River Delta of Lake Baikal, Russia, using high-resolution satellite imagery. Wetl. Ecol. Manag. 2015, 23, 195–214. [Google Scholar] [CrossRef]
- Lane, C.R.; D’Amico, E. Calculating the Ecosystem Service of Water Storage in Isolated Wetlands using LiDAR in North Central Florida, USA. Wetlands 2010, 30, 967–977. [Google Scholar] [CrossRef]
- Tiner, R.; Lang, M.; Klemas, V. Remote Sensing of Wetlands: Applications and Advances; CRC Press: Boca Raton, FL, USA, 2015; ISBN 9781482237351. [Google Scholar]
- Ozesmi, S.L.; Bauer, M.E. Satellite remote sensing of wetland. Wetl. Ecol. Manag. 2002, 10, 381–402. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: A review. Wetl. Ecol. Manag. 2009, 18, 281–296. [Google Scholar] [CrossRef]
- Gallant, A. The challenges of remote monitoring of wetlands. Remote Sens. 2015, 7, 10938–10950. [Google Scholar] [CrossRef]
- Frohn, R.C.; Reif, M.; Lane, C.; Autrey, B. Satellite remote sensing of isolated wetlands using object-oriented classification of Landsat-7 data. Wetlands 2009, 29, 931–941. [Google Scholar] [CrossRef]
- Immitzer, M.; Atzberger, C.; Koukal, T. Tree species classification with random forest using very high spatial resolution 8-band worldview-2 satellite data. Remote Sens. 2012, 4, 2661–2693. [Google Scholar] [CrossRef]
- Costa, H.; Foody, G.M.; Boyd, D.S. Using mixed objects in the training of object-based image classifications. Remote Sens. Environ. 2017, 190, 188–197. [Google Scholar] [CrossRef]
- Ball, G.; Hall, J. ISODATA, A Novel Method of Data Analysis and Pattern Classification, Technical Report; Stanford Research Institute: Menlo Park, CA, USA, 1965; pp. 1–61. [Google Scholar]
- Jain, A.; Dubes, R. Algorithms for Clustering Data; Prentice Hall: Englewood Cliffs, NJ, USA, 1988; ISBN 013022278X. [Google Scholar]
- Earth Resources Data Analysis System (ERDAS). ERDAS Field Guide, 5th ed.; ERDAS Worldwide Headquarters: Buford Highway, NE, USA; Atlanta, GA, USA, 1999; pp. 227–232. [Google Scholar]
- Lillesand, T.; Kiefer, R.; Chipman, J. Remote Sensing and Image Interpretation, 7th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 544–558. [Google Scholar]
- Akar, Ö.; Güngör, O. Classification of multispectral images using random forest algorithm. J. Geodesy Geoinform. 2012, 1, 105–112. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Millard, K.; Richardson, M. On the importance of training data sample selection in random forest image classification: A case study in peatland ecosystem mapping. Remote Sens. 2015, 7, 8489–8515. [Google Scholar] [CrossRef]
- Stumpf, A.; Kerle, N. Object-oriented mapping of landslides using random forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- Puissant, A.; Rougier, S.; Stumpf, A. Object-oriented mapping of urban trees using random forest classifiers. Int. J. Appl. Earth Obs. Geoinform. 2014, 26, 235–245. [Google Scholar] [CrossRef]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Dronova, I. Object-based image analysis in wetland research: A review. Remote Sens. 2015, 7, 6380–6413. [Google Scholar] [CrossRef]
- Husson, E.; Ecke, F.; Reese, H. Comparison of manual mapping and automated object-based image analysis of non-submerged aquatic vegetation from very-high-resolution UAS images. Remote Sens. 2016, 8, 724. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random forest wetland classification using ALOS-2 L-band, RADARSAT-2 C-band, and TerraSAR-X imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
- Ariel, E.; Salas, L.; Boykin, K.; Valdez, R. Multispectral and Texture Feature Application in Image-Object Analysis of Summer Vegetation in Eastern Tajikistan Pamirs. Remote Sens. 2016, 8, 78. [Google Scholar]
- Tian, S.; Zhang, X.; Tian, J.; Sun, Q. Random Forest Classification of Wetland Land covers from Multi-Sensor Data in the Arid Region of Xinjiang, China. Remote Sens. 2016, 8, 954. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanre, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Crippen, R. Calculating the vegetation index faster. Remote Sens. Environ. 1990, 34, 71–73. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Bwangoy, J.; Hansen, M.; Roy, D.; DeGrandi, G.; Justice, C. Wetland mapping in the Congo Basin using optical and radar remotely sensed data and derived topographical indices. Remote Sens. Environ. 2010, 114, 73–86. [Google Scholar] [CrossRef]
- Wright, C.; Gallant, A. Improved wetland remote sensing in Yellowstone National Park using classification trees to combine TM imagery and ancillary environmental data. Remote Sens. Environ. 2007, 107, 582–605. [Google Scholar] [CrossRef]
- Brunello, A. Lake Baikal: Experience and Lessons Learned Brief; Tahoe-Baikal Institute: South Lake Tahoe, CA, USA, 2003. [Google Scholar]
- Rafferty, J. The Living Earth: Lakes and Wetlands; Britannica Educational Publishing: Chicago, IL, USA, 2011; ISBN 139781615304035. [Google Scholar]
- Kolomiets, V.L.; Budaev, R.T. Barguzin rift valley: Sedimentogenesis and paleogeography (Baikalian area, Russia). Quat. Int. 2015, 355, 57–64. [Google Scholar] [CrossRef]
- Plyusnin, V.M. (Ed.) The Ecological Atlas of the Baikal Basin; V.B. Sochava Institute of Geography: Irkutsk, Russia, 2015. [Google Scholar]
- Hogan, C. Lake Baikal Basin, Russian Federation; United Nations Environment Programme-World Conservation: Cambridge, UK, 2015. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Richards, J.A.; Jia, X. Feature reduction. In Remote Sensing Digital Image Analysis; Springer: Berlin/Heidelberg, Germany, 1999; pp. 239–257. [Google Scholar]
- Lane, C.; Liu, H.; Autrey, B.; Anenkhonov, O.; Chepinoga, V.; Wu, Q. Improved wetland classification using eight-band high resolution satellite imagery and a hybrid approach. Remote Sens. 2014, 6, 12187–12216. [Google Scholar] [CrossRef]
- Richardson, A.J.; Everitt, J.H. Using spectral vegetation indices to estimate rangeland productivity. Geocarto Int. 1992, 7, 63–69. [Google Scholar] [CrossRef]
- Yang, C.; Everitt, J.; Bradford, J. Comparison of QuickBird satellite imagery and airborne imagery for mapping grain sorghum yield patterns. Precis. Agric. 2006, 7, 33–44. [Google Scholar] [CrossRef]
- Liu, G.-R.; Liang, C.-K.; Kuo, T.-H.; Lin, T.-H.; Huang, S.-J. Comparison of the NDVI, ARVI and AFRI vegetation index, along with their relations with the AOD using SPOT 4 vegetation data. Terr. Atmos. Ocean. Sci. 2004, 15, 15. [Google Scholar] [CrossRef]
- Gao, B. NDWI-A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Wuest, B.; Zhang, Y. Region based segmentation of Quickbird multispectral imagery through bands ratios and fuzzy comparison. ISPRS J. Photogramm. Remote Sens. 2009, 64, 55–64. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Foody, G.M.; Campbell, N.A.; Trodd, N.M.; Wood, T.F. Derivation and applications of probabilistic measures of class membership from the maximum likelihood classification. Photogramm. Eng. Remote Sens. 1992, 58, 1335–1341. [Google Scholar]
- Foody, G.M.; Palubinskas, G.; Lucas, R.M.; Curran, P.J.; Honzak, M. Identifying terrestrial carbon sinks: Classification of successional stages in regenerating tropical forest from Landsat TM data. Remote Sens. Environ. 1996, 55, 205–216. [Google Scholar] [CrossRef]
- Dingle Robertson, L.; King, D.J.; Davies, C. Object-based image analysis of optical and radar variables for wetland evaluation. Int. J. Remote Sens. 2015, 36, 5811–5841. [Google Scholar] [CrossRef]
- Stehman, S.V.; Czaplewski, R.L. Design and analysis for thematic map accuracy assessment. Remote Sens. Environ. 1998, 64, 331–344. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- McNemar, Q. Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 1947, 12, 153–157. [Google Scholar] [CrossRef] [PubMed]
- Foody, G. Classification accuracy comparison: Hypothesis tests and the use of confidence intervals in evaluations of difference, equivalence and non-inferiority. Remote Sens. 2009, 113, 1658–1663. [Google Scholar] [CrossRef]
- Duro, D.; Franklin, S.; Dubé, M. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Prasad, A.M.; Iverswon, L.R.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Mallinis, G.; Koutsias, N.; Tsakiri-Strati, M.; Karteris, M. Object-based classification using Quickbird imagery for delineating forest vegetation polygons in a Mediterranean test site. ISPRS J. Photogramm. Remote Sens. 2008, 63, 237–250. [Google Scholar] [CrossRef]
- Smith, A. Image segmentation scale parameter optimization and land cover classification using the random forest algorithm. J. Spat. Sci. 2010, 55, 69–79. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Abarca-Hernandez, F.; Atkinson, P.M.; Jeganathan, C. Random forest classification of Mediterranean land cover using multi-seasonal imagery and multi-seasonal texture. Remote Sens. Environ. 2012, 121, 93–107. [Google Scholar] [CrossRef]
- Lowe, B.; Kulkarni, A. Multispectral image analysis using random forest. Int. J. Soft Comput. 2015, 6, 1–14. [Google Scholar] [CrossRef]
- Wessels, K.; van den Bergh, F.; Roy, D.; Salmon, B.; Steenkamp, K.; MacAlister, B.; Swanepoel, D.; Jewitt, D. Rapid land cover map updates using change detection and robust random forest classifiers. Remote Sens. 2016, 8, 888. [Google Scholar] [CrossRef]
- Wolter, P.T.; Johnston, C.A.; Niemi, G.J. Mapping submergent aquatic vegetation in the US Great Lakes using Quickbird satellite data. Int. J. Remote Sens. 2005, 26, 5255–5274. [Google Scholar] [CrossRef]
- Beeri, O.; Phillips, R.; Hendrickson, J.; Frank, A.B.; Kronberg, S. Estimating forage quantity and quality using aerial hyperspectral imagery for northern mixed-grass prairie. Remote Sens. Environ. 2007, 110, 216–225. [Google Scholar] [CrossRef]
- Pelletier, C.; Valero, S.; Inglada, J.; Champion, N.; Dedieu, G. Assessing the robustness of Random Forests to map land cover with high resolution satellite image time series over large areas. Remote Sens. Environ. 2016, 187, 156–168. [Google Scholar] [CrossRef]
- Ouyang, Z.; Zhang, M.; Xie, X.; Shen, Q.; Guo, H.; Zhao, B. A comparison of pixel-based and object-oriented approaches to VHR imagery for mapping saltmarsh plants. Ecol. Inform. 2011, 6, 136–146. [Google Scholar] [CrossRef]
- Vo, Q.; Oppelt, N.; Kuenzer, C. Remote sensing in mapping mangrove ecosystem-An object-based approach. Remote Sens. 2013, 5, 183–201. [Google Scholar] [CrossRef]
- Creed, I.C.; Lane, C.R.; Serran, J.N.; Alexander, L.C.; Basu, N.B.; Calhoun, A.J.K.; Christensen, J.R.; Cohen, M.J.; Craft, C.; D’Amico, E.; et al. Enhancing protection for vulnerable waters. Nat. Geosci. 2017. [Google Scholar] [CrossRef]
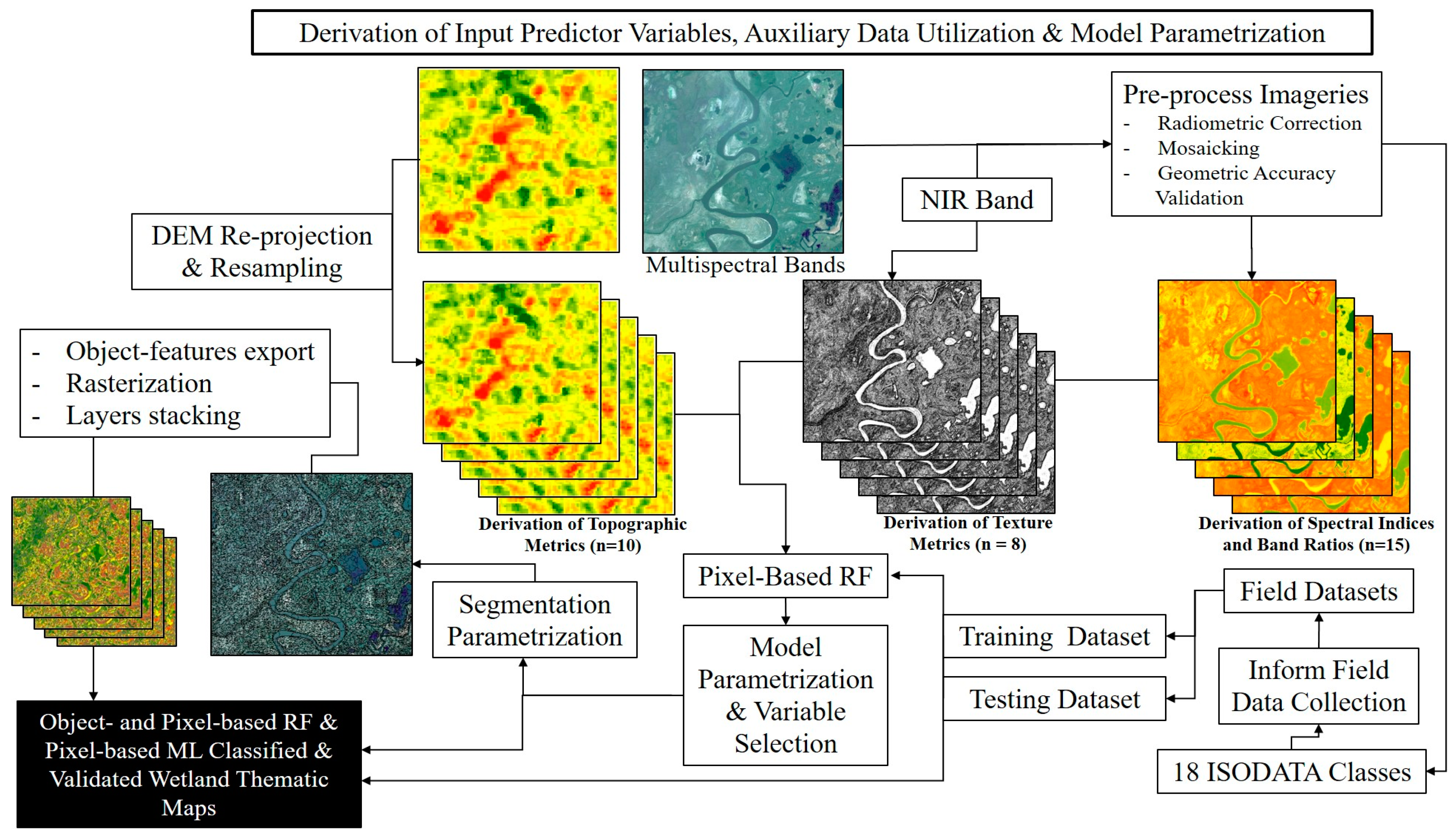


| Input Data Layer (Stack) | Description | Equations |
|---|---|---|
| B1234 | Quickbird multispectral bands | - |
| ARVI (B5) | Atmospherically resistant vegetation index [37,53] | |
| BNDVI (B6) | Blue-normalized difference vegetation index [52] | |
| DVI (B7) | Difference vegetation index [36,51] | |
| GNDVI (B8) | Green-normalized difference vegetation index [52] | |
| IPVI (B9) | Infrared percentage vegetation index [39] | |
| NDVI (B10) | Normalized difference vegetation index [51] | |
| NDWI (B11) | Normalized difference water index [54] | |
| SAVI (B12) | Soil adjusted vegetation index [38] | |
| WRI (B13) | Water ratio index [55] | |
| Ratio Transformation | Ratio of reflectance spectra [52]; B14–B19 | ; ; ; ; ; |
| Texture Metrics | Texture variables (contrast (B20), correlation (B21), dissimilarity (B22), entropy (B23), homogeneity (B24), mean (B25), 2nd moment (B26), and variance (B27)) computed as a measure of Gray Level Co-occurrence Matrix (GLCM) using Band4 (Harris Geospatial Solutions, Herndon, VA, USA, version 5.3). | Source: Harris Geospatial, Texture Metrics Background. Available online: www.harrisgeospatial.com/docs/backgroundtexturemetrics.html (accessed on 26 December 2017). |
| Topography Metrics | Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTERGDEM)-Global Digital Elevation Model (GDEM). GDEM-derived variables (aspect (B28), cross-sectional convexity (B29), DEM (B30), longitudinal convexity (B31), maximum curvature (B32), minimum curvature (B33), plan convexity (B34), profile convexity (B35), RMS error (B36), and slope (%; B37) (Harris Geospatial Solutions, Herndon, VA, USA, version 5.3)). | Source: Harris Geospatial, Topographic Modeling Background. Available online: www.harrisgeospatial.com/docs/backgroundtopographicmodeling.html (accessed on 26 December 2017). |
| Predictor | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 | B11 | B12 | B13 | B14 | B15 | B16 | B17 | B18 | B19 | B20 | B21 | B22 | B23 | B24 | B25 | B26 | B27 | B28 | B29 | B30 | B31 | B32 | B33 | B34 | B35 | B36 | B37 |
| B1 | 1.00 | ||||||||||||||||||||||||||||||||||||
| B2 | 0.96 | 1.00 | |||||||||||||||||||||||||||||||||||
| B3 | 0.96 | 0.96 | 1.00 | ||||||||||||||||||||||||||||||||||
| B4 | 0.62 | 0.74 | 0.62 | 1.00 | |||||||||||||||||||||||||||||||||
| B5 | −0.08 | −0.08 | −0.08 | −0.02 | 1.00 | ||||||||||||||||||||||||||||||||
| B6 | 0.55 | 0.66 | 0.56 | 0.94 | −0.01 | 1.00 | |||||||||||||||||||||||||||||||
| B7 | −0.16 | −0.15 | −0.13 | −0.05 | −0.02 | −0.05 | 1.00 | ||||||||||||||||||||||||||||||
| B8 | 0.5 | 0.6 | 0.49 | 0.93 | 0 | 1 | −0.03 | 1.00 | |||||||||||||||||||||||||||||
| B9 | 0.28 | 0.4 | 0.26 | 0.85 | 0.02 | 0.94 | 0 | 0.96 | 1.00 | ||||||||||||||||||||||||||||
| B10 | 0.28 | 0.4 | 0.26 | 0.85 | 0.02 | 0.94 | 0 | 0.96 | 1 | 1.00 | |||||||||||||||||||||||||||
| B11 | −0.50 | 0.31 | −0.49 | −0.93 | 0 | −1.00 | 0.03 | −1.00 | −0.96 | −0.96 | 1.00 | ||||||||||||||||||||||||||
| B12 | 0.28 | 0.4 | 0.26 | 0.85 | 0.02 | 0.94 | 0 | 0.96 | 1 | 1 | −0.96 | 1.00 | |||||||||||||||||||||||||
| B13 | 0.62 | 0.75 | 0.63 | 0.99 | −0.02 | 0.95 | −0.05 | 0.94 | 0.85 | 0.85 | −0.94 | 0.85 | 1.00 | ||||||||||||||||||||||||
| B14 | −0.68 | −0.86 | −0.74 | −0.82 | 0.05 | −0.77 | 0.11 | −0.71 | −0.59 | −0.59 | 0.71 | −0.59 | −0.85 | 1.00 | |||||||||||||||||||||||
| B15 | 0.93 | 0.94 | 0.99 | 0.65 | −0.07 | 0.62 | −0.12 | 0.56 | 0.32 | 0.32 | −0.56 | 0.32 | 0.68 | −0.77 | 1.00 | ||||||||||||||||||||||
| B16 | 0.9 | 0.84 | 0.95 | 0.51 | −0.06 | 0.51 | −0.10 | 0.46 | 0.2 | 0.2 | −0.46 | 0.2 | 0.53 | −0.59 | 0.96 | 1.00 | |||||||||||||||||||||
| B17 | 0.46 | 0.6 | 0.46 | 0.98 | 0 | 0.95 | −0.02 | 0.95 | 0.91 | 0.91 | −0.95 | 0.91 | 0.98 | −0.75 | 0.51 | 0.37 | 1.00 | ||||||||||||||||||||
| B18 | 0.41 | 0.53 | 0.4 | 0.95 | 0.01 | 0.95 | −0.01 | 0.96 | 0.93 | 0.93 | −0.96 | 0.93 | 0.95 | −0.68 | 0.46 | 0.33 | 0.99 | 1.00 | |||||||||||||||||||
| B19 | 0.17 | 0.31 | 0.14 | 0.85 | 0.03 | 0.85 | 0.02 | 0.88 | 0.93 | 0.93 | −0.88 | 0.93 | 0.84 | −0.54 | 0.2 | 0.06 | 0.94 | 0.96 | 1.00 | ||||||||||||||||||
| B20 | 0.16 | 0.2 | 0.17 | 0.28 | 0.01 | 0.25 | 0.03 | 0.25 | 0.24 | 0.24 | −0.25 | 0.24 | 0.27 | −0.23 | 0.17 | 0.12 | 0.27 | 0.25 | 0.23 | 1.00 | |||||||||||||||||
| B21 | −0.17 | −0.16 | −0.17 | −0.18 | 0 | −0.28 | −0.01 | −0.28 | −0.26 | −0.26 | 0.28 | −0.26 | −0.19 | 0.14 | −0.19 | −0.20 | −0.17 | −0.19 | −0.14 | −0.16 | 1.00 | ||||||||||||||||
| B22 | 0.21 | 0.26 | 0.22 | 0.38 | 0.01 | 0.42 | 0.03 | 0.42 | 0.41 | 0.41 | −0.42 | 0.41 | 0.38 | −0.31 | 0.24 | 0.19 | 0.38 | 0.38 | 0.35 | 0.87 | −0.38 | 1.00 | |||||||||||||||
| B23 | 0.33 | 0.36 | 0.35 | 0.45 | 0 | 0.6 | −0.04 | 0.59 | 0.56 | 0.56 | −0.59 | 0.56 | 0.47 | −0.38 | 0.39 | 0.38 | 0.45 | 0.47 | 0.39 | 0.36 | −0.54 | 0.69 | 1.00 | ||||||||||||||
| B24 | −0.24 | −0.27 | −0.25 | −0.40 | −0.01 | −0.51 | −0.02 | −0.52 | −0.50 | −0.50 | 0.52 | −0.50 | −0.41 | 0.32 | −0.29 | −0.26 | −0.41 | −0.42 | −0.37 | −0.53 | 0.55 | −0.87 | −0.89 | 1.00 | |||||||||||||
| B25 | 0.63 | 0.74 | 0.62 | 1 | −0.02 | 0.94 | −0.05 | 0.93 | 0.85 | 0.85 | −0.93 | 0.85 | 0.99 | −0.82 | 0.65 | 0.51 | 0.98 | 0.95 | 0.85 | 0.28 | −0.18 | 0.38 | 0.46 | −0.40 | 1.00 | ||||||||||||
| B26 | −0.34 | −0.36 | −0.35 | −0.42 | 0.01 | −0.57 | 0.04 | −0.56 | −0.52 | −0.52 | 0.56 | −0.52 | −0.44 | 0.36 | −0.40 | −0.39 | −0.41 | −0.44 | −0.34 | −0.30 | 0.6 | −0.62 | −0.98 | 0.85 | −0.43 | 1.00 | |||||||||||
| B27 | 0.15 | 0.2 | 0.15 | 0.28 | 0.01 | 0.27 | 0.02 | 0.27 | 0.26 | 0.26 | −0.27 | 0.26 | 0.28 | −0.24 | 0.16 | 0.11 | 0.28 | 0.26 | 0.24 | 0.79 | −0.09 | 0.75 | 0.37 | −0.50 | 0.28 | −0.30 | 1.00 | ||||||||||
| B28 | −0.01 | 0 | −0.01 | 0 | −0.01 | 0.02 | −0.01 | 0.02 | 0.02 | 0.02 | −0.02 | 0.02 | 0.01 | −0.01 | 0 | 0 | 0.01 | 0.01 | 0.01 | 0.01 | −0.07 | 0.04 | 0.04 | −0.05 | 0 | −0.05 | 0 | 1.00 | |||||||||
| B29 | −0.01 | −0.01 | −0.01 | 0.01 | 0 | 0.01 | 0 | 0.02 | 0.02 | 0.02 | −0.02 | 0.02 | 0.01 | 0 | −0.01 | −0.01 | 0.02 | 0.02 | 0.03 | 0.02 | −0.02 | 0.02 | 0.02 | −0.02 | 0.01 | −0.02 | 0.02 | −0.01 | 1.00 | ||||||||
| B30 | 0.18 | 0.19 | 0.19 | 0.15 | −0.02 | 0.14 | −0.07 | 0.13 | 0.08 | 0.08 | −0.13 | 0.08 | 0.16 | −0.16 | 0.19 | 0.17 | 0.13 | 0.12 | 0.08 | 0.13 | −0.09 | 0.15 | 0.14 | −0.13 | 0.15 | −0.14 | 0.09 | 0.03 | 0.02 | 1.00 | |||||||
| B31 | 0 | 0.01 | 0.01 | −0.01 | 0.01 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −0.01 | 0.01 | 0.01 | −0.01 | −0.01 | −0.01 | 0.02 | 0 | 0.01 | 0 | 0 | 0 | −0.01 | 0.02 | 0.02 | 0.08 | 0.09 | 1.00 | ||||||
| B32 | −0.01 | −0.01 | 0 | 0.01 | 0.02 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | −0.01 | 0.01 | 0.01 | 0 | 0 | 0 | 0.01 | 0.01 | 0.02 | 0 | −0.03 | 0 | 0.01 | −0.01 | 0.01 | −0.02 | 0 | 0.12 | 0.19 | 0.08 | 0.73 | 1.00 | |||||
| B33 | 0.02 | 0.01 | 0.02 | −0.01 | 0 | 0 | −0.02 | −0.01 | −0.01 | −0.01 | 0.01 | −0.01 | −0.01 | −0.01 | 0.01 | 0.01 | −0.02 | −0.02 | −0.02 | 0.03 | 0.02 | 0.02 | 0 | 0 | −0.01 | 0 | 0.03 | −0.09 | 0.19 | 0.05 | 0.72 | 0.09 | 1.00 | ||||
| B34 | −0.01 | 0 | 0 | −0.01 | 0 | −0.01 | 0 | −0.01 | −0.01 | −0.01 | 0.01 | −0.01 | −0.01 | −0.01 | 0 | 0 | −0.01 | −0.01 | −0.01 | −0.02 | 0.01 | −0.02 | −0.02 | 0.01 | −0.01 | 0.01 | −0.02 | 0.01 | −0.83 | −0.02 | −0.07 | −0.15 | −0.17 | 1.00 | |||
| B35 | 0 | 0 | 0.01 | −0.01 | 0.02 | 0 | 0 | 0 | −0.01 | −0.01 | 0 | −0.01 | 0 | −0.01 | 0.01 | 0.01 | −0.01 | −0.01 | −0.01 | 0.01 | 0.03 | 0 | 0 | 0.01 | −0.01 | 0.01 | 0.01 | 0 | 0.06 | 0.06 | 0.77 | 0.57 | 0.54 | −0.07 | 1.00 | ||
| B36 | 0.01 | 0.01 | 0.01 | 0.04 | 0.01 | 0.04 | −0.02 | 0.04 | 0.04 | 0.04 | −0.04 | 0.04 | 0.03 | −0.02 | 0.01 | 0.01 | 0.04 | 0.04 | 0.04 | 0.01 | 0 | 0.02 | 0.03 | −0.03 | 0.04 | −0.02 | 0.02 | −0.01 | 0.06 | −0.01 | −0.02 | 0.19 | −0.20 | 0.06 | 0.01 | 1.00 | |
| B37 | −0.02 | −0.02 | −0.02 | 0.02 | 0.01 | 0.01 | 0.03 | 0.02 | 0.02 | 0.02 | −0.02 | 0.02 | 0.01 | 0.01 | −0.01 | −0.02 | 0.02 | 0.03 | 0.03 | −0.03 | −0.03 | −0.01 | 0.01 | −0.01 | 0.02 | −0.02 | −0.02 | 0.15 | 0 | 0.02 | 0.02 | 0.67 | −0.66 | 0.02 | 0.03 | 0.27 | 1.00 |
| Classifier | Chi-Squared | p-Value | ||
|---|---|---|---|---|
| Pixel-Based ML | Object-Based RF | Pixel-Based ML | Object-Based RF | |
| Three-Layer Stack | ||||
| Pixel-based RF | 0.083 | 0.078 | 0.774 | 0.780 |
| Pixel-based ML | - | 0.100 | - | 0.752 |
| Five-Layer Stack | ||||
| Pixel-based RF | 0.128 | 0.058 | 0.720 | 0.810 |
| Pixel-based ML | - | 0.096 | - | 0.756 |
| Predictor Variables | Training Data OOB Error (%) | Testing Data | ||
|---|---|---|---|---|
| Overall Accuracy | ||||
| % | 95% CI | |||
| All non-correlated variables (with WRI, not mean texture; 22 variables) | 1.3 | 72.7 | 72.6 | 72.9 |
| All non-correlated variables (with mean texture, not WRI; 22 variables) | 0.3 | 80.1 | 80.0 | 80.2 |
| All non-correlated variables including both WRI and mean texture (23 variables) | 0.4 | 80.1 | 80.1 | 80.2 |
| All (37) variables | 0.8 | 84.6 | 84.5 | 84.7 |
| Ten most important variables | 1.0 | 84.6 | 84.5 | 84.6 |
| Five most important variables | 0.9 | 84.9 | 84.8 | 85.0 |
| Fifteen most important variables | 1.2 | 85.6 | 85.5 | 85.8 |
| Most parsimonious model (three variables: B3, WRI, and mean texture) | 1.4 | 87.9 | 87.8 | 88.0 |
| Wetland Class | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.00 | 55 | 1.00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 5 | 0 | 21 | 0 | 0 | 0 | 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 30 | 68 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 12 | 0 | 63 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 1.00 | 0 | 0 | 0 | 0 | 0 | 51 | 0 | 9 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 58 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 53 | 0 | 0 | 0 | 0 | 15 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 51 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | 0 | 62 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 61 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 84 | 0 | 0 | 0 | 0 | 0 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 40 | 0 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 65 | 0 | 2 | 0 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 7 | 0 | 44 | 3 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 53 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 56 |
| PA (%) | 90.2 | 98.1 | 33.1 | 100 | 100 | 65.5 | 84.3 | 97.0 | 84.2 | 82.9 | 96.9 | 95.3 | 100 | 64.4 | 100 | 100 | 90.0 | 100 |
| UA (%) | 97.2 | 100 | 59.7 | 69.3 | 67 | 100 | 76.8 | 89.3 | 78.0 | 96.7 | 98.4 | 100 | 100 | 95.2 | 97.0 | 77.1 | 100 | 98.3 |
| OA (%) | 87.9 |
| Variable Importance Rank | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Predictor Variable | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th | 10th | 11th | 12th | 13th | 14th | 15th |
| Quickbird B1 | - | - | - | - | - | - | - | 1.00 | 5 | 12 | 30 | 45 | 5 | 2 | - |
| Quickbird B2 | - | - | - | - | 100 | - | - | - | - | - | - | - | - | - | - |
| Quickbird B3 | - | - | 1.00 | 99 | - | - | - | - | - | - | - | - | - | - | - |
| Quickbird B4 | - | 100 | - | - | - | - | - | - | - | - | - | - | - | - | - |
| ARVI | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| B1/B2 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| BNDVI | - | - | - | - | - | 51 | 49 | - | - | - | - | - | - | - | - |
| DVI | - | - | - | - | - | - | - | 57 | 18 | 19 | 3 | 3 | - | - | - |
| GNDVI | - | - | - | - | - | - | - | 12 | 24 | 25 | 25 | 14 | - | - | - |
| IPVI | - | - | - | - | - | - | - | - | - | - | - | 1.00 | 10 | 18 | 20 |
| NDVI | - | - | - | - | - | - | - | - | - | - | - | - | 5 | 20 | 22 |
| B4/B1 | - | - | - | - | - | 49 | 51 | - | - | - | - | - | - | - | - |
| B4/B2 | - | - | - | - | - | - | - | 14 | 25 | 28 | 15 | 17 | 1.00 | - | - |
| B4/B3 | - | - | - | - | - | - | - | - | - | - | - | - | 6 | 24 | 19 |
| B3/B1 | - | - | - | - | - | - | - | - | - | - | - | 8 | 68 | 19 | 4 |
| B3/B2 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| SAVI | - | - | - | - | - | - | - | - | - | - | - | - | 4 | 17 | 35 |
| WRI | - | - | 99 | 1.00 | - | - | - | - | - | - | - | - | - | - | - |
| Mean texture | 100 | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| NDWI | - | - | - | - | - | 1 | - | 16 | 28 | 16 | 27 | 12 | 1 | - | - |
| Wetland Class | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.00 | 51 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 55 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 9 | 4 | 44 | 0 | 20 | 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 17 | 68 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 2 | 0 | 42 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 1.00 | 29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 1.00 | 0 | 0 | 0 | 0 | 21 | 61 | 0 | 20 | 1.00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 1.00 | 0 | 54 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 0 | 1.00 | 0 | 0 | 27 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 0 | 61 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 0 | 62 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 58 | 2 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 6 | 82 | 0 | 0 | 0 | 3 | 0 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | 0 | 0 | 32 | 4 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 61 | 0 | 0 | 0 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 44 | 0 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 55 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 56 |
| PA (%) | 83.6 | 93.2 | 69.8 | 100.0 | 66.7 | 47.5 | 100.0 | 90.0 | 38.1 | 98.4 | 96.9 | 90.6 | 97.6 | 51.6 | 93.8 | 100.0 | 93.2 | 100.0 |
| UA (%) | 100.0 | 100.0 | 50.6 | 80.0 | 95.5 | 96.7 | 58.7 | 98.2 | 46.2 | 91.0 | 76.5 | 96.7 | 90.1 | 86.5 | 100.0 | 93.6 | 100.0 | 98.2 |
| OA (%) | 83.9 |
| Predictor Variables | Training Data OOB Error (%) | Testing Data | ||
|---|---|---|---|---|
| Overall Accuracy | ||||
| % | 95% CI | |||
| B3 + WRI + mean texture | ||||
| Scale 5 | 0.4 | 84.6 | 84.3 | 84.8 |
| Scale 10 | 0.2 | 67.7 | 67.4 | 67.9 |
| Scale 15 | 1.9 | 67.6 | 67.5 | 67.6 |
| Scale 30 | 2.3 | 46.7 | 46.2 | 47.1 |
| Scale 50 | 6.0 | 57.6 | 57.1 | 58.2 |
| Scale 100 | 22.4 | 37.4 | 36.9 | 37.9 |
| Scale 5 B2 + B3 + B4 + WRI + mean texture | 0.3 | 90.4 | 90.3 | 90.4 |
| Wetland Class | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.00 | 60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1.00 | 0 | 37 | 0 | 0 | 0 | 33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 25 | 67 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1.00 | 63 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 1.00 | 0 | 0 | 46 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 15 | 0 | 55 | 0 | 36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 62 | 0 | 0 | 0 | 0 | 21 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 26 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 63 | 0 | 0 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 84 | 0 | 0 | 4 | 0 | 0 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | 0 | 2 | 0 | 0 | 41 | 0 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 65 | 0 | 13 | 0 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | 0 | 0 | 0 | 40 | 0 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 36 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 56 |
| PA (%) | 98.4 | 100.0 | 58.4 | 98.5 | 100.0 | 75.4 | 45.9 | 91.7 | 98.4 | 41.9 | 92.2 | 98.4 | 100.0 | 66.1 | 100.0 | 90.9 | 60.4 | 100.0 |
| UA (%) | 100.0 | 100.0 | 52.0 | 72.7 | 98.4 | 88.5 | 100.0 | 52.0 | 74.7 | 89.7 | 99.7 | 100.0 | 95.5 | 93.2 | 83.8 | 97.6 | 100.0 | 83.9 |
| OA (%) | 84.6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berhane, T.M.; Lane, C.R.; Wu, Q.; Anenkhonov, O.A.; Chepinoga, V.V.; Autrey, B.C.; Liu, H. Comparing Pixel- and Object-Based Approaches in Effectively Classifying Wetland-Dominated Landscapes. Remote Sens. 2018, 10, 46. https://doi.org/10.3390/rs10010046
Berhane TM, Lane CR, Wu Q, Anenkhonov OA, Chepinoga VV, Autrey BC, Liu H. Comparing Pixel- and Object-Based Approaches in Effectively Classifying Wetland-Dominated Landscapes. Remote Sensing. 2018; 10(1):46. https://doi.org/10.3390/rs10010046
Chicago/Turabian StyleBerhane, Tedros M., Charles R. Lane, Qiusheng Wu, Oleg A. Anenkhonov, Victor V. Chepinoga, Bradley C. Autrey, and Hongxing Liu. 2018. "Comparing Pixel- and Object-Based Approaches in Effectively Classifying Wetland-Dominated Landscapes" Remote Sensing 10, no. 1: 46. https://doi.org/10.3390/rs10010046
APA StyleBerhane, T. M., Lane, C. R., Wu, Q., Anenkhonov, O. A., Chepinoga, V. V., Autrey, B. C., & Liu, H. (2018). Comparing Pixel- and Object-Based Approaches in Effectively Classifying Wetland-Dominated Landscapes. Remote Sensing, 10(1), 46. https://doi.org/10.3390/rs10010046







