Bayesian and Classical Machine Learning Methods: A Comparison for Tree Species Classification with LiDAR Waveform Signatures
Abstract
1. Introduction
2. Materials and Methods
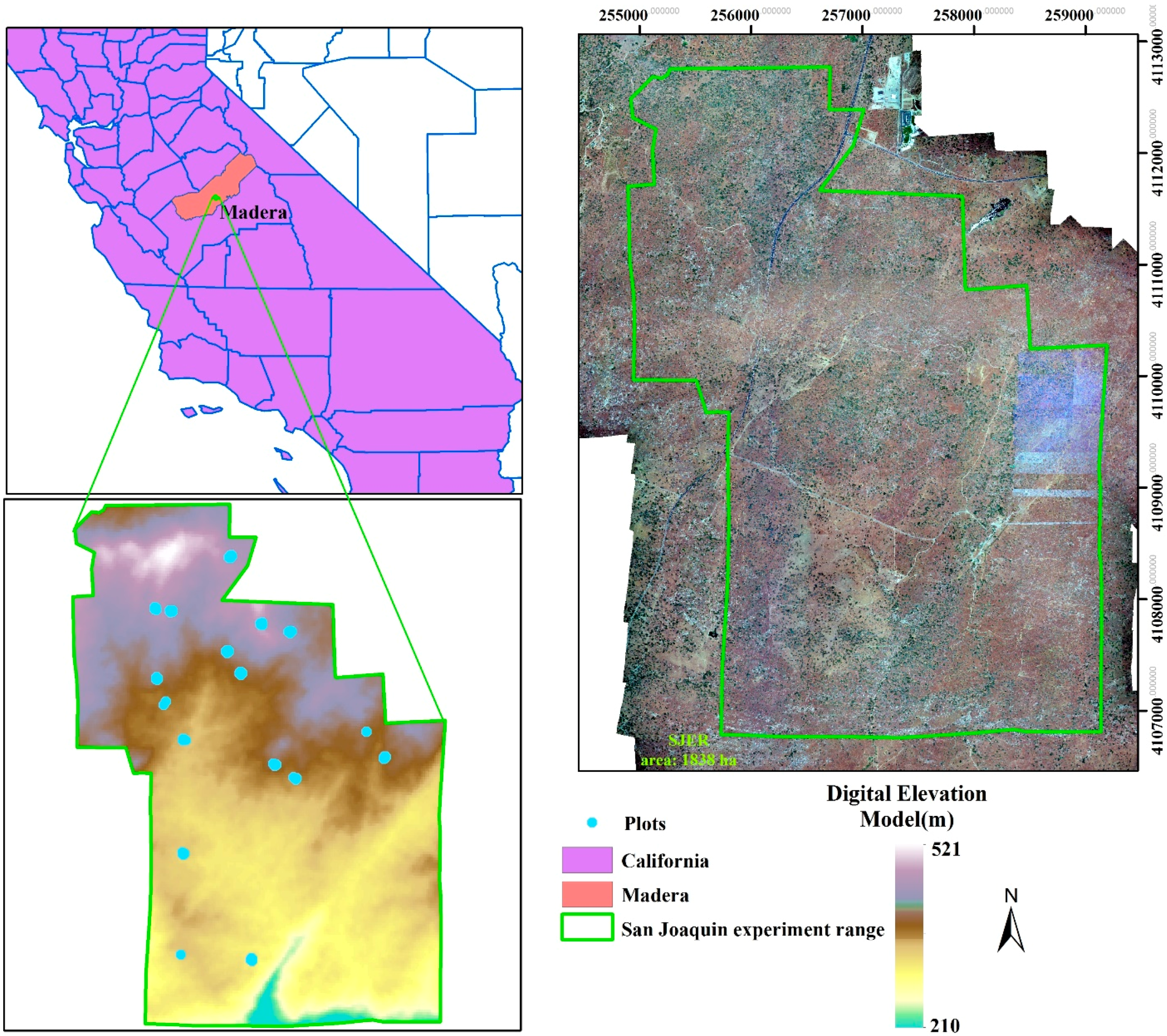
2.1. Study Site
2.2. Data
2.2.1. LiDAR Data
2.2.2. Reference Data
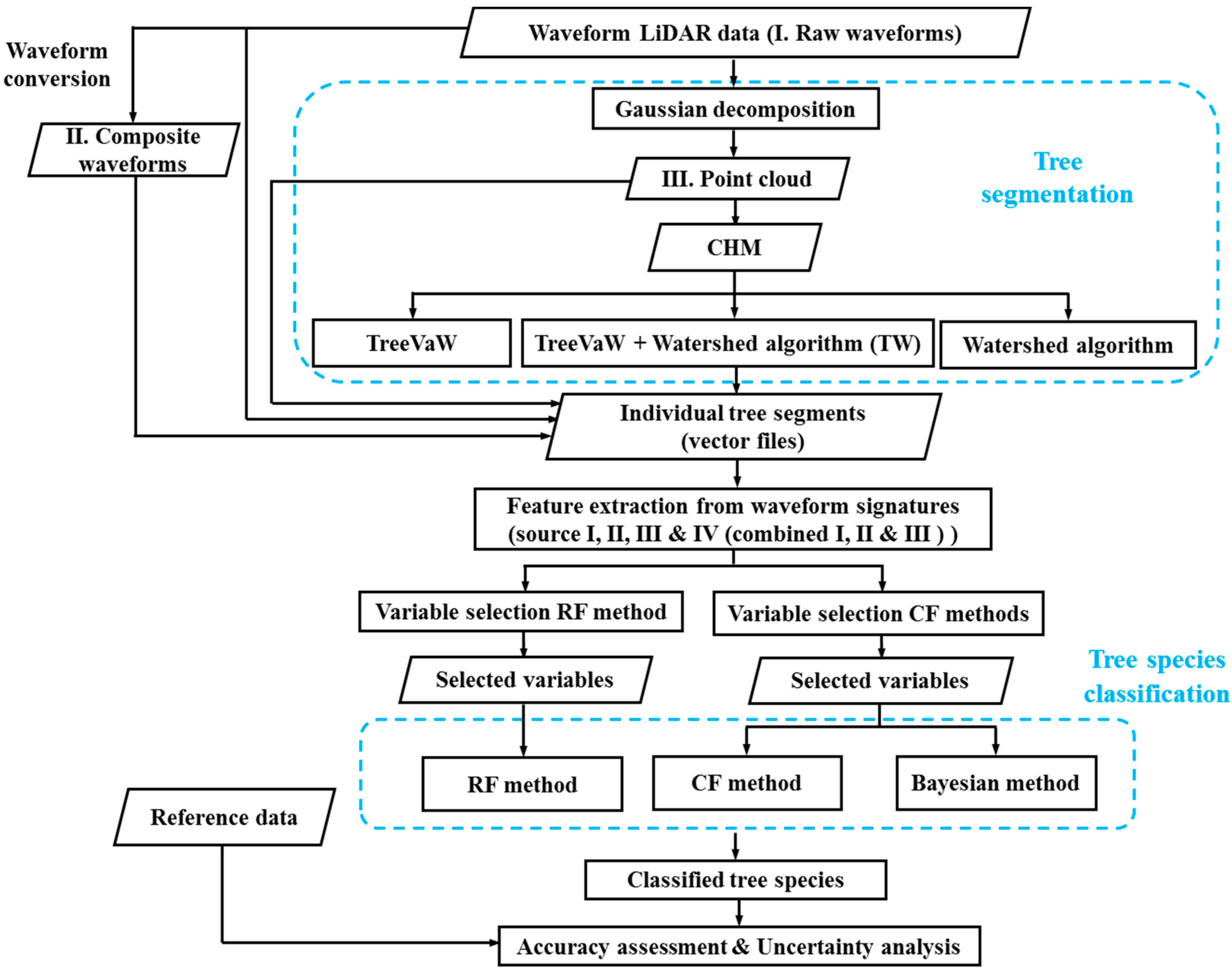
2.3. Methods
2.3.1. Waveform Decomposition
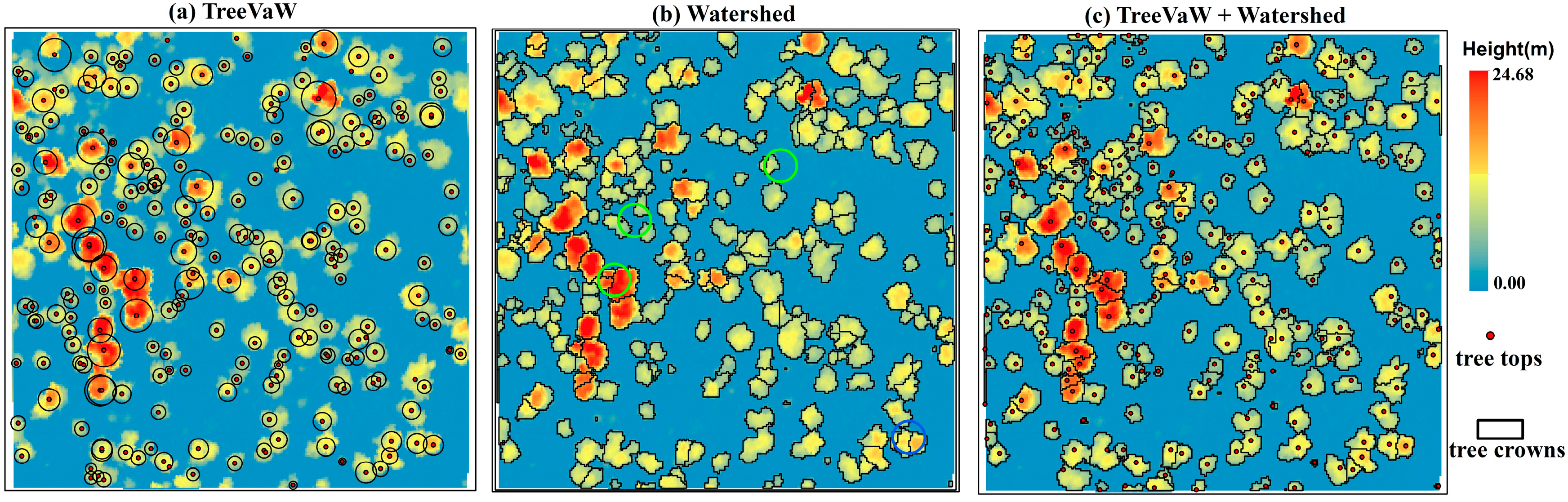
2.3.2. Tree Segmentation
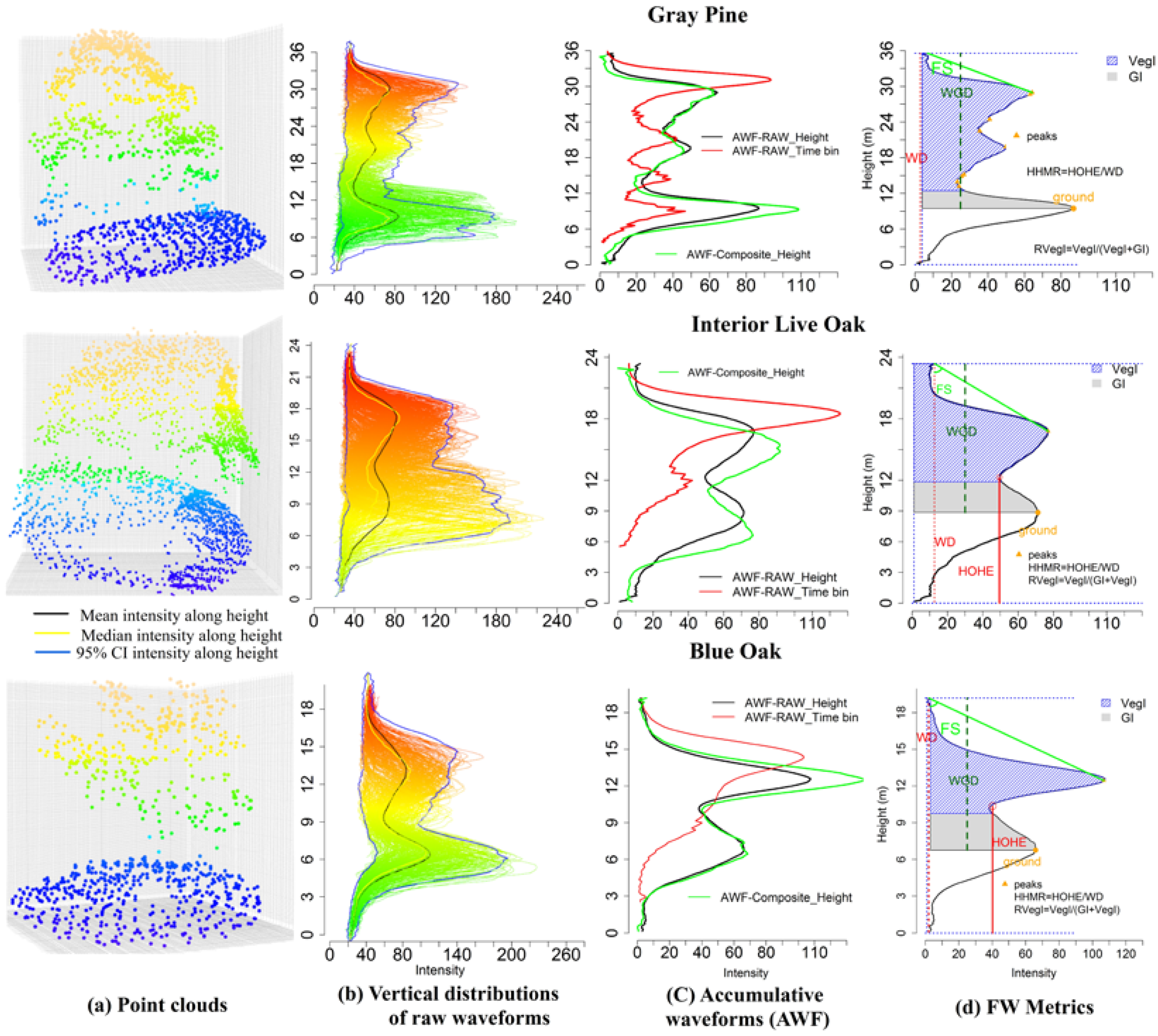
2.3.3. Feature Extraction from Waveform Signatures
2.3.4. Feature Selection
2.3.5. Tree Species Classification
Random Forests and Conditional Inference Forests
Bayesian Inference
3. Results
3.1. Tree Segmentation
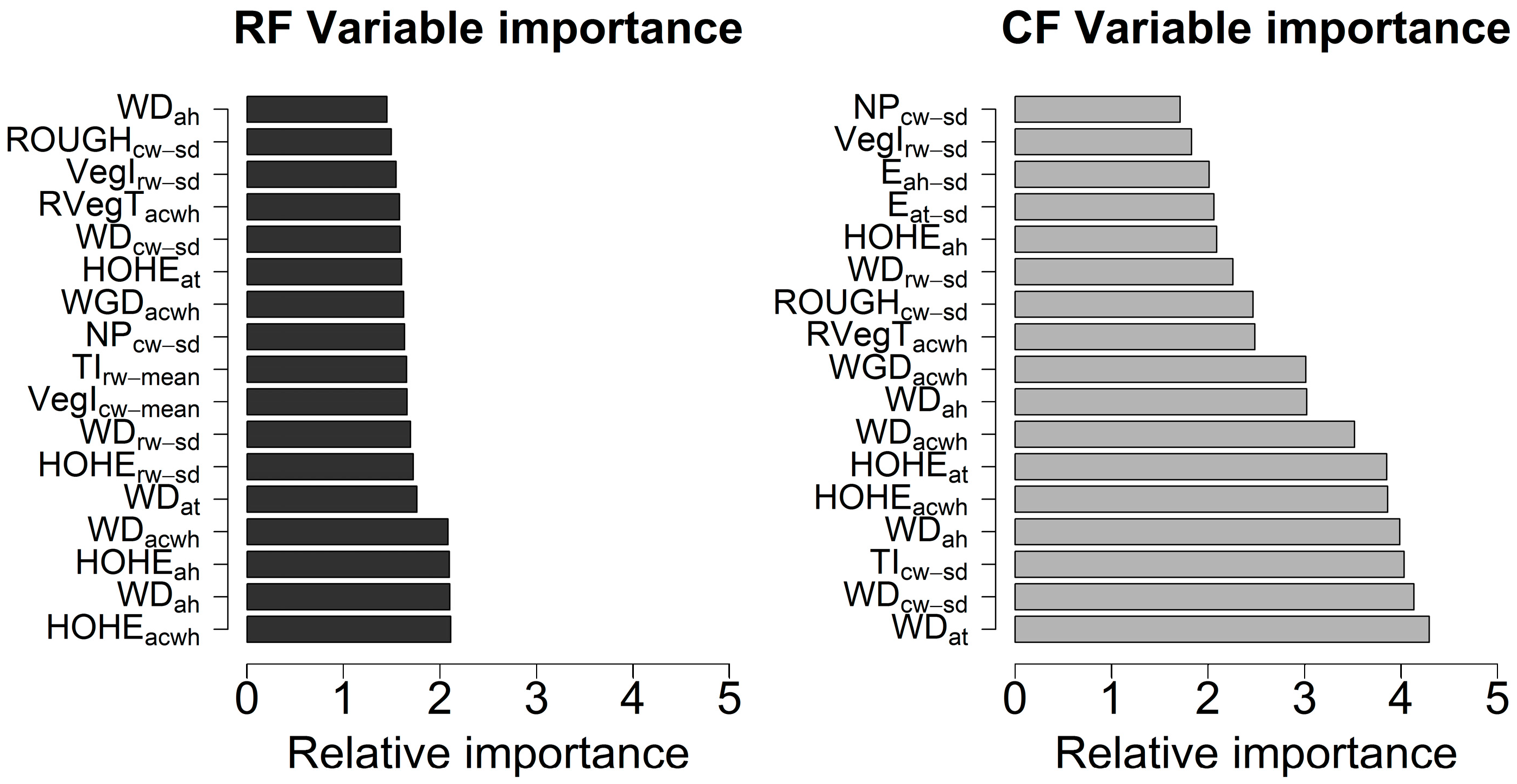
3.2. Feature Extraction & Selection
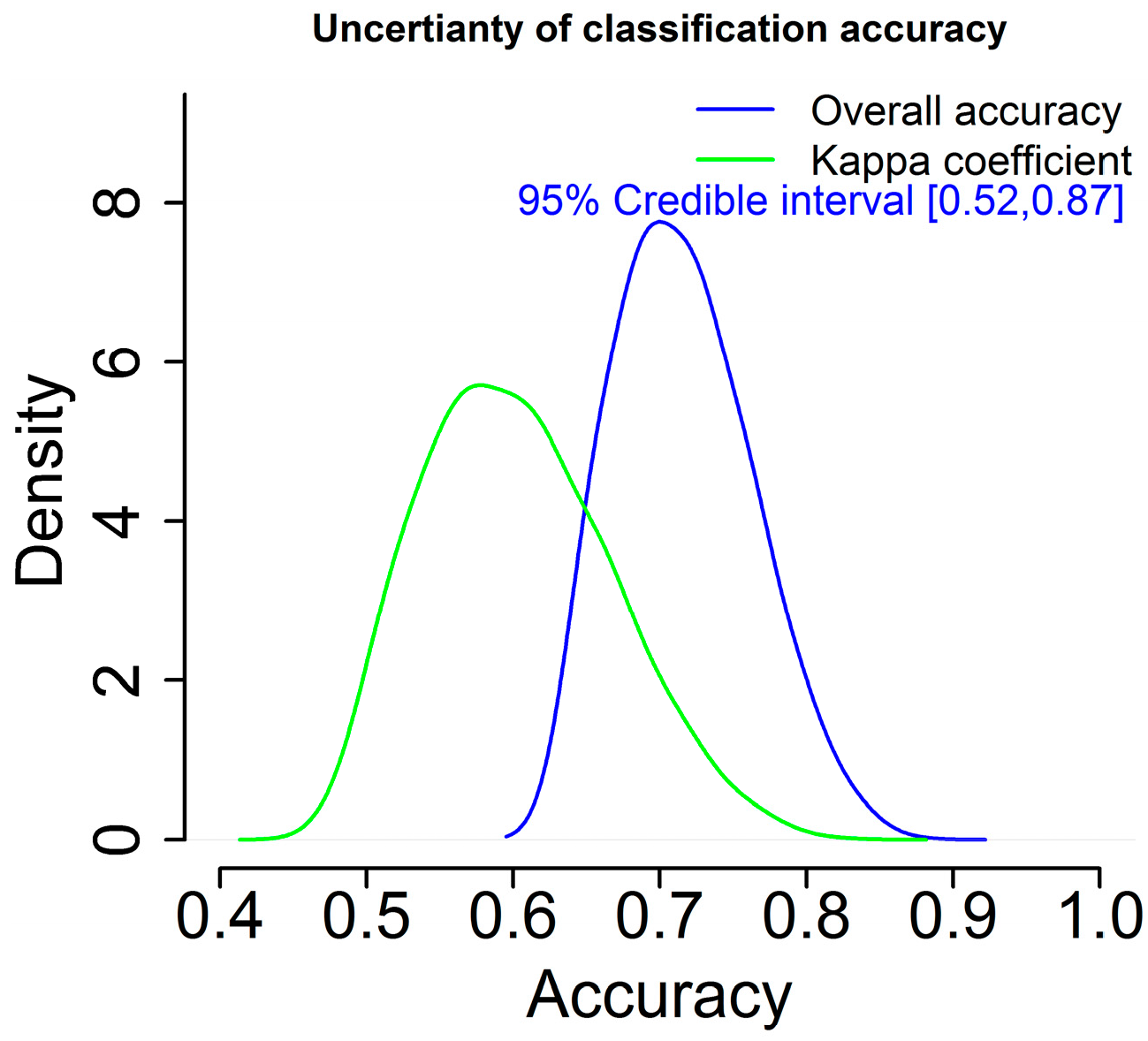
3.3. Classification Results
4. Discussion
4.1. Tree Segmentation
4.2. Individual Trees’ Waveform Signatures
4.3. Waveform Metrics and Feature Selection
4.4. Tree Species Classification and Uncertainty
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Waveform Metrics | Definition (Within an Individual Tree Segments) |
|---|---|
| Individual raw waveforms | |
| Area | The area of an individual tree crown segment |
| NPrw-mean | The average number of detected peaks for raw waveforms |
| NPrw-sd | Standard deviation of NP |
| MaxPrw | Maximum of NP |
| WDrw-mean | The average distance from waveform beginning to waveform ending using raw waveform |
| WDrw-sd | Standard deviation of WDmean |
| HOMErw-mean | The average distance from height of median energy in waveforms to the ground |
| HOMErw-sd | Standard deviation of HOMEmean |
| HTMRrw-mean | The average ration between HOHE and WD |
| HTMRrw-sd | Standard deviation of HTMR |
| HOHErw-mean | The average distance from height of half energy in waveforms to the ground |
| HOHErw-sd | Standard deviation of HOHE |
| HTHRrw-mean | The average ration between HOHE and WD |
| HTHRrw-sd | Standard deviation of HTHR |
| FSrw-mean | The average vertical angle from waveform beginning to the first peak |
| FSrw-sd | Standard deviation of FS |
| ROUGHrw-mean | The average distance form waveform beginning to the first peak |
| ROUGHrw-sd | Standard deviation of ROUGH |
| TErw-mean | The average total energy of raw waveforms |
| MErw-mean | The average energy of each raw waveform |
| MaxIrw-mean | Average maximum intensity of all raw waveforms |
| TIrw-mean | The average integral of energy along height from waveform beginning to the ground |
| VegIrw-mean | The average integral of energy along height from waveform beginning to 3-m above ground |
| RVegTrw-mean | The average ratio between VegI and TI |
| MaxIrw-sd | Standard deviation of maximum intensity |
| TIrw-sd | Standard deviation of the integral of energy along height from waveform beginning to the ground |
| VegIrw-sd | Standard deviation of the integral of energy along height from waveform beginning to 3-m above ground |
| RVegTrw-sd | Standard deviation of the ratio between VegI and TI for all waveforms in the individual tree crown segment |
| Accumulative waveform along the time bin | |
| NPat | The number of peaks in the time bin based accumulative waveform |
| WDat | The distance from waveform beginning to the ground in the time bin based accumulative waveform |
| HOMEat | The distance from height of median energy to ground in the time bin based accumulative waveform |
| HOHEat | The distance from height of half energy to ground in the time bin based accumulative waveform |
| HTMRat | The ration between HOMEat and WDat |
| HTHRat | The ration between HOHEat and WDat |
| FSat | The front slope angle of the time bin based accumulative waveform |
| ROUGHat | The average distance form waveform beginning to the first peak in the time bin based accumulative waveform |
| Eat-mean | The average energy of the time bin based accumulative waveform |
| Eat-sd | Standard deviation of energy of the time bin based accumulative waveform |
| Accumulative waveform along the height | |
| NPah | The number of peaks in the height based accumulative waveform |
| WDah | The distance from waveform beginning to the ground in the height based accumulative waveform |
| HOMEah | The distance from height of median energy to ground in the height based accumulative waveform |
| HOHEah | The distance from height of half energy to ground in the height based accumulative waveform |
| HTMRah | The ration between HOMEah and WDah |
| HTHRah | The ration between HOHEah and WDah |
| FSah | The front slope angle of the height based accumulative waveform |
| ROUGHah | The average distance form waveform beginning to the first peak in the height based accumulative waveform |
| Eah-mean | The average energy of the height based accumulative waveform |
| Eah-sd | Standard deviation of energy of the height based accumulative waveform |
| MaxIah | Maximum intensity in height based accumulative waveform |
| WDah | The distance from waveform beginning to the ground in the height based accumulative waveform |
| TIah | The integral of energy along height from waveform beginning to the ground |
| VegIah | The integral of energy along height from waveform beginning to 3-m above ground |
| RVegTah | The ratio between VegIah and TIah |
| Point cloud | |
| A1p-mean | The average amplitude of detected first peak of all waveforms within an individual tree crown segment |
| A1p-sd | Standard deviation of the amplitude of detected first peak for all waveforms within an individual tree crown segment |
| TB1p-mean | The average time bin locations of detected first peak for all waveforms within an individual tree crown segment |
| TB1p-sd | Standard deviation of the time bin locations of detected first peak for all waveforms within an individual tree crown segment |
| EW1p-mean | The average echo width of detected first peak for all waveforms within an individual tree crown segment |
| EW1p-sd | Standard deviation of the echo width of detected first peak for all waveforms within an individual tree crown segment |
| A2p-mean | The average amplitude of detected second peak of all waveforms within an individual tree crown segment |
| A2p-sd | Standard deviation of the amplitude of detected second peak for all waveforms within an individual tree crown segment |
| TB2p-mean | The average time bin locations of detected second peak for all waveforms within an individual tree crown segment |
| TB2p-sd | Standard deviation of the time bin locations of detected second peak for all waveforms within an individual tree crown segment |
| EW2p-mean | The average echo width of detected second peak for all waveforms within an individual tree crown segment |
| EW2p-sd | Standard deviation of the echo width of detected second peak for all waveforms within an individual tree crown segment |
| Ap-mean | The average amplitude of all detected peaks of waveforms within an individual tree crown segment |
| TBp-mean | The average time bin locations of all detected peaks for waveforms within an individual tree crown segment |
| EWp-mean | The average echo width of all detected peak for waveforms within an individual tree crown segment |
| Ap-sd | Standard deviation of amplitude for all detected peaks for waveforms within an individual tree crown segment |
| TBp-sd | Standard deviation of time bin locations of all detected peaks for waveforms within an individual tree crown segment |
| EWp-sd | Standard deviation of echo width of all detected peak for waveforms within an individual tree crown segment |
| Individual composite waveforms | |
| NPcw-mean | The average number of detected peaks for these composite waveforms |
| NPcw-sd | Standard deviation of NP for the composite waveforms |
| MaxPcw | Maximum of NP for the composite waveforms |
| WDcw-mean | The average distance from waveform beginning to the ground for the composite waveforms |
| WDcw-sd | Standard deviation of WD for the composite waveforms |
| HOMEcw-mean | The average distance from height of median energy in waveforms to the ground for the composite waveforms |
| HOMEcw-sd | Standard deviation of HOME for the composite waveforms |
| HTMRcw-mean | The average ration between HOHE and WD for the composite waveforms |
| HTMRcw-sd | Standard deviation of HTMR for the composite waveforms |
| HOHEcw-mean | The average distance from height of half energy in waveforms to the ground for the composite waveforms |
| HOHEcw-sd | Standard deviation of HOHE for the composite waveforms |
| HTHRcw-mean | The average ration between HOHE and WD for the composite waveforms |
| HTHRcw-sd | Standard deviation of HTHR for the composite waveforms |
| FScw-mean | The average vertical angle from waveform beginning to the first peak for the composite waveforms |
| FScw-sd | Standard deviation of FS for the composite waveforms |
| ROUGHcw-mean | The average distance form waveform beginning to the first peak for the composite waveforms |
| ROUGHcw-sd | Standard deviation of ROUGH for the composite waveforms |
| TEcw-mean | The average total energy of composite waveforms |
| MEcw-mean | The average energy of each composite waveform |
| Accumulative composite waveforms | |
| NPacwh | The number of peaks in the height based accumulative composite waveform |
| WDacwh | The distance from waveform beginning to waveform ending in the height based accumulative composite waveform |
| HOMEacwh | The distance from height of median energy to ground in the height based accumulative composite waveform |
| HOHEacwh | The distance from height of half energy to ground in the time height based accumulative composite waveform |
| HTMRacwh | The ration between HOMEacwh and WDacwh |
| HTHRacwh | The ration between HOHEacwh and WDacwh |
| FSacwh | The front slope angle of the height based accumulative composite waveforms |
| ROUGHacwh | The average distance form waveform beginning to the first peak in height based accumulative composite waveform |
| MEacwh | The average energy of the height based accumulative composite waveforms |
| MaxAacwh | Maximum amplitude of the height accumulative composite waveforms |
| WGDacwh | The distance from waveform beginning to the ground in the height based accumulative composite waveform |
| TIacwh | The integral of energy along height using the accumulative composite waveform |
| VegIacwh | The integral of energy along height using the accumulative composite waveform |
| RVegTacwh | The ratio between VegIacwh and TIacwh using accumulative composite waveforms |
| MaxIcw-mean | Average maximum intensity of composite waveforms |
| TIcw-mean | The average integral of energy along height from waveform beginning to the ground using composite waveforms |
| VegIcw-mean | The average integral of energy along height from waveform beginning to 3 m above ground using composite waveforms |
| groIcw-mean | The average integral of energy along height from 3 m above ground to ground using composite waveforms |
| RVegTcw-mean | The average ratio between VegI and TI using composite waveforms |
| MaxIcw-sd | Standard deviation of maximum intensity using composite waveforms |
| TIcw-sd | Standard deviation of the integral of energy along height from waveform beginning to the ground using composite waveforms |
| VegIcw-sd | Standard deviation of the integral of energy along height from waveform beginning to 3 m above ground using composite waveforms |
| GroIcw-sd | Standard deviation of the integral of energy along height from 3 m above ground to ground using composite waveforms |
| RVegTcw-sd | Standard deviation of the ratio between VegI and TI using composite waveforms |
References
- Treitz, P.; Howarth, P. High spatial resolution remote sensing data for forest ecosystem classification: An examination of spatial scale. Remote Sens. Environ. 2000, 72, 268–289. [Google Scholar] [CrossRef]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using hymap imaging spectrometer data. Remote Sens. Environ. 2005, 95, 177–194. [Google Scholar] [CrossRef]
- Heinzel, J.; Koch, B. Exploring full-waveform lidar parameters for tree species classification. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 152–160. [Google Scholar] [CrossRef]
- Holmgren, J.; Persson, Å. Identifying species of individual trees using airborne laser scanner. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Reitberger, J.; Krzystek, P.; Stilla, U. Analysis of full waveform lidar data for the classification of deciduous and coniferous trees. Int. J. Remote Sens. 2008, 29, 1407–1431. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A new method for segmenting individual trees from the lidar point cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
- Koch, B.; Heyder, U.; Weinacker, H. Detection of individual tree crowns in airborne lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 357–363. [Google Scholar] [CrossRef]
- Ghosh, A.; Fassnacht, F.E.; Joshi, P.K.; Koch, B. A framework for mapping tree species combining hyperspectral and lidar data: Role of selected classifiers and sensor across three spatial scales. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 49–63. [Google Scholar] [CrossRef]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Electron. Agric. 2002, 37, 71–95. [Google Scholar] [CrossRef]
- Chen, Q.; Baldocchi, D.; Gong, P.; Kelly, M. Isolating individual trees in a savanna woodland using small footprint lidar data. Photogramm. Eng. Remote Sens. 2006, 72, 923–932. [Google Scholar] [CrossRef]
- Morsdorf, F.; Meier, E.; Allgöwer, B.; Nüesch, D. Clustering in airborne laser scanning raw data for segmentation of single trees. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2003, 34, W13. [Google Scholar]
- Wang, Y.; Weinacker, H.; Koch, B.; Sterenczak, K. Lidar point cloud based fully automatic 3d single tree modelling in forest and evaluations of the procedure. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 45–51. [Google Scholar]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkänen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2012, 85, 27–40. [Google Scholar] [CrossRef]
- Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An international comparison of individual tree detection and extraction using airborne laser scanning. Remote Sens. 2012, 4, 950–974. [Google Scholar] [CrossRef]
- Hollaus, M.; Mücke, W.; Höfle, B.; Dorigo, W.; Pfeifer, N.; Wagner, W.; Bauerhansl, C.; Regner, B. Tree species classification based on full-waveform airborne laser scanning data. In Proceedings of the SILVILASER, College Station, TX, USA, 14–16 October 2009; pp. 54–62. [Google Scholar]
- Vaughn, N.R.; Moskal, L.M.; Turnblom, E.C. Tree species detection accuracies using discrete point lidar and airborne waveform lidar. Remote Sens. 2012, 4, 377–403. [Google Scholar] [CrossRef]
- Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and dbh based on single tree extraction by exploiting airborne full-waveform lidar data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
- Yu, X.; Litkey, P.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Assessment of low density full-waveform airborne laser scanning for individual tree detection and tree species classification. Forests 2014, 5, 1011–1031. [Google Scholar] [CrossRef]
- Harding, D.J. Icesat waveform measurements of within-footprint topographic relief and vegetation vertical structure. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Drake, J.B.; Dubayah, R.O.; Clark, D.B.; Knox, R.G.; Blair, J.B.; Hofton, M.A.; Chazdon, R.L.; Weishampel, J.F.; Prince, S. Estimation of tropical forest structural characteristics using large-footprint lidar. Remote Sens. Environ. 2002, 79, 305–319. [Google Scholar] [CrossRef]
- Hermosilla, T.; Ruiz, L.A.; Kazakova, A.N.; Coops, N.C.; Moskal, L.M. Estimation of forest structure and canopy fuel parameters from small-footprint full-waveform lidar data. Int. J. Wildland Fire 2014, 23, 224–233. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Dai, J.; Ruan, H.; She, G. Tree species classification in subtropical forests using small-footprint full-waveform lidar data. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 39–51. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S.; Meng, X.; Pang, Y.; Agca, M. Characterizing forest canopy structure with lidar composite metrics and machine learning. Remote Sens. Environ. 2011, 115, 1978–1996. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C.; Hothorn, T.; Zeileis, A. Party on! A New, Conditional Variable Importance Measure for Random Forests Available in the Party Package; Technical Report; University of Munich: München, Germany, 2009. [Google Scholar]
- Das, A.; Abdel-Aty, M.; Pande, A. Using conditional inference forests to identify the factors affecting crash severity on arterial corridors. J. Saf. Res. 2009, 40, 317–327. [Google Scholar] [CrossRef] [PubMed]
- Acevedo, M.A.; Corrada-Bravo, C.J.; Corrada-Bravo, H.; Villanueva-Rivera, L.J.; Aide, T.M. Automated classification of bird and amphibian calls using machine learning: A comparison of methods. Ecol. Inform. 2009, 4, 206–214. [Google Scholar] [CrossRef]
- Zhou, T.; Popescu, S.C. Bayesian decomposition of full waveform lidar data with uncertainty analysis. Remote Sens. Environ. 2017, 200, 43–62. [Google Scholar] [CrossRef]
- Patenaude, G.; Milne, R.; Van Oijen, M.; Rowland, C.S.; Hill, R.A. Integrating remote sensing datasets into ecological modelling: A bayesian approach. Int. J. Remote Sens. 2008, 29, 1295–1315. [Google Scholar] [CrossRef]
- Finley, A.O.; Banerjee, S.; Cook, B.D.; Bradford, J.B. Hierarchical bayesian spatial models for predicting multiple forest variables using waveform lidar, hyperspectral imagery and large inventory datasets. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 147–160. [Google Scholar] [CrossRef]
- Babcock, C.; Finley, A.O.; Cook, B.D.; Weiskittel, A.; Woodall, C.W. Modeling forest biomass and growth: Coupling long-term inventory and lidar data. Remote Sens. Environ. 2016, 182, 1–12. [Google Scholar] [CrossRef]
- Zhou, T.; Popescu, S.C.; Krause, K.; Sheridan, R.D.; Putman, E. Gold—A novel deconvolution algorithm with optimization for waveform lidar processing. ISPRS J. Photogramm. Remote Sens. 2017, 129, 131–150. [Google Scholar] [CrossRef]
- Allouis, T.; Durrieu, S.; Véga, C.; Couteron, P. Stem volume and above-ground biomass estimation of individual pine trees from lidar data: Contribution of full-waveform signals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 924–934. [Google Scholar] [CrossRef]
- Isenburg, M. Lastools-Efficient Tools for Lidar Processing. Available online: http://www.cs.unc.edu/~isenburg/lastools/ (accessed on 9 October 2012).
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 2003, 29, 564–577. [Google Scholar] [CrossRef]
- The R Development Core Team. R: A Language and Environment for Statistical Computing; CB Rank: San Francisco, CA, USA, 2013. [Google Scholar]
- Plowright, A. Foresttools: Analyzing Remotely Sensed Forest Data. R Package Version 0.1.5. 2017. Available online: https://cran.r-project.org/web/packages/ForestTools/index.html (accessed on 26 October 2017).
- Beucher, S.; Meyer, F. The morphological approach to segmentation: The watershed transformation. Opt. Eng. N. Y. 1992, 34, 433. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Frühwirth-Schnatter, S.; Frühwirth, R. Bayesian inference in the multinomial logit model. Austrian J. Stat. 2016, 41, 27–43. [Google Scholar] [CrossRef]
- Kruschke, J. Doing Bayesian Data Analysis: A Tutorial with r, Jags and Stan; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D.B. Bayesian Data Analysis; Chapman & Hall/CRC: Boca Raton, FL, USA, 2014; Volume 2. [Google Scholar]
- Buerkner, P.-C. Brms: An R package for bayesian multilevel models using stan. J. Stat. Softw. 2016, 80, 1–28. [Google Scholar] [CrossRef]
- Karlson, M.; Ostwald, M.; Reese, H.; Sanou, J.; Tankoano, B.; Mattsson, E. Mapping tree canopy cover and aboveground biomass in sudano-sahelian woodlands using landsat 8 and random forest. Remote Sens. 2015, 7, 10017–10041. [Google Scholar] [CrossRef]
- Freeman, E.A.; Frescino, T.S.; Moisen, G.G. Pick Your Flavor of Random Forest. 2016. Available online: https://cran.r-project.org/web/packages/ModelMap/vignettes/Vquantile.pdf (accessed on 26 October 2017).


| Plot ID | Number of Trees | Mean DBH | Mean Tree Height | Mean Crown Diameter | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gray Pine | Blue Oak | Interior Live Oak | Shrubs | Gray Pine | Blue Oak | Interior Live Oak | Shrubs | Gray Pine | Blue Oak | Interior Live Oak | Shrubs | ||
| 1 | 12 | 0.45 | - | 0.16 | 0.07 | 13.95 | - | 6.10 | 2.85 | 8.70 | - | 5.95 | 4.62 |
| 2 | 13 | 0.38 | 0.39 | 0.29 | - | 16.23 | 7.77 | 4.77 | 3.10 | 7.00 | 7.23 | 5.50 | 7.30 |
| 3 | 16 | 0.45 | 0.35 | 0.49 | 0.28 | 14.20 | 7.60 | 7.68 | 3.70 | 10.75 | 6.81 | 8.92 | 6.55 |
| 4 | 8 | - | 0.50 | 0.20 | - | - | 8.43 | 5.36 | - | - | 9.12 | 4.75 | - |
| 5 | 7 | - | - | 0.38 | - | - | - | 7.60 | - | - | - | 9.95 | - |
| 6 | 10 | 0.67 | 0.31 | - | - | 18.20 | 7.55 | - | 2.97 | 13.75 | 6.85 | - | 4.51 |
| 7 | 9 | - | - | 0.35 | - | - | - | 6.77 | - | - | - | 8.67 | - |
| 8 | 12 | 0.14 | - | 0.39 | 0.04 | 7.27 | - | 9.10 | 2.28 | 3.82 | - | 9.96 | 4.40 |
| 9 | 11 | - | 0.33 | 0.21 | 0.14 | - | 8.60 | 4.88 | 3.50 | - | 7.22 | 6.20 | 5.17 |
| 10 | 15 | 0.54 | 0.22 | 0.24 | 0.06 | 17.90 | 9.10 | 6.83 | 2.35 | 13.10 | 4.45 | 7.22 | 3.46 |
| 11 | 7 | - | - | 0.78 | - | - | - | 9.20 | - | - | - | 14.05 | - |
| 12 | 10 | 0.45 | - | - | 0.06 | 7.70 | - | - | 2.13 | 9.35 | - | - | 2.58 |
| 13 | 7 | - | 0.66 | - | - | - | 11.50 | - | - | - | 17.15 | - | - |
| 14 | 7 | - | - | 0.34 | - | - | - | 5.74 | - | - | - | 7.08 | - |
| 15 | 17 | 0.82 | 0.38 | 0.18 | 0.05 | 26.50 | 10.90 | 4.92 | 3.82 | 9.75 | 8.10 | 4.73 | 2.82 |
| 16 | 10 | 0.58 | - | 0.52 | - | 17.85 | - | 6.43 | - | 11.55 | - | 6.56 | - |
| 17 | 10 | - | - | 0.27 | 0.07 | - | - | 6.33 | 1.22 | - | - | 4.51 | 1.33 |
| Total | 181 | ||||||||||||
| Approaches | Function | Minimum Height (m) | Tolerance | Extent |
|---|---|---|---|---|
| TreeVaW | 0.804x + 3.67 | 4 | - | - |
| Watershed | - | 3.5 | 1 | 2 |
| TreeVaW + Watershed (TW) | 0.1x + 2.15 | 2.5 | - | - |
| Acronym (Metrics) | Description |
|---|---|
| WD (waveform distance) | The distance from the waveform beginning to waveform ending. |
| WGD (waveform distance from ground) | The distance from the waveform beginning to assumed ground location. |
| HOHE (height of median energy) | The distance from waveform centroid to the assumed ground location. |
| MEHR (median energy height ratio) | HOHE/WGD |
| ROUGH (roughness of outermost canopy) | The distance from the waveform beginning to the first peak. |
| HOHE (height of half total energy) | The distance from half energy location to waveform ending. |
| HEHR (half energy height ratio) | HOHE/WD |
| FS (front slope angle) | The angle from waveform beginning to the first peak which is assumed to be canopy returns. |
| E (total return energy) | The total energy contained in the waveform from waveform beginning to ending. |
| VegI (integral of the vegetation part) | The integral of vegetation part which is 3 m above the assumed ground location. |
| GI (integral of the ground part) | The integral of ground part which is 3 m from the assumed ground location. |
| RvegT (the ratio between the integral of vegetation and the additive integral of vegetation and ground parts) | VegI/(VegI + GI) |
| Approaches | Tree Detection Rate (%) | False Detection Rate (%) | Over-Segmentation Rate (%) |
|---|---|---|---|
| TreeVaW | 82.87 | 17.13 | 6.07 |
| Watershed | 92.82 | 7.18 | 15.58 |
| TreeVaW + Watershed (TW) | 90.06 | 9.94 | 8.84 |
| Observed | Gray Pine (%) | Blue Oak (%) | Interior Live Oak (%) | Shrub (%) | |
|---|---|---|---|---|---|
| Predicted | |||||
| RF | |||||
| Gray Pine | 95 | 5 | 7 | 0 | |
| Blue Oak | 0 | 45 | 10 | 6 | |
| Interior Live Oak | 5 | 40 | 80 | 6 | |
| Shrub | 0 | 10 | 3 | 88 | |
| Overall accuracy | 80 | Kappa | 72 | ||
| CF | |||||
| Gray Pine | 94 | 0 | 20 | 0 | |
| Blue Oak | 0 | 20 | 0 | 0 | |
| Interior Live Oak | 6 | 80 | 67 | 0 | |
| Shrub | 0 | 0 | 13 | 100 | |
| Overall accuracy | 68 | Kappa | 54 | ||
| Observed | Gray Pine (%) | Blue Oak (%) | Interior Live Oak (%) | Shrub (%) | |
|---|---|---|---|---|---|
| Predicted | |||||
| RF | |||||
| Gray Pine | 94 | 0 | 13 | 0 | |
| Blue Oak | 6 | 50 | 13 | 0 | |
| Interior Live Oak | 0 | 50 | 60 | 0 | |
| shrub | 0 | 0 | 13 | 100 | |
| Overall accuracy | 73 | Kappa | 61 | ||
| CF | |||||
| Gray Pine | 95 | 5 | 10 | 0 | |
| Blue Oak | 0 | 10 | 3 | 0 | |
| Interior Live Oak | 5 | 80 | 83 | 13 | |
| shrub | 0 | 5 | 3 | 88 | |
| Overall accuracy | 74 | Kappa | 63 | ||
| Bayesian | |||||
| Gray Pine | 89 | 0 | 8 | 0 | |
| Blue Oak | 6 | 27 | 8 | 10 | |
| Interior Live Oak | 6 | 73 | 83 | 20 | |
| shrub | 0 | 0 | 0 | 70 | |
| Overall accuracy | 84 | Kappa | 78 | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Popescu, S.C.; Lawing, A.M.; Eriksson, M.; Strimbu, B.M.; Bürkner, P.C. Bayesian and Classical Machine Learning Methods: A Comparison for Tree Species Classification with LiDAR Waveform Signatures. Remote Sens. 2018, 10, 39. https://doi.org/10.3390/rs10010039
Zhou T, Popescu SC, Lawing AM, Eriksson M, Strimbu BM, Bürkner PC. Bayesian and Classical Machine Learning Methods: A Comparison for Tree Species Classification with LiDAR Waveform Signatures. Remote Sensing. 2018; 10(1):39. https://doi.org/10.3390/rs10010039
Chicago/Turabian StyleZhou, Tan, Sorin C. Popescu, A. Michelle Lawing, Marian Eriksson, Bogdan M. Strimbu, and Paul C. Bürkner. 2018. "Bayesian and Classical Machine Learning Methods: A Comparison for Tree Species Classification with LiDAR Waveform Signatures" Remote Sensing 10, no. 1: 39. https://doi.org/10.3390/rs10010039
APA StyleZhou, T., Popescu, S. C., Lawing, A. M., Eriksson, M., Strimbu, B. M., & Bürkner, P. C. (2018). Bayesian and Classical Machine Learning Methods: A Comparison for Tree Species Classification with LiDAR Waveform Signatures. Remote Sensing, 10(1), 39. https://doi.org/10.3390/rs10010039






