Assessing Different Feature Sets’ Effects on Land Cover Classification in Complex Surface-Mined Landscapes by ZiYuan-3 Satellite Imagery
Abstract
1. Introduction
2. Materials and Methods
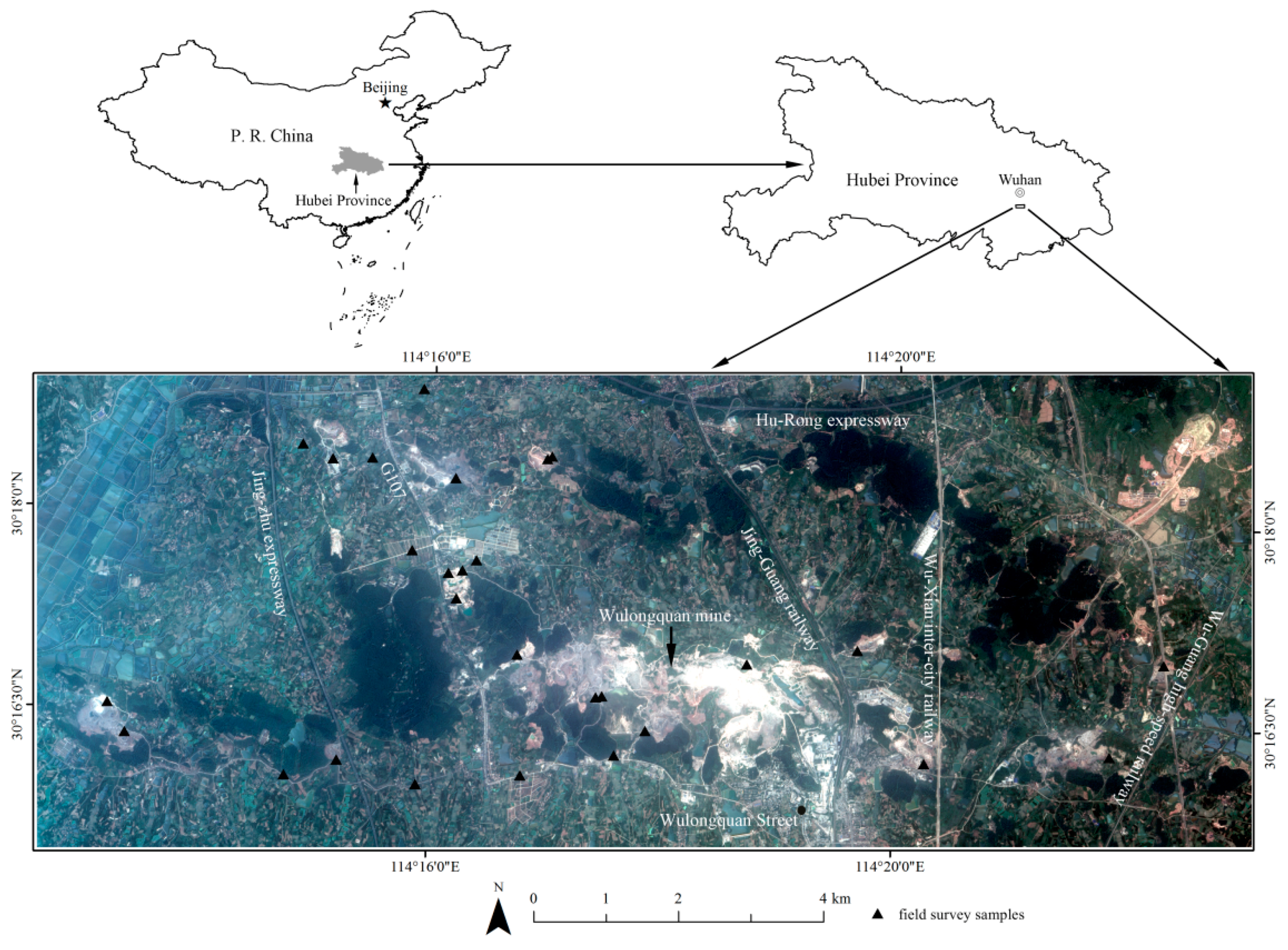
2.1. Test Site and Data Set
2.2. Employed Feature Sets
2.3. Referenced Data
2.4. Feature Set Combinations and Classification Procedure
2.4.1. Feature Combinations
2.4.2. Feature Selection Procedure
2.4.3. Classification Model Construction and Accuracy Assessment
3. Results
3.1. Feature Selection Results for SBs Following the Addition of Some Types of Feature Sets
3.2. Analysis of the Addition of Different Types of Feature Sets to SBs for LCCSML
3.2.1. Overall Accuracy, F1-Measure, and Percentage Deviation
3.2.2. McNemar Test
3.3. Analysis of the Exclusion of Different Types of Feature Sets from Feature Subset for LCCSML
3.3.1. Overall Accuracy, F1-Measure, and Percentage Deviation
3.3.2. McNemar Test
3.4. Analysis of the Addition of Some Types of Feature Sets to SBs with FS for LCCSML
3.4.1. Overall Accuracy, F1-Measure, and Percentage Deviation
3.4.2. McNemar Test
4. Discussion
4.1. Assessment of Feature Sets
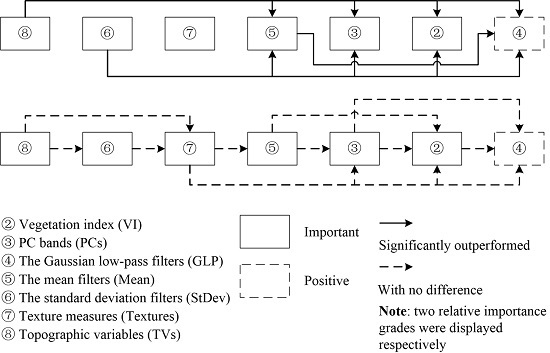
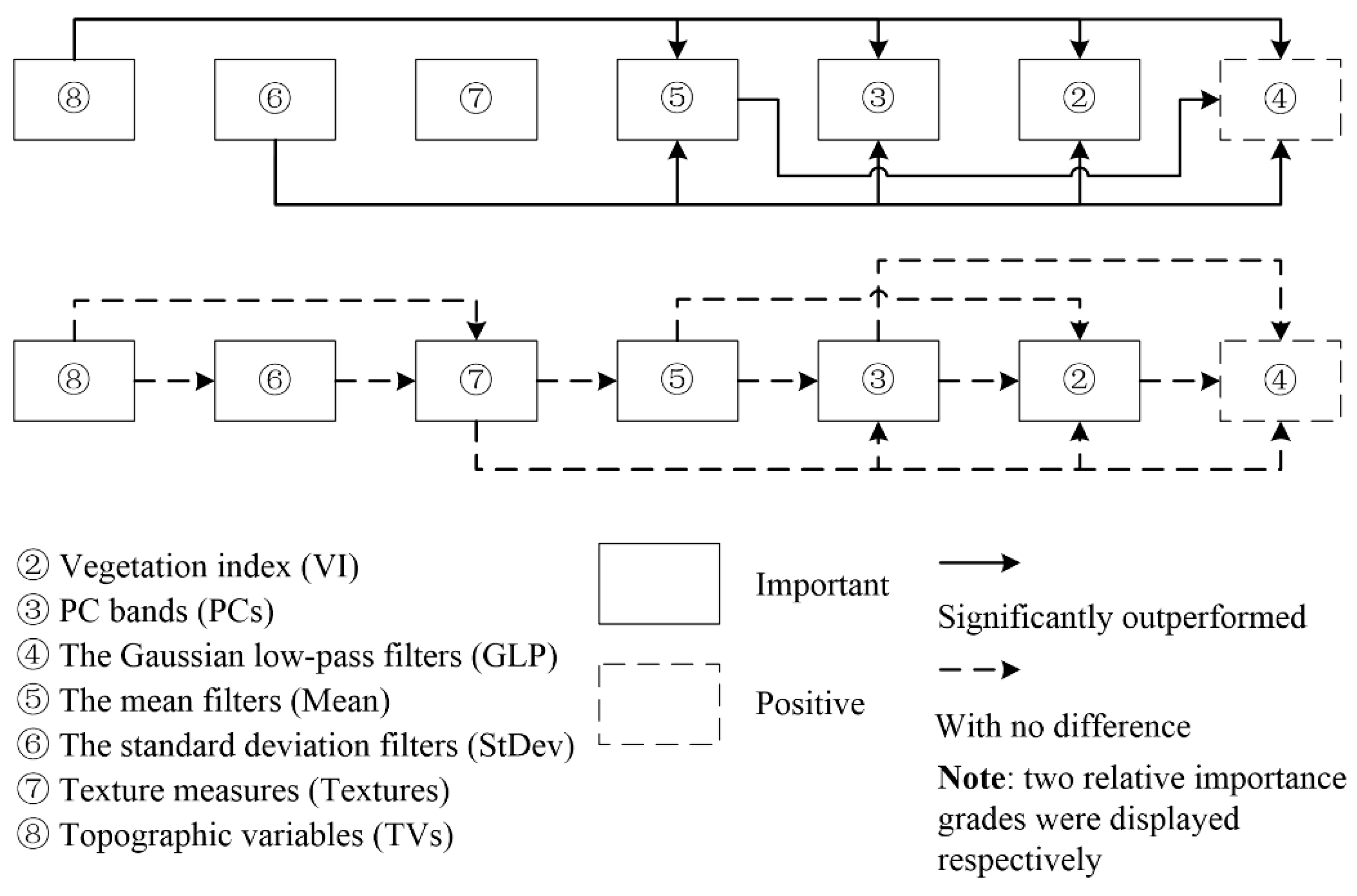
4.1.1. Importance of Feature Sets
Importance of VI and PCs
Importance of GLP, Mean, and StDev
Importance of Textures and TVs
4.1.2. Relative Importance between Different Feature Sets
Relative Importance of VI and PCs
Relative Importance of GLP, Mean, and StDev
Relative Importance among Those Five Feature Sets
Relative Importance of Textures and TVs
Others
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.C.; Zhao, Y.Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Sellers, P.J.; Meeson, B.W.; Hall, F.G.; Asrar, G.; Murphy, R.E.; Schiffer, R.A.; Bretheron, F.P.; Dickinson, R.E.; Ellingson, R.G.; Huemmrich, K.F.; et al. Remote sensing of the land surface for studies of global change: Models—Algorithms—Experiments. Remote Sens. Environ. 1995, 51, 3–26. [Google Scholar] [CrossRef]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-pixel vs. object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
- Senf, C.; Leitão, P.J.; Pflugmacher, D.; van der Linden, S.; Hostert, P. Mapping land cover in complex Mediterranean landscapes using Landsat: Improved classification accuracies from integrating multi-seasonal and synthetic imagery. Remote Sens. Environ. 2015, 156, 527–536. [Google Scholar] [CrossRef]
- Yan, W.Y.; Shaker, A.; El-Ashmawy, N. Urban land cover classification using airborne LiDAR data: A review. Remote Sens. Environ. 2015, 158, 295–310. [Google Scholar] [CrossRef]
- Goodin, D.G.; Anibas, K.L.; Bezymennyi, M. Mapping land cover and land use from object-based classification: An example from a complex agricultural landscape. Int. J. Remote Sens. 2015, 36, 4702–4723. [Google Scholar] [CrossRef]
- Hurni, K.; Hett, C.; Epprecht, M.; Messerli, P.; Heinimann, A. A texture-based land cover classification for the delineation of a shifting cultivation landscape in the Lao PDR using landscape metrics. Remote Sens. 2013, 5, 3377–3396. [Google Scholar] [CrossRef]
- Okubo, S.; Parikesit; Muhamad, D.; Harashina, K.; Takeuchi, K.; Umezaki, M. Land use/cover classification of a complex agricultural landscape using single-dated very high spatial resolution satellite-sensed imagery. Can. J. Remote Sens. 2010, 36, 722–736. [Google Scholar] [CrossRef]
- Piiroinen, R.; Heiskanen, J.; Mõttus, M.; Pellikka, P. Classification of crops across heterogeneous agricultural landscape in Kenya using AisaEAGLE imaging spectroscopy data. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 1–8. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Strager, M.P.; Warner, T.A.; Zegre, N.P.; Yuill, C.B. Comparison of NAIP orthophotography and RapidEye satellite imagery for mapping of mining and mine reclamation. Gisci. Remote Sens. 2014, 51, 301–320. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A. Differentiating mine-reclaimed grasslands from spectrally similar land cover using terrain variables and object-based machine learning classification. Int. J. Remote Sens. 2015, 36, 4384–4410. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Strager, M.P.; Conley, J.F.; Sharp, A.L. Assessing machine-learning algorithms and image- and lidar-derived variables for GEOBIA classification of mining and mine reclamation. Int. J. Remote Sens. 2015, 36, 954–978. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Strager, M.P.; Pal, M. Combining RapidEye satellite imagery and Lidar for mapping of mining and mine reclamation. Photogram. Eng. Remote Sens. 2014, 80, 179–189. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Cheng, X.; Wang, L. A comparison of machine learning algorithms for mapping of complex surface-mined and agricultural landscapes using ZiYuan-3 stereo satellite imagery. Remote Sens. 2016, 8, 514. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Abarca-Hernandez, F.; Atkinson, P.M.; Jeganathan, C. Random forest classification of Mediterranean land cover using multi-seasonal imagery and multi-seasonal texture. Remote Sens. Environ. 2012, 121, 93–107. [Google Scholar] [CrossRef]
- Chen, G.; Li, X.; Chen, W.; Cheng, X.; Zhang, Y.; Liu, S. Extraction and application analysis of landslide influential factors based on LiDar DEM: A case study in the Three Gorges area, China. Nat. Hazards 2014, 74, 509–526. [Google Scholar] [CrossRef]
- Chen, W.; Li, X.; Wang, Y.; Chen, G.; Liu, S. Forested landslide detection using LiDar data and the random forest algorithm: A case study of the Three Gorges, China. Remote Sens. Environ. 2014, 152, 291–301. [Google Scholar] [CrossRef]
- Li, X.; Cheng, X.; Chen, W.; Chen, G.; Liu, S. Identification of forested landslides using LiDar data, object-based image analysis, and machine learning algorithms. Remote Sens. 2015, 7, 9705–9726. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Cheng, X.; Liao, Y.; Chen, G. Comparison and integration of feature reduction methods for land cover classification with RapidEye imagery. Multimed. Tools Appl. 2017. [Google Scholar] [CrossRef]
- Duro, D.C.; Franklin, S.E.; Dube, M.G. Multi-scale object-based image analysis and feature selection of multi-sensor Earth Observation imagery using random forests. Int. J. Remote Sens. 2012, 33, 4502–4526. [Google Scholar] [CrossRef]
- Schuster, C.; Förster, M.; Kleinschmit, B. Testing the red edge channel for improving land-use classifications based on high-resolution multi-spectral satellite data. Int. J. Remote Sens. 2012, 33, 5583–5599. [Google Scholar] [CrossRef]
- Adelabu, S.; Mutanga, O.; Adam, E. Evaluating the impact of red-edge band from Rapideye image for classifying insect defoliation levels. ISPRS J. Photogramm. Remote Sens. 2014, 95, 34–41. [Google Scholar] [CrossRef]
- Kim, H.O.; Yeom, J.M. Effect of red-edge and texture features for object-based paddy rice crop classification using RapidEye multi-spectral satellite image data. Int. J. Remote Sens. 2014, 35, 7046–7068. [Google Scholar] [CrossRef]
- Akar, Ö.; Güngör, O. Integrating multiple texture methods and NDVI to the Random Forest classification algorithm to detect tea and hazelnut plantation areas in northeast Turkey. Int. J. Remote Sens. 2015, 36, 442–464. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Neumann, C.; Förster, M.; Buddenbaum, H.; Ghosh, A.; Clasen, A.; Joshi, P.K.; Koch, B. Comparison of feature reduction algorithms for classifying tree species with hyperspectral data on three central European test sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2547–2561. [Google Scholar] [CrossRef]
- Aguilar, M.A.; Bianconi, F.; Aguilar, F.J.; Fernández, I. Object-based greenhouse classification from GeoEye-1 and WorldView-2 stereo imagery. Remote Sens. 2014, 6, 3554–3582. [Google Scholar] [CrossRef]
- Wright, C.; Gallant, A. Improved wetland remote sensing in Yellowstone National Park using classification trees to combine TM imagery and ancillary environmental data. Remote Sens. Environ. 2007, 107, 582–605. [Google Scholar] [CrossRef]
- Clausi, D.A. Comparison and fusion of co-occurrence, Gabor and MRF texture features for classification of SAR sea-ice imagery. Atmosphere-Ocean 2001, 39, 183–194. [Google Scholar] [CrossRef]
- Diaz-Uriarte, R. Varselrf: Variable Selection Using Random Forests; R Package Version 0.7-3; TU Wien: Vienna, Austria, 2010. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Draguµ, L. Random Forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Pal, M. Random Forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Pelletier, C.; Valero, S.; Inglada, J.; Champion, N.; Dedieu, G. Assessing the robustness of Random Forests to map land cover with high resolution satellite image time series over large areas. Remote Sens. Environ. 2016, 187, 156–168. [Google Scholar] [CrossRef]
- Rodríguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a Random Forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by RandomForest. R News 2002, 2, 18–22. [Google Scholar]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F.; Chang, C.-C.; Lin, C.-C. E1071: Misc Functions of the Department of Statistics (e1071); R Package Version 1.6–4; TU Wien: Vienna, Austria, 2014. [Google Scholar]
- Breiman, L.; Cutler, A. Random Forests Leo Breiman and Adele Cutler—Classification/Clustering—Description. Available online: http://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm (accessed on 4 September 2017).
- Daskalaki, S.; Kopanas, I.; Avouris, N. Evaluation of classifiers for an uneven class distribution problem. Appl. Artif. Intell. 2006, 20, 381–417. [Google Scholar] [CrossRef]
- Manandhar, R.; Odeh, I.O.A.; Ancev, T. Improving the accuracy of land use and land cover classification of Landsat data using post-classification enhancement. Remote Sens. 2009, 1, 330–344. [Google Scholar] [CrossRef]
- Li, X.; Chen, G.; Liu, J.; Chen, W.; Cheng, X.; Liao, Y. Effects of RapidEye imagery’s red-edge band and vegetation indices on land cover classification in an arid region. Chin. Geogr. Sci. 2017, 27, 827–835. [Google Scholar] [CrossRef]
- Corcoran, J.; Knight, J.; Gallant, A. Influence of multi-source and multi-temporal remotely sensed and ancillary data on the accuracy of random forest classification of wetlands in northern Minnesota. Remote Sens. 2013, 5, 3212–3238. [Google Scholar] [CrossRef]
- Dannenberg, M.P.; Hakkenberg, C.R.; Song, C. Consistent classification of Landsat time series with an improved automatic adaptive signature generalization algorithm. Remote Sens. 2016, 8, 691. [Google Scholar] [CrossRef]


| Image Features | Names | No. | |
|---|---|---|---|
| ① | Spectral bands | Band_(b, g, r, n) | 4 |
| ② | Vegetation index | NDVI | 1 |
| ③ | PC bands | PC1, PC2 | 2 |
| ④ | GLP filter features | GLP_(b, g, r, n)_(3, 5, 7) | 12 |
| ⑤ | Mean filter features | Mean_(b, g, r, n)_(3, 5, 7) | 12 |
| ⑥ | StDev filter features | StDev_(b, g, r, n)_(3, 5, 7) | 12 |
| ⑦ | Texture measures | (Con, Cor, Asm, Ent, Hom)_(b, g, r, n)_(3, 5, 7) | 60 |
| ⑧ | Topographic variables | DTM, slope, aspect | 3 |
| ⑨ | Feature subset | 2 spectral bands (Band_(r,n)), vegetation index (NDVI), PC bands (PC1, PC2), 11 GLP filter features (GLP_(b, g, r, n)_(5, 7), GLP_(b, r, n)_3), Mean filter features (Mean_(b, g, r, n)_(3, 5, 7)), 4 StDev filter features (StDev_(b, g, r)_7, StDev_b_5), and 2 topographic variables (DTM, slope) | 34 |
| Combination 1 | No. | Combination 2 | No. | Combination 3 | No. |
|---|---|---|---|---|---|
| ① | 4 | ⑨ | 34 | ① + ④ + FS | - |
| ① + ② | 5 | ⑨ − ② | 33 | ① + ⑤ + FS | - |
| ① + ③ | 6 | ⑨ − ③ | 32 | ① + ⑥ + FS | - |
| ① + ④ | 16 | ⑨ − ④ | 23 | ① + ⑦ + FS | - |
| ① + ⑤ | 16 | ⑨ − ⑤ | 22 | ||
| ① + ⑥ | 16 | ⑨ − ⑥ | 30 | ||
| ① + ⑦ | 64 | ⑨ − ⑧ | 32 | ||
| ① + ⑧ | 7 |
| Features | Selected Times | Mean Ranks | Standard Deviation Value of Ranks |
|---|---|---|---|
| GLP_r_7 | 20 | 1.00 | 0.00 |
| GLP_r_5 | 20 | 2.00 | 0.00 |
| GLP_b_7 | 20 | 3.15 | 0.37 |
| GLP_n_7 | 20 | 3.85 | 0.37 |
| GLP_r_3 | 20 | 5.40 | 0.68 |
| GLP_g_7 | 20 | 6.10 | 0.55 |
| GLP_n_5 | 13 | 6.23 | 0.93 |
| Band_r | 13 | 8.00 | 0.00 |
| GLP_n_3 | 13 | 9.00 | 0.00 |
| GLP_b_5 | 13 | 10.08 | 0.28 |
| Band_n | 13 | 11.08 | 0.49 |
| GLP_g_5 | 13 | 11.85 | 0.38 |
| GLP_g_3 | 13 | 13.31 | 0.48 |
| GLP_b_3 | 8 | 13.50 | 0.53 |
| Band_g | 8 | 15.25 | 0.46 |
| Band_b | 8 | 15.75 | 0.46 |
| Features | Selected Times | Mean Ranks | Standard Deviation Value of Ranks |
|---|---|---|---|
| Mean_r_7 | 20 | 1.00 | 0.00 |
| Mean_r_5 | 20 | 2.00 | 0.00 |
| Mean_b_7 | 20 | 3.00 | 0.00 |
| Mean_r_3 | 20 | 4.00 | 0.00 |
| Mean_g_7 | 20 | 5.00 | 0.00 |
| Mean_n_7 | 20 | 6.00 | 0.00 |
| Mean_n_5 | 14 | 7.14 | 0.53 |
| Mean_n_3 | 14 | 8.36 | 0.50 |
| Mean_b_5 | 14 | 8.50 | 0.65 |
| Mean_g_5 | 14 | 10.00 | 0.00 |
| Features | Selected Times | Mean Ranks | Standard Deviation Value of Ranks |
|---|---|---|---|
| Band_n | 20 | 1.00 | 0.00 |
| Band_r | 20 | 2.00 | 0.00 |
| Band_g | 20 | 3.00 | 0.00 |
| Band_b | 20 | 4.00 | 0.00 |
| StDev_b_7 | 20 | 5.40 | 0.50 |
| StDev_r_7 | 20 | 5.60 | 0.50 |
| StDev_g_7 | 20 | 7.00 | 0.00 |
| StDev_n_7 | 20 | 8.75 | 0.44 |
| StDev_b_5 | 15 | 8.00 | 0.00 |
| StDev_r_5 | 12 | 10.00 | 0.00 |
| StDev_n_5 | 3 | 10.00 | 0.00 |
| Features | Selected Times | Mean Ranks | Standard Deviation Value of Ranks |
|---|---|---|---|
| Band_n | 20 | 1 | 0 |
| Band_r | 20 | 2 | 0 |
| Band_g | 20 | 3 | 0 |
| Band_b | 20 | 4 | 0 |
| Con_r_7 | 20 | 5 | 0 |
| Con_b_7 | 20 | 6 | 0 |
| Con_g_7 | 1 | 7 | 0 |
| Con_n_7 | 1 | 8 | 0 |
| Hom_r_7 | 1 | 9 | 0 |
| ① | ① + ② | ① + ③ | ① + ④ | ① + ⑤ | ① + ⑥ | ① + ⑦ | ① + ⑧ | |
|---|---|---|---|---|---|---|---|---|
| Crop land | 48.5 ± 2.0 | 48.0 ± 2.6 | 47.4 ± 1.6 | 50.9 ± 3.0 | 52.3 ± 2.3 | 52.5 ± 2.5 | 50.9 ± 1.8 | 56.8 ± 2.0 |
| Forest land | 58.1 ± 2.6 | 57.9 ± 1.9 | 57.9 ± 2.5 | 60.0 ± 2.0 | 62.9 ± 2.3 | 67.9 ± 1.7 | 66.4 ± 2.0 | 69.4 ± 1.9 |
| Water | 86.5 ± 0.6 | 86.9 ± 1.0 | 86.6 ± 1.4 | 86.8 ± 1.0 | 86.7 ± 1.3 | 85.7 ± 1.8 | 82.9 ± 1.3 | 90.4 ± 0.7 |
| Road | 28.0 ± 2.6 | 27.4 ± 2.5 | 26.5 ± 2.9 | 30.4 ± 2.2 | 34.6 ± 2.0 | 48.3 ± 1.9 | 45.9 ± 1.7 | 42.8 ± 3.6 |
| Urban and rural residential land | 27.2 ± 4.9 | 27.3 ± 3.8 | 26.1 ± 5.8 | 28.4 ± 2.8 | 41.3 ± 2.9 | 50.8 ± 2.5 | 53.4 ± 2.1 | 40.3 ± 4.3 |
| Bare land | 55.7 ± 2.1 | 54.4 ± 3.3 | 53.2 ± 2.0 | 57.9 ± 2.9 | 58.9 ± 2.7 | 60.8 ± 3.1 | 58.2 ± 2.2 | 60.4± 2.1 |
| Surface-mined land | 76.4 ± 2.9 | 76.0 ± 1.3 | 75.8 ± 2.7 | 78.6 ± 1.3 | 83.1 ± 2.5 | 80.0 ± 1.0 | 76.6 ± 1.6 | 81.4 ± 2.3 |
| OA | 55.6 ± 1.2 | 55.4 ± 1.0 | 54.8 ± 1.3 | 57.7 ± 1.0 | 61.0 ± 1.3 | 63.4 ± 1.0 | 61.6 ± 0.7 | 64.8 ± 1.4 |
| ① + ② | ① + ③ | ① + ④ | ① + ⑤ | ① + ⑥ | ① + ⑦ | ① + ⑧ | |
|---|---|---|---|---|---|---|---|
| ① | 0.00 | 0.43 | 1.74 | 8.70 | 12.55 | 7.67 | 20.90 |
| ① + ② | 0.52 | 2.14 | 10.17 | 13.69 | 8.68 | 24.38 | |
| ① + ③ | 4.17 | 11.57 | 17.01 | 11.16 | 28.16 | ||
| ① + ④ | 4.10 | 6.90 | 3.53 | 14.04 | |||
| ① + ⑤ | 1.31 | 0.12 | 3.60 | ||||
| ① + ⑥ | 0.94 | 0.33 | |||||
| ① + ⑦ | 1.85 |
| ⑨ | ⑨ − ② | ⑨ − ③ | ⑨ − ④ | ⑨ − ⑤ | ⑨ − ⑥ | ⑨ − ⑧ | |
|---|---|---|---|---|---|---|---|
| Crop land | 74.0 | 69.2 ± 2.5 | 68.8 ± 5.9 | 70.7 ± 2.3 | 66.7 ± 2.5 | 59.4 ± 1.0 | 60.2 ± 1.9 |
| Forest land | 79.8 | 74.5 ± 3.2 | 75.9 ± 4.2 | 76.6 ± 3.2 | 73.4 ± 2.1 | 69.8 ± 1.9 | 70.4 ± 1.3 |
| Water | 91.2 | 88.9 ± 1.4 | 89.7 ± 1.3 | 89.2 ± 0.6 | 90.5 ± 1.3 | 87.8 ± 1.4 | 88.1 ± 1.2 |
| Road | 70.5 | 60.3 ± 1.9 | 61.1 ± 9.3 | 61.7 ± 1.8 | 57.9 ± 3.2 | 43.2 ± 3.1 | 54.4 ± 3.6 |
| Urban and rural residential land | 63.0 | 60.6 ± 1.9 | 59.6 ± 6.6 | 63.2 ± 2.1 | 55.2 ± 2.3 | 45.2 ± 3.4 | 56.6 ± 2.9 |
| Bare land | 76.2 | 76.6 ± 2.0 | 73.5 ± 5.5 | 77.7 ± 1.7 | 72.4 ± 2.9 | 65.3 ± 2.3 | 65.4 ± 2.3 |
| Surface-mined land | 86.9 | 88.0 ± 2.0 | 86.5 ± 1.8 | 87.7 ± 1.4 | 85.7 ± 1.4 | 83.5 ± 1.4 | 83.8 ± 1.9 |
| OA | 77.6 | 74.0 ± 0.9 | 73.8 ± 4.3 | 75.3 ± 1.1 | 71.8 ± 1.4 | 66.2 ± 1.0 | 68.5 ± 0.8 |
| ⑨ − ② | ⑨ − ③ | ⑨ − ④ | ⑨ − ⑤ | ⑨ − ⑥ | ⑨ − ⑧ | |
|---|---|---|---|---|---|---|
| ⑨ | 6.58 | 11.64 | 3.04 | 13.45 | 36.50 | 23.84 |
| ⑨ − ② | 0.38 | 0.58 | 2.03 | 17.15 | 8.31 | |
| ⑨ − ③ | 1.89 | 0.80 | 13.23 | 4.88 | ||
| ⑨ − ④ | 6.70 | 23.73 | 12.20 | |||
| ⑨ − ⑤ | 9.03 | 2.56 | ||||
| ⑨ − ⑥ | 1.04 |
| ① + ④ + FS | ① + ⑤ + FS | ① + ⑥ + FS | ① + ⑦ + FS | |
|---|---|---|---|---|
| Crop land | 52.3 ± 1.5 | 51.8 ± 2.0 | 54.6 ± 2.3 | 52.1 ± 2.4 |
| Forest land | 61.3 ± 2.0 | 64.2 ± 1.4 | 67.4 ± 1.9 | 68.3 ± 1.2 |
| Water | 86.6 ± 0.8 | 84.8 ± 1.4 | 86.7 ± 1.4 | 84.2 ± 1.4 |
| Road | 29.9 ± 3.2 | 33.3 ± 1.7 | 50.6 ± 2.9 | 44.0 ± 1.9 |
| Urban and rural residential land | 29.0± 4.3 | 34.4 ± 1.6 | 52.3 ± 2.6 | 46.4 ± 3.4 |
| Bare land | 57.0 ± 3.5 | 61.1 ± 2.5 | 59.9 ± 2.3 | 54.2 ± 3.4 |
| Surface-mined land | 77.6 ± 1.2 | 81.3 ± 3.1 | 80.6 ± 1.2 | 79.5 ± 2.5 |
| OA | 58.1 ± 1.1 | 59.9 ± 0.8 | 64.5 ± 0.9 | 61.3 ± 0.8 |
| ① + ④ + FS | ① + ⑤ + FS | ① + ⑥ + FS | ① + ⑦ + FS | |
|---|---|---|---|---|
| ① + ④ | 0.10 | |||
| ① + ⑤ | 0.62 | |||
| ① + ⑥ | 0.27 | |||
| ① + ⑦ | 0.06 |
| ① + ④ + FS | ① + ⑤ + FS | ① + ⑥ + FS | ① + ⑦ + FS | ① + ⑧ | |
|---|---|---|---|---|---|
| ① | 2.31 | 5.56 | 16.69 | 8.00 | |
| ① + ④ + FS | 1.01 | 8.60 | 2.52 | 11.50 | |
| ① + ⑤ + FS | 4.64 | 0.49 | 5.96 | ||
| ① + ⑥ + FS | 2.77 | 0.04 | |||
| ① + ⑦ + FS | 2.59 |
| NO. | Grade | Description |
|---|---|---|
| 1 | Important | The feature sets could exert statistically significant effects on LCCSML |
| 2 | Positive | The feature sets could provide effective information for the LCCSML but did not result in significant effects |
| 3 | Useless | The feature sets had little effects on LCCSML |
| NO. | Type | Description |
|---|---|---|
| 1 | Significantly outperformed | One feature set statistically significantly outperformed another feature set. |
| 2 | With no difference | One feature set resulted in higher accuracy improvement than another feature set but with no statistically significant difference. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Li, X.; He, H.; Wang, L. Assessing Different Feature Sets’ Effects on Land Cover Classification in Complex Surface-Mined Landscapes by ZiYuan-3 Satellite Imagery. Remote Sens. 2018, 10, 23. https://doi.org/10.3390/rs10010023
Chen W, Li X, He H, Wang L. Assessing Different Feature Sets’ Effects on Land Cover Classification in Complex Surface-Mined Landscapes by ZiYuan-3 Satellite Imagery. Remote Sensing. 2018; 10(1):23. https://doi.org/10.3390/rs10010023
Chicago/Turabian StyleChen, Weitao, Xianju Li, Haixia He, and Lizhe Wang. 2018. "Assessing Different Feature Sets’ Effects on Land Cover Classification in Complex Surface-Mined Landscapes by ZiYuan-3 Satellite Imagery" Remote Sensing 10, no. 1: 23. https://doi.org/10.3390/rs10010023
APA StyleChen, W., Li, X., He, H., & Wang, L. (2018). Assessing Different Feature Sets’ Effects on Land Cover Classification in Complex Surface-Mined Landscapes by ZiYuan-3 Satellite Imagery. Remote Sensing, 10(1), 23. https://doi.org/10.3390/rs10010023