A CNN-Based Method of Vehicle Detection from Aerial Images Using Hard Example Mining
Abstract
:1. Introduction
2. Methodology
2.1. Basic Methodology
2.1.1. Vehicle Detection Methodology
- Threshold a test image by pixel intensity greater than 60 or less than 100 and calculate gradient images, yielding three gradient images (Figure 2).
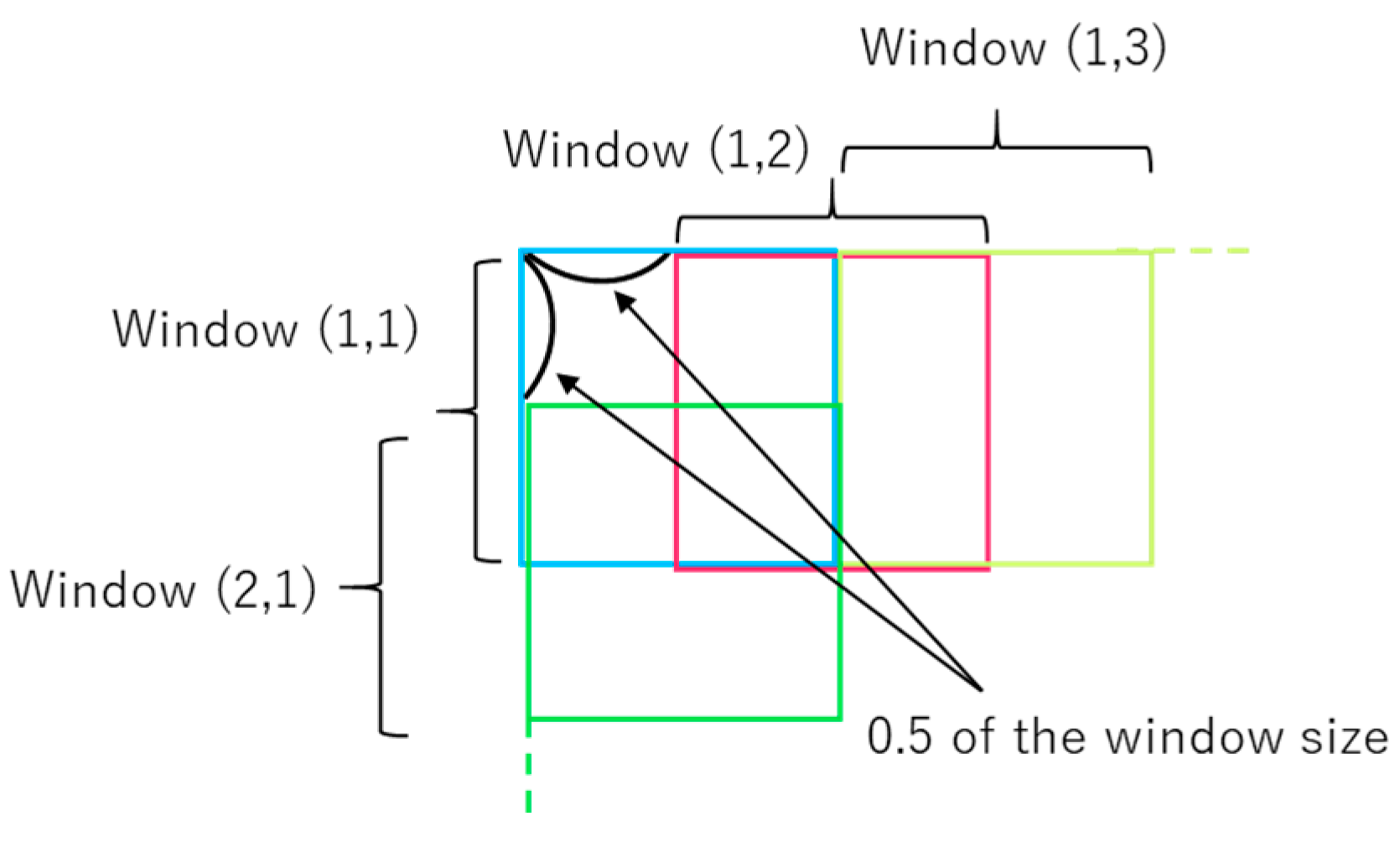
- Generate sliding windows that overlap each other on half of width and height (Figure 3).
- Move centers of the windows to geometric centers, which represent possible positions of objects in windows. Geometric centers are calculated as Equation (1):where is a vector which express a pixel position of a geometric center; and are the width and height of a window patch, respectively (both are equal to the window size); vector is a pixel position ; is a gradient intensity value of a pixel and is the sum of the gradient intensity values at all pixels in a window patch (Figure 4a,b).
- Enlarge them by a factor of , and move them to the new geometric centers (Figure 4c,d).
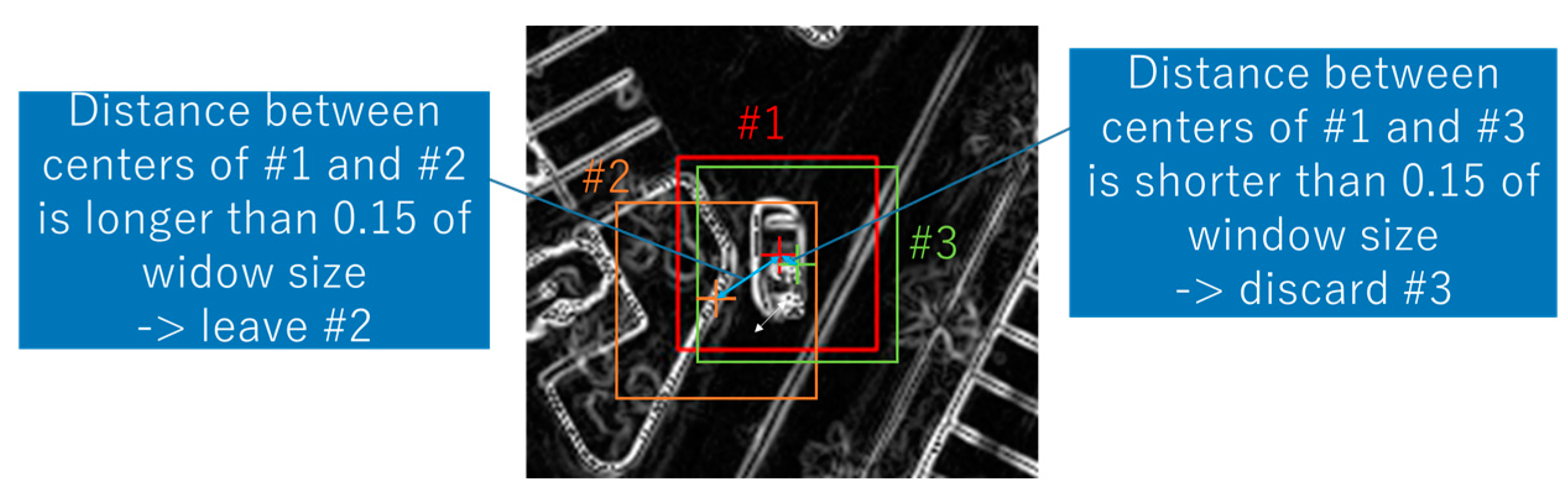
- Discard unnecessary windows that were close to the others. We regarded the windows whose centers were within a distance of 0.15 of window size as unnecessary (Figure 5).
- Apply a CNN to RGB pixels in the windows remaining after the above steps.
- Examine if the windows had overlapping windows with more than 0.5 of IoU from the highest probability of vehicle existence to the lowest. If a window had overlapping windows, the overlapping windows were discarded (this is called non-maximum-suppression).
2.1.2. Stochastic Gradient Descent (SGD) and Room for Improvement
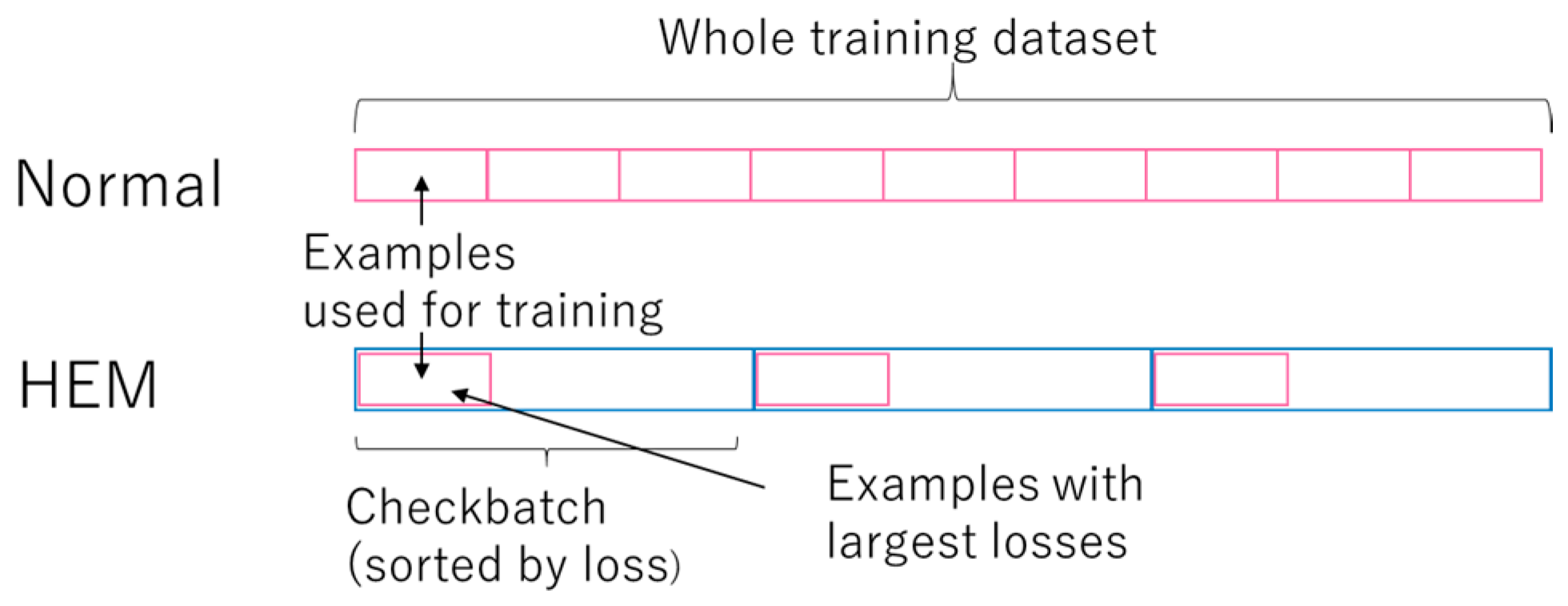
2.2. Hard Example Mining (HEM) in SGD Training
| Algorithm 1: Hard example mining in SGD |
| Input: Training dataset D, nlearn, ncheck, epochs, classifier Output: Trained classifier Initialize variables of For e = 1 to epochs: Shuffle D Split D into size(D)/ncheck checkbatches For each checkbatch: Compute loss values of examples in the checkbatch by Sort the examples in the checkbatch by loss values in descending order Train using the top nlearn examples |
2.3. Accuracy Assesment
2.3.1. Vehicle Detection Criteria
2.3.2. Quantitative Measure
3. Experiment and Results
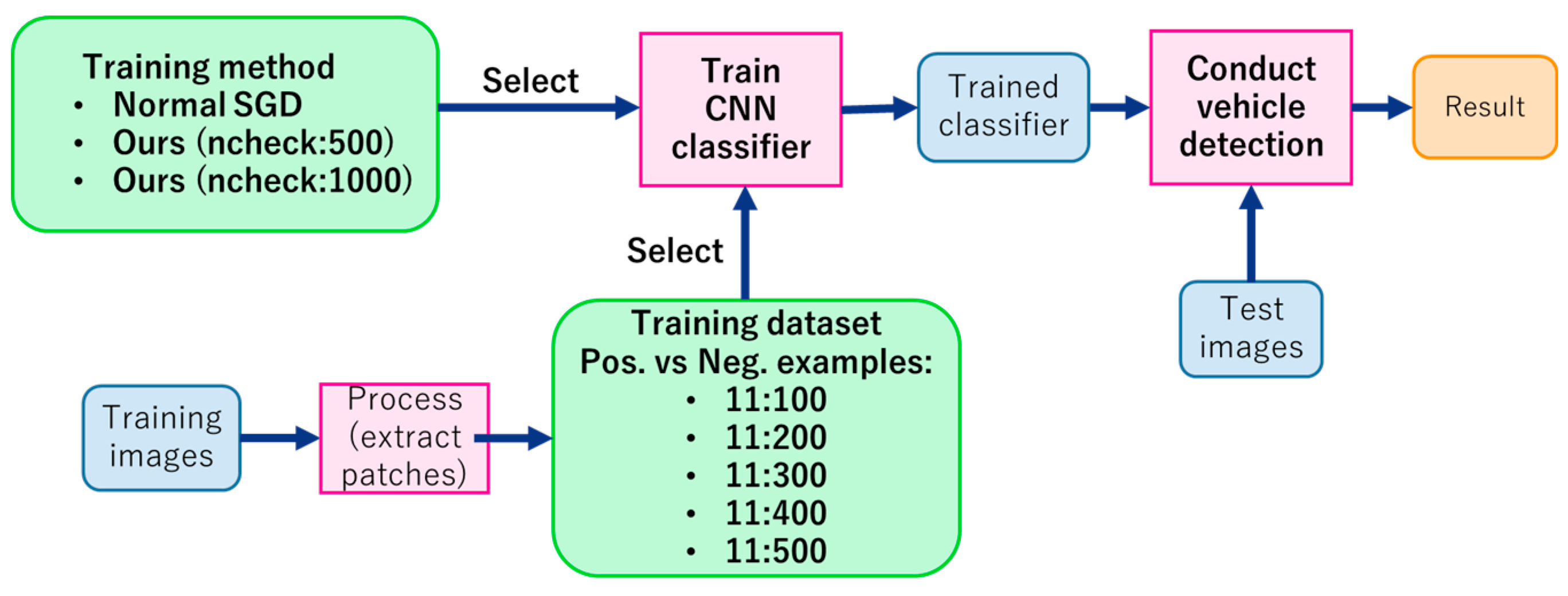
3.1. Training and Test Images
3.2. Data Preparation
3.3. Experiment
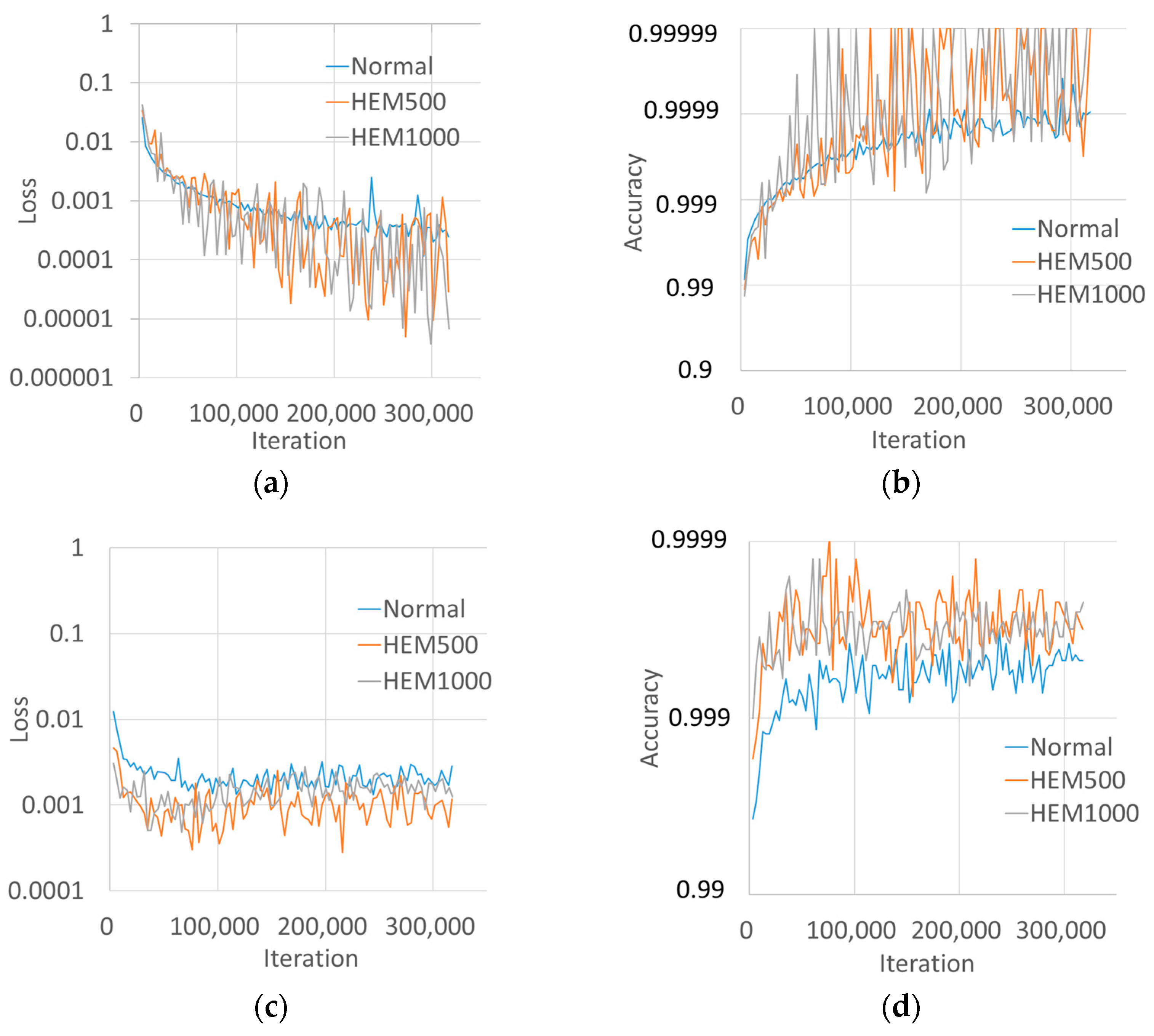
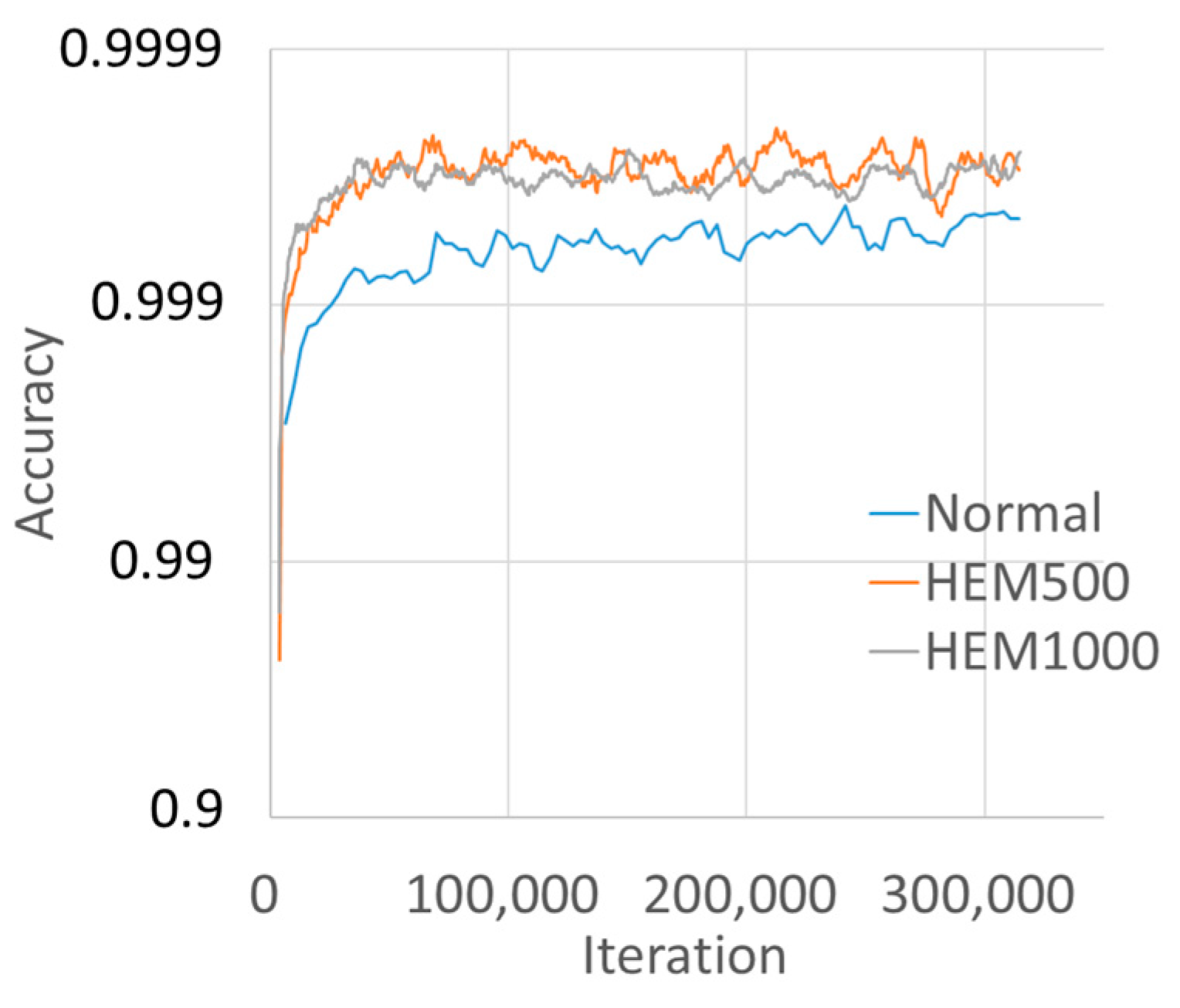
3.4. Training Results
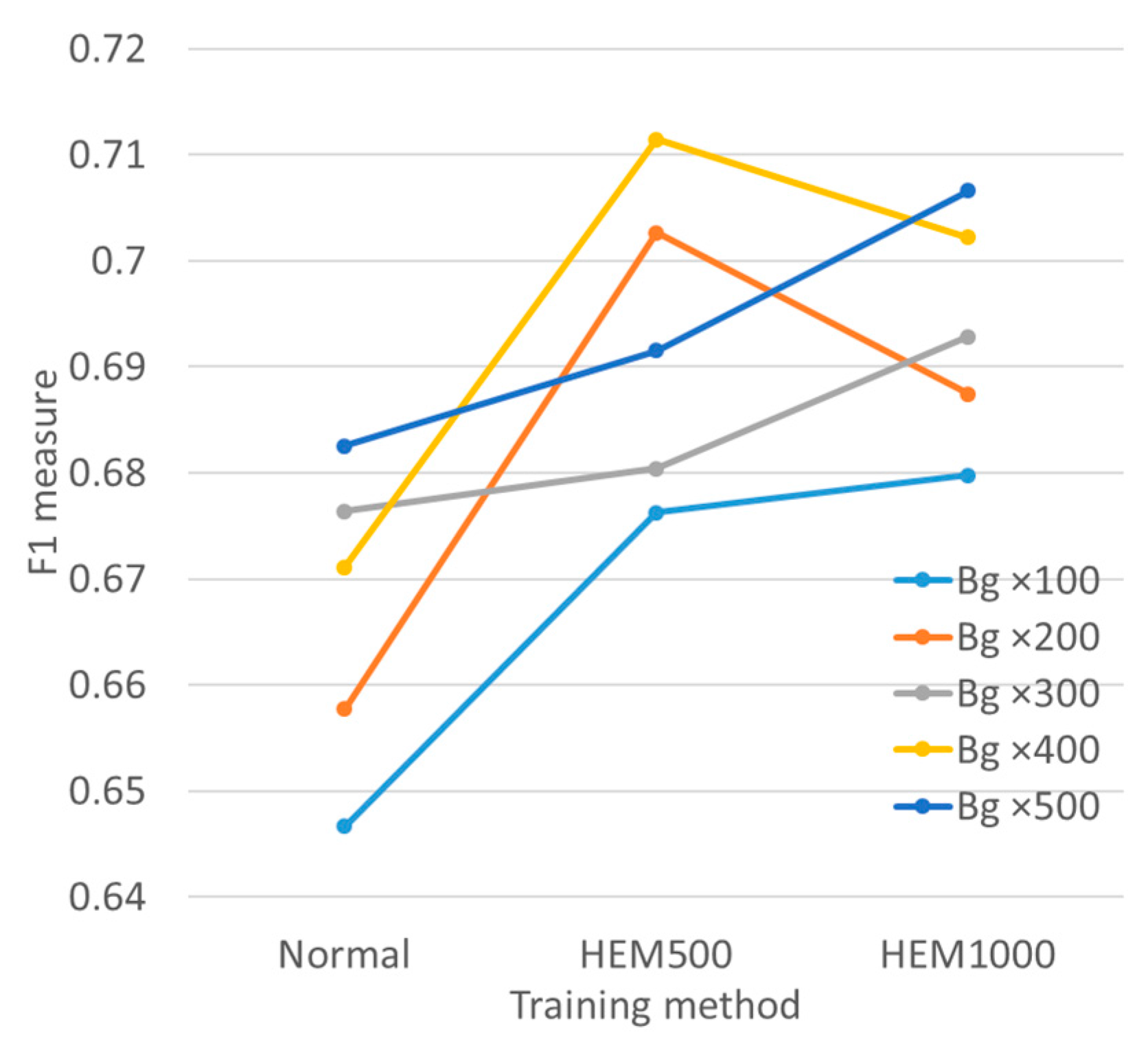
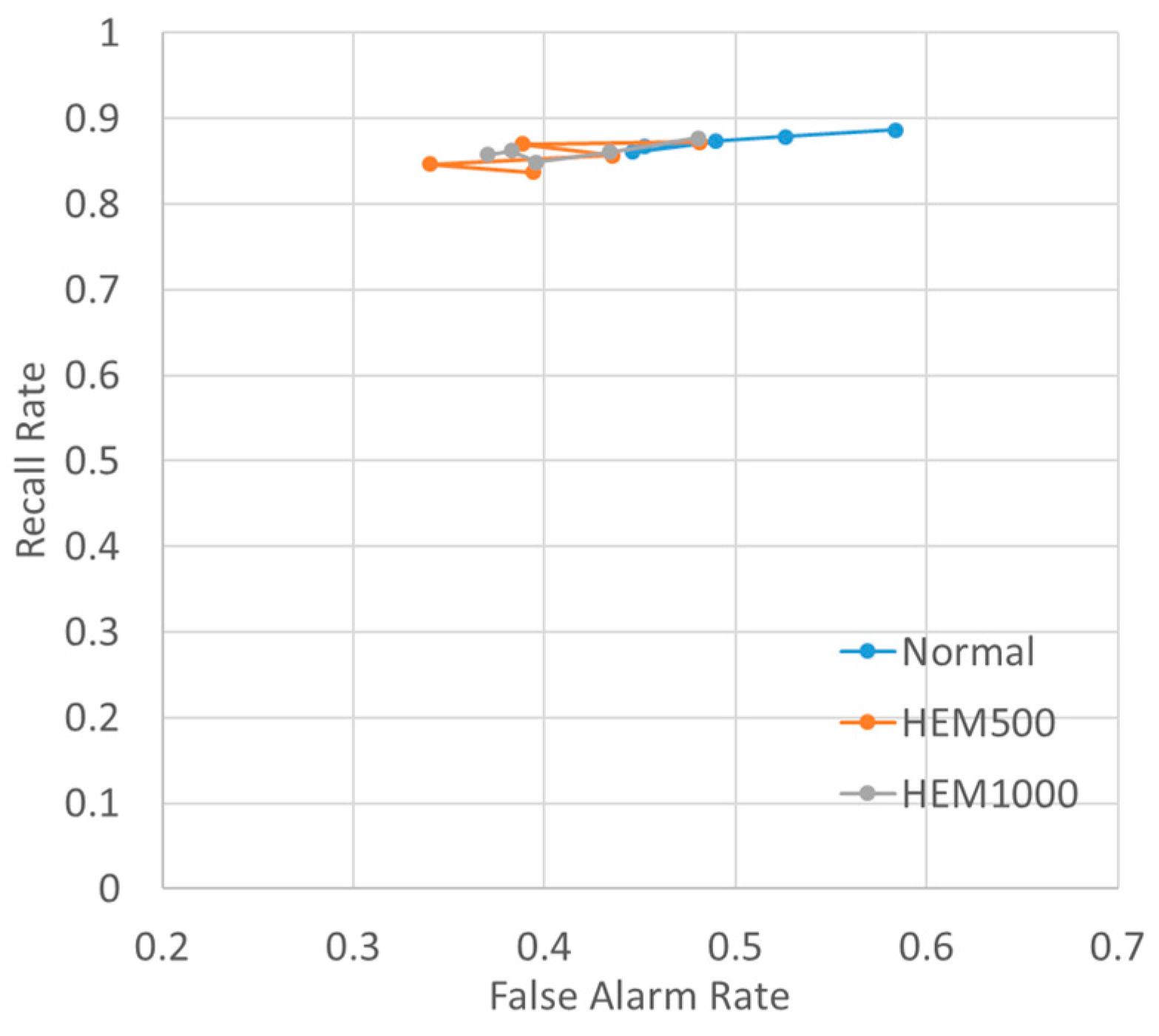
3.5. Vehicle Detection Results
4. Discussion
4.1. Improvement Extent
4.2. Training Loss Values and Duration
4.3. Source of Accuracy Improvement
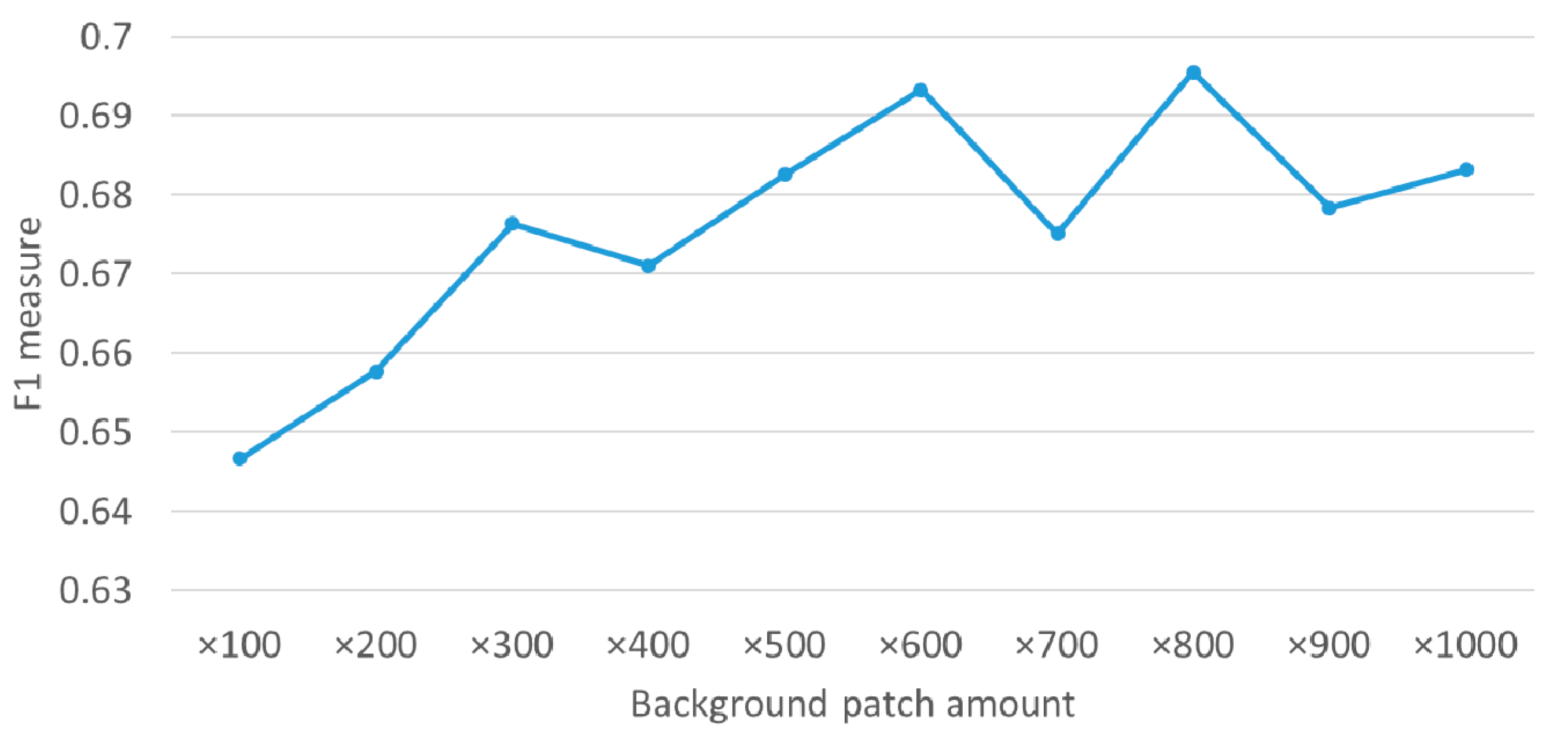
4.4. HEM500 vs. HEM1000
4.5. Usabilty of Our Method
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Effect of Clutters and Shadows


References
- Digital Globe. Available online: https://www.digitalglobe.com/ (accessed on 30 November 2017).
- Planet Labs. Available online: https://www.planet.com/ (accessed on 30 November 2017).
- Black Sky. Available online: https://www.blacksky.com/ (accessed on 30 November 2017).
- NTT Geospace. Available online: http://www.ntt-geospace.co.jp/ (accessed on 30 November 2017).
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR’14), Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Uijlings, J.R.R.; Sande, K.E.A.v.d.; Gevers, T.; Smeulders, A.W.M. Selective Search for Object Recognition. Int. J. Comput. Vis. 2013, 104, 154–171. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV’15), Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef] [PubMed]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NIPS’15), Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Lecture Notes in Computer Science, Proceedings of the ECCV 2016: Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Cham, Switzerland, 2016; Volume 9905, pp. 21–37. [Google Scholar] [CrossRef]
- Chen, X.; Xiang, S.; Liu, C.L.; Pan, C.H. Vehicle Detection in Satellite Images by Hybrid Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1797–1801. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar] [CrossRef]
- Qu, S.; Wang, Y.; Meng, G.; Pan, C. Vehicle Detection in Satellite Images by Incorporating Objectness and Convolutional Neural Network. J. Ind. Intell. Inf. 2016, 4, 158–162. [Google Scholar] [CrossRef]
- Cheng, M.M.; Zhang, Z.; Lin, W.Y.; Torr, P. BING: Binarized Normed Gradients for Objectness Estimation at 300fps. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 3286–3293. [Google Scholar] [CrossRef]
- Tang, T.; Zhou, S.; Deng, Z.; Zou, H.; Lei, L. Vehicle Detection in Aerial Images Based on Region Convolutional Neural Networks and Hard Negative Example Mining. Sensors 2017, 17, 336. [Google Scholar] [CrossRef] [PubMed]
- Car Localization and Counting with Overhead Imagery, an Interactive Exploration. Available online: https://medium.com/the-downlinq/car-localization-and-counting-with-overhead-imagery-an-interactive-exploration-9d5a029a596b (accessed on 27 July 2017).
- Mundhenk, T.N.; Konjevod, G.; Sakla, W.A.; Boakye, K. A Large Contextual Dataset for Classification, Detection and Counting of Cars with Deep Learning. In Lecture Notes in Computer Science, Proceedings of the ECCV 2016: Computer Vision—ECCV 2016, Amsterdam, The Netherlands, 8–16 October 2016; Springer: Cham, Switzerland, 2016; Volume 9907, pp. 785–800. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Schapire, R.E.; Singer, Y. Improved Boosting Algorithms Using Confidence-rated Predictions. Mach. Learn. 1999, 37, 297–336. [Google Scholar] [CrossRef]
- Shrivastava, A.; Gupta, A.; Girshick, R. Training Region-Based Object Detectors with Online Hard Example Mining. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 761–769. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning (ICML’15), Lille, France, 6–11 July 2015; Volume 37, pp. 448–456. [Google Scholar]
- CS231n: Convolutional Neural Networks for Visual Recognition. Available online: http://cs231n.github.io/optimization-1/#gd (accessed on 27 July 2017).
- UFLDL Tutorial. Available online: http://ufldl.stanford.edu/tutorial/supervised/OptimizationStochasticGradientDescent/ (accessed on 27 July 2017).
- Neural Networks and Deep Learning (CHAPTER 2). Available online: http://neuralnetworksanddeeplearning.com/chap2.html (accessed on 27 July 2017).
- Felzenszwalb, P.F.; Girshick, R.B.; McAllester, D.; Ramanan, D. Object Detection with Discriminatively Trained Part-Based Models. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1627–1645. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv, 2014; arXiv:1412.6980v9. [Google Scholar]
- Liu, K.; Mattyus, G. DLR 3k Munich Vehicle Aerial Image Dataset. Available online: http://pba-freesoftware.eoc.dlr.de/3K_VehicleDetection_dataset.zip (accessed on 30 November 2017).





| Training Images | Test Images | |||
|---|---|---|---|---|
 |  |  |  | |
| Name | train_1 | train_2 | test_1 | test_2 |
| City | New York | New York | ||
| Feature | Harbor | Mall | Harbor | Mall |
| Area | 0.16 km2 | 0.08 km2 | 0.16 km2 | 0.12 km2 |
| Vehicle | 687 | 821 | 806 | 510 |
| Training Method | ||||
|---|---|---|---|---|
| Normal | HEM500 | HEM1000 | ||
| BG patch amount | ×100 | (×100, Normal) | (×100, HEM500) | (×100, HEM1000) |
| ×200 | (×200, Normal) | (×200, HEM500) | (×200, HEM1000) | |
| ×300 | (×300, Normal) | (×300, HEM500) | (×300, HEM1000) | |
| ×400 | (×400, Normal) | (×400, HEM500) | (×400, HEM1000) | |
| ×500 | (×500, Normal) | (×500, HEM500) | (×500, HEM1000) | |
| BG Patch | Training Method | Last Validation Loss | Last Validation Accuracy | ||||
|---|---|---|---|---|---|---|---|
| Average | STDDEV | STDERR | Average | STDDEV | STDERR | ||
| ×100 | Normal | 0.0031 | 0.0006 | 0.0002 | 99.932% | 0.013% | 0.004% |
| HEM500 | 0.0030 | 0.0005 | 0.0002 | 99.950% | 0.005% | 0.002% | |
| HEM1000 | 0.0036 | 0.0008 | 0.0003 | 99.949% | 0.014% | 0.005% | |
| ×200 | Normal | 0.0016 | 0.0004 | 0.0001 | 99.957% | 0.008% | 0.003% |
| HEM500 | 0.0015 | 0.0005 | 0.0002 | 99.973% | 0.006% | 0.002% | |
| HEM1000 | 0.0013 | 0.0002 | 0.0001 | 99.973% | 0.002% | 0.001% | |
| ×300 | Normal | 0.0019 | 0.0003 | 0.0001 | 99.963% | 0.007% | 0.002% |
| HEM500 | 0.0022 | 0.0005 | 0.0002 | 99.974% | 0.006% | 0.002% | |
| HEM1000 | 0.0022 | 0.0004 | 0.0001 | 99.973% | 0.003% | 0.001% | |
| ×400 | Normal | 0.0016 | 0.0003 | 0.0001 | 99.969% | 0.004% | 0.001% |
| HEM500 | 0.0017 | 0.0002 | 0.0001 | 99.978% | 0.003% | 0.001% | |
| HEM1000 | 0.0016 | 0.0003 | 0.0001 | 99.981% | 0.003% | 0.001% | |
| ×500 | Normal | 0.0011 | 0.0002 | 0.0001 | 99.978% | 0.003% | 0.001% |
| HEM500 | 0.0010 | 0.0002 | 0.0001 | 99.986% | 0.003% | 0.001% | |
| HEM1000 | 0.0011 | 0.0002 | 0.0001 | 99.986% | 0.002% | 0.001% | |
| BG Patch | Training Method | FAR | PR | RR | F1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Avr. | STDDEV | STDERR | Avr. | STDDEV | STDERR | Avr. | STDDEV | STDERR | Avr. | STDDEV | STDERR | ||
| ×100 | Normal | 0.584 | 0.109 | 0.036 | 0.511 | 0.041 | 0.014 | 0.887 | 0.033 | 0.011 | 0.647 | 0.028 | 0.009 |
| HEM500 | 0.481 | 0.104 | 0.035 | 0.554 | 0.042 | 0.014 | 0.873 | 0.027 | 0.009 | 0.676 | 0.028 | 0.009 | |
| HEM1000 | 0.480 | 0.099 | 0.033 | 0.556 | 0.042 | 0.014 | 0.877 | 0.012 | 0.004 | 0.680 | 0.030 | 0.010 | |
| ×200 | Normal | 0.526 | 0.073 | 0.024 | 0.527 | 0.031 | 0.010 | 0.879 | 0.030 | 0.010 | 0.658 | 0.019 | 0.006 |
| HEM500 | 0.388 | 0.056 | 0.019 | 0.590 | 0.027 | 0.009 | 0.870 | 0.017 | 0.006 | 0.703 | 0.016 | 0.005 | |
| HEM1000 | 0.434 | 0.066 | 0.022 | 0.573 | 0.031 | 0.010 | 0.861 | 0.017 | 0.006 | 0.687 | 0.020 | 0.007 | |
| ×300 | Normal | 0.452 | 0.091 | 0.030 | 0.555 | 0.031 | 0.010 | 0.868 | 0.014 | 0.005 | 0.676 | 0.021 | 0.007 |
| HEM500 | 0.435 | 0.071 | 0.024 | 0.566 | 0.038 | 0.013 | 0.857 | 0.029 | 0.010 | 0.680 | 0.021 | 0.007 | |
| HEM1000 | 0.396 | 0.066 | 0.022 | 0.587 | 0.041 | 0.014 | 0.849 | 0.022 | 0.007 | 0.693 | 0.027 | 0.009 | |
| ×400 | Normal | 0.490 | 0.127 | 0.042 | 0.547 | 0.050 | 0.017 | 0.873 | 0.018 | 0.006 | 0.671 | 0.036 | 0.012 |
| HEM500 | 0.340 | 0.081 | 0.027 | 0.616 | 0.049 | 0.016 | 0.847 | 0.027 | 0.009 | 0.711 | 0.024 | 0.008 | |
| HEM1000 | 0.383 | 0.062 | 0.021 | 0.593 | 0.032 | 0.011 | 0.862 | 0.020 | 0.007 | 0.702 | 0.021 | 0.007 | |
| ×500 | Normal | 0.446 | 0.063 | 0.021 | 0.566 | 0.030 | 0.010 | 0.861 | 0.025 | 0.008 | 0.683 | 0.024 | 0.008 |
| HEM500 | 0.394 | 0.094 | 0.031 | 0.591 | 0.047 | 0.016 | 0.837 | 0.023 | 0.008 | 0.692 | 0.030 | 0.010 | |
| HEM1000 | 0.370 | 0.050 | 0.017 | 0.601 | 0.024 | 0.008 | 0.858 | 0.013 | 0.004 | 0.707 | 0.016 | 0.005 | |
| Image | Method | Improvement | |
|---|---|---|---|
| Normal | HEM500 | ||
| test_1 | 0.83 | 0.82 | −0.01 |
| test_2 | 0.54 | 0.61 | 0.07 |
| Both | 0.67 | 0.71 | 0.04 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koga, Y.; Miyazaki, H.; Shibasaki, R. A CNN-Based Method of Vehicle Detection from Aerial Images Using Hard Example Mining. Remote Sens. 2018, 10, 124. https://doi.org/10.3390/rs10010124
Koga Y, Miyazaki H, Shibasaki R. A CNN-Based Method of Vehicle Detection from Aerial Images Using Hard Example Mining. Remote Sensing. 2018; 10(1):124. https://doi.org/10.3390/rs10010124
Chicago/Turabian StyleKoga, Yohei, Hiroyuki Miyazaki, and Ryosuke Shibasaki. 2018. "A CNN-Based Method of Vehicle Detection from Aerial Images Using Hard Example Mining" Remote Sensing 10, no. 1: 124. https://doi.org/10.3390/rs10010124
APA StyleKoga, Y., Miyazaki, H., & Shibasaki, R. (2018). A CNN-Based Method of Vehicle Detection from Aerial Images Using Hard Example Mining. Remote Sensing, 10(1), 124. https://doi.org/10.3390/rs10010124







