Spatial Club Convergence of Regional Economic Growth in Inland China
Abstract
:1. Introduction
2. The Hypothesis of Spatial Club Convergence
2.1. The Limitations of the Theory of Classical (Temporal) Club Convergence
2.2. The Basic Idea of the Hypothesis of Spatial Club Convergence
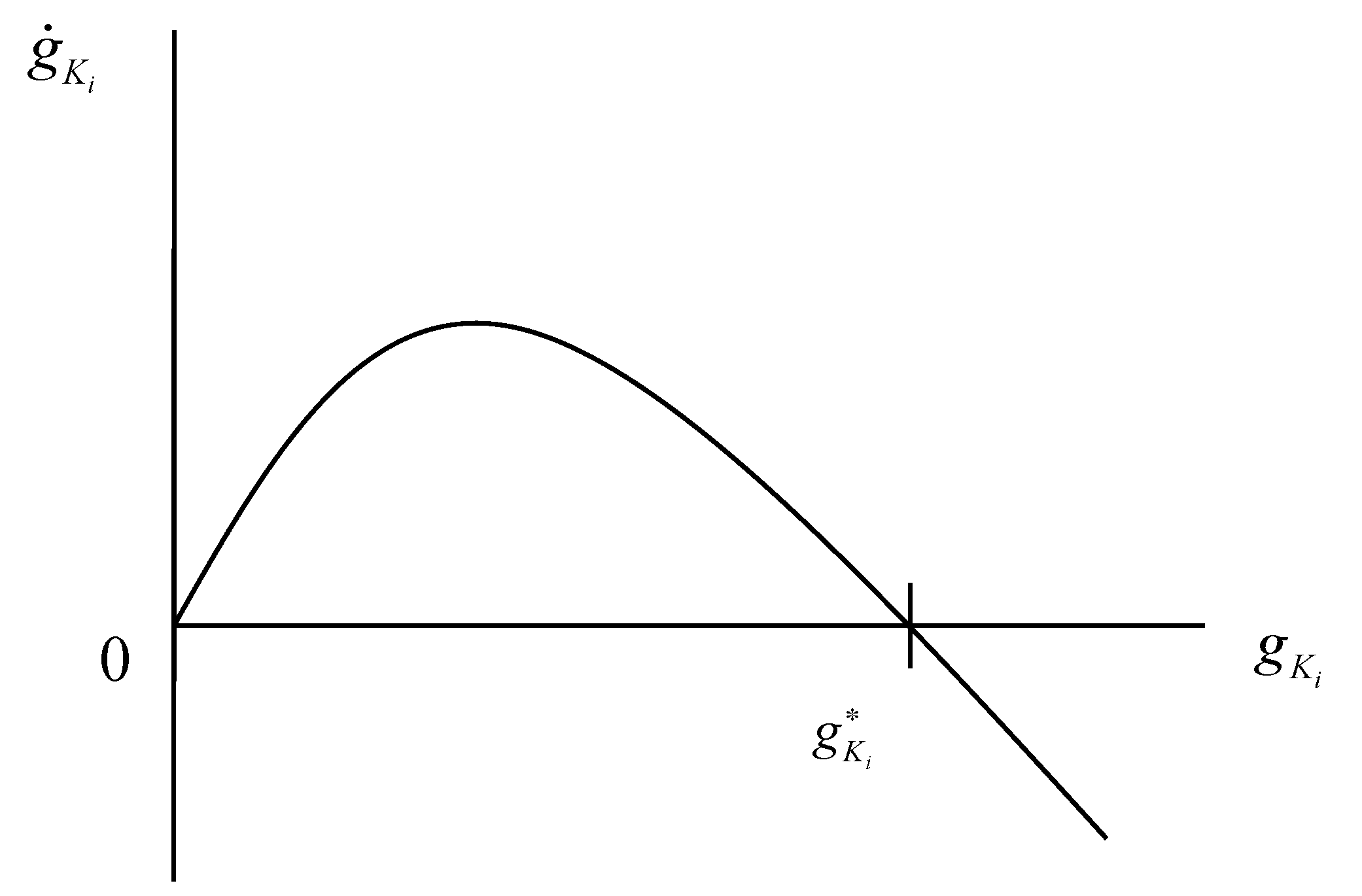
2.3. The Theoretical Model of Spatial Club Convergence
3. An Test of the Hypothesis of Spatial Club Convergence
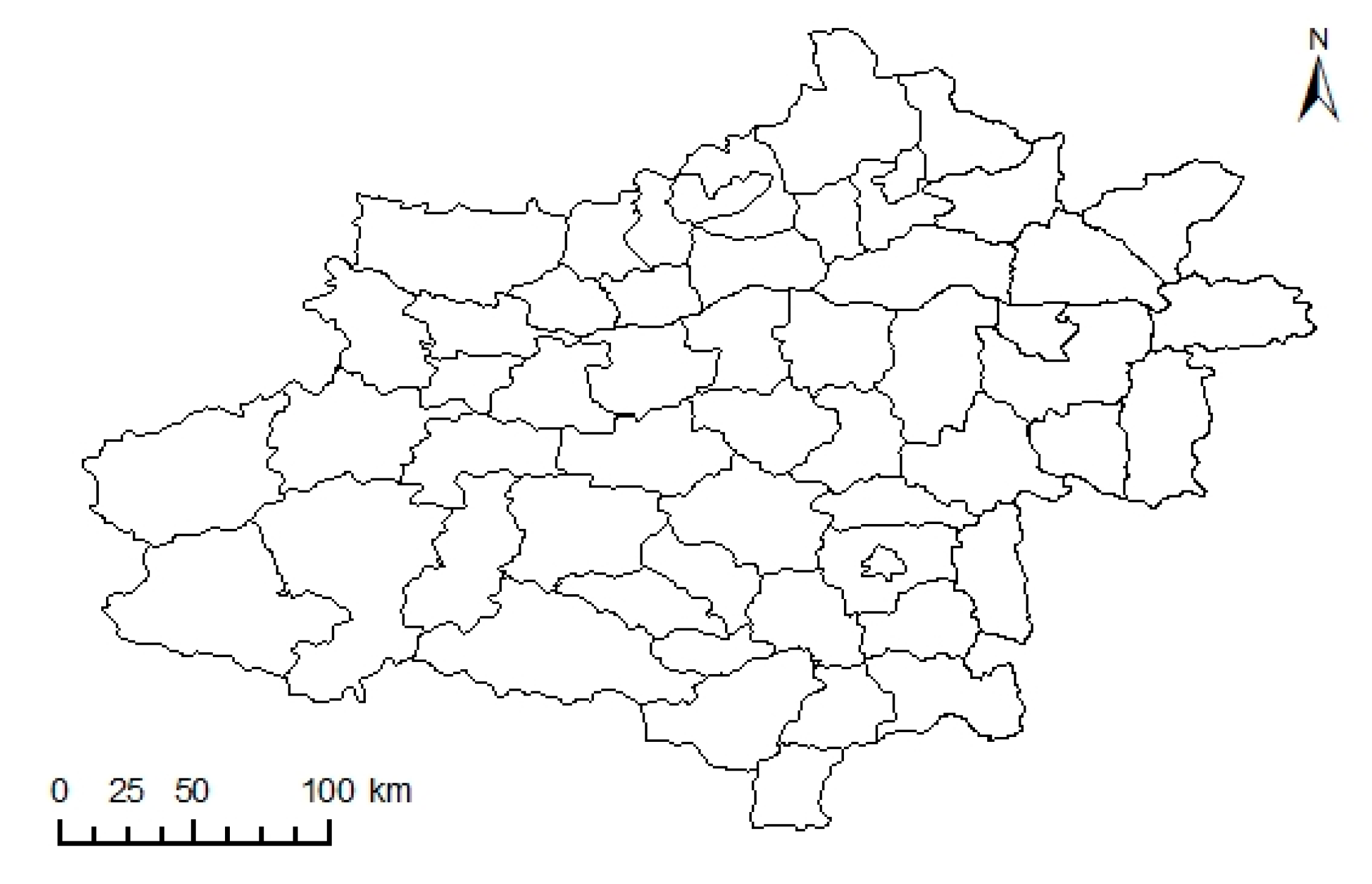
3.1. Regions
3.2. Data
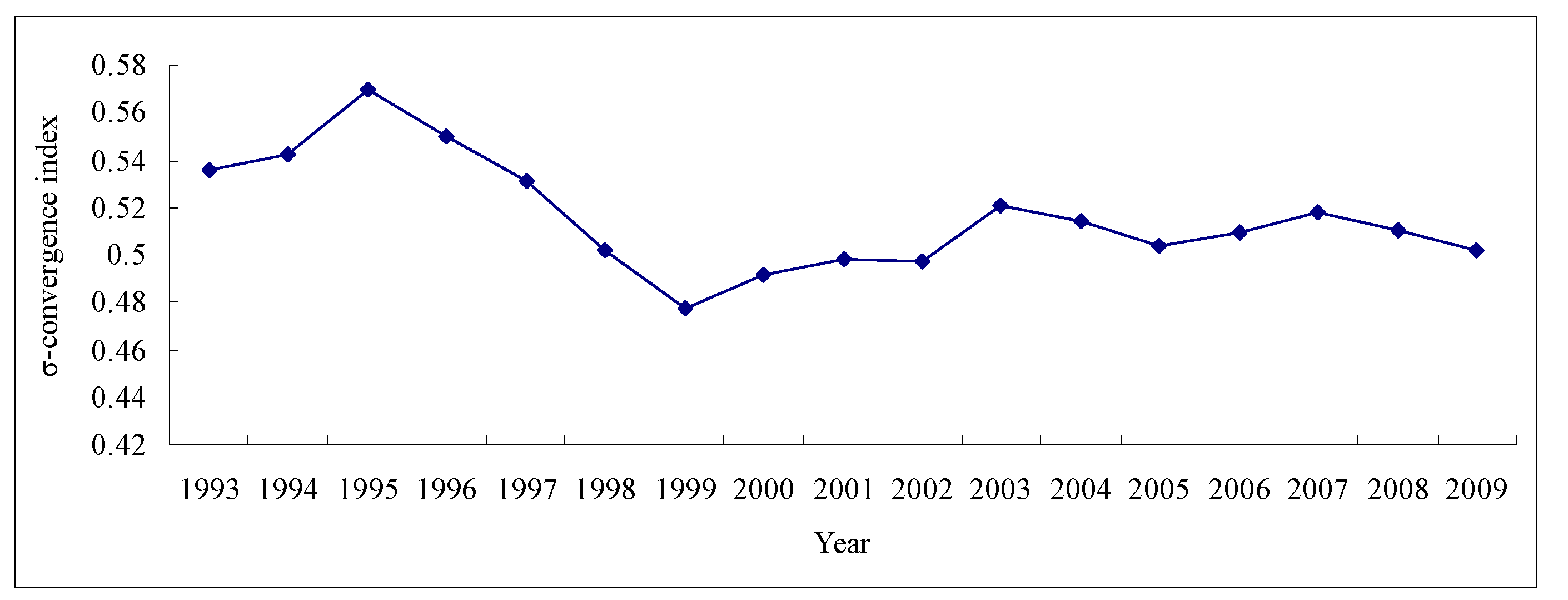
3.3. Test of the Hypothesis of Spatial Club Convergence
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wei, Y.D.; Ye, X. Beyond Convergence: Space, Scale, and Regional Inequality in China. Tijdschr. Econ. Soc. Geogr. 2009, 100, 59–80. [Google Scholar] [CrossRef]
- Fischer, M.M.; Stirböck, C. Pan-European regional income growth and club-convergence insights from a spatial econometric perspective. Ann. Reg. Sci. 2006, 40, 693–721. [Google Scholar] [CrossRef]
- Ye, X.; Wei, Y.D. Regional Development, Disparities and Polices in Globalizing Asia. Reg. Sci. Policy Pract. 2012, 4, 179–182. [Google Scholar] [CrossRef]
- Postiglione, P.; Andreano, M.S.; Benedetti, R. Using constrained optimization for the identification of convergence clubs. Comput. Econ. 2013, 42, 151–174. [Google Scholar] [CrossRef]
- Lim, U. Regional income club convergence in US BEA economic areas: A spatial switching regression approach. Ann. Reg. Sci. 2016, 56, 273–294. [Google Scholar] [CrossRef]
- Ye, X.; Rey, S.J. A Framework for Exploratory Space-Time Analysis of Economic Data. Ann. Reg. Sci. 2013, 50, 315–339. [Google Scholar] [CrossRef]
- Laurini, M.; Andrade, E.; Valls Pereira, P.L. Income convergence clubs for Brazilian municipalities: A non-parametric analysis. Appl. Econ. 2005, 37, 2099–2118. [Google Scholar] [CrossRef]
- Dall’erba, S.; Le Gallo, J. Regional convergence and the impact of European structural funds over 1989–1999: A spatial econometric analysis. Pap. Reg. Sci. 2008, 87, 219–244. [Google Scholar] [CrossRef]
- Olejnik, A. Using the spatial autoregressively distributed lag model in assessing the regional convergence of per-capita income in the EU25. Pap. Reg. Sci. 2008, 87, 371–384. [Google Scholar] [CrossRef]
- Pfaffermayr, M. Conditional β and σ-convergence in space: A maximum likelihood approach. Reg. Sci. Urban Econ. 2009, 39, 63–78. [Google Scholar] [CrossRef]
- Ye, X.; Yue, W. Comparative Analysis of Regional Development: Exploratory Space-Time Data Analysis and Open Source Implementation. Economics. 2014. Available online: http://www.economics-ejournal.org/economics/discussionpapers/2014-20 (accessed on 25 June 2017).
- Ertur, C.; Koch, W. Growth, technological interdependence and spatial externalities: Theory and evidence. J. Appl. Econom. 2007, 22, 1033–1062. [Google Scholar] [CrossRef]
- Fischer, M.M. A spatial Mankiw-Romer-Weil model: Theory and evidence. Ann. Reg. Sci. 2011, 47, 419–436. [Google Scholar] [CrossRef]
- Liu, Y.X.; Qin, C.L. Research of regional economic growth spatial convergence hypothesis. Econ. Perspect. 2010, 2, 99–103. [Google Scholar]
- Abreu, M.; De Groot, H.L.F.; Florax, R.J.G.M. Space and growth: A survey of empirical evidence and methods. Rég. Dév. 2005, 21, 13–44. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Y.H.D. Multidimensional Inequalities in Health Care Distribution in Provincial China: A Case Study of Henan Province. Tijdschr. Econ. Soc. Geogr. 2014, 105, 91–106. [Google Scholar] [CrossRef]
- Lemoine, F.; Poncet, S.; Ünal, D. Spatial rebalancing and industrial convergence in China. China Econ. Rev. 2015, 34, 39–63. [Google Scholar] [CrossRef]
- Barro, R.J.; Sala-i-Martin, X. Convergence across states and regions. Brook Pap. Econ. Act. 1991, 1991, 107–182. [Google Scholar] [CrossRef]
- Qin, C.L.; Zhang, W.L. Test and factor analysis of the club convergence of regional economic growth in China: Based on the information of regional grouping by CART. Manag. World. 2009, 3, 21–35. [Google Scholar]
- Cheng, J.; Dai, S.; Ye, X. Spatiotemporal heterogeneity of industrial pollution in China. China. Econ. Rev. 2016, 40, 179–191. [Google Scholar] [CrossRef]
- Fujita, M.; Krugman, P.; Venables, A. The Spatial Economy: Cities, Regions, and International Trade; MIT Press: Cambridge, UK, 1999. [Google Scholar]
- Dall’erba, S. Productivity convergence and spatial dependence among Spanish regions. J. Geogr. Syst. 2005, 7, 207–227. [Google Scholar] [CrossRef]
- Qin, C.L.; Tang, Y. Club convergence of regional economic growth in Henan Province. Geogr. Res. 2007, 26, 548–556. [Google Scholar]
- Qin, C.L.; Zhang, W.L. Review of regional economic growth club convergence. Econ. Perspect. 2008, 3, 103–108. [Google Scholar]
- Quah, D. Galton’s fallacy and tests of the convergence hypothesis. Scand. J. Econ. 1993, 95, 427–443. [Google Scholar] [CrossRef]
- Quah, D. Empirics for economic growth and convergence. Eur. Econ. Rev. 1996, 40, 1353–1375. [Google Scholar] [CrossRef]
- Quah, D. Twin peaks: Growth and convergence in models of distribution dynamics. Econ. J. 1996, 106, 1045–1055. [Google Scholar] [CrossRef]
- BernadiniPapalia, R.; Bertarelli, S. Identification and Estimation of Club Convergence Models with Spatial Dependence. Int. J. Urban Reg. Res. 2013, 37, 2094–2115. [Google Scholar] [CrossRef]
- Pan, X.; Liu, Q.; Peng, X. Spatial club convergence of regional energy efficiency in China. Ecol. Indic. 2015, 51, 25–30. [Google Scholar] [CrossRef]
- Rumayya, W.W.; Erlangga, A.L. Club convergence & regional spillovers in East JAVA. Reg. Econ. Dev. 2005, 17, 1315–1445. [Google Scholar]
- Egger, P.; Pfaffermayr, M. Spatial convergence. Pap. Reg. Sci. 2006, 85, 199–215. [Google Scholar] [CrossRef]
- Barro, R.J.; Sala-i-Martin, X. Convergence. J. Polit. Econ. 1992, 100, 223–251. [Google Scholar] [CrossRef]
- Barro, R.J.; Mankiw, N.G.; Sala-i-Martin, X. Capital mobility in neoclassical models of growth. Am. Econ. Rev. 1995, 85, 103–115. [Google Scholar]
- Lei, H. Estimating capital stock and investment efficiency in China. Economist 2009, 9, 75–83. [Google Scholar]
- Zhang, J.; Wu, G.Y.; Zhang, J.P. The estimation of China’s provincial capital stock: 1952–2000. Econ. Res. J. 2004, 39, 35–44. [Google Scholar]
- Wang, X.L.; Fan, G. Sustainability of China’s Economic Growth; Economic Science Press: Beijing, China, 2000. [Google Scholar]
- Guo, Q.W.; Jia, J.X. Estimating total factor productivity in China. Econ. Res. J. 2005, 40, 51–60. [Google Scholar]
- Zhang, X.L. Economic convergence and its effect mechanism in Yangtze River Delta Region: 1993–2006. J. World Econ. 2010, 3, 126–140. [Google Scholar]
- Zhang, Z.Q. Type of spatial Weight on Spatial Panel Parameters estimation and testing efficiency. J. Quant. Tech. Econ. 2014, 10, 122–138. [Google Scholar]
- López-Bazo, E.; Vayá, E.; Manuel, A. Regional externalities and growth: Evidence from European regions. J. Reg. Sci. 2004, 44, 43–73. [Google Scholar] [CrossRef]
| 1993–2009 | 1993–1999 | 2000–2009 | ||||
|---|---|---|---|---|---|---|
| RW | GW | RW | GW | RW | GW | |
| constant | −2.13(−1.12) | −0.14(−1.23) | −0.68(−1.04) | −0.04(−0.23) | 0.33(0.22) | −0.003(−0.02) |
| −0.17(−3.79) *** | 0.02(2.03) ** | −0.15(−3.08) *** | −0.01(0.86) | −0.19(−2.31) ** | 0.009(0.55) | |
| φ1 | 0.44(2.23) ** | −0.008(−0.39) | −0.001(−0.02) | −0.001(−0.07) | 0.28(1.71) * | 0.009(0.10) |
| φ2 | 1.74(1.44) | −0.16(−0.09) | −0.15(−0.08) | −3.12(−0.94) | 2.65(2.61) ** | 1.33(0.80) |
| φ3 | −0.43(−0.86) | −0.81(−1.32) | 0.11(0.14) | −1.09(−1.03) | −0.50(−1.29) | −0.24(−0.39) |
| φ4 | 0.39(2.88) *** | −0.02(−2.53) *** | 0.006(0.12) | −0.002(−0.15) | 0.29(2.61) ** | −0.02(−1.32) |
| φ5 | 0.64(2.98) *** | 0.03(2.77) *** | 0.41(3.33) *** | 0.01(1.07) | 0.19(0.96) | 0.02(0.95) |
| φ6 | −0.05(−0.46) | −0.01(1.18) | −0.18(3.08) *** | −0.001(−0.09) | −0.23(−2.65) ** | 0.01(0.80) |
| R2 | 0.32 | 0.19 | 0.51 | 0.09 | 0.43 | 0.07 |
| F | 4.11 | 1.62 | 7.25 | 0.73 | 4.89 | 0.56 |
| LIK | −8.79 | 127.47 | 24.15 | 103.6 | 1.96 | 103.24 |
| AIC | 33.65 | −238.94 | −32.30 | −191.2 | 12.23 | −190.48 |
| SC | 50.23 | −222.74 | −16.10 | −174.99 | 28.45 | −174.28 |
| Moran’ I | 0.22[0.48] | − | 0.15[0.38] | − | 0.21[0.46] | − |
| Breusch-Pagan | 13.42[0.08] | 4.52[0.71] | 13.50[0.06] | 4.5[0.71] | 13.31[0.07] | 3.77[0.80] |
| Jarque-Bera | 2.19[0.38] | 2.50[0.28] | 7.26[0.03] | 1.15[0.56] | 5.29[0.08] | 26.05[0.00] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, C.; Ye, X.; Liu, Y. Spatial Club Convergence of Regional Economic Growth in Inland China. Sustainability 2017, 9, 1189. https://doi.org/10.3390/su9071189
Qin C, Ye X, Liu Y. Spatial Club Convergence of Regional Economic Growth in Inland China. Sustainability. 2017; 9(7):1189. https://doi.org/10.3390/su9071189
Chicago/Turabian StyleQin, Chenglin, Xinyue Ye, and Yingxia Liu. 2017. "Spatial Club Convergence of Regional Economic Growth in Inland China" Sustainability 9, no. 7: 1189. https://doi.org/10.3390/su9071189
APA StyleQin, C., Ye, X., & Liu, Y. (2017). Spatial Club Convergence of Regional Economic Growth in Inland China. Sustainability, 9(7), 1189. https://doi.org/10.3390/su9071189





