Wind Speed for Load Forecasting Models
Abstract
:1. Introduction
2. Background
2.1. Multiple Linear Regression Models for Load Forecasting
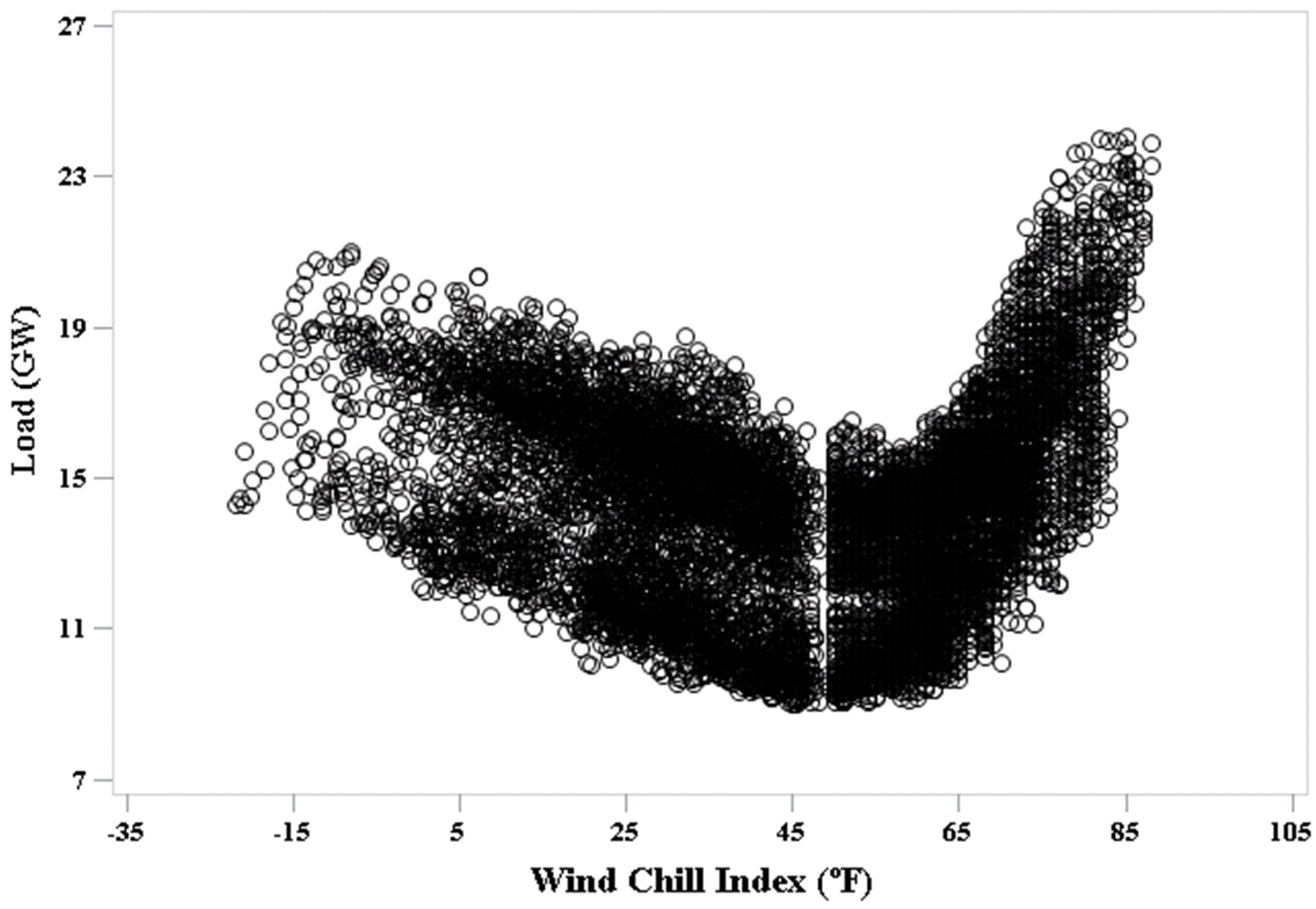
2.2. Wind Chill Index
2.3. Cross-Validation
2.4. Out-of-Sample Test
3. Data
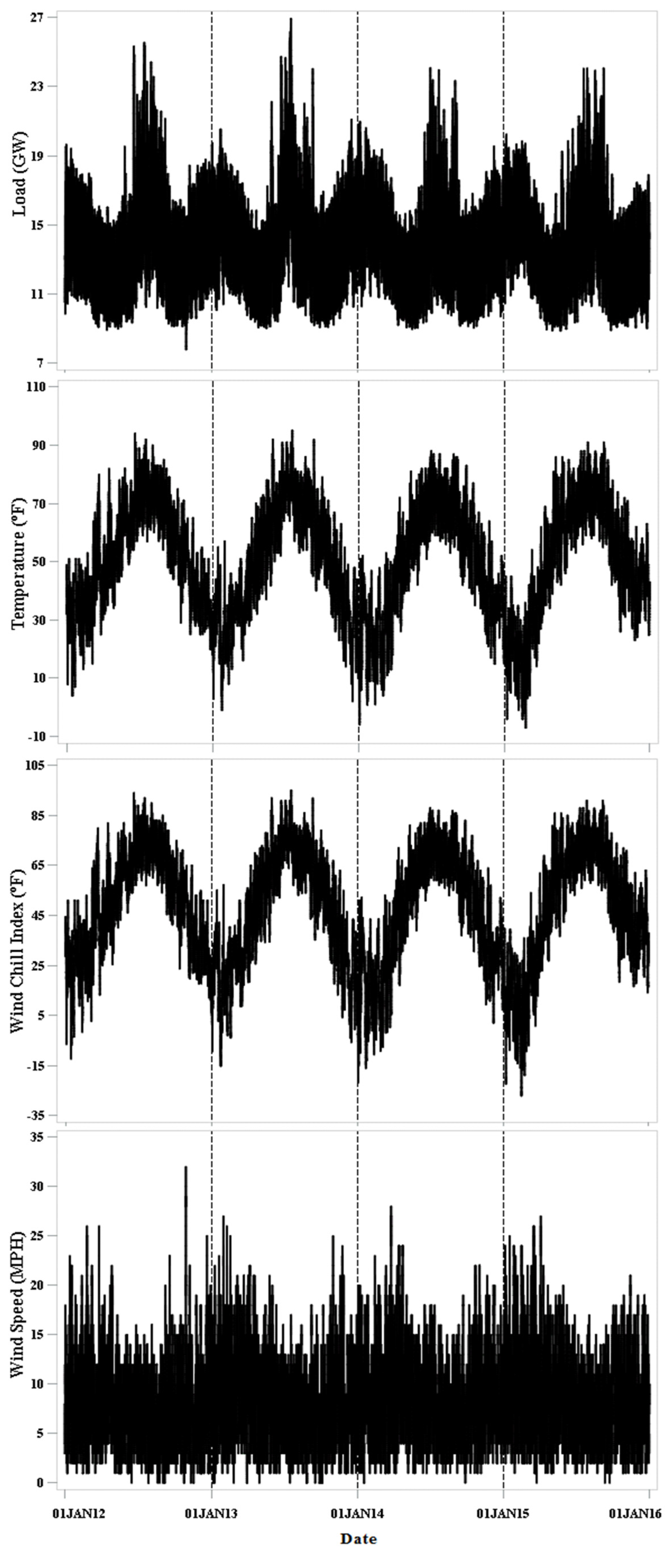
3.1. Data Description
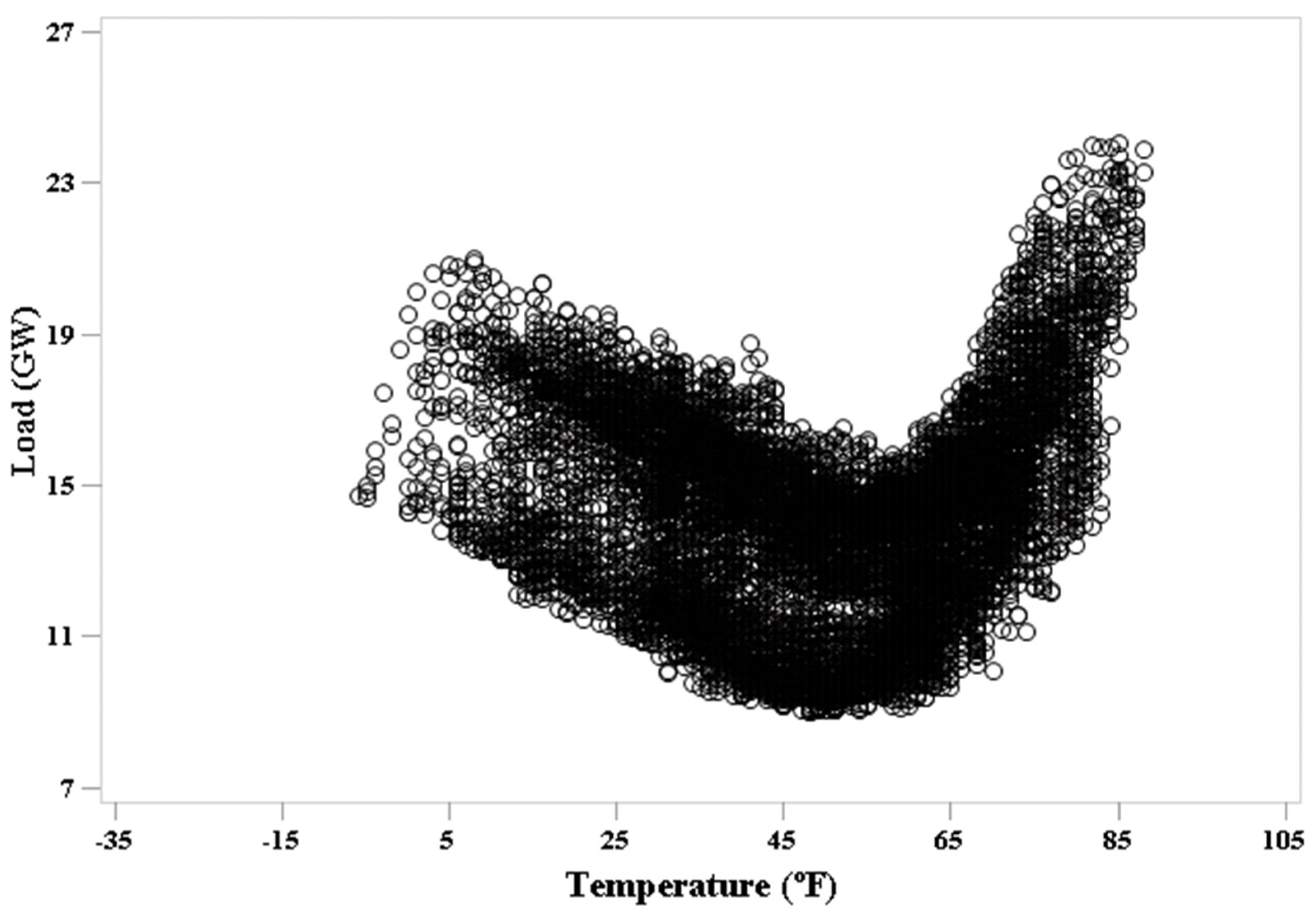
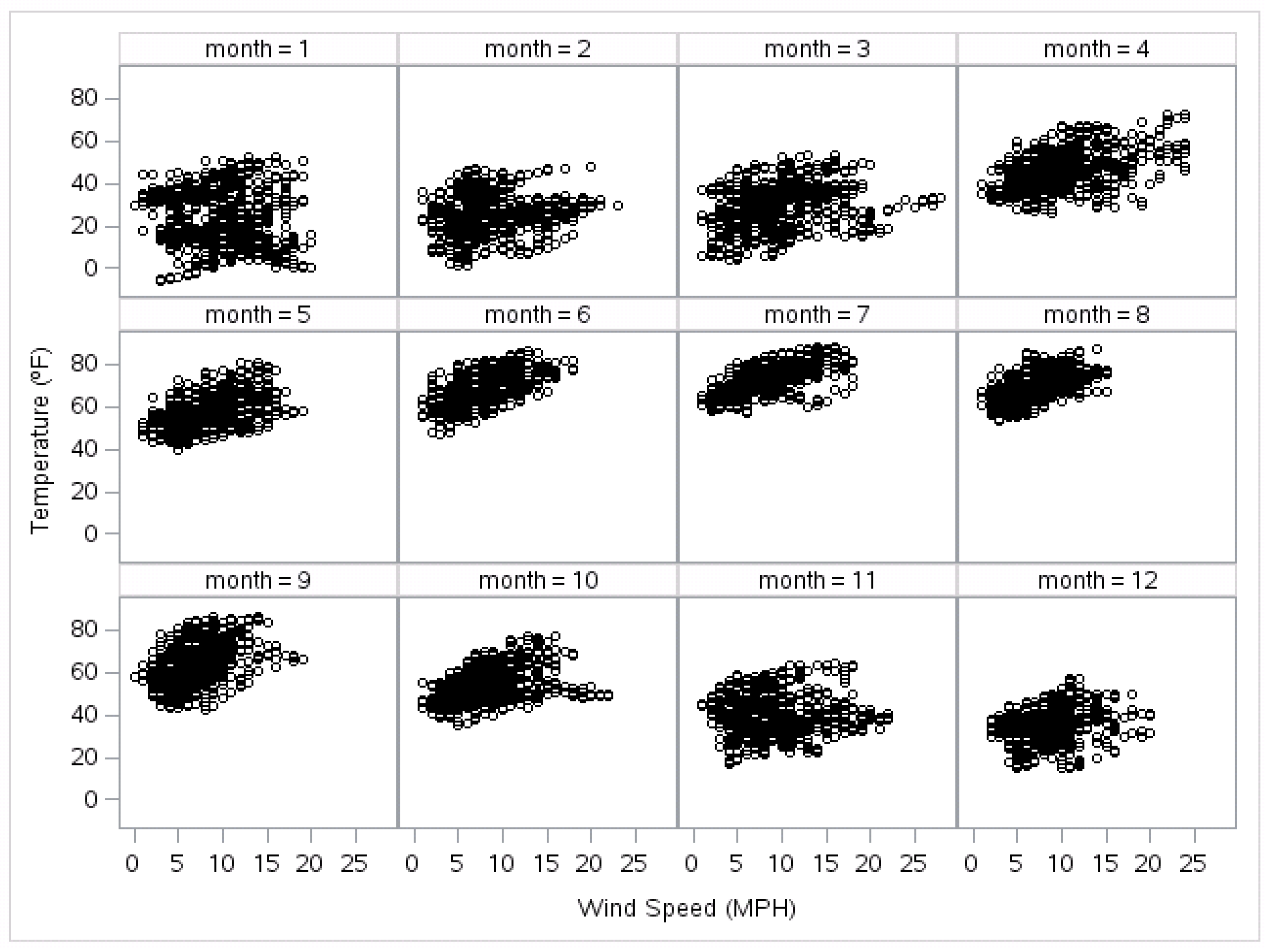
3.2. Exploratory Data Analysis
4. Models
4.1. Wind Speed-Related Variables
4.2. Two WCI-Based Models
5. Results and Discussion
5.1. Out-of-Sample Test
5.2. Ex Ante Forecasting
5.3. Future Research Directions
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Weron, R. Modeling and Forecasting Electricity Loads and Prices: A Statistical Approach; Wiley Finance: New York, NY, USA, 2006. [Google Scholar]
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 1–32. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Khotanzad, A.; Afkhami-Rohani, R. ANNSTLF—Artificial neural network short-term load forecaster-generation three. IEEE Trans. Power Syst. 1998, 13, 1413–1422. [Google Scholar] [CrossRef]
- Ramanathan, R.; Engle, R.; Granger, C.W.J.; Vahid-Araghi, F.; Brace, C. Short-run forecasts of electricity loads and peaks. Int. J. Forecast. 1997, 13, 161–174. [Google Scholar] [CrossRef]
- Chen, B.; Chang, M.; Lin, C. Load forecasting using support vector machines: A study on EUNITE competition 2001. IEEE Trans. Power Syst. 2004, 19, 1821–1830. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S. Global energy forecasting competition 2012. Int. J. Forecast. 2014, 30, 357–363. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S.; Zareipour, H.; Troccoli, A.; Hyndman, R.J. Probabilistic energy forecasting: Global Energy Forecasting Competition 2014 and beyond. Int. J. Forecast. 2016, 32, 896–913. [Google Scholar] [CrossRef]
- Xie, J.; Liu, B.; Lyu, X.; Hong, T.; Basterfield, D. Combining load forecasts from independent experts. In Proceedings of the 2015 North American Power Symposium, NAPS 2015, Charlotte, NC, USA, 4–6 October 2015. [Google Scholar]
- Xie, J.; Hong, T. GEFCom2014 probabilistic electric load forecasting: An integrated solution with forecast combination and residual simulation. Int. J. Forecast. 2015, 32, 1012–1016. [Google Scholar] [CrossRef]
- Xie, J.; Hong, T.; Stroud, J. Long-term retail energy forecasting with consideration of residential customer attrition. IEEE Trans. Smart Grid 2015, 6, 2245–2252. [Google Scholar] [CrossRef]
- Xie, J.; Hong, T. Temperature scenario generation for probabilistic load forecasting. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- Fan, S.; Methaprayoon, K.; Lee, W.-J. Multiregion load forecasting for system with large geographical area. IEEE Trans. Ind. Appl. 2009, 45, 1452–1459. [Google Scholar] [CrossRef]
- Nedellec, R.; Cugliari, J.; Goude, Y. GEFCom2012: Electric load forecasting and backcasting with semi-parametric models. Int. J. Forecast. 2014, 30, 375–381. [Google Scholar] [CrossRef]
- Wang, P.; Liu, B.; Hong, T. Electric load forecasting with recency effect: A big data approach. Int. J. Forecast. 2016, 32, 585–597. [Google Scholar] [CrossRef]
- Xie, J.; Chen, Y.; Hong, T.; Laing, T.D. Relative humidity for load forecasting models. IEEE Trans. Smart Grid 2016. [Google Scholar] [CrossRef]
- McSharry, P.E.; Bouwman, S.; Bloemhof, G. Probabilistic forecasts of the magnitude and timing of peak electricity demand. IEEE Trans. Power Syst. 2005, 20, 1166–1172. [Google Scholar] [CrossRef]
- Chen, Y.; Luh, P.B.; Guan, C.; Zhao, Y.; Michel, L.D.; Coolbeth, M.A.; Friedland, P.B.; Rourke, S.J. Short-term load forecasting: Similar day-based wavelet neural networks. IEEE Trans. Power Syst. 2010, 25, 322–330. [Google Scholar] [CrossRef]
- Apadula, F.; Bassini, A.; Elli, A.; Scapin, S. Relationships between meteorological variables and monthly electricity demand. Appl. Energy 2012, 98, 346–356. [Google Scholar] [CrossRef]
- Ružić, S.; Vučković, A.; Nikolić, N. Weather sensitive method for short term load forecasting in electric power utility of Serbia. IEEE Trans. Power Syst. 2003, 18, 1581–1586. [Google Scholar] [CrossRef]
- Black, J.D.; Henson, W.L.W. Hierarchical load hindcasting using reanalysis weather. IEEE Trans. Smart Grid 2014, 5, 447–455. [Google Scholar] [CrossRef]
- Hoverstad, B.A.; Tidemann, A.; Langseth, H.; Ozturk, P. Short-term load forecasting with seasonal decomposition using evolution for parameter tuning. IEEE Trans. Smart Grid 2015, 6, 1904–1913. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. Wind Chill Temperature Index. 2001. Available online: http://www.nws.noaa.gov/om/cold/resources/wind-chill-brochure.pdf (accessed on 14 March 2017).
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surverys 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Tashman, L.J. Out-of-sample tests of forecasting accuracy: An analysis and review. Int. J. Forecast. 2000, 16, 437–450. [Google Scholar] [CrossRef]
- ISO New England. ISO New England Zonal Information. 2016. Available online: https://www.iso-ne.com/isoexpress/web/reports/pricing/-/tree/zone-info (accessed on 26 October 2016).
- Xie, J.; Hong, T. Variable selection methods for probabilistic load forecasting: Empirical evidence from seven States of the United States. IEEE Trans. Smart Grid 2017. [Google Scholar] [CrossRef]
- Hong, T.; Wang, P.; White, L. Weather station selection for electric load forecasting. Int. J. Forecast. 2015, 31, 286–295. [Google Scholar] [CrossRef]


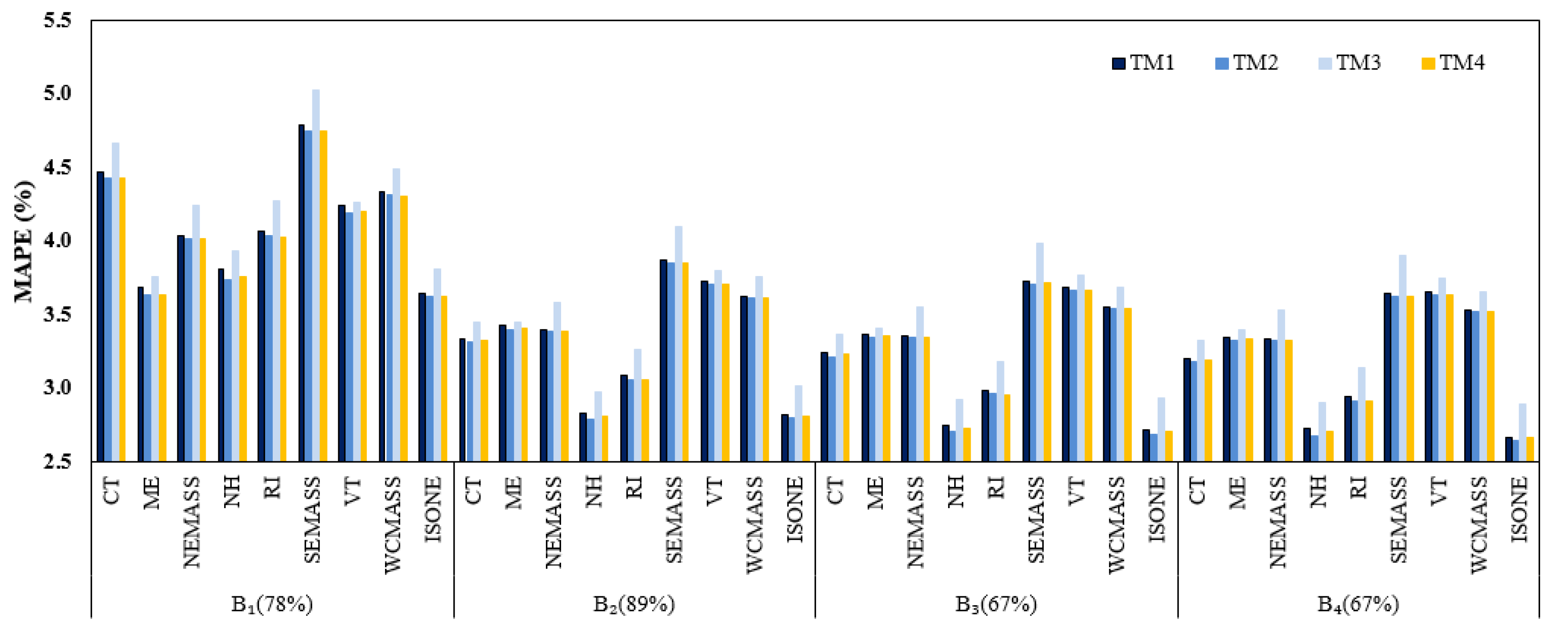
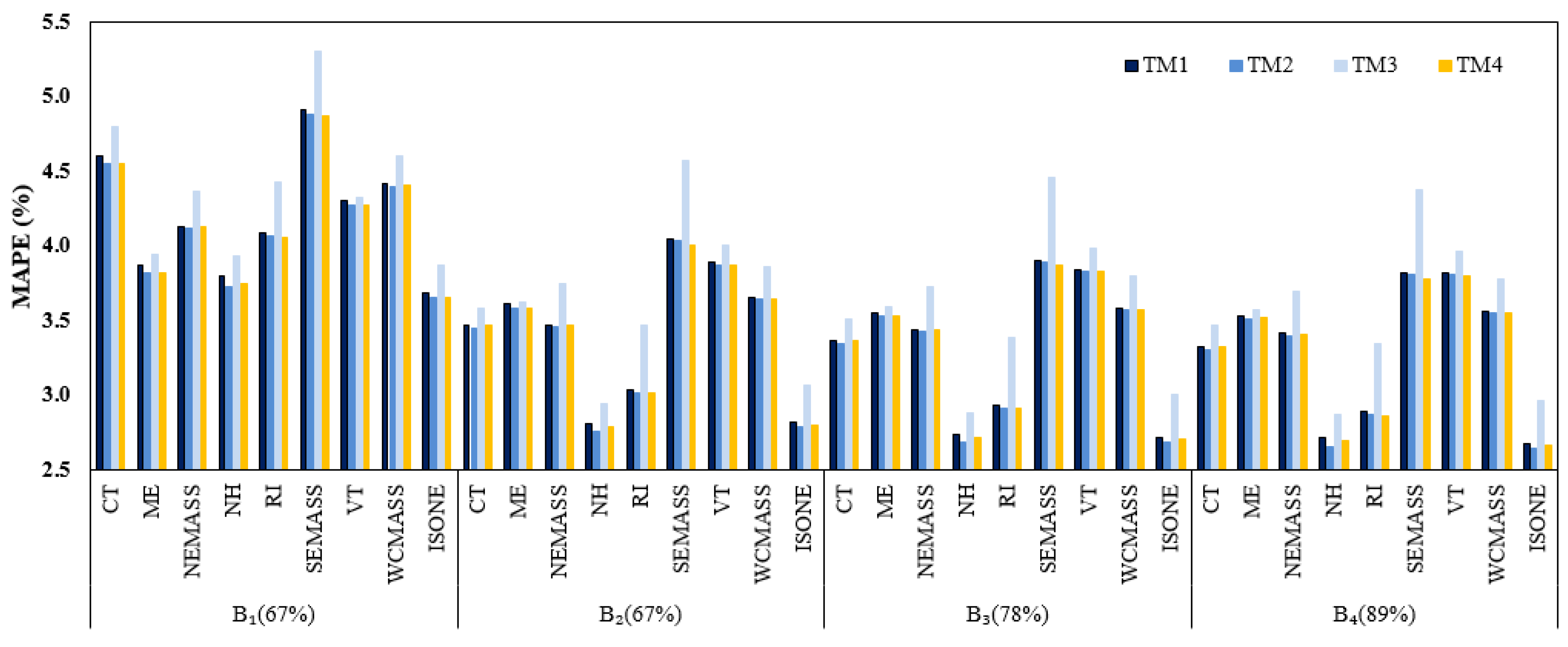
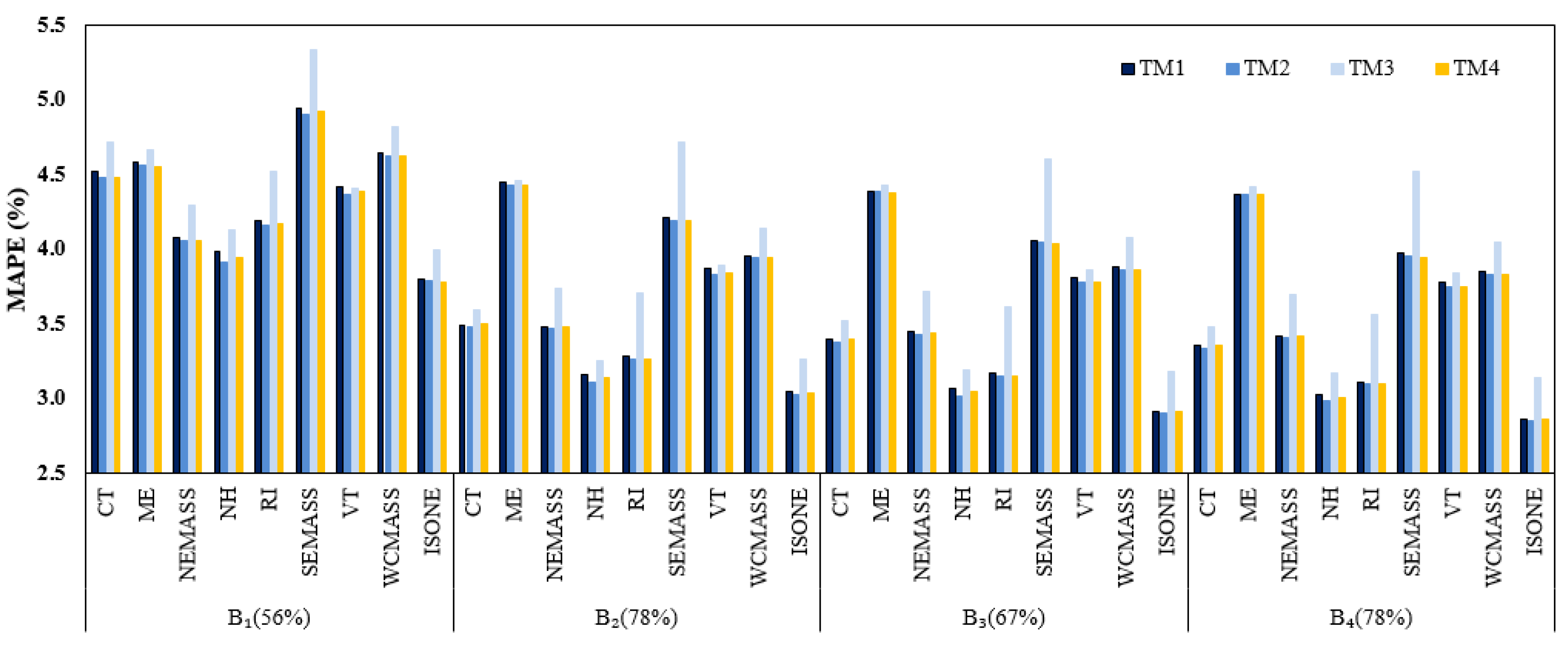
| Zone | Weather Station | Load (MW) | Temperature (°F) | WCI (°F) | Wind Speed (MPH) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | STD. | Mean | STD. | Mean | STD. | Mean | STD. | ||
| CT | KBDL | 3516.14 | 766.52 | 51.61 | 19.44 | 49.17 | 22.31 | 7.32 | 5.20 |
| ME | KPWM | 1320.56 | 202.01 | 47.80 | 18.57 | 44.86 | 21.81 | 7.40 | 5.21 |
| NEMASS | KBOS | 2914.24 | 571.68 | 52.08 | 17.95 | 48.79 | 21.86 | 10.47 | 2.33 |
| NH | KCON | 1331.56 | 265.15 | 47.45 | 20.35 | 45.21 | 22.86 | 5.45 | 5.24 |
| RI | KPVD | 934.15 | 202.94 | 52.17 | 18.20 | 49.62 | 21.30 | 8.41 | 5.23 |
| VT | KBTV | 653.32 | 106.66 | 47.95 | 21.28 | 44.91 | 24.62 | 7.55 | 5.55 |
| SEMASS | KPVD | 1711.79 | 387.60 | 52.17 | 18.20 | 49.62 | 21.30 | 8.41 | 5.23 |
| WCMASS | KORH | 1980.58 | 379.29 | 48.69 | 18.99 | 44.81 | 23.30 | 9.92 | 5.06 |
| ISONE | N/A | 14,362.35 | 2825.33 | 50.05 | 18.85 | 46.96 | 22.39 | 8.18 | 4.11 |
| Base Model (h,d) | None | |||
|---|---|---|---|---|
| B1(h = 0, d = 0) | 3.669 | 3.666 | 3.671 | 3.639 |
| B2(h = 0, d = 1) | 3.066 | 3.061 | 3.055 | 3.028 |
| B3(h = 1, d = 1) | 2.977 | 2.971 | 2.962 | 2.941 |
| B4(h = 2, d = 1) | 2.959 | 2.953 | 2.941 | 2.924 |
| Tested Model Groups | Model Equation |
|---|---|
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Hong, T. Wind Speed for Load Forecasting Models. Sustainability 2017, 9, 795. https://doi.org/10.3390/su9050795
Xie J, Hong T. Wind Speed for Load Forecasting Models. Sustainability. 2017; 9(5):795. https://doi.org/10.3390/su9050795
Chicago/Turabian StyleXie, Jingrui, and Tao Hong. 2017. "Wind Speed for Load Forecasting Models" Sustainability 9, no. 5: 795. https://doi.org/10.3390/su9050795
APA StyleXie, J., & Hong, T. (2017). Wind Speed for Load Forecasting Models. Sustainability, 9(5), 795. https://doi.org/10.3390/su9050795





