Abstract
Data centers have become ubiquitous in the last few years in an attempt to keep pace with the processing and storage needs of the Internet and cloud computing. The steady growth in the heat densities of IT servers leads to a rise in the energy needed to cool them, and constitutes approximately 40% of the power consumed by data centers. However, many data centers feature redundant air conditioning systems that contribute to inefficient air distribution, which significantly increases energy consumption. This remains an insufficiently explored problem. In this paper, a typical, small data center with tiles for an air supply system with a raised floor is used. We use a fluent (Computational Fluid Dynamics, CFD) to simulate thermal distribution and airflow, and investigate the optimal conditions of air distribution to save energy. The effects of the airflow outlet angle along the tile, the cooling temperature and the rate of airflow on the beta index as well as the energy utilization index are discussed, and the optimal conditions are obtained. The reasonable airflow distribution achieved using 3D CFD calculations and the parameter settings provided in this paper can help reduce the energy consumption of data centers by improving the efficiency of the air conditioning.
1. Introduction
With the rapid development of the Internet, the mobile Internet, cloud computing and big data applications, the pace of construction of data centers has accelerated worldwide. At the same time, environmental and energy-related problems arising from the growth of data centers have drawn increasing attention. To date, the worldwide energy consumption of data centers accounts for approximately 1.3% of the world’s total electricity usage [1]. In 2013, U.S. data centers consumed an estimated 91 billion kWh of electricity. Data center electricity consumption is projected to increase to roughly 140 billion kWh annually by 2020 [2,3].
Moreover, the energy consumption of data centers is expected to double every five years, which will incur a massive cost to both business and the environment [4,5]. Therefore, both researchers and data center owners have made efforts to improve the energy efficiency of data centers to minimize their environmental impact, lower the cost of energy and optimize the operation of these centers [6].
Statistics pertaining to the energy consumption of data centers from several surveys are summarized in Figure 1, mainly covering the cost of computational and physical resources [7,8,9]. Server computation accounts for approximately 40% of total cost [10], the energy consumption of the communication equipment for 5%, storage devices consume 5%, and power supply systems and miscellaneous factors account for approximately 10%. Surveys have also shown that refrigeration systems, mainly air conditioning, account for 40% of total energy consumption at data centers, which is also a major energy consumption part.
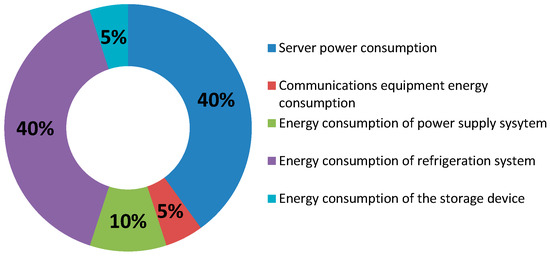
Figure 1.
Energy consumption distribution of data centers.
Research has revealed that a primary cause of the high energy consumption of air conditioning systems in data centers is inefficient airflow. Investment in air conditioning equipment rises due to inefficient air distribution, which leads to higher cost. Therefore, the optimization of air distribution in data centers is important for improving the efficiency of air conditioning systems and reducing emissions.
In the last decade, most researchers have used numerical methods to study indoor airflow and analyze its energy saving effect. Different modeling methods have been used to simulate air circulation in data centers [7], including reduced order models (ROM), flow network modeling (FNM), and CFD. Tang et al. [11] presented an abstract heat flow model that used temperature information from onboard and ambient sensors, characterized hot air recirculation based on this information and accelerated the thermal evaluation process for high performance data centers. Simulation results confirmed that heat recirculation could be characterized as cross-interference in their abstract heat flow model. Moreover, fast thermal evaluation based on cross-interference can be used in online thermal management to predict temperature distribution in real time. Moreover, Tang et al. [12] provided the most elaborate way to describe recirculation through a computational fluid dynamics (CFD) model. They also claimed that CFD models are not suitable solutions for online decisions on task placement. Cho et al. [13] studied the profiles of temperature and airflow in a data center a using a CFD simulation, and used four performance metrics to analyze air management systems. Wang et al. [14] established a unified model for pricing and energy cost, and obtained the optimal conditions for the operation of the entire data center based on dynamic pricing. Zhang et al. [15] showed that air distribution improved with the addition of an intelligent fan system to regions with excessive heat. Annual energy consumption in normal ventilation systems can be reduced by 38% by using numerical models.
Axley et al. [16] and Dols et al. [17] evaluated the influence of demand-controlled ventilation systems on energy and indoor air quality by building airflow and thermal load models; subsequently, Dols and Emmerich developed coupled thermal/airflow solutions to simulate and verify a three-zone combined heat transfer/airflow analytical BESTEST case [18]. Alissa et al. [19] provided a validated dynamic airflow prediction model and a testing methodology for server storage based on the RPM of fans and simple, facility-level pressure measurements, which are beneficial to the platform and facility-level control to assess the cooling needs of each storage unit. Wang et al. [20] simulated the airflow configuration of a computer room and computed the data for the velocity fields, temperature fields, PMV and PPD using CFD technology with two air supply systems for a computer room. Lang et al. [21] analyzed the influence of different inlet wind directions on airflow characteristics for an underground air distribution system and presented airflow characteristics resulting from experimental and numerical simulations. These characteristics were similar when the wind incidence angles were 60° and 90°, and the maximum velocities were recorded at the center of the room. Indoor air was more mixed when the wind incidence angle was 60° than when it was 90°. Hasson [22] presented an analysis of the airflow, the temperature and the pressure distribution of data centers using the CFD code Fluent, and investigated the effect of various parameters on the temperature distribution and the flow field. The model can evaluate airflow rates and thermal loads to optimize an existing data center or design a new one.
The above-mentioned research indicates that, as a common tool, CFD is widely used to analyze and optimize the airflow and temperature distribution in communication rooms and data processing equipment, the equipment layout and the effects of different layouts and frames on the computer room. However, studies on indoor air distribution to data rooms have either focused on temperature and airflow at the scale of a room or on vectors and contours of velocity and temperature in the macro scale. Airflow in a hot aisle/cold aisle remains an insufficiently explored field.
Solutions to energy saving in data centers equipped with air conditioning machines fall into three main categories: (1) selecting air conditioning machines with a high energy efficiency ratio; (2) managing auxiliary facilities or the automatic control of air conditioning to reduce energy consumption; and (3) designing a layout of the indoor air conditioners to optimize airflow to the server rooms, which is the most important approach. A perfect air conditioning system with optimal airflow according to the requirements of the equipment is the main problem in the design of data centers. Appropriately designed airflow can help achieve the best cooling effect, improve efficiency and reduce energy consumption [23,24,25,26].
To this end, a typical, small data center with tiles for a raised floor in an air supply system is used as the target model in this study. CFD is used to simulate airflow and thermal distribution in order to investigate the influence of the operating conditions on airflow in the hot aisle/cold aisle and optimize it to save energy using Fluent 6.3. The effect of the airflow outlet angle at the tile, the cooling temperature and the airflow rate on the beta index and the energy utilization index are discussed and optimum conditions are obtained. Furthermore, the problem of high energy consumption due to poor air distribution in the small data center is analyzed to improve air conditioning efficiency and reduce energy consumption.
2. Methodology
In this paper, a typical data center with an air supply system with a raised floor was chosen as target model to provide boundary conditions to simulate the pattern of airflow and confirm the results.
2.1. Physical Model of Data Center
Fluent 6.3 was used to obtain the thermal distribution of various scheduling algorithms and the cooling efficiency of the small-scale data center in a confined space, as shown in Figure 2. This methodology has been validated in prior studies [20,21,22,23,24,25,26,27,28].
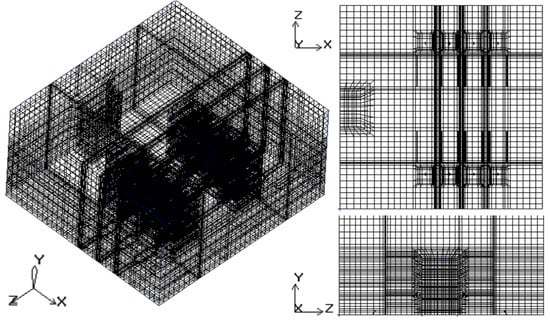
Figure 2.
The small scale data center with meth.
A three-dimensional (3D) model of an analyzed data center was built with dimensions 10.0 m × 9.6 m × 3.2 m (see Table 1 for the parameters). A corresponding physical model was created using the modeling software Gambit, which contained two rows of industry-standard 2U racks arranged in a typical cold aisle and a hot aisle. An unstructured hexahedral mesher was used to create the mesh, and the grid was refined around the openings, servers and vents. A total of 161,142 cells, 503,912 faces and 173,475 nodes were generated. The quality of the mesh was satisfactory because the calculated face alignment was greater than 0.7, which meant that no element had been severely distorted. Cold air was supplied by an air conditioner at a rate of 3.6–10 m3/s. The cold air rose from the raised floor plenum through vent tiles and hot air returned to the air conditioner. The data center contained two rows of racks, and four R520 2U racks (Rack 1, Rack 2, Rack 3, Rack 4, …, Rack 8) were arranged in each row; each rack was equipped with five chassis (marked from bottom to top as A, B, C, D and E). The servers were Lenovo R520 GT containing two processors each. The total power consumption of the data center was 9.6 KW when idle and 13.6 KW at full utilization. The data center also contained one CRAC unit that pushed chilled air at a temperature between 13 °C and 21 °C into the raised floor at a certain rate.

Table 1.
Equipment parameters in numerical simulation.
During the simulation, the room was isolated and the effects of heat transfer outside it were neglected. Adiabatic walls were chosen for the room. For the chassis as heat source, a black box model was used that allowed no flow through the servers, and a chassis load was added to generate the profile of the thermal exhaust and heat exchange with the environment through a heat transfer area. The black box method has been shown to be feasible in past work [29,30,31].
2.2. Mathematical Model
The commercial CFD software package Fluent 6.3 was used as basic tool for the simulation [32]. Since design factors can affect the efficiency of airflow in the data center, several physical conditions based on the standard modulus of design and architecture variables were investigated.
In room-level data center airflow modeling, the major flow regime is commonly taken to be turbulent mixed convection because of the scale of the room, flow conditions through the perforations and the server racks [33,34].
Past investigations have indicated that the k-ε turbulent model exhibits better performance and results, in good agreement with experimental data, than the k-ω, SST, the RSM and the RNG k-ε models [29]. The governing equations of the Euler–Euler model are provided in Section 2.2.1.
Since the equation involves the flow and characteristics of typical dimensions and flow turbulence, the simulation process with the equation model was assumed to be as follows [35,36,37]: (1) Air could be regarded as an incompressible fluid and the flow as steady turbulent flow because indoor air velocity was lower than the velocity of sound. (2) Heat transfer on the surface of the external wall and the server was uniform, and the effects of radiation were ignored in the room according to the steady heat assumption. (3) We ignored the impact of such disturbance as air leakage or personnel movement.
2.2.1. Continuity and Momentum Equations
The motion of each phase was governed by the corresponding mass and momentum conservation equations. The continuity equation is:
where ui is the velocity of the i-th phase. The subscript i represents the x-, y- or z-axis.
The equation for the conservation of momentum is:
where is density in kg/m3; fi is the interfacial force acting on phase i due to the presence of phase j, which includes drag force, interphase turbulent dispersion force, virtual mass and lift force [32,34]; μ is shear viscosity in N·s/m2; and p is pressure in N/m2.
The energy equation is as follows:
where T is the fluid temperature in K, cp is the specific heat capacity of the fluid at constant pressure in J/gK, k is the fluid thermal transfer coefficient in m2/s and ST is the term for viscous dissipation.
2.2.2. Turbulence Model
In order to solve Reynolds’ stress in the turbulence momentum equations, the standard k-ε model was used to simulate introduction of the liquid phase with the Boussinesq assumption, obtained as follows:
where i represents the x-, y- or z-axis, is the turbulent kinetic energy at the mean velocity gradient ; is the turbulent kinetic energy generated by buoyancy ; Pr is the Prandtl number, ; β is the expansion coefficient,; is the turbulent viscosity, ; and , , , and are parameters in the standard k-ε model. The turbulent viscosity of the liquid phase was modeled using the conventional shear-induced turbulent viscosity, which was obtained from the standard k-ε model as:
and Boussinesq assumption,
2.3. Boundary Conditions
For the calculations of the CFD, a finite-volume approximation of the Reynolds-averaged Navier–Stokes equations and energy equations with the standard k-ε turbulence model were solved. The effects of buoyancy were included, but constant properties for the air were assumed otherwise. Grid generation is very important for CFD calculations because it is directly related to its success or failure. The grid should meet the following criteria: the change in density in the grid domain should be based on the variables, and the change in elements in the entire solution domain should be smooth. According to the geometry of the data room, the minimum volume was 2.961 × 10−7 m3 and the maximum was 8.001 × 10−3 m3. This grid level was used to obtain all CFD data for a numerical comparison with the zonal modeling.
The boundary conditions, the initial conditions and the iteration scheme were set for the numerical simulations in the Fluent 6.3 software package. The continuity equations were discretized using the QUICK scheme and the others through the second-order upwind differencing scheme. The relaxation factors are shown in Table 2. In all simulations, a time step of 0.001 s was used. The convergence criterion for flow was set at 1 × 10−3 and that for energy and H2O specie was set at 1 × 10−6. The simulation was stopped when it was determined to have reached a steady state.

Table 2.
Factors concerning relaxation.
For validation purposes, a CFD simulation was also carried out in this study, for which the standard k-ε turbulence model was used. The following turbulence model constants were employed: C1 = 1.44, C2 = 1.92, C3 = 1, C = Ck = 0.09, σk = 1.0 and σε = 1.3.
2.4. Evaluation Method
A data center is usually designed as a raised floor with racks arranged in a hot/cold aisle layout. In computer room air conditioning (CRACs), hot exhaust air from the racks is cooled and supplied with chilled air through the floor plenum. In the hot/cold aisle layout, several researchers have raised airflow and temperature management problems, such as the hotspot phenomenon, bypass airflow and recirculation air. A number of thermal metrics have been proposed to evaluate airflow and thermal management. Sharma et al. [38] proposed the dimensionless parameters of supply heat index and return heat index, and Herrlin [39,40] proposed the rack cooling index. These indices can provide a macroscopic evaluation of the recirculation phenomena but fail to present the effect of bypass on recirculation and other information pertaining to local IT equipment. Other thermal metrics were proposed in [41].
In response to the thermal and bypass phenomena, we used two kinds of evaluation indices, the beta index and the energy utilization index. The β index was proposed to evaluate temperature increase in local racks [42], and can be defined as:
where Tin is the airflow inlet mean temperature for each rack that corresponds with Tout, the airflow outlet mean temperature for each rack, and Tref is the airflow cooling mean temperature for the floor. The temperature symbols are shown in Figure 3. Schmidt tried to solve this problem by proposing the β Index [42]. This index provides information about local temperatures in a rack, and is obtained from the ratio of the punctual temperature difference across a rack to the average difference across the racks. The common value of β ranges between 0 and 1. A β value of 0 means no air recirculation, whereas a β value above 1 indicates self-heating.
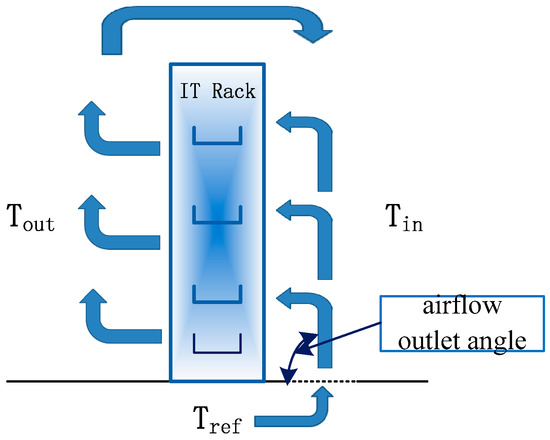
Figure 3.
A typical temperature distribution layout.
The other index is the energy utilization index [43,44]. This index is defined as:
where Tp is the temperature in the outlet and Ts is that in the inlet. Tn is the temperature in the working space. It indicates the efficiency of airflow in the workspace used to cool the equipment; the higher the value of η, the higher the air cooling rate. The value of η can be used to evaluate the utilization efficiency of air distribution with respect to the air cooling capacity as well as the energy saving obtained through the air distribution scheme.
In order to calculate the energy efficiency of airflow in the data center, the energy utilization index was modified as [45]:
where Tout is the exhaust air temperature and Tin the inlet air temperature. Tref is the cooling air temperature in the rack area. In Equation (13), the difference between the average temperature of the inlet and exhaust air and the reference temperature are used as reference to measure the intensity of the mixing of hot and cold air. It can reflect a local hotspot due to equipment failure. Smaller values represent higher the comprehensive evaluation of airflow organization. It represents the exhaust air circulation of the IT rack.
3. Results and Discussion
3.1. Effect of Airflow Outlet Angle of Tiles on Air Distribution
Early simulations of data centers focused on modeling a raised floor and perforated tiles to accurately predict the boundary conditions [46,47,48,49,50,51,52]. We believe that not only does heterogeneous airflow in the cold aisle (hot air recirculation and cold air bypass) depend on airflow distribution from the tiles, the airflow outlet angle also influences the distribution of cold air.
The airflow vectors of the CFD simulation at airflow angles of 30° and 45° are shown in Figure 4. In the cold aisle, the vectors of the cooling air were clearly observed near the surface of the tile, flowing toward the cold aisle space, following a small volume of re-circulated cold air in the lower parts of the room. A majority of the flow streamed toward the right end and moved into the server inlets. However, a small amount of airflow, especially in the top parts of the room, simply streamed past the open cold aisle and mixed with the hot air in hot aisle in Figure 4A. As the figure shows, a similar bypass cooling air phenomenon was observed in the same region of Figure 4C.
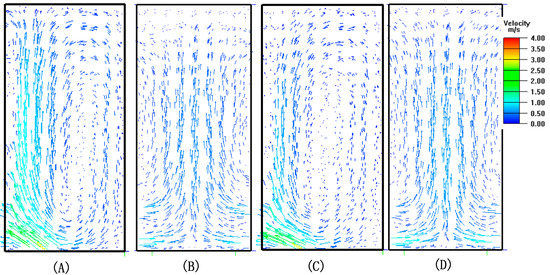
Figure 4.
Airflow characteristics in the cold and hot aisles at an airflow rate of 4.22 m3/s: (A) 45°, cold aisle, Z = 0–1.6 m; (B) 45°, hot aisle, Z = 2.4–3.9 m; (C) 30°, cold aisle, Z = 0–1.6 m; and (D) 30°, hot aisle, Z = 2.4–3.9 m.
In the hot aisle, airflow from the outlets of servers led directly into the main flow in the hot aisle from bottom to the top, as shown Figure 4B,D. However, the hot airflow mixed with a small part of the cold flow. Some degree of heterogeneous flow at the top of the room was also observed.
Figure 5 shows the contours of local temperature in the selected cross-sections through the computational domain. These figures provide useful insights into the thermal tendencies of the domain corresponding to the observed airflow. The thermal distribution at an airflow outlet angle of 45° at the tiles was better than that of 30°. Particularly at the ceiling, a mixing of cold and hot airflows and the airflow in the cold aisle generated greater circulation. Moreover, the temperature of the upper region of the plotted area appeared slightly higher than the surrounding area.
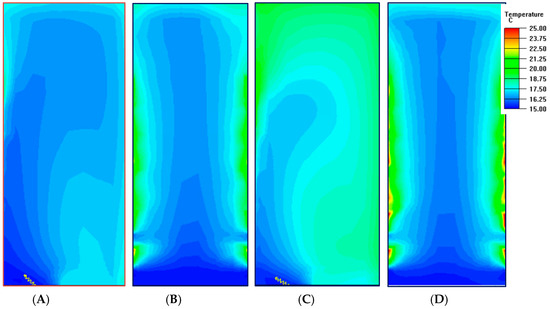
Figure 5.
The contours of the selected cross-sections of temperature in the cold and hot aisles: (A) 45°, cold aisle, Z = 0–1.6 m; (B) 45°, hot aisle, Z = 2.4–3.9 m; (C) 30°, cold aisle, Z = 0–1.6 m; and (D) 30°, hot aisle, Z = 2.4–3.9 m.
In Figure 6, the velocity of the air at the axis gradually weakened from the exit along the direction of flow. Compared with Figure 6A,B, at airflow outlet angles of 60° and 90° with the tiles, the airflow of the cold aisle at 60° was evenly mixed, and the difference in the inlet of the rack could be reduced. Moreover, airflow in the hot aisle had a uniform distribution, and only at the top part of the room was there a mixture of hot and cold air. On the other hand, at a 90° angle with the perforated tiles, airflow first reached the ceiling, and then moved to the center along the ceiling. Part of the airflow occurred through the outlet, and the other part reached the center after the downward movement. In the upper part of the room, the indoor air formed a vortex, appearing in the position of circular flow vortex several times, and then continued to flow downward. Large air circulation typically occurs in this condition, which is not conducive to heat exchange in the server.
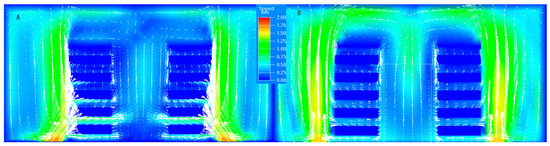
Figure 6.
The velocity vectors and contours of local temperature in selected cross-sections with X = 2.95 m through the computational domain: (A) 60°; and (B) 90°.
To further illustrate the influence of the airflow outlet angle (as shown in Figure 3), the simulation results of the CFD showed the effect this angle on the β index and the energy utilization index as shown in Figure 7. Because the simulation of the two row racks was symmetrically structured, this paper only discusses the impact of one of them. In Figure 7, we see that the airflow outlet angle influenced flow and thermal distribution. With an increase in the airflow outlet angle, the β index decreased and the energy utilization index increased, which represented a clear difference between the punctual temperature and the average temperature across the rack. In addition, at an angle of 60°, the β index was minimum and the energy utilization index maximum: the airflow was more uniform.
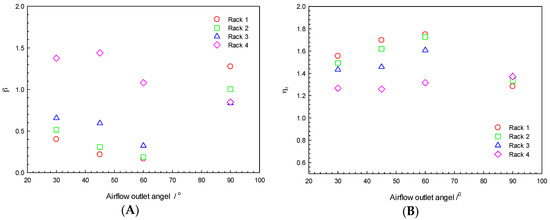
Figure 7.
The relationship between airflow outlet angle and: β (A); and ηr (B) (airflow rate 4.22 m3/s, the cooling air temperature 15 °C).
3.2. The Temperature of the Cold Air on the Airflow Distribution
Due to the complex nature of airflow inside the data center, some of the hot exhaust from the outlets of the servers was re-circulated into the inlets of the other servers. A reason for the extra cost of cooling systems is the mixture of cold air with the re-circulated hot air in the inlet. To provide an acceptable inlet temperature for all servers, the supplied air temperature needed to be reduced, which often increases cost. Thus, understanding and reducing the recirculation of hot air should be explored to reduce the energy cost of data centers.
The temperature of the cold air was a parameter that influenced airflow. The effects of the temperature of the cold air on the β index and the energy utilization index are shown in Figure 8. With the increase in the temperature of the cold air, the β index decreased and the energy utilization index increased. While the temperature was over 17 °C, the β index occupied a stable region. However, for Rack A4, which was far from the air conditioner, only cold air at a temperature of 17 °C has a low value, which meant little recirculation. Under other conditions, when the β value was above 1, indicating a mixing of cold and hot airflows, local hot point in racks may present.
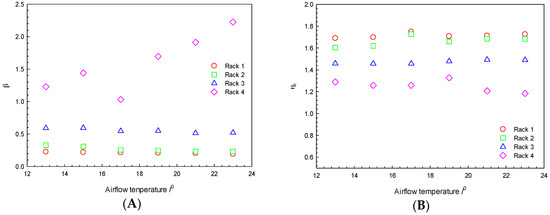
Figure 8.
Effect of temperature of cooling airflow on: the β index (A); and the energy utilization index ηr (B) (airflow outlet angle 60°, airflow rate 4.22 m3/s).
Furthermore, the energy utilization index increased with increase in the temperature of the cooling airflow. For cold air at 17 °C, the energy utilization index recorded its maximum value-airflow was more uniform. The results show that air at 15 °C and 17 °C was more conducive for the full utilization of the cooling capacity than at other temperatures. This showed that the variation in air temperature has a certain impact on the thermal environment and air distribution in a confined room. The unit energy consumption also changed. Hence, we needed to find the optimal operating conditions through the thermal and airflow simulations, including suitable airflow temperature, and the quantitative relationship between room temperature and the air distribution evaluation indices.
Figure 9 shows the inlet and outlet temperatures of the chassis at the reference temperatures of 15 °C and 17 °C. Regardless of the inlet temperature, chassis E at each rack had the worst mixing of cold and hot airflows: the hot air backflow phenomenon occurred. However, the thermal environment of the other chassis profile was better. At the same time, the higher is the rate of utilization rate of airflow, the higher the thermal safety of the rack. In addition, for the outlet temperature, the results in Figure 9B are better than those in Figure 9D. Thus, an inlet temperature of 15 °C is recommended as the temperature of the cold air, since it ensures high efficiency and a safe working environment for the heat transfer in the racks and the arrangement of the equipment, according to the results of the index for each location.
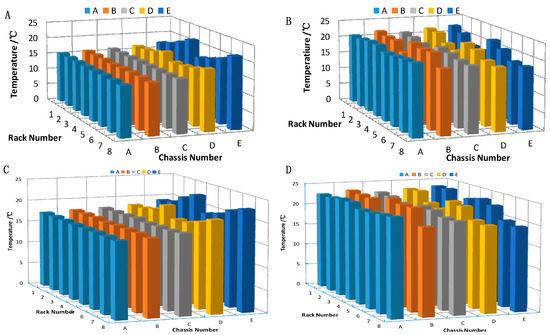
Figure 9.
The inlet and outlet temperatures of the chassis at reference temperatures 15 °C and 17 °C: (A) inlet temperature 15 °C; (B) outlet temperature 15 °C; (C) inlet temperature 17 °C; and (D) outlet temperature 17 °C (airflow rate 4.22 m3/s, airflow outlet angle 60°).
3.3 The Effect of Airflow Rate on the Air Distribution
Floor air supply is related to heat transfer in servers in the data center, but the rate of airflow can also affect the circulation in the data center. The contours of local temperature in a z-axis 2.48 m plane is shown in Figure 10, which is indicate the contours of outlet temperature in Rack 1, Rack 2, Rack 3 and Rack 4. From the CFD simulation, the hot aisle presents a uniform distribution of temperature at small airflow rate, and the temperature of chassis increase from the bottom to top of room; there is a heterogeneous distribution of temperature at larger airflow rate, and the temperature of bottom chassis close to 15 °C and the temperature of the top chassis 25–27 °C. In order to evaluate the thermal and bypass phenomena, the beta index and the energy utilization index were used, as shown Figure 11.
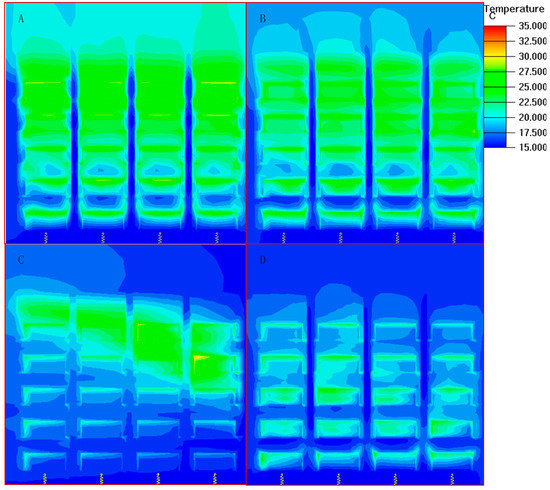
Figure 10.
The contours of local temperature in selected cross-sections with Z = 2.48 m through the computational domain (airflow outlet angle 60°, the cooling air temperature 15 °C): (A) airflow rate 2.0 m3/s; (B) airflow rate 3.1 m3/s; (C) airflow rate 4.22 m3/s; and (D) airflow rate 5.64 m3/s.
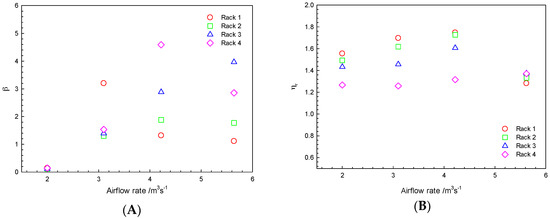
Figure 11.
The effect of airflow rate on: the β index (A); and the energy utilization index ηr (B) (airflow outlet angle 45°, the cooling air temperature 15 °C).
Figure 11 shows the relationships between airflow and the β index and the energy utilization index. The β index at an airflow rate of 2.0 m3/s was better than those at other velocities, which is consistent with the phenomenon in Figure 10A. Moreover, as shown in Figure 10B, the energy utilization index at this rate was the best. In China, the national standard of the thermal environment of data centers is outlined in the Code for the Design of Electronic Information System Rooms [53], which stipulates the temperature for data centers at 22–24 °C, but does not specify the sample points of the test temperature in the data center. Therefore, based on the room temperature requirements of the data center, the airflow rate required for the data center can be calculated through the cooling load on it, the air thermodynamic constant and the inlet and outlet temperatures, as shown in Equation (14):
where n is the number of servers in the data center, Cp represents the specific heat of air (a thermodynamic constant), mi is the mass of the flow of air through servers and is the inlet temperature of the servers.
Therefore, a volume of airflow should be considered according to Equation (14) and the results of the simulation.
Figure 12 shows the velocity vectors and contours of the local temperature in the selected cross-sections under different airflow conditions. There were some local hot spots at the top of the room, for which we need to consider the design of airflow in the mixing of hot and cold flows to increase thermal efficiency.
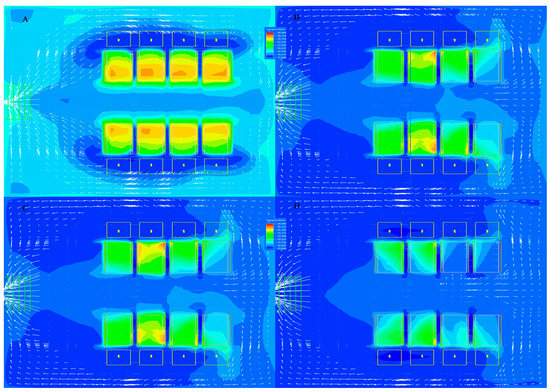
Figure 12.
The velocity vectors and contours of local temperature in selected cross-sections with Y = 1.8 m through the computational domain: (A) 2 m3/s; (B) 3.1 m3/s; (C) 4.22 m3/s; and (D) 5.64 m3/s.
In addition, the increase in airflow can increase the heat transfer rate and decrease the local temperature of the chassis. However, the chance of the local mixing of cold and hot airflows increases, especially where there is obvious recirculation air at high airflow, which can lead to wasted energy and can increase the load on the CRAC.
Therefore, better airflow distribution and a uniform local temperature are needed. Hence, the CFD simulation, the models and the parameter settings in our research can provide secure foundations for further study.
4. Conclusions
The consumption of energy in data centers has consistently increased due to the rapid development of big data. A very important issue in the design of data centers is the balancing of the airflow distribution through the tiles to fulfill the cooling requirements of the adjacent computer equipment. By using CFD simulation software, a series of influence parameters for a confined data room were simulated in this paper. According to the thermal and the bypass phenomena, we used two kinds of evaluation indices, the beta index and the energy utilization index. By analyzing the relation between the airflow outlet angle with the tiles and airflow distribution, we found a minimum β index and a maximum energy utilization index at an angle of 60°, which represented better, more uniform air distribution. The variation in air temperature affects the thermal environment and air distribution in the confined room, and the unit energy consumption also changed. The simulation results showed that an air supply temperature of 15–17 °C is most suitable for the full utilization of the cooling capacity. Moreover, floor air supply is related to the heat transfer in the servers of the data center, and the airflow rate affects its airflow circulation. According to the results of the CFD simulation, the β index at lower airflow rates has an ideal value, whereas the energy utilization index at a higher airflow rate is the best. Therefore, through the thermal and airflow simulations, we found the optimal operating conditions, suitable airflow temperatures, as well as the quantitative relationship between the room temperature and the room air distribution evaluation indices. The utility model implemented high-efficiency heat transfer in the data room, which improved the efficiency of the cooling process and the effective utilization of the air conditioner.
The outcome of this study has the potential to contribute to treating the problems of airflow and thermal distribution in data centers through simulation models and computational analysis involving detailed 3D CFD calculations. Optimal parameter settings for the tiles and severs can be generated and used to obtain the desired distribution of flow rates of cold air. This study can also be used as the foundation for further research on airflow distribution and thermal consumption by considering such parameters as equipment arrangement, rack loadings, airflow rate, airflow outlet angel, heat load distribution and other cases of cooling.
Acknowledgments
The work described in this paper is supported by the National Natural Science Foundation of China (91634101), Education Ministry Funding Project for the Development of Liberal Arts and Social Sciences (No. 12YJA87001, 15YJAZH052) and Beijing Social Science Fund (No. 14SHB010).The work is also supported by The Research Center for Beijing Modern Industrial Development.
Author Contributions
Jing Ni and Bowen Jin established the model. Jing Ni, Bo Zhang and Xiaowei Wang carried out experiment and simulation. Jing Ni and Bowen Jin prepared the manuscript. Xiaowei Wang revised manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Koomey, J.G. Growth in Data Center Electricity Use 2005 to 2010; Analytics Press: Oakland, CA, USA, 2011. [Google Scholar]
- Ni, J.; Bai, X. A review of air conditioning energy performance in data centers. Renew. Sustain. Energy Rev. 2017, 67, 625–640. [Google Scholar] [CrossRef]
- Whitney, J.; Delforge, P. Data Center Efficiency Assessment; Natural Resources Defense Council: New York, NY, USA, 2014. [Google Scholar]
- Ristic, B.; Madani, K.; Makuch, Z. The water footprint of data centers. Sustainability 2015, 7, 11260–11284. [Google Scholar] [CrossRef]
- Shehabi, A.; Ganguly, S.; Traber, K.; Price, H.; Horvath, A.; Nazaroff, W.W.; Gadgil, A.J. Energy Implications of Economizer Use in California Data Centers; Lawrence Berkeley National Laboratory: Monterey, CA, USA, 2008.
- Qian, X.; Li, Z.; Li, Z.X. Entransy and exergy analyses of airflow organization in data centers. Int. J. Heat Mass Trans. 2015, 81, 252–259. [Google Scholar] [CrossRef]
- Joshi, Y.; Kumar, P. Energy Efficient Thermal Management of Data Centers; Springer: New York, NY, USA, 2012. [Google Scholar]
- Patel, C.D.; Sharma, R.; Bash, C.E. Thermal considerations in cooling large scale high compute density data centers. In Proceedings of the 2002 Inter Society Conference on Thermal Phenomena, San Diego, CA, USA, 30 May–2 June 2002. [Google Scholar]
- Jeffrey, R.; Yogendra, J. Modeling of data center airflow and heat transfer: State of the art and future trends. Distrib. Parallel Databases 2007, 21, 193–225. [Google Scholar]
- Uddin, M.; Darabidarabkhani, Y.; Shah, A.; Memon, J. Evaluating power efficient algorithms for efficience and carbon emissions in cloud data centers: A review. Renew. Sustain. Energy Rev. 2015, 51, 1553–1563. [Google Scholar] [CrossRef]
- Tang, Q.; Mukherjee, T.; Sandeep, K.S.; Cayton, G.P. Sensor-based fast thermal evaluation model for energy efficient high-performance datacenters. In Proceedings of the International Conference on Intelligent Sensing Information Processing, Bangalore, India, 15–18 December 2006; pp. 203–208. [Google Scholar]
- Tang, Q.; Gupta, S.K.S.; Varsamopoulos, G. Energy-efficient, thermal-aware task scheduling for homogeneous, high performance computing data centers: A cyber-physical approach. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 1458–1472. [Google Scholar] [CrossRef]
- Cho, J.; Yang, J.; Park, W. Evaluation of air distribution system’s airflow performance for cooling energy savings in high-density data centers. Energy Build. 2014, 68, 270–279. [Google Scholar] [CrossRef]
- Wang, W.; Luo, J.; Song, A. Dynamic pricing based energy cost optimization in data center environments. Chin. J. Comput. 2013, 36, 599–612. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, H.; Feng, Z.; Sun, C.; Jin, Z.; Long, Z. Optimization on air distribution and energy consumption of a small data center. J. Tianjin Univ. Sci. Technol. 2014, 47, 647–652. [Google Scholar]
- Axley, J.W.; Emmerich, S.J.; George, N.W. Modeling the performance of a naturally ventilated commercial building with a multizone coupled thermal/airflow simulation tool. ASHRAE Trans. 2002, 108, 1260–1275. [Google Scholar]
- Dols, W.S.; Emmerich, S.J.; Polidoro, B.J. Using coupled energy, airflow and indoor air quality software (TRNSYS/CONTAM) to evaluate building ventilation strategies. Build. Serv. Eng. Res. Technol. 2016, 37, 163–175. [Google Scholar] [CrossRef] [PubMed]
- Dols, W.S.; Emmerich, S.J.; Polidoro, B.J. Coupling the multizone airflow and contaminant transport software contam with energy plus using co-simulation. Build. Simul. 2016, 9, 469–479. [Google Scholar] [CrossRef] [PubMed]
- Alissa, H.A.; Nemati, K.; Puvvadi, U.L.N.; Sammaki, B.G.; Schneebeli, K.; Seymour, M.; Gregory, T. Analysis of airflow imbalances in an open compute high density storage data center. Appl. Therm. Eng. 2016, 108, 937–950. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, F.; Jiang, L. CFD analysis of airflow configuration in the computer room. Refrig. Air Cond. Electr. Powder Mach. 2008, 28, 32–35. [Google Scholar]
- Lang, N.; Li, C.; Wang, M.A. Study on the influence of different inlet wind directions on airflow pattern of under floor air distribution system. World Sci. Tech. R D 2009, 31, 913–916. [Google Scholar]
- Hassan, N.M.S.; Khan, M.M.K.; Rasul, M.G. Temperature monitoring and CFD Analysis of Data Centre. Procedia Eng. 2013, 56, 551–559. [Google Scholar] [CrossRef]
- Wang, I.N.; Tsui, Y.Y.; Wang, C.C. Improvements of Airflow Distribution in a Container Data Center. Energy Proc. 2015, 75, 1819–1824. [Google Scholar] [CrossRef]
- Cho, J.; Lim, T.; Kim, B.S. Measurements and predictions of the air distribution systems in high compute density(internet)data centers. Energy Build. 2009, 41, 1107–1115. [Google Scholar] [CrossRef]
- Lu, T.; Lü, X.; Remes, M. Investigation of air management and energy performance in a data center in Finland: Case study. Energy Build. 2011, 43, 3360–3372. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Shokry, E.; Ahmadian Hosseini, A.J.; Ahmadi, G.; Calautit, J.K. Evaluation of airflow and thermal comfort in buildings ventilated with wind catchers: Simulation of conditions in Yazd City, Iran. Energy Sustain. Dev. 2016, 35, 7–24. [Google Scholar] [CrossRef]
- Bartrand, T.A.; Farouk, B.; Haas, C.N. Countercurrent gas/liquid flow and mixing: Implications for water disinfection. Int. J. Multiph. Flow 2009, 35, 171–184. [Google Scholar] [CrossRef]
- Fakhim, B. Multifaceted Analysis of Data Centre Cooling Using CFD, Experiment and Second Law of Thermodynamics. Ph.D. Thesis, University of Sydney, Sydney, Australia, March 2014. [Google Scholar]
- Alkharabsheh, S.; Fernandes, J.; Gebrehiwot, B.; Agonafer, D.; Ghose, K.; Ortega, A.; Joshi, Y.; Sammakia, B. A brief overview of recent developments in thermal management in data center. J. Electron. Packag. 2015, 137, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.S.; VanGilder, J.W.; Iyengar, M.; Schmidt, R.R. Effect of rack modeling detail on the numerical results of a data center test cell. In Proceedings of the IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronics Systems (ITHERM 2008), Lake Buena Vista, FL, USA, 28–31 May 2008; pp. 1183–1190. [Google Scholar]
- Zhai, J.Z.; Hermansen, K.A.; Al-Saadi, S. The development of simplified rack boundary conditions for numerical data center models. ASHRAE Trans. 2012, 118, 436–449. [Google Scholar]
- Ansys Incorported. ANSYS FLUENT-Solver Release 10.0; Ansys Inc.: Canonsbury, PA, USA, 2005; p. 131. [Google Scholar]
- Abanto, J.; Barrero, D.; Reggio, M.; Ozell, B. Airflow modeling in a computer room. Build. Environ. 2004, 39, 1393–1402. [Google Scholar] [CrossRef]
- Song, Z. Thermal performance of a contained data center with fan-assisted perforations. Appl. Therm. Eng. 2016, 102, 1175–1184. [Google Scholar] [CrossRef]
- Patel, C.D.; Bash, C.E.; Belady, C.; Stahl, L.; Sullivan, D. Computational fluid dynamics modeling of high compute density data centers to assure system inlet air specifications. In Proceedings of the Pacific Rim Technical Conference and Exposition of Packaging and Integration of Electronic and Photonic Systems (IPACK), Kauai, HI, USA, 8–13 July 2001. [Google Scholar]
- Dun, Z.; Qin, Y.; Guan, X. Simulation optimization and evaluation analysis of the data center airflow distribution. Build. Energy Effic. 2015, 43, 27–33. [Google Scholar]
- Gao, T.; David, M.; Geer, J. Experimental and numerical dynamic investigation of an energy efficient liquid cooled chiller-less data center test facility. Energy Build. 2015, 91, 83–96. [Google Scholar] [CrossRef]
- Hannaford, P. Ten steps to solving cooling problems cause by high-density server deployment. In Proceedings of the INTELEC 05-Twenty-Seventh International Telecommunications Conference, Berlin, Germany, 18–22 September 2005; pp. 609–616. [Google Scholar]
- Herrlin, M.K. Rack cooling effectiveness in data centers and telecom central offices: The Rack Cooling Index (RCI). ASHRAE Trans. 2005, 111, 725–731. [Google Scholar]
- Herrlin, M.K. Airflow and cooling performance of DC: Two performance metrics. ASHRAE Trans. 2008, 114, 182–187. [Google Scholar]
- Capozzoli, A.; Serale, G.; Liuzzo, L.; Chinnici, M. Thermal metrics for data centers: A critical review. Energy Procedia 2014, 62, 391–400. [Google Scholar] [CrossRef]
- Schmidt, R.R.; Cruz, E.E.; Iyengar, M.K. Challenges of data center thermal management. IBM J. Res. Dev. 2005, 49, 709–723. [Google Scholar] [CrossRef]
- VanGilder, J.W.; Lee, T. A hybrid flow network-CFD method for achieving any desired flow partitioning through floor tiles of a raised-floor data center. Adv. Electron. Packag. 2003, 1, 377–382. [Google Scholar]
- Sorell, V.; Escalante, S.; Yang, J. Comparison of overhead and underfloor air delivery systems in a data center environment using CFD modeling. ASHRAE Trans. 2005, 111, 756–764. [Google Scholar]
- Xu, Q.X. Energy Consumption and Air Distribution Simulation of a Substation Data Room; Zhejiang University: Hangzhou, China, 2015. [Google Scholar]
- Kang, S.; Schmidt, R.; Kelkar, K.M.; Radmehr, A.; Patankar, S.V. A Methodology for the Design of Perforated Tiles in Raised Floor Data Centers Using Computational Flow Analysis. IEEE Trans. Compon. Packag. Technol. 2001, 24, 177–183. [Google Scholar] [CrossRef]
- Karki, K.; Patankar, S. Airflow distribution through perforated tiles in raised-floor data centers. Build. Environ. 2006, 41, 734–744. [Google Scholar] [CrossRef]
- VanGilder, J.W.; Schmidt, R. Airflow Uniformity through Perforated Tiles in a Raised-Floor Data Center. In Proceedings of the ASME 2005 Pacific Rim Technical Conference and Exhibition on Integration and Packaging of MEMS, NEMS, and Electronic Systems collocated with the ASME 2005 Heat Transfer Summer Conference, San Francisco, CA, USA, 17–22 July 2005. [Google Scholar]
- Abdelmaksoud, W.A.; Khalifa, H.E.; Dang, T.Q.; Elhadidi, B.; Schmidt, R.R.; Iyengar, M. Experimental and Computational Study of Perforated Floor Tile in Data Centers. In Proceedings of the 12th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronics Systems (ITHERM), Las Vegas, NV, USA, 2–5 June 2010. [Google Scholar]
- Arghode, V.K.; Kumar, P.; Joshi, Y.; Weiss, T.; Meyer, G. Rack Level Modeling of Air Flow Through Perforated Tile in a Data Center. ASME J. Electron. Packag. 2013, 135, 030902. [Google Scholar] [CrossRef]
- Karki, K.C.; Radmehr, A.; Patankar, S.V. Use of computational fluid dynamics for calculating flow rates through perforated tiles in raised-floor data centers. HVAC R Res. 2003, 9, 153–166. [Google Scholar] [CrossRef]
- Beitelmal, A.H. Numerical investigation of data center raised-floor plenum. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015. [Google Scholar]
- Code for Design of Electronic Information System Room; GB 50174-2008; China Electronics Engineering Design Institute: Beijing, China, 2009.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).