Eco-Efficiency Evaluation Considering Environmental Stringency

Abstract

This paper proposes an extended data envelopment analysis (DEA) model for deriving eco-efficiency. In order to derive eco-efficiency, the proposed model utilizes the concepts of operational efficiency and environmental efficiency. Since DEA can separately measure operational efficiency and environmental efficiency, the treatment for constructing the unified indicator is required to ultimately evaluate eco-efficiency through balancing operational and environmental concerns. To achieve this goal, we define the environmental stringency as the business condition reflecting the degree of enforcing environmental regulations across the firms or particular industries in different countries. The proposed model provides flexibility, as required by the pollution-intensity of industry, in that it allows the decision maker to evaluate DMU’s (decision-making unit) eco-efficiency appropriately depending on the business environment. We present a case of agricultural production systems to help readers understand what eco-efficiency becomes when we vary the stringency conditions. Through the illustrative example, this paper presents the potential application by which different environmental stringencies can successively be incorporated in DEA.

1. Introduction

Recently, sustainability has become an undoubtedly critical issue, and many researchers involved in environment studies have been paying serious attention to the challenging topic in order to achieve both economic and environmental goals. Since the concept of eco-efficiency was first proposed by Schaltegger and Sturm [1], a number of researchers as well as organizations suggested their own definitions and also tried to link business with environmental issues, ultimately for sustainability. For example, according to the World Business Council for Sustainable Development, eco-efficiency is achieved by “the delivery of competitively priced goods and services that satisfy human needs and bring quality of life, while progressively reducing ecological impacts and resource intensity throughout the life cycle, to a level at least in line with the earth’s carrying capacity” [2]. Although the definitions are slightly different, in essence they have the common core that eco-efficiency means to “efficiently produce with less pollutants and energy”. Obviously, it is worth noting that the major concern of measuring eco-efficiency is on how to improve economic performance while diminishing environmental damages. So, currently, eco-efficiency is of high concern in many business areas.

Data envelopment analysis (DEA), first proposed by [3], is an effective tool in evaluating the efficiencies of a set of decision-making units (DMUs), which use multiple inputs to produce multiple outputs. DEA does not require the parametric specifications of a particular function and it also does not require the predetermined weights to be attached to each input and output. Since the original model was carried out, many researchers have contributed to the refinement and extension of DEA for the various fields of their interests. Traditional DEA models allow the users to evaluate the economic performance of individual DMUs, depending on a profitability perspective. However, because addressing the environmental performance of organizations has become one of the important issues, it is necessary to extend the present DEA techniques or develop new DEA techniques that take into account environmental impacts on the performance evaluation.

Over the past two decades, the efforts for environmental application using DEA have increased considerably (e.g., [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]). In general, the efficiency is derived from a fractional formulation that either minimizes inputs while holding outputs constant or maximizes outputs while holding inputs constant. Also, there are other approaches for maximizing outputs and minimizing inputs simultaneously. Under these optimization schemes, the result of DEA is directly affected by clearly defined input and output variables. Therefore, the inputs and outputs should be selected for a particular problem context. However, in the production process, traditional DEA models cannot provide accurate results if there are important variables that have a negative effect on the environment. Such environmentally detrimental factors can be considered undesirable outputs, which are often produced along with desirable outputs and are expected to be minimized. As Färe et al. [23] pointed out, the performances of DMUs turn out to be very sensitive to whether or not undesirable outputs are included. There are DEA studies that tried to incorporate undesirable outputs. For example, Färe and Grosskopf [24], Seiford and Zhu [25], and Liu et al. [26] clarified the issue of efficiency evaluation of undesirable outputs and provided the mathematical models to solve it.

Usually, the performance measure incorporating both desirable and undesirable outputs is used as a form of environmental efficiency in environment studies. Since DEA can separately measure the operational (technical) and environmental efficiency, the treatment for constructing the unified measure is required to ultimately evaluate eco-efficiency through balancing operational and environmental concerns. Among the aforementioned environmental studies, Korhonen and Luptacik [6], Zhang et al. [20], and Mahdiloo et al. [8] provided the DEA-based eco-efficiency models considering environmental variables by setting them to undesirable outputs. To derive eco-efficiency, they used an environmental efficiency (ecological efficiency) measure as the ratio of undesirable outputs to desirable outputs and combined it with traditional operational efficiency, defined as the ratio of desirable outputs to inputs. That is, the undesirable outputs behave like inputs for environmental efficiency calculation. Mahdiloo et al. [8] criticized the so-called three-step methods, suggested by [6,20], in that the combination of operational and environmental efficiency does not provide a valid eco-efficiency score. Furthermore, Mahdiloo et al. [8] suggested multiple objective linear programming (MOLP) to incorporate technical and environmental efficiency so as to reduce the computational burden resulting from the three-step methods. The MOLP model recognizes DMUs as being eco-efficient if and only if they are both operationally and environmentally efficient, while the former models identify them if a DMU is either operationally or environmentally efficient.

In this research, a modified DEA model is suggested for taking into account the environment-related factors. Along this line of research, this study attempts to determine eco-efficiency on the basis of the operational and environmental aspects without directly unifying both operational and environmental efficiency. In order to reflect environmental concern across business situations, we propose a new model with parametric constraints that represent the situational context of environmental concern. As pointed out by [6], studies on the impact of environmental policy on the efficiency measure across the firms or particular industries in different countries are required. Our research aimed at addressing this challenge.

To show applicability, agricultural production systems are illustrated by a new model suggested in this research. That is, we apply the modified DEA model to soybean data gathered from 94 farms in Iran. Recently, many agricultural applications have been examined to derive eco-efficiency using DEA methodology, focusing on regional specific evaluation (China [27], Canada [28], Iran [29], Japan [30], Spain [31]). In addition, other applications for eco-efficiency are employed for the evaluation of factories [4,9,15,19], power plants [6,10,14,18,32], supplier selection [8], regions and cities [7,12,13,16,17,21], and transportation [33]. Particularly, unlike previous studies, we present a generalized way to evaluate any condition with regard to the different levels of environmental pressures or environmental concerns.

The remainder of this paper is organized as follows. In Section 2, DEA formulations of operational and environmental efficiency are introduced with input decomposition. Also, the proposed model for eco-efficiency is presented. In Section 3, we illustrate the proposed method using soybean data collected from 94 farms in Iran. Finally, conclusions are given in Section 4.

2. Proposed Method

The conceptual DEA framework of eco-efficiency evaluation for sustainability is depicted in Figure 1.

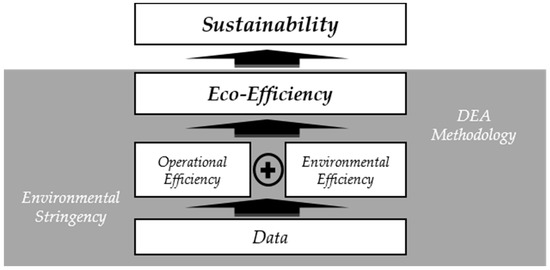
Figure 1. The conceptual framework.

Consistent with previous studies [6,20], the underlying eco-efficiency of the proposed model is based on the idea that undesirable outputs can be treated as inputs in a fractional form for efficiency calculation.

2.1. Input Decomposition

As a preliminary work, we decompose inputs in the proposed DEA model into two types, which are operational inputs and environmental inputs. Operational inputs consist of labor, machinery, resources, energy, etc. In some DEA studies, energy has evolved as an important measurement, and it has been widely investigated not only as an energy efficiency measurement [34,35,36] but also as an input variable [8,20]. Since our study is not limited to the efficient use of energy, the proposed model considers it as an input variable along with traditional inputs such as labor, machinery, and resources. It is reasonable to consider the energy (e.g., electricity, gasoline, diesel, natural gas, and so on) as an input because it is a key and basic resource in most production processes. Environmental inputs are defined as undesirable outputs, e.g., emission of CO₂, SO₂, or NO, which are generated from the entire production process. In this study, the life cycle inventory (LCI) information, which describes all the resources used and all the emissions released into the environment connected with the production process, is employed to determine environmental inputs more specifically.

2.2. Operational Efficiency

In general, the operational efficiency accounts for the capability of an organization that produces products or services in a cost-effective manner while ensuring the quality. Typically, it is defined as the ratio of the outputs to the inputs in a system. Thus, we define operational efficiency as the ratio of desirable outputs to operational inputs.

The traditional DEA model is the basis for developing a new model for eco-efficiency. This model implicitly assumes that all DMUs operate a constant returns to scale (CRS) transformation of the inputs into outputs. We adopt a CRS assumption in this study. When there are m operational inputs $x_{ij}$ (i = 1, 2, …, m) and s outputs $y_{rj}$ (r = 1, 2, …, s) for each DMU j (j = 1, 2, …, n), the operational efficiency of a particular DMU o can be formulated as the following fractional programming model:

$$\begin{array}{l}\max \frac{{\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}}}{{\displaystyle \sum _{i=1}^m{v}_i{x}_{io}}}\\ \mathrm{s}.\mathrm{t}.\\ \frac{{\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}}}\le 1\\ v_i\ge 0\\ u_r\ge 0\end{array}$$

(1)

where v_i and u_r are unknown non-negative weights for operational inputs and outputs, respectively. Also, Model (1) can be transformed into a linear model through the Charnes-Cooper transformation [37]:

$$\begin{array}{l}\max {\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}}\\ \mathrm{s}.\mathrm{t}.\\ {\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}}-{\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}}\le 0\\ {\displaystyle \sum _{i=1}^m{v}_i{x}_{io}}=1\\ v_i\ge 0\\ u_r\ge 0\end{array}$$

(2)

If the optimal value of the objective function in Model (2) equals to one, then it can be said of the specific DMU o that it is on the efficient frontier.

2.3. Environmental Efficiency

Compared to operational efficiency, environmental efficiency explains how efficiently produced the outputs are relative to the environmental inputs, as defined above. Thus, environmental efficiency is calculated as the ratio of outputs to environmental inputs. Assume there are p environmental inputs $z_{kj}$ (k = 1, 2, …, p) for each DMU j (j = 1, 2, …, n), the environmental efficiency of a particular DMU o can be formulated as follows:

$$\begin{array}{l}\max \frac{{\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}}}{{\displaystyle \sum _{k=1}^p{w}_k{z}_{ko}}}\\ \mathrm{s}.\mathrm{t}.\\ \frac{{\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}}}\le 1\\ w_k\ge 0\\ u_r\ge 0\end{array}$$

(3)

Model (3) also can be transformed to a linear model using the Charnes-Cooper transformation as follows:

$$\begin{array}{l}\max {\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}}\\ \mathrm{s}.\mathrm{t}.\\ {\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}}-{\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}}\le 0\\ {\displaystyle \sum _{k=1}^p{w}_k{z}_{ko}}=1\\ w_k\ge 0\\ u_r\ge 0\end{array}$$

(4)

2.4. A Model for Eco-Efficiency

At this stage, we proposed a more concrete DEA method for eco-efficiency using both operational and environmental efficiency simultaneously. If there are m operational inputs and p environmental inputs, the total weighted sum of the inputs to a DMU j can be calculated as ${\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}}+{\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}}$. Thus, eco-efficiency incorporating operational and environmental impacts on the process performance could be expressed as the ratio of the weighted sum of outputs to the weighted sum of total inputs. Accordingly, the eco-efficiency of a particular DMU o is formulated as follows:

$$\begin{array}{l}\max \frac{{\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}}}{{\displaystyle \sum _{i=1}^m{v}_i{x}_{io}}+\delta {\displaystyle \sum _{k=1}^p{w}_k{z}_{ko}}}\\ \mathrm{s}.\mathrm{t}.\\ \frac{{\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}}+\delta {\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}}}\le 1\\ v_i\ge 0\\ u_r\ge 0\\ w_k\ge 0\end{array}$$

(5)

In Model (5), the parameter δ reflects environmental regulation in a particular production problem. That is, in order for the decision maker to respond appropriately to a given situation, the parameter plays an adjusting role toward operational or environmental orientation. Specifically, the smaller δ explains the situation that focuses more on the operational excellence, while the larger δ implies the higher environment pressure that exists in the industry. Thus, we call this parameter δ the degree of environmental stringency that explains environmental sensitivity.

Also, this model is a generalized version of [6,20] because the two models lead to identical outcomes to the proposed model if δ = 1. This parameter illustrates the relative importance between operational and environmental inputs and is specified by the decision maker. By assigning the approporiate value to δ, the evaluation method for eco-efficiency can be flexibly applied to a variety of business situations with regard to the different levels of environmental pressures or environmental concerns. Using the Charnes-Cooper transformation with an additional constraint, this fractional programming Model (5) can be represented by the following linear programming model:

$$\begin{array}{l}\max {\displaystyle \sum _{r=1}^s{u}_r{y}_{ro}}\\ \mathrm{s}.\mathrm{t}.\\ {\displaystyle \sum _{r=1}^s{u}_r{y}_{rj}-{\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}}-\delta {\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}}}\le 0\\ {\displaystyle \sum _{i=1}^m{v}_i{x}_{io}}+\delta {\displaystyle \sum _{k=1}^p{w}_k{z}_{ko}}=1\\ v_i\ge 0\\ u_r\ge 0\\ w_k\ge 0\end{array}$$

(6)

We refer to this linear Model (6) as the base model in this study. To reflect the relative importance between a set of operational inputs and a set of environmental inputs, the base model can be modified by using adjustment parameter δ. If δ is larger than 1, the following constraint should be added to the base Model (6):

$${\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}}-\frac{1}{\delta }{\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}}\le 0$$

(7)

Constraint (7) implies the business condition that a set of environmental inputs is δ times more important than a set of operational inputs for any DMU. For example, if δ = 2, the constraint ensures that all DMUs will be assessed by satisfying $2{\displaystyle {\sum }_{i=1}^m{v}_i{x}_{ij}}\le {\displaystyle {\sum }_{k=1}^p{w}_k{z}_{kj}}$, meaning that a set of environmental inputs is at least two times more important than a set of operational inputs. In a similar manner, if δ is less than 1, the following constraint should be added to Model (6):

$$-{\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}}+\frac{1}{\delta }{\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}}\le 0$$

(8)

The balanced condition can be formulated by assigning δ equal to 1. In addition, as described above, if δ equals 1, the following equality condition should be included:

$${\displaystyle \sum _{i=1}^m{v}_i{x}_{ij}}-{\displaystyle \sum _{k=1}^p{w}_k{z}_{kj}}=0$$

(9)

By adding Constraint (7) or (8) or (9) to base Model (6), the pollution-intensity of an industry can successively be taken into account. Therefore, we call these constraints environmental stringency constraints.

Even though Model (5), when the value of δ equals to 1, is identical to the models of [6,20], the enhanced Model (6) with Constraint (9) is distinguished. Constraint (9) restricts the weights by satisfying the weighted sum of the operational inputs as equal to the weighted sum of the environmental inputs for all DMUs, while the earlier two models permit the most favorable weights to be chosen freely in the usual DEA manner. Namely, Constraint (9) explains a business environment that takes into account the equal importance of operational and environmental concerns for eco-efficiency evaluation. However, by adding Constraint (9), the programs may often become infeasible because it strictly restricts the decision space. Furthermore, it is difficult and unrealistic to extract an explicit recognition of a business environment that represents the exactly equal importance between operational and environmental concerns. To avoid infeasibility and unreality, the use of Constraints (7) and (8) is recommended. Through the non-strict inequality in Constraints (7) and (8), the results from the two independent models can be compared and analyzed in the situation in which the equal importance between operational and environmental aspects is elicited by the decision maker.

This restriction looks similar to a traditional restriction called Type II Assurance Region (ARII), which represents the relationships between input weights and output weights. However, the restriction suggested in this research is different in that it is imposed on a group of input variables while ARII imposes it on each single input. In other words, this restriction does not control the weights on all input variables directly but allows the most favorable weights to be chosen within a narrower condition. In addition, the use of such constraints can increase the discriminatory power of DEA because discriminatory power may be decreased if large numbers of inputs and outputs are involved relative to the number of DMUs [38]. As noted in [39], weight restrictions may be useful if one wishes to reduce the number of efficient DMUs. It may be especially helpful in environment studies where a large number of variables are extracted from the LCI data.

3. Illustrated Example

In this section, the proposed method is applied to agricultural production systems. The agricultural production system is suitable for applying the proposed approach since it consumes traditionally used inputs in typical production processes such as labor and machinery, as well as environment-related inputs such as chemicals and fertilizers. In addition, undesirable outputs are produced with desirable outputs. We adopted the LCI data presented by [29] for soybean farming evaluation. The inputs and outputs are selected from life cycle impact assessment, but the efficiency measure does not clearly identify the operational efficiency and environmental efficiency since they do not differentiate environmental inputs from operational inputs. The former study considered environment-related variables as aggregated measures such as chemicals and fertilizers. These variables were incorporated as inputs in the DEA model with other input measures of labor, machinery, diesel, water, electricity, farmyard manure (FYM), seeds, and the output of soybeans. However, the LCI data provides the original sources of chemicals and fertilizers. Specifically, the components of the chemicals are herbicides, insecticides, and K₂O, and the components of the fertilizers are urea and P₂O₅. Emissions of CH₄ and N₂O are also selected in the LCI data, but these are not directly considered variables in DEA. In this problem, a redefined input-output setting is summarized in the following Table 1.

Table 1. Input decomposition.

Operational Inputs	Traditional Inputs	Labor (h)
		Machinery (h)
		Water (m3)
		Seed (kg)
	Energy	Diesel (L)
		Electricity (kWh)
Environmental Inputs	Chemicals	Herbicides (kg)
		Insecticides (kg)
		K2O (kg)
	Fertilizers	Urea (kg)
		P2O5 (kg)
		FYM (kg)
	Undesirable Outputs	CH4 (kg)
	(direct gas emission)	N2O (kg)

To illustrate an application of the proposed eco-efficiency DEA model, the modified dataset of soybean farming is presented in Table 2. The data presented herein is collected for a combinational use of LCI and DEA data analyzed in [29]. The reader is referred to Mohammadi et al. [29] for the complete data. It is also noted that a rule of thumb by [38] is satisfied because the number of DMUs is over three times greater than the total number of input and output variables, although a large number of variables are utilized through the use of LCI data.

Table 2. Data set for the analysis.

DMU	Labor (h)	Machinery (h)	Water (m3)	Diesel (L)	Electricity (kWh)	Seed (kg)	Herbicides (kg)	Insecticides (kg)	Urea (kg)	P2O5 (kg)	K2O (kg)	FYM (kg)	CH4 (kg)	N2O (kg)	Soybean (kg)	Straw (kg)
1	169	16	2016	70	0	60	4	1.5	110	46	0	0	9.3	3.2	3500	4312
2	142	15	2150	65	0	60	3	0.5	55	23	0	2500	8.4	3.1	3000	3889
3	197	22	3360	88	1953	70	2	1	96	69	0	2500	8.4	3.2	3000	3889
4	254	35	2722	122	1286	70	3	2	110	46	0	7500	9.5	3.4	3600	4397
5	138	32	2464	111	1432	100	2	2.5	78	23	0	2222	0	3.2	3000	3889
6	152	28	2419	98	0	60	3	2	110	46	0	2000	0	3.7	3150	4016
7	148	28	2419	109	703	60	3	3	110	46	0	563	0	3.2	4150	4862
8	213	27	4838	109	1406	100	1	2	137	115	0	1250	9.3	3.3	3500	4312
9	159	18	2822	76	0	80	0	2	76	46	0	0	7.1	3.1	2300	3296
10	137	28	2822	96	0	70	3	3.5	76	46	0	0	0	3.4	2300	3296
11	272	26	2016	105	0	63	3	2	103	115	0	750	9.3	3.2	3500	4312
12	185	31	2419	126	1406	60	3	4.5	82	92	0	1500	0	3.6	3400	4227
13	228	35	1344	119	781	80	3	5	82	92	0	7500	8.4	3.4	3000	3889
14	264	22	1890	91	0	100	3	2	100	72	0	0	7.1	3.2	2315	3309
15	200	45	4032	150	1758	80	0	1.5	92	0	0	16,667	9.8	3.6	3750	4524
16	289	32	3528	115	2179	75	3	1.5	114	115	0	7500	0	3.4	3250	4100
17	282	35	3024	130	1758	60	3	2.5	105	92	0	4500	0	3.3	3500	4312
18	209	24	2621	83	1524	80	3	1	92	0	0	6000	7.7	3.3	2600	3550
19	268	33	7258	119	2901	80	3	8	92	0	0	12,500	8.4	3.5	3000	3889
20	210	55	3024	168	1538	60	0	1	64	46	0	10,000	9.3	3.4	35,007	4312
21	139	27	1260	108	732	60	3	4.5	114	115	0	9375	0	3.9	3500	4312
22	179	23	4536	109	1154	80	5	0.5	69	0	0	4000	0	3.8	4000	4735
23	200	40	2822	131	820	70	3	3.5	114	115	0	1111	8.6	3.2	3115	3986
24	245	29	2016	106	1172	80	3	1.5	87	46	0	3750	9.3	3.3	3500	4312
25	222	31	3226	93	1289	80	3	8	0	0	0	11,000	10.6	3.3	4200	4904
26	263	54	5443	175	2175	70	3	3.5	92	0	0	12,500	8.6	3.5	3100	3974
27	285	64	5443	203	2175	70	3	2.5	92	0	0	25,000	8.4	3.9	3000	3889
28	124	17	2419	69	0	55	3	0.5	78	23	25	0	0	3.5	3200	4058
29	215	15	5645	88	3282	70	0	1	87	46	0	0	9.3	3.1	3500	4312
30	134	14	4838	76	1406	70	0	1.5	69	0	0	0	6.6	3.1	2000	3043
31	137	17	2016	64	1318	60	3	3	78	23	0	833	0	3.1	3300	4143
32	201	17	3024	68	879	60	3	0.5	110	46	0	0	0	3.2	3600	4397
33	159	38	3528	128	2051	70	3	2.5	110	46	0	7500	9.3	3.4	3500	4312
34	269	50	2016	160	732	60	3	5.5	64	46	0	0	10.6	3.1	4200	4904
35	223	10	4838	65	2813	60	3	4.5	64	46	0	1500	8.4	3.1	3000	3889
36	145	24	3360	101	2075	60	0	3	64	46	0	0	7.5	3.1	2500	3466
37	176	29	4032	108	1172	70	3	2	64	46	0	2083	0	3.6	3500	4312
38	183	29	3629	100	1450	60	3	10.6	48	35	0	208	0	3.1	2800	3720
39	167	23	6048	93	3076	60	3	2.5	50	69	0	0	0	3.5	3000	3889
40	238	26	4032	95	879	55	3	2.5	64	46	0	0	9	3.1	3330	4168
41	290	34	6048	117	3516	90	3	6	197	92	0	0	9.3	3.4	3500	4312
42	206	24	3528	93	2051	60	3	5	128	92	0	3000	10.2	3.3	4000	4735
43	350	21	4032	120	1538	60	4	5	159	92	0	3000	9.1	3.4	3400	4227
44	133	31	3024	100	1154	75	3	6.5	96	69	0	0	9.3	3.2	3500	4312
45	169	25	3528	92	1025	70	3	3.5	0	0	0	6250	0	3.7	4000	4735
46	157	34	2822	108	820	70	3	3	110	46	0	3750	8	3.3	2800	3720
47	239	35	2822	120	1641	70	3	3.6	156	46	0	15,000	0	4.3	4000	4735
48	170	21	3360	89	855	60	3	1.5	115	0	150	0	9.3	3.2	3500	4312
49	220	50	3110	146	1582	80	3	4	135	81	13	10,000	9.3	3.5	3500	4312
50	277	29	4838	117	2813	60	1.25	4.5	110	46	0	0	9.9	3.2	3800	4566
51	186	48	2952	165	1791	65	1.5	3	92	0	0	21,429	0	4.3	3700	4481
52	189	20	2688	81	781	60	0	1.5	64	46	0	0	7.8	3.1	2666	3606
53	104	35	4838	124	2110	60	3	3	83	23	0	12,000	7.7	3.5	2600	3550
54	170	19	2520	75	1465	60	3	2	92	0	0	0	7.9	3.2	2700	3635
55	112	20	3226	101	2110	70	2	3	92	0	125	0	9.1	3.2	3400	4227
56	144	25	2112	106	1074	60	3.5	0.3	110	46	0	1500	0	3.7	3570	4371
57	179	15	3024	86	1978	60	0	1.5	92	0	100	0	8.4	3.2	3000	3889
58	215	30	3024	109	769	55	3	3	123	138	0	22,500	0	3.9	3500	4312
59	146	34	3629	134	1846	70	3	2.5	87	46	0	15,000	0	4.1	3800	4566
60	162	40	4657	147	2369	70	3	2.5	87	46	0	15,000	9.3	3.6	3500	4312
61	245	34	3528	119	1410	70	3	3	92	0	100	10,000	8.4	3.4	3000	3889
62	196	9	2016	61	513	100	3	2.5	32	23	0	417	0	3.4	2500	3466
63	187	19	2957	79	1934	70	2	2.5	137	115	0	0	8	3.3	2800	3720
64	163	21	2880	88	1465	70	3	3	115	0	50	2500	9.4	3.3	3570	4371
65	243	21	3024	86	824	55	3	3	123	138	0	5000	9.7	3.4	3700	4481
66	196	22	3326	103	2175	70	3	2.5	137	115	0	0	8	3.3	2800	3720
67	178	26	2150	100	0	60	3.5	0.3	110	46	0	1500	0	3.6	3000	3889
68	214	33	2688	132	1367	70	3.5	3	110	46	0	7500	0	3.9	3500	4312
69	169	27	2520	92	1282	70	3.5	0.5	92	0	50	7500	0	3.9	3600	4397
70	208	28	2464	104	1432	70	3	3	123	138	0	20,000	8	3.8	2800	3720
71	165	37	4032	124	1758	70	3	2	77	0	0	15,000	0	4	3500	4312
72	261	32	3528	124	2179	70	3	1.5	114	115	0	7500	0	3.8	2900	3804
73	283	38	3024	138	1758	70	3	1.5	69	0	100	5000	9.4	3.2	3550	4354
74	167	37	3276	136	1904	70	3	1	92	0	0	7500	7.7	3.4	2600	3550
75	211	31	2903	122	1477	60	0	1	46	0	50	10,000	9.1	3.3	3400	4227
76	155	36	3780	129	1030	70	3	2.5	69	0	0	10,000	0	3.4	3800	4566
77	154	30	2520	96	1007	70	3	2	110	46	0	7500	0	3.4	3300	4143
78	176	28	6451	119	2344	80	3	2.5	92	0	50	0	7.7	3.2	2600	3550
79	195	18	3629	89	1846	80	3	6	119	69	0	10,000	8.9	3.5	3300	4143
80	144	21	3226	93	1641	70	2	3	137	115	0	0	0	3.8	3900	4651
81	108	29	1613	98	820	60	3.5	1.5	64	46	0	7500	0	3.8	3700	4481
82	279	27	3360	116	916	90	4	4.5	160	115	0	15,000	8.9	3.7	3300	4143
83	309	12	2822	55	820	80	1	1	128	92	0	0	9.5	3.2	3600	4397
84	95	12	4704	66	0	60	3.5	2.5	87	46	50	10,000	0	3.4	3400	4227
85	141	25	2268	105	0	60	2	1.5	174	92	0	0	0	3.3	3200	4058
86	152	27	2100	103	0	60	0	2.5	91	115	0	12,500	0	3.9	3150	4016
87	127	19	2520	82	0	65	3	4.5	114	115	0	9375	8.5	3.5	3050	3931
88	121	21	2016	84	1172	60	3	2	46	0	0	10,000	0	3.8	3100	3974
89	213	6	2688	47	1074	70	2	1.5	105	92	0	0	0	3.2	2000	3043
90	171	17	4032	69	2344	70	3	1	92	0	0	0	0	3.5	2500	3466
91	192	18	6451	87	328	75	3	1	64	46	0	18,667	0	4	3000	3889
92	217	6	2688	48	1074	70	3	1.5	105	92	0	0	6.6	3.2	2000	3043
93	199	19	3629	72	2110	60	3	2	64	46	0	0	8.4	3.1	3000	3889
94	211	16	2520	58	1007	60	3	1.5	110	46	0	0	0	3.2	3200	4058

DMU: decision-making unit; FYM: farmyard manure.

3.1. Subsection Model (6) with δ = 1

First of all, base Model (6) is applied to this case study by assigning 1 to δ. As presented in Section 2.4, this setting makes Model (6) identical to the common model of [6,20]. The efficiency scores by Model (6) with δ = 1 are presented in the second column of Table 3. As shown in Table 3, 57 out of 94 DMUs are reported as eco-efficient in this setting (δ = 1). From the decision maker’s view, this figure may be regarded as unsatisfactory with respect to discriminatory power. As noted by [40], the single input and output, possibly minor, can be overweighed as a whole for a certain DMU; accordingly it may not really reflect the model’s performance. In this manner, DEA is more likely to produce such results since the unrestricted Model (6) identifies the efficient DMUs through the extremely optimistic schemes, even though the rule of thumb for the number of DMUs and variables is satisfied.

Table 3. Data envelopment analysis (DEA) results.

DMU	Model (6) (δ = 1)	OE	δ = 1/10	δ = 1/3	δ = 1/2	δ = 1	δ = 2	δ = 3	δ = 10	EE
1	1	1	1	1	1	1	1	0.968	0.94	0.937
2	1	0.94	0.944	0.977	1	1	1	1	1	1
3	0.836	0.706	0.709	0.732	0.759	0.823	0.834	0.832	0.824	0.823
4	0.888	0.76	0.761	0.773	0.786	0.86	0.882	0.88	0.875	0.874
5	1	0.67	0.674	0.705	0.743	0.938	1	1	1	1
6	1	0.901	0.908	0.976	1	0.981	0.827	0.8	0.774	0.772
7	1	1	1	1	1	1	1	1	1	1
8	0.97	0.625	0.63	0.673	0.731	0.914	0.939	0.921	0.895	0.892
9	1	0.615	0.621	0.68	0.762	1	1	0.956	0.869	0.861
10	1	0.642	0.645	0.68	0.719	0.918	0.879	0.82	0.765	0.76
11	1	1	1	1	1	1	0.945	0.92	0.9	0.897
12	0.895	0.818	0.819	0.83	0.845	0.88	0.871	0.866	0.854	0.852
13	0.903	0.804	0.806	0.831	0.86	0.832	0.702	0.684	0.67	0.669
14	0.783	0.706	0.707	0.719	0.733	0.727	0.644	0.624	0.609	0.607
15	1	0.678	0.683	0.737	0.812	1	1	1	1	1
16	0.823	0.659	0.661	0.673	0.686	0.774	0.823	0.823	0.823	0.823
17	0.872	0.84	0.843	0.848	0.854	0.869	0.862	0.861	0.86	0.86
18	0.923	0.605	0.607	0.632	0.665	0.832	0.788	0.776	0.765	0.764
19	0.704	0.572	0.575	0.599	0.624	0.688	0.703	0.702	0.701	0.701
20	1	0.838	0.845	0.909	0.997	1	1	1	1	1
21	1	1	1	1	1	0.945	0.793	0.77	0.753	0.751
22	1	0.827	0.832	0.88	0.946	1	1	1	1	1
23	0.745	0.643	0.644	0.651	0.659	0.716	0.745	0.745	0.745	0.745
24	0.983	0.821	0.823	0.847	0.871	0.956	0.963	0.942	0.92	0.917
25	1	0.897	0.904	0.963	1	1	1	1	1	1
26	0.797	0.635	0.638	0.659	0.685	0.789	0.785	0.781	0.777	0.777
27	0.78	0.614	0.616	0.64	0.666	0.762	0.716	0.707	0.7	0.699
28	1	1	1	1	1	1	1	1	1	1
29	1	0.87	0.878	0.964	1	1	1	1	1	1
30	1	0.517	0.522	0.571	0.638	0.966	1	1	1	1
31	1	1	1	1	1	1	1	1	1	1
32	1	1	1	1	1	1	1	1	1	1
33	0.841	0.747	0.748	0.758	0.769	0.824	0.834	0.831	0.828	0.828
34	1	1	1	1	1	1	1	1	1	1
35	1	1	1	1	1	0.98	0.846	0.788	0.749	0.745
36	1	0.629	0.634	0.68	0.739	0.976	0.984	0.966	0.95	0.948
37	0.964	0.769	0.772	0.797	0.814	0.915	0.959	0.956	0.953	0.953
38	1	0.689	0.692	0.722	0.743	0.897	1	1	1	1
39	1	0.762	0.766	0.798	0.825	0.943	1	1	1	1
40	1	0.884	0.887	0.913	0.931	0.988	1	1	1	1
41	0.834	0.623	0.625	0.64	0.658	0.778	0.83	0.813	0.798	0.796
42	1	1	1	1	1	0.996	0.958	0.946	0.914	0.911
43	0.881	0.866	0.869	0.881	0.881	0.864	0.799	0.784	0.753	0.75
44	1	0.819	0.823	0.868	0.926	0.985	0.913	0.87	0.835	0.832
45	1	0.939	0.946	1	1	1	1	1	1	1
46	0.666	0.63	0.631	0.64	0.65	0.666	0.663	0.662	0.661	0.661
47	0.901	0.845	0.846	0.855	0.864	0.882	0.847	0.835	0.825	0.824
48	1	0.908	0.913	0.95	0.991	1	1	1	1	1
49	0.77	0.639	0.64	0.651	0.663	0.737	0.77	0.77	0.77	0.77
50	1	0.915	0.919	0.958	1	1	1	0.993	0.988	0.988
51	1	0.821	0.825	0.859	0.904	1	1	1	1	1
52	1	0.71	0.715	0.769	0.836	1	1	1	1	1
53	0.83	0.721	0.723	0.748	0.769	0.773	0.651	0.636	0.625	0.623
54	1	0.746	0.749	0.773	0.803	0.954	1	1	1	1
55	1	0.932	0.937	0.991	1	1	1	1	1	1
56	1	0.924	0.927	0.957	0.997	1	1	1	1	1
57	1	0.858	0.867	0.948	1	1	1	1	1	1
58	0.92	0.918	0.92	0.92	0.92	0.872	0.781	0.77	0.762	0.761
59	0.932	0.837	0.838	0.853	0.869	0.923	0.901	0.881	0.864	0.862
60	0.837	0.741	0.743	0.756	0.771	0.822	0.829	0.824	0.82	0.819
61	0.78	0.628	0.631	0.655	0.681	0.766	0.78	0.779	0.776	0.775
62	1	0.98	0.988	1	1	1	1	1	1	1
63	0.781	0.693	0.696	0.725	0.747	0.771	0.741	0.723	0.707	0.705
64	1	0.871	0.875	0.903	0.934	1	1	1	1	1
65	1	1	1	1	1	0.965	0.875	0.861	0.85	0.848
66	0.75	0.647	0.649	0.663	0.673	0.721	0.727	0.714	0.703	0.701
67	1	0.857	0.865	0.945	0.999	1	1	0.946	0.865	0.859
68	0.766	0.733	0.734	0.739	0.744	0.764	0.752	0.746	0.741	0.74
69	1	0.859	0.862	0.895	0.934	1	1	1	1	1
70	0.656	0.635	0.636	0.65	0.656	0.64	0.605	0.597	0.588	0.587
71	0.958	0.737	0.74	0.769	0.808	0.946	0.933	0.926	0.92	0.919
72	0.695	0.602	0.603	0.615	0.627	0.685	0.695	0.695	0.695	0.695
73	1	0.732	0.735	0.763	0.799	0.967	1	1	1	1
74	0.798	0.544	0.546	0.569	0.599	0.757	0.742	0.733	0.726	0.726
75	1	0.818	0.824	0.886	0.969	1	1	1	1	1
76	1	0.818	0.822	0.855	0.901	1	1	1	1	1
77	0.855	0.787	0.788	0.801	0.815	0.852	0.837	0.828	0.821	0.82
78	0.883	0.511	0.512	0.53	0.555	0.76	0.883	0.883	0.883	0.883
79	0.853	0.762	0.765	0.789	0.812	0.839	0.767	0.75	0.719	0.716
80	1	0.965	0.971	1	1	1	1	1	1	1
81	1	1	1	1	1	1	1	0.992	0.965	0.962
82	0.715	0.606	0.607	0.623	0.639	0.696	0.701	0.694	0.679	0.678
83	1	1	1	1	1	1	1	1	0.997	0.992
84	1	1	1	1	1	1	0.912	0.867	0.833	0.829
85	1	0.966	0.973	1	1	1	1	1	1	1
86	1	0.943	0.952	1	1	1	1	1	1	1
87	1	0.927	0.932	0.986	1	0.914	0.723	0.696	0.669	0.666
88	1	0.909	0.912	0.941	0.981	1	0.944	0.912	0.885	0.882
89	1	1	1	1	1	0.942	0.718	0.681	0.656	0.653
90	1	0.668	0.672	0.715	0.754	0.95	1	1	1	1
91	1	0.683	0.686	0.715	0.749	0.954	0.961	0.942	0.928	0.926
92	1	1	1	1	1	0.823	0.577	0.557	0.537	0.535
93	1	0.82	0.822	0.847	0.864	0.958	0.987	0.972	0.958	0.957
94	1	0.988	0.993	1	1	0.976	0.912	0.9	0.89	0.889

OE: Operational efficiency; EE: Environmental efficiency.

Also, this model may look like it considers the relative importance of operational and environmental impacts due to δ in the normalization constraint. However, it does not appropriately consider the environmental impacts because no environmental stringency constraint is imposed, not only for a DMU o but also for other DMUs. Assume that the decision maker takes into account the business conditions such that both operational and environmental concerns are equally important. The stringency parameter may play a role in reflecting this condition to the DEA model by setting δ = 1. The model constrains the total weighted sum of operational and environmental inputs to be unity. Therefore, the weights v_i and w_k behave like homogeneous ones that constitute a single virtual input, without discriminating between operational and environmental inputs.

3.2. Operational Efficiency and Environmental Efficience

Operational efficiency and environmental efficiency are measured by Models (2) and (4), and these are presented in the third and the last column, respectively, in Table 3. As shown in Table 3, we see that 16 DMUs are operationally efficient and 34 DMUs are environmentally efficient. In the three-step methods, if a DMU is either operationally or environmentally efficient, it is identified as being eco-efficient. This characteristic is also criticized by [8]. However, eco-efficiency does not always pick the maximum value between the operational and environmental efficiency scores. Among efficient DMUs by Model (6), this feature is not applied to 12 DMUs (specifically DMU 6, 9, 10, 36, 44, 50, 67, 87, 88, 91, 93, and 94). For example, DMU 6’s eco-efficiency derived by Model (6) is neither operationally nor environmentally efficient (operational efficiency = 0.901, environmental efficiency = 0.772). We believe that this model is limited in measuring eco-efficiency appropriately because it provides misunderstandings, which stem from not being able to discriminate between operations- and environment-oriented processes and the eco-efficiency of DMUs. Specifically, for example, both DMU 20 and 21 are eco-efficient by the former model, but DMU 20 is more environment-oriented, while DMU 21 is more operations-oriented.

3.3. Eco-Efficiency

DEA is performed by adding Constraints (7) and (8) to Model (6). The fourth to the tenth columns of Table 4 present the eco-efficiency as parameter δ changes. It also noted that the settings δ = 1/10 and δ = 10 describe the extremely operations-oriented and environmental-oriented business envirionment, thus these could hardly be regarded as eco-efficiency. However, in this case study, we utilize these settings for the purpose of comparison to operational and environmental efficiency.

Table 4. The number of efficient decision-making units (DMUs).

	Model (6) with δ = 1	OE	δ = 1/10	δ = 1/3	δ = 1/2	δ = 1	δ = 2	δ = 3	δ = 10	EE
No. of DMUs	57	16	16	22	30	35	40	35	34	34

As expected, eco-efficiency converges to the operational efficiency as δ decreases. On the contrary it converges to the environmental efficiency as δ increases. Accordingly, the results of these two extreme conditions are very similar to the operational or environmental efficiency. First, we set the parameter δ to be 1 for both conditions by adding Constraints (7) and (8). Since both constraints share the equality condition although the directions are different, the two results provide the basis for deriving eco-efficiency from the conditions that reflects exactly same importance for operational and environmental concerns. As pointed out in Section 2.4, this condition is not realistic, but it is meaningful in that it provides the criterion for considering the different business environments. In this example, to incorporate the environmental stringency that reflects the equal importance of operational and environmental concerns, we use the average score of the models under Constraints (7) and (8) rather than using of Constraint (9).

The figures in Table 3 show the changes of efficiency as the environmental stringency. Among 94 DMUs, the eco-efficiency scores of DMU 7, 28, 31, 32, and 34 are 1 regardless of the value of the stringency parameter. In other words, one can interpret that these five DMUs are efficiently operating under any business conditions. Furthermore, these DMUs are not only operationally efficient but also environmentally efficient. In addition, comparing the number of efficient DMUs by Model (6), the proposed method overcomes the poor discriminatory power, a commonly reported problem in DEA. The numbers of efficient DMUs for the various settings of δ are presented in the Table 4.

As shown in Figure 2, 11 DMUs (DMU 1, 11, 21, 35, 42, 65, 81, 83, 84, 89, 92) are operationally efficient but environmentally inefficient. Under Model (6) with δ = 1, all these DMUs are eco-efficient. However, the proposed method cannot carry out such a result because the environmental stringency is not identified. Therefore, in order to simluate the proposed method, we tried to derive the eco-effiency by changing the degree of environmental stringency. Figure 2 presents the changes of efficiency scores of 11 operationally efficient DMUs by changing δ from 1/10 to 10. From the results, we conclude that these 11 DMUs are eco-efficient when the operational concern is at least two times more important than the environmental concern. However, eco-efficiency scores are decreased as δ increases. In other words, eco-efficient DMUs in certain environments may not be eco-inefficient in other environments.

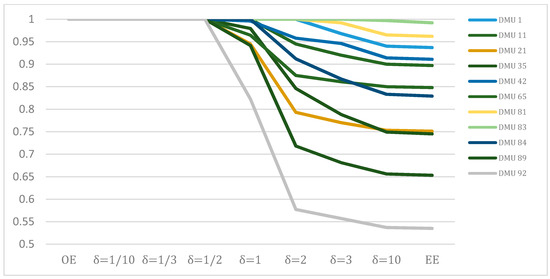
Figure 2. Changes of operationally efficient DMUs.

Figure 3 illustrates the efficiency changes of 29 DMUs, which are environmentally efficient but operationally inefficient. These 29 DMUs are regarded as being eco-efficient under Model (6) with δ = 1. However, the proposed model recognizes eco-efficient DMUs according to the environmental stringencty parameter. The simulation results show that all 29 DMUs are eco-efficient only when δ ≥ 2. The changes of the eco-efficiency of 29 DMUs are presented in Figure 3.

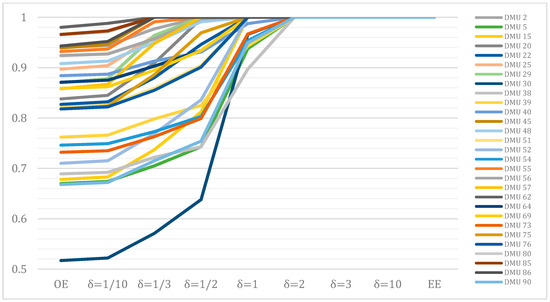
Figure 3. Changes of environmentally efficient DMUs.

Again, we highlight that five DMUs are eco-efficient regardless of the environmental stringency. Now, in order to evaluate DMUs under the specified business conditions, we assume that the decision maker specifies the value of the stringency parameter. Assume δ equals one. Then 35 DMUs are eco-efficient. Among them, 26 DMUs are either operationally efficient or environmentally efficient. However, there are four DMUs (DMU 9, 50, 67, 88), as shown in Figure 4, which are neither operationally efficient nor environmental efficiency but are eco-efficient.

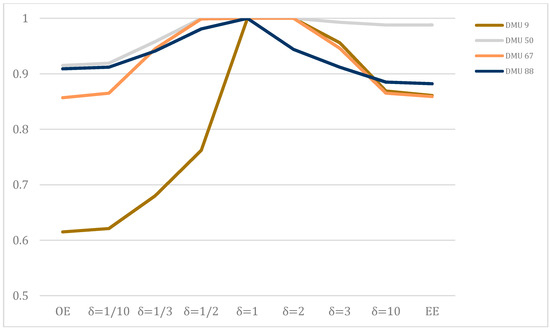
Figure 4. Efficiency changes of DMU 9, 50, 67, and 88.

Additionally, the eco-efficiency scores of some DMUs are not skewed towards either operations-oriented situations or environment-oriented situations. For example, DMU 9, 50, 67, and 88 are eco-efficient on the condition that equal importance is given to operational and environmental concerns. However, we should note that the scores of operational efficiency and/or environmental efficiency are not equal to 1. This result explains that some DMUs can be evaluated as being eco-efficient under a certain condition, even if they are not operationally efficient or environmentally efficient.

4. Conclusions

In this paper, we proposed a more concrete and flexible DEA method for evaluating eco-efficiency. By using the environmental stringency constraints, the proposed model allows users to evaluate DMUs’ performance in accordance with their business conditions. We analyzed a case example to present the results by varying the value of the stringency parameter. Also, the results were compared with the results from Model B in [6,20].

The main contributions of this study are three-fold. Firstly, the proposed model provides the flexibility, as required by the pollution-intensity of industry, in that it allows the decision maker to appropriately evaluate a DMU’s eco-efficiency depending on the business environment. This approach overcomes the disadvantage in the earlier studies, which provide eco-efficiency evaluation models without considering environmental stringency. Different environmental stringencies can successively be incorporated in DEA. Through the use of selective parametric restrictions, DEA can flexibly be applied to the eco-efficiency evaluation problem. Secondly, the proposed model provides clarification or a link between operational and environmental efficiency in a different way from previous eco-efficiency research. In the previous studies, a particular DMU is treated as being eco-efficient if it is either operationally or environmentally efficient. In other words, eco-efficiency is derived by picking a more favorable score between operational efficiency and environmental efficiency. However, the proposed method shows that this property cannot be applied when the environmental stringency is considered. Thirdly, the proposed method enhances the discriminant power. This contribution may seem relatively minor, but it is worth noticing that it can generate a reasonable number of efficient DMUs and produce more realistic results in real-world applications because unconstrained weights on its inputs and outputs are usually unacceptable [41].

Some of the further research opportunities are as follows. First, this study examines eco-efficiency by decomposing inputs into operational and environmental inputs. However, both undesirable outputs and undesirable inputs are considered as environmental inputs in the illustrative example, although environmental inputs are defined as undesirable outputs in the proposed model. Therefore, a technique for treating these two factors separately will be helpful for the input-output context. Second, the role of the stringency parameter described in the Section 2.4 provides some other ideas for future studies, particularly including possible extensions of our method to situations where equal importance between operational and environmental aspects exists. Finally, we can expect that much further improvement by a more detailed case study will enhance the practical use of DEA for eco-efficiency evaluation.

However, there are some limitations to the proposed model. First, the major limitation is the process of eco-efficiency approximation by taking an average of two scores when both operational and environmental concerns are equally important. Since incorporating equal importance between operational and environmental concerns is unrealistic when it applied to the evaluation model, it requires convincing ways of systematical improvement on a theoretical basis. Second, the proposed method only considers the evaluation problem, where all DMUs follow the same environmental stringency. Therefore, one should adopt a different approach if several DMUs belong to different business environments. This limitation also provides opportunities for further studies. The last limitation is the non-statistical property of DEA. Since efficiency scores are obtained by deterministic computation based on the data without statistical assumptions, the results are very sensitive to the data. This inherent weakness of DEA made it difficult to interpret the statistical reliability of the results. However, it is expected that statistical techniques such as bootstrapping can be better incorporated into a DEA-based eco-efficiency study.