Simplified I-V Characteristic Tester for Photovoltaic Modules Using a DC-DC Boost Converter
Abstract
:1. Introduction
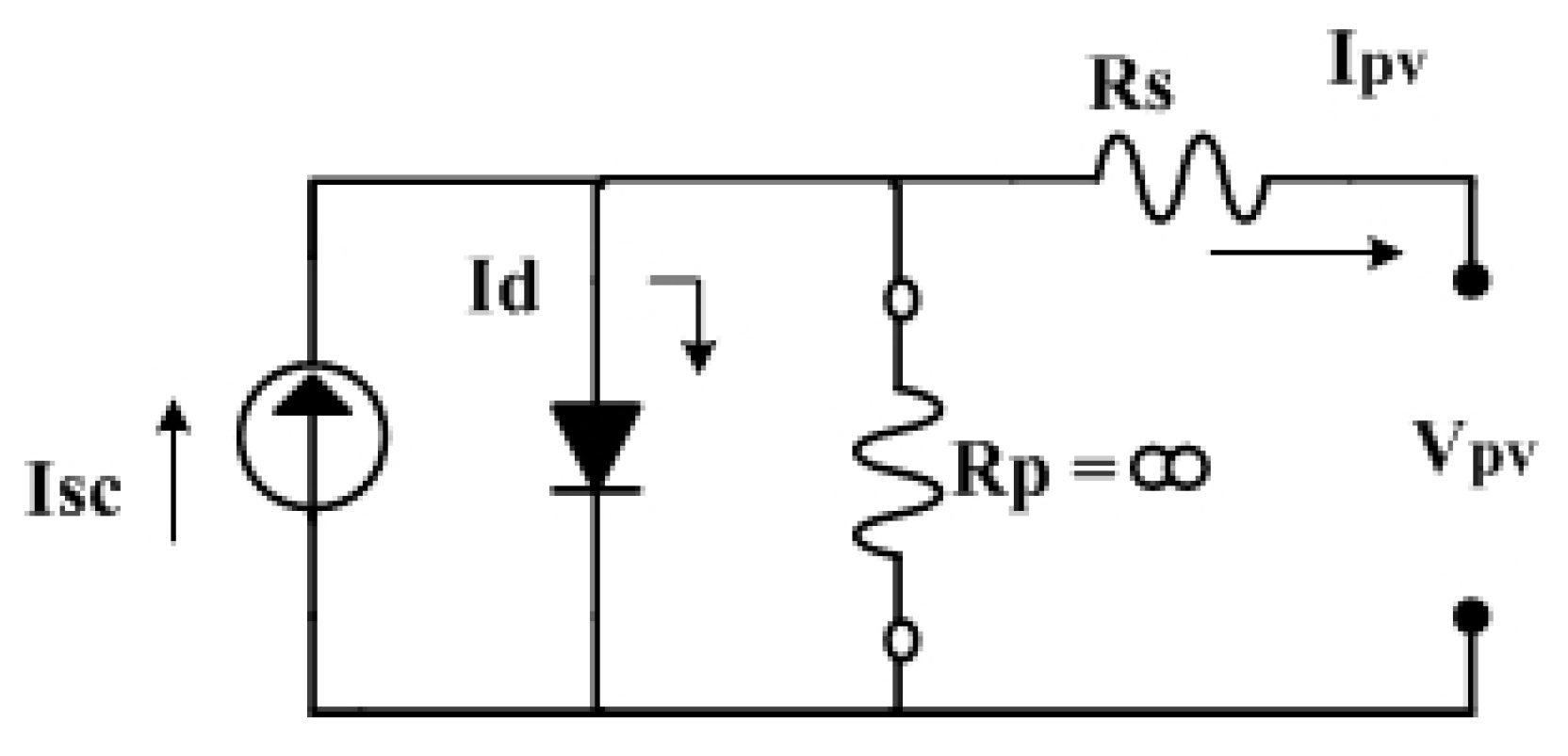
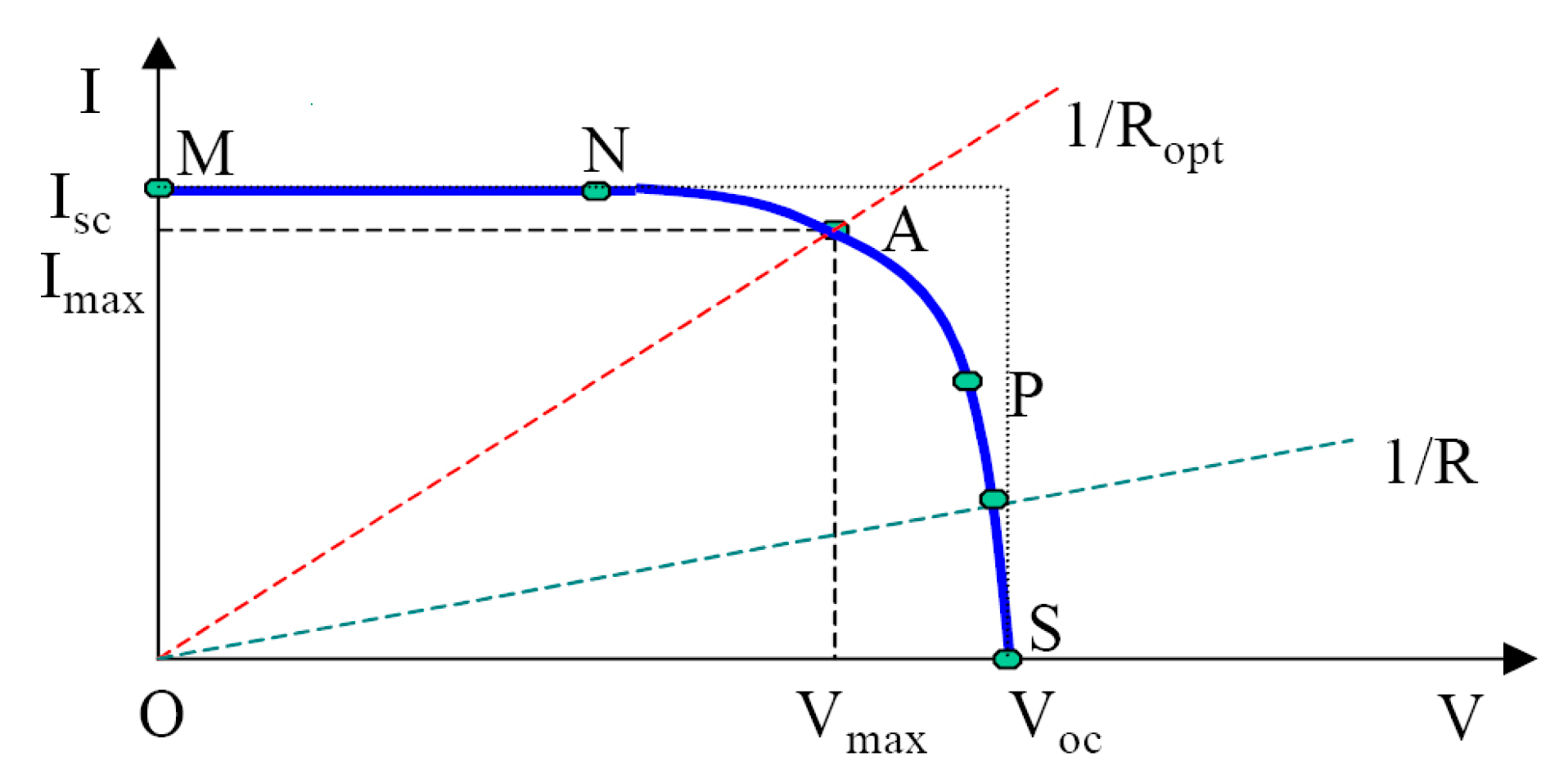
2. Solar Cell Mathematical Model
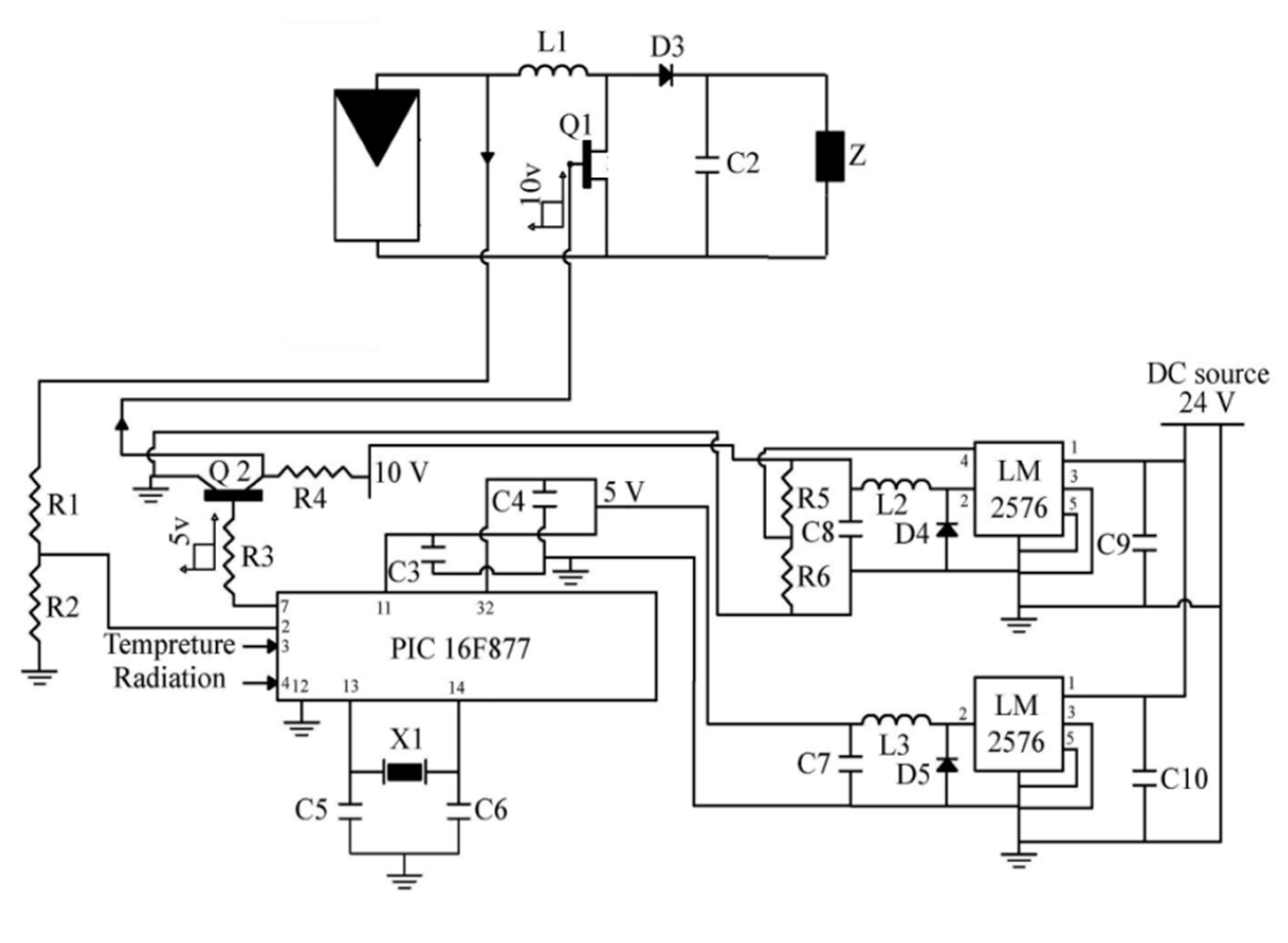
3. Proposed I-V Curve Testing System
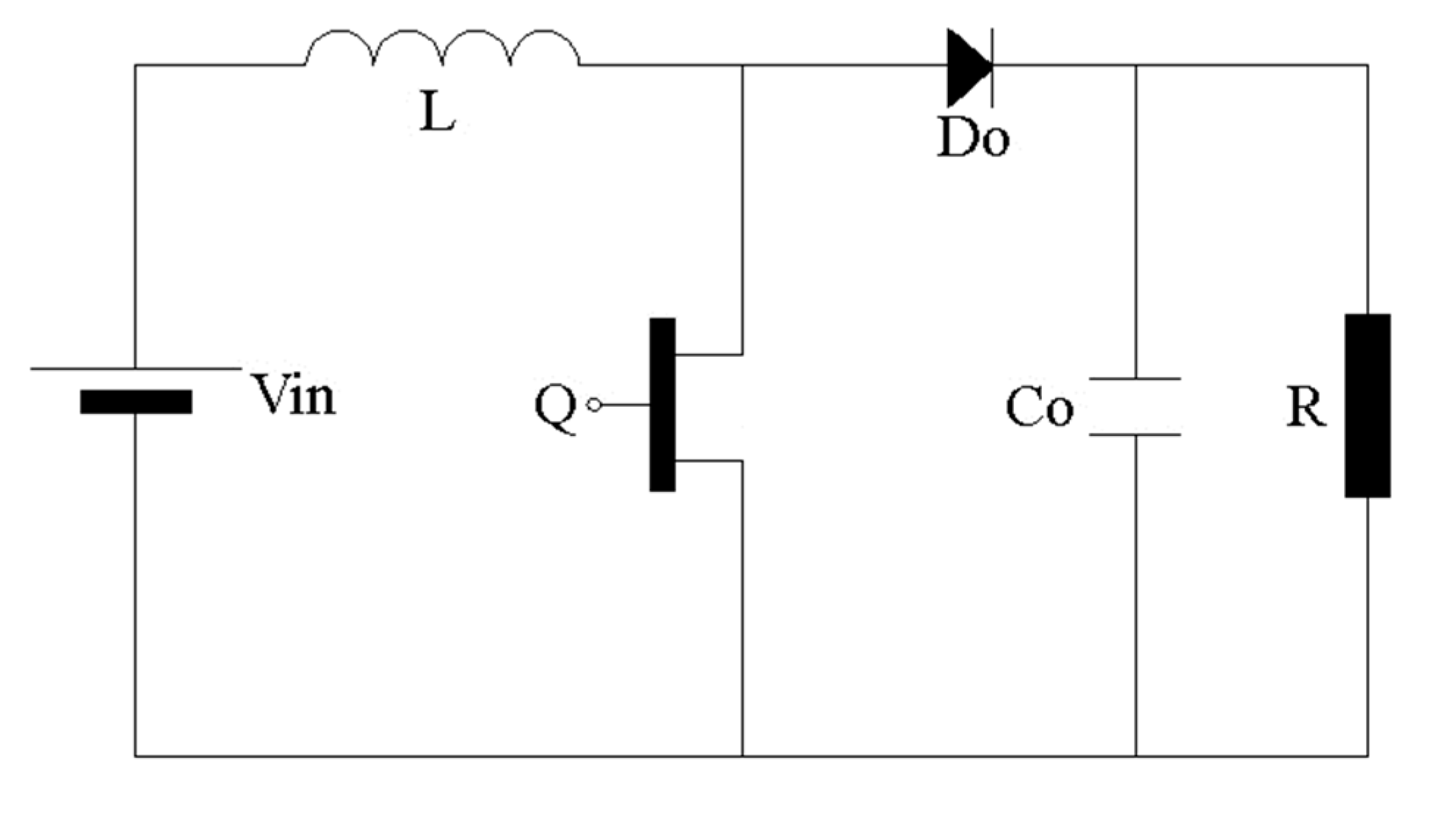
3.1. DC-DC Boost Converter Analysis
3.2. Control of the Proposed I-V Curve Testing System
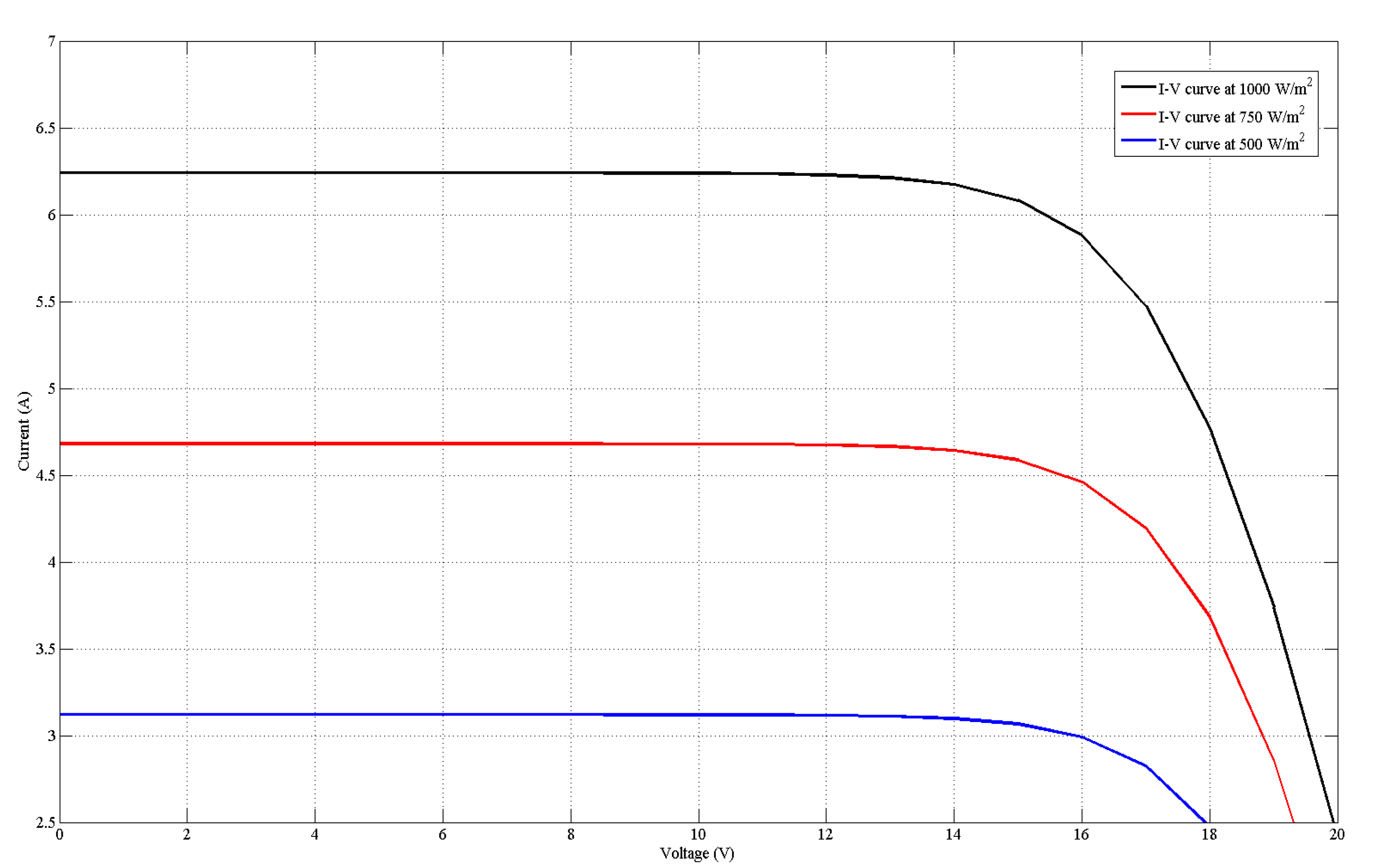
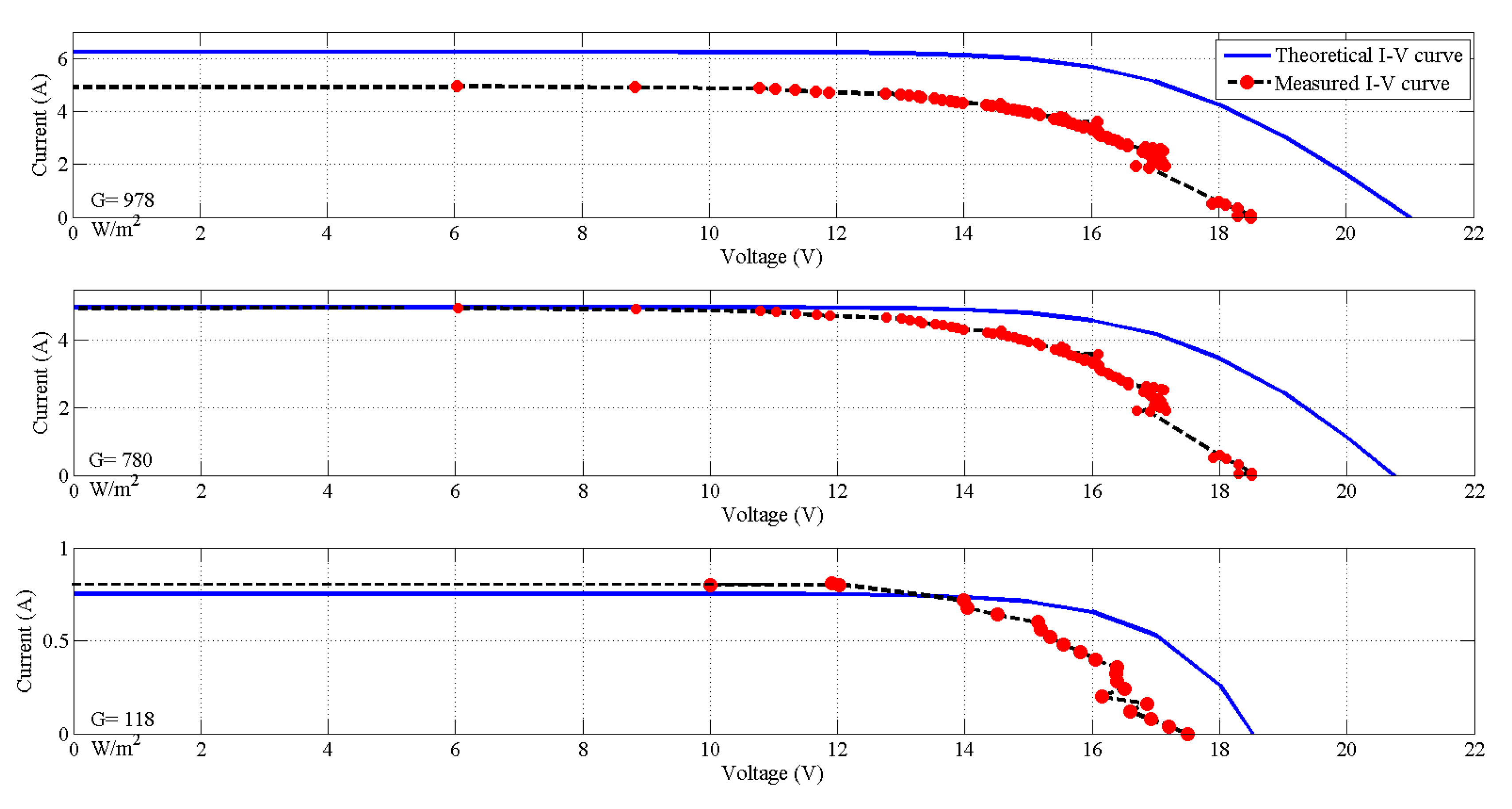
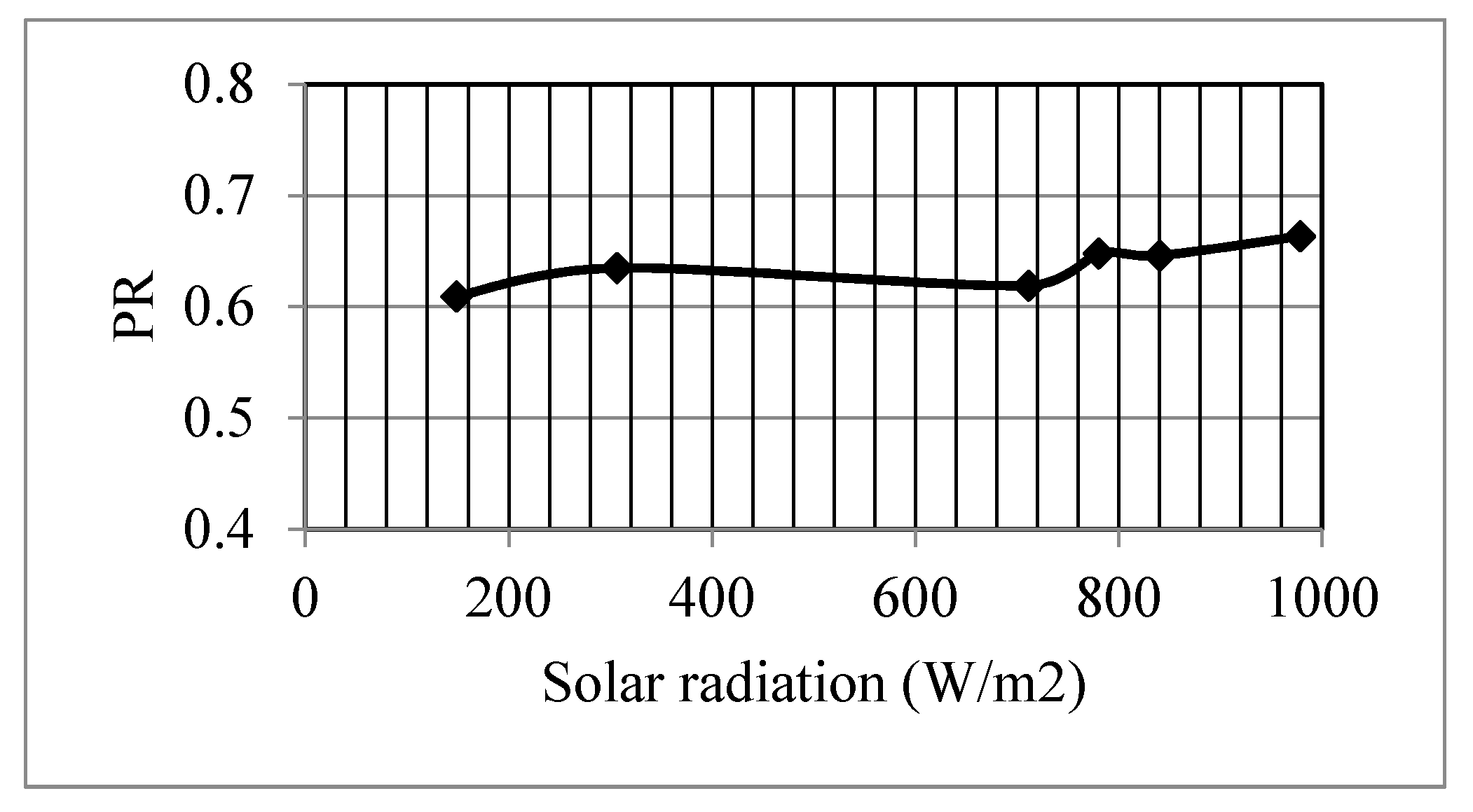
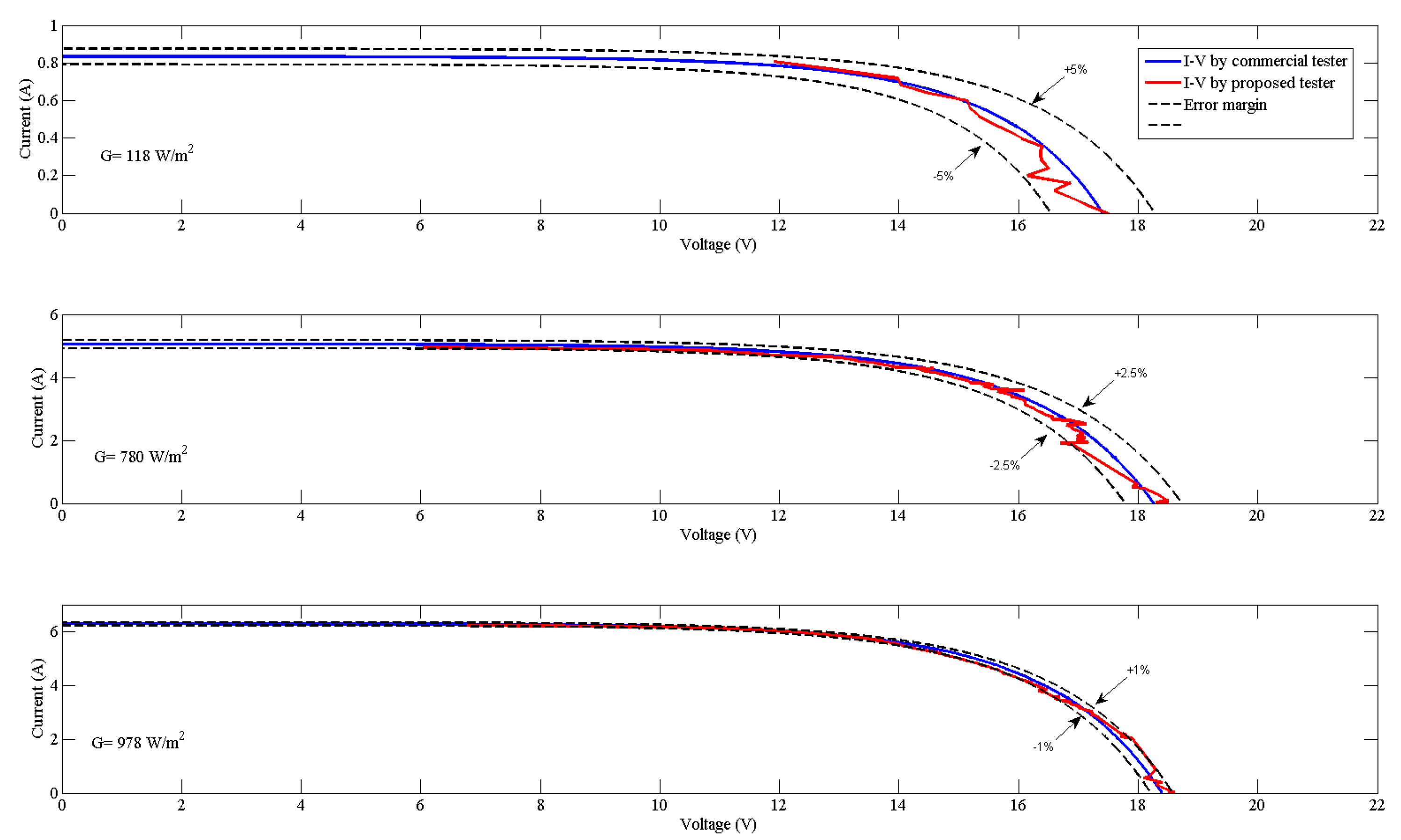
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Durán, E.; Andújar, J.M.; Galán, J.; Sidrach-De-Cardona, M. Methodology and experimental system for measuring and displaying I-V characteristic curves of PV facilities. Prog. Photovolt. Res. Appl. 2009, 17, 574–586. [Google Scholar] [CrossRef]
- Malik, A.Q.; Damit, S.J.B.H. Outdoor testing of single crystal silicon solar cells. Renew. Energy 2003, 28, 1433–1445. [Google Scholar] [CrossRef]
- Van Dyk, E.E.; Gxasheka, A.R.; Meyer, E.L. Monitoring current-voltage characteristics and energy output of silicon photovoltaic modules. Renew. Energy 2005, 30, 399–411. [Google Scholar] [CrossRef]
- Mahmoud, M.M. Transient analysis of a PV power generator charging a capacitor for measurement of the I-V characteristics. Renew. Energy 2006, 31, 2198–2206. [Google Scholar] [CrossRef]
- Muñoz, J.; Lorenzo, E. Capacitive load based on IGBTs for on-site characterization of PV arrays. Sol. Energy 2006, 80, 1489–1497. [Google Scholar] [CrossRef]
- Kuai, Y.; Yuvarajan, S. An electronic load for testing photovoltaic panels. J. Power Sources 2006, 154, 308–313. [Google Scholar] [CrossRef]
- Forero, N.; Hernandez, J.; Gordillo, G. Development of a monitoring system for a PV solar plant. Energy Convers. Manag. 2006, 47, 2329–2336. [Google Scholar] [CrossRef]
- Guvench, M.G.; Gurcan, C.; Durgin, K.; MacDonald, D. Solar simulator and I-V measurement system for large area solar cell testing. In Proceedings of the American Society for Engineering Education Annual Conference & Exposition, Washington, DC, USA, 20–23 June 2004; pp. 12747–12753. [Google Scholar]
- Fernandez-Reche, J.; Canadas, I.; Sáncheza, M.; Ballestrín, J.; Yebra, L.; Monterreala, R.; Rodrígueza, J.; Garcíaa, G.; Alonsob, M.; Chenlo, F. PSA Solar furnace, A facility for testing PV cells under concentrated solar radiation. Sol. Energy Mater. Sol. Cells 2006, 90, 2480–2488. [Google Scholar] [CrossRef]
- De Bias, M.A.; Torres, J.L.; Prieto, E.; Garcia, A. Selecting a suitable model for characterizing photovoltaic devices. Renew. Energy 2002, 25, 371–380. [Google Scholar] [CrossRef]
- Enrique, J.M.; Duran, E.; Sidrach-de-Cardona, M.; Andujar, J.M.; Boh6rquez, M.A.; Carretero, J.E. A new approach to obtain I-V and P-V curves of PV panels by using DC-DC converters. In Proceedings of the 31st IEEE PVSC, Lake Buena Vista, FL, USA, 3–7 January 2005; pp. 1769–1772. [Google Scholar]
- Duran, E.; Galan, J.; Sidrach-de-Cardona, M.; Andujar, J.M. A new Application of the Buck-Boost-Derived Converters to obtain the I-V curve of PV Modules. In Proceedings of the 38th IEEE PESC, Orlando, FL, USA, 17–21 June 2007; pp. 413–417. [Google Scholar]
- Sanchis, P.; Lopez, J.; Ursua, A.; Marroyo, L. Electronic Controlled Device for the Analysis and Design of Photovoltaic Systems. IEEE Power Electron. Lett. 2005, 3, 1748–1753. [Google Scholar] [CrossRef]
- Durán, E.; Andújar, J.M.; Pérez-Oria, M.E.M. Determination of PV Generator I-V/P-V Characteristic Curves Using a DC-DC Converter Controlled by a Virtual Instrument. Int. J. Photoenergy 2012, 2012, 13. [Google Scholar] [CrossRef]
- Durán, E.; Piliougine, M.; Sidrach-de-Cardona, M.; Galán, J.; Andujar, J.M. Different methods to obtain the I-V curve of PV modules: A review. In Proceedings of the 33rd IEEE Photovoltaic Specialists Conference (PVSC ‘08), San Diego, CA, USA, 11–16 May 2008. [Google Scholar]
- Castaner, L. Modeling Photovoltaic Systems Using PSPICE; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Gow, J.; Manning, C. Development of a photovoltaic array model for use in power electronics simulation studies. IEE Proc. Electr. Power Appl. 1999, 146, 193–200. [Google Scholar] [CrossRef]
- Xu, J. An Analytical Technique for the Analysis of Switching DC-DC Converters. Available online: http://ieeexplore.ieee.org/document/176586/ (accessed on 14 April 2017).
- Rashid, M.H. Power Electronics Handbook; Florida Academic Press: Miami, FL, USA, 2001. [Google Scholar]
- Khatib, T.; Sopian, K.; Kazem, H. Actual performance and characteristic of a grid connected photovoltaic power system in the tropics: A short term evaluation. Energy Convers. Manag. 2013, 71, 115–119. [Google Scholar] [CrossRef]
- Ya’acob, M.; Hizam, H.; Khatib, T.; Radzi, M. Acomparative study of three types of grid connected photovoltaic systems based on actual performance. Energy Convers. Manag. 2014, 78, 8–13. [Google Scholar] [CrossRef]
- Farhoodnea, M.; Mohamed, A.; Khatib, T.; Elmenreich, W. Performance evaluation and characterization of a 3-kWp grid-connected photovoltaic system based on tropical field experimental results: New results and comparative study. Renew. Sustain. Energy Rev. 2015, 42, 1047–1054. [Google Scholar] [CrossRef]
- Dihrab, S.; Khatib, T.; Sopian, K.; Al-Ani, H. On the Performance of hybrid PV/ unitized regenerative fuel cell system in the tropics. Int. J. Photoenergy 2012, 2012, 1–7. [Google Scholar] [CrossRef]
- Sopian, K.; Shaari, S.; Amin, N.; Zulkifli, R.; Nizam, M. Abdul Rahman. Performance of a grid-connected photovoltaic system in Malaysia. Int. J. Eng. Technol. 2007, 4, 57–65. [Google Scholar]
- Hussin, M.Z.; Omar, A.M.; Zain, Z.M.; Shaari, S. Performance of Grid-Connected Photovoltaic System in Equatorial Rainforest Fully Humid Climate of Malaysia. Int. J. Appl. Power Eng. (IJAPE) 2013, 2, 105–114. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khatib, T.; Elmenreich, W.; Mohamed, A. Simplified I-V Characteristic Tester for Photovoltaic Modules Using a DC-DC Boost Converter. Sustainability 2017, 9, 657. https://doi.org/10.3390/su9040657
Khatib T, Elmenreich W, Mohamed A. Simplified I-V Characteristic Tester for Photovoltaic Modules Using a DC-DC Boost Converter. Sustainability. 2017; 9(4):657. https://doi.org/10.3390/su9040657
Chicago/Turabian StyleKhatib, Tamer, Wilfried Elmenreich, and Azah Mohamed. 2017. "Simplified I-V Characteristic Tester for Photovoltaic Modules Using a DC-DC Boost Converter" Sustainability 9, no. 4: 657. https://doi.org/10.3390/su9040657
APA StyleKhatib, T., Elmenreich, W., & Mohamed, A. (2017). Simplified I-V Characteristic Tester for Photovoltaic Modules Using a DC-DC Boost Converter. Sustainability, 9(4), 657. https://doi.org/10.3390/su9040657




