Organic vs. Non-Organic Food Products: Credence and Price Competition

Abstract

We analyze the organic and non-organic production choices of two firms by considering customers’ trust in organic food products. In the context of customers’ possible willingness to pay a premium price and their mistrust in organic food products, two firms first make choices on offering organic and non-organic food products. If offering organic products, a firm can further invest in the credence system to increase customers’ trust in their organic products. At the final stage, two firms determine prices. We provide serval insights. First, we characterize the market conditions in which only one firm, both firms or neither firm will choose to offer organic food products. We find that the higher the production costs or credence investment costs for organic food products are, the more likely firms are to choose to produce non-organic food products. Second, if it is expensive enough to invest in organic credence, offering organic food products may still be uncompetitive, even if organic production cost appears to have no disadvantage compared to non-organic food products. Third, we highlight how the prices of organic food products in equilibrium are affected by market parameters. We show that when only one firm offers organic food products, this firm tends to offer a relatively low price if organic credence investment is expensive. Fourth, we highlight how one firm’s credence investment decision in equilibrium can be affected by the product type choice of the other firm. We find that the investment in organic credence is lower when both firms offer organic food products compared with the case when only one firm offers organic food products.

1. Introduction

The consumption of organic food has grown rapidly over the past two decades. Global sales for organic food increased from $23 billion in 2002 to 63 billion in 2011, accounting for 1–2% of total food production worldwide [1,2]. Such growth could be explained partially by consumers’ great concerns for personal health, and the environment since the organic production meets these two requirements [3]. The high nutritional value and the awareness of the risk of some diet-related diseases contribute to the health aspects of organic consumption motivation [3]. Besides, the belief that organic production overcomes the sustainable shortcomings of conventional farming, e.g., soil degradation, nutrient runoff, greenhouse gas emissions, biodiversity loss, and pesticide-born damage, etc. [4], contributes to sustainable aspects of organic consumption motivation.

On the demand side, consumers are willing to pay a premium price for organic food, which typically costs 10% to several times more than non-organic food [5]. However, lack of consumer trust is a barrier for the development of a market for organic food in some countries. On the supply side, despite the potential premium price, the organic producers (farmers/farming firms) usually face lower yields and higher production cost than conventional (non-organic) ones. For example, Seufert et al. [6] use a comprehensive meta-analysis to examine the relative yield performance of organic and conventional farming systems and find that organic yields are typically between 5% and 34% lower than conventional ones. Production costs for organic food are typically higher due to restricting the use of certain pesticides and fertilizers in farming which means that, the greater labor inputs, the high expense on fertility, weed control, and pest and disease control, etc.

Although increasing demand and potential premium price for organic food are motivating producers (farmers/farming companies) to transit to organic production, they face the following challenging questions: First, what are the profitable market conditions for producers of organically/non-organically produced food? Second, if organic production is chosen, how much should producers invest in their own credence systems to respond to consumers’ mistrust in organic producers and control systems? Organic food belongs to credence goods which means that customers cannot verify the organic attributes even after purchase and consumption [7]. Many customers fear being cheated while buying organic food even in the case where the products are labeled. To build the customers’ trust in organic products, many producers invest heavily in their own credence system to increase customer’s trust, e.g., by using a traceability system [8]. Pivato et al. [9] show that the corporate social performance of organic food firms may also increase consumer trust on a firm’s organic products. Thirdly, how should firms set a price for organically- and conventionally-produced food in a competitive market? To the best of our knowledge, there is no existing study on the topic of individual credence system investment in organic production although it has great and practical significance.

To address the above questions, we construct a Bertrand game-theoretic duopoly model where two firms have the choices of offering organic or non-organic products. Firms first make choices on the products types including organic products, which fit the customers’ organic preferences but incur higher production cost, and non-organic products, which do not fit the customers’ organic preferences but incur only moderate production cost. If the firm chooses to offer organic products, she can further make a decision on their credence systems investment to increase consumers’ trust in their organic products. Dependent on the previous decisions, firms finally make a pricing decision. The insights from our model are: First, we find that the product-type choice strategy depends on its cost efficiencies of production and organic investment credence investment, as well as the attractiveness of organic products. Specifically, the organic production cost, the credence investment cost, and the attractiveness of organic products can influence firms’ likelihood of offering organic products. The smaller the organic production cost and the credence investment cost are, the higher the attractiveness of organic products in the market and the more likely a firm offers organic products. Further more, we show that, even if organic production cost is the same as that of non-organic production, firms may still have no motivations to offer organic products if it is expensive enough to invest in organic credence. Second, we show that when only one firm offers organic food products, this firm tends to offer a relatively low price if it is expensive to invest in organic credence systems. Third, a firm offering organic products tends to invest more in organic credence when the rival offers non-organic products than when both firms offer organic products.

The rest of this paper is organized as follows. In Section 2, we analyze relevant previous literature. The model formulation and equilibrium analysis are presented in Section 3. Several numerical experiments are reported in Section 4 to examine the impacts of market parameters on the final equilibrium. We conclude this paper in Section 5, followed by all proofs in the appendix.

2. Related Literature

Three streams of literature are related to our model: the literature on organic production, the literature on the consumer trust and consumption of organic products, and the literature on the model based on the Hotelling’s model [10].

There are considerable studies that have attempted to gain insight into producers’ decision on the adoption of organic production [11]. The vast majority of the work in this area focuses on the economic determinants of adoption of organic production, although there are also some studies involving noneconomic factors, such as farmers’ personal characteristics, geographical issues, etc. [12]. Pietola and Lansink [13] investigate factors determining the choice between standard and organic farming technology in Finland and foud that decreasing output prices and increasing subsidies induce a switch to organic production. Läpple [14], utilizing Irish data, investigates empirically the adoption and abandonment of organic farming of the drystock sector, and reveal that offering fixed organic price premiums and better market outlets may encourage farmers not only to convert but also may secure the long-term economic viability of organic farms. Vollmer et al. [15] analyze whether the farmers’ investment behavior varies when given the option to invest in organic and conventional production methods. Acs et al. (2009) [16] investigate the effect of yield and price risk on the conversion decision from conventional to organic farming using a model maximizing the expected utility of the farmer depending on the farmers’ risk attitude. It is revealed that, for a risk-neutral farmer, converting to organic farming is optimal while for a more risk-averse farmer, it is optimal only if policy incentives are applied or if the market for the organic food products becomes more stable. Doernberg et al. [17] study potentials and limitations of regional organic food supply in the Berlin metropolitan region. They show that demand for regional organic food is higher than regional supply. However, the limitation is that regional organic food supply need to overcome some obstacles. Cavaliere et al. [3] analyze characteristics of vertical relationships of organic supply chains with a specific focus on the processing and retailing sectors. They show that the majority of the processing firms indicate quite a low bargaining power on the side of their customers. Brzezina et al. [4] adopt a system dynamics approach to study whether organic farming can reduce vulnerabilities and enhance the resilience of the European food system. They argue that organic farming has potential to bring resilience to the European food system, but it has to be carefully designed and implemented. Our work focuses on farmers’ choice between offering organic food products and non-organic food products in the competition environment, and results in several new insights.

Our work is also broadly related to the consumer trust and consumption of organic products. A large number of studies discuss consumers’ attitude and preference regarding organic food [18,19,20,21,22,23]. However, the analysis about the influences of trust on consumer decision-making is very limited although consumer trust is a key prerequisite for establishing a market for organic products [7,24]. Pivato et al. [9] study the impact of corporate social responsibility on consumer trust and the impact of that trust on consumers behaviors. Some papers consider consumer trust in organic consumption without systematically controlling for other important determinants of consumer choices [25,26,27]. Nuttavuthisit and Thøgersen [7] first explicitly investigate the importance of consumer trust for the emergence of a market for organic products, and find that the lack of consumer trust is a barrier for the development of a market for organic food. On the measures of building customers trust, labeling is the most widely studied. Rousseau [28] empirically investigates the effect of organic labeling on consumers’ purchasing behavior of chocolate. They find that, for most of the consumers, the organic label seems to become superfluous when selecting self-indulgent products. McCluskey [29] studies a series of game models where producers and customers sequentally make decisions. They show that repeat-purchase relationships and third-party monitoring are required for high-quality credence goods to be available. Amacher et al. [30] study a three stage game model including green production choices (eco-labeling), environmental quality provision and price. In their model, the consumers are able to observe the quality of the product; thus, customers trust is not a problem. Baksi and Bose [31] study producers’ optimal labeling decisions in signal game, where they can either self-label their products, or have them certified by a third party. They show that the government needs to supplement the labeling policy with costly monitoring activities in conditions under which corrupt producers can affix spurious labels. Bonroy and Constantatos [32] analyze credence goods markets in the case of two firms. They study the impacts of perfect labeling providing full information and imperfect labeling providing partial information on the outcome of the competition. A detailed and updated review about the labeling on credence is referred to [33]. Our paper differs from the above studies on labeling of credence goods in that we focus on firms’ own credence system of trust, such as building firms’ own traceability system and making advertisements.

In the model of our paper, two firms are competing on a product line, where customers are located. The distance from customers position to the ends of the product line represents the preference for a firm. This model is based on the Hotelling’s model, in which two firms compete in location and price within a linear city. The classic model has been widely applied in much work [34,35,36]. Gabszewicz and Thisse [34] study the product differentiation problem. Syam and Kumar [35], and Xia and Rajagopalan [36] analyze competition with customized and standard goods. In the above models, firms’ variety or customization decisions can directly change customers’ utility. Similar to this area of the literature, in our model, organic food products bring additional benefits to customers. The major difference is that we further introduce an organic trust attribute to customers. Firms’ investments on credence influences customers’ trust, and the customers’ buying behavior is based on their trust. To the best of our knowledge, the model in this paper first builds a connection from credence investment, to the consumer trust, then to consumer buying behavior, and finally to the firms’ demand function.

3. Model Formulation and Analysis

3.1. Model Setting

We consider a model where two symmetric firms which may be farmers/farming firms, denoted as Firm 1 and Firm 2 respectively, are competing in a market with M customers. Each firm can offer organic or non-organic food products. The customers are distributed uniformly on a product line of length 1 between the two firms, with Firm 1’s food products located at the left end, denoted by $x=0$, and Firm 2’s food products at the right end, denoted by $x=1$. A customer’s location at the product line is denoted as $x\in [0,1],$ representing their relative preference for two firms’ food products. A customer located at the left end of the product line ($x=0$) treats Firm 1’s product as an ideal product, and a customer located at the right end ($x=1$) treats Firm 2’s as their favorite. The distance from a customer’s location to the left (or right) end of this line, which is x (or $1-x$), denotes the difference between the customer’s ideal food products from Firm 1 (or Firm 2)’s food products. We assume that each customer has a unitary demand.

As mentioned in Section 1, organic food products fit the customers’ organic preferences and bring extra utility, but incur lower yields and higher production cost than non-organic food products. Thus, it is reasonable to assume that $c_o\ge c_n$ and define $c_{\Delta }=c_o-c_n$, where $c_o$ and $c_n$ denote the unit production cost of organic food products and non-organic food products, respectively. Note in some special cases, organic production cost may not be higher than non-organic production cost [37]. In our paper, we consider the general cases where organic production incurs higher cost.

As organic food is difficult to distinguish from non-organic food, firms offering organic products also need to invest in credence to respond to consumers’ potential mistrust in organic products. In this paper, a firm’s credence investment is spent on building their own credence system, thus we assume that the belief of consumers in two firms’ credence is independent. This setting is different from the authority-certified labeling investment where trusts are towards all labeled firms. Thus, the credence investment cost function is assumed as $C_B\left(a\right)=c_B{\left(1-a\right)}^{-1}$, where $a\in [0,1)$ is the ratio of customers in the whole market who trust the credence of organic products, and $c_B$ is a parameter which captures the cost of organic credence investment. This function is concave and increasing, which reflects that the cost $C_B$ and the marginal cost are both increasing in a. Besides, when a tends to 1, the investment cost tends to infinity. This property is in accordance with reality, where it is difficult to make all customers trust a firm’s organic products. For analysis convenience, we also assume that when the credence investment of a firm is less than a threshold value, i.e., $C_B\le c_B$, there will be no customers who trust their organic products. This assumption can be relaxed in future study. As in the more general case, there already exists some customer trust in a firm’s organic products even when the firm does not invest in any credence system. The monotonicity of cost function indicates that the credence cost $C_B\left(a\right)$ and the trust ratio a form a one-to-one mapping, e.g., for any fixed $C_B^{\prime }\ge c_B$, there always exists a $a\in [0,1)$ such that $C_B^{\prime }=c_B{\left(1-a\right)}^{-1}$. Thus, although the firms’ real decision is the investment, i.e., the value of $C_B$, we can use $a_i$ as a decision variable of firm i in the later sections for the sake of analysis convenience.

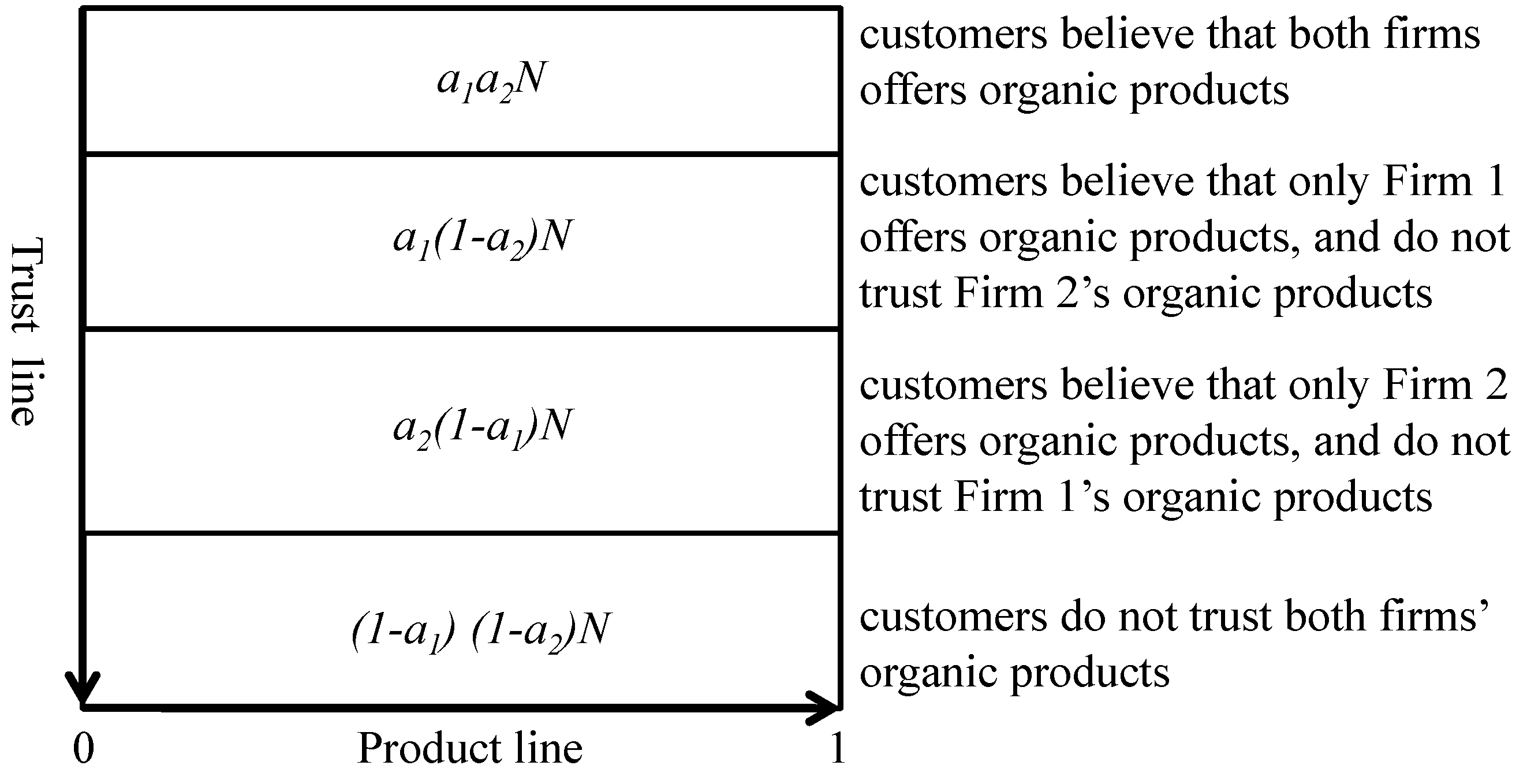
In addition to the product line, customers are also uniformly distributed along an organic trust line, where customers have different beliefs regarding the firms’ organic credence system. The product line and the trust line constitute a rectangular space, which represents the whole market where the customers are uniformly distributed. When both firms offer organic food products, given two firms’ organic credence system investment, the trust ratio $a_1$ and $a_2$ are determined. Along the trust line, the probability that a customer trusts both firms’ organic food products is $a_1{a}_2$, the probability that a customer trusts Firm1’s organic food products but does not trust Firm 2’s organic food products is $a_1(1-a_2)$, the probability that a customer trusts in Firm2’s organic food products but does not trust Firm 1’s organic food products is $a_2(1-a_1)$, and the probability that a customer does not trust both firms’ organic food products is $(1-a_1)(1-a_2)$. Thus, we can see that the whole market can be divided into four parts: $a_1{a}_{2}M$ customers trusting both Firms’ organic food products, $a_1(1-a_2)M$ customers only believing that firm 1’s food products are organic, $a_2(1-a_1)M$ customers only believing that Firm 2’s food products are organic, and the rest $(1-a_1)(1-a_2)$ of the customers trust neither of the two firms. The market structure is illustrated in Figure 1.

Customers choose organic or non-organic food products of the two firms based on their own food product preference, the price, and their trust as to whether the food products are organic. Suppose that Firm 1 offers organic food products to customers at a price $p_1$. For the customer at location x of product line believing that the product is organic, the net utility of buying an organic product from Firm 1 is $U+u_o-p_1-tx$, where U is the utility for a customer getting their ideal non-organic product for free, $u_o$ is the additional utility from an organic product compared to a non-organic product, and U and $u_o$ are the same for all customers. In general, customers may have different utility in organic products, for example sometimes the willingness to pay for organic food is even negative [28]. However, for the sake of analysis convenience, we assume homogeneity in organic utility. Similar homogeneity in utility assumption can be seen in [32]. This utility function is quite intuitive. A customer’s utility is linearly decreasing in the charged price $p_1$ and the degree of difference to customer’s ideal product, x. The term $tx$ represents the loss of utility due to the difference between Firm 1’s food products and the ideal food products of a customer at x, where t is the intensity of relative preference of firms. When t is very small, e.g., $t=0$, customers have almost no preference differences between two firms. A higher t implies a bigger difference between two firms. If the customer does not trust the organic food products, they treats them as non-organic food products. Thus, the net utility of buying an organic product from Firm 1 is $U-p_1-tx$. Suppose that Firm 1 offers non-organic food products to customers at a price $p_1$. For the customer located at x of product line, the net utility of buying a non-organic product from Firm 1 is $U-p_1-tx$. Similarly, when Firm 2 offers organic food products, the customer trusts that the organic food products gets utility $U+u_o-p_2-t(1-x)$, while the customer that does not trust organic food products gets utility $U-p_2-t(1-x)$. A customer buys organic or non-organic food products from the firm that offers them a higher utility. In this study, we consider the case that the whole market is covered by the two firms, and thus assume U is large enough so that all customers’ net utility are nonnegative. Here, we also assume $u_o>c_{\Delta }$, i.e., the additional utility of a organic product is higher than the required additional production cost.

We consider an three-stage game. At the first stage, both firms decide whether to offer organic or non-organic food products. We denote the first stage decision of Firm i, $i\in (1,2)$, as $S_i\in \{O,N\}$, where O represents the decision to offer organic food products, and N represents the decision to offer non-organic food products, respectively. We use $(S_1,S_2)$ to denote the outcome of the first stage decisions. At the second stage, given the strategy decisions $(S_1,S_2)$, firms choosing to offer organic food products determine the investment on the organic credence while the ones choosing to offer non-organic food products do not make a decision. At the final stage, two firms determine the prices for organic or non-organic food products. After the price decision, the demand is realized. For such a multi-stage game, it is more analytically convenient to consider a simultaneous decision game than sequential game, e.g., [30,36]. Besides, in a sequential decision game, the sequence of decision will have an impact on the final equilibrium, where the first mover may have more advantages. To avoid such additional first mover advantage and focus on the impacts of market conditions, we consider a simultaneous decision game.

3.2. Equilibrium Analysis

At stage 1, since each firm can decide to offer organic or non-organic food products, we analyze the following subgames induced by the outcomes of the first stage before analyzing the overall game: (1) Both firms offer non-organic food products, denoted as $(N,N)$; (2) Both firms offer organic food products, denoted as $(O,O)$; (3) Firm 1 offers organic food products while Firm 2 offers non-organic food products, denoted as $(N,O)$. In this model, as we assume that two firms are symmetric, the analysis of $(O,N)$ is same to that of $(N,O)$.

3.2.1. Both Firms Offer Non-Organic Food Products

When both firms decide to offer non-organic food products, they just need to determine the price at the final stage. Using standard backward induction, we first consider the firms’ pricing decisions at the final stage.

From the utility function, we can see that a customer located at $x^{<N,N>}$ is indifferent between the two firm’s food products iff:

$$U-p_1-t{x}^{<N,N>}=U-p_2-t(1-x^{<N,N>}).$$

(1)

It can be derived from the Equation (1) that the customer’s location is $x^{<N,N>}={\displaystyle \frac{p_2-p_1+t}{2t}}$. Those customers whose locations are at the left to $x^{<N,N>}$, i.e., $x\le x^{<N,N>}$, will buy one unit of non-organic food products from Firm 1, and the rest customers, i.e., $x\ge x^{<N,N>}$ will purchase one unit of Firm 2’s non-organic food products. Thus the demands of Firm 1 and Firm 2 are $D_1^{<N,N>}={\displaystyle \frac{p_2-p_1+t}{2t}}M$ and $D_2^{<N,N>}={\displaystyle \frac{p_1-p_2+t}{2t}}M$, respectively.

Back to the pricing decision stage, two firms determine the prices to maximize their own profits, which are ${\pi }_1^{<N,N>}={\displaystyle \frac{p_2-p_1+t}{2t}}M(p_1-c_n)$ and ${\pi }_2^{<N,N>}={\displaystyle \frac{p_1-p_2+t}{2t}}M(p_2-c_n)$. Using first order conditions, we can obtain the equilibrium solutions in the subgame $(N,N)$, which are stated in Proposition 1.

Proposition 1.

If both firms choose to offer non-organic food products to customers at the first stage, the equilibrium prices are: $p_1^{<N,N>}=p_2^{<N,N>}=t+c_n$, and the equilibrium profits are: ${\pi }_1^{<N,N>}={\pi }_2^{<N,N>}={\displaystyle \frac{tM}{2}}$.

In the subgame $(N,N)$, both firms charge the same price that exceeds unit production cost $c_n$ by t. While t represents the difference between two firms’ food products, firms can charge a higher price when t is larger. This is in accordance with the conclusion of prior literature, i.e., [38], that increasing firm differentiation will lower the intensity of price competition. The expected profits of two firms are the same and increasing with the market size M and t. Thus, a larger market size or a bigger firm differentiation will lead to higher expected profits of the two firms.

3.2.2. Both Firms Offer Organic Food Products

When both firms decide to offer organic food products to customers at the first stage, they need to determine the investment on the credence of organic food products at the second stage and the prices at the final stage.

We first analyze the market structure for given credence investment decisions. Given Firm 1’s decision $a_1$ and Firm 2’s decision $a_2$, the whole market can be divided into four parts as discussed in Section 3. Now we analyze the two firms’ market share for given price and credence investment decisions. We analyze the two firms’ demand in four parts of the market respectively, and then we sum up these demands to get the total demands.

For the $a_1{a}_{2}M$ customers who believe that both firms offer organic food products, a customer located at $x_1^{<O,O>}$ is indifferent between two firm’s food products iff:

$$U+u_o-p_1-t{x}_1^{<O,O>}=U+u_o-p_2-t(1-x_1^{<O,O>}).$$

(2)

It can be derived from the above equation that the customer’s location is $x_1^{<O,O>}={\displaystyle \frac{p_2-p_1+t}{2t}}$. Those customers whose locations are at the left to $x_1^{<O,O>}$, i.e., $x\le x_1^{<O,O>}$, will buy a unit of organic food products from Firm 1, while the rest customers will purchase a unit of organic food products from Firm 2. Thus, the demands of Firm 1 and Firm 2 in this part of market are $D_{1,1}^{<O,O>}={\displaystyle \frac{p_2-p_1+t}{2t}}{a}_1{a}_{2}M$ and $D_{2,1}^{<O,O>}={\displaystyle \frac{p_1-p_2+t}{2t}}{a}_1{a}_{2}M$, respectively.

For $a_1\left(1-a_2\right)M$ customers who trust Firm 1’s organic food products and do not trust Firm 2’s organic food products, a customer located at $x_2^{<O,O>}$ is indifferent between the two firm’s food products iff:

$$U+u_o-p_1-t{x}_2^{<O,O>}=U-p_2-t(1-x_2^{<O,O>}).$$

(3)

It can be derived from the above equation that the customer’s location is $x_2^{<O,O>}={\displaystyle \frac{p_2-p_1+u_o+t}{2t}}$. Since we are interested in a more general case when both firms are in the market, we impose a condition $x_2^{<O,O>}\in [0,1]$, which requires an assumption $t\ge u_o$, i.e., firm differentiation is sufficiently large. Those customers located at the left to $x_2^{<O,O>}$, i.e., $x\le x_2^{<O,O>}$, will buy one unit of organic food products from Firm 1, and the other customers will purchase a unit of organic food products from Firm 2. Thus, the demands of Firm 1 and Firm 2 in this part of market are $D_{1,2}^{<O,O>}={\displaystyle \frac{p_2-p_1+u_o+t}{2t}}{a}_1\left(1-a_2\right)M$ and $D_{2,2}^{<O,O>}={\displaystyle \frac{p_2-p_1-u_o+t}{2t}}{a}_1\left(1-a_2\right)M$, respectively.

For $a_2\left(1-a_1\right)M$ customers who trust Firm 2’s organic food products and do not trust Firm 1’s organic food products, a customer located at $x_3^{<O,O>}$ is indifferent between the two firm’s food products iff:

$$U-p_1-t{x}_3^{<O,O>}=U+u_o-p_2-t(1-x_3^{<O,O>}).$$

(4)

It can be derived from the above equation that the customer’s location is $x_3^{<O,O>}={\displaystyle \frac{p_2-p_1-u_o+t}{2t}}$. Those customers located at the left to $x_3^{<O,O>}$, i.e., $x\le x_3^{<O,O>}$, will buy one unit of organic food products from Firm 1, and the other customers will purchase a unit of organic food products from Firm 2. Thus, the demands of Firm 1 and Firm 2 in this part of market are $D_{1,3}^{<O,O>}={\displaystyle \frac{p_2-p_1-u_o+t}{2t}}{a}_2\left(1-a_1\right)M$ and $D_{2,3}^{<O,O>}={\displaystyle \frac{p_2-p_1+u_o+t}{2t}}{a}_2\left(1-a_1\right)N$, respectively. For the rest $\left(1-a_1\right)\left(1-a_2\right)M$ customers who do not trust both firms’ organic food products, a customer located at $x_4^{<O,O>}$ is indifferent between the two firm’s food products iff:

$$U-p_1-t{x}_4^{<O,O>}=U-p_2-t(1-x_4^{<O,O>}).$$

(5)

It can be derived from the above equation that the customer’s location is $x_4^{<O,O>}={\displaystyle \frac{p_2-p_1+t}{2t}}$. Those customers whose locations are at the left to $x_4^{<O,O>}$, i.e., $x\le x_4^{<O,O>}$, will buy a unit of organic food products from Firm 1, and the rest customers will purchase a unit of organic food products from Firm 2. Thus, the demands of Firm 1 and Firm 2 in this part of market are $D_{1,4}^{<O,O>}={\displaystyle \frac{p_2-p_1+t}{2t}}(1-a_1)$$\left(1-a_2\right)M$ and $D_{2,4}^{<O,O>}={\displaystyle \frac{p_1-p_2+t}{2t}}(1-a_1)\left(1-a_2\right)M$, respectively. Thus the total demands of two Firms are:

$$D_1^{<O,O>}=D_{1,1}^{<O,O>}+D_{1,2}^{<O,O>}+D_{1,3}^{<O,O>}+D_{1,4}^{<O,O>}={\displaystyle \frac{M}{2t}}\left[p_2-p_1+t+u_o(a_1-a_2)\right],$$

(6)

$$D_2^{<O,O>}=D_{2,1}^{<O,O>}+D_{2,2}^{<O,O>}+D_{2,3}^{<O,O>}+D_{2,4}^{<O,O>}={\displaystyle \frac{M}{2t}}\left[p_1-p_2+t-u_o(a_1-a_2)\right].$$

(7)

Now we analyze the equilibrium price and organic credence investment decisions. Using standard backward induction, we first consider two firms’ pricing decisions at the final stage. Two firms determine their prices to maximize their own profits:

$${\pi }_1^{<O,O>}={\displaystyle \frac{M}{2t}}\left[p_2-p_1+t+u_o(a_1-a_2)\right](p_1-c_o)-c_B{\left(1-a_1\right)}^{-1},$$

(8)

$${\pi }_2^{<O,O>}={\displaystyle \frac{M}{2t}}\left[p_1-p_2+t-u_o(a_1-a_2)\right](p_2-c_o)-c_B{\left(1-a_2\right)}^{-1}.$$

(9)

Optimizing these profits with respect to $p_1$ and $p_2$, respectively, we obtain two firms’ optimal prices: $p_1^{<O,O>}=c_o+t+{\displaystyle \frac{1}{3}}{u}_o(a_1-a_2)$ and $p_2^{<O,O>}=c_o+t-{\displaystyle \frac{1}{3}}{u}_o(a_1-a_2)$. By substituting the optimal prices into two firms profit functions, we can then solve the equilibrium credence investment decision in the subgame $(O,O)$, which are summarized in Proposition 2.

Proposition 2.

If both firms choose to offer organic food products to customers, the equilibrium organic credence investment decisions are: $a_1^{<O,O>}=a_2^{<O,O>}=1-\sqrt{{\displaystyle \frac{3c_B}{u_{o}M}}}$, the cost of organic credence investment are $C_{B1}=C_{B2}=\sqrt{{\displaystyle \frac{c_B{u}_{o}M}{3}}}$, the equilibrium prices are $p_1^{<O,O>}=p_2^{<O,O>}=t+c_o$, and the equilibrium profits are ${\pi }_1^{<O,O>}={\pi }_2^{<O,O>}={\displaystyle \frac{Mt}{2}}-\sqrt{{\displaystyle \frac{c_B{u}_{o}M}{3}}}$.

We can see that the equilibrium profits when both firms offering organic food products, are less than when both firms offering non-organic food products, and the gap is just the cost of organic credence investment. Due to the fixed market size assumption, this observation is reasonable. As compared to non-organic food products, offering organic food products leads to additional competition in credence investment, but does not increase the total demand. It can also be observed that the additional cost of credence investment is increasing in $u_o$ and $c_B$. The former is intuitive as the more customers value organic food products, the more firms would invest in organic credence. The explanation of the latter maybe that firms need to invest more in credence when it costs more.

3.2.3. Firm 1 Offers Organic Food Products and Firm 2 Offers Non-Organic Food Products

In the subgame $(O,N)$, where Firm 1 offers organic food products and Firm 2 offers non-organic food products, Firm 1 needs to determine the organic credence investment at the second stage and both firms need to determine the price at the final stage.

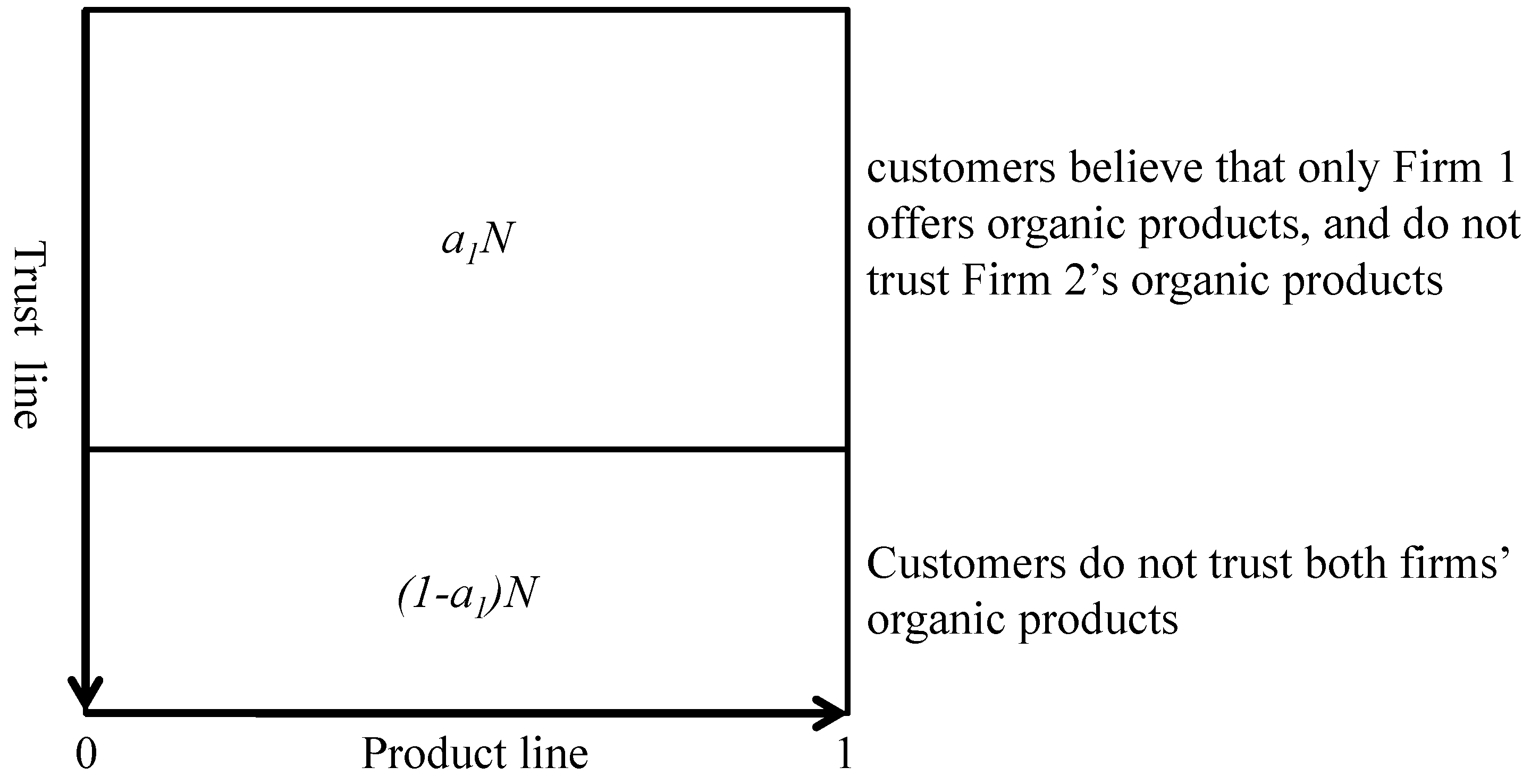
We first analyze the market structure given Firm 1’s credence investment decisions. For given $a_1$, the whole market can be divided into two parts. $a_{1}M$ customers trust the organic food products offered by Firm 1, while $\left(1-a_1\right)M$ customers do not trust Firm 1’s organic food products, and thus treat both two firms’ food products as normal non-organic food products. The market structure is illustrated in Figure 2.

Following similar analysis in last subsection, we can obtain that the market share of two firms in the first part of market are $D_{1,2}^{<O,N>}={\displaystyle \frac{p_2-p_1+t}{2t}}\left(1-a_1\right)M$ and $D_{2,2}^{<O,N>}={\displaystyle \frac{p_1-p_2+t}{2t}}\left(1-a_1\right)M$, respectively. The market share of two firms in the second part of market are $D_{1,2}^{<O,N>}={\displaystyle \frac{p_2-p_1+t}{2t}}\left(1-a_1\right)M$ and $D_{2,2}^{<O,N>}={\displaystyle \frac{p_1-p_2+t}{2t}}\left(1-a_1\right)M$, respectively.

The total demands of two firms are:

$$D_1^{<O,N>}=D_{1,1}^{<O,N>}+D_{1,2}^{<O,N>}={\displaystyle \frac{M}{2t}}\left(p_2-p_1+t+u_o{a}_1\right),$$

(10)

$$D_2^{<O,N>}=D_{2,1}^{<O,N>}+D_{2,2}^{<O,N>}={\displaystyle \frac{M}{2t}}\left(p_1-p_2+t-u_o{a}_1\right).$$

(11)

Now we study two firms’ optimal decisions and equilibrium outcomes. At the third stage, two firms determine price to maximize their own profits:

$${\pi }_1^{<O,N>}={\displaystyle \frac{M}{2t}}\left(p_2-p_1+t+u_o{a}_1\right)(p_1-c_o)-c_B{\left(1-a_1\right)}^{-1},$$

(12)

$${\pi }_2^{<O,N>}={\displaystyle \frac{M}{2t}}\left(p_1-p_2+t-u_o{a}_1\right)(p_2-c_n).$$

(13)

The first order conditions lead to the equilibrium price decisions:

$$p_1^{<O,N>}=t+{\displaystyle \frac{1}{3}}{u}_o{a}_1+{\displaystyle \frac{2}{3}}{c}_o+{\displaystyle \frac{1}{3}}{c}_n,$$

(14)

$$p_2^{<O,N>}=t-{\displaystyle \frac{1}{3}}{u}_o{a}_1+{\displaystyle \frac{1}{3}}{c}_o+{\displaystyle \frac{2}{3}}{c}_n.$$

(15)

Now back to the second stage, Firm 1 makes the organic credence investment decision $a_1$ to maximize their profit:

$${\pi }_1^{<O,N>}={\displaystyle \frac{M}{2t}}{\left(t+{\displaystyle \frac{1}{3}}{u}_o{a}_1-{\displaystyle \frac{1}{3}}{c}_{\Delta }\right)}^2-c_B{\left(1-a_1\right)}^{-1}.$$

(16)

From the first order condition, we can see that the optimal $a_1^{*}$ satisfies:

$${\displaystyle \frac{M{u}_o}{3t}}\left(t+{\displaystyle \frac{1}{3}}{u}_o{a}_1^{*}-{\displaystyle \frac{1}{3}}{c}_{\Delta }\right){\left(1-a_1^{*}\right)}^2-c_B=0.$$

(17)

Lemma 1 guarantees that there exists a unique solution for Equation (17).

Lemma 1.

Equation ${\displaystyle \frac{M{u}_o}{3t}}\left(t+{\displaystyle \frac{1}{3}}{u}_o{a}_1-{\displaystyle \frac{1}{3}}{c}_{\Delta }\right){\left(1-a_1\right)}^2-c_B=0$ has a unique solution for $a_1\in [0,1)$.

By substituting $a_1^{*}$ into the expressions of equilibrium prices and profits, we can further derive all equilibrium solutions in the subgame $(O,N)$, which are summarized in the following proposition.

Proposition 3.

Let $a_1^{*}$ be the solution in $[0,1)$ of following Equation (17). If Firm 1 offers organic food products and Firm 2 offers non-organic food products , the equilibrium prices are $p_1^{<O,N>}=t+{\displaystyle \frac{1}{3}}{u}_o{a}_1^{*}+{\displaystyle \frac{2}{3}}{c}_o+{\displaystyle \frac{1}{3}}{c}_n$ and $p_2^{<O,N>}=t-{\displaystyle \frac{1}{3}}{u}_o{a}_1^{*}+{\displaystyle \frac{1}{3}}{c}_o+{\displaystyle \frac{2}{3}}{c}_n$. Firm 1’s organic credence investment decision is $a_1^{<O,N>}=a_1^{*}$. The equilibrium profits are: ${\pi }_1^{<O,N>}={\displaystyle \frac{M}{2t}}{\left(t+{\displaystyle \frac{1}{3}}{u}_o{a}_1^{*}-{\displaystyle \frac{1}{3}}{c}_{\Delta }\right)}^2-c_B{\left(1-a_1^{*}\right)}^{-1}$ and ${\pi }_2^{<O,N>}={\displaystyle \frac{M}{2t}}{\left(t-{\displaystyle \frac{1}{3}}{u}_o{a}_1^{*}+{\displaystyle \frac{1}{3}}{c}_{\Delta }\right)}^2$.

Note that we do not have a closed form of $a_1^{*}$ in Proposition 3, and all the equilibrium solutions are dependent on the value of $a_1^{*}$. Thus the impacts of market parameters over the equilibrium outcomes are still not clear. In the following we further uncover the impacts of market parameters over the equilibrium credence investment decision, the equilibrium prices and the equilibrium profits, which are stated in Corollary 1.

Corollary 1.

In the subgame $(O,N)$:

1. 

Firm 1’s organic credence investment decision $a_1^{<O,N>}$ is increasing in $u_o$ and decreasing in $c_{\Delta }$ and $c_B$.

2. 

Firm 1’s equilibrium price $p_1^{<O,N>}$ is increasing in $u_o$ and decreasing in $c_B$; Firm 2’s equilibrium price $p_2^{<O,N>}$ is decreasing in $u_o$ and increasing in $c_B$.

3. 

Firm 1’s equilibrium profit ${\pi }_1^{<O,N>}$ is increasing in $u_o$ and decreasing in $c_{\Delta }$, $c_B$; Firm 2’s equilibrium profit ${\pi }_2^{<O,N>}$ is decreasing in $u_o$ and increasing in $c_{\Delta }$, and $c_B$.

The majority of Corollary 1 is intuitive, except one counter-intuitive result in Corollary 1-(2). It is interesting to see that $p_1^{<O,N>}$ is decreasing in $c_B$ while $p_2^{<O,N>}$ is increasing in $c_B$. Usually, a higher cost will lead to a higher price. An explanation is that $c_B$ captures the cost to make customers trust the organic food products. A lower $c_B$ means that the firm offering organic food products is more competitive and thus can offer a higher price.

In Corollary 2, we compare the equilibrium solutions and market shares in different subgames under a general condition.

Corollary 2.

If $c_B<{\displaystyle \frac{M{u}_o}{3}}{\left(1-{\displaystyle \frac{c_{{}_{\Delta }}}{u_o}}\right)}^2$, then:

1. 

$a_1^{<O,O>}=a_2^{<O,O>}>a_1^{<O,N>}$.

2. 

the equilibrium prices in different subgames satisfy the following relationships: $p_1^{<O,N>}\ge p_1^{<O,O>}=p_2^{<O,O>}>p_1^{<N,N>}=p_2^{<N,N>}\ge p_2^{<O,N>}$.

3. 

the market shares in different subgames satisfy the following relationships: $D_1^{<O,N>}\ge D_1^{<O,O>}=D_2^{<O,O>}=D_1^{<N,N>}=D_2^{<N,N>}\ge D_2^{<O,N>}$.

The condition $c_B>{\displaystyle \frac{M{u}_o}{3}}{\left(1-{\displaystyle \frac{c_{\Delta }}{u_o}}\right)}^2$ is quite general condition, which will be discussed in next section. As $C_B\left(a\right)$ is increasing in a, Corollary 2-(1) also indicates that Firm 1 would invest more on organic credence when only Firm 1 offers organic food products than when both firms offer organic food products. This is an interesting result as one might expect the opposite that competitive pressures would force firms to invest more in organic credence. The reason is that in our model, when firms make credence investment decisions, they can recognize its strategic effect on the price competition of next stage. When both firms offer organic food products, investing too much in organic credence intensifies price competition. Internalizing this effect, firms keep the equilibrium credence investment cost low. When only one firm offers organic food products, their organic food products competes with the rival’s non-organic food products. Although increasing the degree of competition does intensify prices competition, but the magnitude of this effect is not the same as in the case when both firms offer organic food products. The remaining part of Corollary 2 is quite intuitive.

3.3. Strategy Equilibrium

Now we consider two firms’ strategy choices at the first stage. We compare the outputs of all subgames first. Define ${\Delta }_1={\pi }_1^{<O,N>}-{\pi }_1^{<N,N>}$ and ${\Delta }_2={\pi }_2^{<O,N>}-{\pi }_2^{<O,O>}$. Notice that the sign of ${\Delta }_1$ (${\Delta }_2$) determines if Firm 1 (Firm 2) would offer organic or non-organic food products when Firm 2 (Firm 1) offers non-organic (organic) food products. Thus the final equilibrium depends the signs of ${\Delta }_1$ and ${\Delta }_2$. We further rewrite ${\Delta }_1$ and ${\Delta }_2$ as follows:

$${\Delta }_1={\displaystyle \frac{M}{2t}}{\left(t+{\displaystyle \frac{1}{3}}{u}_o{a}_1^{*}-{\displaystyle \frac{1}{3}}{c}_{\Delta }\right)}^2-c_B{\left(1-a_1^{*}\right)}^{-1}-{\displaystyle \frac{Mt}{2}},$$

(18)

$${\Delta }_2={\displaystyle \frac{M}{2t}}{\left(t-{\displaystyle \frac{1}{3}}{u}_o{a}_1^{*}+{\displaystyle \frac{1}{3}}{c}_{\Delta }\right)}^2-\left[{\displaystyle \frac{Mt}{2}}-\sqrt{{\displaystyle \frac{c_B{u}_{o}M}{3}}}\right].$$

(19)

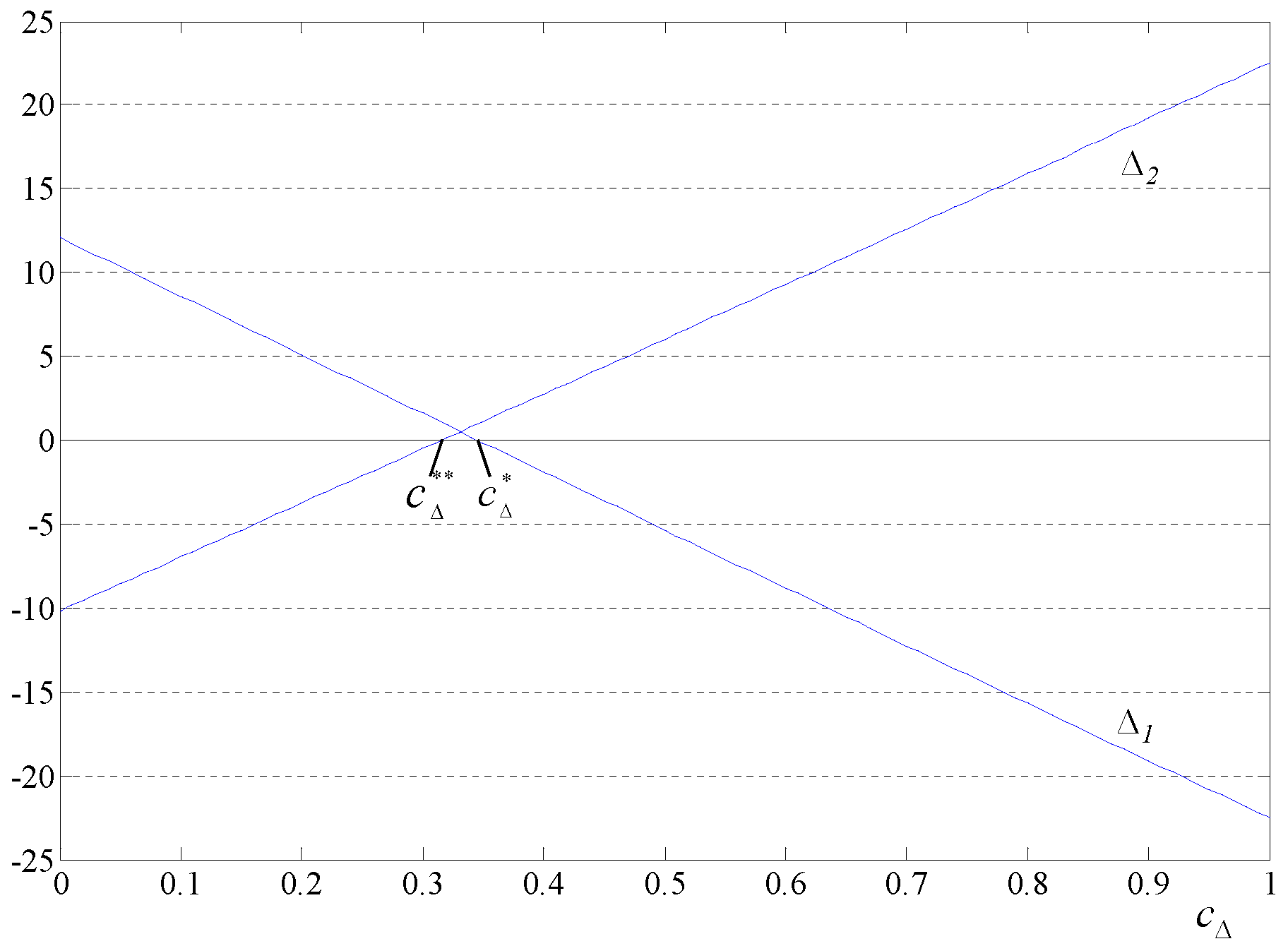
When $a_1^{*}\le {\displaystyle \frac{c_{\Delta }}{u_o}}$, it can be seen that ${\Delta }_1<0$ and ${\Delta }_2>0$ always hold, which indicates that both firms have no motivations to offer organic food products. To avoid such an extreme case, we need to identify conditions ensuring $a_1^{*}>{\displaystyle \frac{c_{\Delta }}{u_o}}$. This condition is stated in Lemma 2.

Lemma 2.

Let $a_1^{*}$ be the solution of ${\displaystyle \frac{M{u}_o}{3t}}\left(t+{\displaystyle \frac{1}{3}}{u}_o{a}_1-{\displaystyle \frac{1}{3}}{c}_{\Delta }\right){\left(1-a_1\right)}^2-c_B=0$. If $c_B<{\displaystyle \frac{M{u}_o}{3}}{\left(1-{\displaystyle \frac{c_{{}_{\Delta }}}{u_o}}\right)}^2$, then $a_1^{*}>{\displaystyle \frac{c_{{}_{\Delta }}}{u_o}}$, ${\Delta }_1<0$ and ${\Delta }_2>0$.

From Lemma 2 we have Proposition 4, which identifies a condition on organic product credence investment cost under which the final equilibrium is $(N,N)$.

Proposition 4.

If $c_B\ge {\displaystyle \frac{M{u}_o}{3}}{\left(1-{\displaystyle \frac{c_{{}_{\Delta }}}{u_o}}\right)}^2$, ${\Delta }_1<0$ and ${\Delta }_2>0$, the equilibrium is $(N,N)$, both firms offer non-organic food products.

Proposition 4 shows that if the credence investment cost is sufficiently large, firms will have no motivations offering organic food products. Note that when $c_{\Delta }=0$, which is mostly favourable for offering organic food products, firms may still have no motivations if the credence investment is too expensive, e.g., $c_B>{\displaystyle \frac{M{u}_o}{3}}$. Generally, production costs for organic food products are typically higher due to restricting the use of certain pesticides and fertilizers in farming which brings the greater labor inputs, the high expense on fertility, weed control, as well as pest and disease control, etc. However, there are still several arguments that the production costs for for organic food products may be similar to those of non-organic food products. Our above result indicates that even if under the case that production costs for both organic and non-organic food products are identical, firms still may not offer organic food products. The reason is that if it is expensive to make customers trust organic food products, offering organic food products still can not be competitive even if organic production cost appears to have no disadvantage compared to non-organic.

Lemma 3 characterizes a condition on $c_B$ such that when $c_{\Delta }=0$, ${\Delta }_2>0$, i.e., at most one firm will offer organic food products.

Lemma 3.

There exists a $c_B^{*}$, such that when $c_{\Delta }=0$ and $c_B>c_B^{*}$:

$${\Delta }_2={\displaystyle \frac{M}{2t}}{\left(t-{\displaystyle \frac{1}{3}}{u}_o{a}_1^{*}\right)}^2-\left[{\displaystyle \frac{Mt}{2}}-\sqrt{{\displaystyle \frac{c_B{u}_{o}M}{3}}}\right]>0,$$

(20)

where $a_1^{*}$ is the solution of ${\displaystyle \frac{\Delta M}{3t}}\left(t+{\displaystyle \frac{1}{3}}{u}_o{a}_1\right){\left(1-a_1\right)}^2=c_B$.

We can also see that $c_B^{*}$ is the solution of the following equations:

$$\left\{\begin{array}{c}{\displaystyle \frac{M}{2t}}{\left(t-{\displaystyle \frac{1}{3}}{u}_o{a}_1\right)}^2-\left[{\displaystyle \frac{Mt}{2}}-\sqrt{{\displaystyle \frac{c_B{u}_{o}M}{3}}}\right]=0,\\ {\displaystyle \frac{M{u}_o}{3t}}\left(t+{\displaystyle \frac{1}{3}}{u}_o{a}_1\right){\left(1-a_1\right)}^2=c_B.\end{array}\right.$$

(21)

From Lemma 3, we have Proposition 5 which further identifies a sufficient condition of organic product credence investment cost under which the final equilibrium will not be $(O,O)$.

Proposition 5.

If $c_B>c_B^{*}$, ${\Delta }_2>0$, the equilibrium may be $(N,N)$, $(O,N)$ or $(N,O)$, firms may offer organic food products or non-organic food products, except the case that both firms offer organic food products.

Note that the conditions in Proposition 5 are independent of the value of $c_{\Delta }$. Proposition 5 further provides important managerial insights on firms strategy choices between offering organic and non-organic food products: when $c_B$ is sufficiently large, at most one firm will offer organic food products, regardless of the cost of organic production. The insights from Proposition 4 and 5 are intuitive. When it is expensive to invest in organic credence, firms are less likely to offer organic food products.

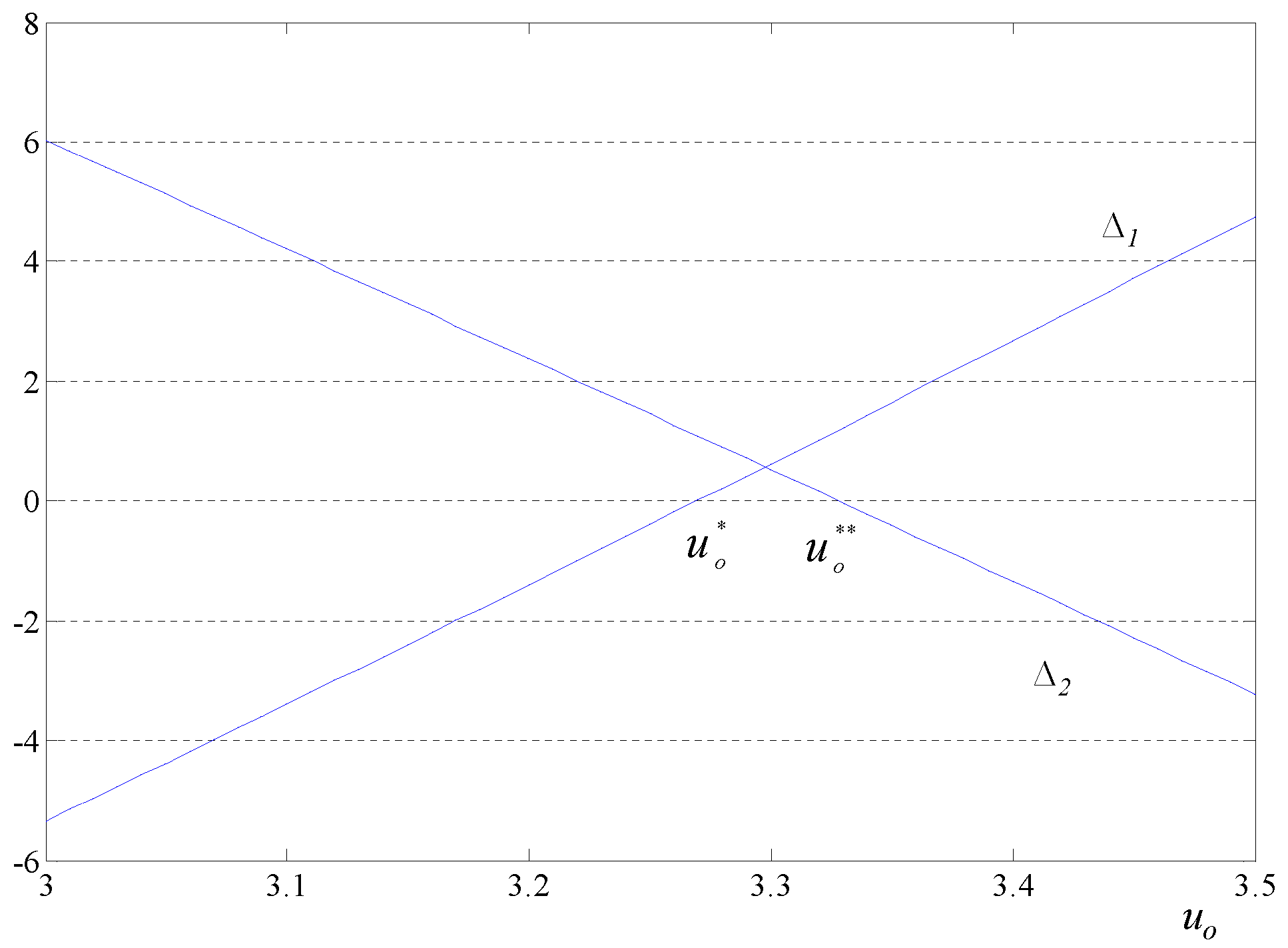
We are also interested in the impacts of organic production cost over the final equilibrium. Before introducing the main results, we have Lemma 4, which characterizes the value of ${\Delta }_1$ and ${\Delta }_2$ over different spaces of $c_{\Delta }$.

Lemma 4.

If $c_B<{\displaystyle \frac{M{u}_o}{3}}{\left(1-{\displaystyle \frac{c_{{}_{\Delta }}}{u_o}}\right)}^2$and $c_B\le c_B^{*}$, for $c_{\Delta }\in [0,u_o]$:

(1) 

There exists a critical value $c_{\Delta }^{*}$ such that: when $c_{\Delta }\le c_{\Delta }^{*}$, ${\Delta }_1\ge 0$; when $c_{\Delta }>c_{\Delta }^{*}$, ${\Delta }_1<0$,

(2) 

There exists a critical value $c_{\Delta }^{**}$ such that: when $c_{\Delta }\ge c_{\Delta }^{**}$, ${\Delta }_2\ge 0$; when $c_{\Delta }<c_{\Delta }^{**}$, ${\Delta }_2<0$,

(3) 

$c_{\Delta }^{*}\ge c_{\Delta }^{**}$.

From Lemma 4 we directly have Proposition 6, which describes how the cost difference between organic and non-organic food products impacts the final equilibrium.

Proposition 6.

If $c_B<{\displaystyle \frac{M{u}_o}{3}}{\left(1-{\displaystyle \frac{c_{{}_{\Delta }}}{u_o}}\right)}^2$and $c_B\le c_B^{*}$, then:

(1) 

If $c_{\Delta }<c_{\Delta }^{**}$, ${\Delta }_1\ge 0$, ${\Delta }_2<0$, the final equilibrium is $(O,O)$, both firms offer organic food products.

(2) 

If $c_{\Delta }^{**}\le c_{\Delta }\le c_{\Delta }^{*}$, ${\Delta }_1\ge 0$, ${\Delta }_2\ge 0$, the final equilibrium is $(O,N)$ or $(N,O)$, only one firm offers organic food products and the other firm offers non-organic food products.

(3) 

If $c_{\Delta }>c_{\Delta }^{*}$, ${\Delta }_1<0$, ${\Delta }_2>0$, the final equilibrium is $(N,N)$, both firms offer non-organic food products.

Proposition 6 has important managerial implications for firms making strategy choices between offering organic and non-organic food products. For fixed organic credence investment cost, the production cost difference between organic and non-organic food products determines the final equilibrium. As one may expect, firms’ choices are dependent on the production cost difference: (i) if it is large enough, both firms will offer non-organic food products to customers; (ii) if it is moderately large, only one firm offers organic food products to customers; (iii) if it is relatively low, both firms offer organic food products to customers. These observations are consistent with the practice in industry. In 2014, a lot of organic food producers in Wuhan China abandoned organic production due to the high organic production costs [39].

4. The Impacts of Market Conditions on the Final Equilibrium

In this section, we numerically investigate the impacts of organic credence cost and organic product attractiveness on the final equilibrium. In these numerical studies, the basic model parameters are set as follows unless stated: $M=100$, $t=10$, $u_o=3$, $c_{\Delta }=0.5$, $c_B=20$. Note these parameters satisfy the condition $c_B<{\displaystyle \frac{M{u}_o}{3}}{\left(1-{\displaystyle \frac{c_{\Delta }}{u_o}}\right)}^2$, as well as the required assumptions.

4.1. The Impacts of Organic Food Production Cost

The effect of changing $c_{\Delta }$ on final equilibrium is illustrated in Figure 3.

The values of $c_{\Delta }^{*}$ and $c_{\Delta }^{**}$ in Proposition 6 can be found in Figure 3. When $c_{\Delta }>c_{\Delta }^{*}$, ${\pi }_1^{<O,N>}<{\pi }_1^{<N,N>}$ and ${\pi }_2^{<O,N>}>{\pi }_2^{<O,O>}$, if any firm offers organic food products rather than non-organic food products, they will only earn a lower profit no matter what strategy its rival takes. Therefore, both firms prefer to offer non-organic food products to customers. When $c_{\Delta }^{**}\le c_{\Delta }\le c_{\Delta }^{*}$, ${\pi }_1^{<O,N>}\ge {\pi }_1^{<N,N>}$ and ${\pi }_2^{<O,N>}\ge {\pi }_2^{<O,O>}$, if any one firm offers organic (non-organic) food products, the other firm will prefer to offer non-organic (organic) food products. Consequently, the equilibrium is $(O,N)$ or $(N,O)$. When $c_{\Delta }<c_{\Delta }^{**}$, ${\pi }_1^{<O,N>}>{\pi }_1^{<N,N>}$ and ${\pi }_2^{<O,N>}<{\pi }_2^{<O,O>}$, if any firm offers non-organic food products, the other firm will prefer to offer organic food products since ${\pi }_2^{<N,O>}={\pi }_1^{<O,N>}>{\pi }_1^{<N,N>}={\pi }_2^{<N,N>}$; while if any firm offers organic food products, the other firm will not like to offer non-organic food products since ${\pi }_1^{<N,O>}={\pi }_2^{<O,N>}<{\pi }_2^{<O,O>}={\pi }_1^{<O,N>}$. Thus in this situation, both firms will offer organic food products.

4.2. The Impacts of Organic Food Products’ Credence Investment Cost

To understand the impacts of organic product credence investment cost $c_B$ on the final equilibrium, we illustrate the relationship between ${\Delta }_1$, ${\Delta }_2$ and $c_B$ in Figure 4.

We can observe that as $c_B$ increases, ${\Delta }_1$ decreases and ${\Delta }_2$ increases. Figure 4 also shows that there are two threshold values $c_B^{*}$ and $c_B^{**}$ of organic product credence investment cost such that: (i) if the organic product credence investment cost is small ($c_B<c_B^{**}$), ${\Delta }_1>0$ and ${\Delta }_2<0$, both firms offer organic food products to customers, and the final equilibrium is $(O,O)$; (ii) if the organic product credence investment cost is moderately big ($c_B^{**}\le c_B\le c_B^{*}$), ${\Delta }_1>0$ and ${\Delta }_2>0$, one firm offers organic food products and the other firm offers non-organic food products to customers, the final equilibrium is $(O,N)$ or $(N,O)$; (iii) if the market size is relatively big ($c_B>c_B^{*}$), ${\Delta }_1<0$ and ${\Delta }_2>0$, both firms offer non-organic food products to customers, and the final equilibrium is $(N,N)$. As $c_B$ refers to the cost of organic food products’ credence investment, it is easy to understand that when organic food products’ credence investment is expensive, offering organic food products becomes a less competitive choice.

4.3. The Impacts of Organic Food Products’ Attractiveness

The additional utility of organic food products reflects the attractiveness. We test the impacts of organic food products’ utility $u_o$ on the final equilibrium. The relationships between ${\Delta }_1$, ${\Delta }_2$ and $u_o$ are presented in Figure 5.

Figure 5 shows that as $u_o$ increases, ${\Delta }_1$ increases and ${\Delta }_2$ decreases. We can observe that there are two threshold values $u_o^{*}$ and $u_o^{**}$ such that: (i) if the utility of the organic product is small ($u_o<u_o^{*}$), ${\Delta }_1<0$ and ${\Delta }_2>0$, both firms offer non-organic food products to customers, and the final equilibrium is $(N,N)$; (ii) if the utility of the organic product is moderately big ($u_o^{*}\le u_o\le u_o^{**}$) , ${\Delta }_1>0$ and ${\Delta }_2>0$, one firm offers organic food products and the other firm offers non-organic food products to customers, the final equilibrium is $(O,N)$ or $(N,O)$; (iii) if the utility of the organic product is relatively big ($u_o>u_o^{**}$), ${\Delta }_1>0$ and ${\Delta }_2<0$, both firms offer organic food products to customers, and the final equilibrium is $(O,O)$. This result is very intuitive. If customers’ utility over organic food products are high, offering organic food products becomes a more competitive choice. This explains why we tend to see less organic food products in the clothing industry than in the food industry, especially the baby food industry, where safety and health are key concerns.

5. Discussion and Conclusions

In this paper, we study competition between two firms to investigate their strategy choices in offering organic and non-organic food products. The two firms compete for customers through their choices of production type, organic credence investment and price. Consumers have heterogeneous preferences for firms as well as heterogeneous sensitivity to organic credence investment. The main results we found are as follows: (1) We show that in equilibrium, whether firms choose to offer organic or non-organic food products depends on the cost efficiencies of production and organic credence investment. The higher the production cost or credence investment costs for organic food products are, the more likely firms would choose to offer non-organic food products. Furthermore, we find that if it is expensive enough to invest in organic credence, offering organic food products may still be uncompetitive, even if organic production cost appears to have no disadvantage compared to the non-organic case; (2) We also find that when only one firm offers organic products, they tend to offer a relatively low price if organic credence investment is expensive. Usually, a higher cost will lead to a higher price. An explanation for this is that if it is expensive to make customers trust the organic credence system, the firm offering organic food products is less competitive and thus can only offer a lower price; (3) Besides, we find that when only one firm offers organic products, the investment on organic credence is higher than when both firms offer organic products. This is different from our intuition that competitive pressures would force firms to invest more in organic credence. The explanation for this is that when both firms offer organic food products, investing too much in organic credence intensifies price competition. Thus, firms may keep the equilibrium credence investment cost low to internalize this effect. When only one firm offers organic food products, their organic food products competes with the rival’s non-organic food products. Although increasing the degree of competition does intensify price competition, the magnitude of this effect is not the same as in the case when both firms offer organic food products.

The main value of this model is that our results illustrate the key points of organic production, credence investment and pricing in determining whether a firm should offer organic food products. As the organic industry is growing in both length and breadth, the importance of exploring the the business of organic food products will only increase. It is thus our hope that this work can help firms understand when to offer organic or non-organic food products and how much firms should invest in their own credence systems.

Our study has some limitations. First, in our model we assume that without firms’ own credence system investment, no customers will trust a firm’s organic products. While in general, the public investment in certified labeling system can influence customers’ trust even firms do not invest their own credence system. Thus an important future research direction is considering an existing level of public trust on the market, and study the impacts of the public investment in certified labeling on firms’ decisions. Second, we assume that the additional utility of organic products is the same for the customers who trust organic products. In general, even the customers trusting organic products may have different interests in organic products. Assuming heterogeneity in organic utility may lead to more interesting results, which is a potential future research path. Third, we assume that the market is fully covered. Relaxing this assumption may leads to more insights. For example, in equilibrium, firms may tend to offer low prices or invest a lot in organic credence in order to attract more customers.