Risk Assessment for Distribution Systems Using an Improved PEM-Based Method Considering Wind and Photovoltaic Power Distribution
Abstract
:1. Introduction
2. Distribution of Wind and Photovoltaic DGs
2.1. Output Uncertainty of Wind Generators
2.2. Output Uncertainty of Photovoltaic Generators
3. Risk Assessment Indices and Method
3.1. Risk Assessment Indices
3.2. Improved Point Estimate Methods
3.3. Optimal Power Flow Algorithm in Distribution Systems
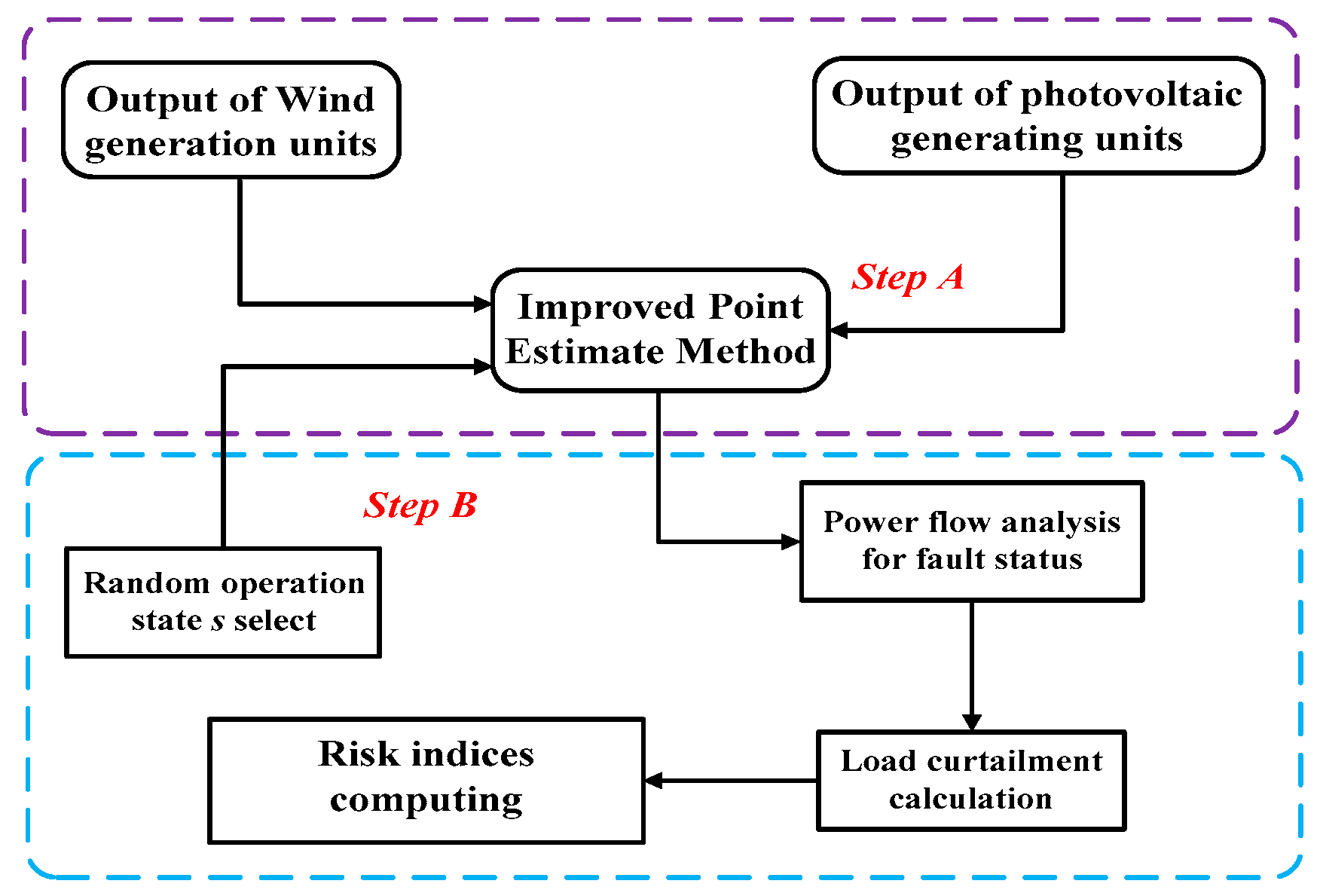
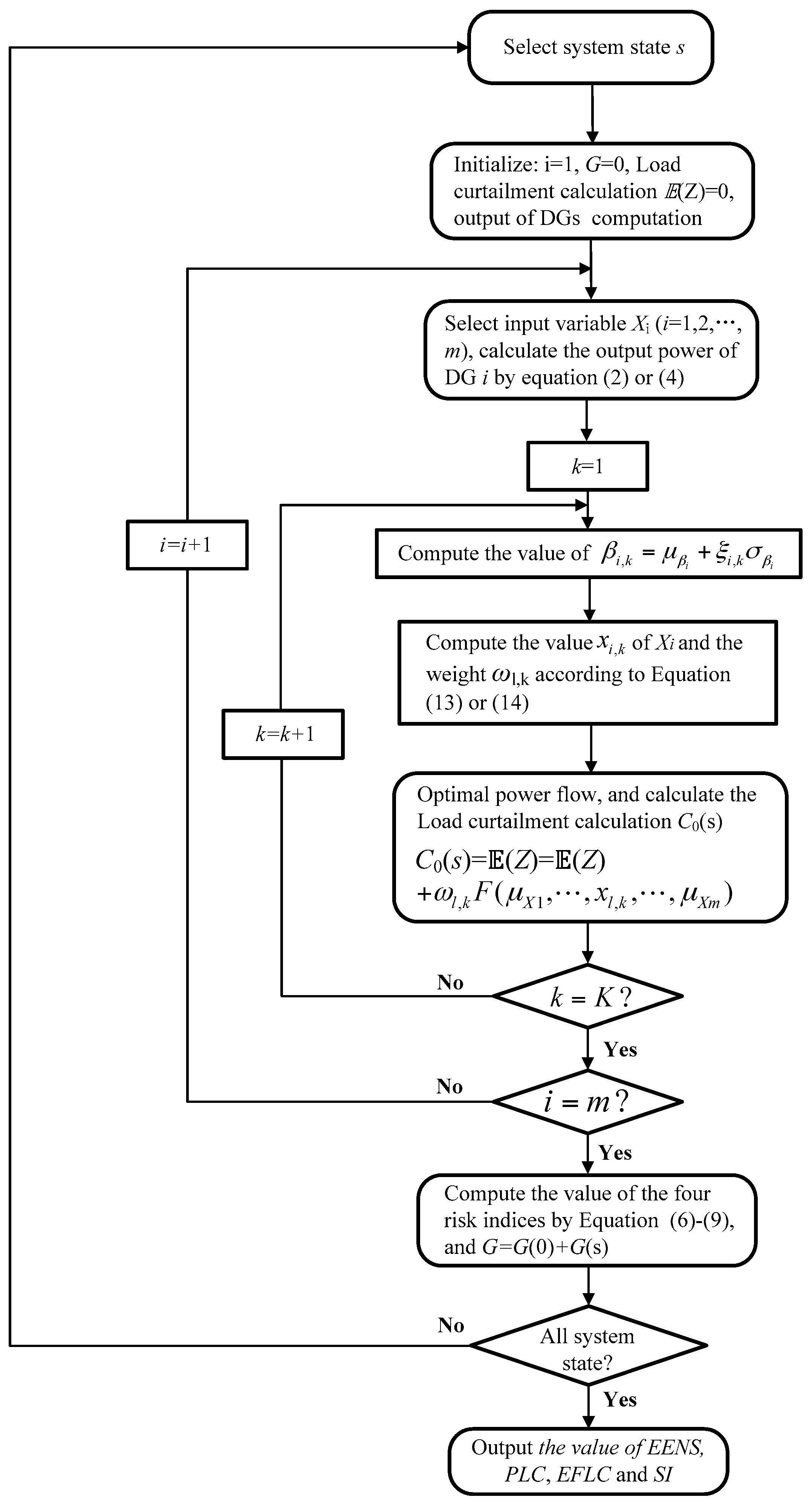
4. Risk Assessment Procedure for Distribution Systems
4.1. Structure for Risk Assessment
4.2. Procedure for Calculating Risk Indices
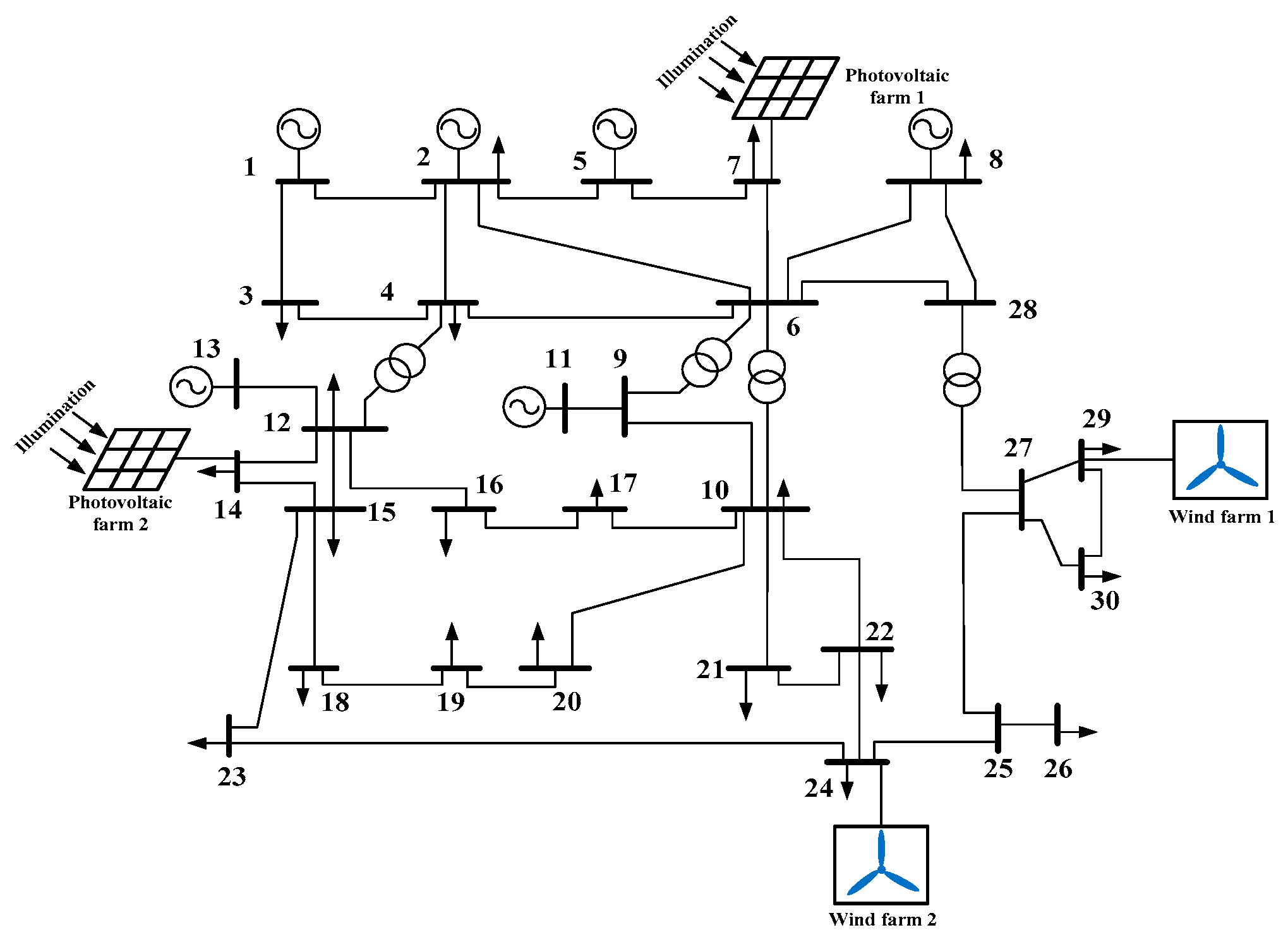
5. Case Studies
5.1. Calculation of Risk Indices Based on PEM
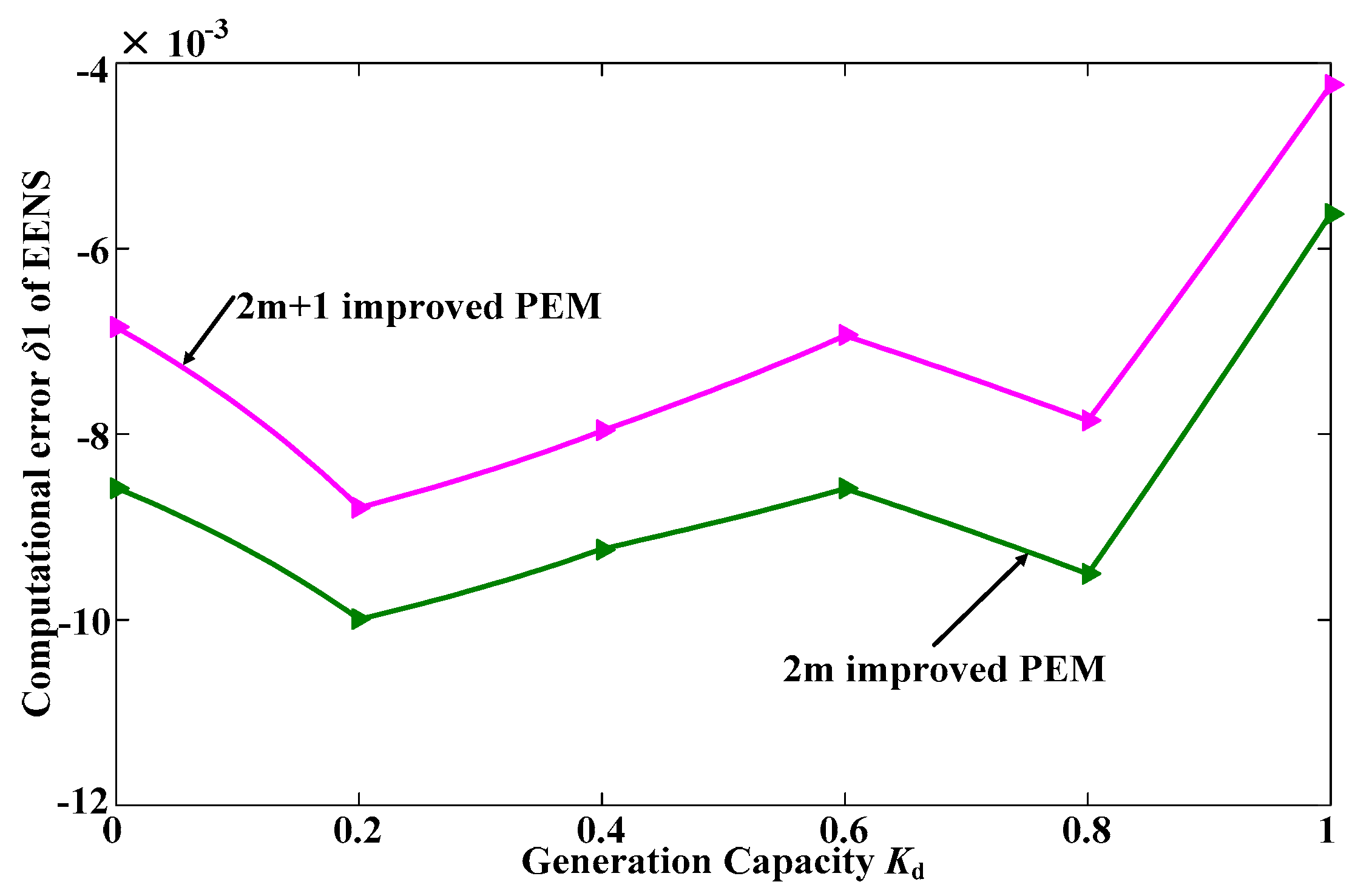
5.2. Deviation and Computational Cost Comparison
5.3. Influence of DGs on System Risk
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Arabali, A.; Ghofrani, M.; Etezadi-Amoli, M. Stochastic Performance Assessment and Sizing for a Hybrid Power System of Solar/Wind/Energy Storage. IEEE Trans. Sustain. Energy 2014, 5, 363–371. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, S. External Benefit Evaluation of Renewable Energy Power in China for Sustainability. Sustainability 2015, 7, 4783–4805. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, C. Comprehensive Benefit Evaluation of the Power Distribution Network Planning Project Based on Improved IAHP and Multi-Level Extension Assessment Method. Sustainability 2016, 8, 796. [Google Scholar] [CrossRef]
- Al Kaabi, S.S.; Zeineldin, H.H.; Khadkikar, V. Planning Active Distribution Networks Considering Multi-DG Configurations. IEEE Trans. Power Syst. 2014, 29, 785–793. [Google Scholar] [CrossRef]
- Negnevitsky, M.; Nguyen, D.H.; Piekutowski, M. Risk Assessment for Power System Operation Planning with High Wind Power Penetration. IEEE Trans. Power Syst. 2015, 30, 1359–1368. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Wu, L. Transmission Line Overload Risk Assessment for Power Systems with Wind and Load-Power Generation Correlation. IEEE Trans. Smart Grid 2015, 3, 1233–1242. [Google Scholar] [CrossRef]
- Marsadek, M.; Mohamed, A.; Mohd, Z. Assessment and classification of line overload risk in power systems considering different types of severity functions. WSEAS Transcr. Power Syst. 2010, 3, 182–191. [Google Scholar]
- Feng, Y.Q.; Wu, W.C.; Zhang, B.; Li, W.Y. Power system operation risk assessment using credibility theory. IEEE Trans. Power Syst. 2008, 23, 1309–1318. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, P. Reliability and price risk assessment of a restructured power system with hybrid market structure. IEEE Trans. Power Syst. 2006, 21, 108–116. [Google Scholar] [CrossRef]
- Celli, G.; Ghiani, E.; Pilo, F.; Soma, G.G. Active distribution network reliability assessment with a pseudo sequential Monte Carlo method. In Proceedings of the IEEE PowerTech, Trondheim, Norway, 19–23 June 2011; pp. 1–8. [Google Scholar]
- Atwa, Y.M.; El-Saadany, E.F. Reliability evaluation for distribution system with renewable distributed generation during islanded mode of operation. IEEE Trans. Power Syst. 2009, 24, 572–581. [Google Scholar] [CrossRef]
- Li, W.; Zhou, J.; Lu, J.; Yan, W. Incorporating a combined fuzzyand probabilistic load model in power system reliability assessment. IEEE Trans. Power Syst. 2007, 22, 1386–1388. [Google Scholar] [CrossRef]
- Jia, H.; Qi, W.; Liu, Z.; Wang, B. Hierarchical Risk Assessment of Transmission System Considering the Influence of Active Distribution Network. IEEE Trans. Power Syst. 2015, 2, 1084–1093. [Google Scholar] [CrossRef]
- Li, W.; Zhou, J.; Xie, K.; Xiong, X. Power system risk assessment using a hybrid method of fuzzy set and Monte Carlo simulation. IEEE Trans. Power Syst. 2008, 23, 336–343. [Google Scholar]
- Billinton, R.; Wang, P. Reliability cost/worth assessment ofdistribution systems incorporating time-varying weather conditions andrestorations resources. IEEE Trans. Power Deliv. 2002, 17, 260–265. [Google Scholar]
- Soroudi, A.; Amraee, T. Decision making under uncertainty in energy systems: State of the art. Renew. Sustain. Energy Rev. 2013, 28, 376–384. [Google Scholar] [CrossRef]
- Soroudi, A.; Ehsan, M. IGDT based robust decision making tool for DNOs in load procurement under severe uncertainty. IEEE Trans. Smart Grid 2013, 4, 886–895. [Google Scholar] [CrossRef]
- Bertsimas, D.; Litvinov, E.; Sun, X.A.; Zhao, J.; Zheng, T. Adaptive robust optimization for the security constrained unit commitment problem. IEEE Trans. Power Syst. 2013, 28, 52–63. [Google Scholar] [CrossRef]
- Baudrit, C.; Dubois, D.; Guyonnet, D. Joint propagation and exploitation of probabilistic and possibilistic information in risk assessment. IEEE Trans. Fuzzy Syst. 2006, 14, 593–608. [Google Scholar] [CrossRef]
- Liu, K.Y.; Sheng, W.; Hu, L.; Liu, Y. Simplified probabilistic voltage stability evaluation considering variable renewable distributed generation in distribution systems. IET Gener. Transm. Distrib. 2015, 9, 1464–1473. [Google Scholar] [CrossRef]
- Liu, Z.; Wen, F.; Ledwich, G. Optimal siting and sizing of distributed generators in distribution systems considering uncertainties. IEEE Trans. Power Deliv. 2011, 26, 2541–2551. [Google Scholar] [CrossRef]
- Rei, A.M.; Schilling, M.T. Reliability assessment of the Brazilianpower system using enumeration and Monte Carlo. IEEE Trans. Power Syst. 2008, 23, 1480–1487. [Google Scholar] [CrossRef]
- Martinez-Velasco, J.A.; Guerra, G. Parallel Monte Carlo approach for distribution reliability assessment. IET Gener. Transm. Distrib. 2014, 8, 1810–1819. [Google Scholar] [CrossRef]
- Conejo, A.J.; Carrión, M.; Morales, J.M. Decision Making under Uncertainty in Electricity Markets; Springer: New York, NY, USA, 2010; Volume 1. [Google Scholar]
- Hong, H.P. An efficient point estimate method for probabilistic analysis. Reliab. Eng. Syst. Saf. 1998, 59, 261–267. [Google Scholar] [CrossRef]
- Morales, J.M.; Perez-Ruiz, J. Point estimate schemes to solve the probabilistic power flow. IEEE Trans. Power Syst. 2007, 4, 1594–1601. [Google Scholar] [CrossRef]
- Su, C.L. Probabilistic load-flow computation using point estimate method. IEEE Trans. Power Syst. 2005, 20, 1843–1851. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Oren, S.S.; O’Neill, R.P. Reserve requirements for wind power integration: A scenario-based stochastic programming framework. IEEE Trans. Power Syst. 2011, 26, 2197–2206. [Google Scholar] [CrossRef]
- Li, J.; Wei, W.; Xiang, J. A simple sizing algorithm for stand-alone PV/wind/battery hybrid microgrids. Energies 2012, 5, 5307–5323. [Google Scholar] [CrossRef]
- Kratochvil, J.A.; Boyson, W.E.; King, D.L. Photovoltaic Array Performance Model; Technical Report; Sandia National Laboratories: New Mexico, NM, USA, 2004.
- Saaty, T.L. Analytic hierarchy process. In Encyclopedia of Biostatistics; John Wiley and Sons, Inc.: Somerset, NJ, USA, 2001; pp. 19–28. [Google Scholar]
- Stott, B.; Marinho, J.L. Linear programming for power-system network security applications. IEEE Trans. Power Appl. Syst. 1979, 3, 837–848. [Google Scholar] [CrossRef]
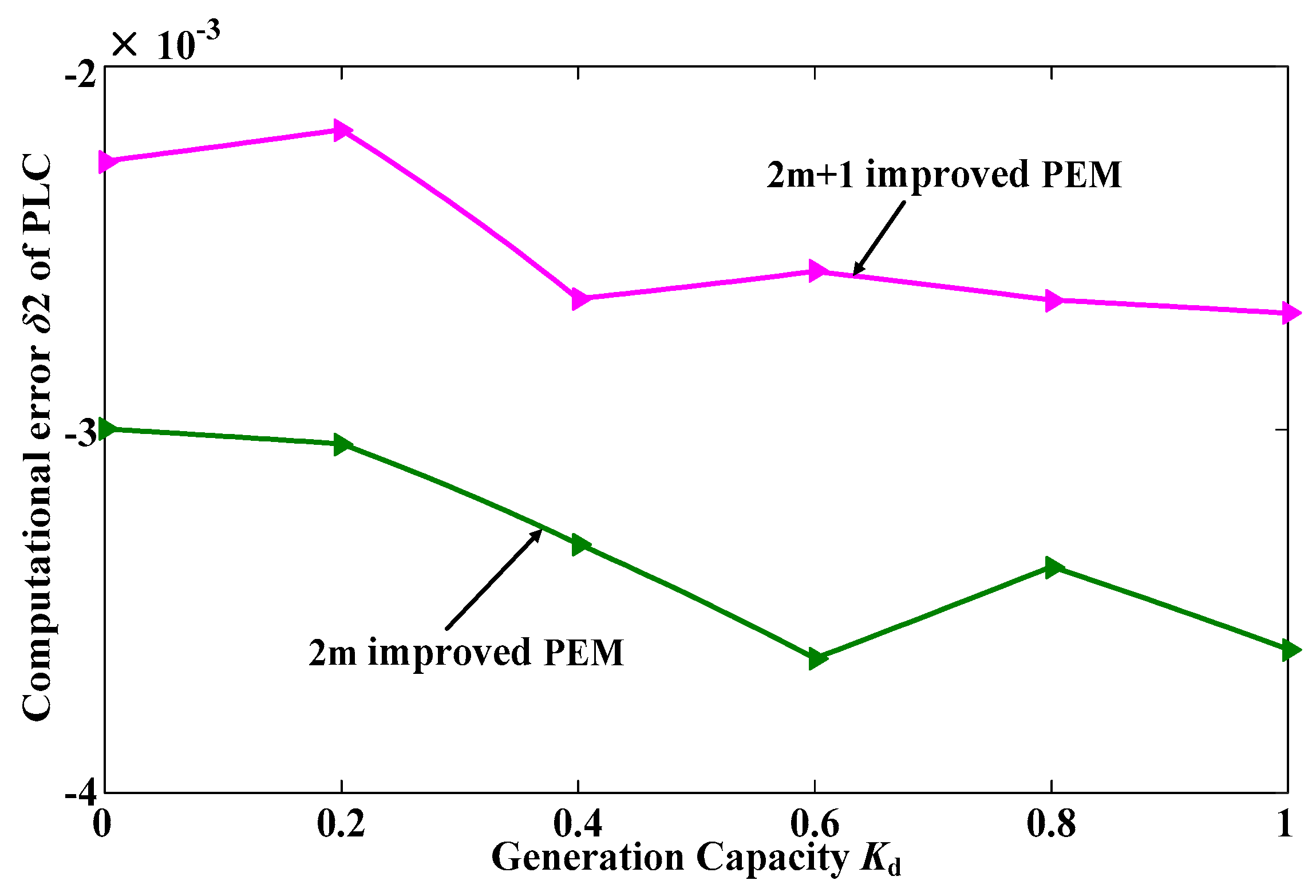
| Kd | 2m PEM | |||
|---|---|---|---|---|
| EENS (MWh/y) | PLC | EFLC (Times/y) | SI (min/y) | |
| 0 | 3151.2 | 62,247 × 10−7 | 2.4899 | 66.716 |
| 0.2 | 2382.5 | 59,981 × 10−7 | 2.3992 | 50.441 |
| 0.4 | 1945.7 | 53,176 × 10−7 | 2.1285 | 41.193 |
| 0.6 | 1744.4 | 48,635 × 10−7 | 1.9454 | 36.932 |
| 0.8 | 1619.1 | 47,516 × 10−7 | 1.9006 | 34.279 |
| 1 | 1580.3 | 45,243 × 10−7 | 1.8097 | 33.457 |
| Kd | 2m + 1 PEM | |||
|---|---|---|---|---|
| EENS (MWh/y) | PLC | EFLC (Times/y) | SI (min/y) | |
| 0 | 3156.7 | 62,293 × 10−7 | 2.4917 | 66.832 |
| 0.2 | 2385.4 | 60,033 × 10−7 | 2.4013 | 50.502 |
| 0.4 | 1948.2 | 53,212 × 10−7 | 2.1285 | 41.246 |
| 0.6 | 1747.3 | 48,687 × 10−7 | 1.9475 | 36.993 |
| 0.8 | 1621.8 | 47,551 × 10−7 | 1.9020 | 34.336 |
| 1 | 1582.5 | 45,285 × 10−7 | 1.8114 | 33.504 |
| Kd | Hierarchical Method | |||
|---|---|---|---|---|
| EENS (MWh/y) | PLC | EFLC (Times/y) | SI (min/y) | |
| 0 | 3178.5 | 62,434 × 10−7 | 2.4974 | 67.293 |
| 0.2 | 2406.6 | 60,164 × 10−7 | 2.4066 | 50.95 |
| 0.4 | 1963.8 | 53,353 × 10−7 | 2.1341 | 41.577 |
| 0.6 | 1759.5 | 48,812 × 10−7 | 1.9525 | 37.251 |
| 0.8 | 1634.6 | 47,677 × 10−7 | 1.9071 | 34.608 |
| 1 | 1589.2 | 45,407 × 10−7 | 1.8163 | 33.646 |
| Risk Indices | The Computational Costs of Risk Indices(s) | ||
|---|---|---|---|
| 2m Improved PEM | 2m + 1 Improved PEM | Hierarchical Method | |
| EENS | 25.845 | 27.742 | 67.293 |
| PLC | 1.985 | 2.031 | 5.950 |
| EFLC | 2.157 | 2.192 | 6.107 |
| SI | 25.845 | 27.742 | 67.293 |
| Kd | 2m + 1 Improved PEM | |||
|---|---|---|---|---|
| EENS (MWh/y) | PLC | EFLC (Times/y) | SI (min/y) | |
| 0.2 | 2131.7 | 56,823 × 10−7 | 2.2729 | 45.131 |
| Kd | 2m + 1 Improved PEM | |||
|---|---|---|---|---|
| EENS (MWh/y) | PLC | EFLC (Times/y) | SI (min/y) | |
| 0.2 | 2193.6 | 57,232 × 10−7 | 2.2893 | 46.442 |
| Kd | 2m + 1 Improved PEM | |||
|---|---|---|---|---|
| EENS (MWh/y) | PLC | EFLC (Times/y) | SI (min/y) | |
| 0.2 | 2058.4 | 55,785 × 10−7 | 2.2314 | 43.579 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Q.; Lei, J.; Qiao, H.; Qiu, J. Risk Assessment for Distribution Systems Using an Improved PEM-Based Method Considering Wind and Photovoltaic Power Distribution. Sustainability 2017, 9, 491. https://doi.org/10.3390/su9040491
Gong Q, Lei J, Qiao H, Qiu J. Risk Assessment for Distribution Systems Using an Improved PEM-Based Method Considering Wind and Photovoltaic Power Distribution. Sustainability. 2017; 9(4):491. https://doi.org/10.3390/su9040491
Chicago/Turabian StyleGong, Qingwu, Jiazhi Lei, Hui Qiao, and Jingjing Qiu. 2017. "Risk Assessment for Distribution Systems Using an Improved PEM-Based Method Considering Wind and Photovoltaic Power Distribution" Sustainability 9, no. 4: 491. https://doi.org/10.3390/su9040491
APA StyleGong, Q., Lei, J., Qiao, H., & Qiu, J. (2017). Risk Assessment for Distribution Systems Using an Improved PEM-Based Method Considering Wind and Photovoltaic Power Distribution. Sustainability, 9(4), 491. https://doi.org/10.3390/su9040491





