Virtual Sensors for Biodiesel Production in a Batch Reactor
Abstract
:1. Introduction
2. Transesterification Model
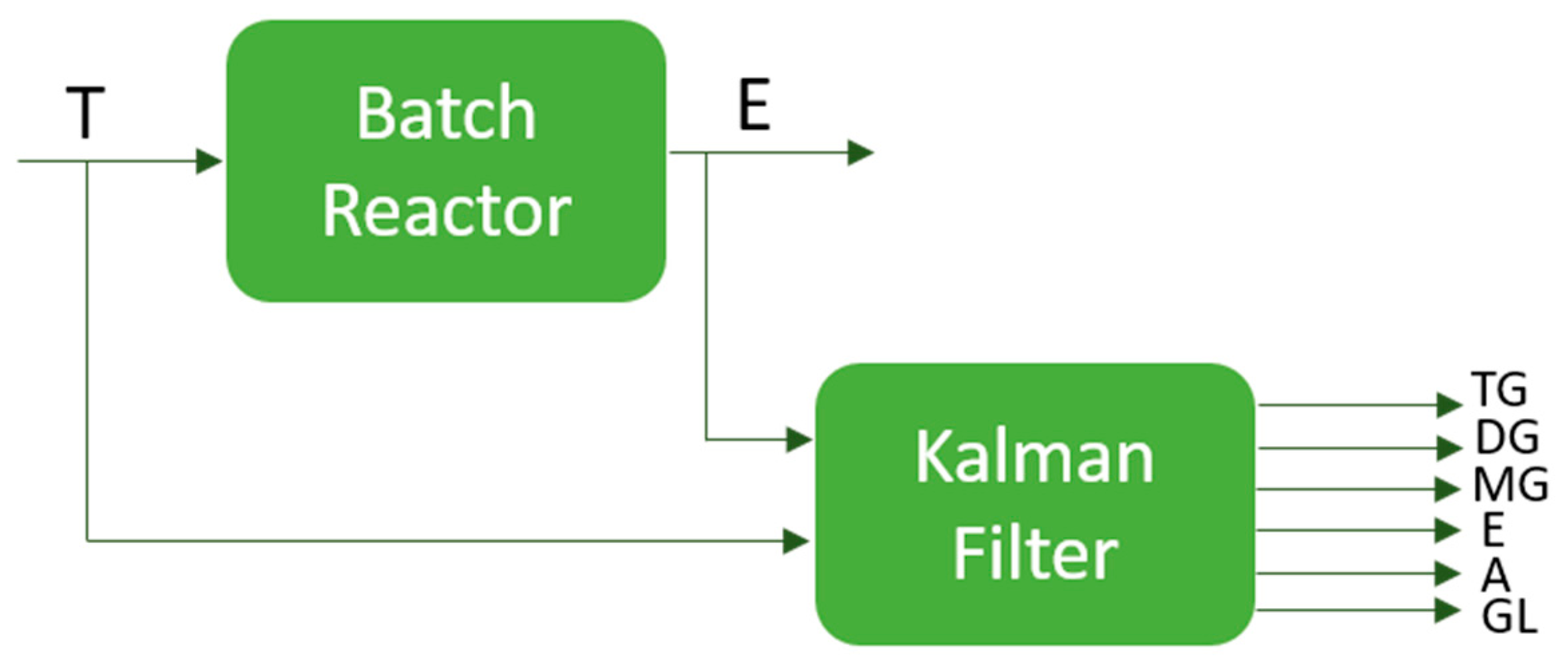
3. Extended Kalman Filter
4. Results and Discussion
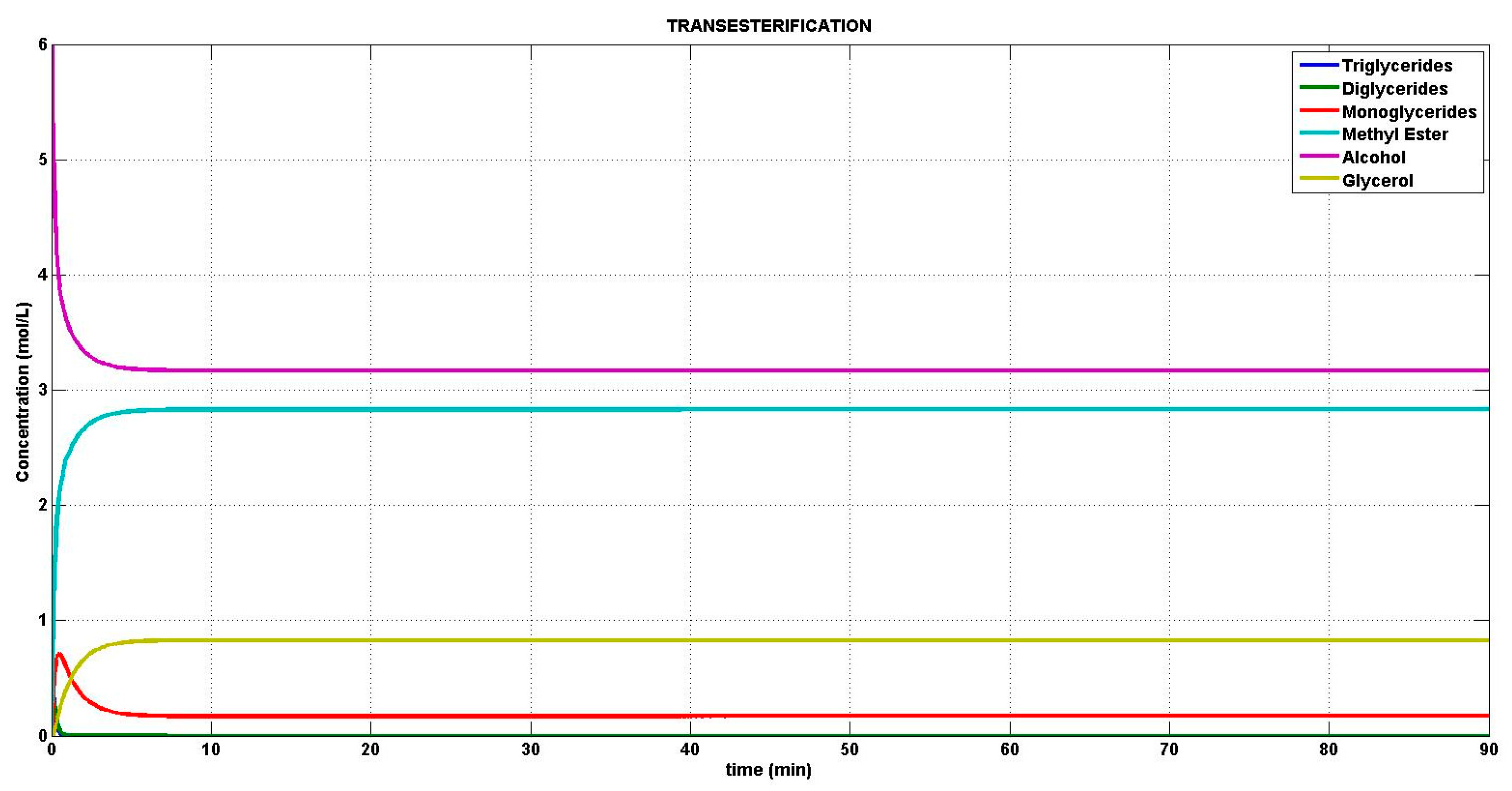
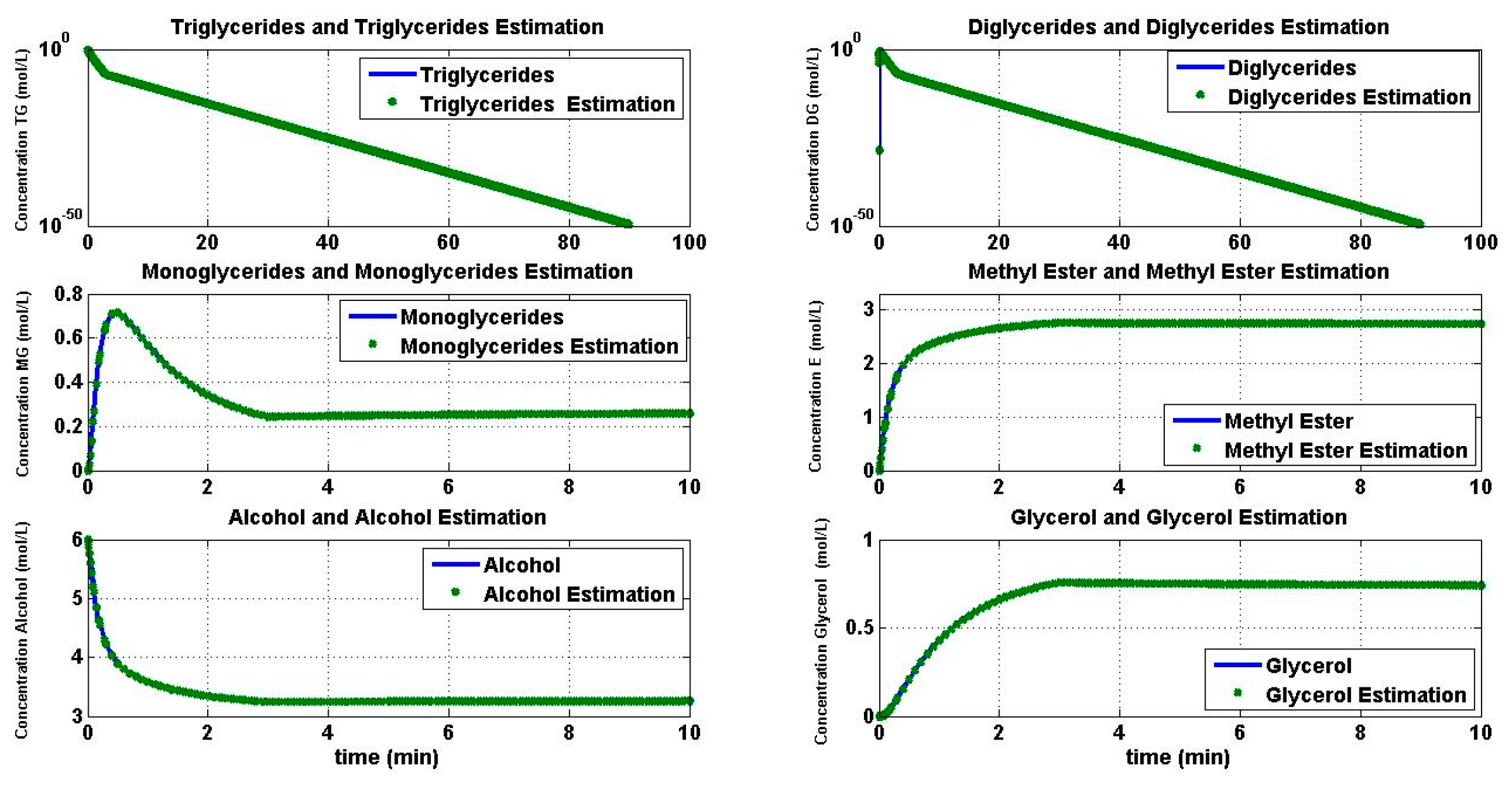
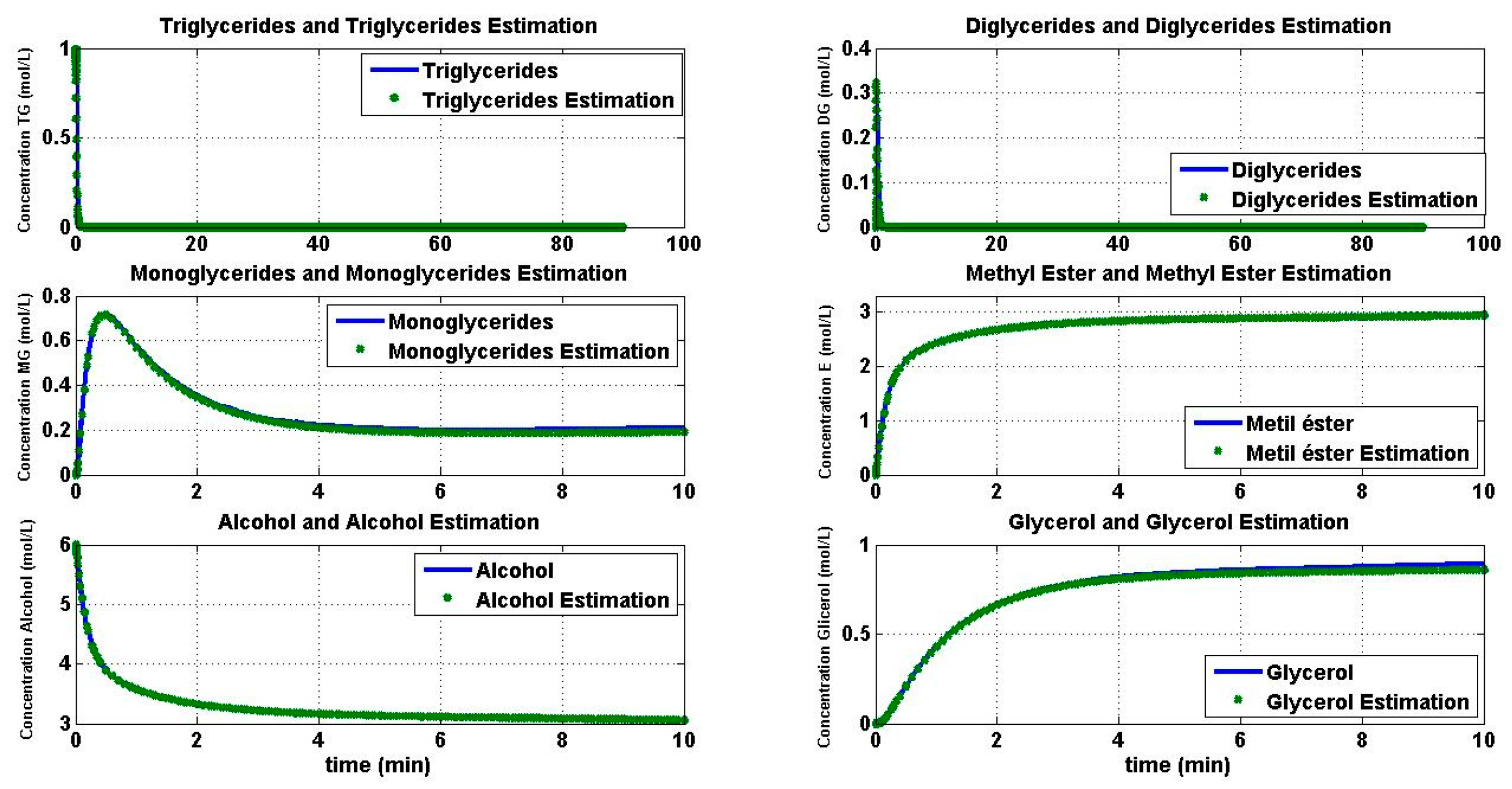
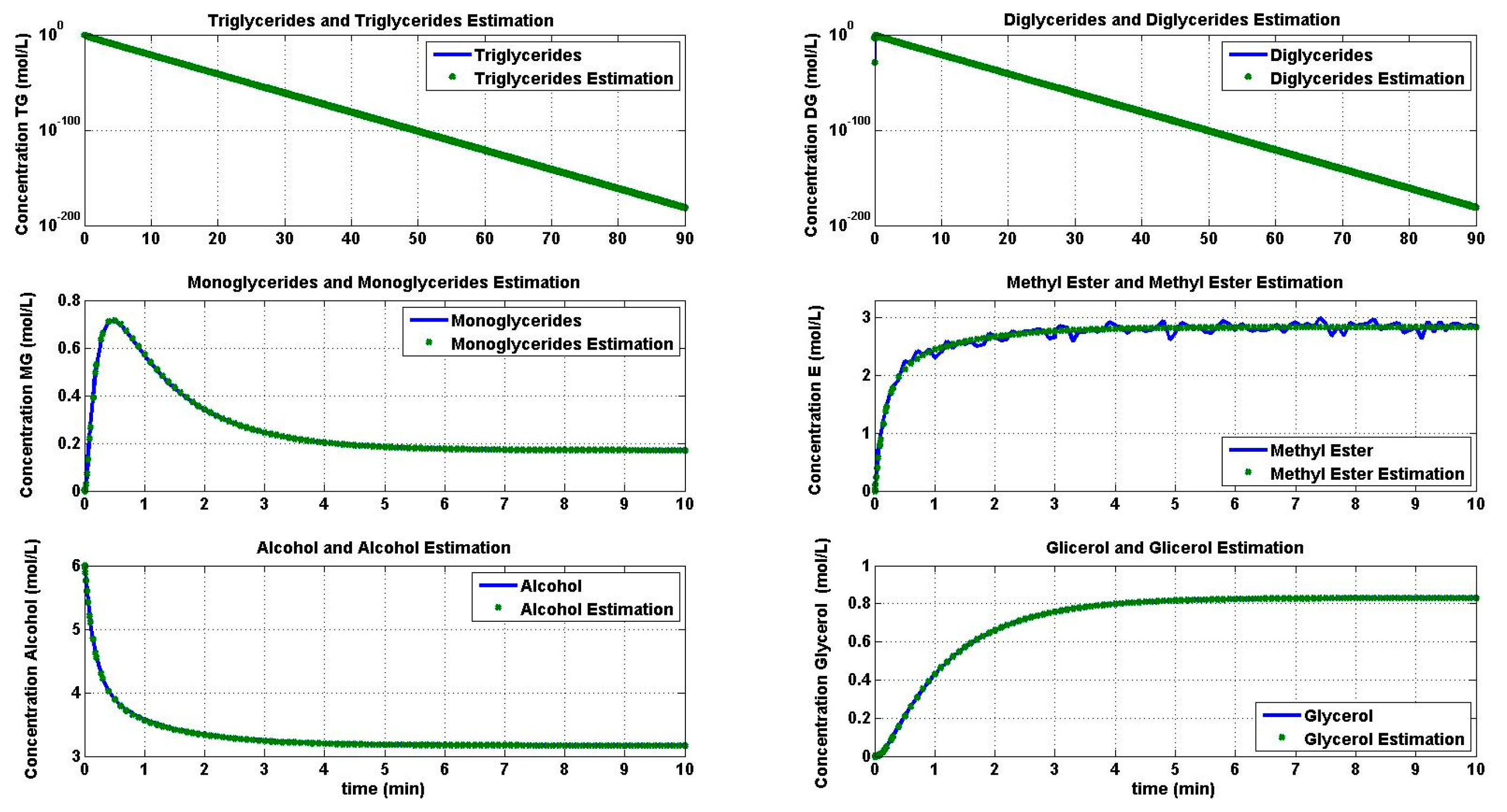
4.1. Simulation of the Transesterification Reaction
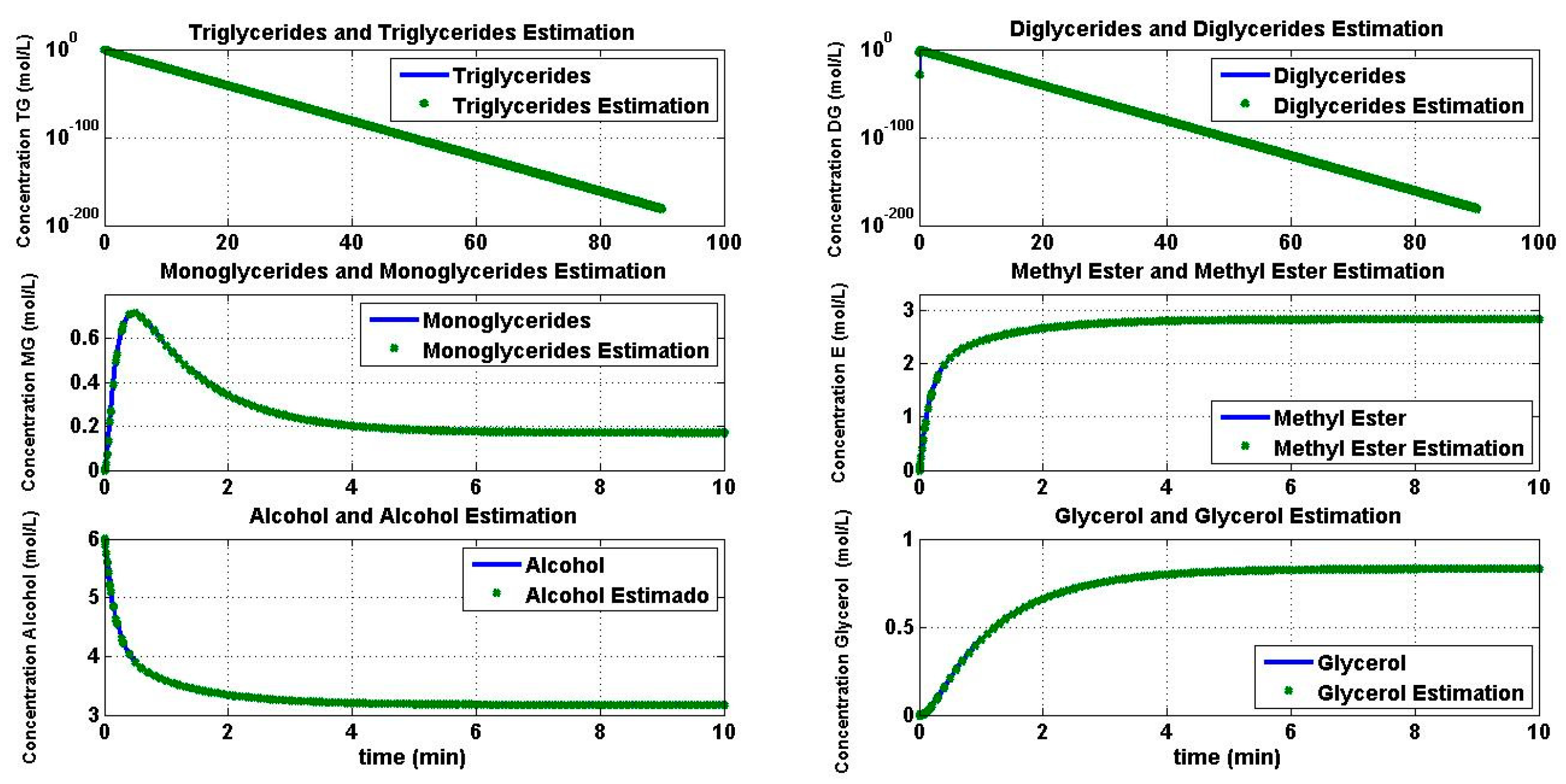
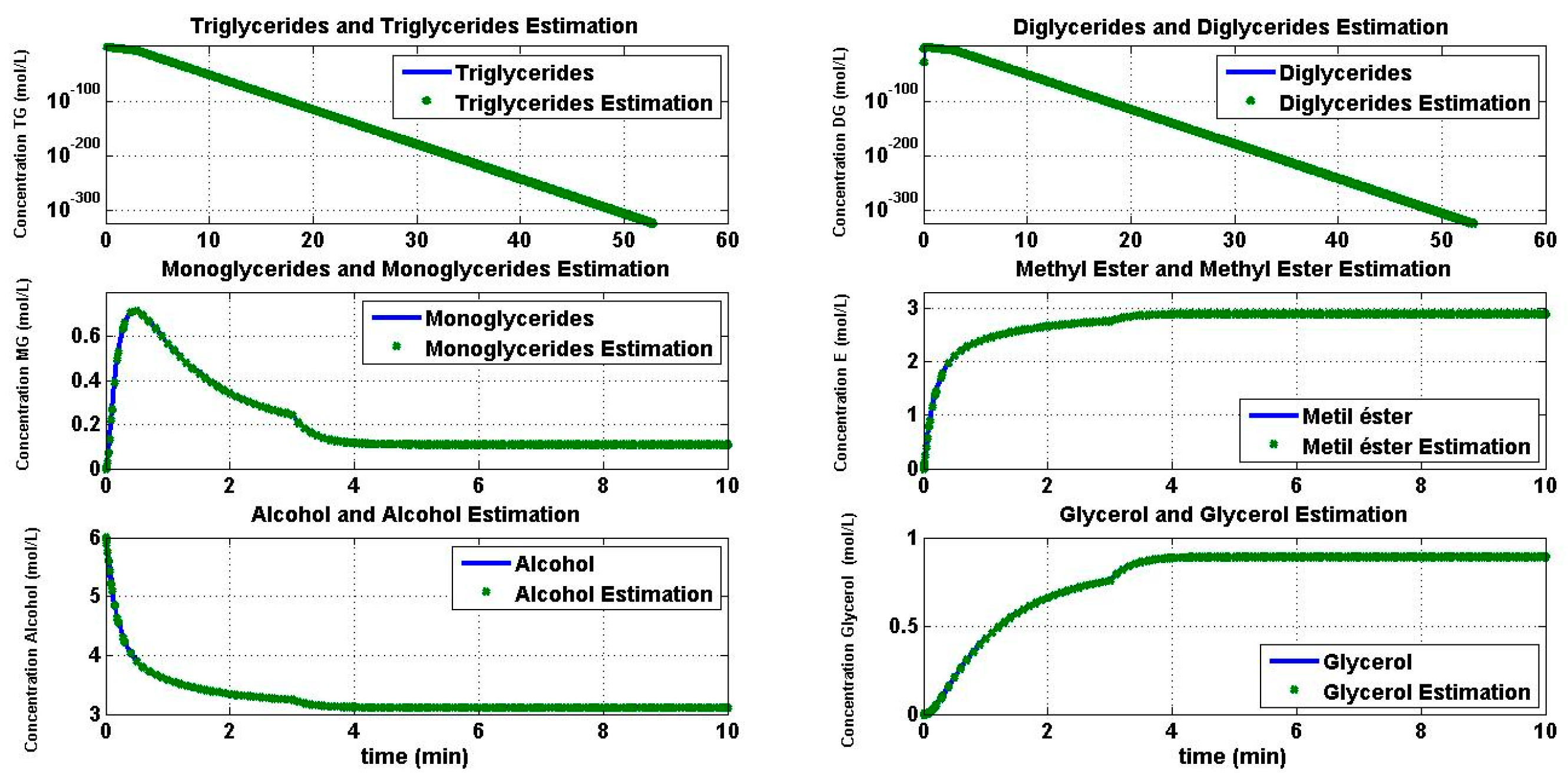
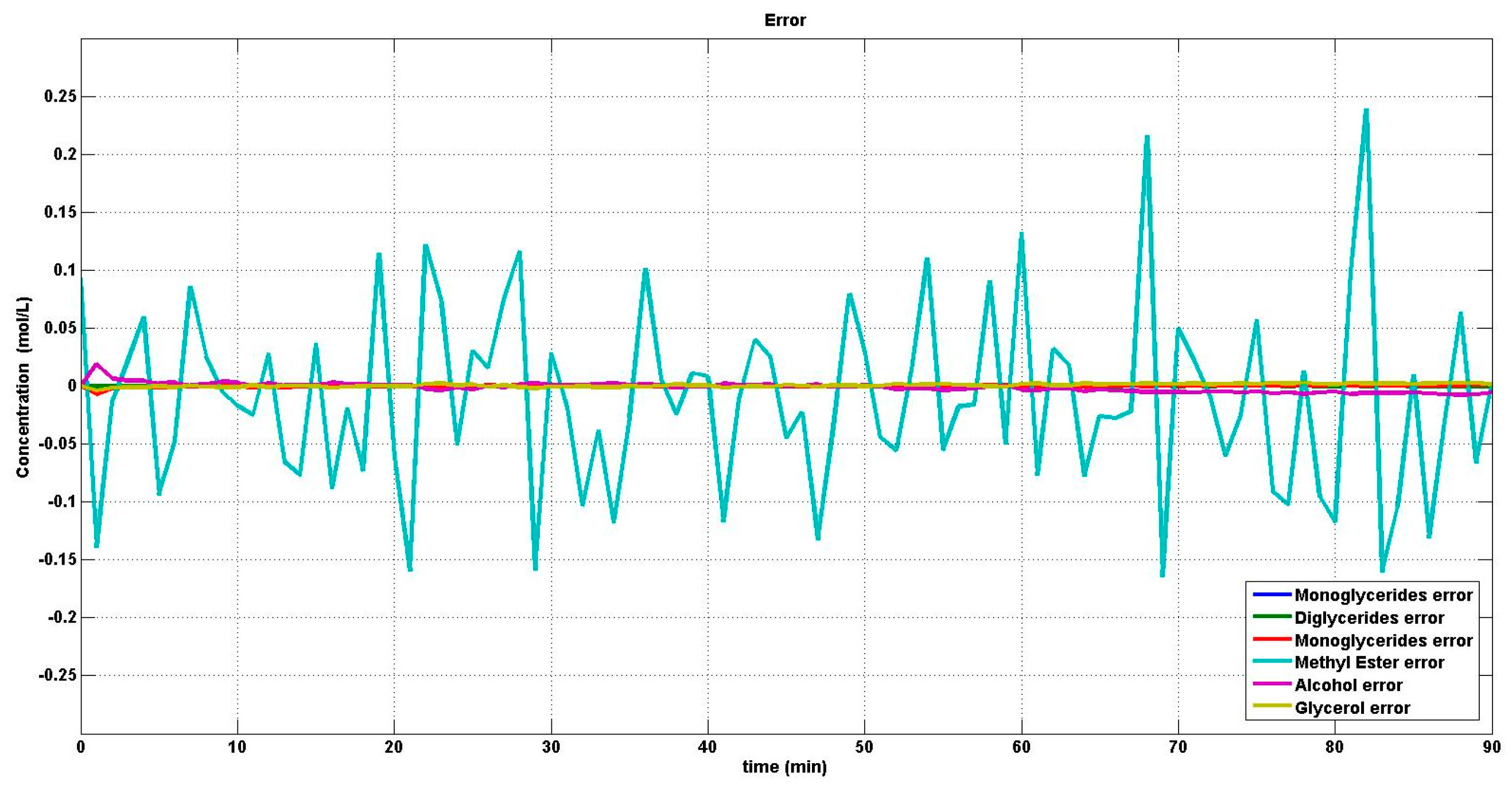
4.2. Reaction Estimation
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Demirbas, M.F.; Mehmet, B. Progress and recent trends in biodiesel fuels. Int. J. Green Energy 2009, 50, 14–34. [Google Scholar] [CrossRef]
- Felizardo, P.; Baptista, P.; Menezes, J.C.; Correia, M.J.N. Multivariate near infrared spectroscopy models for predicting the methyl esters content in biodiesel. Anal. Chim. Acta 2008, 607, 153–159. [Google Scholar]
- Fukuda, H.; Kondo, A.; Noda, H. Biodiesel fuel production by transesterification of oils. J. Biosci. Bioeng. 2001, 92, 405–416. [Google Scholar] [CrossRef]
- Mansouri, S.S.; Ismail, M.I.; Babi, D.K.; Simasatitkul, L.; Huusom, J.K.; Gani, R. Systematic Sustainable Process Design and Analysis of Biodiesel Processes. Processes 2013, 1, 167–202. [Google Scholar] [CrossRef]
- Ovando-Medina, I.; Espinosa-García, F.; Núñez-Farfán, J.; Salvador-Figueroa, M. Does biodiesel from Jatropha Curcas represent a sustainable alternative energy source? Sustainability 2009, 1, 1035–1041. [Google Scholar] [CrossRef]
- Ma, F.; Hanna, M.A. Biodiesel production: A review. Bioresour. Technol. 1999, 70, 1–15. [Google Scholar] [CrossRef]
- Knothe, G. Biodiesel and renewable diesel: A comparison. Prog. Energy Combust. Sci. 2010, 36, 364–373. [Google Scholar] [CrossRef]
- Franco, M. Simulación del Proceso de Producción de Biodiesel a Partir de Aceites Vegetales en Condiciones Súper-Críticas. Master’s Thesis, Escola Tecnica Superior d’Enginyeria Industrial de Barcelona, Barcelona, Espana, 2013. [Google Scholar]
- Holčapek, M.; Jandera, P.; Fischer, J.; Prokeš, B. Analytical monitoring of the production of biodiesel by high-performance liquid chromatography with various detection methods. J. Chromatogr. A 1999, 858, 13–31. [Google Scholar] [CrossRef]
- Dubé, M.A.; Zheng, S.; McLean, D.D.; Kates, M. A comparison of attenuated total reflectance-FTIR spectroscopy and GPC for monitoring biodiesel production. J. Am. Oil Chem. Soc. 2004, 81, 599–603. [Google Scholar] [CrossRef]
- Monteiro, M.R.; Ambrozin, A.R.P.; Lião, L.M.; Ferreira, A.G. Critical review on analytical methods for biodiesel characterization. Talanta 2008, 77, 593–605. [Google Scholar] [CrossRef]
- Richard, R.; Li, Y.; Dubreuil, B.; Thiebaud-Roux, S.; Prat, L. On-line monitoring of the transesterification reaction between triglycerides and ethanol using near infrared spectroscopy combined with gas chromatography. Bioresour. Technol. 2011, 102, 6702–6709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Boni, L.A.B.; Da Silva, I.N.L. Monitoring the transesterification reaction with laser spectroscopy. Fuel Process. Technol. 2011, 92, 1001–1006. [Google Scholar] [CrossRef]
- Fontalvo-Gómez, M.; Colucci, J.A.; Velez, N.; Romanach, R.J. In-line near-infrared (NIR) and raman spectroscopy coupled with principal component analysis (PCA) for in situ evaluation of the transesterification reaction. Appl. Spectrosc. 2013, 67, 1142–1149. [Google Scholar] [CrossRef] [PubMed]
- Kouame, S.D.B.; Perez, J.; Eser, S.; Benesi, A. 1H-NMR Monitoring of the transesterification process of Jatropha oil. Fuel Process. Technol. 2012, 97, 60–64. [Google Scholar] [CrossRef]
- Knothe, G. Analyzing biodiesel: Standards and other methods. JAOCS J. Am. Oil Chem. Soc. 2006, 83, 823–833. [Google Scholar] [CrossRef]
- Reddy, S.R.; Titu, D.; Chadha, A. A novel method for monitoring the transesterification reaction of oil in biodiesel production by estimation of glycerol. JAOCS J. Am. Oil Chem. Soc. 2010, 87, 747–754. [Google Scholar] [CrossRef]
- Xie, W.; Li, H. Hydroxyl content and refractive index determinations on transesterified soybean oil. JAOCS J. Am. Oil Chem. Soc. 2006, 83, 869–872. [Google Scholar] [CrossRef]
- Ellis, N.; Guan, F.; Chen, T.; Poon, C. Monitoring biodiesel production (transesterification) using in situ viscometer. Chem. Eng. J. 2008, 138, 200–206. [Google Scholar] [CrossRef]
- Oisiovici, R.M.; Cruz, S.L. State estimation of batch distillation columns using an extended Kalman filter. Chem. Eng. Sci. 2000, 55, 4667–4680. [Google Scholar] [CrossRef]
- Patnaik, P.R. Improvement of the microbial production of streptokinase by controlled filtering of process noise. Process Biochem. 1999, 35, 309–315. [Google Scholar] [CrossRef]
- Torres, L.; Verde, C.; Vázquez-Hernández, O. Parameter identification of marine risers using Kalman-like observers. Ocean Eng. 2015, 93, 84–97. [Google Scholar] [CrossRef]
- Eftekhar, S.; Chatzi, E.; Papadimitriou, C. A dual Kalman filter approach for state estimation via output-only acceleration measurements. Mech. Syst. Signal Process. 2015, 60–61, 866–886. [Google Scholar] [CrossRef]
- Beyer, M.A.; Grote, W.; Reinig, G. Adaptive exact linearization control of batch polymerization reactors using a Sigma-Point Kalman Filter. J. Process Control 2008, 18, 663–675. [Google Scholar] [CrossRef]
- Docimo, D.J.; Ghanaatpishe, M.; Mamun, A. Extended Kalman Filtering to estimate temperature and irradiation for maximum power point tracking of a photovoltaic module. Energy 2017, 120, 47–57. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, L.; Yu, T. On-line estimation in fed-batch fermentation process using state space model and unscented kalman filter. Chin. J. Chem. Eng. 2010, 18, 258–264. [Google Scholar] [CrossRef]
- Rezaei, N.; Rahimpour, M.R.; Khayatian, A.; Jahanmiri, A. A new hybrid approach in the estimation of end-states of a tubular plug-flow reactor by Kalman filter. Chem. Eng. Process. Process Intensif. 2008, 47, 770–779. [Google Scholar] [CrossRef]
- Kupilik, M.J.; Vincent, T.L. Estimation of biogas composition in a catalytic reactor via an extended Kalman filter. In Proceedings of the IEEE International Conference on Control Applications, Denver, CO, USA, 28–30 September 2011; pp. 768–773.
- Noureddini, H.; Zhu, D. Kinetics of transesterification of soybean oil. J. Am. Oil Chem. Soc. 1997, 74, 1457–1463. [Google Scholar] [CrossRef]
- Jain, S.; Sharma, M.P. Kinetics of acid base catalyzed transesterification of Jatropha curcas oil. Bioresour. Technol. 2010, 101, 7701–7706. [Google Scholar] [CrossRef] [PubMed]
- Noriega, M.A.; Narváez, P.C.; Heinz, C. Kinetics of Jatropha oil methanolysis. Fuel 2014, 134, 244–249. [Google Scholar] [CrossRef]
- Berchmans, H.J.; Morishita, K.; Takarada, T. Kinetic study of hydroxide-catalyzed methanolysis of Jatropha curcas–waste food oil mixture for biodiesel production. Fuel 2013, 104, 46–52. [Google Scholar] [CrossRef]
- William, M.C.; Medeiros, N.J.; Boyd, D.J.; Snell, J.R. Biodiesel transesterification kinetics monitored by pH measurement. Bioresour. Technol. 2013, 136, 771–774. [Google Scholar]
- Baras, J.S.; Bensoussan, A.; James, R.M. Dynamic observers as asymptotic limits of recursive filters: Special cases. Appl. Math. 1988, 48, 1147–1158. [Google Scholar] [CrossRef]
| Type of Oil | Jatropha Oil |
|---|---|
| Alcohol:oil molar ratio | 6:1 |
| Alcohol | Methanol (CH4O) |
| Ng’s reaction time | 90 min |
| Catalyst | Sodium hydroxide (NaOH) |
| Amount of catalyst | 0.20 wt % of sodium oxide hydraulic oil |
| Temperature on reaction | 323.15 K (50 °C) |
| Mixing intensity | 600 rpm |
| Parameters | Units |
|---|---|
| Initial conditions | |
| Stability parameter | |
| Initial condition of S | |
| Covariance Matrix | |
| Covariance Matrix |
| Component | MSE (%) |
|---|---|
| TG | |
| DG | |
| MG | 0.0094 |
| E | 0.0202 |
| A | 0.0033 |
| GL | 0.1250 |
| Component | MSE (%) |
|---|---|
| TG | |
| DG | |
| MG | |
| E | |
| A | |
| GL |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Zapata, B.Y.; Adam-Medina, M.; Álvarez-Gutiérrez, P.E.; Castillo-González, J.P.; León, H.R.H.-d.; Vela-Valdés, L.G. Virtual Sensors for Biodiesel Production in a Batch Reactor. Sustainability 2017, 9, 455. https://doi.org/10.3390/su9030455
López-Zapata BY, Adam-Medina M, Álvarez-Gutiérrez PE, Castillo-González JP, León HRH-d, Vela-Valdés LG. Virtual Sensors for Biodiesel Production in a Batch Reactor. Sustainability. 2017; 9(3):455. https://doi.org/10.3390/su9030455
Chicago/Turabian StyleLópez-Zapata, Betty Y., Manuel Adam-Medina, Peggy E. Álvarez-Gutiérrez, Juan P. Castillo-González, Héctor R. Hernández-de León, and Luis G. Vela-Valdés. 2017. "Virtual Sensors for Biodiesel Production in a Batch Reactor" Sustainability 9, no. 3: 455. https://doi.org/10.3390/su9030455
APA StyleLópez-Zapata, B. Y., Adam-Medina, M., Álvarez-Gutiérrez, P. E., Castillo-González, J. P., León, H. R. H.-d., & Vela-Valdés, L. G. (2017). Virtual Sensors for Biodiesel Production in a Batch Reactor. Sustainability, 9(3), 455. https://doi.org/10.3390/su9030455






