Modeling Post-Fire Mortality in Pure and Mixed Forest Stands in Portugal—A Forest Planning-Oriented Model
Abstract
:1. Introduction
2. Materials and Methods
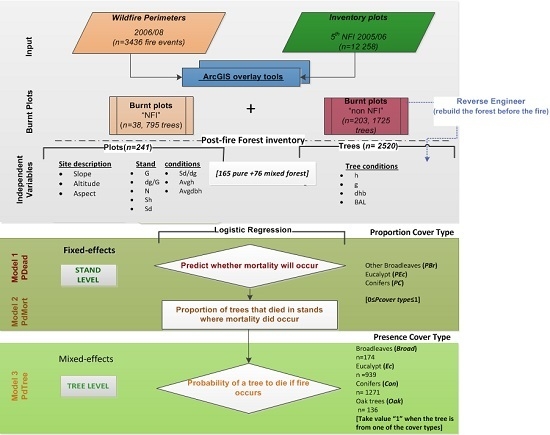
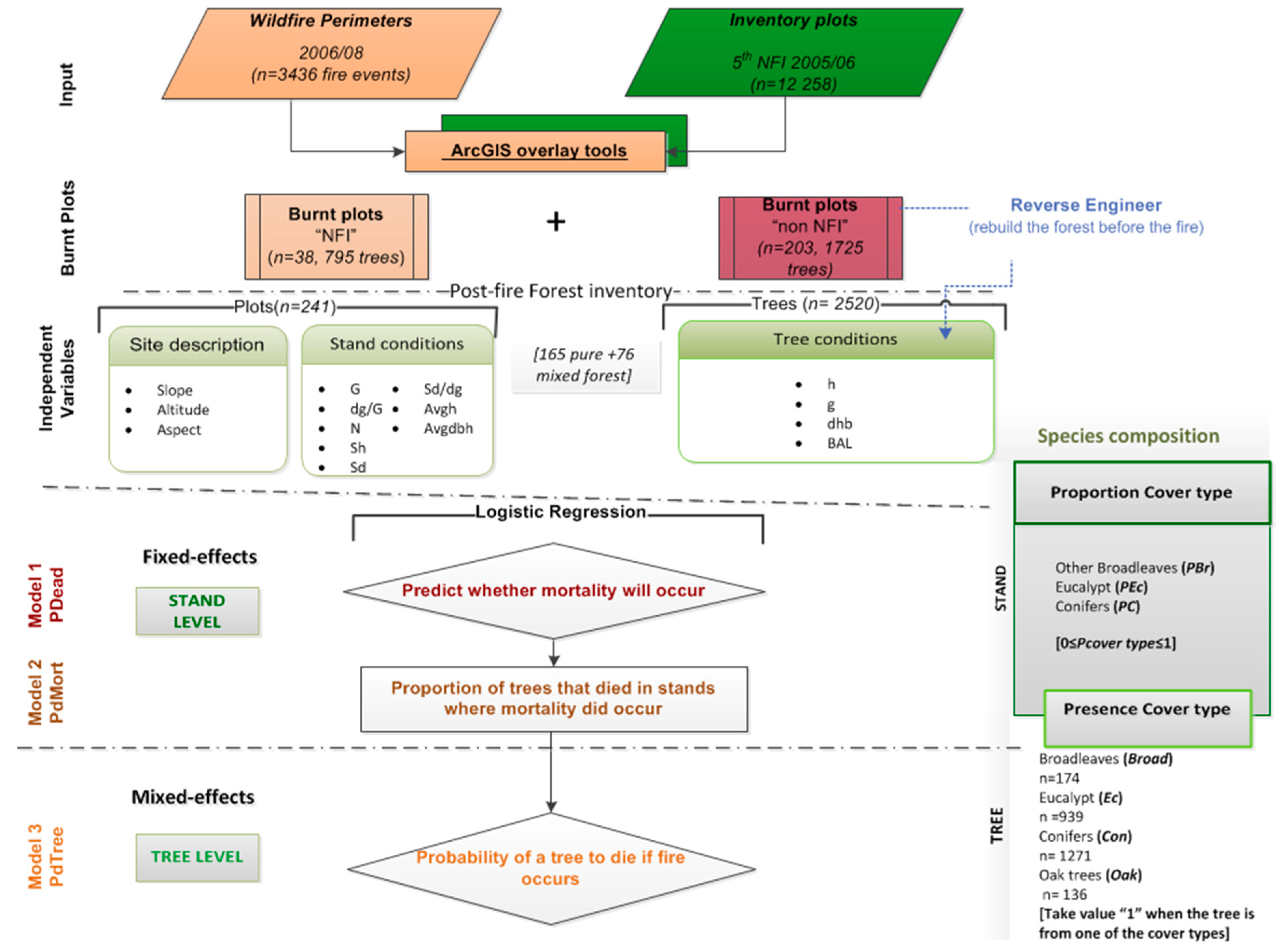
2.1. Data Collection
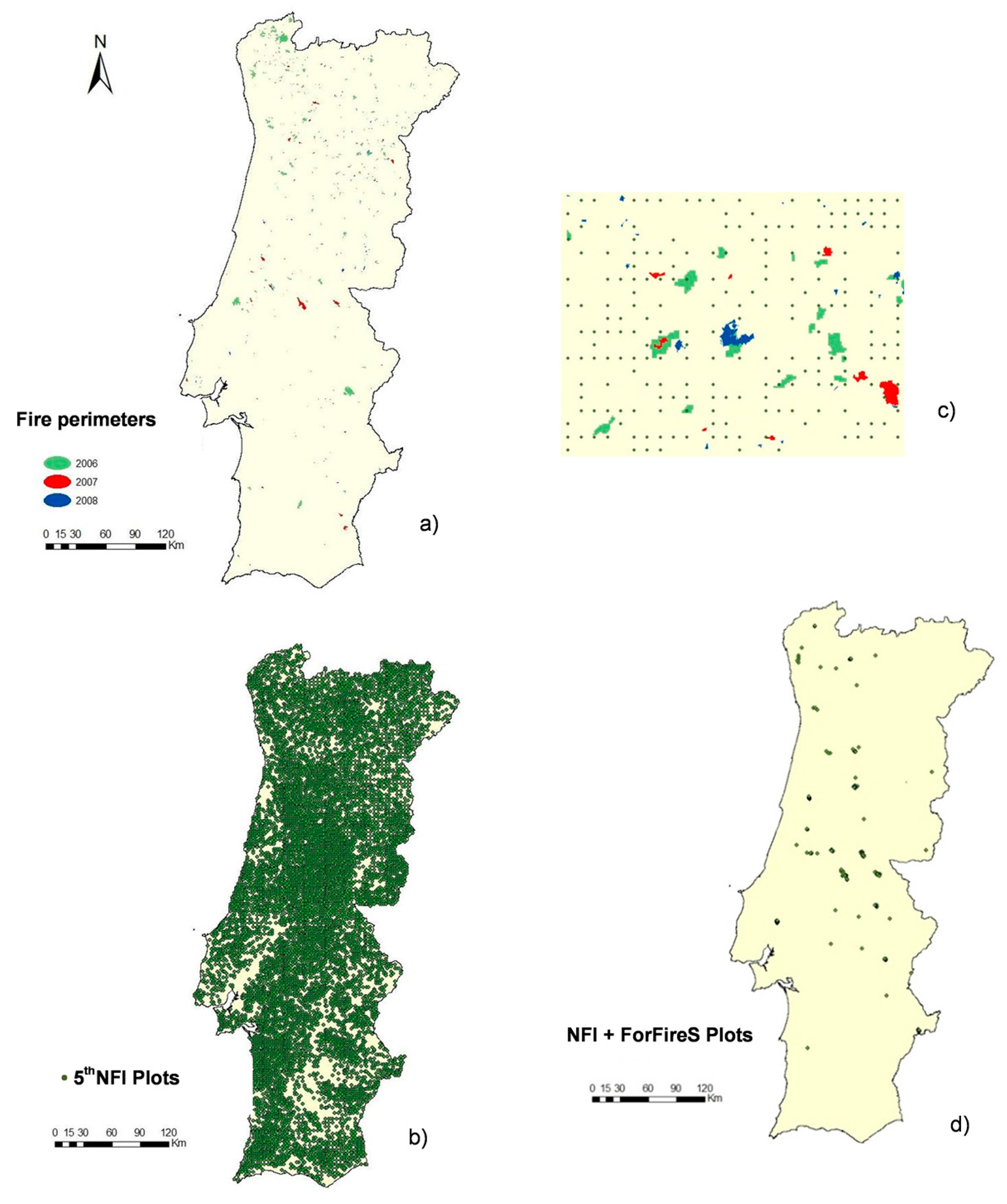
2.1.1. Wildfire Perimeters and Inventory Plots Status
2.1.2. Reverse Engineering to Rebuild the Tree Characteristics
2.2. Post-Fire Model Description
2.2.1. Statistical Approach
Fixed-Effects Logistic Regression
Mixed-Effects Logistic Regression
2.2.2. Stand-Level Modeling
2.2.3. Tree-Level Modeling
2.2.4. Assessment of Model Selection
3. Results
3.1. General Response Patterns
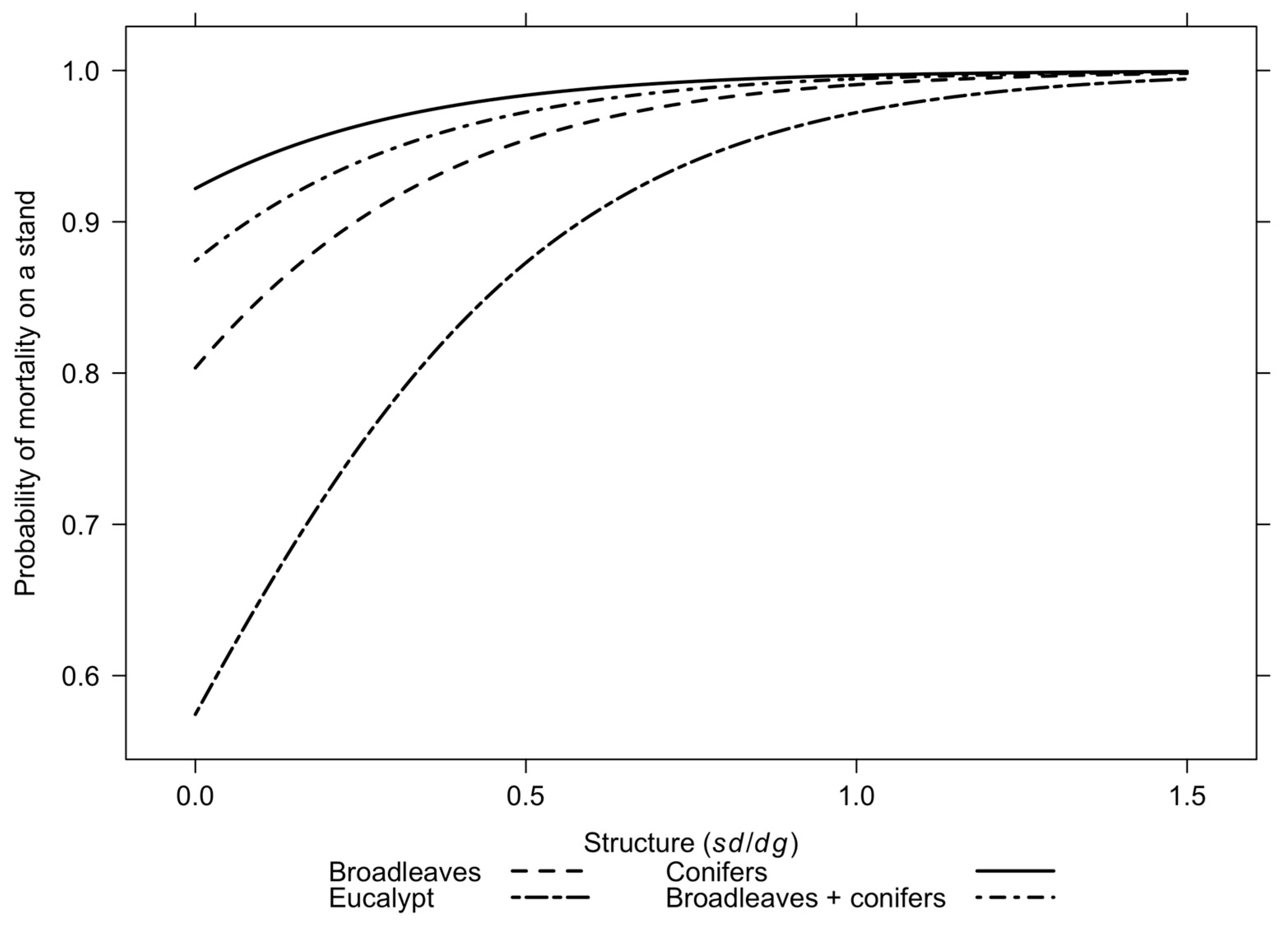
3.2. Stand-Level Mortality
3.2.1. Predicting Whether Stand Level Mortality Will Occur
3.2.2. Estimating Stand-Level Post-Fire Mortality
3.3. Estimating Post-Fire Tree Mortality
3.4. Cut-Off Point Value Selection
4. Discussion
4.1. Forest Composition, Heterogeneity and Structure
4.2. Pre and Post-Fire Smart Management: Applicability
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- ICNF. Áreas Dos Usos Do Solo E Das Espécies Florestais de Portugal Continental. Resultados Preliminares, 6º Inventário Florestal Nacional. 2013, p. 34. Available online: http://www.icnf.pt/portal/florestas/ifn/resource/ficheiros/ifn/ifn6-res-prelimv1-1 (accessed on 8 August 2016). (In Portuguese)
- Pereira, M.G.; Aranha, J.; Amraoui, M. Land cover fire proneness in Europe. For. Syst. 2014, 23, 598–610. [Google Scholar] [CrossRef]
- Rothermel, R.C. How to Predict the Spread and Intensity of Forest and Range Fires; U.S. Department of Agriculture, Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1983.
- Silva, J.S.; Moreira, F.; Vaz, P.; Catry, F.; Godinho-Ferreira, P. Assessing the Relative Fire Proneness of Different Forest Types in Portugal. Plant Biosyst. 2009, 143, 597–608. [Google Scholar] [CrossRef]
- Mateus, P.; Fernandes, P.M. Forest Fires in Portugal: Dynamics, Causes and Policies. In Forest Context and Policies in Portugal; Springer: Berlin, Germany, 2014; pp. 97–115. [Google Scholar]
- Catry, F.X.; Pausas, J.G.; Moreira, F.; Fernandes, P.M.; Rego, F. Post-Fire Response Variability in Mediterranean Basin Tree Species in Portugal. Int. J. Wildland Fire 2013, 22, 919–932. [Google Scholar] [CrossRef]
- Del Río, M.; Pretzsch, H.; Alberdi, I.; Bielak, K.; Bravo, F.; Brunner, A.; Condés, S.; Ducey, M.J.; Fonseca, T.; von Lüpke, N. Characterization of the Structure, Dynamics, and Productivity of Mixed-Species Stands: Review and Perspectives. Eur. J. For. Res. 2016, 135, 23–49. [Google Scholar] [CrossRef]
- Lee, S.-W.; Lee, M.-B.; Lee, Y.-G.; Won, M.-S.; Kim, J.J.; Hong, S. Relationship between Landscape Structure and Burn Severity at the Landscape and Class Levels in Samchuck, South Korea. For. Ecol. Manag. 2009, 258, 1594–1604. [Google Scholar] [CrossRef]
- Kint, V.; Geudens, G.; Mohren, G.M.J.; Lust, N. Silvicultural Interpretation of Natural Vegetation Dynamics in Ageing Scots Pine Stands for Their Conversion into Mixed Broadleaved Stands. For. Ecol. Manag. 2006, 223, 363–370. [Google Scholar] [CrossRef]
- Jactel, H.; Nicoll, B.C.; Branco, M.; Gonzalez-Olabarria, J.R.; Grodzki, W.; Långström, B.; Moreira, F.; Netherer, S.; Orazio, C.; Piou, D. The Influences of Forest Stand Management on Biotic and Abiotic Risks of Damage. Ann. For. Sci. 2009, 66, 1–18. [Google Scholar] [CrossRef]
- Nunes, L.; Lopes, D.; Rego, F.C.; Gower, S.T. Aboveground Biomass and Net Primary Production of Pine, Oak and Mixed Pine-oak Forests on the Vila Real District, Portugal. For. Ecol. Manag. 2013, 305, 38–47. [Google Scholar] [CrossRef]
- Finney, M.A.; Andrews, P.L. FARSITE—A Program for Fire Growth Simulation. Fire Manag. Notes 1999, 59, 13–15. [Google Scholar]
- Finney, M.A. An Overview of FlamMap Fire Modeling Capabilities. Fuels Management—How to Measure Success. USDA Forest Service Proceedings RMRS-P-41. Andrews, P.L., Butler, B.W., Eds.; pp. 213–220. Available online: https://www.fs.fed.us/rm/pubs/rmrs_p041.pdf (accessed on 6 March 2017).
- Ryan, K.C. Evaluating Potential Tree Mortality from Prescribed Burning. In Proceedings of the Site Preparation and Fuels Management on Steep Terrain, Pullman, WA, USA, 15–17 February 1982; pp. 167–179.
- Keyser, T.L.; Smith, F.W.; Lentile, L.B.; Shepperd, W.D. Modeling Postfire Mortality of Ponderosa Pine Following a Mixed-Severity Wildfire in the Black Hills: The Role of Tree Morphology and Direct Fire Effects. For. Sci. 2006, 52, 530–539. [Google Scholar]
- Hull Sieg, C.; McMillin, J.D.; Fowler, J.F.; Allen, K.K.; Negron, J.F.; Wadleigh, L.L.; Anhold, J.A.; Gibson, K.E. Best Predictors for Postfire Mortality of Ponderosa Pine Trees in the Intermountain West. For. Sci. 2006, 52, 718–728. [Google Scholar]
- González, J.R.; Trasobares, A.; Palahi, M.; Pukkala, T. Predicting Stand Damage and Tree Survival in Burned Forests in Catalonia (North-East Spain). Ann. For. Sci. 2007, 64, 733–742. [Google Scholar] [CrossRef]
- Garcia-Gonzalo, J.; Marques, S.; Borges, J.G.; Botequim, B.; Oliveira, M.M.; Tomé, J.; Tomé, M. A Three-Step Approach to Post-Fire Mortality Modelling in Maritime Pine (Pinus pinaster Ait) Stands for Enhanced Forest Planning in Portugal. Forestry 2011, 84, 197–206. [Google Scholar] [CrossRef]
- Linder, P.; Jonsson, P.; Niklasson, M. Tree Mortality after Prescribed Burning in an Old-Growth Scots Pine Forest in Northern Sweden. Silva Fenn. 1998, 32, 339–349. [Google Scholar] [CrossRef]
- Hély, C.; Flannigan, M.; Bergeron, Y. Modeling Tree Mortality Following Wildfire in the Southeastern Canadian Mixed-Wood Boreal Forest. For. Sci. 2003, 49, 566–576. [Google Scholar]
- McHugh, C.W.; Kolb, T.E. Corrigendum to: Ponderosa Pine Mortality Following Fire in Northern Arizona. Int. J. Wildland Fire 2003, 12, 245. [Google Scholar] [CrossRef]
- Fernandes, P.M. Combining Forest Structure Data and Fuel Modelling to Classify Fire Hazard in Portugal. Ann. For. Sci. 2009, 66, 1–9. [Google Scholar] [CrossRef]
- Fernandes, P.M.; Luz, A.; Loureiro, C. Changes in Wildfire Severity from Maritime Pine Woodland to Contiguous Forest Types in the Mountains of Northwestern Portugal. For. Ecol. Manag. 2010, 260, 883–892. [Google Scholar] [CrossRef]
- Agee, J.K.; Skinner, C.N. Basic Principles of Forest Fuel Reduction Treatments. For. Ecol. Manag. 2005, 211, 83–96. [Google Scholar] [CrossRef]
- Gonzalez, J.R.; Palahi, M.; Trasobares, A.; Pukkala, T. A Fire Probability Model for Forest Stands in Catalonia (North-East Spain). Ann. For. Sci. 2006, 63, 169–176. [Google Scholar] [CrossRef]
- Marques, S.; Garcia-Gonzalo, J.; Borges, J.G.; Botequim, B.; Oliveira, M.M.; Tomé, J.; Tomé, M. Developing Post-Fire Eucalyptus globulus Stand Damage and Tree Mortality Models for Enhanced Forest Planning in Portugal. Silva Fenn. 2011, 45, 69–83. [Google Scholar] [CrossRef]
- Gonzalez, J.R.; Palahí, M.; Pukkala, T. Integrating Fire Risk Considerations in Forest Management Planning in Spain—A Landscape Level Perspective. Landsc. Ecol. 2005, 20, 957–970. [Google Scholar] [CrossRef]
- Garcia-Gonzalo, J.; Pukkala, T.; Borges, J.G. Integrating Fire Risk in Stand Management Scheduling. An Application to Maritime Pine Stands in Portugal. Ann. Oper. Res. 2011, 219, 379–395. [Google Scholar] [CrossRef]
- Pasalodos-Tato, M.; Pukkala, T.; Alboreca, A.R. Optimal Management of Pinus pinaster in Galicia (Spain) under Risk of Fire. Int. J. Wildland Fire 2010, 19, 937–948. [Google Scholar] [CrossRef]
- Botelho, H.S.; Rego, F.C.; Ryan, K.C. Tree Mortality Models for Pinus Pinaster of Northern Portugal. In Proceedings of the 13th Conference on Fire and Forest Meteorology; IAWF: Lorne, Australia, 1998; pp. 235–240. [Google Scholar]
- Fernandes, P.A.; Loureiro, C.A.; Botelho, H.S. Fire Behaviour and Severity in a Maritime Pine Stand under Differing Fuel Conditions. Ann. For. Sci. 2004, 61, 537–544. [Google Scholar] [CrossRef]
- Fernandes, P.M.; Rigolot, E. The Fire Ecology and Management of Maritime Pine (Pinus pinaster Ait.). For. Ecol. Manag. 2007, 241, 1–13. [Google Scholar] [CrossRef]
- Catry, F.X.; Moreira, F.; Duarte, I.; Acácio, V. Factors Affecting Post-Fire Crown Regeneration in Cork Oak (Quercus suber L.) Trees. Eur. J. For. Res. 2009, 128, 231–240. [Google Scholar] [CrossRef]
- Catry, F.X.; Rego, F.; Moreira, F.; Fernandes, P.M.; Pausas, J.G. Post-Fire Tree Mortality in Mixed Forests of Central Portugal. For. Ecol. Manag. 2010, 260, 1184–1192. [Google Scholar] [CrossRef]
- Catry, F.X.; Moreira, F.; Tujeira, R.; Silva, J.S. Post-Fire Survival and Regeneration of Eucalyptus globulus in Forest Plantations in Portugal. For. Ecol. Manag. 2013, 310, 194–203. [Google Scholar] [CrossRef]
- Nunes, L.; Coutinho, J.; Nunes, L.F.; Rego, F.C.; Lopes, D. Growth, Soil Properties and Foliage Chemical Analysis Comparison. For. Syst. 2011, 20, 496–507. [Google Scholar] [CrossRef]
- Kolström, M.; Lindner, M.; Vilén, T.; Maroschek, M.; Seidl, R.; Lexer, M.J.; Netherer, S.; Kremer, A.; Delzon, S.; Barbati, A. Reviewing the Science and Implementation of Climate Change Adaptation Measures in European Forestry. Forests 2011, 2, 961–982. [Google Scholar] [CrossRef]
- Keeley, J.E.; Bond, W.J.; Bradstock, R.A.; Pausas, J.G.; Rundel, P.W. Fire in Mediterranean Ecosystems: Ecology, Evolution and Management; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Naeslund, B.A. Simulation of Damage and Mortality in Young Stands and Associated Stand Development Effects [Incl. Betula Pendula, Betula Verrucosa, Betula Pubescens]; Sveriges lantbruksuniv.: Uppsala, Sweden, 1986; ISBN 9789157626493. [Google Scholar]
- Ferreira, L.; Constantino, M.; Borges, J.G. Optimizing Management of Pinus pinaster Ait Stands, under Risk of Fire. An Application in Portugal. Ann. Oper. Res. 2011, 219, 359–377. [Google Scholar] [CrossRef]
- Ferreira, L.; Constantino, M.F.; Borges, J.G.; Garcia-Gonzalo, J. A Stochastic Dynamic Programming Approach to Optimize Short-Rotation Coppice Systems Management Scheduling: An Application to Eucalypt Plantations under Wildfire Risk in Portugal. For. Sci. 2012, 58, 353–365. [Google Scholar] [CrossRef]
- Oliveira, S.L.; Pereira, J.M.; Carreiras, J.M. Fire Frequency Analysis in Portugal (1975–2005), Using Landsat-Based Burnt Area Maps. Int. J. Wildland Fire 2012, 21, 48–60. [Google Scholar] [CrossRef]
- Bergeot, F.; Oliveira, T. Development of a Simple and Efficient Method for Field Assessment of Fire Severity; (ForFireS) Contract Number 382167 FISC, Final Report; Inventaire Forestier National: Maurin, France, 2008. [Google Scholar]
- Botequim, B.; Garcia-Gonzalo, J.; Marques, S.; Ricardo, A.; Borges, J.G.; Oliveira, M.M.; Tomé, J.; Tomé, M. Assessing wildfire risk probability in Eucalyptus globulus Labill stands in Portugal. iForest 2013, 6, 217–227. [Google Scholar] [CrossRef]
- Dieguez, U.; Barrio, M.; Castedo, F.; Balboa, M. Estimacion Del Diametro Normal Y Del Volumen Del Tronco a Partir de Las Dimensiones Del Tocon Para Seis Especies Forestales Comerciales de Galicia; Instituto Nacional de Investigacion y Tecnologia Agraria y Alimentaria, Madrid (España). Sist. Recur. For. 2003, 12, 131–139. [Google Scholar]
- Tomé, M.; Meyer, A.; Ramos, T.; Barreiro, S.; Faias, S.P.; Cortiçada, A. Relações Hipsométricas E Equações de Diâmetro Da Copa Desenvolvidas No Âmbito Do Tratamento Dos Dados Do Inventário Florestal Nacional 2005–2006; Publicações GIMREF RT, Universidade Técnica de Lisboa; Instituto Superior de Agronomia: Lisboa, Portugal, 2007; p. 23. (In Portuguese) [Google Scholar]
- Soares, P.; Tomé, M. Height-diameter Equation for First Rotation Eucalypt Plantations in Portugal. For. Ecol. Manag. 2002, 166, 99–109. [Google Scholar] [CrossRef]
- Monserud, R.A.; Sterba, H. Modeling Individual Tree Mortality for Austrian Forest Species. For. Ecol. Manag. 1999, 113, 109–123. [Google Scholar] [CrossRef]
- Vanclay, J.K. Modelling Forest Growth and Yield: Applications to Mixed Tropical Forests; School of Environment, Science and Engineering Papers; CAB International: Wallingford, UK, 1994; p. 537. [Google Scholar]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2000. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2016. [Google Scholar]
- Hamilton, D.A. A Logistic Model of Mortality in Thinned and Unthinned Mixed Conifer Stands of Northern Idaho. For. Sci. 1986, 32, 989–1000. [Google Scholar]
- Das, A.J.; Battles, J.J.; Stephenson, N.L.; Van Mantgem, P.J. The Relationship between Tree Growth Patterns and Likelihood of Mortality: A Study of Two Tree Species in the Sierra Nevada. Can. J. For. Res. 2007, 37, 580–597. [Google Scholar] [CrossRef]
- Bates, D.M.; Maechler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Fridman, J.; Ståhl, G. A Three-Step Approach for Modelling Tree Mortality in Swedish Forests. Scand. J. For. Res. 2001, 16, 455–466. [Google Scholar] [CrossRef]
- DeBano, L.F.; Neary, D.G.; Ffolliott, P.F. Fire Effects on Ecosystems; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Freire, J.P.A. Modelação Do Crescimento E Da Produção de Pinha No Pinheiro Manso; Tese de Doutoramento, Instituto Superior de agronomia, Universidade de Lisboa: Lisboa, Portugal, 2009; p. 215. (In Portuguese) [Google Scholar]
- Kleinbaum, D.G. Logistic Regression: A Self-Learning Text. S. 5: 103–104. Stat. Methods Med. Res. 1994, 5, 103–104. [Google Scholar]
- Ryan, T.P. Modern Regression Methods; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Kozak, A.; Kozak, R. Does cross validation provide additional information in the evaluation of regression models? Can. J. For. Res. 2003, 33, 976–987. [Google Scholar] [CrossRef]
- Jalkanen, A.; Mattila, U. Logistic Regression Models for Wind and Snow Damage in Northern Finland Based on the National Forest Inventory Data. For. Ecol. Manag. 2000, 135, 315–330. [Google Scholar] [CrossRef]
- Beverly, J.L.; Martell, D.L. Modeling Pinus Strobus Mortality Following Prescribed Fire in Quetico Provincial Park, Northwestern Ontario. Can. J. For. Res. 2003, 33, 740–751. [Google Scholar] [CrossRef]
- Botelho, H.S.; Fernandes, P.M.; Ruas, L.L.S. Modeling Pinus pinaster Induced by up-Slope Wind Driven Prescribed Fires in Northern Portugal. In Proceedings of the 13th Fire and Forest Meteorology Conference, Lorne, Australia, 27–31 October 1996; pp. 473–476.
- Regelbrugge, J.C.; Conard, S.G. Modeling Tree Mortality Following Wildfire in Pinus Ponderosa Forests in the Central Sierra-Nevada of California. Int. J. Wildland Fire 1993, 3, 139–148. [Google Scholar] [CrossRef]
- Rigolot, E. Predicting Postfire Mortality of Pinus halepensis Mill. and Pinus pinea L. Plant Ecol. 2004, 171, 139–151. [Google Scholar] [CrossRef]
- Eid, T.; Øyen, B.-H. Models for Prediction of Mortality in Even-aged Forest. Scand. J. For. Res. 2003, 18, 64–77. [Google Scholar]
- González, J.G.Á.; Dorado, F.C.; González, A.D.R.; Sánchez, C.A.L.; Von Gadow, K. A Two-Step Mortality Model for Even-Aged Stands of Pinus Radiata D. Don in Galicia (Northwestern Spain). Ann. For. Sci. 2004, 61, 439–448. [Google Scholar] [CrossRef]
- Peterson, D.L.; Ryan, K.C. Modeling Postfire Conifer Mortality for Long-Range Planning. Environ. Manag. 1986, 10, 797–808. [Google Scholar] [CrossRef]
- Lohmander, P.; Helles, F. Windthrow Probability as a Function of Stand Characteristics and Shelter. Scand. J. For. Res. 1987, 2, 227–238. [Google Scholar] [CrossRef]
- Bond, W.J.; van Wilgen, B.W. Fire and Plants—Population and Community Biology Series 14; Springer: Berlin, Germany, 1996; p. 263. ISBN 978-94-009-1499-5. [Google Scholar]
- Moreira, F.; Ferreira, P.G.; Rego, F.C.; Bunting, S. Landscape Changes and Breeding Bird Assemblages in Northwestern Portugal: The Role of Fire. Landsc. Ecol. 2001, 16, 175–187. [Google Scholar] [CrossRef]
- Moreira, F.; Vaz, P.; Catry, F.; Silva, J.S. Regional Variations in Wildfire Susceptibility of Land-Cover Types in Portugal: Implications for Landscape Management to Minimize Fire Hazard. Int. J. Wildland Fire 2009, 18, 563–574. [Google Scholar] [CrossRef]
- Pausas, J.G. Resprouting of Quercus suber in NE Spain after Fire. J. Veg. Sci. 1997, 8, 703–706. [Google Scholar] [CrossRef]
- Retana, J.; Riba, M.; Castell, C.; Espelta, J.M. Regeneration by Sprouting of Holm-Oak (Quercus Ilex) Stands Exploited by Selection Thinning. In Quercus ilex L. Ecosystems: Function, Dynamics and Management; Springer: Berlin, Germany, 1992; pp. 355–364. [Google Scholar]
- Pollet, J.; Omi, P.N. Effect of Thinning and Prescribed Burning on Crown Fire Severity in Ponderosa Pine Forests. Int. J. Wildland Fire 2002, 11, 1–10. [Google Scholar] [CrossRef]
- Catry, F.X.; Moreira, F.; Pausas, J.G.; Fernandes, P.M.; Rego, F.; Cardillo, E.; Curt, T. Cork Oak Vulnerability to Fire: The Role of Bark Harvesting, Tree Characteristics and Abiotic Factors. PLoS ONE 2012, 7, e39810. [Google Scholar] [CrossRef] [PubMed]
- Pyne, S.J.; Andrews, P.L.; Laven, R.D. Introduction to Wildland Fire; John Wiley and Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Ventura, J.; Vasconcelos, M.J. O Fogo Como Processo Físico-Químico E Ecológico. Incêndios Florestais em Portugal Impactes E Prevenção; Instituto Superior de Agronomia: Lisboa, Portugal, 2006; pp. 93–113. [Google Scholar]
- Garcia-Gonzalo, J.; Zubizarreta-Gerendiain, A.; Ricardo, A.; Marques, S.; Botequim, B.; Borges, J.G.; Oliveira, M.M.; Tomé, M.; Pereira, J.M.C. Modelling wildfire risk in pure and mixed forest stands in Portugal. Allgemeine Forst und Jagdzeitung (AFJZ) 2012, 183, 238–248. [Google Scholar]
- Marques, S.; Garcia-Gonzalo, J.; Botequim, B.; Ricardo, A.; Borges, J.G.; Tomé, M.; Oliveira, M.M. Assessing wildfire risk probability in Pinus pinaster Ait. stands in Portugal. For. Syst. 2011, 21, 111–120. [Google Scholar]
- González, J.R.; Pukkala, T.; Palahí, M. Optimising the Management of Pinus sylvestris L. Stand under Risk of Fire in Catalonia (North-East of Spain). Ann. For. Sci. 2005, 62, 493–501. [Google Scholar] [CrossRef]
- González-Olabarría, J.R.; Palahí, M.; Pukkala, T.; Trasobares, A. Optimising the Management of Pinus nigra Arn. Stands under Endogenous Risk of Fire in Catalonia. For. Syst. 2008, 17, 10–17. [Google Scholar] [CrossRef]
- González-Olabarria, J.-R.; Pukkala, T. Integrating Fire Risk Considerations in Landscape-Level Forest Planning. For. Ecol. Manag. 2011, 261, 278–287. [Google Scholar] [CrossRef]
- Von Gadow, K. Evaluating Risk in Forest Planning Models. Silva Fenn. 2000, 34, 181–191. [Google Scholar]
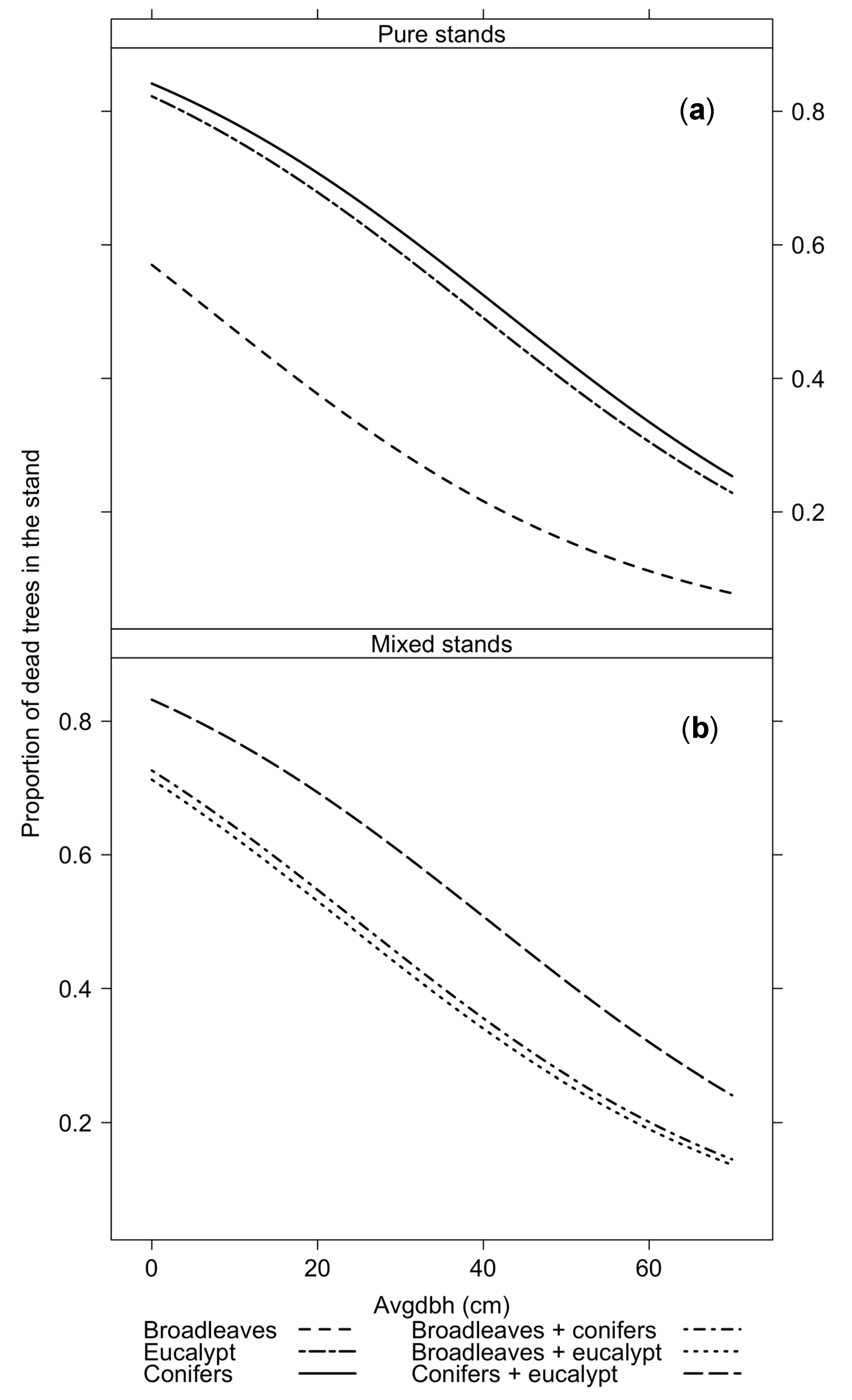
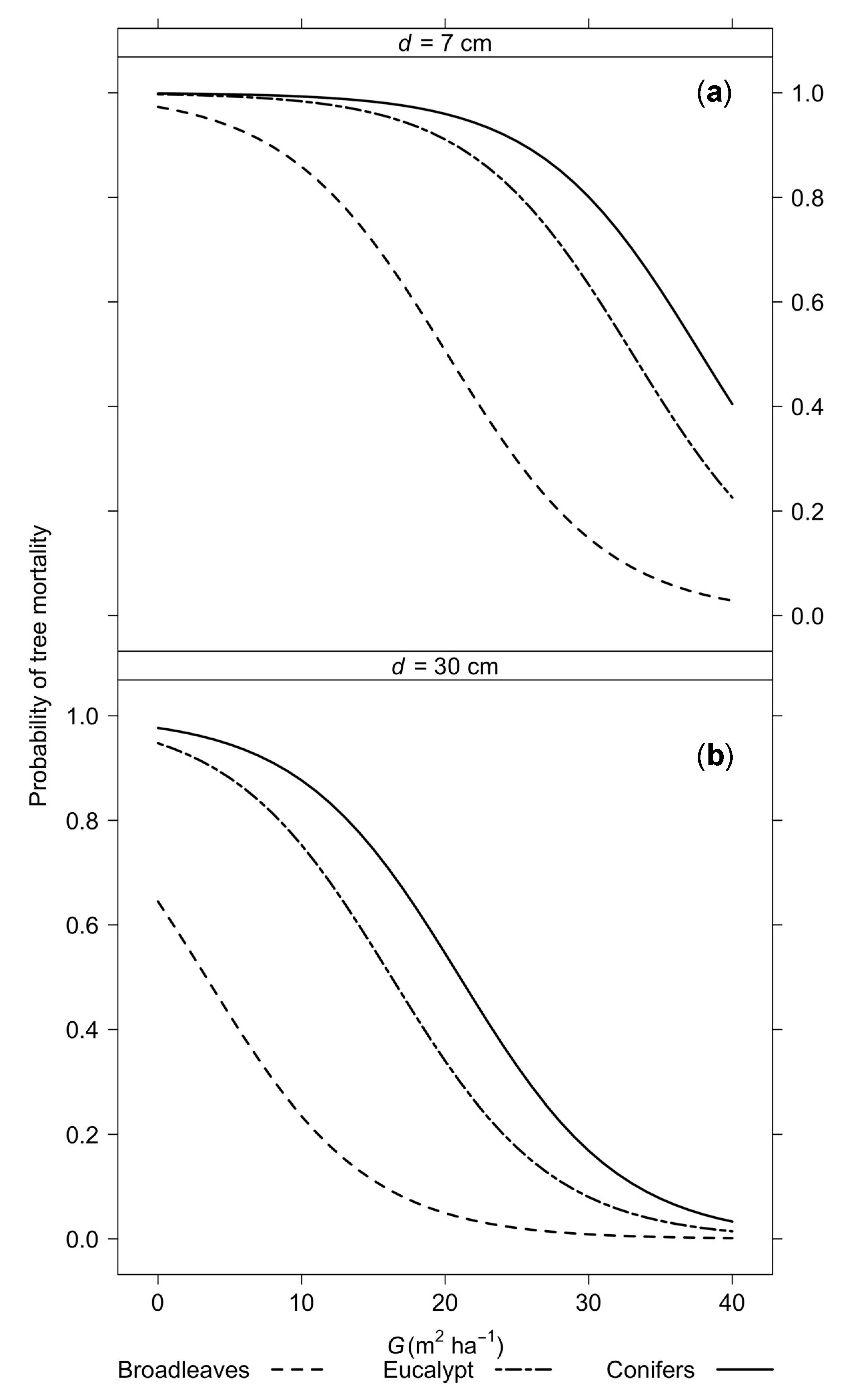
| Tree Species | Tree Status | n | dbh (cm) | h (m) | g (m2) | |||
|---|---|---|---|---|---|---|---|---|
| Mean | Range | Mean | Range | Mean | Range | |||
| Ec | S | 177 | 15.24 | 5.20–59.30 | 15.13 | 5.40–30.40 | 0.022 | 0.002–0.276 |
| D | 762 | 10.06 | 5.00–46.30 | 12.24 | 1.40–28.20 | 0.008 | 0.002–0.168 | |
| OB | S | 37 | 10.88 | 7.00–21.00 | 6.92 | 4.90–11.60 | 0.010 | 0.004–0.035 |
| D | 43 | 10.19 | 7.00–23.00 | 5.97 | 3.12–9.90 | 0.009 | 0.004–0.042 | |
| OC | S | 11 | 25.09 | 7.00–59.00 | 15.09 | 7.98–26.90 | 0.073 | 0.004–0.273 |
| D | 5 | 13.40 | 9.00–21.00 | 9.79 | 8.22–11.44 | 0.015 | 0.006–0.035 | |
| Pp | S | 263 | 19.17 | 6.00–51.00 | 13.89 | 5.50–28.50 | 0.035 | 0.003–0.204 |
| D | 981 | 14.63 | 7.00–51.00 | 11.09 | 3.80–28.50 | 0.021 | 0.004–0.149 | |
| Ppi | S | 7 | 31.23 | 18.00–43.00 | 17.45 | 7.35–24.40 | 0.086 | 0.025–0.145 |
| D | 4 | 13.70 | 8.50–22.60 | 7.22 | 3.97–8.90 | 0.017 | 0.006–0.040 | |
| Qr | S | 20 | 16.82 | 8.00–39.00 | 5.09 | 3.83–7.60 | 0.028 | 0.005–0.119 |
| D | 10 | 19.08 | 7.00–64.00 | 4.99 | 3.40–7.50 | 0.051 | 0.004–0.321 | |
| Qs | S | 58 | 20.01 | 4.30–62.00 | 6.72 | 2.70–13.90 | 0.044 | 0.001–0.302 |
| D | 48 | 17.53 | 4.50–59.80 | 6.34 | 2.95–10.70 | 0.042 | 0.002–0.281 | |
| Qsp | S | 42 | 12.21 | 7.00–24.00 | 8.61 | 5.00–13.80 | 0.013 | 0.004–0.045 |
| D | 52 | 10.09 | 7.00–21.30 | 7.25 | 4.20–12.50 | 0.009 | 0.004–0.035 | |
| Stands with Dead Trees (n = 96) | Stands without Dead Trees (n = 68) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eucalyptus | Conifers | Other Broadleaves | Eucalyptus | Conifers | Other Broadleaves | |||||||
| Variable (Code) | Range | Mean (S.d.) | Range | Mean (S.d.) | Range | Mean (S.d.) | Range | Mean (S.d.) | Range | Mean (S.d.) | Range | Mean (S.d.) |
| Avgdbh | 2.92–14.50 | 9.03 (3) | 7–26.25 | 13.75 (5.81) | 7.5–38.03 | 18.85 (9.05) | 7–27.45 | 11.49 (3.63) | 13–32.8 | 20.18 (6.76) | 8–73.36 | 30.11 (17) |
| Avgh | 3.49–15.24 | 10.18 (3.35) | 3.8–19.37 | 9.78 (4.08) | 3.93–9.4 | 6.45 (1.53) | 6.5–21.9 | 13.84 (3.68) | 3.47–19.73 | 12.01 (4.42) | 4.7–18.23 | 8.12 (4.23) |
| dg | 5.59–26.03 | 8.98 (4.17) | 5.14–45.09 | 18.64 (11.9) | 13.6–45.09 | 28.77 (10.14) | 6.03–45.09 | 13.54 (8.13) | 10.08–45.09 | 27.16 (15.78) | 17.04–45.09 | 34.14 (9.96) |
| G | 0.31–11.04 | 4.91 (2.57) | 0.077–38.16 | 7.15 (9.46) | 0.08–26.51 | 3.9 (6.54) | 0.08–29.73 | 7.62 (7.2) | 0.27–33.13 | 8.2 (11.01) | 0.1–13.81 | 4.09 (3.75) |
| G/dg | 0.012–1.80 | 0.66 (0.42) | 0.0017–3.78 | 0.78 (1.1) | 0.002–1.95 | 0.23 (0.48) | 0.002–3.4 | 0.8 (0.84) | 0.006–3.2 | 0.71 (1.1) | 0.002–0.81 | 0.15 (0.19) |
| N | 60–1299 | 691.48 (347.55) | 20–1539 | 318.7 (353.86) | 20–220 | 72 (57.09) | 20–1811 | 617.4 (429.62) | 20–623 | 181.62 (213.82) | 20–140 | 46.96 (33.91) |
| Sd | 0.78–5.37 | 3.28 (1.3) | 0–12.41 | 3.63 (3.13) | 0–26.02 | 7.31 (8.67) | 0–7.91 | 2.88 (1.89) | 0–11.72 | 4.3 (4.27) | 0–19.8 | 4.58 (6.01) |
| Sh | 0.4–6.96 | 3.43 (1.98) | 0–5.46 | 1.57 (1.38) | 0–3.81 | 0.96 (1.08) | 0–5.07 | 2.2 (1.23) | 0–4.09 | 1.34 (1.46) | 0–5.91 | 0.75 (1.28) |
| Sd/dg | 0.03–0.88 | 0.45 (0.25) | 0–1.34 | 0.33 (0.35) | 0–1.26 | 0.34 (0.43) | 0–1.07 | 0.27 (0.21) | 0–1.13 | 0.33 (0.37) | 0–0.93 | 0.18 (0.25) |
| Altitude | 0–272 | 179 (81) | 0–893 | 330.42 (171.77) | 76–800 | 296.55 (152.55) | 0–491 | 192 (150.53) | 106–931 | 441 (331.3) | 0–861 | 313.39 (224.44) |
| Slope | 0–26.6 | 10.27 (6.2) | 0–29 | 13.3 (7.92) | 0–22.8 | 8.27 (6.53) | 0.6–32 | 13.09 (8.68) | 1.8–27 | 11.48 (6.8) | 0–25.2 | 9.38 (6.27) |
| Stands with Dead Trees | Stands without Dead Trees | |||
|---|---|---|---|---|
| (n = 56) | (n = 20) | |||
| Variable (Code) | Range | Mean | Range | Mean |
| (S.d.) | (S.d.) | |||
| Altitude | 0–940 | 337.78 | 0–919 | 268.15 |
| (232.79) | (285.51) | |||
| Avgdbh | 7.64–25.67 | 15.41 | 7.99–26.88 | 14.7 |
| (4.84) | (5.54) | |||
| Avgh | 3.72–22.7 | 10.99 | 4.92–17.06 | 11.15 |
| (4.19) | (3.48) | |||
| dg | 5.64–31.88 | 13.04 | 10.08–26.03 | 13.66 |
| (5.31) | (4.93) | |||
| G | 0.55–30.52 | 9.29 | 0.93–33.18 | 8.81 |
| (7.89) | (8.76) | |||
| G/dg | 0.02–3.33 | 0.95 | 0.051–3.29 | 0.79 |
| (0.94) | (0.88) | |||
| N | 40–1279 | 398.02 | 60–1769 | 486.3 |
| (297.73) | (433.8) | |||
| PBr | 0–0.98 | 0.27 | 0–0.82 | 0.25 |
| (0.33) | (0.29) | |||
| PCon | 0–0.99 | 0.56 | 0–0.95 | 0.4 |
| (0.35) | (0.29) | |||
| PEc | 0–0.97 | 0.16 | 0–0.95 | 0.35 |
| (0.3) | (0.41) | |||
| Sd | 0.7–15.4 | 6.57 | 1.42–16.96 | 6.54 |
| (3.31) | (4.53) | |||
| Sh | 0.55–6.49 | 3.13 | 0.69–6.53 | 3.37 |
| (1.58) | (1.82) | |||
| Sd/dg | 0.06–1.54 | 0.58 | 0.09–1.02 | 0.49 |
| (0.37) | (0.3) | |||
| Altitude | 0–940 | 337.78 | 0–919 | 268.15 |
| (232.79) | (285.51) | |||
| Slope | 0–32 | 13.53 | 0.6–22.6 | 13.7 |
| (7.77) | (6.06) | |||
| Proportion of Dead Trees (%) | 0 | 1–20 | 21–40 | 41–60 | 61–80 | 81–99 | 100 |
|---|---|---|---|---|---|---|---|
| No. of plots | 88 | 19 | 16 | 18 | 11 | 15 | 74 |
| Effect | Variables | Estimate | SE | Z Value | p-Value |
|---|---|---|---|---|---|
| β0 | Intercept | 1.3816 | 0.3380 | 4.0876 | <0.0001 |
| β1 | PEc | −2.1698 | 0.4192 | −5.1757 | <0.0001 |
| β2 | PBr | −1.0619 | 0.4438 | −2.3929 | 0.0167 |
| β3 | G | −0.5553 | 0.1264 | −4.3934 | <0.0001 |
| β4 | G/dg | 4.3280 | 1.1765 | 3.6790 | 0.0002 |
| β5 | Sd/dg | 3.2549 | 0.8187 | 3.9760 | <0.0001 |
| Effect | Variables | Estimate | SE | Z Value | p-Value |
|---|---|---|---|---|---|
| β0 | Intercept | 0.3573 | 0.0392 | 9.118 | <0.0001 |
| β1 | PEc | −0.1364 | 0.0258 | −5.293 | <0.0001 |
| β2 | PBr | −1.3878 | 0.0361 | −38.495 | <0.0001 |
| β3 | Slope | 0.0525 | 0.0013 | 39.118 | <0.0001 |
| β4 | Altitude | 0.0017 | 0.0001 | 28.711 | <0.0001 |
| β5 | Avgdbh | −0.0393 | 0.0018 | −20.832 | <0.0001 |
| Effect | Variables | Estimate | SE | Z Value | p Value |
|---|---|---|---|---|---|
| β0 | Intercept | 4.493 | 0.9044 | 4.968 | <0.0001 |
| β1 | Ec | 2.296 | 0.6599 | 3.480 | <0.0001 |
| β2 | Con | 3.143 | 0.4721 | 6.657 | <0.0001 |
| β3 | G | −0.1778 | 0.04572 | −3.890 | <0.0001 |
| β4 | dbh | −0.1299 | 0.04559 | −2.849 | 0.00438 |
| - | 12.54 | - | - | - | |
| - | 0.06780 | - | - | - | |
| - | −0.3681 | - | - | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Botequim, B.; Arias-Rodil, M.; Garcia-Gonzalo, J.; Silva, A.; Marques, S.; Borges, J.G.; Oliveira, M.M.; Tomé, M. Modeling Post-Fire Mortality in Pure and Mixed Forest Stands in Portugal—A Forest Planning-Oriented Model. Sustainability 2017, 9, 390. https://doi.org/10.3390/su9030390
Botequim B, Arias-Rodil M, Garcia-Gonzalo J, Silva A, Marques S, Borges JG, Oliveira MM, Tomé M. Modeling Post-Fire Mortality in Pure and Mixed Forest Stands in Portugal—A Forest Planning-Oriented Model. Sustainability. 2017; 9(3):390. https://doi.org/10.3390/su9030390
Chicago/Turabian StyleBotequim, Brigite, Manuel Arias-Rodil, Jordi Garcia-Gonzalo, Andreia Silva, Susete Marques, José G. Borges, Maria Manuela Oliveira, and Margarida Tomé. 2017. "Modeling Post-Fire Mortality in Pure and Mixed Forest Stands in Portugal—A Forest Planning-Oriented Model" Sustainability 9, no. 3: 390. https://doi.org/10.3390/su9030390
APA StyleBotequim, B., Arias-Rodil, M., Garcia-Gonzalo, J., Silva, A., Marques, S., Borges, J. G., Oliveira, M. M., & Tomé, M. (2017). Modeling Post-Fire Mortality in Pure and Mixed Forest Stands in Portugal—A Forest Planning-Oriented Model. Sustainability, 9(3), 390. https://doi.org/10.3390/su9030390