Temporal Variability and Trends of Rainfall and Streamflow in Tana River Basin, Kenya
Abstract
:1. Introduction
2. Data and Methods
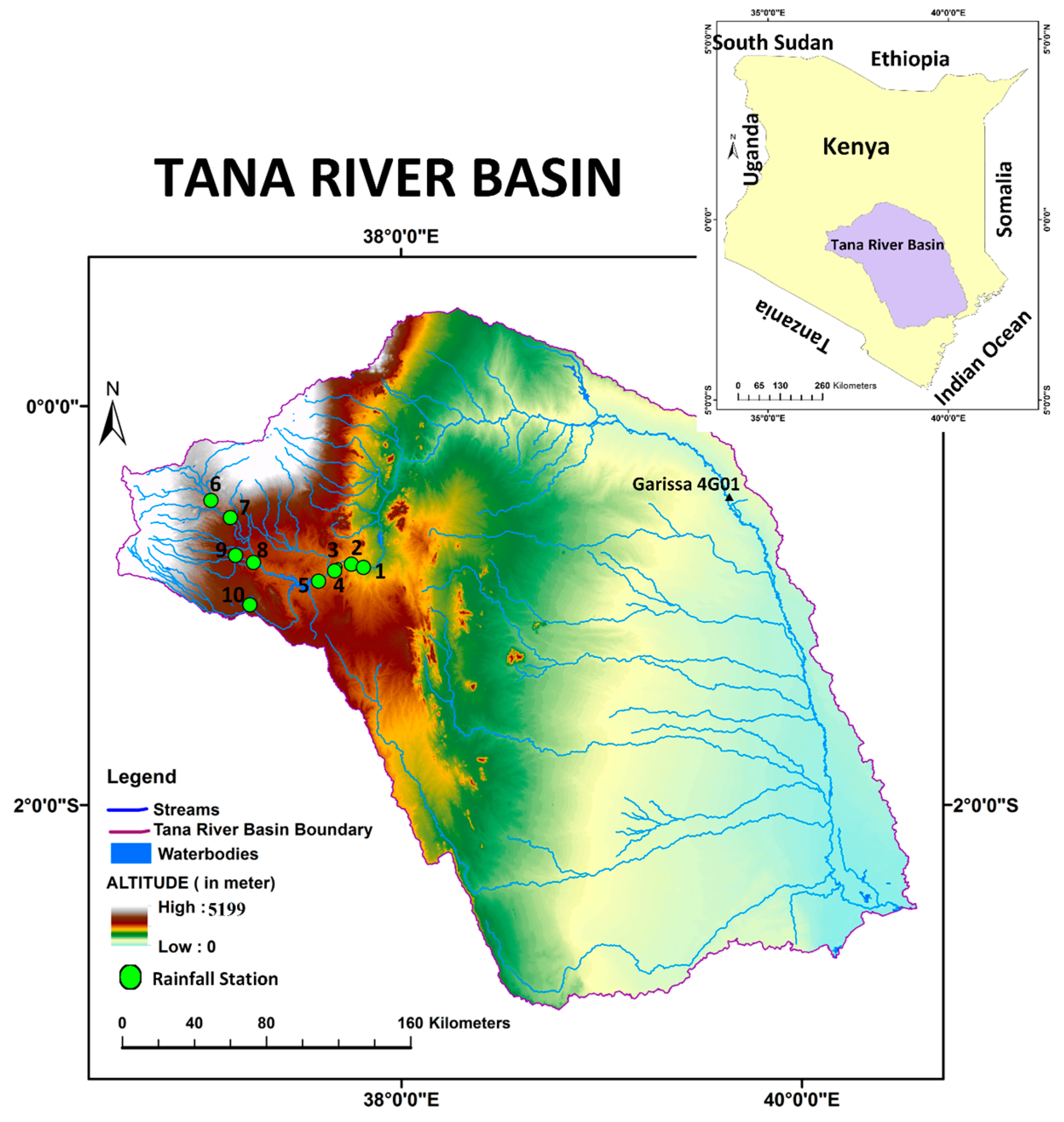
2.1. Description of the Study Area
2.2. Datasets
2.3. Method
3. Results and Discussions
3.1. Rainfall Characteristics
3.2. Annual Rainfall MK’s Trend-Test Analysis of Each Station
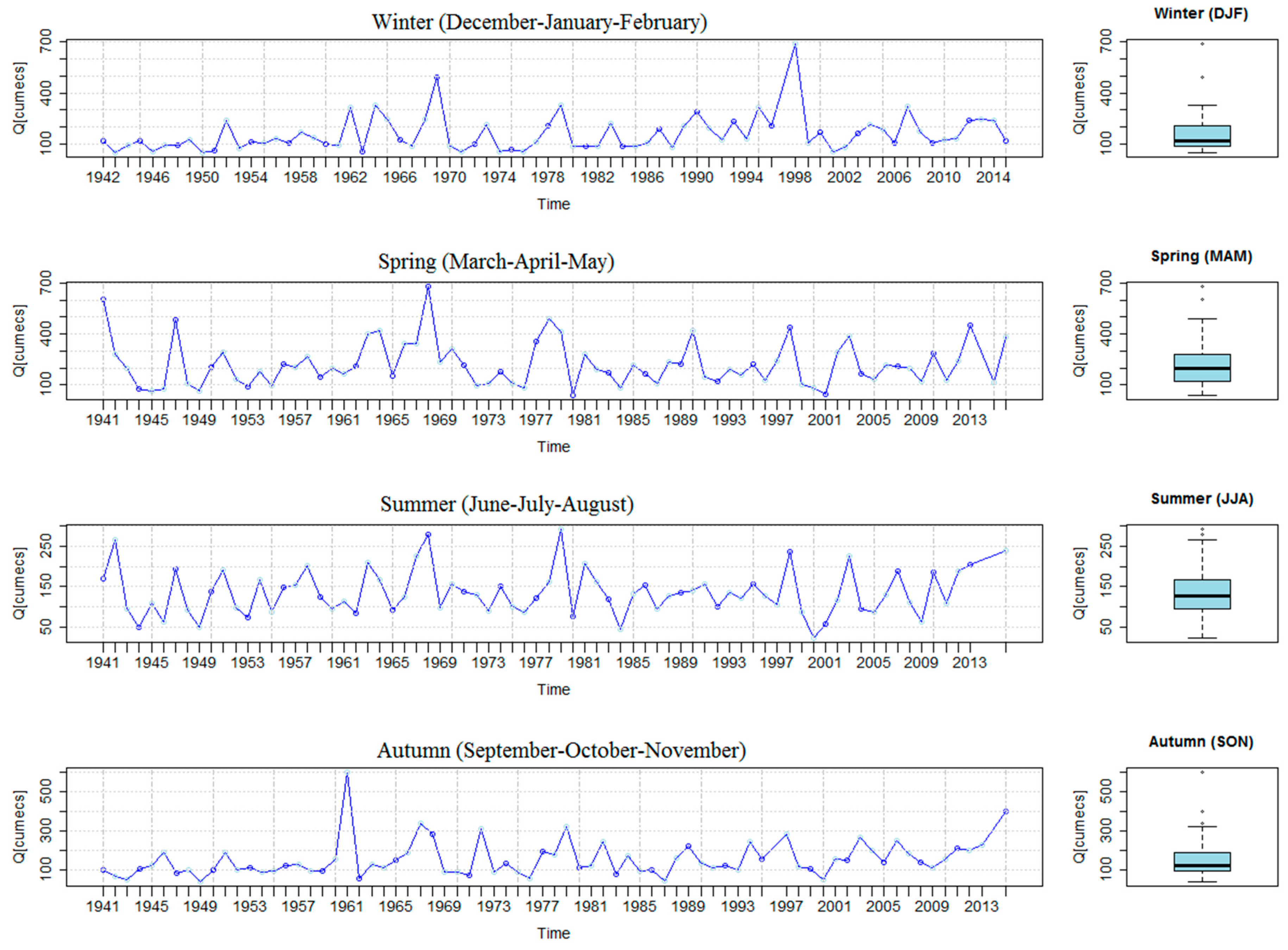
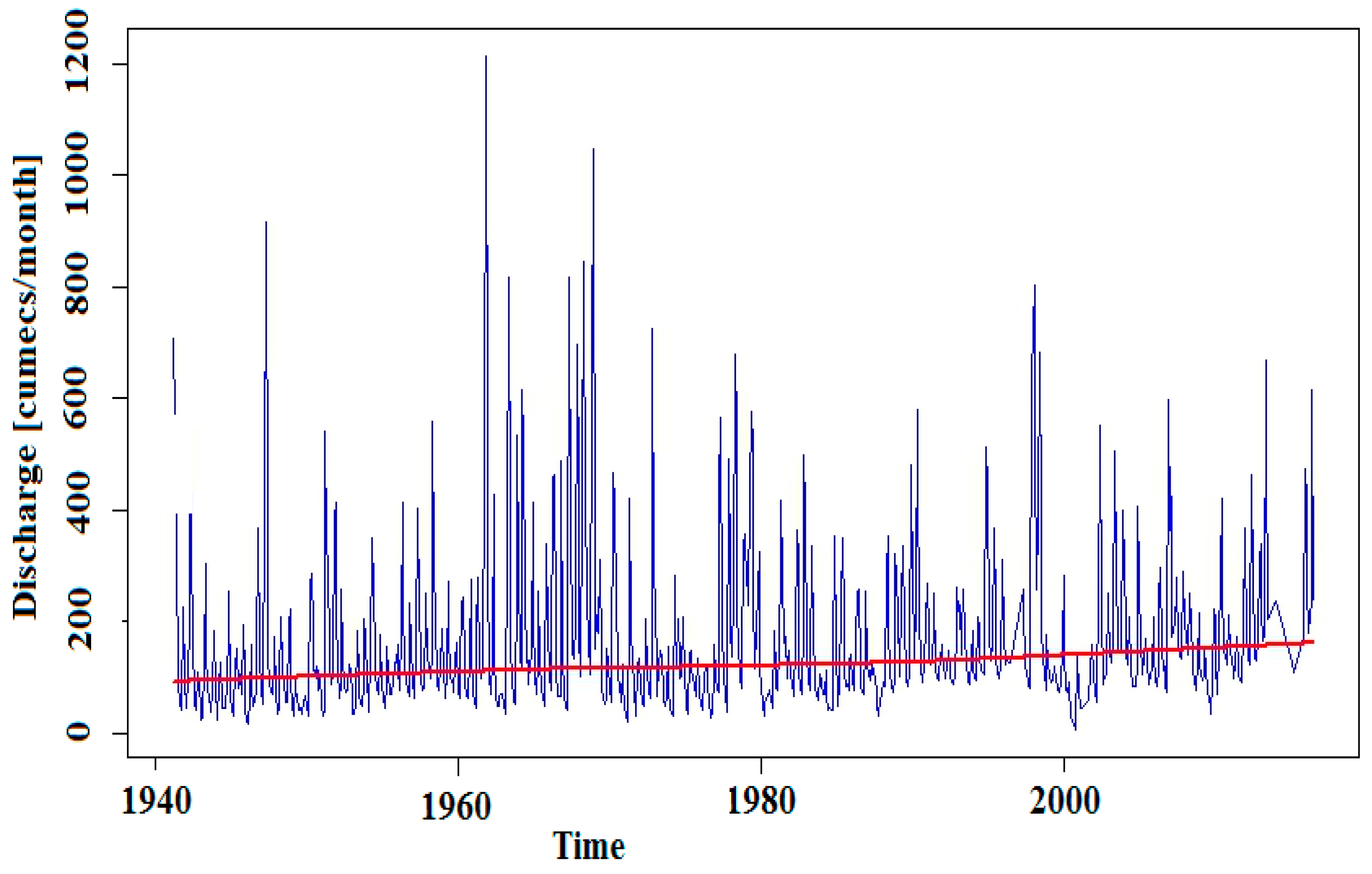
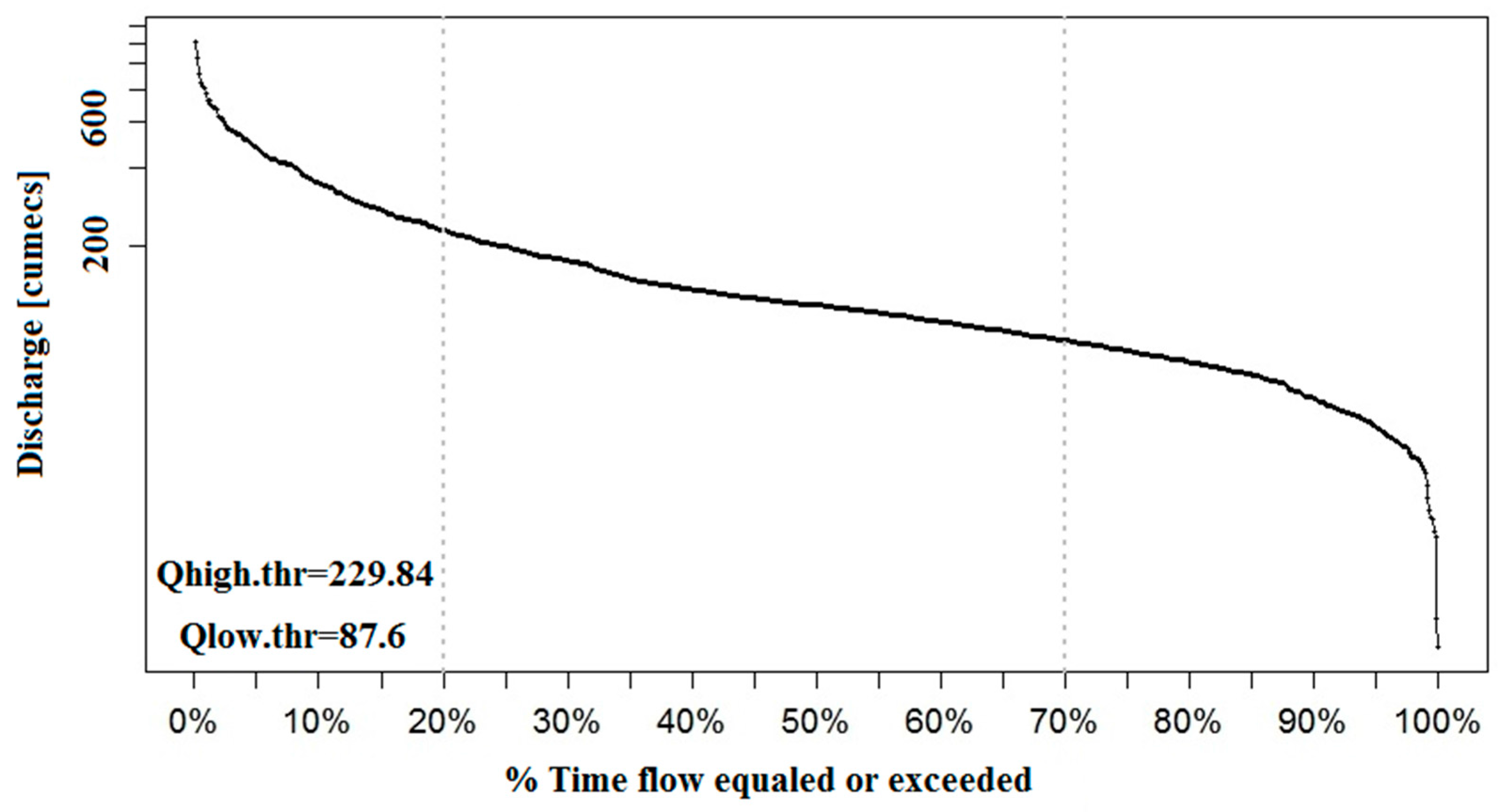
3.3. Stream Flow Statistical Characteristics
3.4. Streamflow Trend Analysis
3.5. Discussion
4. Preliminary Findings and Conclusions
- (a)
- Annual rainfall trend analysis showed negative monotonic trend in seven rainfall stations and positive trends in three stations, indicating an increasing rainfall in high elevation areas, and more drying conditions for low areas within the basin.
- (b)
- The annual rainfall time series exhibited very small temporal variabilities in most areas in the basin and were insignificant in most of the stations.
- (c)
- The statistically significant trend were positive and consisted 30% of the annual and monthly rainfall datasets.
- (d)
- The results from the trend analysis showed significant increasing annual streamflow trends and that there was a strong significant upward monotonic trend in streamflow suggesting increasing base flow in the basin with reduced high flows.
- (e)
- The seasonal rainfall series in the basin have non-significant positive trend in areas of altitude of more than 1000 m and negative trends in areas of altitude of less than 1000 m above sea level.
- (f)
- The construction of reservoirs have not adversely modified the Tana River’s hydrological flow regime.
Author Contributions
Conflicts of Interest
References
- Delitala, A.M.S.; Cesari, D.; Chessa, P.A.; Ward, M.N. Precipitation over Sardinia(Italy) during the 1946–1993 rainy seasons and associated large-scale climate variations. Int. J. Climatol. 2000, 20, 519–541. [Google Scholar] [CrossRef]
- Kuczera, G.; Renard, B.; Thyer, M.; Kavetski, D. There are no hydrological monsters, just models and observations with large uncertainties! Hydrol. Sci. J. 2010, 55, 980–991. [Google Scholar] [CrossRef]
- Oguntunde, P.G.; Friesen, J.; Van De Giesen, N.; Savenije, H.H.G. Hydroclimatology of the Volta River Basin in West Africa: Trends and variability from 1901 to 2002. Phys. Chem. Earth 2006, 31, 1180–1188. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Kirby, J.M.; Paydar, Z.; Podger, G.; Mainuddin, M.D.; Marvanek, S.; Peña-Arancibia, J. Uncertainty in river modelling across the Murray-Darling Basin. In A Report to the Australian Government from the CSIRO Murray-Darling Basin Sustainable Yields Project; CSIRO: Canberra, Australia, 2008. [Google Scholar]
- Restrepo, P.; Liu, Y.; Weerts, A.H.; Clark, M.; Hendricks Franssen, H.-J.; Kumar, S.; Moradkhani, H.; Seo, D.-J.; Schwanenberg, D.; Smith, P.; et al. Advancing data assimilation in operational hydrologic forecasting: Progresses, challenges, and emerging opportunities. Hydrol. Earth Syst. Sci. 2012, 16, 3863–3887. [Google Scholar]
- Da Silva, R.M.; Santos, C.A.G.; Moreira, M.; Corte-Real, J.; Silva, V.C.L.; Medeiros, I.C. Rainfall and river flow trends using Mann–Kendall and Sen’s slope estimator statistical tests in the Cobres River basin. Nat. Hazards 2015, 77, 1205–1221. [Google Scholar] [CrossRef]
- Jain, S.K.; Kumar, V. Trend analysis of rainfall and temperature data for India. Curr. Sci. 2012, 102, 37–49. [Google Scholar]
- Machiwal, D.; Kumar, S.; Dayal, D. Characterizing rainfall of hot arid region by using time-series modeling and sustainability approaches: A case study from Gujarat, India. Theor. Appl. Climatol. 2016, 124, 593–607. [Google Scholar] [CrossRef]
- Ghanem, A. Trends in Mean Seasonal and Annual Rainfall Amounts over Jordan. Hum. Soc. Sci. 2011, 38, 1041–1049. [Google Scholar]
- Muchuru, S.; Botai, J.O.; Botai, C.M.; Landman, W.A.; Adeola, A.M. Variability of rainfall over Lake Kariba catchment area in the Zambezi river basin, Zimbabwe. Theor. Appl. Climatol. 2016, 124, 325–338. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. Trend analysis of annual and seasonal rainfall time series in the Mediterranean area. Int. J. Climatol. 2010, 30, 1538–1546. [Google Scholar] [CrossRef]
- Cook, C.; Reason, C.J.; Hewitson, B.C. Wet and dry spells within particularly wet and dry summers in the South African summer rainfall region. Clim. Res. 2004, 26, 17–31. [Google Scholar] [CrossRef]
- Haile, M. Weather patterns, food security and humanitarian response in sub-Saharan Africa. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2005, 360, 2169–2182. [Google Scholar] [CrossRef] [PubMed]
- Frenken, K. Irrigation in Africa in Figures: AQUASTAT Survey, 2005; Food and Agriculture Organization: Rome, Italy, 2005; Volume 29. [Google Scholar]
- Food and Agriculture Organization of the United Nations (FAO). Survey of the Irrigation Potential of the LowerTana River Basin, Kenya; FAO: Rome, Italy, 1968. [Google Scholar]
- Maingi, J.K.; Marsh, S.E. Quantifying hydrologic impacts following dam construction along the Tana River, Kenya. J. Arid Environ. 2002, 50, 53–79. [Google Scholar] [CrossRef]
- Baker, T.; Kiptala, J.; Olaka, L.; Oates, N.; Hussain, A.; McCartney, M. Baseline Review and Ecosystem Services Assessment of the Tana River Basin, Kenya; IWMI Working Paper 165; International Water Management Institute (IWMI): Colombo, Sri Lanka, 2015. [Google Scholar]
- Koei, N. The Project on the Development of the National Water Master Plan 2030. Final Report. Volume V Sectorial Report (E)–Agriculture and Irrigation; Water Resources Management Authority: Nairobi, Kenya, 2013. [Google Scholar]
- Ihaka, R.; Gentleman, R. R: A language for data analysis and graphics. J. Comput. Graph. Stat. 1996, 5, 299–314. [Google Scholar]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M. HydroTSM: Time Series Management, Analysis and Interpolation for Hydrological Modelling. Available online: https://cran.r-project.org/package=hydroTSM (accessed on 25 October 2017).
- Cisty, M.; Celar, L. Using R in Water Resources Education. Int. J. Innov. Educ. Res. 2015, 3, 97–117. [Google Scholar]
- Duhan, D.; Pandey, A. Statistical analysis of long term spatial and temporal trends of precipitation during 1901–2002 at Madhya Pradesh, India. Atmos. Res. 2013, 122, 136–149. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Ahmadi, M. Long-term variations of water quality parameters in the Maroon River, Iran. Environ. Monit. Assess. 2011, 177, 273–287. [Google Scholar] [CrossRef] [PubMed]
- Tabari, H.; Talaee, P.H. Temporal variability of precipitation over Iran: 1966–2005. J. Hydrol. 2011, 396, 313–320. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Modarres, R.; da Silva, V.D.P.R. Rainfall trends in arid and semi-arid regions of Iran. J. Arid Environ. 2007, 70, 344–355. [Google Scholar] [CrossRef]
- Yue, S.; Hashino, M. Long term trends of annual and monthly precipitation in Japan. J. Am. Water Resour. Assoc. 2003, 39, 587–596. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997; Volume 1. [Google Scholar]
- Hipel, K.W.; McLeod, A.I. Time Series Modelling of Water Resources and Environmental Systems; Elsevier: Amsterdam, The Netherlands, 1994; Volume 45. [Google Scholar]
- Kahya, E.; Kalaycı, S. Trend analysis of streamflow in Turkey. J. Hydrol. 2004, 289, 128–144. [Google Scholar] [CrossRef]
- Siraj, K.T.; Mohammed, A.; Bam, S.; Addisu, S. Long years comparative climate change trend analysis in terms of temperature, coastal Andhra Pradesh, India. Available online: https://s3.amazonaws.com/academia.edu.documents/39406158/my_own_work_publication.pdf?AWSAccessKeyId=AKIAIWOWYYGZ2Y53UL3A&Expires=1509331015&Signature=TJd%2BGIPTX4IxW0nKUNeRQYXwvJ4%3D&response-content-disposition=inline%3B%20filename%3DLONG_YEARS_COMPARATIVE_CLIMATE_CHANGE_TR.pdf (accessed on 25 October 2017).
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Timmermann, A.; Oberhuber, J.; Bacher, A.; Esch, M.; Latif, M.; Roeckner, E. Increased El Niño frequency in a climate model forced by future greenhouse warming. Nature 1999, 398, 694. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: New York, NY, USA, 2001. [Google Scholar]
- Hughes, F.M.R. The Tana River Floodplain Forest, Kenya: Ecology and the Impact of Development; University of Cambridge: Cambridge, UK, 1985. [Google Scholar]
- Frans, C.; Istanbulluoglu, E.; Mishra, V.; Munoz-Arriola, F.; Lettenmaier, D.P. Are climatic or land cover changes the dominant cause of runoff trends in the Upper Mississippi River Basin? Geophys. Res. Lett. 2013, 40, 1104–1110. [Google Scholar] [CrossRef]
- Wang, D.; Hejazi, M. Quantifying the relative contribution of the climate and direct human impacts on mean annual streamflow in the contiguous United States. Water Resour. Res. 2011, 47, W00J12. [Google Scholar] [CrossRef]
- Novotny, E.V.; Stefan, H.G. Stream flow in Minnesota: Indicator of climate change. J. Hydrol. 2007, 334, 319–333. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, L.; Wang, Z.; Hong, Y.; Zheng, H. Quantitative assessment of climate and human impacts on surface water resources in a typical semi-arid watershed in the middle reaches of the Yellow River from 1985 to 2006. Int. J. Climatol. 2015, 35, 97–113. [Google Scholar] [CrossRef]
- Kyambia, M.M.; Mutua, B.M. Analysis of drought effect on annual stream flows of River Malewa in the Lake Naivasha basin, Kenya. Int. J. Curr. Res. Rev. 2014, 6, 1. [Google Scholar]
- Hurford, A.; Harou, J. Balancing ecosystem services with energy and food security-assessing trade-offs for reservoir operation and irrigation investment in Kenya’s Tana basin. Hydrol. Earth Syst. Sci. 2014, 11, 1343–1388. [Google Scholar] [CrossRef]
- Ovuka, M.; Lindqvist, S. Rainfall variability in Murang’a District, Kenya: Meteorological data and farmers’ perception. Geogr. Ann. 2000, 82, 107–119. [Google Scholar] [CrossRef]
- Recha, C.W.; Makokha, G.L.; Traore, P.S.; Shisanya, C.; Lodoun, T.; Sako, A. Determination of seasonal rainfall variability, onset and cessation in semi-arid Tharaka district, Kenya. Theor. Appl. Climatol. 2012, 108, 479–494. [Google Scholar] [CrossRef]
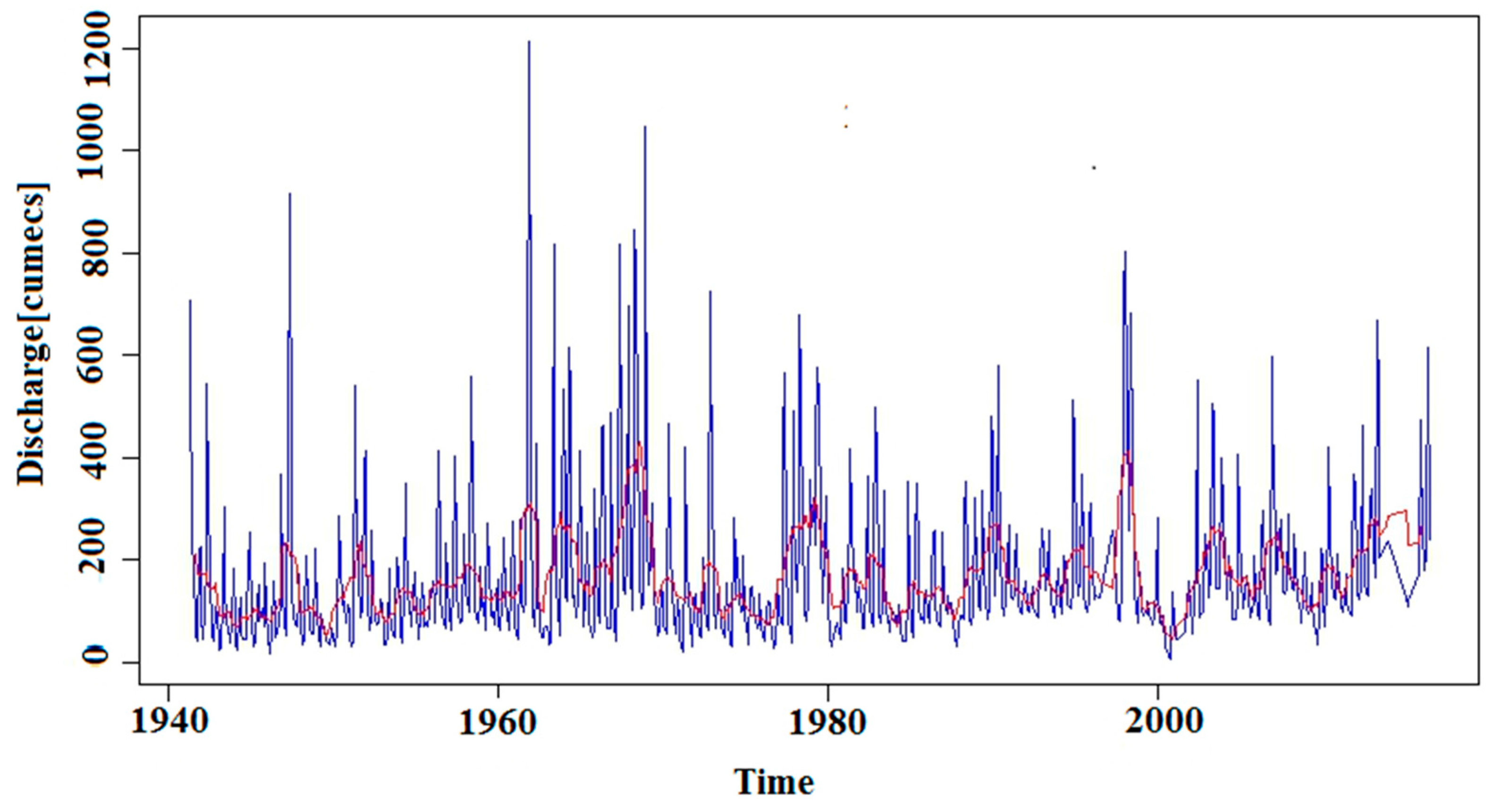
 ) and fitted (
) and fitted (  ) varables.
) varables.
 ) and fitted (
) and fitted (  ) varables.
) varables.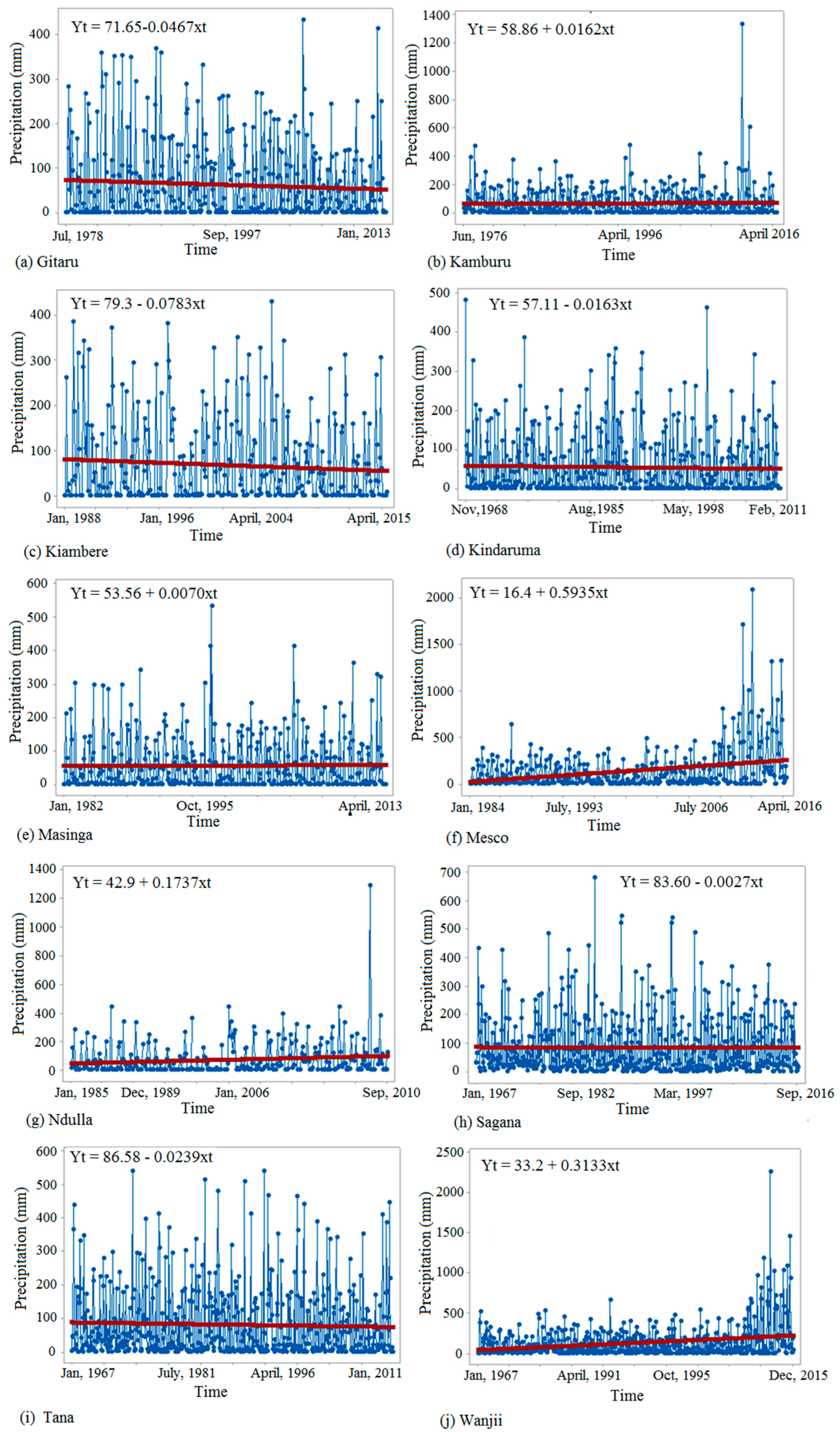
| Station | Elevation (m) | Commencement Date | End Date | Number of Years Spanned | Missing Data |
|---|---|---|---|---|---|
| Gitaru | 932 | July-78 | October-16 | 38 | December-82 |
| Kamburu | 990 | June-76 | October-16 | 40 | No missing data |
| Kiambere | 680 | January-88 | November-16 | 28 | April 1991, May–June 1992, August 1992, July 1993, January 1994 |
| Kindaruma | 766 | November-68 | November-16 | 48 | January–December 1970, January–December 1991, January–December 1992, January–September 1993, January–August 1994, May 1995, July–September 1995 |
| Masinga | 927 | January-82 | October-16 | 34 | No missing data |
| Mesco | 1060 | January-84 | October-16 | 32 | No missing data |
| Ndula | 1414 | January-85 | October-16 | 31 | No missing data |
| Sagana | 1609 | January-67 | October-16 | 49 | January–December 1970 |
| Tana | 1089 | January-67 | October-16 | 49 | January–December 1970 |
| Wanjii | 1146 | January-67 | October-16 | 49 | January–December 1970 |
| Rainfall Station | Elevation (M) | Basic Statistical Property | |||||
|---|---|---|---|---|---|---|---|
| Mean (mm) | Standard Deviation (mm) | Maximum (mm) | Coefficient of Variation (%) | Skewness | Kurtosis | ||
| Gitaru | 932 | 60.87 | 86.22 | 432.00 | 14.2 | 1.70 | 2.52 |
| Kamburu | 990 | 62.82 | 105.2 | 1338.00 | 16.7 | 4.9 | 46.01 |
| Kindaruma | 680 | 52.82 | 79.40 | 482.30 | 15.0 | 2.04 | 4.77 |
| Kiambere | 766 | 66.19 | 93.96 | 428.60 | 14.2 | 1.60 | 1.83 |
| Masinga | 927 | 55.02 | 80.00 | 532.30 | 14.6 | 2.15 | 5.72 |
| Mesco | 1060 | 133.50 | 228.01 | 2084.00 | 17.1 | 3.94 | 22.53 |
| Ndulla | 1414 | 69.99 | 119.28 | 1290.00 | 17.0 | 4.38 | 35.09 |
| Sagana | 1609 | 82.82 | 101.30 | 680.00 | 12.2 | 2.08 | 5.36 |
| Tana | 1089 | 79.57 | 104.18 | 541.30 | 13.1 | 1.88 | 3.69 |
| Wanjii | 1146 | 123.00 | 205.62 | 2260.00 | 16.6 | 4.01 | 26.27 |
| Station | Elevation (M) | Mann–Kendall Test Statistical Property | |||
|---|---|---|---|---|---|
| p-Value | Mann–Kendall Tau | Mann–Kendall Score S | Var (Score) | ||
| Gitaru | 932 | 0.9496 * | (−)0.00453 | (−)435 | 9,999,084 |
| Kamburu | 990 | 0.53044 * | (−)0.0197 | (−)2125 | 118,890,472 |
| Kiambere | 680 | 0.40877 * | (−)0.0266 | (−)1396 | 4,024,238 |
| Kindaruma | 766 | 0.25818 * | (−)0.0343 | (−)5760 | 14,411,660 |
| Masinga | 927 | 0.87395 * | (−)0.0054 | (−)445 | 7,833,073 |
| Mesco | 1060 | 0.127 * | 0.000209 | 9593 | 669,506 |
| Ndulla | 1414 | 0.029618 ** | 0.0851 | 5399 | 3,105,362 |
| Sagana | 1609 | 0.55988 * | (−)0.0163 | (−)2711 | 21,606,354 |
| Tana | 1089 | 0.0366 ** | (−)0.0582 | (−)9859 | 22,260,774 |
| Wanjii | 1146 | 0.005695 ** | 0.077 | 11,594 | 21,900,136 |
| Station | Elevation (M) | Mann–Kendall Test Statistical Property | |||
|---|---|---|---|---|---|
| p-Value | Mann–Kendall Tau | Mann–Kendall Score S | Var (Score) | ||
| Gitaru | 932 | 0.2329 * | (−)0.045 | −2487 | 4,343,414 |
| Kamburu | 990 | 0.6932 * | (−)0.015 | −816 | 4,267,526 |
| Kiambere | 680 | 0.4868 * | (−)0.0266 | −1396 | 4,024,238 |
| Kindaruma | 766 | 0.2057 * | (−)0.0519 | −2096 | 2,740,651 |
| Masinga | 927 | 0.5919 * | (−)0.0201 | −1129 | 4,428,360 |
| Mesco | 1060 | 0.0004 ** | 0.128 | 7468 | 4,527,455 |
| Ndulla | 1414 | 0.0004 ** | 0.149 | 5148 | 2,134,379 |
| Sagana | 1609 | 0.7371 * | 0.0122 | 716 | 4,537,381 |
| Tana | 1089 | 0.0504 ** | (−)0.0712 | −4200 | 4,606,167 |
| Wanjii | 1146 | 0.0021 ** | 0.113 | 6421 | 4,371,048 |
| Station | Elevation (M) | Mann–Kendall Seasonal Test Statistical Property | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Winter | Spring | Summer | Autumn | ||||||
| p-Value | MK Tau | p-Value | MK Tau | p-Value | MK Tau | p-Value | MK Tau | ||
| Gitaru | 932 | * 0.109 | (−)0.217 | * 0.358 | (−)0.123 | * 0.823 | (−)0.034 | * 0.068 | (−)0.241 |
| Kamburu | 990 | * 0.527 | (−)0.087 | * 0.749 | 0.044 | * 0.665 | 0.065 | * 0.586 | (−)0.073 |
| Kiambere | 680 | ** 0.035 | 0.286 | * 0.445 | 0.103 | ** 0.00 | 1.00 | * 0.081 | (−)0.232 |
| Kindaruma | 766 | * 0.591 | 0.08 | * 0.559 | (−)0.086 | * 0.671 | 0.070 | * 0.182 | (−)0.185 |
| Masinga | 927 | * 0.797 | (−)0.037 | * 0.079 | 0.5609 | * 0.364 | (−)0.124 | * 0.358 | (−)0.123 |
| Mesco | 1060 | ** 0.035 | 0.286 | ** 0.004 | 0.379 | * 0.084 | 0.23 | ** 0.009 | 0.348 |
| Ndulla | 1414 | * 0.290 | 0.062 | * 0.225 | 0.139 | * 0.323 | 0.046 | * 0.202 | 0.187 |
| Sagana | 1609 | * 0.828 | 0.0317 | * 0.955 | (−)0.01 | * 0.749 | (−)0.044 | * 0.399 | 0.113 |
| Tana | 1089 | * 0.295 | (−)0.143 | * 0.209 | (−)0.167 | ** 0.026 | (−)0.296 | * 0.311 | (−)0.136 |
| Wanjii | 1146 | * 0.291 | 0.031 | * 0.31 | 0.019 | * 0.21 | 0.115 | * 0.246 | 0.06 |
| Annual Discharge Time Series Basic Statistical Properties | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min | 1st QU | Mean | 3rd Q | Median | Sd | Max | CV (%) | Skewness | Kurtosis | IQR |
| 0.2158 | 75 | 168 | 191 | 112.7 | 168 | 1974 | 1.0045 | 3.1193 | 13.897 | 117 |
| Streamflow Data Sets | Mann–Kendall Properties | Bootstrap Statistics | |||||
|---|---|---|---|---|---|---|---|
| MK Tau Statistic | Two-Sided p-Value | Mann–Kendall Score S | Variance of Kendall Score | MK Tau Original | Bias | Std. Error | |
| Whole dataset | 0.151 | <2.22 × 10−16 | 45,725,556 | 1.664506 × 1012 | t1* 0.1506114 | −0.0150 | 0.0091 |
| Pre-dam Dataset | 0.0991 | <2.22 × 10−16 | 9,010,393 | 272,615,424,000 | t1* 0.2645801 | −0.2708 | 0.0853 |
| Post dam dataset | 0.0523 | <2.22 × 10−16 | 1,825,937 | 65,182,507,008 | t1* 0.2645801 | −0.2639 | 0.08496 |
| Season | MK Tau | p-Value | MK Score | Variance of Kendall Score |
|---|---|---|---|---|
| Winter | 0.29 | 0.0003 | 4,244,587 | 2.5902 × 1010 |
| Spring | 0.195 | 0.0135 | 2,310,821 | 27,459,989,504 |
| Summer | 0.205 | 0.009 | 937,297 | 2,514,449,920 |
| Autumn | 0.316 | 7.8797 × 10−5 | 3,346,066 | 24,818,937,856 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Langat, P.K.; Kumar, L.; Koech, R. Temporal Variability and Trends of Rainfall and Streamflow in Tana River Basin, Kenya. Sustainability 2017, 9, 1963. https://doi.org/10.3390/su9111963
Langat PK, Kumar L, Koech R. Temporal Variability and Trends of Rainfall and Streamflow in Tana River Basin, Kenya. Sustainability. 2017; 9(11):1963. https://doi.org/10.3390/su9111963
Chicago/Turabian StyleLangat, Philip Kibet, Lalit Kumar, and Richard Koech. 2017. "Temporal Variability and Trends of Rainfall and Streamflow in Tana River Basin, Kenya" Sustainability 9, no. 11: 1963. https://doi.org/10.3390/su9111963
APA StyleLangat, P. K., Kumar, L., & Koech, R. (2017). Temporal Variability and Trends of Rainfall and Streamflow in Tana River Basin, Kenya. Sustainability, 9(11), 1963. https://doi.org/10.3390/su9111963





