Multi-Objective Optimization of a Hybrid ESS Based on Optimal Energy Management Strategy for LHDs
Abstract
:1. Introduction
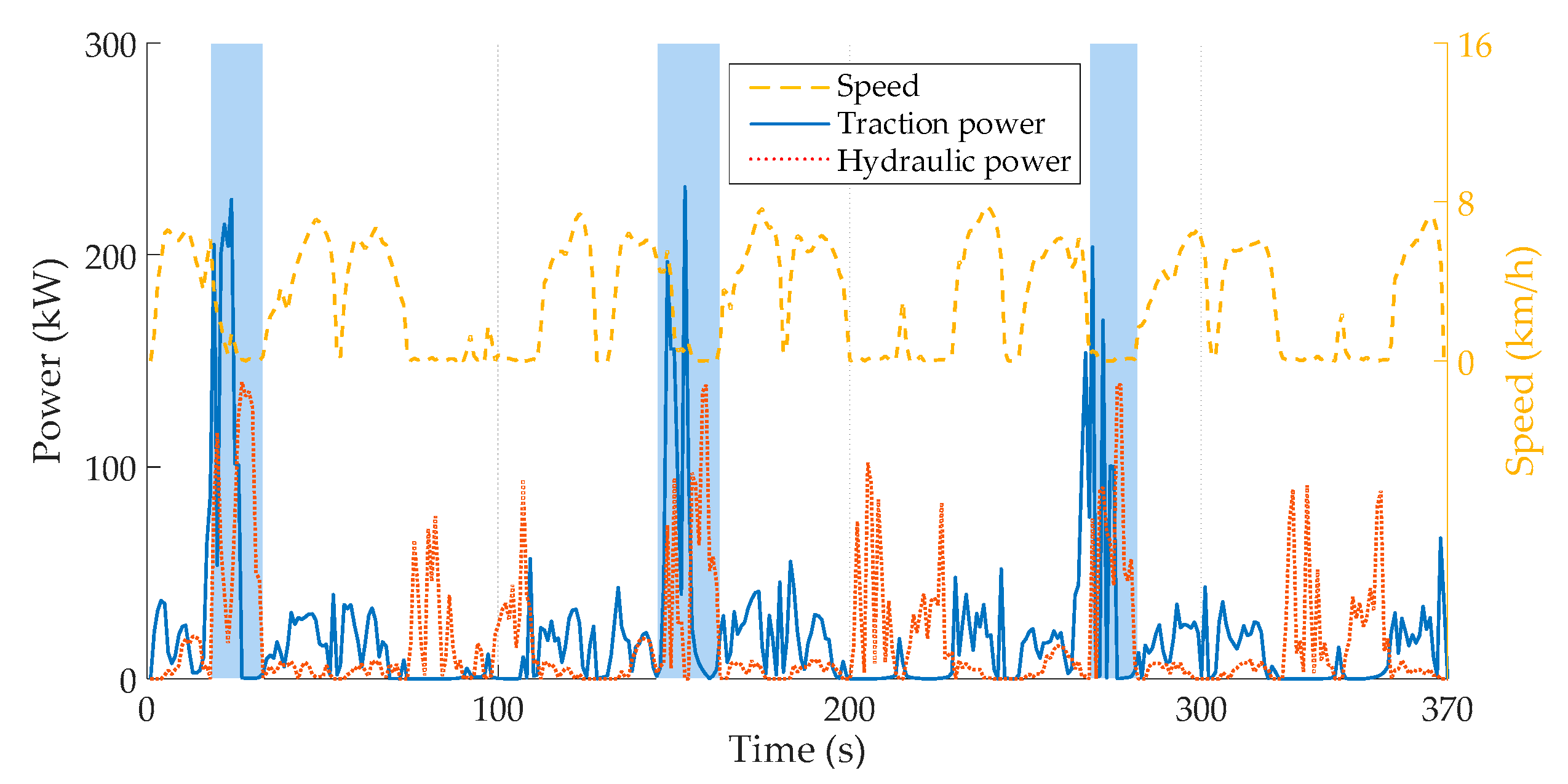
2. Driving Cycle Description
3. Powertrain Configuration and Model of a Hybrid ESS Based LHD
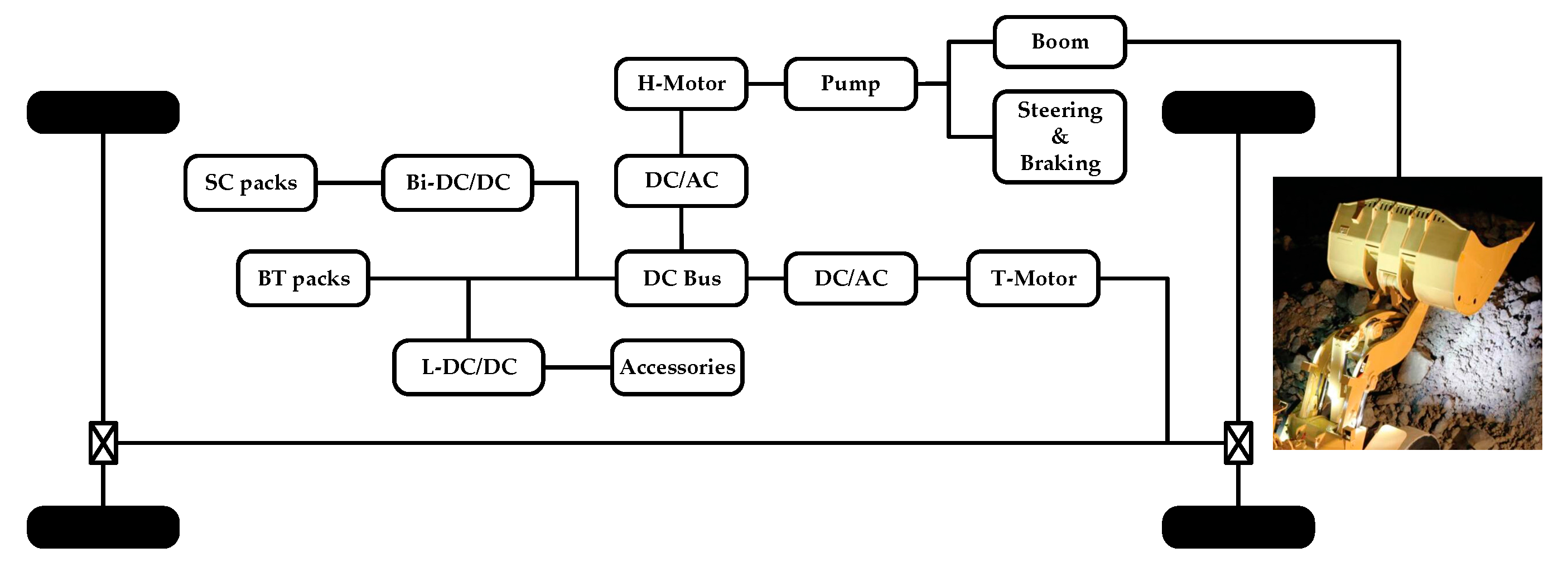
3.1. Powertrain Structure
3.2. Theoretical Model
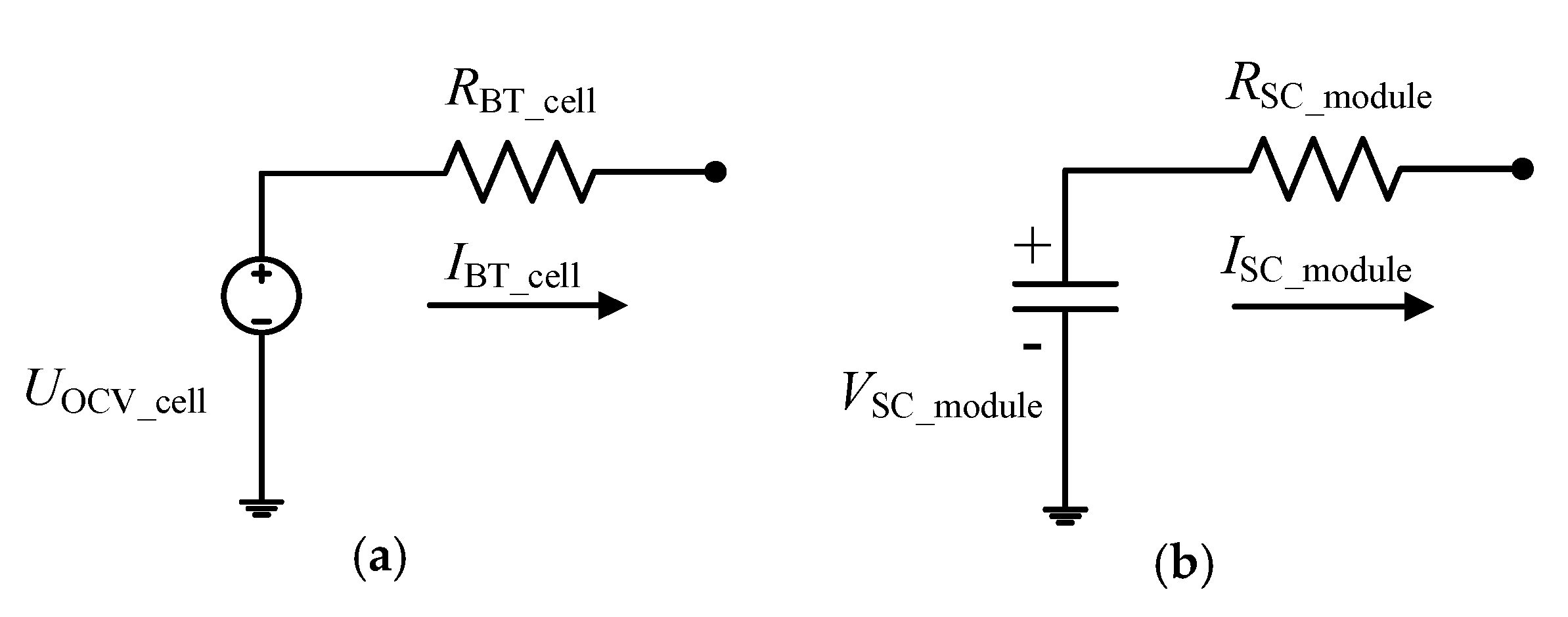
3.2.1. Battery Rint Model
3.2.2. Supercapacitor Model
3.2.3. Battery Capacity Degradation Model
3.2.4. Other Powertrain Elements
4. Multi-Objective Optimization Problem
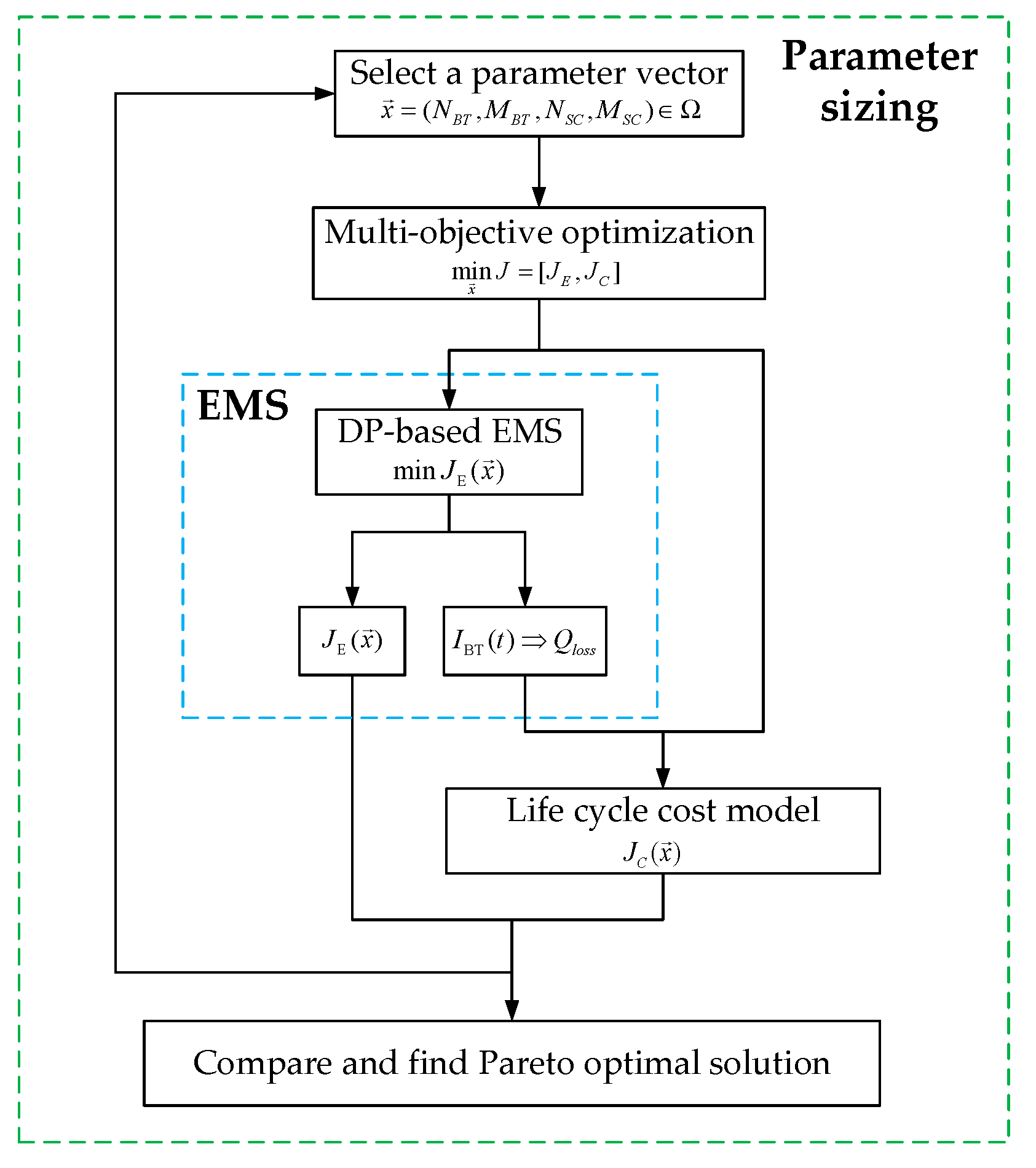
4.1. Optimization Framework for Hybrid ESS Parameter Sizing
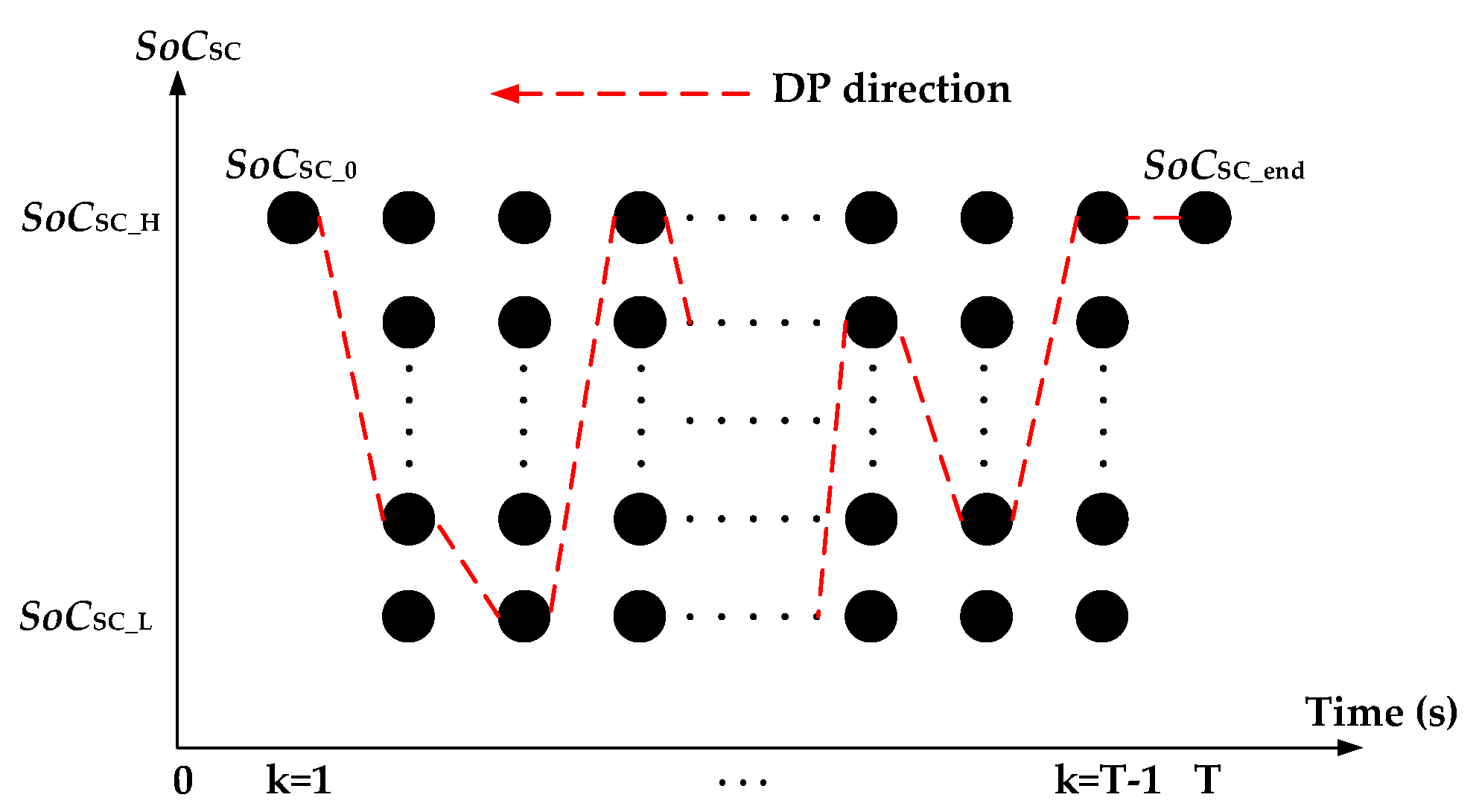
4.2. DP-Based Energy Management Strategy
4.3. Life Cycle Cost Model of Hybrid ESS
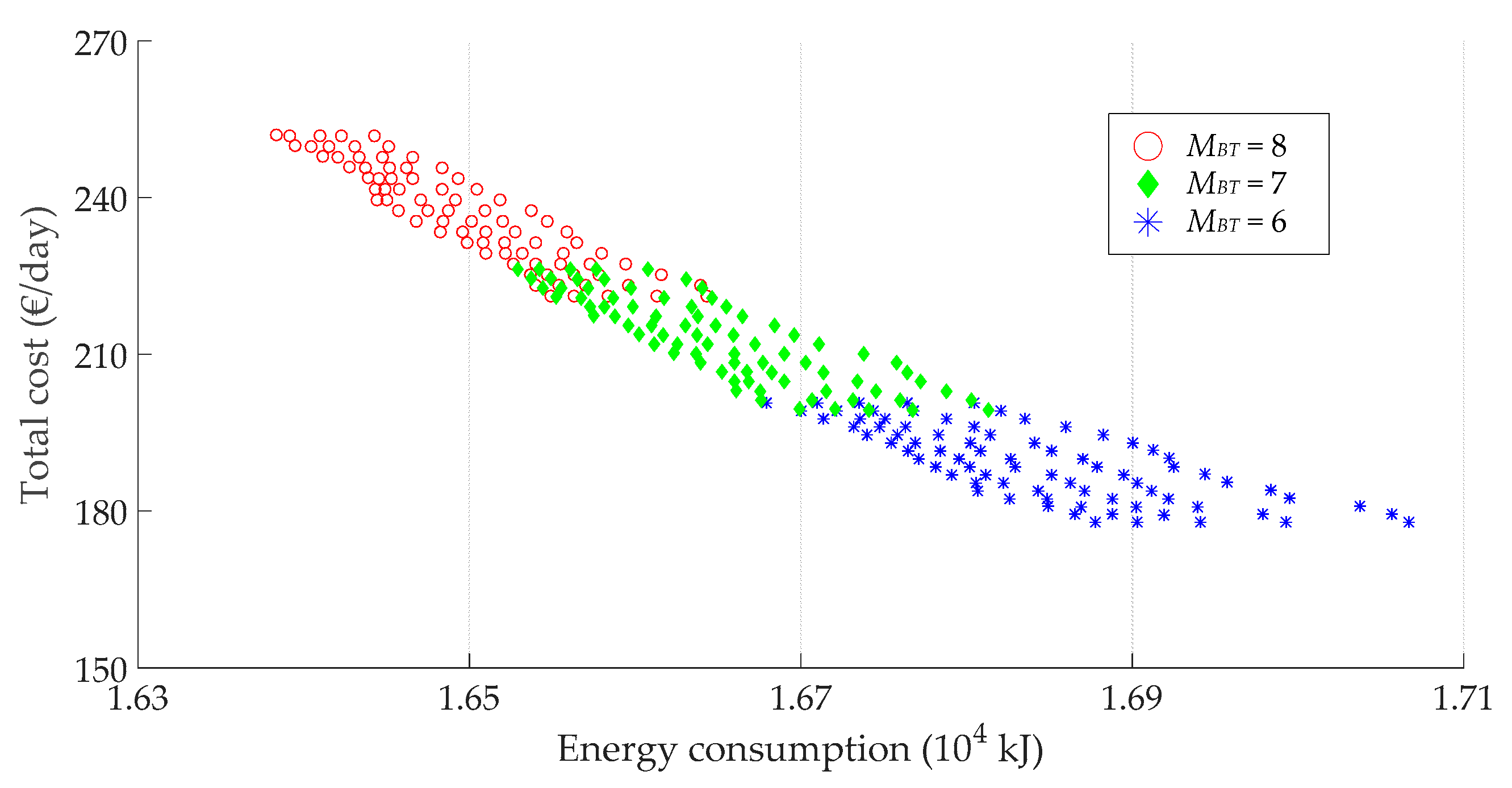
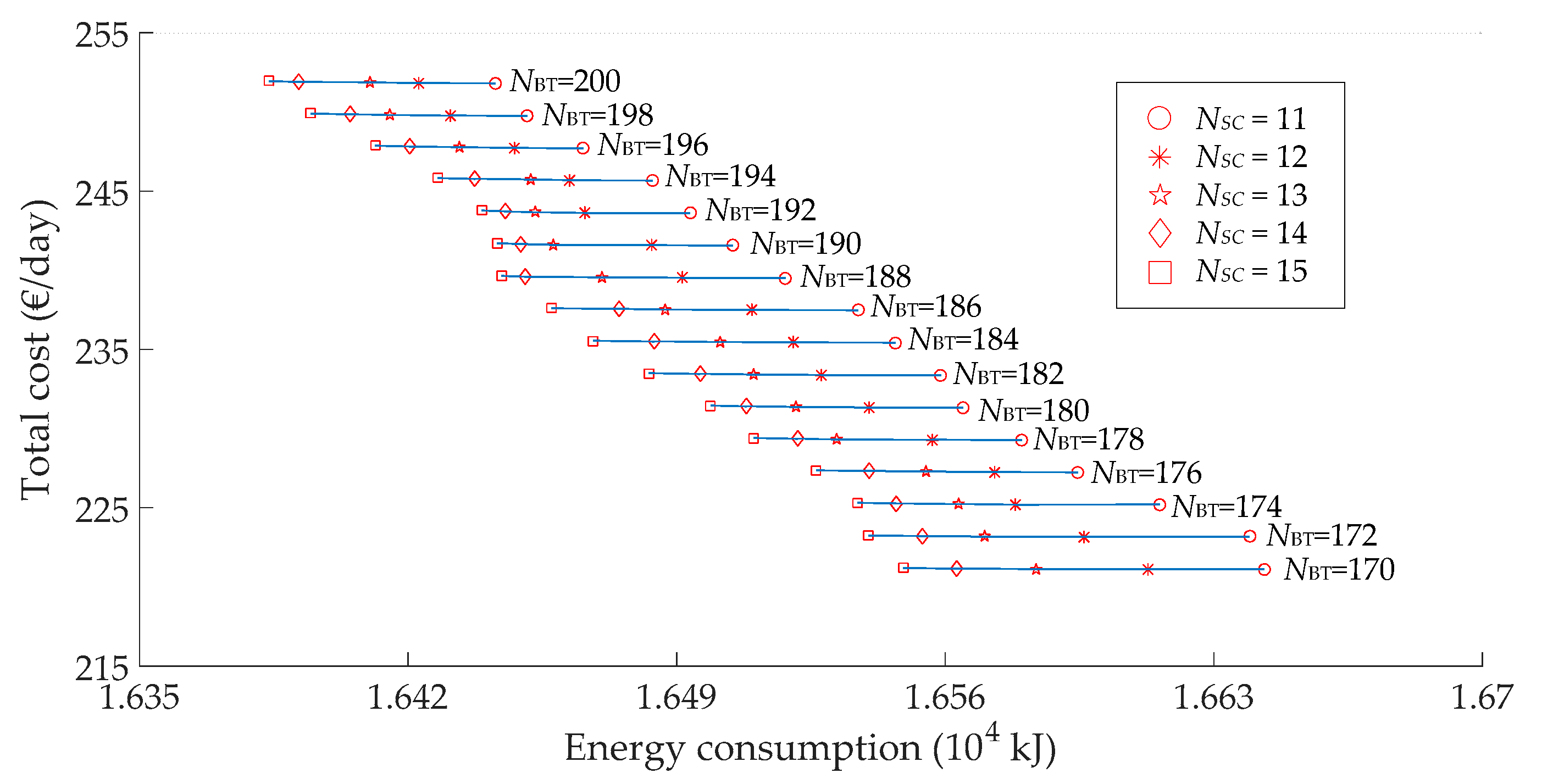
4.4. Pareto Optimal Solution
5. Comparison with Battery-Only Option
6. Conclusions
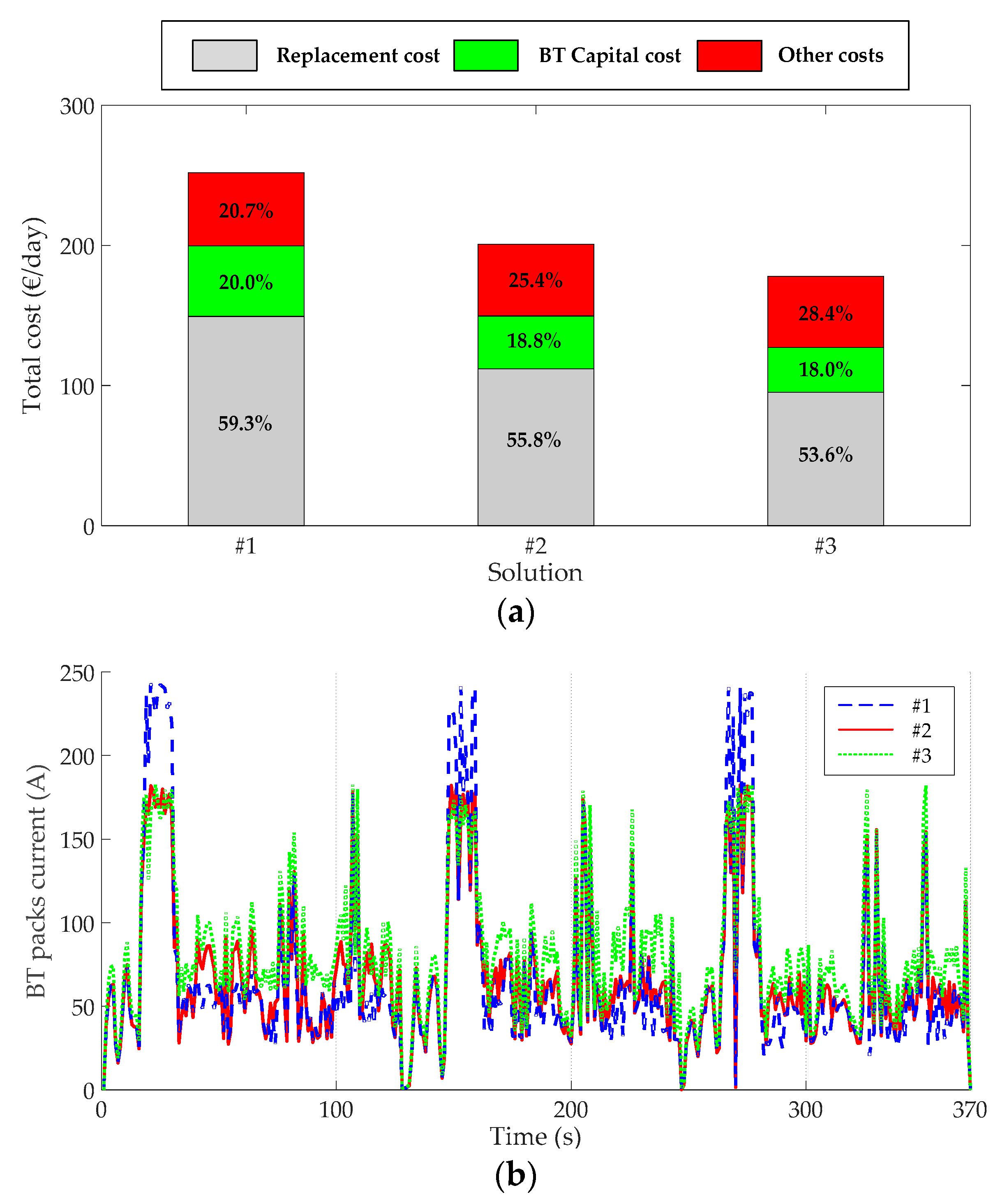
- The sum of BT replacement and capital costs has reached over 71.6% of the total cost of hybrid ESS, which highlights the importance of considering the battery capacity degradation when evaluating the total cost of hybrid ESS-based LHDs.
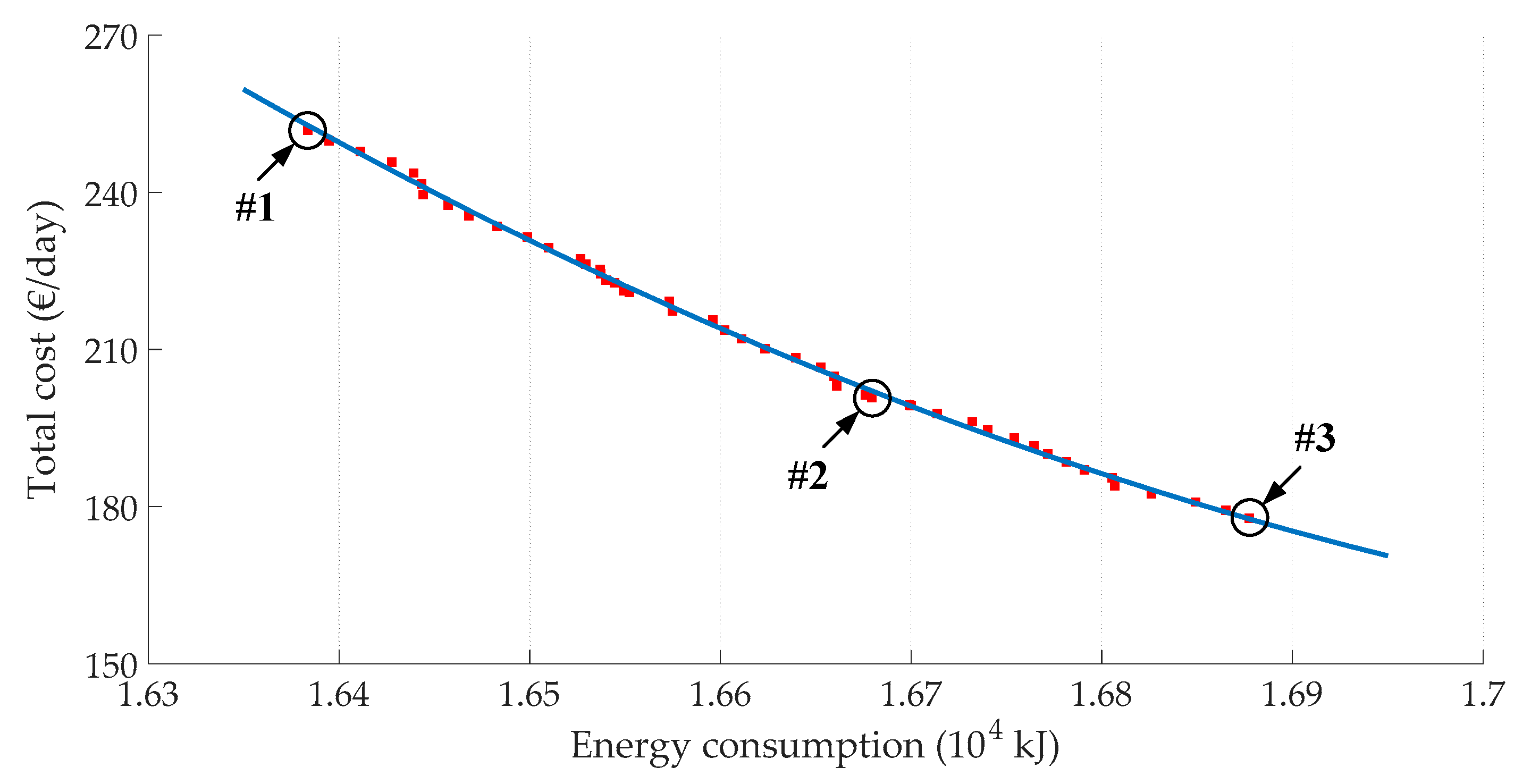
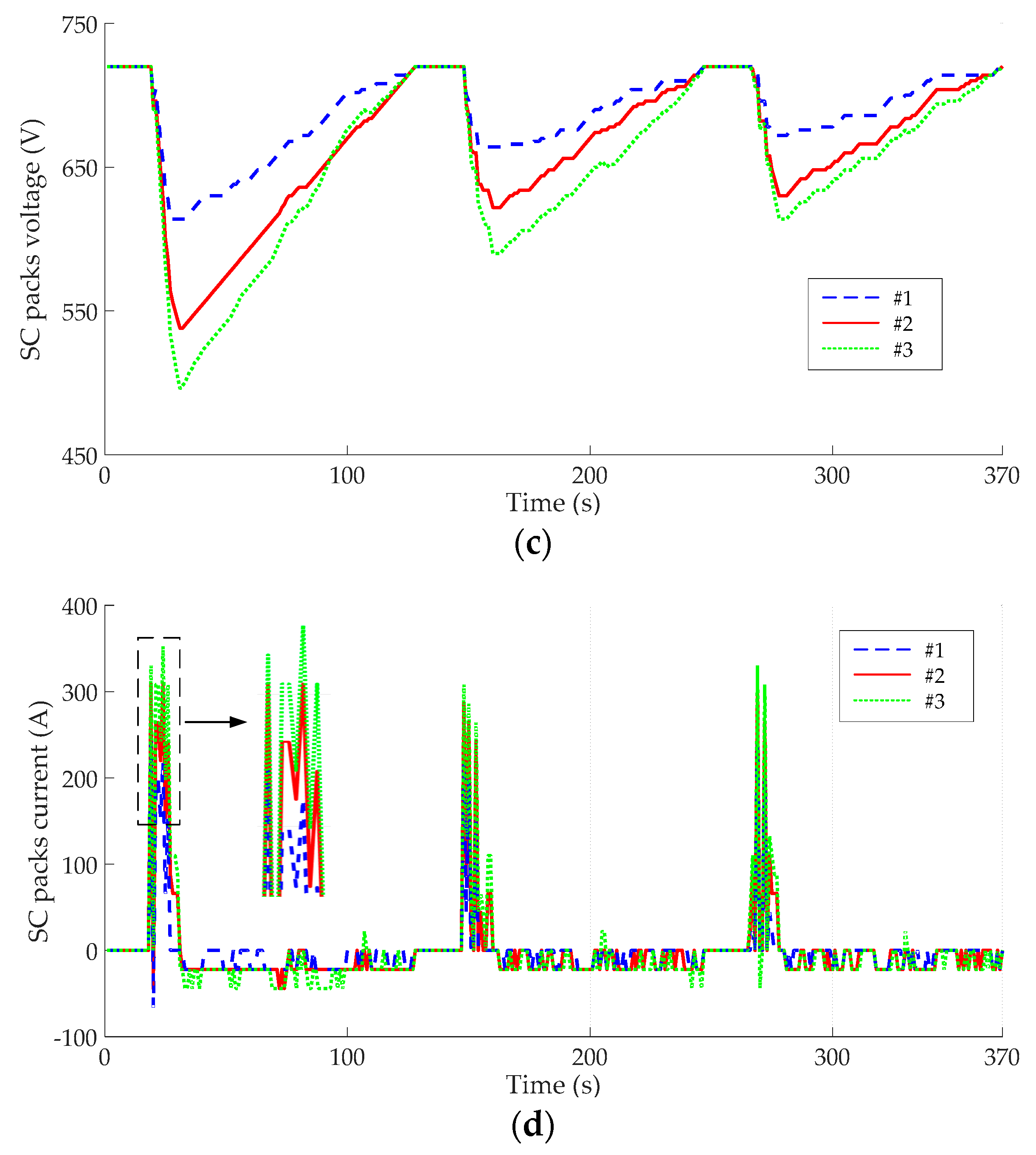
- As the total cost of hybrid ESS increases, the energy consumption becomes smaller. Three solutions chosen from the Pareto front are compared comprehensively, and #2 (, , and ) is selected as the Pareto optimal solution, which can make an ideal trade-off between the two objectives, where the energy consumption and the total cost is 1.668 × 104 kJ and 200.74 €/day, respectively.
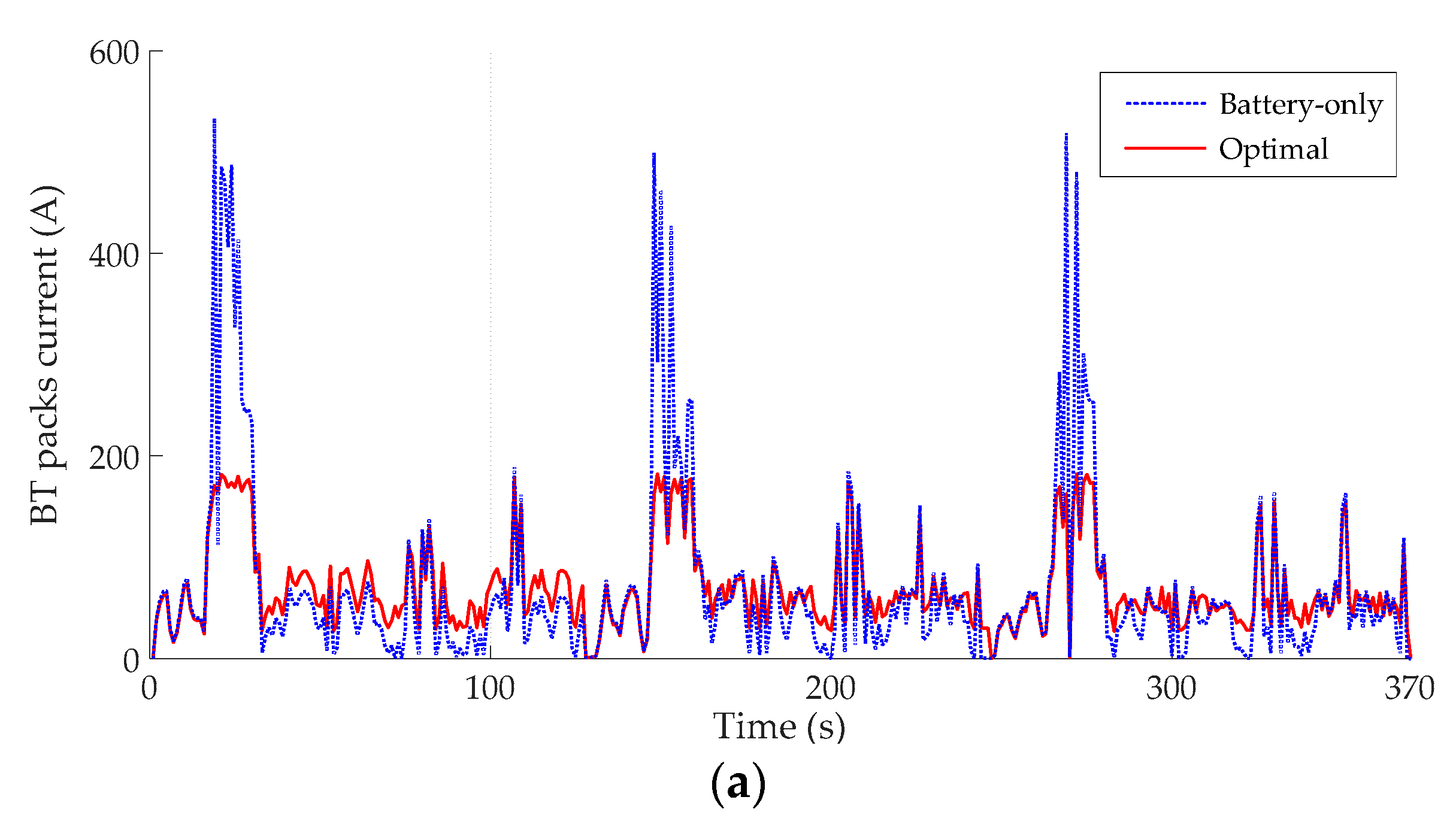
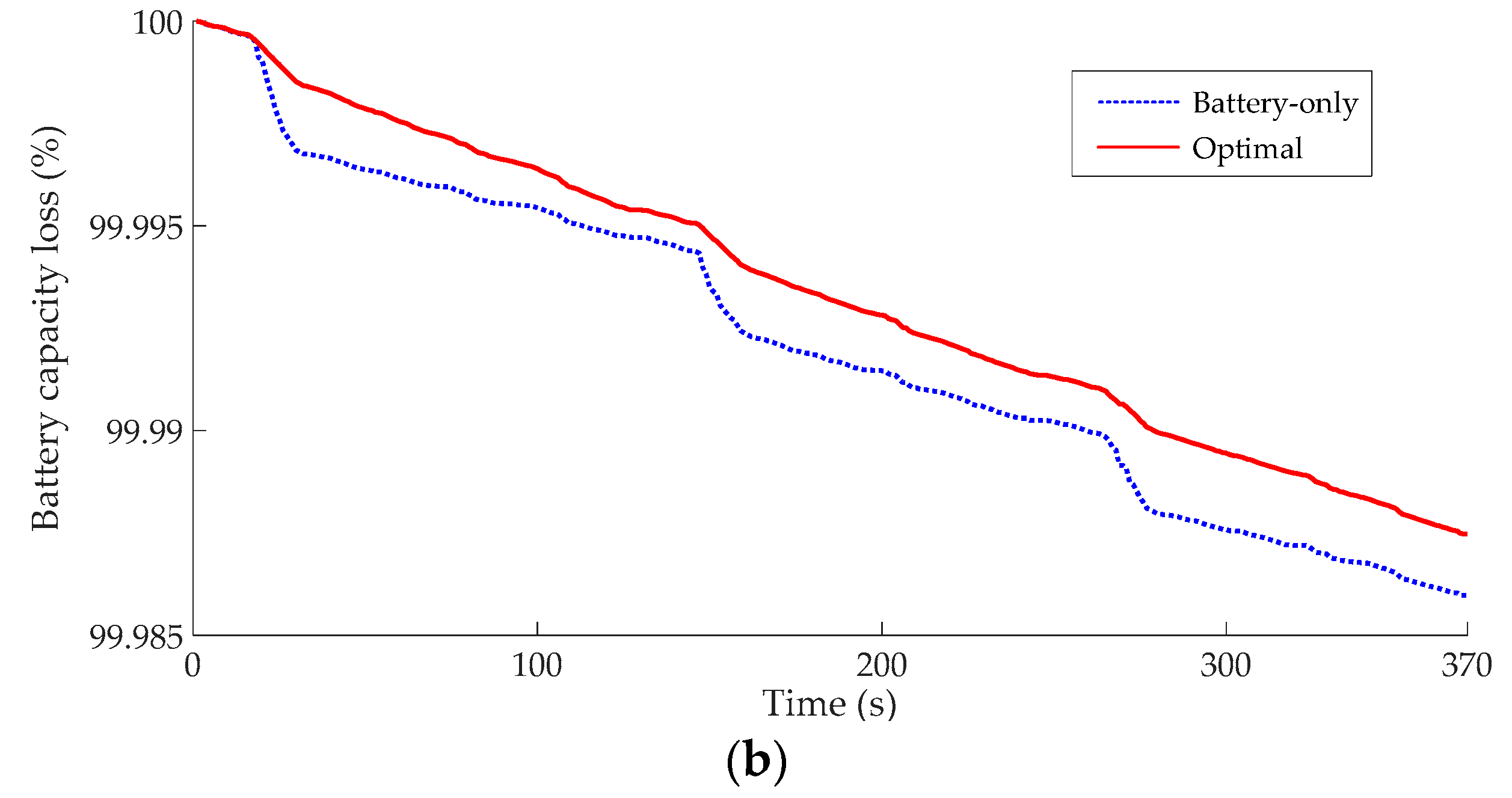
- Comparison with battery-only option indicates that the optimal hybrid ESS is a more economical and efficient option.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jacobs, W.; Hodkiewicz, M.; Bräunl, T. A Cost-Benefit Analysis of Electric Loaders to Reduce Diesel Emissions in Underground Hard Rock Mines. IEEE Trans. Ind. Electron. 2015, 51, 2565–2573. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Lajunen, A.; Suomela, J. Evaluation of energy storage system requirements for hybrid mining loaders. IEEE Trans. Veh. Technol. 2012, 61, 3387–3393. [Google Scholar] [CrossRef]
- Zeng, X.; Yang, N.; Peng, Y.; Zhang, Y.; Wang, J. Research on energy saving control strategy of parallel hybrid loader. Autom. Constr. 2014, 38, 100–108. [Google Scholar] [CrossRef]
- Nilsson, T.; Fröberg, A.; Åslund, J. Predictive control of a diesel electric wheel loader powertrain. Control Eng. Pract. 2015, 41, 47–56. [Google Scholar] [CrossRef]
- Kwon, T.; Lee, S.; Sul, S.; Park, C.; Kim, N.; Kang, B.; Hong, M. Power Control Algorithm for Hybrid Excavator with Supercapacitor. IEEE Trans. Ind. Appl. 2010, 46, 1447–1455. [Google Scholar] [CrossRef]
- Wang, D.; Guan, C.; Pan, S.; Zhang, M.; Lin, X. Performance analysis of hydraulic excavator powertrain hybridization. Autom. Constr. 2009, 18, 249–257. [Google Scholar] [CrossRef]
- Unger, J.; Kozek, M.; Jakubek, S. Nonlinear model predictive energy management controller with load and cycle prediction for non-road HEV. Control Eng. Pract. 2015, 36, 120–132. [Google Scholar] [CrossRef]
- Yoon, J.; Truong, D.; Ahn, K. A generation step for an electric excavator with a control strategy and verifications of energy consumption. Int. J. Precis. Eng. Manuf. 2013, 14, 755–766. [Google Scholar] [CrossRef]
- Kim, M.; Peng, H. Power management and design optimization of fuel cell/battery hybrid vehicles. J. Power Sour. 2007, 165, 819–832. [Google Scholar] [CrossRef]
- Song, Z.; Hofmann, H.; Li, J.; Han, X.; Ouyang, M. Optimization for a hybrid energy storage system in electric vehicles using dynamic programing approach. Appl. Energy 2015, 139, 151–162. [Google Scholar] [CrossRef]
- Song, Z.; Hou, J.; Xu, S.; Ouyang, M.; Li, J. The influence of driving cycle characteristics on the integrated optimization of hybrid energy storage system for electric city buses. Energy 2017, 135, 91–100. [Google Scholar] [CrossRef]
- Hung, Y.; Wu, C. A combined optimal sizing and energy management approach for hybrid in-wheel motors of EVs. Appl. Energy 2015, 139, 260–271. [Google Scholar] [CrossRef]
- Liu, C.; Liu, L. Optimal power source sizing of fuel cell hybrid vehicles based on Pontryagin’s minimum principle. Int. J. Hydrog. Energy 2015, 40, 8454–8464. [Google Scholar] [CrossRef]
- Murgovski, N.; Johannesson, L.; Sjöberg, J.; Egardt, B. Component sizing of a plug-in hybrid electric powertrain via convex optimization. Mechatronics 2012, 22, 106–120. [Google Scholar] [CrossRef]
- Hu, X.; Johannesson, L.; Murgovski, N.; Egardt, B. Longevity-conscious dimensioning and power management of the hybrid energy storage system in a fuel cell hybrid electric bus. Appl. Energy 2015, 137, 913–924. [Google Scholar] [CrossRef]
- Hu, X.; Moura, S.; Murgovski, N.; Egardt, B.; Cao, D. Integrated Optimization of Battery Sizing, Charging, and Power Management in Plug-In Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2016, 24, 1036–1043. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, J.; Egardt, B.; Cao, D. Advanced power-source integration in hybrid electric vehicles: Multicriteria optimization approach. IEEE Trans. Ind. Electron. 2015, 62, 7847–7858. [Google Scholar] [CrossRef]
- Xu, L.; Mueller, C.; Li, J.; Ouyang, M.; Hu, Z. Multi-objective component sizing based on optimal energy management strategy of fuel cell electric vehicles. Appl. Energy 2015, 157, 664–674. [Google Scholar] [CrossRef]
- Ebbesen, S.; Dönitz, C.; Guzzella, L. Particle swarm optimization for hybrid electric drive-train sizing. Int. J. Veh. Des. 2012, 58, 181–199. [Google Scholar] [CrossRef]
- Herrera, V.; Milo, A.; Gaztañaga, H.; Otadui, I.; Villarreal, I.; Camblong, H. Adaptive energy management strategy and optimal sizing applied on a battery-supercapacitor based tramway. Appl. Energy 2016, 169, 831–845. [Google Scholar] [CrossRef]
- Song, Z.; Li, J.; Han, X.; Xu, L.; Lu, L.; Ouyang, M.; Hofmann, H. Multi-objective optimization of a semi-active battery/supercapacitor energy storage system for electric vehicles. Appl. Energy 2014, 135, 212–224. [Google Scholar] [CrossRef]
- Hu, Z.; Li, J.; Xu, L.; Song, Z.; Fang, C.; Ouyang, M.; Dou, G.; Kou, G. Multi-objective energy management optimization and parameter sizing for proton exchange membrane hybrid fuel cell vehicles. Energy Convers. Manag. 2016, 129, 108–121. [Google Scholar] [CrossRef]
- Martinez, C.; Hu, X.; Cao, D.; Velenis, E.; Gao, B.; Wellers, M. Energy management in plug-in hybrid electric vehicles: Recent progress and a connected vehicles perspective. IEEE Trans. Veh. Technol. 2017, 66, 4534–4549. [Google Scholar] [CrossRef]
- Silvas, E.; Hofman, T.; Murgovski, N.; Etman, L.; Steinbuch, M. Review of optimization strategies for system-level design in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2017, 66, 57–70. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Xu, L.; Ouyang, M. Optimization for a fuel cell/battery/capacity tram with equivalent consumption minimization strategy. Energy Convers. Manag. 2017, 134, 59–69. [Google Scholar] [CrossRef]
- Hemi, H.; Ghouili, J.; Cheriti, A. Combination of Markov chain and optimal control solved by Pontryagin’s Minimum Principle for a fuel cell/supercapacitor vehicle. Energy Convers. Manag. 2015, 91, 387–393. [Google Scholar] [CrossRef]
- Wieczorek, M.; Lewandowski, M. A mathematical representation of an energy management strategy for hybrid energy storage system in electric vehicle and real time optimization using a genetic algorithm. Appl. Energy 2017, 192, 222–233. [Google Scholar] [CrossRef]
- Scooptram ST7 Battery. Available online: https://www.atlascopco.com/en-cn/mrba/products/loaders-and-trucks/electric-loaders/scooptram-st7-battery (accessed on 7 July 2017).
- MUCKMASTER 300EB. Available online: http://www.rdhminingequipment.com/product/muckmaster-300eb/ (accessed on 12 July 2017).
- MUCKMASTER 600EB. Available online: http://www.rdhminingequipment.com/product/muckmaster-600eb/ (accessed on 12 July 2017).
- 153-Artisan Vehicle Systems. Available online: http://artisanvs.com/project/153/ (accessed on 13 July 2017).
- Catherino, H.; Burgel, J.; Shi, P.; Rusek, A.; Zou, X. Hybrid power supplies: A capacitor-assisted battery. J. Power Sour. 2006, 162, 965–970. [Google Scholar] [CrossRef]
- Pagano, M.; Piegari, L. Hybrid electrochemical power sources for onboard applications. IEEE Trans. Energy Convers. 2007, 22, 450–456. [Google Scholar] [CrossRef]
- Lu, S.; Corzine, K.; Ferdowsi, M. A new battery/ultracapacitor energy storage system design and its motor drive integration for hybrid electric vehicles. IEEE Trans. Veh. Technol. 2007, 56, 1516–1523. [Google Scholar] [CrossRef]
- Schaltz, E.; Khaligh, A.; Rasmussen, P. Influence of battery/ultracapacitor energy-storage sizing on battery lifetime in a fuel cell hybrid electric vehicle. IEEE Trans. Veh. Technol. 2009, 58, 3882–3891. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sour. 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Ouyang, M.; Feng, X.; Han, X.; Lu, L.; Li, Z.; He, X. A dynamic capacity degradation model and its applications considering varying load for a large format Li-ion battery. Appl. Energy 2016, 165, 48–59. [Google Scholar] [CrossRef]
- Cericola, D.; Ruch, P.; Kötz, R.; Novák, P.; Wokaun, A. Simulation of a supercapacitor/Li-ion battery hybrid for pulsed applications. J. Power Sour. 2010, 195, 2731–2736. [Google Scholar] [CrossRef]
- Trovão, J.; Pereirinha, P.; Jorge, H.; Antunes, C. A multi-level energy management system for multi-source electric vehicles-An integrated rule-based meta-heuristic approach. Appl. Energy 2013, 105, 304–318. [Google Scholar] [CrossRef]
- Hung, Y.; Wu, C. An integrated optimization approach for a hybrid energy system in electric vehicles. Appl. Energy 2012, 98, 479–490. [Google Scholar] [CrossRef]
- Cao, J.; Emadi, A. A new battery/ultracapacitor hybrid energy storage system for electric, hybrid, and plug-in hybrid electric vehicles. IEEE Trans. Power Electron. 2012, 27, 122–132. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Zhao, Y.; Yang, L.; Chen, W. A Fuzzy-Logic Power Management Strategy Based on Markov Random Prediction for Hybrid Energy Storage Systems. Energies 2016, 9, 25. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sour. 2012, 198, 359–367. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Einhorn, M.; Conte, F.; Kral, C.; Fleig, J. Comparison, selection, and parameterization of electrical battery models for automotive applications. IEEE Trans. Power Electron. 2013, 28, 1429–1437. [Google Scholar] [CrossRef]
- Plett, G. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs Part 2. Modeling and identification. J. Power Sour. 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Marler, R.; Arora, J. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Ansarey, M.; Panahi, M.; Ziarati, H.; Mahjoob, M. Optimal energy management in a dual-storage fuel-cell hybrid vehicle using multi-dimensional dynamic programming. J. Power Sour. 2014, 250, 359–371. [Google Scholar] [CrossRef]
- Santucci, A.; Sorniotti, A.; Lekakou, C. Power split strategies for hybrid energy storage systems for vehicular applications. J. Power Sour. 2014, 258, 395–407. [Google Scholar] [CrossRef]
- Pérez, L.; Bossio, G.; Moitre, D.; García, G. Optimization of power management in an hybrid electric vehicle using dynamic programming. Math. Comput. Simul. 2006, 73, 244–254. [Google Scholar] [CrossRef]
- Xu, L.; Yang, F.; Li, J.; Ouyang, M.; Hua, J. Real time optimal energy management strategy targeting at minimizing daily operation cost for a plug-in fuel cell city bus. Int. J. Hydrogen Energy 2012, 37, 15380–15392. [Google Scholar] [CrossRef]
- Zakeri, B.; Syri, S. Electrical energy storage systems: A comparative life cycle cost analysis. Renew. Sustain. Energy Rev. 2015, 42, 569–596. [Google Scholar] [CrossRef]


| BT Cell | SC Module | ||
|---|---|---|---|
| Nominal voltage (V) | 3.3 | Nominal voltage (V) | 48 |
| Nominal capacity (Ah) | 60 | Nominal capacity (F) | 165 |
| Stored energy (kWh) | 0.198 | Stored energy (kWh) | 0.0528 |
| Internal resistance (mΩ) | 1.5 | Internal resistance (mΩ) | 7.1 |
| Volume (L) | 1.15 | Volume (L) | 14.5 |
| Coefficient | Value | Unit |
|---|---|---|
| 370 | s | |
| 50 | % | |
| 100 | % | |
| 100 | % | |
| −250 | kW | |
| 250 | kW | |
| 0.5 C 1 | A |
| Coefficient | Value | Unit |
|---|---|---|
| 500 [21] | €/kWh | |
| 4000 [21] | €/kWh | |
| 150 [21] | €/kW | |
| 0.05 [53] | €/kWh | |
| 2.5 [53] | % | |
| 60 [1] | % | |
| 10 [1] | Years | |
| 303.15 | K | |
| 5 | kW |
| Solution | ( kJ) | (%) | (€/Day) | The Volume of Hybrid ESS (L) | ||||
|---|---|---|---|---|---|---|---|---|
| #1 | 200 | 8 | 15 | 1 | 1.639 | 60.214 | 251.95 | 2058 |
| #2 | 200 | 6 | 15 | 1 | 1.668 | 63.100 | 200.74 | 1598 |
| #3 | 170 | 6 | 15 | 1 | 1.707 | 75.234 | 177.92 | 1333 |
| Option | Hybrid ESS Capital Cost (€/Day) | Battery Loss during 370 s (10−4%) | Replacement Cost (€/Day) | ( kJ) | (€/Day) |
|---|---|---|---|---|---|
| Optimal | 50.62 | 1.25 | 112.01 | 1.668 | 200.74 |
| Battery-only | 37.71 | 1.41 | 129.24 | 1.679 | 204.15 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Jin, T.; Liu, L.; Chen, Y.; Yuan, K. Multi-Objective Optimization of a Hybrid ESS Based on Optimal Energy Management Strategy for LHDs. Sustainability 2017, 9, 1874. https://doi.org/10.3390/su9101874
Liu J, Jin T, Liu L, Chen Y, Yuan K. Multi-Objective Optimization of a Hybrid ESS Based on Optimal Energy Management Strategy for LHDs. Sustainability. 2017; 9(10):1874. https://doi.org/10.3390/su9101874
Chicago/Turabian StyleLiu, Jiajun, Tianxu Jin, Li Liu, Yajue Chen, and Kun Yuan. 2017. "Multi-Objective Optimization of a Hybrid ESS Based on Optimal Energy Management Strategy for LHDs" Sustainability 9, no. 10: 1874. https://doi.org/10.3390/su9101874
APA StyleLiu, J., Jin, T., Liu, L., Chen, Y., & Yuan, K. (2017). Multi-Objective Optimization of a Hybrid ESS Based on Optimal Energy Management Strategy for LHDs. Sustainability, 9(10), 1874. https://doi.org/10.3390/su9101874




