3.1. Daily Optimization Result
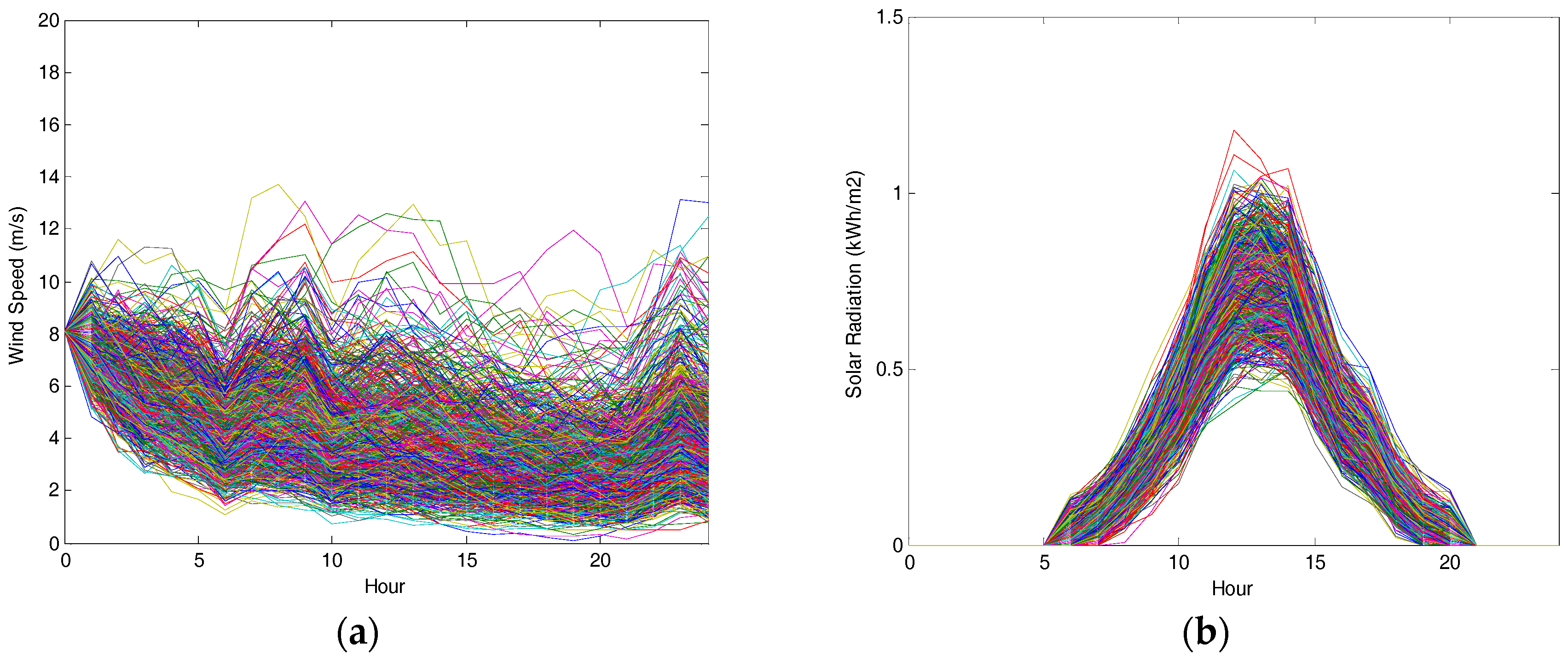
Table 5 describes each scenario that we studied to analyze the effect of energy storage on power systems with different renewable sources. The wind-only scenario is a basic Korean power system with a wind capacity of 8064 MW, which is the government’s target capacity by 2029. The solar-only scenario is a basic Korean power system with a solar photovoltaic capacity of 16,565 MW, and the combined scenario is a basic Korean power system with both wind and solar generation at the capacities used above. For each scenario, the effects of base and net demand were computed, and optimum demand was estimated based on optimization with 10 GWh of energy storage.
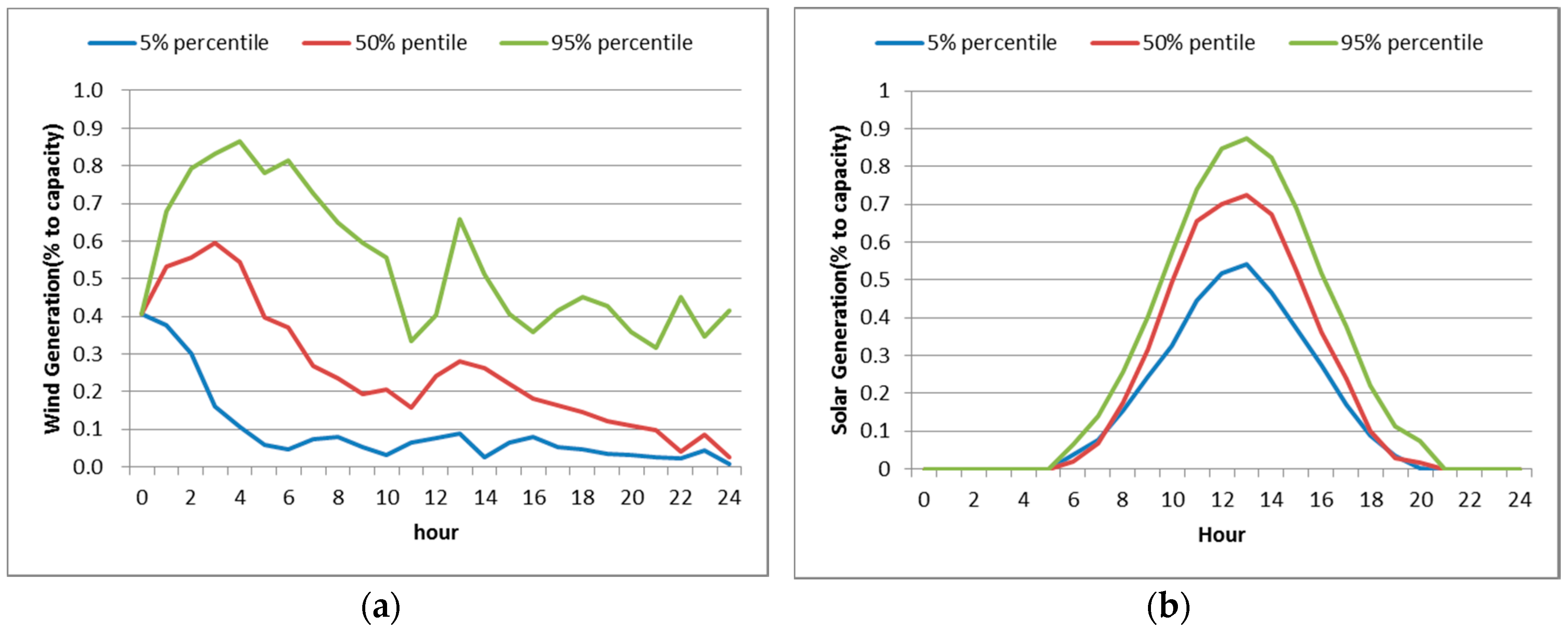
The same methodology was applied to generate sample profiles for solar photovoltaic power generation. From the 1000 simulated solar generation profiles in
Figure 2b, the 5%, 50%, and 95% percentile profiles were estimated and used as inputs for optimization, as shown in
Figure 3b.
For each scenario, analysis was conducted for low, mid, and high days for each renewable source, which were the 5%, 50%, and 95% percentile profiles of the simulations, respectively. The energy storage capacity was assumed to be 10 GWh. 10 GWh is chosen because it is approximately 10% of peak electricity demand of Korea, and thus can start to create some meaningful impacts on the Korean power system. Also, the target capacity of wind and solar photovoltaic power used in this study is 8064 MW and 16,565 MW, respectively. Hence, this storage capacity is approximately the size that can manage the variability caused by these renewable power sources.
The charging and discharging hourly power limits were assumed to be one-third of capacity level. The storage efficiency was assumed to be 95% for each charging and discharging cycle. The charging and discharging efficiency of a Lithium ion battery varies from 90% to 99% by its technology and specification. This paper uses 95% for efficiency based on products manufactured by KOKAM [
17].
(a) Wind-Only Scenario
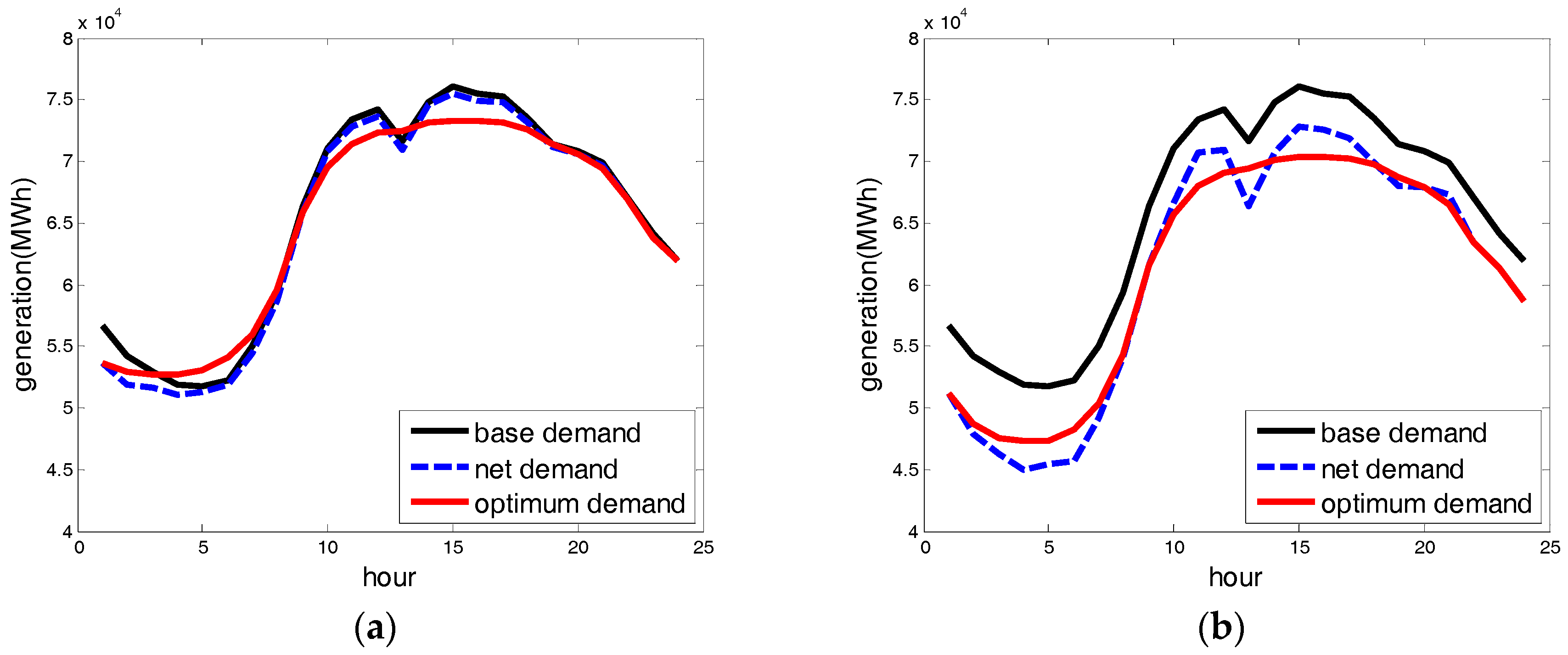
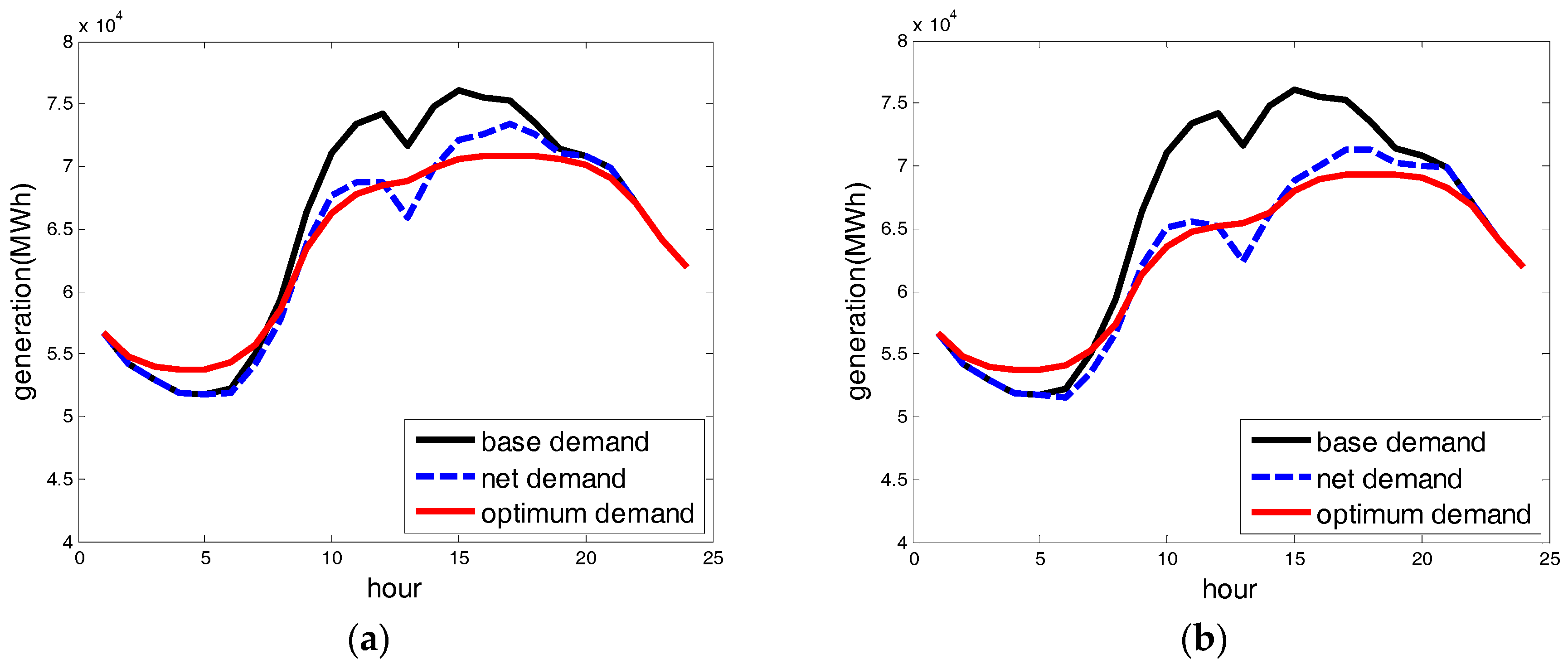
Figure 4 shows the 24-h profiles of base and optimum demand, which is net demand optimized by energy storage to minimize the energy and reserve costs on the chosen summer day. To compare high and low wind days, two sets of optimization results are presented. The optimization results show that, in both the high and low wind-only scenarios, energy storage charged during the early hours and discharged during the peak hours for price arbitrage, and it almost smoothed the net demand profiles to minimize reserve costs.
Table 6 presents the operation costs of base, net, and optimum demand of two of the wind-only scenarios on the peak summer day. For the high wind-only scenario, meeting net demand has significantly lower energy costs and much higher reserve costs than meeting base demand. This is because wind generation effectively replaces expensive fossil-fuel generation, but inherent variability increases the reserve costs by about 31%. Compared with net demand, the energy costs of meeting optimum demand are smaller again, as the expensive peak demand is moved to off-peak hours. Reserve costs are also significantly smaller, as energy storage effectively mitigates for the variability of wind generation. As seen in
Figure 4b, net demand is smoothed by energy storage. The low wind-only scenario has similar results to the high wind-only scenario, but increases in reserve costs are limited as wind power generation is not as variable. Thus, the low wind-only scenario saves only
$748,000/day in operation costs, while the high wind-only scenario saves
$1,042,000/day. The peak demand of each scenario indicates how much the energy storage reduces the maximum energy required for system adequacy.
(b) Solar-only scenario
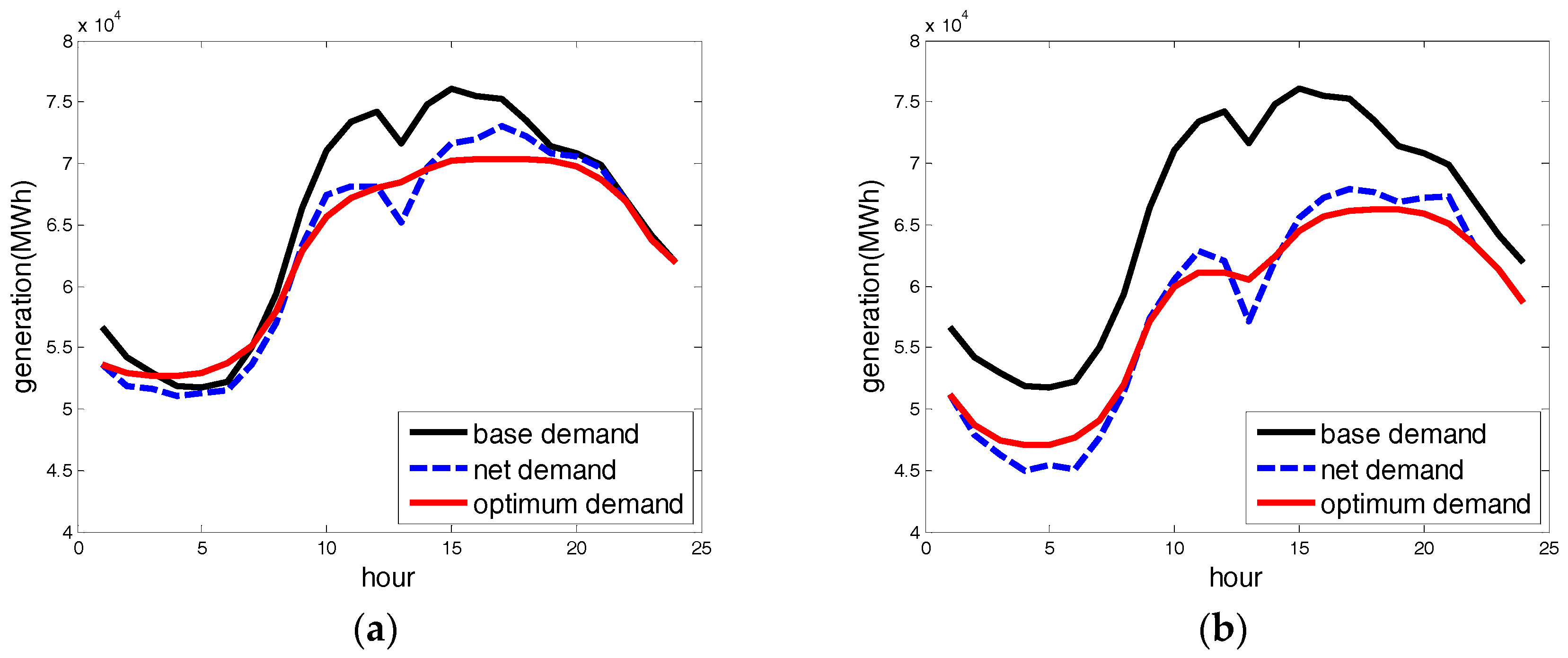
Figure 5 shows the base, net, and optimum demand of the solar-only scenario for the same summer day. The net demand of the solar-only scenario is less variable, and the difference between off-peak and peak demand is less noticeable than that of the wind-only scenario, as solar power is typically produced during peak hours. Hence, although optimum demand includes price arbitrage and demand profile smoothing, cost saving would be limited, as the price difference between peak and off-peak hours is also limited, and the net demand of the solar-only scenario is less variable than the wind-only scenario.
This is confirmed in
Table 7. In the high solar-only scenario, energy storage only reduces energy costs by
$241,000/day, reserve costs by
$422,000/day, and operating costs by
$664,000/day in meeting optimum demand, while the costs of the wind-only scenario (
Table 6) are reduced by
$390,000/day,
$652,000/day, and
$1,042,000/day, respectively. This indicates that energy storage is more valuable for wind power generation than solar power generation.
(c) Combined scenario
Figure 6 shows the 24-h profiles of base, net, and optimum demand of the combined scenario for the chosen summer day. The main advantage of combining wind and solar sources in a power system is that variability is reduced due to the disparity between the variability of the two sources. As seen in
Figure 6, wind is more abundant during the night, while solar power is only produced during the day. Hence, when these two variable sources are combined, overall variability reduces. There is less difference between day–night demand in
Figure 5b and
Figure 6b.
In
Table 8, the high combined scenario demonstrates the advantages of a combined system more clearly. The reserve cost of meeting net demand is
$1,439,000/day, which is much lower than the
$1,766,000/day for meeting net demand in the wind-only scenario. Energy storage in meeting optimum demand saves
$326,000/day,
$657,000/day, and
$983,000/day of energy, reserve, and operating costs, respectively. These savings are slightly lower than those made by energy storage in the wind-only scenario. This is because the difference in day–night demand and net demand variability in the combined scenario is less severe than in the wind-only scenario. Therefore, there are fewer challenges for energy storage to mitigate for, thus there is less of a demand for it.
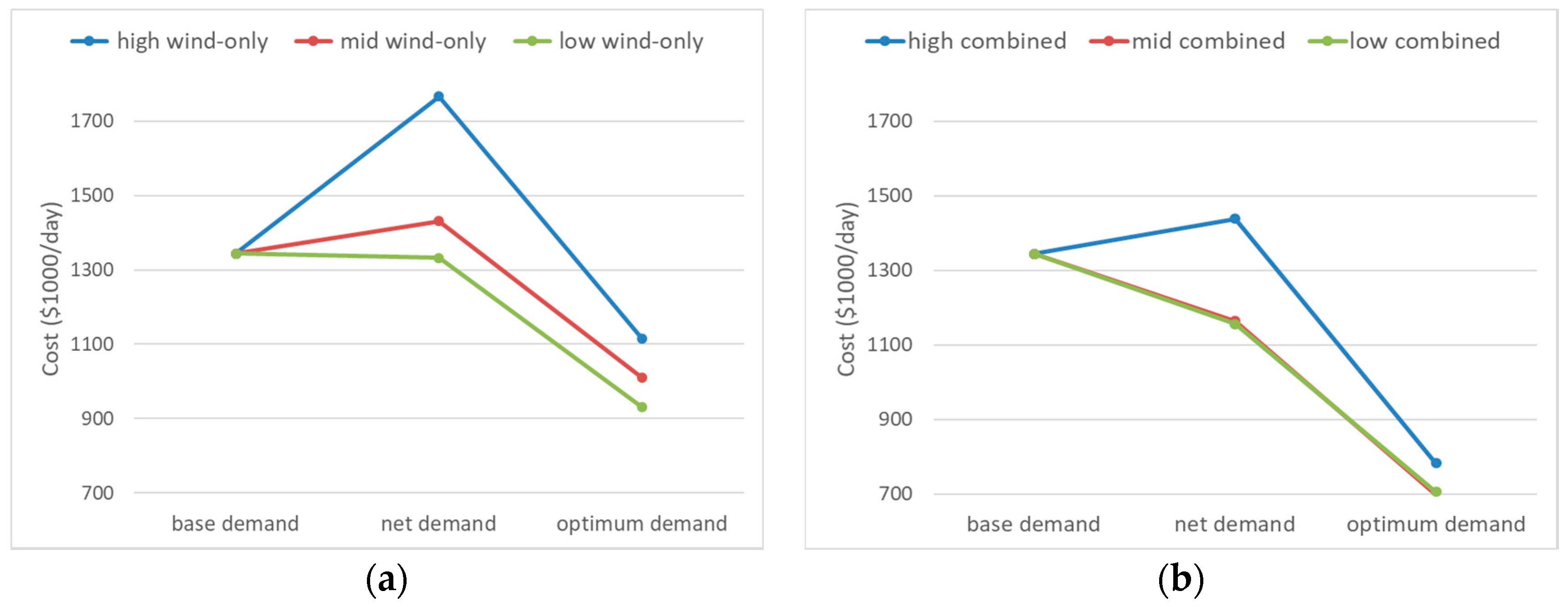
The advantages of the combined scenario over the wind-only scenario are demonstrated in
Figure 7. In the wind-only scenario, the reserve costs of meeting net demand are significantly higher in the high-wind-only scenario, which is due to the variability of wind power, than when wind is combined with solar generation (
Figure 7b).
Figure 7b shows that a balanced installation of wind and solar power capacities in the electricity sector will benefit the operation of the power system, as it faces less variability.
3.2. Optimization with Energy Cost Alone vs. Co-Optimization with Energy and Reserve Cost
This section analyzes changes in the operation costs of the power system in scenarios when the aim of energy storage is to reduce energy costs, and when the aim is to reduce both energy and reserve costs. The value of energy storage is typically evaluated by energy cost savings from moving expensive peak demand to off-peak hours. This is not because using storage for reliability issue is less beneficial, but rather because the current rate structure under real-time pricing can compensate for price arbitrage, but not for variability mitigation. However, from the system operator’s perspective, it would be more efficient to use storage to minimize operating costs as well as energy costs. Hence, in this section, in addition to the original model for minimizing operating costs, we provide the optimization result from minimizing energy costs alone, which is what demand-side storage companies do, and compare how the efficiency of the power system varies under two different optimization schemes.
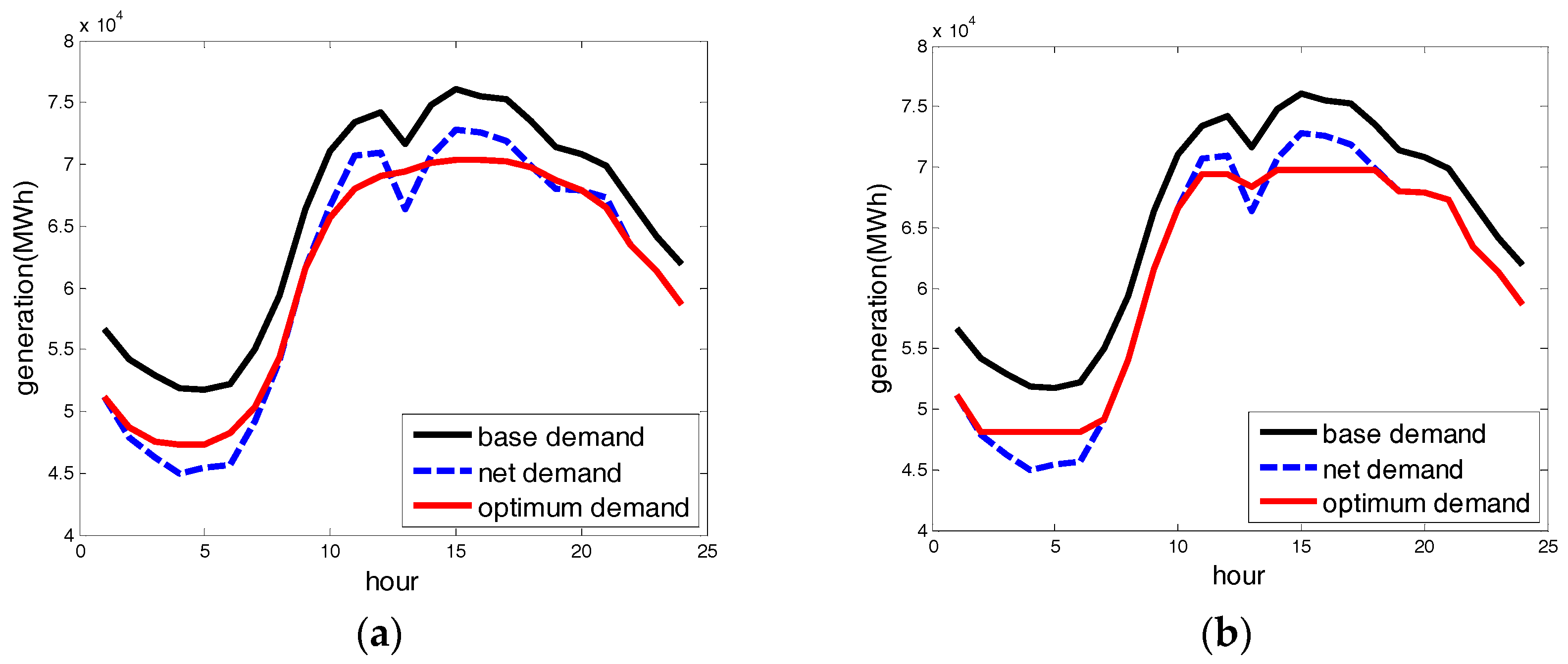
Figure 8 shows the difference between optimum demand when it is co-optimized with both energy and reserve costs, and optimum demand when it is only optimized with energy costs in the high wind-only scenario. As noted in Equation (1-1), the system operator minimizes operating costs, which are the sum of energy and reserve costs. However, energy storage is often used solely for reducing energy costs by moving expensive peak demand to off-peak hours, and this price arbitrage benefit was the most valuable factor of energy storage.
Figure 8b shows the optimum demand under the optimization scheme that solely reduces energy costs. As expected, it moves as many demand peaks as possible to off-peak hours. Thus, optimum demand has several kinks that create additional costs to the system, while the optimum demand of
Figure 8a is smooth.
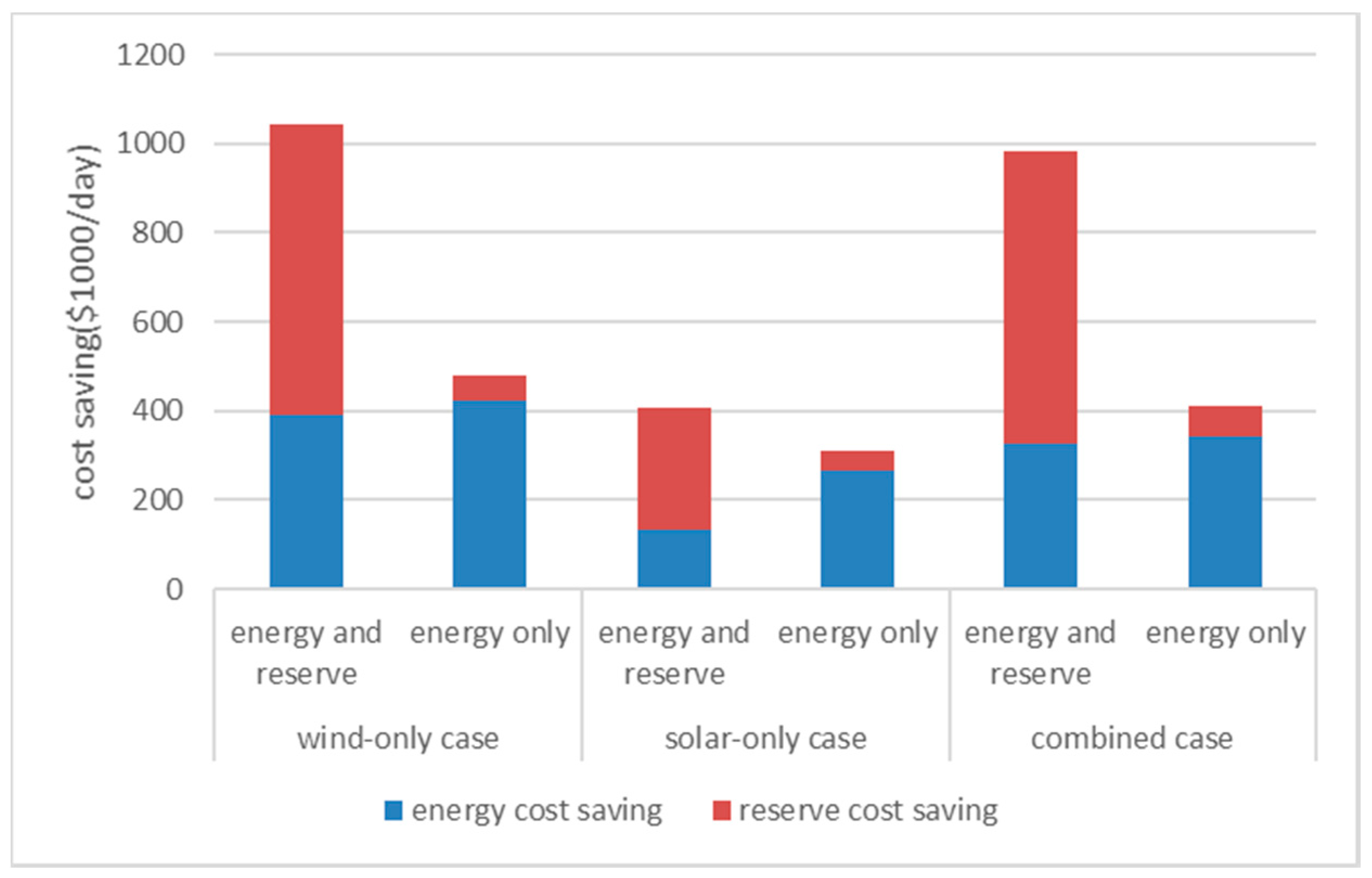
Figure 9 shows the amount of energy and reserve costs saved for each scenario when they are co-optimized for both energy and reserve costs, and optimized for energy costs alone. In all three scenarios, energy storage saves reserve costs by as much as or larger than energy costs alone when energy and reserve costs are co-optimized, whereas when energy costs are optimized alone, energy cost savings increase very marginally, and there is almost no saving of reserve costs. Energy cost savings increase very little, even when the system operator’s optimization focuses on reducing energy costs, because the benefit of arbitrage becomes saturated when more storage is used for this purpose, due to the reduction of the price difference between peak and off-peak periods. Another reason for this is storage charging/discharging inefficiency, which further reduces the price difference between peak and off-peak periods. For these reasons, allocating energy storage to reduce both energy and reserve costs is more economically viable.
3.3. Annual Cost Savings of Energy Storage
Table 9 shows the annual operating costs and peak demand for the base, net, and optimum demand of the three scenarios. To estimate annual costs, three representative days of each season were selected and the Piecewise Cubic Hermite Interpolating Polynomial (PCHIP) interpolation method was followed to estimate annual costs, with peak demand as the highest demand observed on the chosen representative days. The result shows that reserve costs are increased significantly for meeting the net demand of the wind-only scenario, while reserve and energy costs for meeting optimum demand are effectively reduced. In the combined scenario, the reserve cost of meeting net demand is lower than that of the wind-only scenario, indicating that the combined scenario faces less variability in net demand, as there is disparity between wind and solar power generation. Again, there are effective savings in both the reserve and energy costs of meeting optimum demand in the combined scenario.
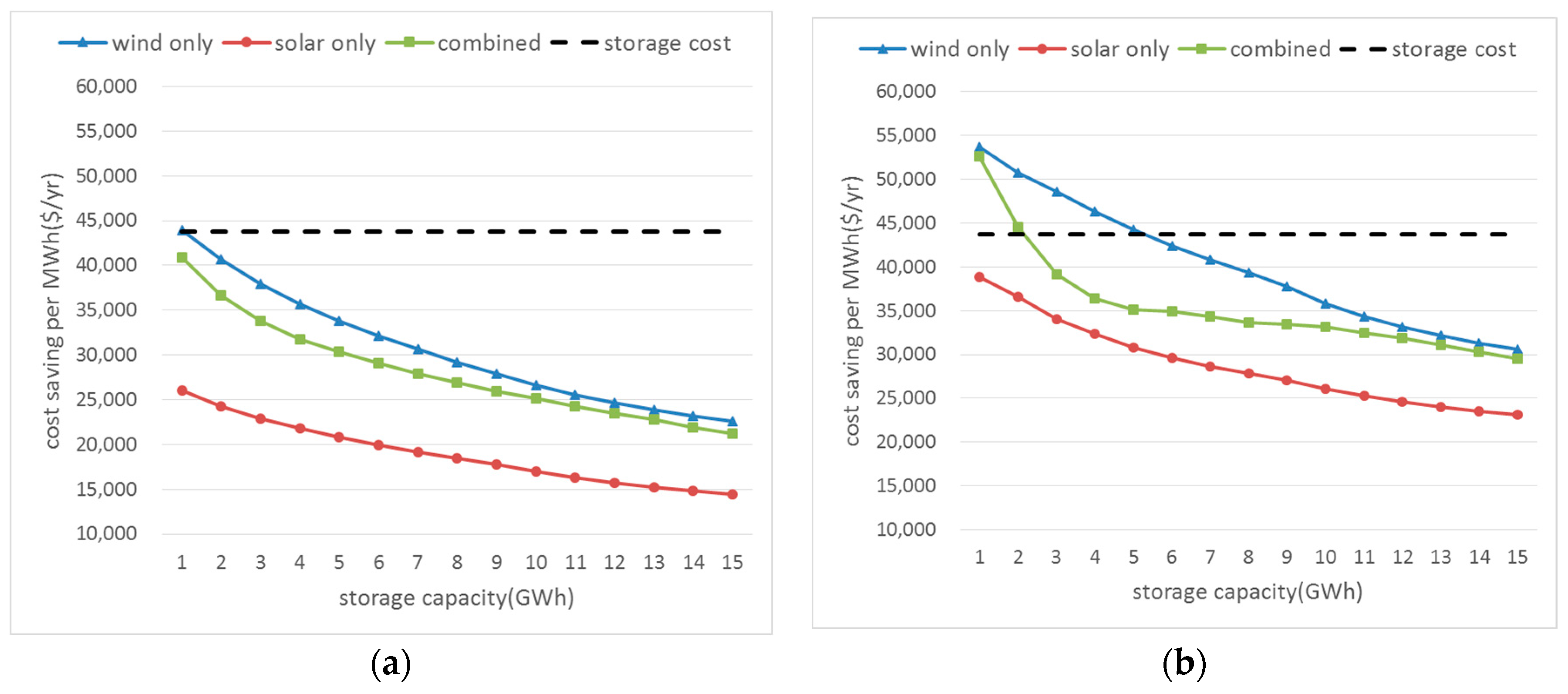
Figure 10 shows the annual costs saved per MWh of energy storage with varying storage capacities for the wind-only, solar-only, and combined scenarios and
Table 10 presents composition of annual system cost savings with varying storage capacities for the combined scenario.
Figure 10a shows cost savings when operating costs were considered alone. The annual costs saved per MWh of storage decrease as storage capacity increases, because when storage size increases, the effect of reducing energy and reserve costs per unit MWh becomes less significant. The black dashed line shows the annual capital cost of storage per MWh, which is
$43,750/MWh/year (based on the cost of a lithium battery cell:
$350/kWh, life cycle: 10 years, PCS (Power Control System) cost and degrading cost). The annual storage cost provides a reference level for evaluating the cost effectiveness of energy storage for grid operation.
As shown in
Figure 10, storage is most valuable for the wind-only scenario, followed by the combined scenario, and the solar-only scenario benefits very little from storage, as there is little variability that storage can mitigate for. As discussed above, wind power is highly variable and abundant during the night, which makes the price difference between day and night larger; therefore, it provides a better opportunity for arbitrage and a chance to reduce high reserve costs. With the current costs of storage, storage in the wind-only scenario just achieved economic viability, while in the other scenarios, the benefit is below the cost of storage.
Figure 10b shows the annual system cost savings per unit MWh of storage, which is the operating cost saving plus capacity cost saving. Capacity cost-saving was computed based on the contribution of storage to reducing peak demand, as reported in
Table 8. The annual capacity cost of a gas turbine plant,
$53,200/MW/year (EIA [
18]) was used when computing the capacity cost saving by storage through reducing peak demand. When capacity cost reduction by storage is considered, in addition to operating cost reduction, cost savings by storage exceed costs in the wind-only and combined cases. This means that energy storage is already economic viable when its contribution to grid operation is correctly evaluated, and properly compensated at the current storage cost levels.