Sustainability Analysis and Buy-Back Coordination in a Fashion Supply Chain with Price Competition and Demand Uncertainty

Abstract

Supply chain sustainability has become significantly important in the fashion industry, and more and more fashion brands have invested in developing sustainable supply chains. We note that dual channel system comprising a brand-owned direct channel and retail outsourcing channel is quite common in the fashion industry, and in the latter, buy-back contract is popular between brands and retailers. Therefore, we build a stylized dual channel model with price competition and demand uncertainty to characterize the main properties of a fashion supply chain. Our foci are the sustainability analysis and the channel coordination mechanism. We first design a buy-back contract with return cost to coordinate the channel. We then study supply chain sustainability and examine the effect of two key influencing factors, i.e., price competition and demand uncertainty. Interestingly, we find that a fiercer price competition will lead to a more sustainable supply chain. From the perspective of supply chain managers, we conclude that (1) if managers care about environmental sustainability, fierce price competition is not a suggested strategy; (2) if managers care about economic sustainability, fierce price competition is an advantageous strategy. We also find that high demand uncertainty results in a less sustainable supply chain, in both an environmental and economic sustainability sense.

1. Introduction

In the fashion industry, sustainability has received more and more attention and become a crucial competing factor in the recent years [1,2]. Fashion companies, including manufactures and retailers, are increasingly developing eco-fashion to promote sustainable supply chain [3,4,5]. According to Shen [1], some apparel firms suffer reputation loss due to their unsustainable supply chains, such as Benetton, Adidas, and C&A. Therefore, more and more apparel firms have realized the importance of sustainability and incorporated sustainable practice into their supply chain to project a positive brand image. Typical examples include Nike, H&M, UNIQLO, and New Balance [6]. For instance, H&M has applied some sustainable operations such as sustainable manufacturing and green retailing, and established a win-win-win strategy for the customers, H&M and environment. Fashion brands like Nike, GAP, and Levi’s expand investments to develop sustainable fashion collections. In addition, H&M and MUJI have launched organic collections and fair trade products. These industrial observations indicate that supply chain sustainability is of decisive importance in a fashion supply chain.

In practice, supply chain sustainability includes environmental sustainability, such as reducing goods leftovers, and economic sustainability, such as increasing return on investment. We focus on sustainable supply chain operations, in which less amount of left-over goods means efficient inventory management, transportation (environmental sustainability), and larger expected sales (economic sustainability). Choi and Chiu [7] and Shen and Li [8] adopt sustainability analysis including these two aspects. Therefore, product return is the main influence of sustainability. Intuitively, more product returns indicate a lower degree of supply chain sustainability. To help retailers and to sustain the fashion business, according to our observations, the buy-back contract has been widely adopted in fashion industry. For example, fashion stores such as Saks, Kohl’s, and J.C. Penny always receive a buy-back contract from fashion brands like Tommy Hilfiger, Ralph Lauren, and the Jones Apparel Group. This is because the retailers always hold large amount of unsold product (25%–40%) at the end of the selling season [8], which greatly hurts their enthusiasm and profits. A large amount of unsold products are also disadvantageous to the sustainability of fashion business. The buy-back policy can reduce the risk of retailers and increase the residual value of the unsold products, which is significant to the sustainability of a fashion supply chain. During the design process of a buy-back contract, a practical problem arises. That is, who should be responsible for the return cost, which may include logistics cost, repacking cost, etc.? This is an important and unavoidable problem in the contracting process.

Another important property in fashion industry is dual channel system. It is common for fashion brands (e.g., UNIQLO and H&M) to operate both a self-owned direct channel and a retail outsourcing channel, such as direct-sales stores and franchisees. In general, direct channel can increase control on pricing and branding more effectively, but always imply more operation costs and inventory pressure. In contrast, retail outsourcing channel can help avoid higher operation cost and inventory risk, while the control on pricing and branding is much weaker. In general, building a dual channel can effectively spread risk and provide differentiated service. However, price competition and channel conflict are the main problems in such a dual channel supply chain. Retailers often view the brand-owned direct channels as a competitive threat [9], and price competition may lead to a lower profitability, which is disadvantageous to both channels.

Based on the above business practice and properties in fashion industry, we build stylized game theoretic models to answer the following research questions:

(1)

How to design a buy-back contract with return cost to achieve supply chain coordination?

(2)

What are the effects of price competition and demand uncertainty on supply chain sustainability in each channel?

We consider a fashion brand that develops a self-owned direct channel and a retail outsourcing channel. These two channels compete in price and both face demand uncertainty. We model the horizontal price competition between brand-owned direct and retail outsourcing channels, and the vertical cooperation between the fashion brand and the retailer. We also design a buy-back contract with return cost to achieve supply chain coordination and eliminate channel conflicts. In each channel, we conduct a sustainability analysis, and investigate how price competition and demand uncertainty affect supply chain sustainability. Our main findings are summarized as follows.

First, we find that a buy-back contract with return cost can indeed coordinate the dual channel supply chain. In the retail outsourcing channel, the return price is decreasing in return cost when the fashion brand bears the return cost. In contrast, when the retailer bears the return cost, the return price is independent on return cost. To explain, we find that the fashion brand always has to bear the return cost in the self-owned channel. This makes the effect of the return cost on direct channel and retail channel remain the same when retailer bears the return cost. Moreover, we find that the fashion brand can quote a high wholesale price and a high return price if he bears the return cost when the price competition is fierce. Clearly, a high wholesale price can increase the retailer’s cost and retail price, and help the fashion brand to control the degree of price competition between the direct and retail outsourcing channels.

Second, we conduct a sustainability analysis, and investigate the effects of price competition and demand uncertainty on supply chain sustainability. Under price competition, we find that fiercer price competition between the brand-owned direct channel and retail outsourcing channel leads to a more sustainable supply chain. It is because fierce price competition increases the market demand, which is good for economic sustainability. From the perspective of supply chain managers, we find that if supply chain managers care more about environmental sustainability, fierce price competition is not a suggested strategy. However, if supply chain managers care more about economic sustainability, fierce price competition is an advantageous strategy. If supply chain managers care about both environmental and economic sustainability, we still suggest fierce price competition. This is essentially because fierce price competition brings an increasing demand in quantity. The utility gains from economic sustainability dominate that from environmental sustainability.

We then investigate the effect of demand uncertainty on supply chain sustainability. First, we find that the expected goods leftover at the end the selling season depends on the amount of safety stock held in each channel. We then use the standard deviation to measure the demand uncertainty, and find that large demand uncertainty leads to a lower supply chain sustainability. This is because a larger volatility of demand makes for more leftover goods at the end of the selling season, which finally leads to a less sustainable supply chain in both an environmental and economic sustainability sense.

The remainder of this paper is organized as follows: We briefly review the most related literature in Section 2. The model settings including game structure and optimal decisions are provided in Section 3. In Section 4, we design a buy-back contract scheme with a return cost to coordinate the dual channel system. A sustainability analysis is conducted in Section 5. The conclusion and future research directions are presented in Section 6.

2. Literature Review

Our work is related to the study of supply chain sustainability analysis. Shen et al. [6] studied the perception of fashion sustainability in online community. They categorized the main concerns of sustainable fashion into four aspects, those are: sustainable production and remanufacturing, green marketing, green information sharing, and green attitude and education. In supply chain management, supply chain sustainability is related to the environmental friendship and economic sustainability. Most of the literature focuses on environmental sustainability, such as Culaba and Purvis [10], Dou and Sarkisb [11], Hua et al. [12], and Shen [1]. There is little literature studying supply chain sustainability including environmental sustainability and economic sustainability. Choi and Chiu [7] propose three factors to measure supply chain sustainability, which is the expected amount of goods leftover (representing environmental sustainability), the rate of return on investment (representing economic sustainability), and the expected sales compared to the expected amount leftover (representing both environmental and economic sustainability). There are lots of studies which use these factors to analyze supply chain sustainability. Our work contributes to this line of literature, and the most related paper is Shen and Li [8], which studied the sustainability in a retail outsourcing fashion supply chain with returning unsold products. In particular, they studied the impact of the return cost on a sustainability level in a retail outsourcing channel. They also compared the wholesale price contract and return policy contract, and concluded that the wholesale price contract is more sustainable than the coordinating return policy contract. However, the main differences of our work exist in (1) we study a dual channel model with brand-owned direct channel and retail outsourcing channel, and there is a price competition between these two channels; (2) the retail price in our model is endogenous, while it is assumed exogenous in Shen and Li [8] a setting which makes the game structure totally different; and (3) the market demand is considered uncertain in our paper. We also study the impact of demand uncertainty on supply chain sustainability.

Our work is also related to the studies on competition between direct channel and retail outsourcing channel in a dual channel system. A comprehensive review of competition between the direct channel and retail channel can be found in Ryan et al. [13]. Most of the studies focus on competition on inventory [14,15], price [16,17], both inventory and price [18,19], and joint price and lead time [20]. There are other related studies considering the impact of sales effort [9], impact of search costs [21], etc. In a recent work, Dong et al. [22] studied sustainability investment under cap-and-trade regulation. Differently, we design a different contract scheme, a buy-back contract with return cost, to coordinate the supply chain. We conduct a sustainability analysis to analyze the influence of price competition and demand uncertainty on supply chain sustainability.

The third related stream of literature is on supply chain coordination and buy-back contracts. Supply chain coordination is influenced by the channel structure. Most of the studies focus on a one-supplier-one-retailer structure, in which there are lot of contracts that can coordinate the supply chain, such as buy-back, revenue sharing, quantity discount, etc. [23]. In this paper, we design a buy-back contract with return cost to coordinate the dual channel system. The buy-back contract has been extensively investigated in the literature on supply chain coordination [24,25], especially the fashion supply chain [26,27]. Choi [26] studies optimal return service-charging policy for a fashion mass customization program, and finds that fashion firms offer free return service to registered members, which is similar to our findings in Proposition 4. Li et al. [27] conduct a mean-variance analysis of a fast fashion supply chain with returns policy. They find that returns policy can coordinate the fast fashion supply chain, even in the presence of multiple retailers. However, buy-back contracts with return costs have received less attention. Tsay [28] studied buy-back contracts with a markdown money policy and found that the return cost cannot be ignored in the buy-back contract. Shen and Li [8] argue that the logistics cost should be considered in the fashion supply chain, because it is not unbearable for the retailer. They compare the scenario where the manufacturer bears the return cost and the scenario where retailer bears return cost, and analyze the impact of return cost. Similar to Shen and Li [8], we consider the scenario where a fashion brand bears the return cost and the scenario where the retailer bears the return cost. We further investigate the impact of price competition on this dual channel system, and analyze the impact of return cost from the perspective of strategic price competition.

3. Model Formulation

3.1. Notation and Game Structure

We consider a dual channel model, which includes a brand-owned direct channel and a retail outsourcing channel. There is price competition between these two channels. We focus on channel coordination and sustainability analysis under price competition and demand uncertainty. The following notations are for easy reference.

Parameters: ($\mathit{i}\mathit{ϵ}\left\{\mathit{D},\mathit{R}\right\}$)

• $a$: Market potential (maximum attainable without cross-effects).
• $b$: Cross-price sensitivity on demand.
• $q_i$: Demand in channel $i$.
• ${ϵ}_i$: Random demand in channel $i$.
• $w$: Wholesale price in retail channel.
• $c_M$: Production cost of fashion brand.
• $v$: Unit salvage value at the end of the selling season.
• $f_i(·),F_i(·),{\mu }_i,{\sigma }_i$: Probability density function, cumulative distribution function, mean, and standard deviation of random variable ${ϵ}_i$.
• $X_i,Y_i$: Lower bound and upper bound of ${ϵ}_i$.
• $m$: Return price from the retailer.
• $n$: Return cost (including logistics cost, repacking cost, etc.).

Decision variables:

• $p_i$: Selling price in channel $i$.
• $Q_i$: Order quantity in channel $i$.
• ${\tau }_i$: Safety stock in channel $i$.

Following Petruzzi and Dada [29], Ryan et al. [13], in each channel, demand is linearly dependent on its channel price, cross price parameter, and a random demand factor. Thus, the demand in channel $i$ ($i\in \left\{D,R\right\}$, where $D$ represents a brand-owned direct channel, and $R$ represents a retail outsourcing channel) can be expressed as

$$q_D=a-p_D+b{p}_R+{ϵ}_D,$$

(1)

$$q_R=a-p_R+b{p}_D+{ϵ}_R$$

(2)

$b$ is in range in (0,1] and used to measure the intensity degree of channel competition [30]; ${ϵ}_i$ is a random factor in range $\left[X_i,Y_i\right]$ with probability density function $f_i(·)$, cumulative distribution function $F_i(·)$, mean ${\mu }_i$, and deviation ${\sigma }_i$.

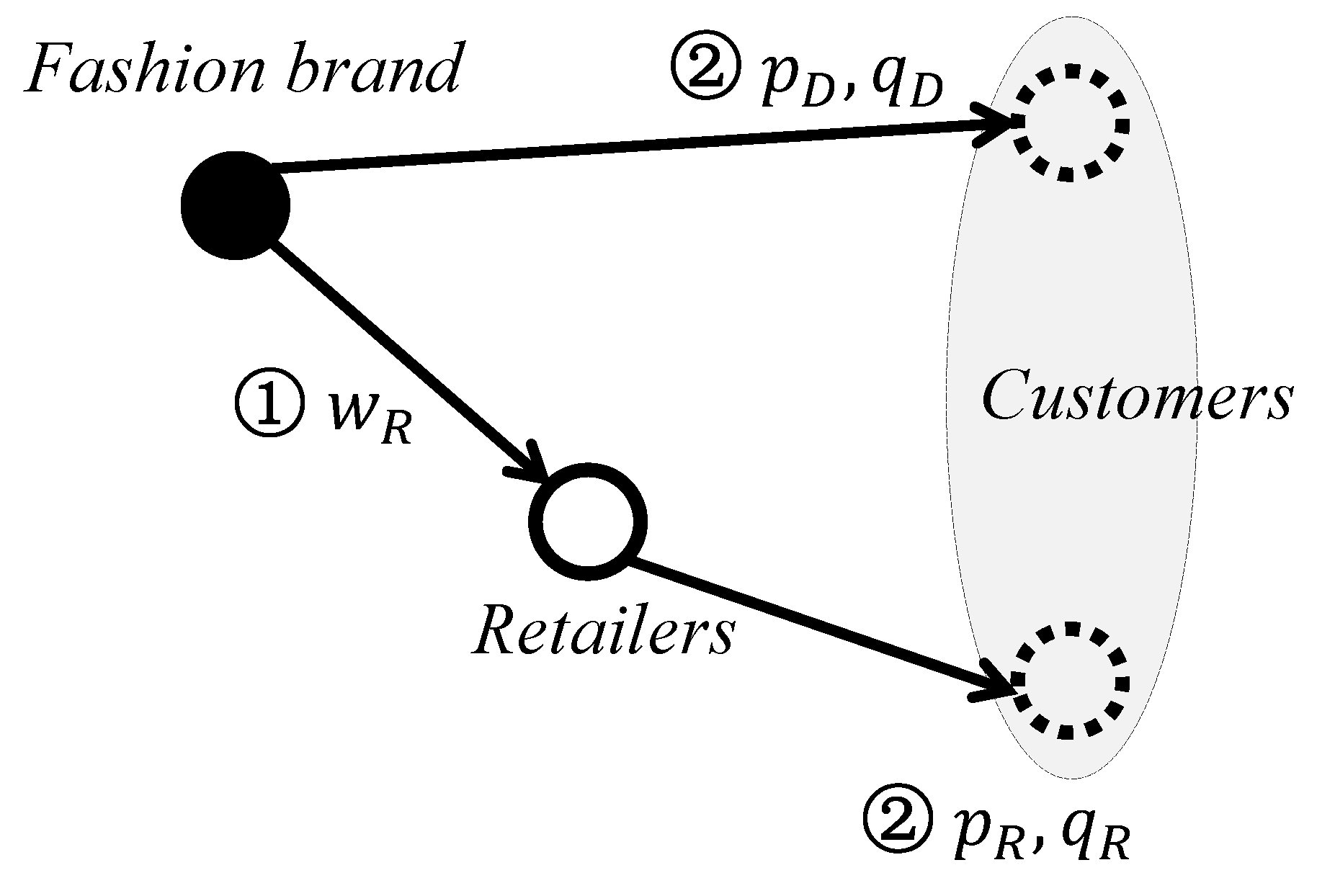
According to Figure 1, the events sequence is illustrated as follows: in the first stage, the fashion brand anticipates the retailer’s price $p_R$ and the direct channel’s price $p_D$, determines the optimal wholesale price $w_R$ to maximize its profits gained from both self-owned channel and retail outsourcing channel:

$$\begin{array}{c}{\Pi }_M={\Pi }_{MR}+{\Pi }_{MD}=\left(w-c_M\right)\left(a-p_R+b{p}_D+{ϵ}_R\right)\\ +\left(p_D-c_M\right)\left(a-p_D+b{p}_R+{ϵ}_D\right)-\left(p_D-v\right){{\displaystyle \int }}_{X_D}^{{\tau }_D}\left({\tau }_D-{ϵ}_D\right)f_D\left({ϵ}_D\right)d{ϵ}_D.\end{array}$$

(3)

In the second stage, the retailer determines the optimal retail price, $p_R$, to maximize its own profits:

$${\Pi }_R=\left(p_R-w\right)\left(a-p_R+b{p}_D+{ϵ}_R\right)-\left(p_R-v\right){\int }_{X_R}^{{\tau }_R}\left({\tau }_R-{ϵ}_R\right)f_R\left({ϵ}_R\right)d{ϵ}_R.$$

(4)

At the same time, the fashion brand determines the optimal direct selling price to maximize its profits gained in the self-owned direct channel:

$${\Pi }_{MD}=\left(p_D-c_M\right)\left(a-p_D+b{p}_R+{ϵ}_D\right)-\left(p_D-v\right){\int }_{X_D}^{{\tau }_D}\left({\tau }_D-{ϵ}_D\right)f_D\left({ϵ}_D\right)d{ϵ}_D.$$

(5)

Assuming the order quantity and safety stock in channel $i$ are $Q_i$ and ${\tau }_i$, for model simplified, the order quantity in each channel can be formulated as:

$$Q_D=a-p_D+b{p}_R+{\tau }_D,$$

(6)

$$Q_R=a-p_R+b{p}_D+{\tau }_R.$$

(7)

Therefore, according to the reformulated demand model, the fashion brand decides $p_D$ and ${\tau }_D$, and simultaneously, the retailer decides $p_R$ and ${\tau }_R$ to maximize their expected profit. Following that, we solve the game and derive the optimal decisions.

3.2. Optimal Decisions

For the fashion brand, the expected profit is from both direct channel and retail outsourcing channels. Hence, we derive the expected profit for the fashion brand as:

$${\Pi }_M=E\left(p_D\min \left(q_D,Q_D\right)+v\max \left(\left(Q_D-q_D\right),0\right)-c_M\left(Q_R+Q_D\right)+w{Q}_R\right).$$

(8)

According to Petruzzi and Dada [29] and Ryan et al. [13], given $p_R$ and ${\tau }_R$, the optimal direct retail price is a function of $p_R$ and ${\tau }_D$, see Lemma 1.

Lemma 1.

For a given $w$, the optimal direct retail price is determined uniquely as a function of $p_R$ and ${\tau }_D$, and can be written as

$$p_D^{\ast }=p_D^0\left(p_R\right)-\frac{U_D\left({\tau }_D\right)}{2},$$

(9)

where $U_D\left({\tau }_D\right)={\int }_{{\tau }_D}^{Y_D}\left({ϵ}_D-{\tau }_D\right)d{F}_D\left({ϵ}_D\right)$, and $p_D^0\left(p_R\right)=\frac{a+c_M+b\left(p_R+w-c_M\right)+{\mu }_D}{2}$ is the optimal price without demand uncertainty.

We substitute the optimal price $p_D^{\ast }$ in to the profit function, and then characterize the conditions where there exists a unique solution to the first-order-condition (FOC) for ${\tau }_D$. The FOC for ${\tau }_D$ is

$$\frac{\partial {\Pi }_M}{\partial {\tau }_D}=-\left(c_M-v\right)+\left(p_D^0\left(p_R\right)-v-\frac{U_D\left({\tau }_D\right)}{2}\right)\ast \left(1-F_D\left({\tau }_D\right)\right)=0.$$

(10)

If $2{\left(\frac{f_D\left({\tau }_D\right)}{1-F_D\left({\tau }_D\right)}\right)}^2+\frac{d(\frac{f_D\left({\tau }_D\right)}{1-F_D\left({\tau }_D\right)})}{d{\tau }_D}>0$, and $1+b{p}_D-w+X_R>0$, the solution for the FOC is unique. Let ${\tau }_D^{\ast }\left(p_R\right)$ denote the solution of ${\tau }_D$ in the FOC function, then the optimal order quantity in the direct channel can be characterized as $Q_D^{\ast }=a-p_D^{\ast }\left(p_R\right)+b{p}_R+{\tau }_D^{\ast }\left(p_R\right)$.

For the retailer, the expected profit is specified as

$${\Pi }_R=E\left(p_R\min \left(q_R,Q_R\right)+v\max \left(\left(Q_R-q_R\right),0\right)-w{Q}_R\right).$$

(11)

Therefore, given $p_D$ and ${\tau }_R$, the optimal retail price in the outsourcing channel is

$$p_R^{\ast }=p_R^0\left(p_D\right)-\frac{U_R\left({\tau }_R\right)}{2}$$

(12)

where $U_R\left({\sigma }_R\right)={\int }_{{\tau }_R}^{Y_R}\left({ϵ}_R-{\tau }_R\right)d{F}_R\left({ϵ}_R\right)$, and $p_R^0\left(p_D\right)=\frac{a+w+b{p}_D+{\mu }_R}{2}.$ After arithmetic manipulation, we derive the conditions and FOC functions, which are analogous to the fashion brand’s decision. Similarly, let ${\tau }_R^{\ast }\left(p_D\right)$ denote the solution of ${\tau }_R$ in the FOC function for the retailer, then the optimal order quantity in the retail channel can be characterized as $Q_R^{\ast }=a-p_R^{\ast }\left(p_D\right)+b{p}_D+{\tau }_R^{\ast }\left(p_D\right)$.

Ryan et al. [13] have proven that, for a given wholesale price ($w_R$) and under certain general conditions, a unique Nash equilibrium exists. They also exhibit that the equilibrium wholesale price can be characterized by ($p_D^{\ast },p_R^{\ast },{\tau }_D^{\ast },{\tau }_R^{\ast }$). Here, we focus on the supply chain coordination under buy-back contract with return cost and supply chain sustainability analysis, which do not require a specific form of solutions.

4. Supply Chain Coordination under a Buy-Back Contract

In this section, we consider a buy-back contract to achieve channel coordination, because buy-back contracts are popular in the fashion industry and extensively used to coordinate the fashion supply chain [26,27]. Specially, we consider a buy-back contract with return cost (repacking, logistics, etc.) [8,28]. In the brand-owned direct channel, the fashion brand has to bear this return cost, while in the retail outsourcing channel, this return cost can be borne by either the fashion brand or the retailer. Thus, there are two scenarios: (i) the fashion brand bears the return cost (scenario M); and (ii) the retailer bears the return cost (scenario R). We now investigate a contract that will enable supply chain coordination. We consider return cost $n$ and a return price $m$. Therefore, by assuming that $p_R>w>max\left(m,c_M\right)>min\left(m,c_M\right)>v$ in the retail outsourcing channel, the expected profits of fashion brand and the retailer in each scenario are characterized as follows:

A Fashion brand bears return cost in retail outsourcing channel

In this scenario, the expected profit of the fashion brand is

$$\begin{array}{c}{\Pi }_M=\left(p_D-c_M\right)\left(a-p_D+b{p}_R+{\tau }_D\right)-\left(p_D-v+n\right){{\displaystyle \int }}_{X_D}^{{\tau }_D}\left({\tau }_D-{ϵ}_D\right)f_D\left({ϵ}_D\right)d{ϵ}_D\\ +\left(w_R-c_M\right)\left(a-p_R+b{p}_D+{\tau }_R\right)-\left(m-v+n\right){\int }_{X_R}^{{\tau }_R}\left({\tau }_R-{ϵ}_R\right)f_R\left({ϵ}_R\right)d{ϵ}_R.\end{array}$$

(13)

Similarly, the expected profit of the retailer is

$${\Pi }_R=\left(p_R-w\right)\left(a-p_R+b{p}_D+{\tau }_R\right)-\left(p_R-m\right){\int }_{X_R}^{{\tau }_R}\left({\tau }_R-{ϵ}_R\right)f_R\left({ϵ}_R\right)d{ϵ}_R.$$

(14)

Thus, the expected profit of the dual channel system is

$${\Pi }_S\left(p_D,{\tau }_D,p_R,{\tau }_R\right)={\Pi }_M\left(p_D,{\tau }_D\right)+{\Pi }_R\left(p_R,{\tau }_R\right).$$

(15)

Comparing the first order conditions for ${ϵ}_D$ and ${ϵ}_R$ with those in the dual channel system, we have Proposition 1.

Proposition 1.

When $w^M=c_M+\frac{\left(m^M-v+n\right){\displaystyle {\int }_{X_R}^{{\tau }_R}{F}_R\left({\mathsf{\tau }}_R\right)}}{{\mathsf{\tau }}_R}$ a buy-back contract coordinates the dual-channel system. Then the return price is $m^M=\frac{\left(w^M-c_M\right){\tau }_R}{{\int }_{X_R}^{{\tau }_R}{F}_R\left({\tau }_R\right)}+v-n$.

Thus, a buy-back contract under which the fashion brand bears the return cost in the retail outsourcing channel can always coordinate the dual channel supply chain. We find that, under such a buy-back contract, the return price is increasing in the unit salvage value while decreasing in the return cost. Intuitively, a higher unit salvage value implies a higher return price, no matter who bears the return cost (see Proposition 2). When the fashion brand bears the return cost, they quote a lower return price to protect the profitability given a high return cost. To further develop the buy-back contract, we next investigate the scenario where the retailer bears the return cost.

B Retailer bears return cost in retail outsourcing channel

In this scenario, the retailer bears return cost in the retail outsourcing channel, and the fashion brand bears the return cost in self-owned direct channel. The expected profit of the fashion brand is

$$\begin{array}{c}{\Pi }_M=\left(p_D-c_M\right)\left(a-p_D+b{p}_R+{\tau }_D\right)-\left(p_D-v+n\right){{\displaystyle \int }}_{X_D}^{{\tau }_D}\left({\tau }_D-{ϵ}_D\right)f_D\left({ϵ}_D\right)d{ϵ}_D\\ +\left(w-c_M\right)\left(a-p_R+b{p}_D+{\tau }_R\right)-\left(m-v\right){\int }_{X_R}^{{\tau }_R}\left({\tau }_R-{ϵ}_R\right)f_R\left({ϵ}_R\right)d{ϵ}_R.\end{array}$$

(16)

Similarly, the expected profit of the retailer is

$${\Pi }_R=\left(p_R-w\right)\left(a-p_R+b{p}_D+{\tau }_R\right)-\left(p_R-m+n\right){\int }_{X_R}^{{\tau }_R}\left({\tau }_R-{ϵ}_R\right)f_R\left({ϵ}_R\right)d{ϵ}_R.$$

(17)

Comparing the first order conditions for ${ϵ}_D$ and ${ϵ}_R$ with those in the dual channel system, we derive Proposition 2.

Proposition 2.

When $w^R=c_M+\frac{\left(m^R-v\right){\int }_{X_R}^{{\tau }_R}{F}_R\left({\tau }_R\right)}{{\tau }_R}$, a buy-back contract coordinates the dual-channel system. Then the return price is $m^R=\frac{\left(w^R-c_M\right){\tau }_R}{{\int }_{X_R}^{{\tau }_R}{F}_R\left({\tau }_R\right)}+v$.

Similar to Proposition 1, Proposition 2 indicates that a buy-back contract with the retailer bearing the return cost in the retail outsourcing channel can coordinate the dual channel supply chain. Differently, when the retailer bears the return cost, the return price is independent of the return cost. This is contrary to conventional wisdom, in which a fashion brand may quote a higher return price when the retailer-borne return cost increases. To explain, we find that in this dual channel system, the fashion brand always bears the return cost in the brand-owned direct channel, and the effects of a higher return cost on the fashion brand and the retailer are the same to that when the retailer bears the cost. Therefore, the quoted return price of the fashion brand remains constant when the retailer-born return cost changes. We compare Proposition 1 and 2 and derive the following Proposition 3.

Proposition 3.

Given $w^M$ and $w^R$, $m^M$ is decreasing in $n$, while $m^R$ is independent on $n$. If $w^R\ge w^M$, then $m^R>m^M$ always holds.

Proposition 3 first summarizes different characters of the buy-back contract between fashion brand and retailer bears return cost. Proposition 3 also states that in the retail outsourcing channel, when the quoted wholesale price given the retailer bearing the return cost is higher than that given the fashion brand bearing the return cost, the return price at the end of selling season will synchronously be higher. In general, a higher wholesale price always implies a higher salvage value, which makes the fashion brand quote a higher return price (see Propositions 1 and 2). Therefore, when there is a higher salvage value with the retailer bearing the return cost ($w^R\ge w^M$), the return price will also be higher. In addition, we know that $m^R$ is independent on the return cost while $m^M$ is decreasing in the return cost. From Propositions 1 and 2, the fashion brand bearing return cost leads to a lower return price.

Proposition 4.

Given ${\tau }_R$, when $w^M-w^R>\frac{n{\int }_{X_R}^{{\tau }_R}{F}_R\left({\tau }_R\right)}{{\tau }_R}$, we have $m^M>m^R$, which indicates the fashion brand may bear the return cost, but quote a higher return price.

Proposition 4 reveals an interesting phenomenon, that is, the fashion brand may bear the return cost but quote a high return price. This finding is similar to Choi [26], which indicates that fashion firms may offer free return service to their registered members. In our model setting, this happens when the fashion brand quotes a sufficiently higher wholesale price in scenario M than that in scenario R. For the fashion brand, which strategy is better? Bearing the return cost and a higher return price but with a higher wholesale price, or, leaving the return cost but quoting a lower return price and wholesale price? It depends on the price competition intensity. For the former, when the competition between the direct channel and the retail outsourcing channel is intensified, a higher wholesale price can put more pressure on the retailer and bring a greater price advantage for the direct channel. The profits of the fashion brand are from both direct channel and retail sourcing channel. Therefore, when the price competition between the brand-owned channel and the retail outsourcing channel is intensified, quoting a higher wholesale price can increase the retailer’s cost, which prevents the retailer from determining a low retail price $p_R$ and hence, prevents a bleeding price war. This induces the fashion brand to be willing to quote a higher return price and bear the return cost to establish a good cooperative relationship with the retailer.

5. Sustainability Analysis

In this section, we analyze the sustainability of this dual channel system, where price competition and demand uncertainty are the critical influencing factors. Choi and Chiu [7] propose three indicators to examine supply chain sustainability performance. They are expected quantity of goods leftover $L\left(Q\right)$, the ratio of expected sales to expected quantity of goods leftover $SLR\left(Q\right)$, and expected rate of return on investment $R\left(Q\right)$. We use these indicators to investigate the impact of price competition and demand uncertainty on supply chain sustainability. The indicators in each channel are specified as follows:

A. Brand-owned direct channel

$$L_D\left(Q_D\right)=\max \left(\left(Q_D-q_D\right),0\right)={{\displaystyle \int }}_{X_D}^{{\tau }_D}\left({\tau }_D-{ϵ}_D\right)f_D\left({ϵ}_D\right)d{ϵ}_D,$$

(18)

$$SL{R}_D\left(Q_D\right)=\frac{Q_D}{L_D\left(Q_D\right)}-1,$$

(19)

$$R_D\left(Q_D\right)=\frac{{\Pi }_{MD}}{c_M{Q}_D}.$$

(20)

B. Retail outsourcing channel

$$L_R\left(Q_R\right)=\max \left(\left(Q_R-q_R\right),0\right)={{\displaystyle \int }}_{X_R}^{{\tau }_R}\left({\tau }_R-{ϵ}_R\right)f_R\left({ϵ}_R\right)d{ϵ}_R,$$

(21)

$$SL{R}_R\left(Q_R\right)=\frac{Q_R}{L_R\left(Q_R\right)}-1,$$

(22)

$$R_R\left(Q_R\right)=\frac{{\Pi }_{MR}+{\Pi }_R}{c_M{Q}_R}.$$

(23)

5.1. Effect of Price Competition on Supply Chain Sustainability

Proposition 5.

Given $p_D, p_R$, fierce price competition (higher $b$) leads to a higher $SL{R}_D\left(Q_D\right), and SL{R}_R\left(Q_R\right)$ and a higher $R_D\left(Q_D\right) and R_R\left(Q_R\right)$, while $L_D\left(Q_D\right) and L_R\left(Q_R\right)$ remains constant.

From Proposition 5, we reveal that the goods leftover at the end of the selling season is independent on the intensified degree of price competition. From the demand model, we know that fierce price competition increases the market demand. However, supply chain parties increase their stock to fit this volatility. Hence, the goods leftover at the end of selling season remain unchanged. This indicates that the environmental sustainability is independent of channel price competition.

Proposition 5 also indicates that fiercer price competition leads to a higher ratio of expected sales to expected quantity of goods leftover ($SLR\left(Q\right)$) and a higher expected rate of return on investment ($R\left(Q\right)$). To explain, we find that fiercer price competition increases the demand quantity, which makes the ratio of expected sales to expected quantity of goods leftover increase. Similarly, the increase of demand quantity increases the expected rate of return on investment at the end of the selling season. This indicates a better economic performance of the supply chain. Because a lower $L\left(Q\right)$, a higher $SLR\left(Q\right)$, or a higher $R\left(Q\right)$ is more desirable in the supply chain for both environmental and economic sustainability [8], we find that fiercer price competition is more sustainable than weaker price competition.

However, if supply chain managers care more about environmental sustainability, price competition is not a suggested strategy, because the amount of goods leftover ($L\left(Q\right)$) is independent with the intensified degree of price competition, and fierce price competition leads to a lower profitability. If supply chain managers care more about economic sustainability, fiercer price competition is a beneficial strategy, because it results in a higher expected rate of return on investment ($R\left(Q\right))$. Moreover, if supply chain managers care about both environmental and economic sustainability, fierce price competition is also a beneficial strategy because it can result in a higher ratio of expected sales to expected quantity of good leftover ($SLR\left(Q\right)$). This is essentially because fiercer price competition leads to a better economic sustainability, though the environmental sustainability is constant. Therefore, these findings help the supply chain managers conduct sustainability analysis and make decisions in supply chain management.

5.2. Effect of Demand Uncertainty on Sustainability

Proposition 6.

Assuming ${ϵ}_D={ϵ}_R=ϵ$, if ${\tau }_D^{\ast }>{\tau }_R^{\ast }$, $L_D\left(Q_D\right)>L_R\left(Q_R\right)$; if ${\tau }_D^{\ast }\le {\tau }_R^{\ast }$, $L_D\left(Q_D\right)\le L_R\left(Q_R\right)$. $L_i\left(Q_i\right)$ is increasing in ${\tau }_i$, $i\in \left\{D,R\right\}$.

We assume that the brand-owned direct channel and retail outsourcing channel face the same market uncertainty. According to Proposition 6, we find that the expected of goods leftover at the end of the selling season depends on the amount of safety stock held in each channel. Intuitively, when facing a similar market demand uncertainty, a larger amount of stock always implies a larger amount of goods leftover at the end of selling season.

Aiming to investigate the effect of demand uncertainty, we then consider two markets (Market 1 and Market 2) with different market uncertainty, which is represented as variables ${ϵ}_1$ and ${ϵ}_2$, with standard deviation ${\sigma }_1$ and ${\sigma }_2$ (${\sigma }_1>{\sigma }_2$). By analyzing the effect of demand uncertainty on supply chain sustainability, we derive Proposition 7.

Proposition 7.

Comparing these two markets with different demand uncertainty levels, we have $L_1\left(Q_1\right)>L_2\left(Q_2\right)$, $SL{R}_1\left(Q_1\right)< SL{R}_2\left(Q_2\right)$ and $R_1\left(Q_1\right)< R_2\left(Q_2\right)$.

Proposition 7 implies that a larger market demand uncertainty will lead to a larger goods leftover at the end of the selling season, while it leads to a smaller ratio of expected sales to expected quantity of goods leftover, and a smaller expected rate of return on investment. We have mentioned that a lower $L\left(Q\right)$, a higher $SLR\left(Q\right)$ or a higher $R\left(Q\right)$ is more desirable in supply chain about both environmental and economic sustainability. Hence, we conclude that a large demand uncertainty will leads to a lower supply chain sustainability. Intuitively, when facing a more uncertain market demand, the volatility of demand makes the goods leftover become large at the end of selling season. A higher $SLR\left(Q\right)$ and $R\left(Q\right)$ imply that the supply chain becomes less sustainable both in environmental and economic sustainability. Therefore, we know that a relatively stable market demand is of great value to supply chain sustainability.

6. Conclusions

Supply chain sustainability is an important property of the fashion industry, and more and more fashion brands have paid attention to supply chain sustainability. In the fashion industry, dual channel structure is another common practice. In this paper, we developed a dual channel model with price competition and demand uncertainty, and designed a buy-back contract with return costs to coordinate the dual channel system. We also conducted a sustainability analysis to analyze the environmental and economic sustainability of this dual channel system. The main findings are summarized as follows.

First, we demonstrate that a buy-back contract with cost of return (logistic cost, etc.) can coordinate the dual channel system. In the retail outsourcing channel, we find that the return price decreases the return cost when fashion brand bears the return cost. While, when retailer bears the return cost, the return price is independent of the return cost. This is because fashion brand always bear the return cost in the direct channel. Hence, when the retailer bears the return cost, the effect of return cost on the fashion brand and retailer remains the same.

From the perspective of a fashion brand, we show that, to quote a high wholesale price and high return price and to bear the return cost may be an advantageous strategy under intensified price competition. This is because a higher wholesale price can increase the cost of retailer and avoid bleeding price war, which helps the fashion brand to control the competition between the direct and retail outsourcing channels.

Second, we analyze the supply chain sustainability from the perspectives of environmental and economic sustainability, and examine the effect of price competition and demand uncertainty on supply chain sustainability. Under price competition, we find that fiercer price competition between the direct channel and retail outsourcing channel can result in a more sustainable supply chain than weaker price competition. Finally, from the perspective of supply chain managers, we find that if supply chain managers care about environmental sustainability, fierce price competition is not advantageous because it does nothing to the amount of goods leftover. If supply chain managers care about economic sustainability, or both environmental and economic sustainability, fierce price competition is an advantageous strategy. It is essentially because fierce price competition brings an increasing demand quantity.

By analyzing the effect of demand uncertainty, we derive that the expected leftover goods at the end of the selling season depend on the amount of safety stock held in each channel. Further, using standard deviation to measure the demand uncertainty, we find that larger demand uncertainty leads to a lower level of supply chain sustainability. This is because a large volatility of demand makes the goods leftover become large at the end of the selling season, which finally leads to a less sustainable supply chain in both an environmental and economic sustainability sense.

We suggest three directions of future research to conclude this paper. First, we design a buy-back contract with return cost to coordinate the dual channel system. In fact, there are other contracts in the fashion industry, although they are not as popular as buy-back contracts. Designing other contracts to coordinate the dual channel system is worthy of investigation. Second, in our buy-back contract, we assume the manufacturer or retailer bears the return cost. In practice, contracts might be reached via a long-term dynamic negotiation process. The supply chain parties’ relative bargaining powers will play a critical role in the returning process of unsold products under competition. Third, in this paper, we investigate price competition between the direct channel and the retail outsourcing channel. It would be interesting to consider two dimensions of competition, such as joint price and inventory competition, joint price and service competition, etc.