4.1. MACs in Industrial Level
The subdivision of industry enables us to understand the MACs in industrial level. The results are shown in
Figure 3 and the detailed calculation results are shown in
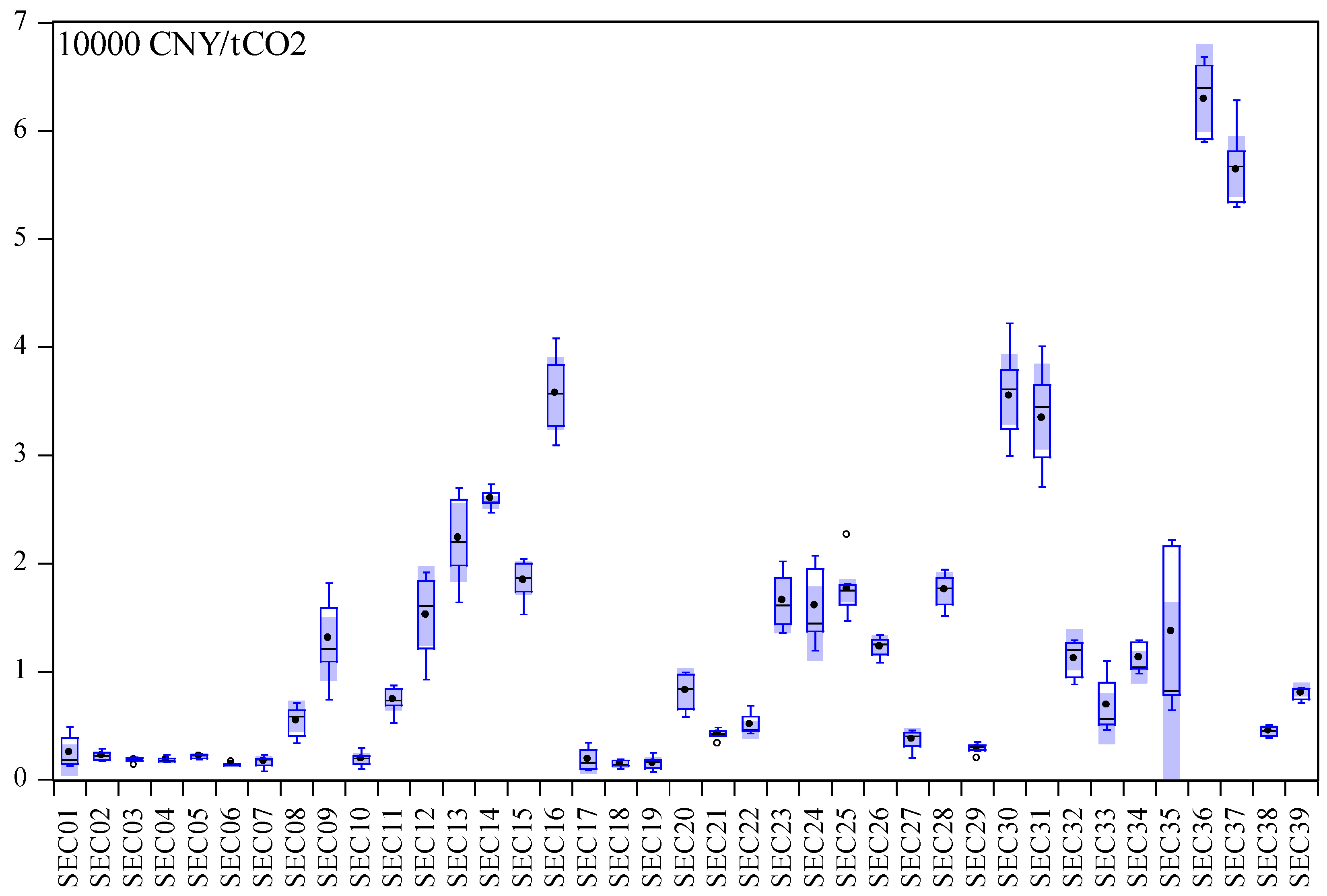
Appendix B. There are two situations that need to be tested. First, the results in boxplots demonstrated that MACs across industries may vary dramatically. For instance, the marginal abatement costs in some sectors are markedly lower than others and the gap between the lowest one and the highest one reached 60,000 CNY/ton CO
2. In order to find out the internal causes, the carbon intensity that is most closely related to both desirable and undesirable output is taken into consideration. Furthermore, we can see that MACs in the same industry fluctuate widely over time, such as Manufacture of electrical machinery and equipment (SEC 16), Printing, reproduction of recording media (SEC 30), Manufacture of articles for culture, education and sport activity (SEC 31), Manufacture of communication equipment, computers and other electronic equipment (SEC 36), and Manufacture of measuring instruments and machinery for cultural activity and office work (SEC 37), most of which manifest a growing trend over time. Can we say with certainty that the MACs show a positive correlation with time? To verify this, we applied the kernel density function.
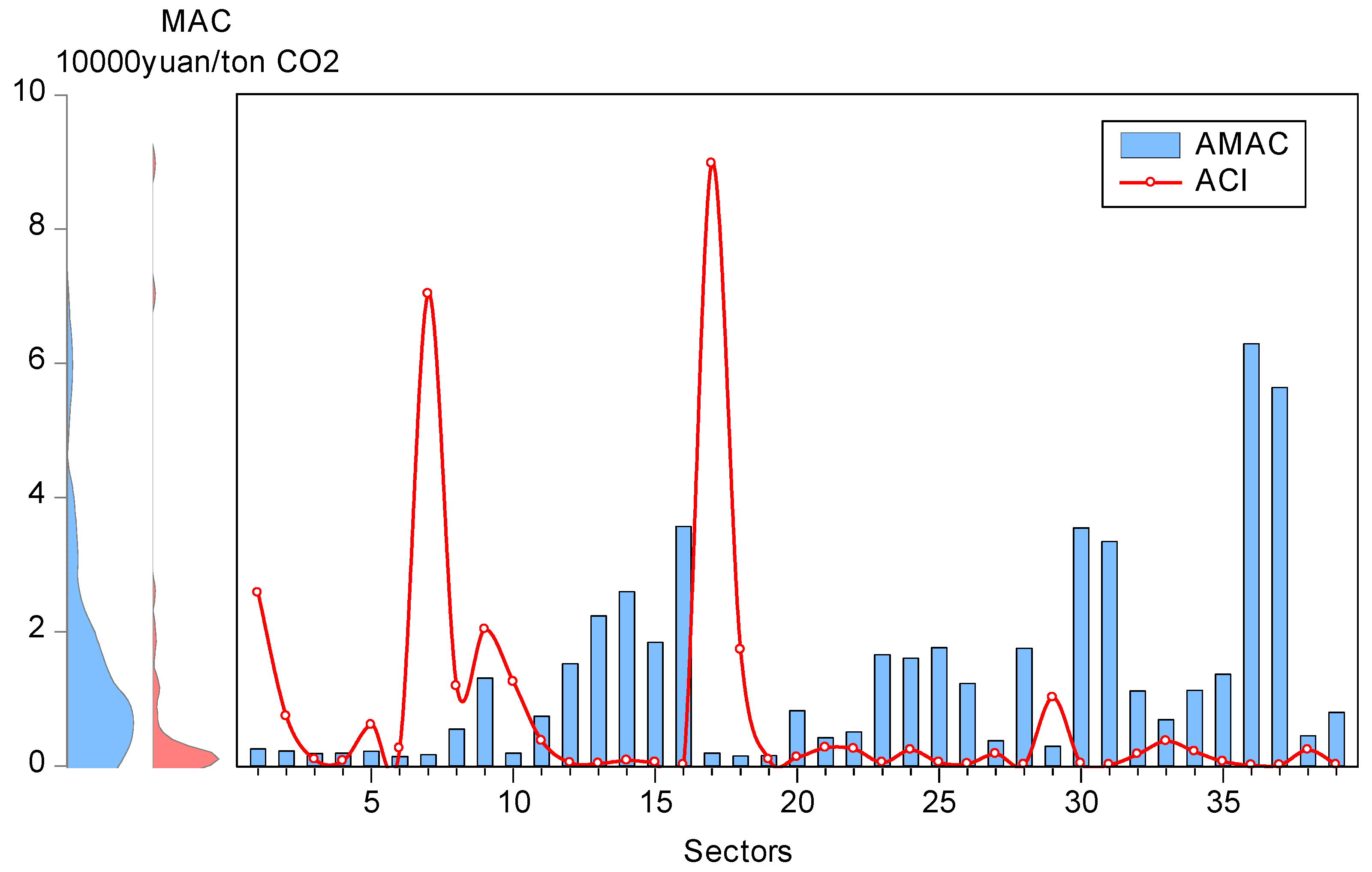
Carbon intensity, as an indicator for the relationship between carbon dioxide emissions and gross domestic product (GDP), has become a restrictive indicator used in China’s emissions reduction campaign. The average carbon intensities (denoted as ACI) from 2005 to 2011 in 39 industries are shown with red lines in
Figure 4; the average MACs (denoted as AMAC) from 2005 to 2011 in 39 industries are also displayed. The vertical axis depicts the kernel probability density estimation, which is applied to estimate the density of unknown functions. The kernel density of ACI reveals that ACI mainly concentrates in 0 to 0.5 intervals, which implies that the majority of ACIs are relatively low. Nevertheless, in several sectors such as Mining and washing of coal (SEC 01), Processing of petroleum, coking, and nuclear fuel (SEC 07), and Production and distribution of electric power and heat power (SEC 17), all of which are energy-intensive industries, the ACIs are significantly higher than in others.
It is noticed that the figure roughly represents a trend that a high AMAC always occurs in an industry with a low ACI and vice versa. In other words, compared with those heavy industries, the light industries tend to have higher MACs. Although the highest ACI appeared in Production and distribution of electric power and heat power (SEC 17), its AMAC only reached 1870 CNY/ton CO2. Conversely, Manufacture of communication equipment, computers and other electronic equipment (SEC 36), whose ACI is lowest, evidences the highest AMAC of 62,923 CNY/ton CO2.
It is not peculiar to obtain this result. Obviously, CO2 emissions mainly come from the use of fossil fuels. Hence, energy utilization, which is the reason for CO2 emissions, can exert a great influence on CO2 emissions. Given the low potential for CO2 abatement induced by high energy efficiency, advanced energy saving technology, and relatively low energy consumption, further energy savings and emissions mitigation in those light industries would be cost-inefficient. On the contrary, energy-intensive heavy industries have relatively large flexibility in reducing CO2 emissions owing to their lower energy efficiency and tremendously wasteful use of energy. Thus, energy saving in energy-intensive heavy industry is more promising and less costly. From the perspective of emissions reduction technology, the large-scale application of emissions reduction technology in energy-intensive industry can lead to a scale effect, which can also reduce MAC in energy-intensive industries. Additionally, a basic principle of environmental economics states that the marginal abatement cost is inversely related to emissions when the production process is inefficient, which has perfectly verified the above conclusions.
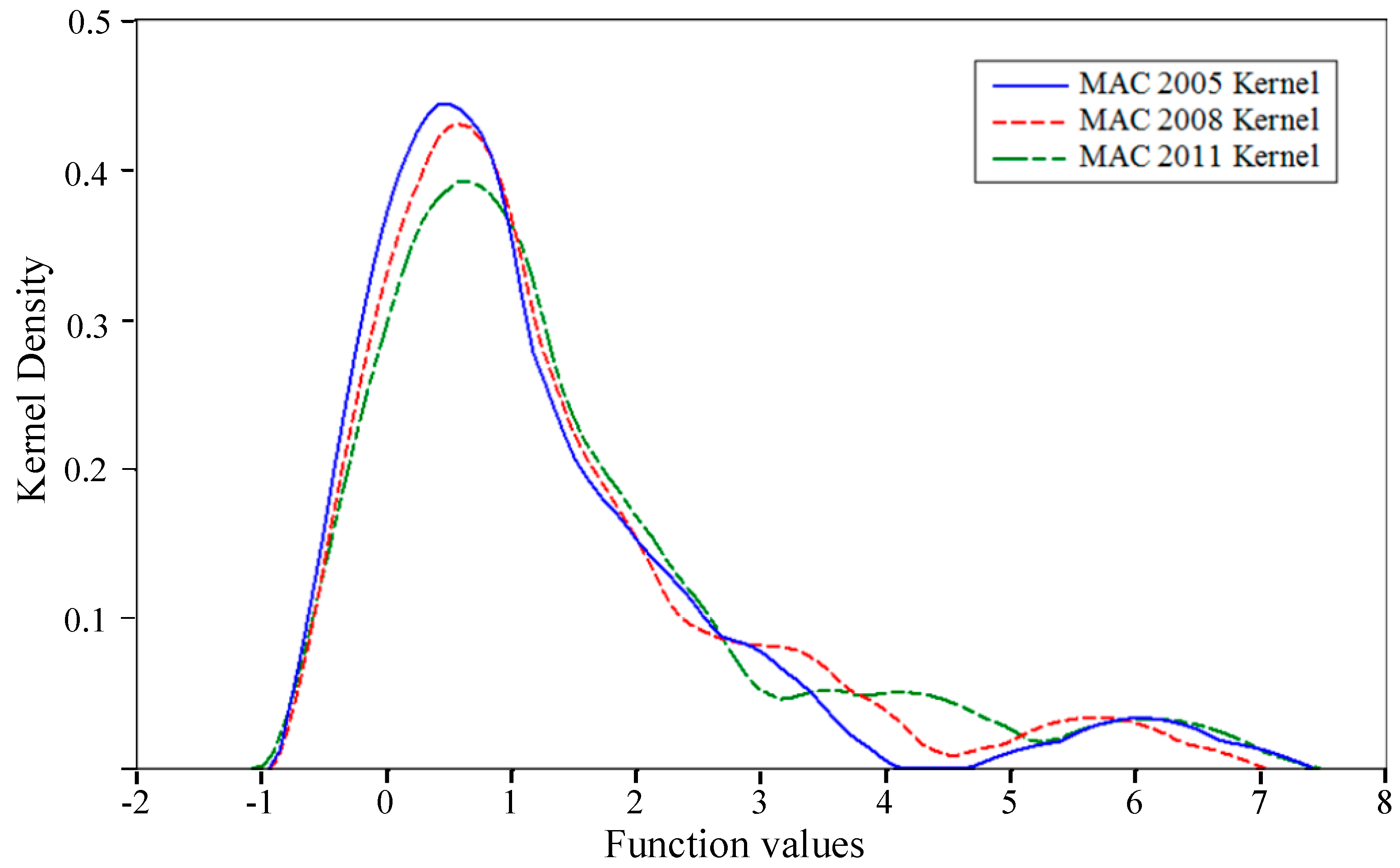
Then, in order to testify whether the MACs have a conspicuous rising tendency over time, the kernel probability density estimation is used for the second time. The kernel density of MAC in 2005, 2008, and 2011 are reported individually in
Figure 5. In 2005, the MACs mainly deviate from about 0 to 10,000 CNY/ton CO
2 with the majority of the estimates clustering around the 7000 CNY/ton CO
2 mark. In 2011, the MACs deviate from about 0 to 15,000 CNY/ton CO
2, with the majority of the estimates clustering around the 9000 CNY/ton CO
2 mark.
Different from previous studies [
23,
42], the rightward shift of kernel density curves is not obvious enough in our research. It is co-determined by two major opposite effects. First, the space for resetting the given resources to cut CO
2 emissions is getting squeezed over time, which means that the potential for cutting CO
2 emissions will be compressed in the future. So the MAC of CO
2 emissions will inevitably go up. Meanwhile, in consideration of technology improvement, industrial structure adjustment, energy conservation measures, rational allocation of energy resources, and learning effects, the ongoing advancement of technology and learning effects, in both energy conservation and emissions reduction, can continuously lift the efficiency of the DMU and reduce the MAC of CO
2 emissions. However, large-scale technological innovations and obvious learning effects are difficult to get and spread in the short term. Hence, there is a weak increasing trend over time.
4.2. Comparative Analysis
Before a deeper analysis, the validity and rationality of the results of MACs in our paper need to be tested. Nine relevant previous studies were selected to testify the rationality of the results and find similarities between the different cases. A summary of the literature is shown in
Table 5.
All the previous studies can be divided into four categories. The first category is MAC of industrial sector in China; the second category is MAC of industrial sector in a certain province or region; the third is MAC at provincial level in China; and the last is the nationwide MAC. Meanwhile, the undesirable output is not limited to CO2; other pollutants are also taken into consideration, such as SO2, NOx, BOD, COD, waste water, etc.
Compared with Zhou et al. [
30] and Chen et al. [
43], the results of our study are apparently higher than those industrial sectors in a certain province, which can be attributed to the changes in production frontier. It should also be noted that “efficiency” is the real driving factor determining the changes in production frontier, but efficiency varies dramatically within the same industry in different regions. Hence, the different results are not at all surprising in view of the tremendous differences between countries and regions. Although there are notable divergences among the results, what is noteworthy is that the trend of MACs in our paper is consistent with the relevant research. Furthermore, although MAC at a provincial level is smallest in the above studies at first sight, such estimates are not comparable due to the different objects. When analyzing our study and Yuan and Cheng [
41], we can conclude that the rank of MAC for different pollutants is as follows: SO
2 > Soot > CO
2 > Waste water. This conclusion is reasonable because it is directly proportional to its negative externality.
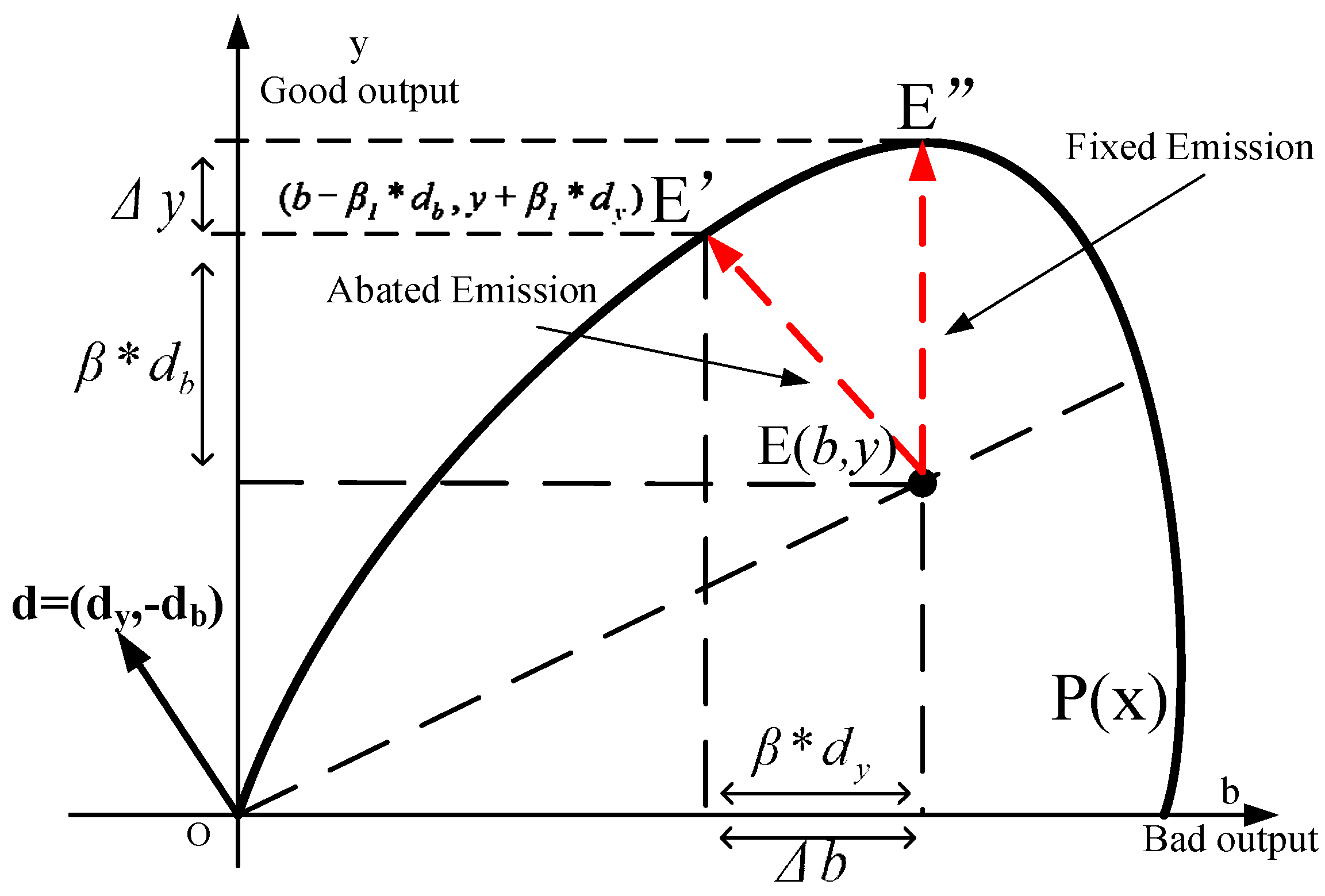
By comparing DDF (Directional distance function) and SDF (Shephard distance function), we find that the results calculated by the former method are basically larger than that of the latter. For the DMU , if and only if , the equation ideally holds. Or, put another way, the emissions reduction path in DDF is artificially selected, whereas the path in SDF is model-driven. Different from the simultaneous expansion between desirable and undesirable outputs in the Shephard function, the directional distance function can increase economic output while cutting the growth in CO2 emissions. Therefore, MACs calculated by DDF are greater than SDF. In addition, the direction vector, as another key factor, is a reflection of environmental policy. Generally speaking, a flat vector always corresponds to a more stringent policy environment, which means the increase in total output is accompanied by a significant reduction in CO2 emissions.
In brief, different evaluation objects, time spans, estimation methods, and in particular, direction vectors, can significantly affect the results.
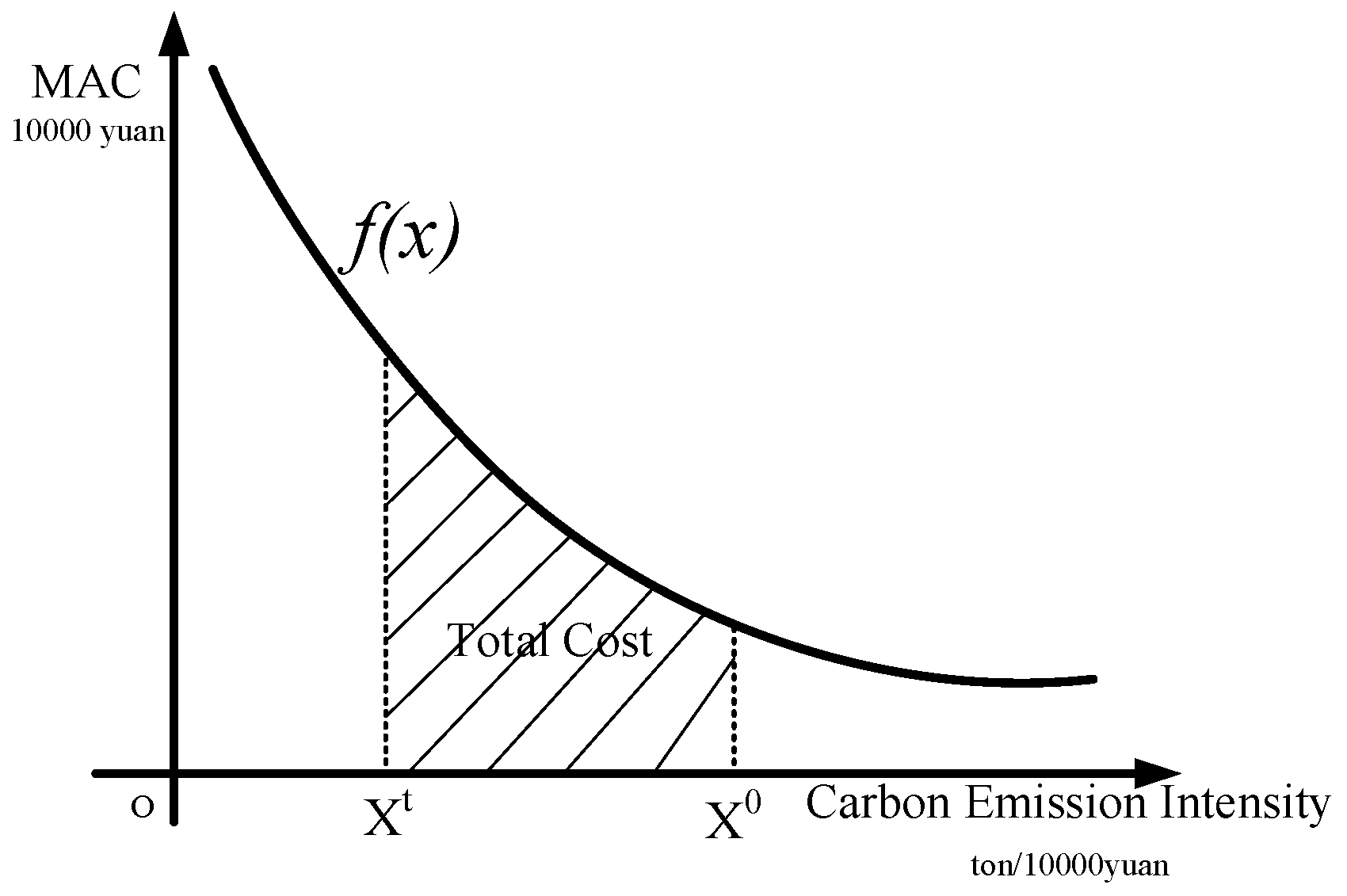
4.3. Estimation of MACC
Empirically, there are commonly five kinds of non-linear functional forms, including quadratic, logarithmic, exponential, power, and hyperbolic functional forms. In order to select the optimal fitting function, the scatter diagram is shown in
Figure 6.
From the above analyses, we can conclude that AMAC and ACI basically change in the reverse direction, and the marginal abatement cost curve is on a downward slope. We can observe an unambiguous nonlinear relationship between these two variables. The downward sloping curve implies that it is more costly to reduce an additional unit of CO
2 emissions for those sectors with lower carbon intensities. To estimate the relationship between the marginal abatement cost and carbon intensity, a hyperbolic function is taken into consideration. The statistics of Equation (14) are depicted in
Table 6.
The
t-statistics show that the null hypotheses for both of the parameters are overwhelmingly rejected.
means the equation passes the hypothesis testing.
R-squared means the fitting equation can interpret 70% of the dependent variable changes. It is considered that this equation can be applied to explain the relationship between the MAC and CI. The function plot is depicted in
Figure 6 in a red line, and its overall trend basically agrees with the sample data.
4.4. The Abatement Distribution Scheme
“The Improved Action to Address Climate Change” submitted to U.N. top climate officials by the Chinese government suggested that the peak value of carbon emissions will be achieved around 2030, and meanwhile the CO2 emissions per unit of GDP is required to be reduced by 60%–65% compared to 2005. Affected by international commitment, an energy revolution involving emissions mitigation, improvement of energy efficiency, and transformation of the energy structure was proposed by the Chinese government. Since the nationwide emissions reduction target was issued, how to allocate the total emissions reduction target to every industry has been a burning question. Our detailed classification of industry not only enables us to look at the MACs at an industrial level, but also to seek the most applicable and optimal allocation scheme of CO2 abatement for the Chinese government.
In this part, we calculated the abatement distribution scheme with minimum total abatement cost under four different emissions reduction targets, i.e., 5%, 10%, 15%, and 20%. The results are demonstrated in
Table 7. What is noteworthy is that the change of abatement distribution scheme is broadly consistent across the four scenarios. Therefore, we only illustrate the results under the circumstance of 20% emissions reduction.
The results show that nearly all sectors must contribute to the emissions reduction, but the emissions reduction rates vary greatly from industry to industry. Along with the transformation of China’s economic development mode, emissions reduction becomes an important task. As the focus of the national implementation of energy saving and emissions reduction, heavy industry will face greater pressure and more challenges. Mining and washing of coal (SEC 01), Extraction of petroleum and natural gas (SEC 02), Processing of petroleum, coking, and nuclear fuel (SEC 07), Manufacture of raw Chemical materials and chemical products (SEC 08), Smelting and pressing of ferrous metals (SEC 10), and Production and distribution of electric power and heat power (SEC 17), whose reduction rates reach 21.84%, 23.23%, 21.57%, 31.13% 29.73%, and 19.25%, respectively, are the six main energy saving and pollution emissions reduction industries. Moreover, besides the above six sectors, there are several sectors whose reduction rates are maintained above 10%, i.e., Manufacture of non-metallic mineral products (SEC 09), Smelting and pressing of non-ferrous metals (SEC 11), Manufacture of general purpose machinery (SEC 13), Production and distribution of gas (SEC 18), and Production and distribution of water (SEC 19). The rest contribute poorly to the abatement, with an emissions reduction rate below 10%.
These findings are understandable. First, as for those sectors with high emissions reduction proportions, they are a group with something in common—lower MACs and higher carbon intensities. Under a circumstance of 20% nationwide emissions reduction target, the allocated emissions reduction rate in Manufacture of raw chemical materials and chemical products (SEC 08) reaches 31.13%, ranking first. Undoubtedly, low MACs and a large amount of energy consumption in these sectors result in a promising future in CO2 reduction. Then, the question arises: why does the Production and distribution of electric power and heat power (SEC 17), whose carbon intensity is highest, not make the greatest contribution to emissions reduction? The electric and heat power industry, which relies heavily on coal, has its own particularity. The reason can be traced back to inter-links between upstream and downstream industries. Apparently, it is a downstream industry of the coal sector and upstream of most economic sectors. Emissions reduction is subject to the conditions of upstream and downstream industries. To put it another way, big cuts in CO2 emissions may induce capacity cutting and price booming, which can induce a contracting demand upstream and rising cost downstream. The co-effects of upstream and downstream constrained the potential for emissions reduction in the electric and heat power industry.
Compared with those industries that have high emissions reduction rates, the emissions reduction rates in light industries and some equipment manufacturing industries are lower than 10%. Among them, the lowest emissions reduction rate appears in Manufacture of measuring instruments and machinery for cultural activity and office work (SEC 37), which scarcely contribute to the emissions reduction. These industries should not become the focus of the emissions reduction; otherwise society will pay a high cost.