Numerical Analysis of the Factors Influencing a Vertical U-Tube Ground Heat Exchanger
Abstract
:1. Introduction
2. Methods
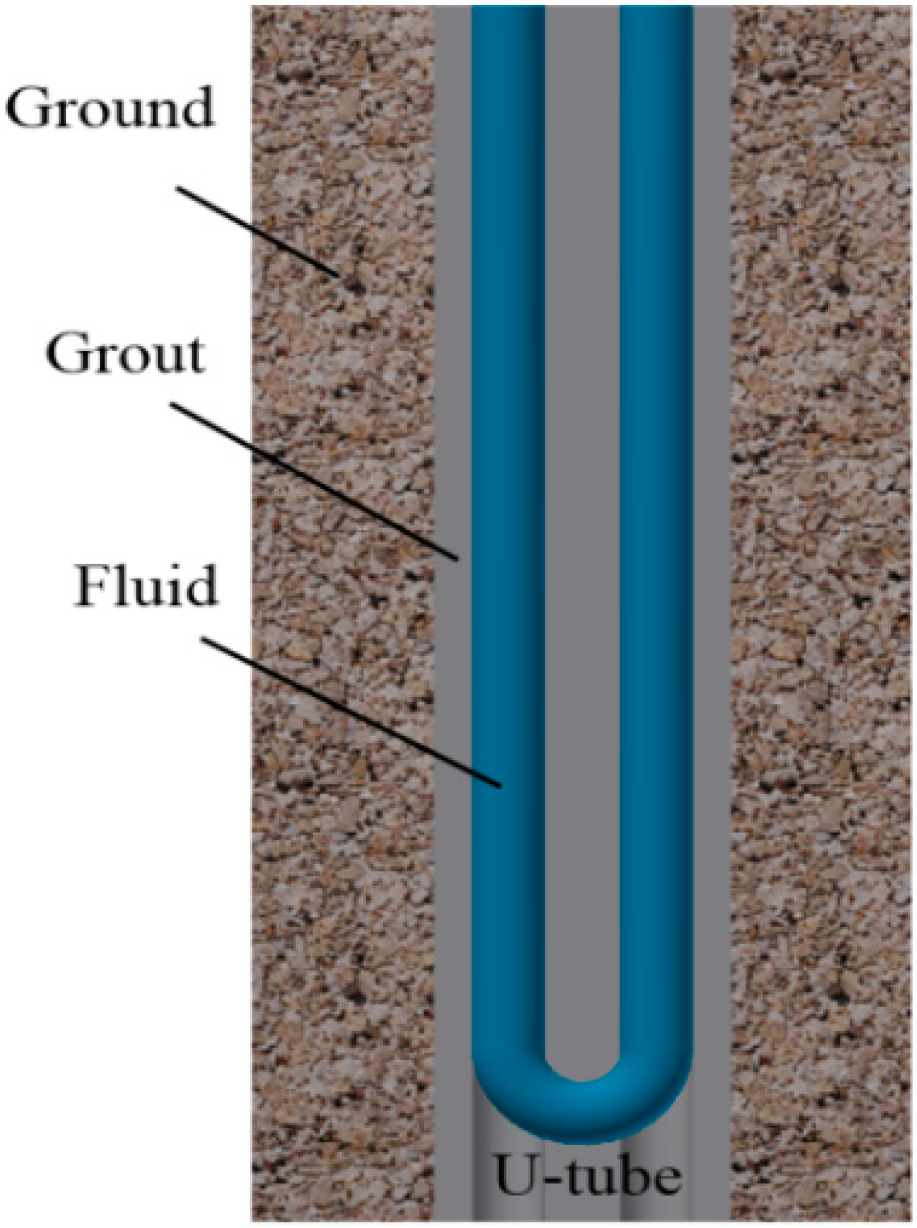
2.1. Model Description
2.2. The Governing Equations
2.3 Data Processing
- (1)
- The initial temperature is a constant of 290.6 K.
- (2)
- The far-field and bottom surfaces are set as undisturbed boundaries.
- (3)
- The top ground surface is set as a convective boundary with an air temperature of 289.0 K and a heat transfer coefficient of 10 W/(m2·K).
- (4)
- The inlet is set as a velocity-inlet boundary, and the outlet is set as a pressure-outlet boundary.
- (5)
- The reference parameters for simulation are listed in Table 2.
3. Analysis of Influencing Factors of Heat Transfer
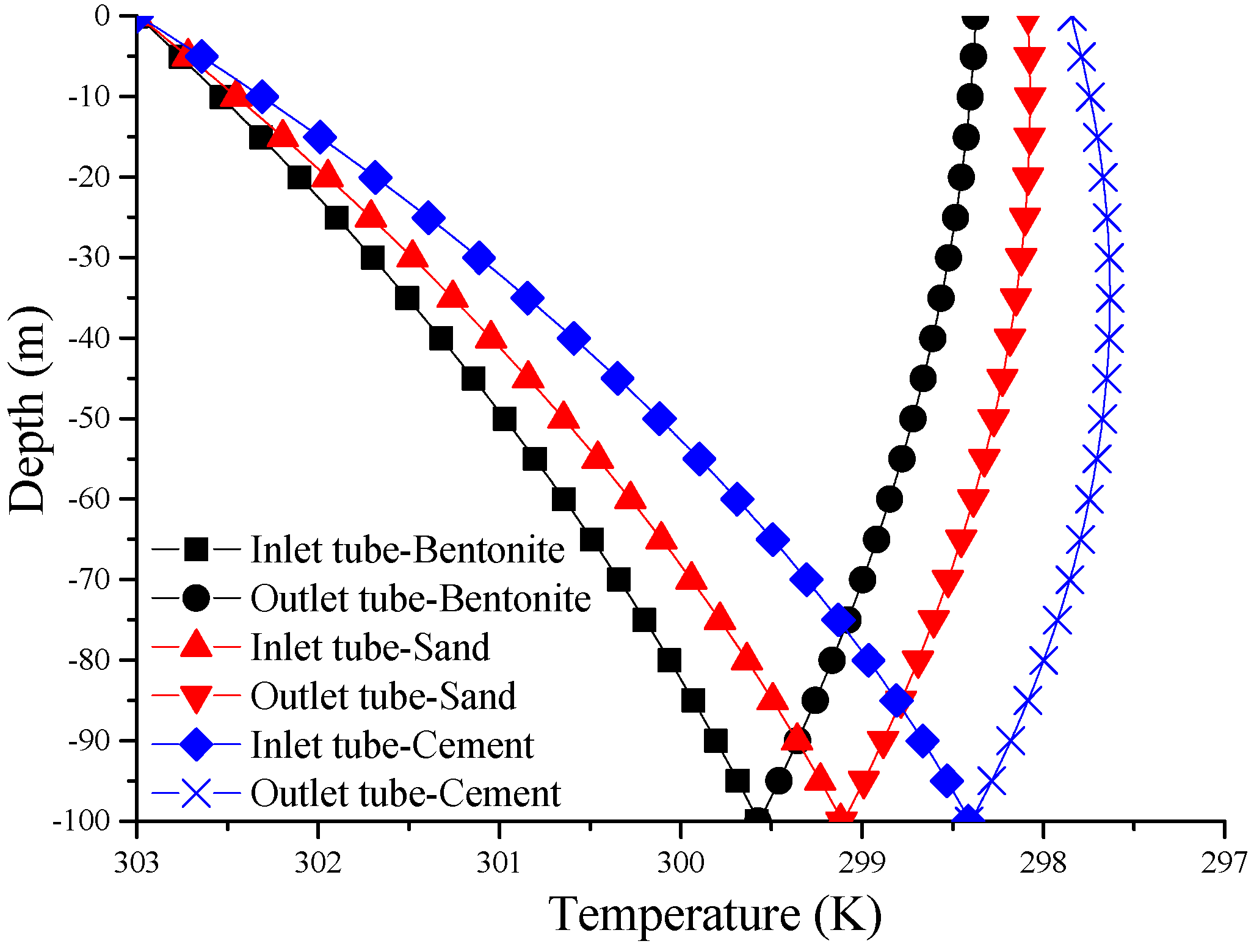
3.1. Influence of Grout Materials
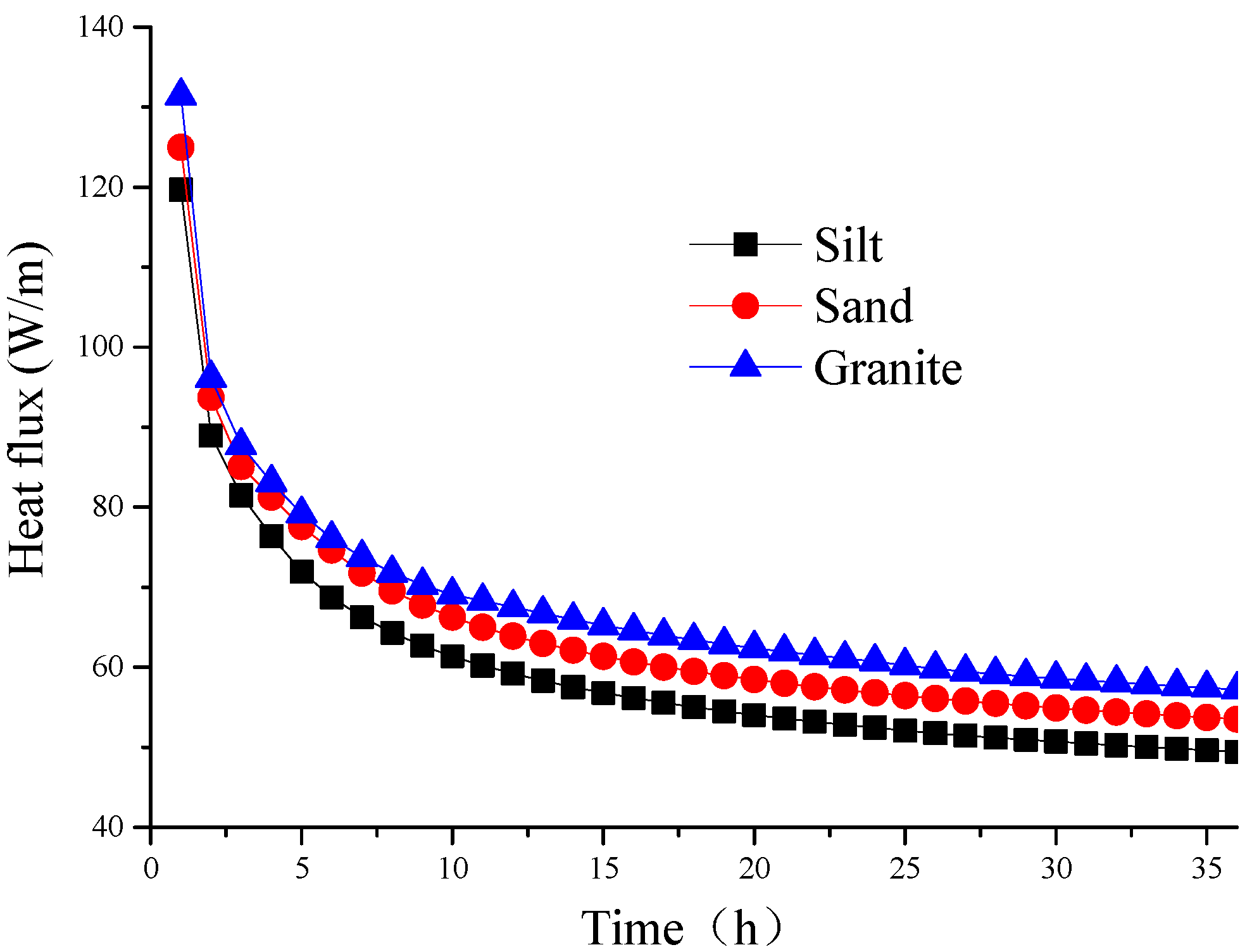
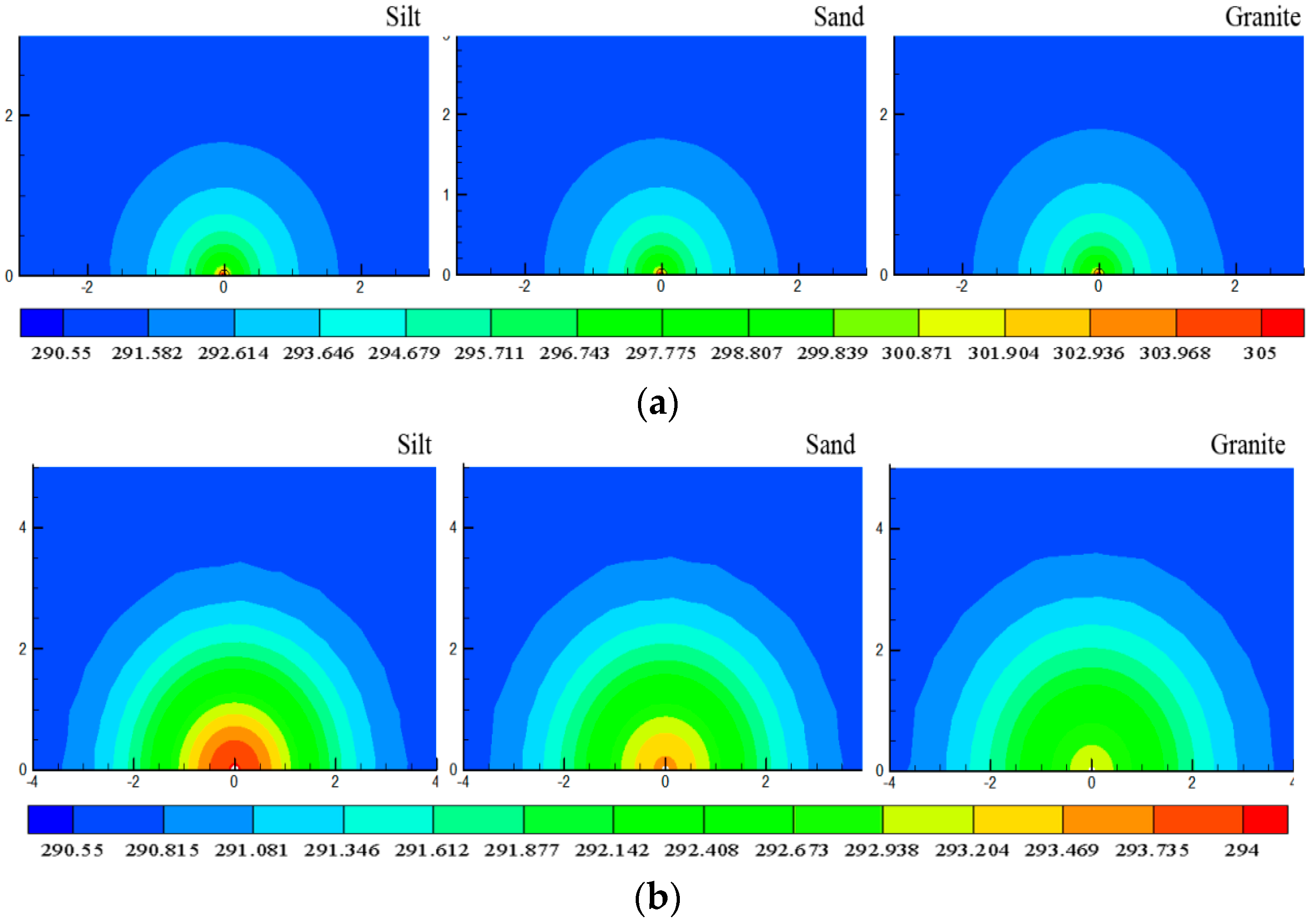
3.2. Influence of Soil
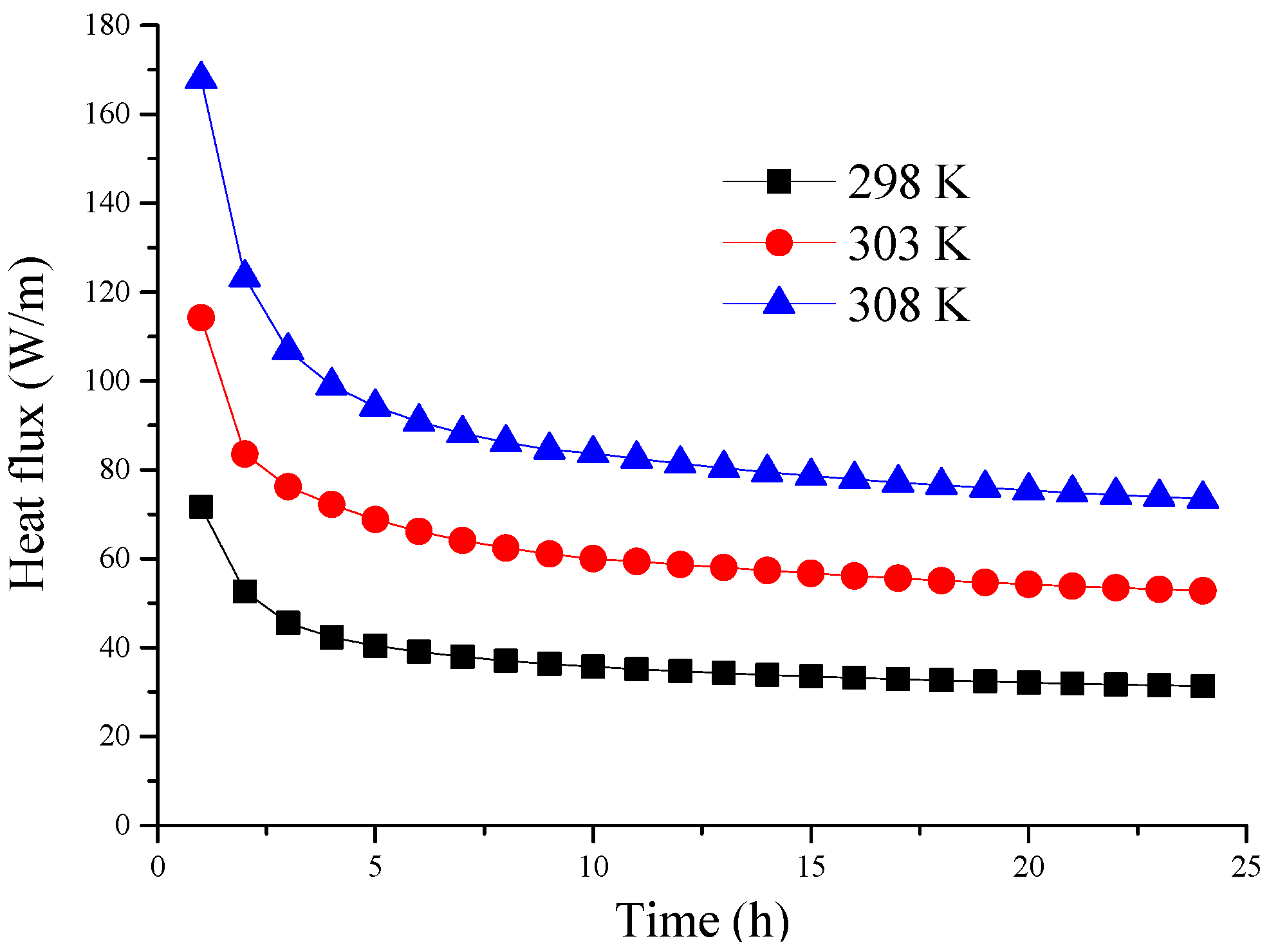
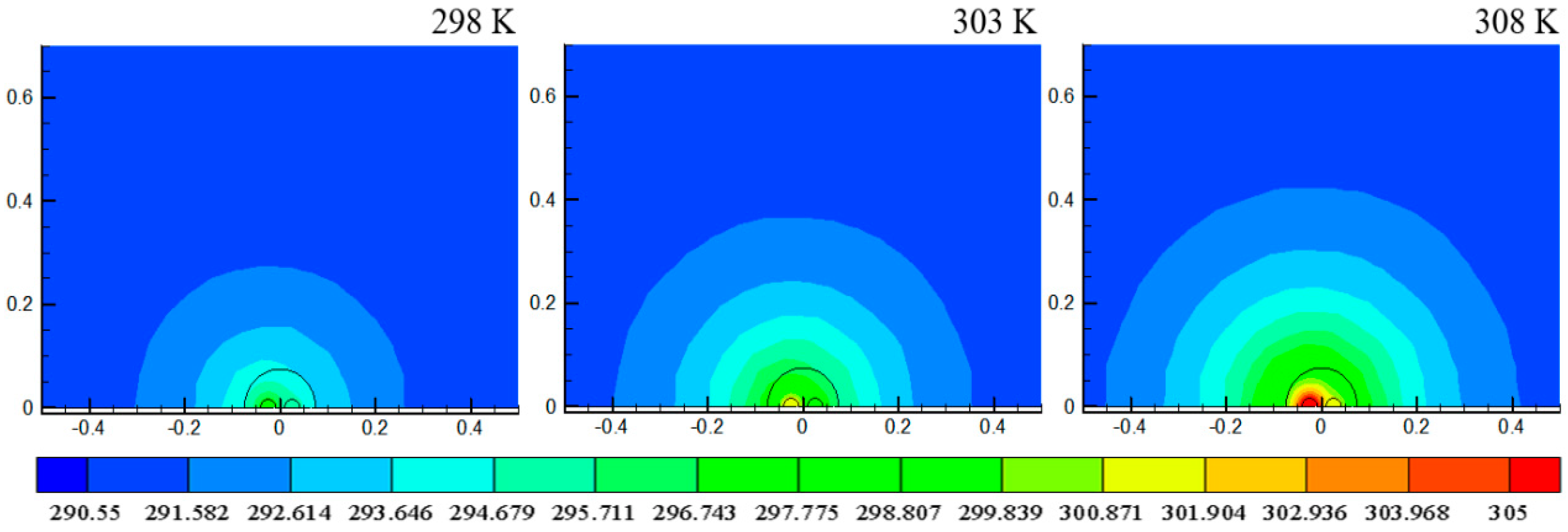
3.3. Influence of Inlet Water Temperature
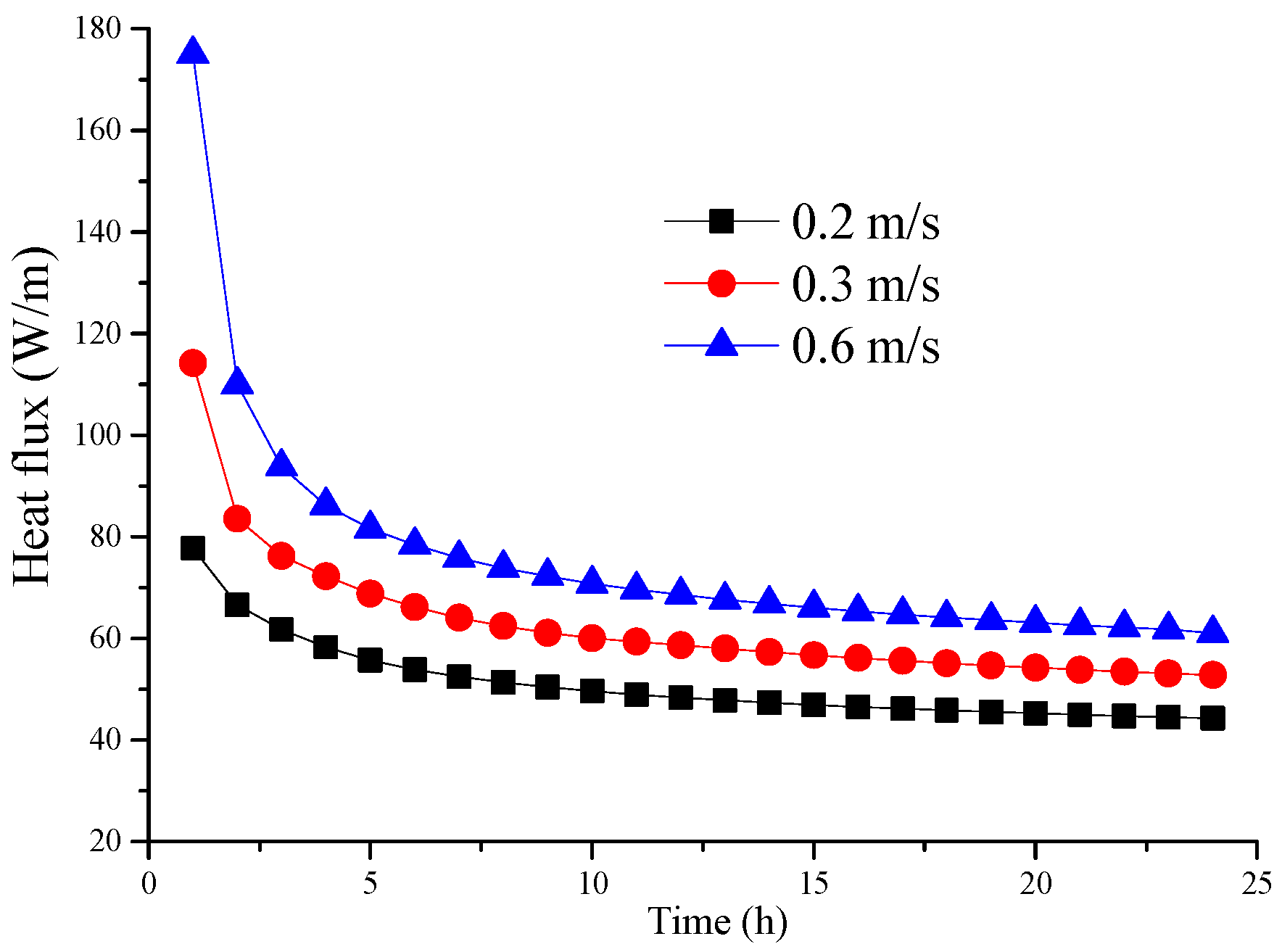
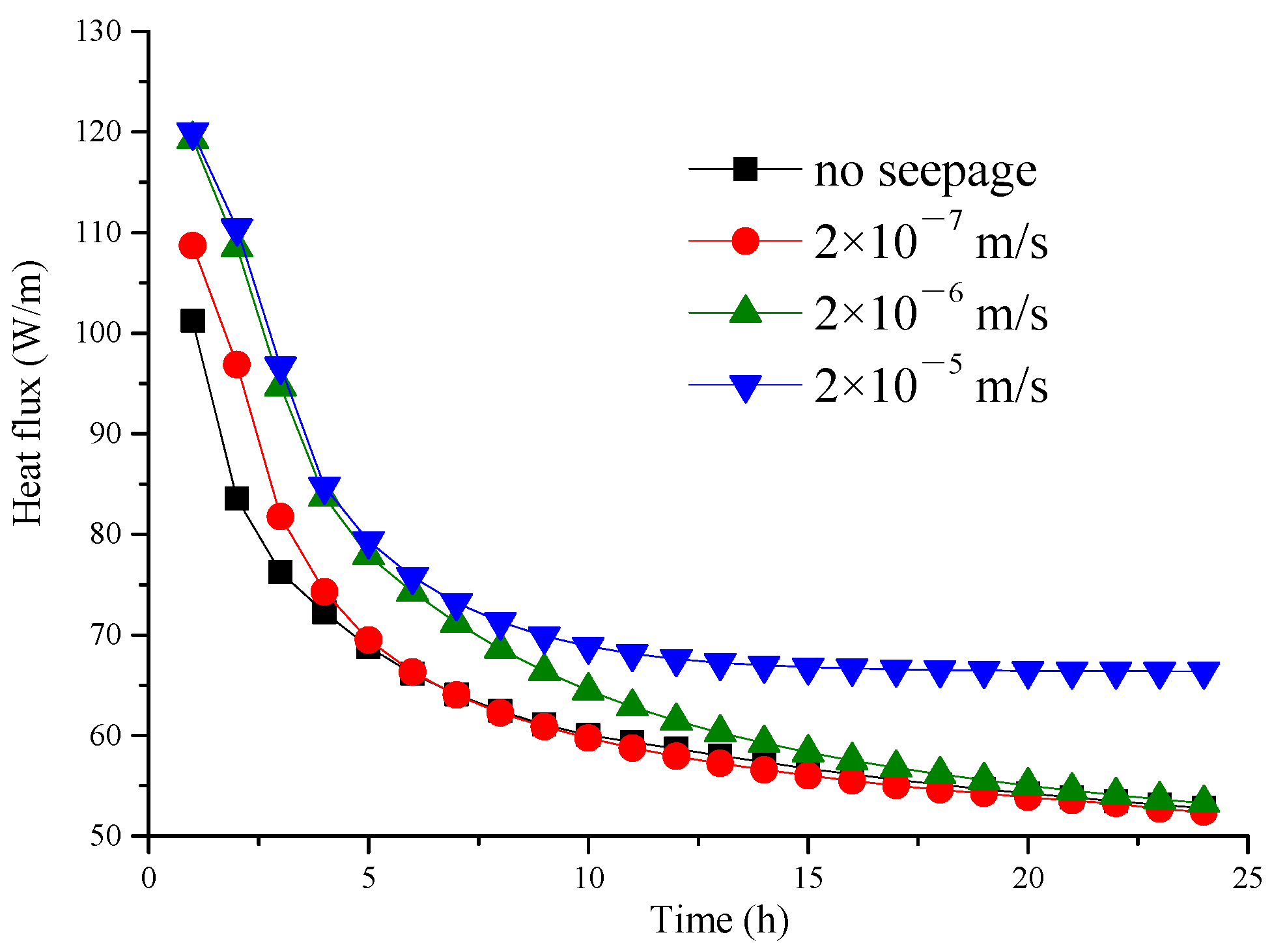
3.4 Influence of Inlet Water Velocity
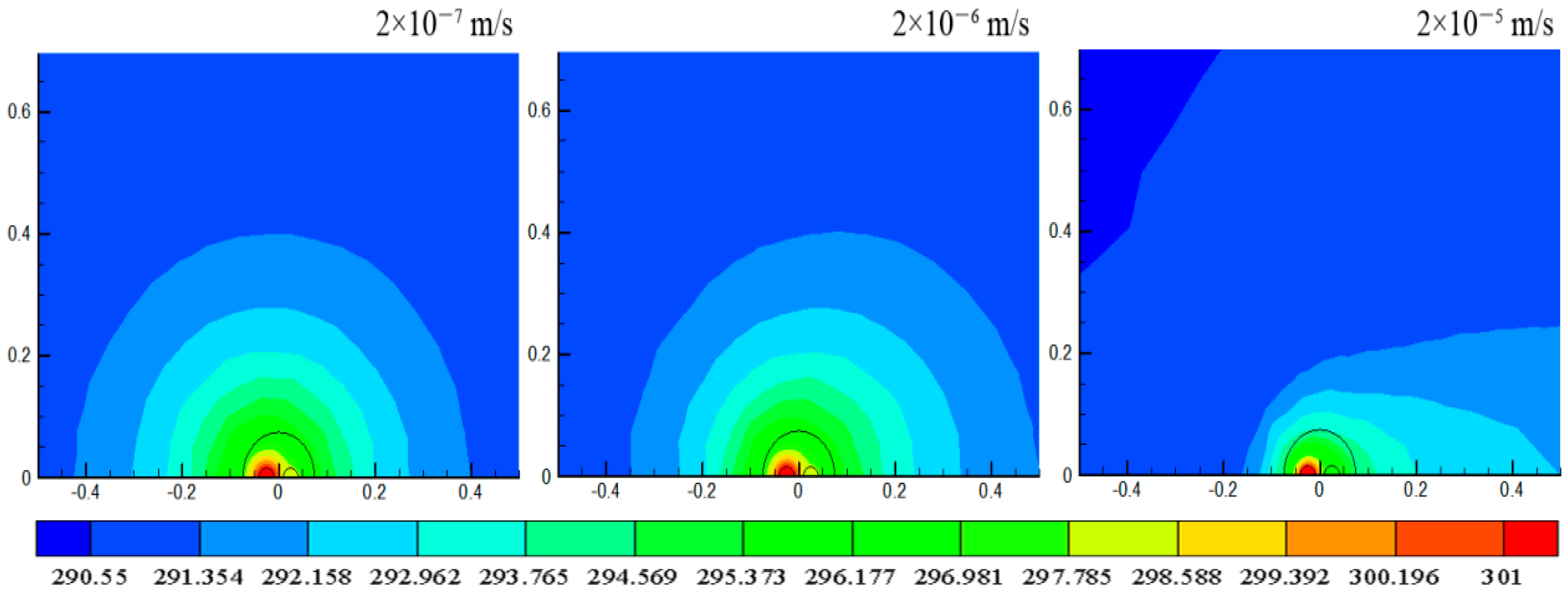
3.5. Influence of Groundwater Flow
4. Conclusions
- (1)
- Before the heat in the borehole is saturated, the heat flux in the GHE is directly proportional to the thermal conductivity coefficient of the grout materials.
- (2)
- The greater the thermal diffusion coefficient of the soil materials, the larger the radius of the thermal effect of the GHE and the faster the recovery rate of the temperature in the soil.
- (3)
- Increasing the inlet water temperature strengthens the heat transfer in the GHE, but it can cause heat buildup problems.
- (4)
- Increasing the inlet water velocity can enlarge the heat convection in the tube; when the inlet water velocity values are 0.2 m/s, 0.3 m/s, and 0.6 m/s, the computed average surface heat transfer coefficients are 17.97 W/(m2·K), 21.06 W/(m2·K), and 25.95 W/(m2·K), respectively.
- (5)
- The thermal-seepage coupling effect in groundwater can remove the accumulated heat, and therefore, can effectively enhance the heat transfer in the GHE.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Main symbols | |
| H | borehole depth (m) |
| heat flux per unit borehole depth (W/m) | |
| S | source term |
| T | temperature (K) |
| velocity vector | |
| velocity components in directions | |
| Cartesian coordinates | |
| Greek symbols | |
| soil permeability (m2) | |
| turbulent dissipation rate (m2/s3) | |
| turbulent kinematic energy (m2/s2) | |
| thermal conductivity (W/m·K) | |
| dynamic viscosity (N·s/m2) | |
| turbulent viscosity (N·s/m2) | |
| inlet flow (m3/h) | |
| temperature recovery rate | |
| density (kg/m3) | |
| volumetric heat capacity (kJ/(m3·K)) | |
| time (h) | |
| soil porosity | |
| generalized variable | |
| Subscripts | |
| f | underground water |
| inlet and outlet | |
| s | soil |
References
- Sarbu, I.; Sebarchievici, C. General review of ground-source heat pump systems for heating and cooling of buildings. Energy Build. 2014, 70, 441–454. [Google Scholar] [CrossRef]
- Hepbasli, A. A key review on exergetic analysis and assessment of renewable energy resources for a sustainable future. Renew. Sustain. Energy Rev. 2008, 12, 593–661. [Google Scholar] [CrossRef]
- Florides, G.; Kalogirou, S. Ground heat exchangers—A review of systems, models and applications. Renew. Energy 2007, 32, 2461–2478. [Google Scholar] [CrossRef]
- Gao, Q.; Li, M.; Yu, M.; Spitler, J.D.; Yan, Y.Y. Review of development from GSHP to UTES in China and other countries. Renew. Sustain. Energy Rev. 2009, 13, 1383–1394. [Google Scholar] [CrossRef]
- Sanner, B.; Karytsas, C.; Mendrinos, D.; Rybach, L. Current status of ground source heat pumps and underground thermal energy storage in Europe. Geothermics 2003, 32, 579–588. [Google Scholar] [CrossRef]
- Liu, X.B.; Lu, S.L.; Hughes, P.; Cai, Z. A comparative study of the status of GSHP applications in the United States and China. Renew. Sustain. Energy Rev. 2015, 48, 558–570. [Google Scholar] [CrossRef]
- Eskilson, P. Thermal Analysis of Heat Extraction Boreholes. Ph.D. Thesis, University of Lund, Lund, Sweden, 1987. [Google Scholar]
- Yang, H.; Cui, P.; Fang, Z. Vertical-borehole ground-coupled heat pumps: A review of models and systems. Appl. Energy 2010, 87, 16–27. [Google Scholar] [CrossRef]
- Jalaluddin; Miyara, A. Thermal performance investigation of several types of vertical ground heat exchangers with different operation mode. Appl. Therm. Eng. 2012, 33, 167–174. [Google Scholar]
- Starace, G.; Congedo, P.M.; Colangelo, G. Horizontal heat exchangers for GSHPs. Efficiency and cost investigation for three different applications. In Proceedings of the 18th International Conference on Efficiency, Cost, Optimization, Simulation, and Environmental Impact of Energy Systems (ECOS 2005), Trondheim, Norway, 20–22 June 2005.
- Jayakumar, J.S.; Mahajani, S.M.; Mandal, J.C.; Vijayan, P.K.; Bhoi, R. Experimental and CFD estimation of heat transfer in helically coiled heat exchangers. Chem. Eng. Res. Des. 2008, 86, 221–232. [Google Scholar] [CrossRef]
- Congedo, P.M.; Colangelo, G.; Starace, G. CFD simulations of horizontal ground heat exchangers: A comparison among different configurations. Appl. Therm. Eng. 2012, 33, 24–32. [Google Scholar] [CrossRef]
- Wagner, V.; Bayer, P. Numerical sensitivity study of thermal response tests. Renew. Energy 2012, 41, 245–253. [Google Scholar] [CrossRef]
- Bouhacina, B.; Saim, R.; Oztop, H.F. Numerical investigation of a novel tube design for the geothermal borehole heat exchanger. Appl. Therm. Eng. 2015, 79, 153–162. [Google Scholar] [CrossRef]
- Lous, M.L.; Larroque, F. Thermal performance of a deep borehole heat exchanger: Insights from a synthetic coupled heat and flow model. Geothermics 2015, 57, 157–172. [Google Scholar] [CrossRef]
- Gustafsson, A.M.; Westerlund, L.; Hellström, G. CFD-modeling of natural convection in a groundwater-filled borehole heat exchanger. Appl. Therm. Eng. 2010, 30, 683–691. [Google Scholar] [CrossRef]
- Yang, W.B.; Chen, Y.P. Numerical investigation on the underground thermal imbalance of ground-coupled heat pump operated in cooling-dominated district. Appl. Therm. Eng. 2013, 58, 626–637. [Google Scholar] [CrossRef]
- Dehkordi, S.E.; Schincariol, R.A. Effect of thermal-hydrogeological and borehole heat exchanger properties on performance and impact of vertical closed-loop geothermal heat pump systems. Hydrogeol. J. 2014, 22, 189–203. [Google Scholar] [CrossRef]
- Chen, S.Y.; Mao, J.F. Heat transfer analysis of a vertical ground heat exchanger using numerical simulation and multiple regression model. Energy Build. 2016, 129, 81–91. [Google Scholar] [CrossRef]
- Kaltreider, C.; Krarti, M.; McCartney, J. Heat transfer analysis of thermo-active foundations. Energy Build. 2015, 86, 492–501. [Google Scholar] [CrossRef]
- Walton, W.C. Practical Aspects of Groundwater Modeling-Flow, Mass and Heat Transport and Subsidence and Computer Models; National Water Well Association: Westerville, OH, USA, 1985. [Google Scholar]
- Molina-Giraldo, N.; Bayer, P.; Blum, P. Evaluating the influence of thermal dispersion on temperature plumes from geothermal systems using analytical solutions. Int. J. Therm. Sci. 2011, 50, 1223–1231. [Google Scholar] [CrossRef]
- Campbell, G.S.; Jungbauer, J.D.; Bidlake, W.R.; Hungerford, R.D. Predicting the effect of temperature on soil thermal conductivity. Soil Sci. 1994, 158, 307–313. [Google Scholar] [CrossRef]
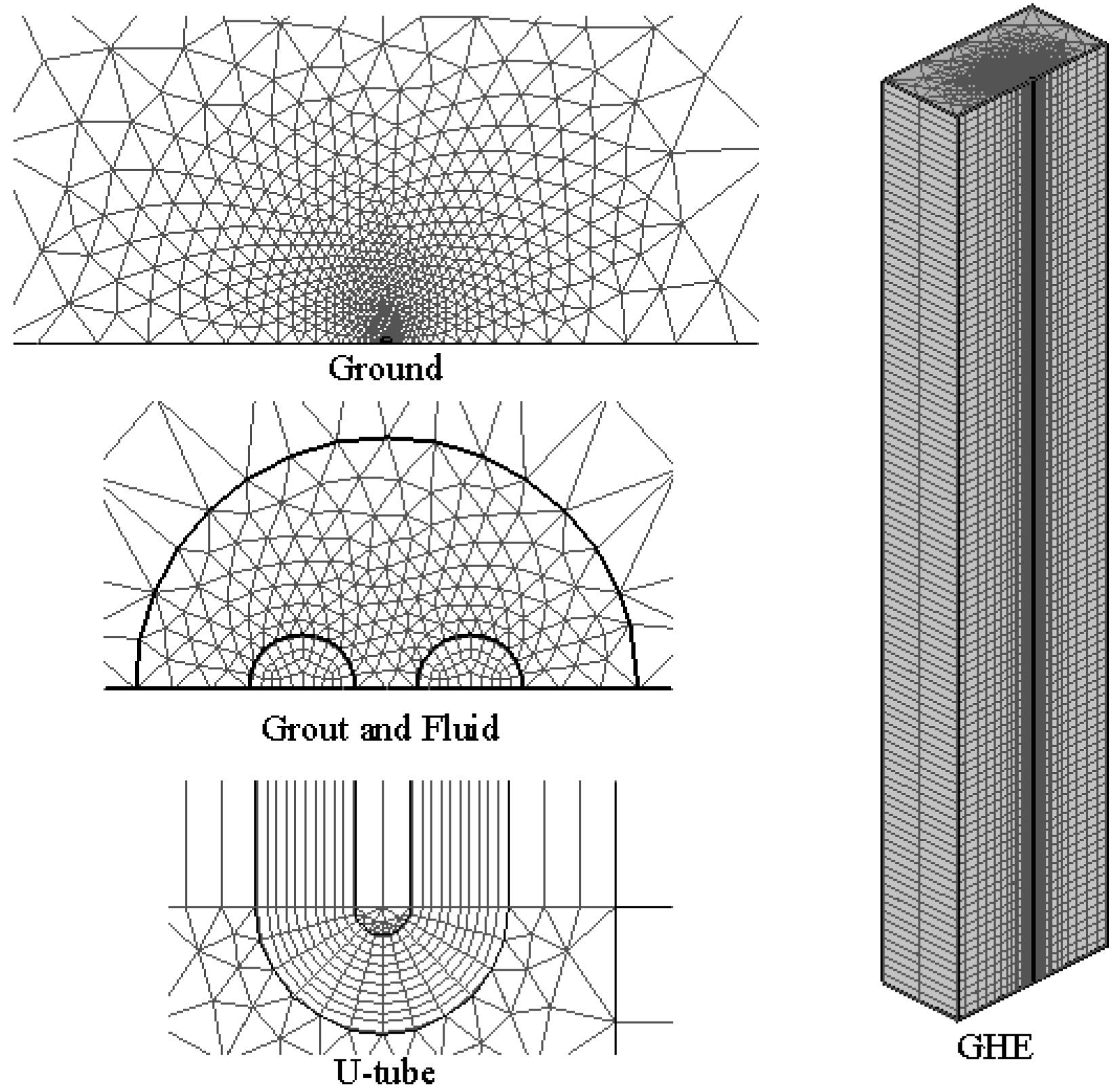

| Coarse Mesh | Medium Mesh | Finer Mesh | Experiment | |
|---|---|---|---|---|
| Mesh number | 353,127 | 485,227 | 692,570 | - |
| Heat flux (W/(m·K)) | 51.81 | 52.77 | 53.62 | 53.31 |
| Difference (%) | 2.81 | 1.01 | 0.6 |
| Parameters | Units | Values |
|---|---|---|
| Soil thermal conductivity | W/(m·K) | 2 |
| Soil density | kg/m3 | 2183 |
| Soil heat capacity | J/(kg·K) | 996 |
| Soil porosity | % | 39 |
| Soil permeability | m2 | 2.3 × 10−10 |
| Grout thermal conductivity | W/(m·K) | 2 |
| Grout density | kg/m3 | 2500 |
| Grout heat capacity | J/(kg·K) | 1110 |
| Inlet temperature | K | 303 |
| Inlet velocity | m/s | 0.3 |
| Groundwater seepage | m/s | 0 |
| Grout | Density | Specific Heat | Thermal Conductivity Coefficient | Thermal Diffusion Coefficient |
|---|---|---|---|---|
| kg/m3 | J/(kg·K) | W/(m·K) | m2/s | |
| Bentonite | 2600 | 720 | 1.6 | 8.5 × 10−7 |
| Sand | 2500 | 1110 | 2.0 | 7.2 × 10−7 |
| Cement | 1631 | 900 | 2.8 | 1.9 × 10−6 |
| Soils | Density | Specific Heat | Thermal Conductivity Coefficient | Thermal Diffusion Coefficient |
|---|---|---|---|---|
| kg/m3 | J/(kg·K) | W/(m·K) | m2/s | |
| Silt | 1760 | 1510 | 1.6 | 6.0 × 10−7 |
| Sand | 2500 | 1110 | 2.0 | 7.2 × 10−7 |
| Granite | 2500 | 840 | 2.4 | 1.14 × 10−6 |
| Inlet Velocity | Reynolds Numbers | Nusselt Numbers | Heat Transfer Coefficient |
|---|---|---|---|
| m/s | - | - | W/(m2·K) |
| 0.2 | 6568 | 29.95 | 17.97 |
| 0.3 | 9852 | 35.09 | 21.06 |
| 0.6 | 19,705 | 43.25 | 25.95 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Mao, J.; Han, X.; Li, C.; Liu, L. Numerical Analysis of the Factors Influencing a Vertical U-Tube Ground Heat Exchanger. Sustainability 2016, 8, 882. https://doi.org/10.3390/su8090882
Chen S, Mao J, Han X, Li C, Liu L. Numerical Analysis of the Factors Influencing a Vertical U-Tube Ground Heat Exchanger. Sustainability. 2016; 8(9):882. https://doi.org/10.3390/su8090882
Chicago/Turabian StyleChen, Shangyuan, Jinfeng Mao, Xu Han, Chaofeng Li, and Liyao Liu. 2016. "Numerical Analysis of the Factors Influencing a Vertical U-Tube Ground Heat Exchanger" Sustainability 8, no. 9: 882. https://doi.org/10.3390/su8090882
APA StyleChen, S., Mao, J., Han, X., Li, C., & Liu, L. (2016). Numerical Analysis of the Factors Influencing a Vertical U-Tube Ground Heat Exchanger. Sustainability, 8(9), 882. https://doi.org/10.3390/su8090882






