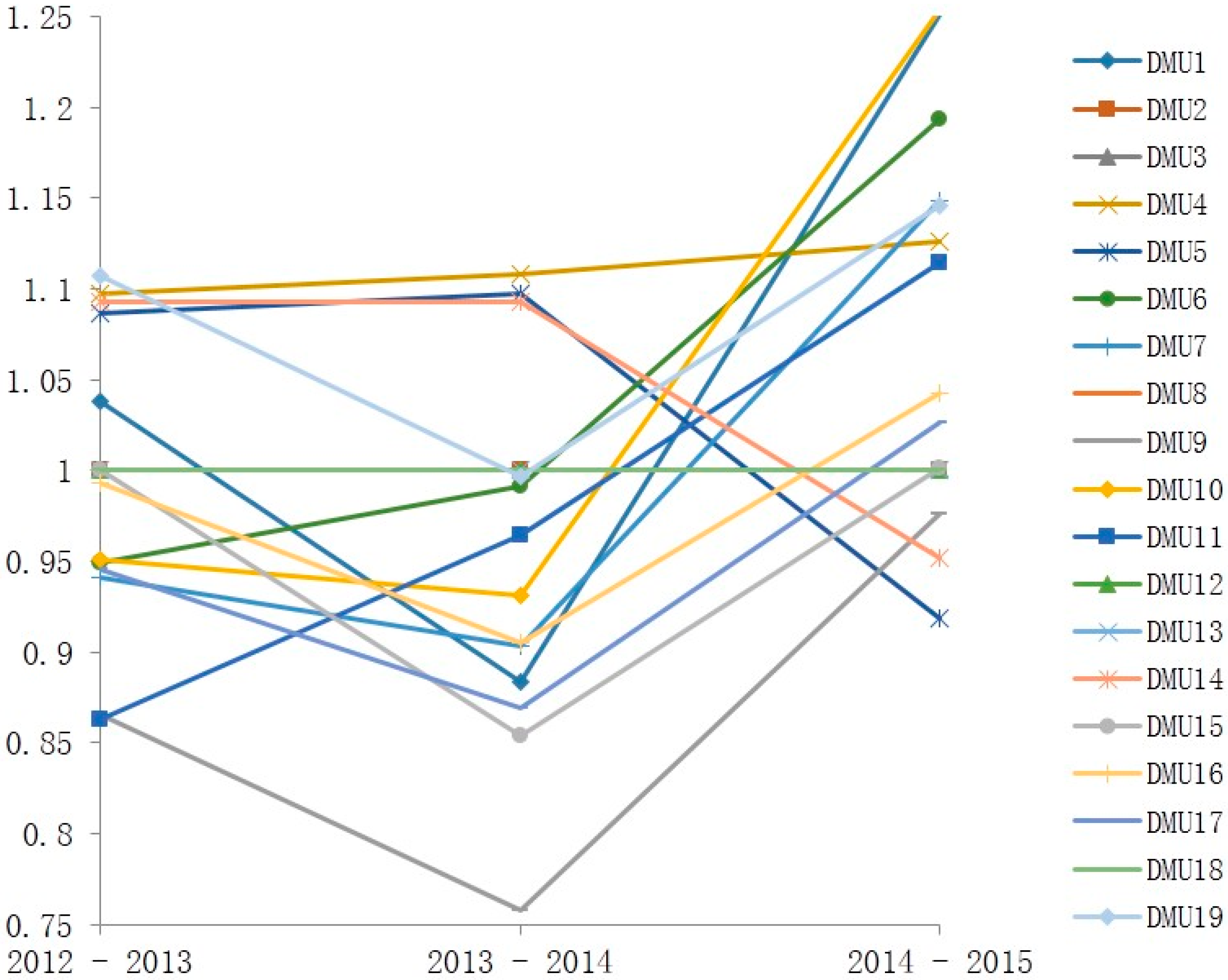
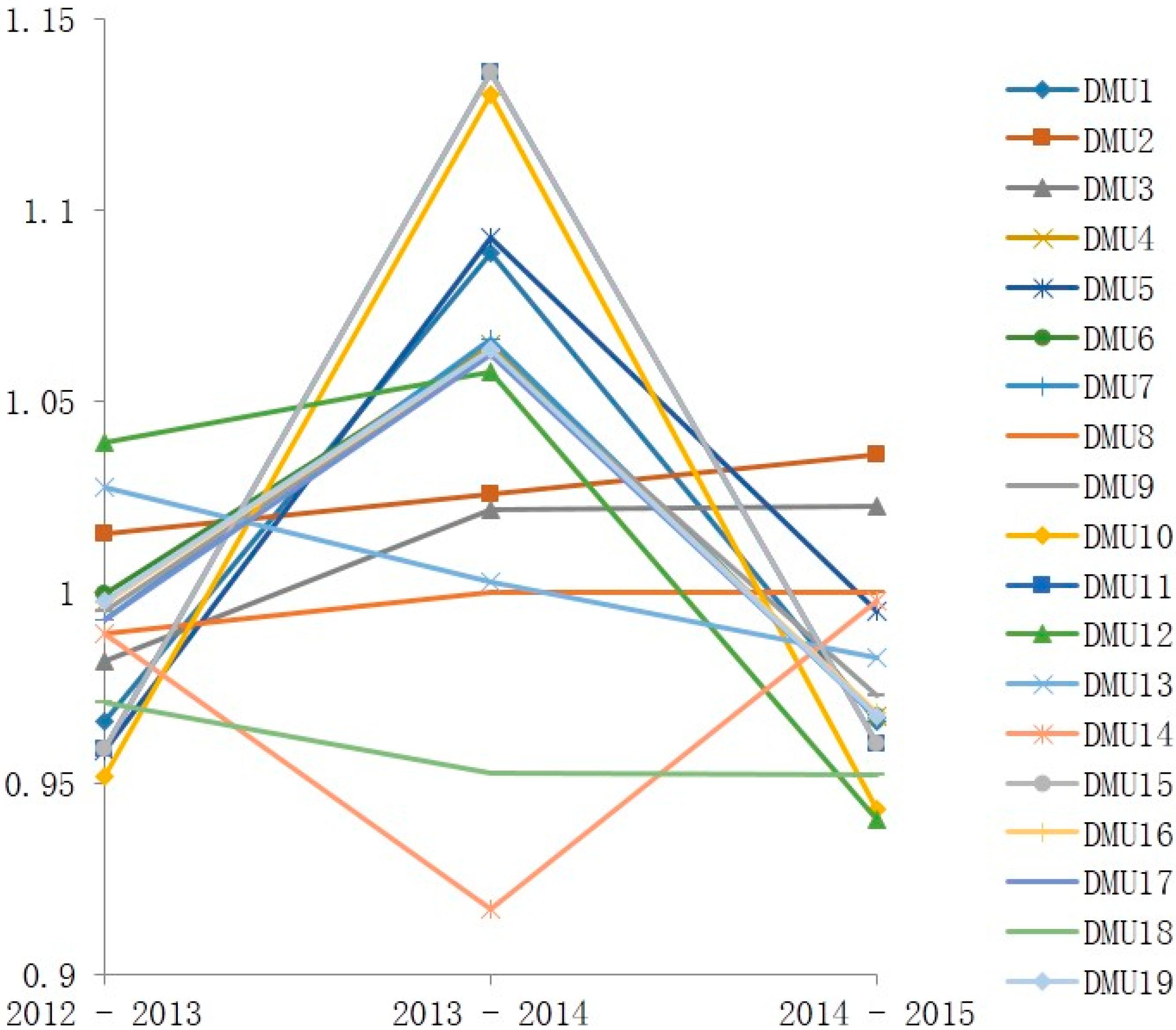
3.1. Grey Forecasting Generation Theory
GM (1,1) is the central model that has been most widely employed, and discrete grey models are a class of new models we initially developed [
22].
Let be a sequence of raw data. Denote its accumulation-generated sequence by . Then, is referred to as the original form of the GM (1,1) model, where the symbol GM (1,1) stands for “first order grey model in one variable”.
Let be the sequence generated from by the adjacent neighbor means; that is, Then, is referred to as the basic form of the GM (1,1) model.
Theorem: Let
,
, and
be the same as the above, except that
is non-negative. If
is the sequence of parameters:
The least squares estimate sequence of the GM (1,1) model satisfies
[
1]. Continuing all of the notations from Theorem 1, if
, then
is a whitenization equation of the GM (1,1).The time response sequence of the GM (1,1) is given below.
The parameters
and
of GM (1,1) are referred to as the development coefficient and Grey action quantity, respectively. The former reflects the development states of
and
[
22]. In general, the variables that act upon the system of interest should be external or pre-defined. Because GM (1,1) is a model constructed on a single sequence, it uses only the behavioral sequence (referred to as the output sequence or background values) of the system without considering any externally-acting sequences (referred to as input sequences or driving quantities). The Grey action quantity in GM (1,1) is a value derived from the background values. It reflects changes contained in the data, and its exact intension is grey. This quantity realizes the extension of the relevant intension. Its existence distinguishes grey systems modeling from the general input-output modeling. It is also an important test of the conclusions of grey systems and grey boxes.
3.3. Malmquist Productivity Index
The Malmquist productivity index (MPI) was introduced by Caves in 1982 [
23]. The researchers expanded upon an idea of Malmquist (1953), who in a consumer context used ratios of input distance functions to construct an input quantity index. Färe et al. [
24] followed and developed the work of Caves, Christensen and Diewert. They calculated an adjacent Malmquist productivity index consisting of the geometric mean of two Malmquist indexes as defined by Caves, Christensen and Diewert. Later, Berg introduced a base period Malmquist productivity index, which (except for the fixed base period technology) is the same as one of the indexes defined by Caves [
23]. Consequently, they argue that one desirable property of an index covering a longer period of time is the possibility to chain it; the index obeys the circular relation, and the price we must pay for the fulfillment of the circular test seems reasonable [
12]. If we use the base period Malmquist productivity index instead of the adjacent index, we fulfill the circular test, but pay with base period dependency and with an underlying reference to a fixed technology that might have nothing in common with the technologies of the two periods under consideration.
Productivity measurement was an important research topic, and DEA introduced a useful approach; productivity measurement in DEA was the Malmquist productivity index (MPI), which was named after Malmquist, to give ideas for the MPI [
6]. In addition, other scholars assumed that Malmquist calculates the relative performance of a DMU in different periods of time using the technology of the base period [
24].
In this research, we adopted the theorem of Chen (2003) [
25] and selected
n ; each
produces a vector of outputs
by using a vector of inputs
at each time period
t, which could be the CCR (Chames, Cooper and Rhodes) DEA model as:
,
s.
t ,
, where
and
means input and output vectors of
, among others. Theorem is shown to be input-oriented, because it acknowledges that the possible redial reductions of all inputs are fixed at current levels of the company [
12].
If , then is (radially) efficient in time period ; otherwise, if , then is (radially) invalid. We observe that: (i) if , then is on the empirical production frontier (EPF); and (ii) if , then can reduce its inputs, and therefore, is operating below the EPF. Note that the possible non-zero input and output slacks are likely to present at the optimal solutions.
Replacing
and
with
and
, respectively, we have the technical efficiency of
for
at the time period
. From
to
technical efficiency may change or the EPF may shift. Based on this model, the radial Malmquist productivity index can be calculated via [
24].
- (i)
Comparing to EPF at time t, calculating ;
- (ii)
Comparing
to EPF at time
t + 1, calculating
through the following linear program:
The Malmquist productivity index is defined as
:
measures the productivity change between periods and . Productivity declines if , remains unchanged if and improves if . Note that is expressed by the radial efficiency scores obtained from several input-oriented DEA models. Therefore, this is called the input-oriented radial Malmquist productivity index.
The following modification of
makes it possible to measure the change in technical efficiency and the movement of EPF for
:
The first term on the right-hand side measures the magnitude of technical efficiency change between period
and
and whether technical efficiency improves, remains or declines, accordingly. The second term measures the shift in the EPF between periods
and
:
We should note the possibility that two different period EPFs may have intersections. The facets of EPF may not shift in the same direction; some facets may shift forward and some backward. In this situation, the movement of EPF is DMU-specific. The Malmquist productivity index measures the performance of a specific DMU in terms of the change or referent DMUs.
The selection of is independent of the corresponding input units. Possible choices of can be and . However, if additional information (e.g., con ratios) is available, then the lower bounds on multipliers can be used as weights .
Furthermore, if , then , where, which can be interpreted as the weighted output for at time period . Thus, we may use to estimate un-normalized given the information on . can be obtained from additional information (e.g., the total expenditure for each in a particular time period or the prices on outputs).