1. Introduction
Recently, environmental regulations have spurred increased interest in activities that enable the utilization of post-consumer products. As a result, the design and implementation of a reverse supply chain is an important requirement for many companies. The reverse supply chain focuses on collecting products from customers and reusing them to generate value. This loop consists of a traditional forward supply chain, with products sold via retailers, and a reverse supply chain, with used products returned via reverse channels.
The value generated by reverse supply chains is threefold: First, the manufacturer uses the returned products in a remanufacturing process. Second, customer participation in the product return enables partners in the supply chain to sell new products to participating customers. Third, for auxiliary and consumable products dependent on another device, such as printer ink for printers, the manufacturer can encourage customers to buy new products rather than refurbish or refill used ones when the reverse supply chain is employed.
Because the collection of used products for remanufacture and resale is an increasingly important component of corporate profits, many companies are now engaged in this process. Participants in the supply chain attempt to generate additional value by cooperating with other participants in the same chain. In particular, manufacturers are considering cooperative strategies such as working with supply chain partners, including retailers and third party logistics (3PL) companies, to increase their used product collection rate [
1]. Generally, various cooperation strategies can be developed using contraction methods such as benefit-sharing or sharing the burden of expense [
2,
3,
4,
5].
Yu et al. [
6] highlights the efficiency of decentralized decision-making (distribution of decision rights to most relevant department) when a large organization manages timely decision effectively. A supply chain consists of partners who can decide independently. Thus, most of this study assumed each supply chain member’s acts in their own benefit regardless of the act of other members under the decentralized supply chain environment. This paper reviews some of the contract options available to manufacturers and retailers to increase the return rate of used products from consumers through the reverse supply chain. Compared with decentralized models (no sharing of benefits or costs with supply chain partners), the effects of coordinative options will be tested from the perspective of individual participants or total supply chain profits through a simulation approach.
We consider the example of ink cartridges used in printers and the following process. We firstly divide customer into two types. The first type are customers who prefer refill cartridge for cost saving. The second type are customers who prefer new cartridge for guaranteeing product quality. When a customer visits a retailer, he/she suggests returning used-cartridge and buying new cartridge to customer by paying collect payment. After, when used cartridges reach a proper inventory level, the retailer distributes them to a manufacturer. All used cartridges that have arrived at the manufacturer will go through a sorting process and then will be remanufactured based on their condition. Lastly, the manufacturer will resell the remanufactured products to the customers at an economical price.
This study focuses on understanding the detailed implementation procedure involved in determining the optimal contracts agreed by the manufacturer and retailer.
2. Literature Review
The tendency towards environmental issues, adaptation to the competitive market, and increasingly controlled legislation in the global market has increased the need for corporate entities to focus on developing sustainable practices. To keep pace with this trend, reverse supply chain management has emerged as one strand of a sustainable strategy [
2]. Li et al. [
3] stated that manufacturers more and more prefer integrating the remanufacturing process with the original manufacture process of producing new products for manufacture cost reduction. The remanufacturing system integrates the forward supply chain, with its cycle of production, distribution, and delivery to customers, and the reverse supply chain, which involves the collection, delivery, remanufacturing, and resale of used products [
7,
8]. Because collecting used products for remanufacture and resale is increasingly important to corporate profits, many companies have engaged their customers in this process. Manufacturers, in particular, are considering strategies such as working with supply chain partners, including retailers and third party logistics (3PL) companies, to increase their used product collection rate. Savaskan [
1] proposed a three revers supply channel formats. Firstly, manufacturers utilize a direct collection method from customers like Xerox Corporation. Another collect method is that manufacturers utilize retailer channel for collecting used products. Last, manufacturers occasionally utilize third-party logistics companies such as GENCO Distribution System to collect used products.
Numerous formats for the contract between manufacturer and retailer have been studied, such as buy-back, quantity-flexibility, revenue-sharing, price-discount, sales-rebate, and quantity-discount [
7,
9,
10,
11,
12]. Hu et al. [
13] applied five contracts to a reverse supply chain in which consumers make strategic decisions based on the payment offered by a collector. They designed coordination strategies consisting of the wholesale price contract, double-phase price contract, cost-pooling contract, subsidy contract, and indemnity contract, and analyzed the impact of each on the performance of supply chain members. Li et al. [
3] studied an incentive contract model for a manufacturer who assigns the used product collection to a company, but has imperfect information on the company’s collecting costs under the Extended Producer Responsibility law. The manufacturer designs the contract to incorporate a level of investment for its partner and the collection rate of the partner. Huang et al. [
14] proposed a quantity discount contract as one of the strategies to increase profit of supply chain partners. Walther et al. [
15] developed a negotiation-oriented decomposition approach to coordinate between manufacturer and retailer for the purpose of maximizing their profit.
Most of the above studies have focused on the impact of coordination contracts on the performance of supply chain members. However, some researchers have considered the process of contracts between the participants in a reverse supply chain model. For example, Gerchak and Wang [
16] considered two different types of contract between retailer and suppliers: one was a vendor management inventory with revenue sharing, and the other was a wholesale-price-driven contract. They explored the resulting delivery quantities in this decentralized supply chain, and discussed the implications for the participants’ and total expected profits. Through a series of experiments, they found that revenue sharing was the best option for the supplier to maximize its own profits. Cachon [
9] found revenue sharing contracts outperform alternative contracts such as buy-back contracts, price-discount contracts, quantity-flexibility contracts, sales rebate contracts, franchise contracts and quantity discounts in a traditional supply chain.
Wang and Zipkin [
17] investigated how the behavior of participant’s decision making affects the supply chain performance under a two-stage supplier-retailer model. Under a buy-back contract, they identified the scenarios under which the retailer is the leader and the supplier is the leader. The results showed that, all other conditions being equal, total system profits are maximized when the supplier is the leader. Kanda and Deshmukh [
18] evaluated the wholesale price, buy-back, and quantity flexibility in relation to the decentralized model and, in terms of performance measures, the improvement offered by three-level supply chains with a single supplier, assembler, and retailer. Kannan et al. [
19] investigated a series of contracts applied to a two-echelon supply chain, and found that revenue-sharing contracts offer the highest profit margins for the manufacturer.
3. Reverse Supply Chain Management
Rogers et al. [
20] defined reverse supply chain as the process collecting products from customers and reusing them to generate value. It is one of sustainable methods worth paying attention to enterprises. The main reasons they engage in it is to increase profit by reusing used-products, follow government regulations, or to protect brand-image from customers who are sensitive to environmental issues. Then, what are important issues in the reverse supply chain management?
One of the most reviewed themes in the literature is the coordination between supply chain members. Kanda and Deshmukh [
21] proposed four coordination mechanisms: coordination contracts, information technology, information sharing and joint decision making. This paper focuses on how to coordinate through contracts between channel participants and its effects in reverse supply chain.
Govindan et al. [
22] stated that contracts are important key to coordinate between supply chain partners. In addition, optimal contract design is that all of coordination member are satisfied with the contractual terms in the cooperative game. If there is just one partner who loses benefit, there is no coordination. Raut et al. [
23], who studied contracts between exhibitor and producer in movie industry, emphasized that optimal contract design between manufacturer and retailer is affecting profit of coordination members. It is an extremely complicated mechanism given that a reverse supply chain consists of complex decision-making of partners in interdependent and interconnected business relation.
In forward supply chain, price discounts, quantity discounts, quantity flexibility, and incentives based on lead times, deadlines, and quantity have been utilized as contract options. Otherwise, in the case of reverse supply chain, there can be a series of incentives offered by manufacturers to their channel partners in order to achieve their coordination. We then consider the following incentive contracts, namely revenue sharing, sharing of channel cost such as return logistics cost, and sharing incentive aid to customers by retailer.
Revenue sharing is a coordination mechanism offered by the manufacturer to the retailer, which increases the retailer’s profit so that retailer can offer more incentive. It will ultimately have an effect on increasing return rate of used products. Sharing the reverse logistics cost can also be a solution between manufacturer and retailer in reverse supply chain. From this contract, retailer can expect to increase the indirect profit through cost reduction, as manufacturer bears a portion of the logistics costs that retailer have to pay for delivering used product to manufacturer. Sharing the incentive paid to customer is that manufacturer directs pay to the incentive to customer, and retailer should pay it. This strategy is for securing a certain amount of return rate regardless of retailer’s profit in manufacturer perspective.
This paper has focused on investigating which type of contract will generate higher profit in the retailer perspective and how the retailer and manufacturer are going to adjust to a mutual agreement for maximizing total (or coordinated) profits.
4. Research Model
4.1. Model Procedure
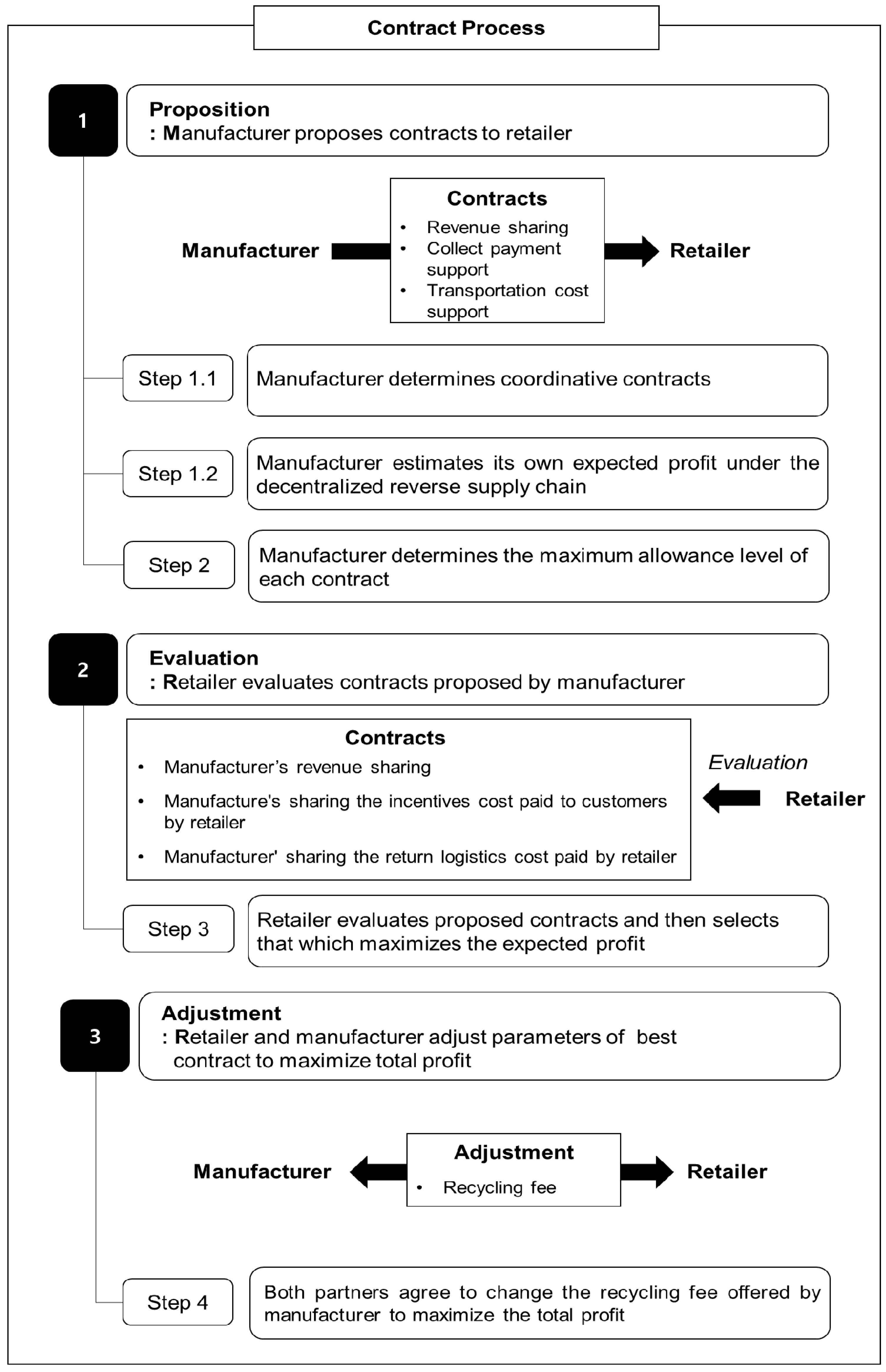
Our research model involves the following four steps (see
Figure 1).
(1) Proposition
Step 1.1. Manufacturer determines coordinative contracts
In Step 1.1, we design three cooperative strategies between the manufacturer and retailer: (1) manufacturer revenue sharing; (2) manufacturer sharing the incentives cost paid to customers by retailer (an additional payment to the retailer to accelerate the return activity, separate from the basic return fee); and (3) manufacturer sharing the return logistics cost paid by retailer.
Step 1.2. Manufacturer estimates its own expected profit under the non-coordinative reverse supply chain
First, we design the reverse supply chain model with two partners, manufacturer and retailer, using a system dynamics simulation technique. We then conduct experiments to estimate the individual profits of the manufacturer and retailer in a decentralized supply chain. In the decentralized scheme, there are no cooperative contracts between the manufacturer and retailer, and they each seek to maximize their own profit. The profit under this decentralized scenario is considered as the maximum allowance in any contracts between the manufacturer and retailer.
Step 2. Manufacturer determines the maximum allowance of each contract
For the contracts proposed in Step 1.1, we determine the maximum allowance that the manufacturer can offer to the retailer. Because the manufacturer expects to increase its own profits through cooperation (the contract) with a partner, the maximum allowance of each cooperative contract will be determined when the expected profit in the coordinative model is greater than the expected profit in the decentralized model.
(2) Evaluation
Step 3. Retailer evaluates proposed contracts based on which will lead to the maximum expected profit
The manufacturer offers the retailer three contracts, which state the maximum allowance level that will be offered to the retailer. The retailer then simulates its own profit effects under the three contracts, and determines the best as that which gives the highest expected profit.
(3) Adjustment
Step 4. Both partners agree to change the recycling fee offered by the manufacturer to maximize total profit
After the retailer has made a decision, the details of the contract are followed by both partners. In a cooperative supply chain, it is more important to maximize total profits than individual profits. Thus, if the retailer’s decision does not satisfy the maximization of total profits, we assume that the contract parameters will be adjusted by the partners. In this study, we consider the basic return fee as the adjustable contract parameter. From the initial basic return fee, we examine the change in total profits given by a smooth decrement in the value of the basic return fee. Finally, we select the return fee that maximizes the total profits and the corresponding maximum allowance level.
4.2. Framework of the Reverse Supply Chain Model
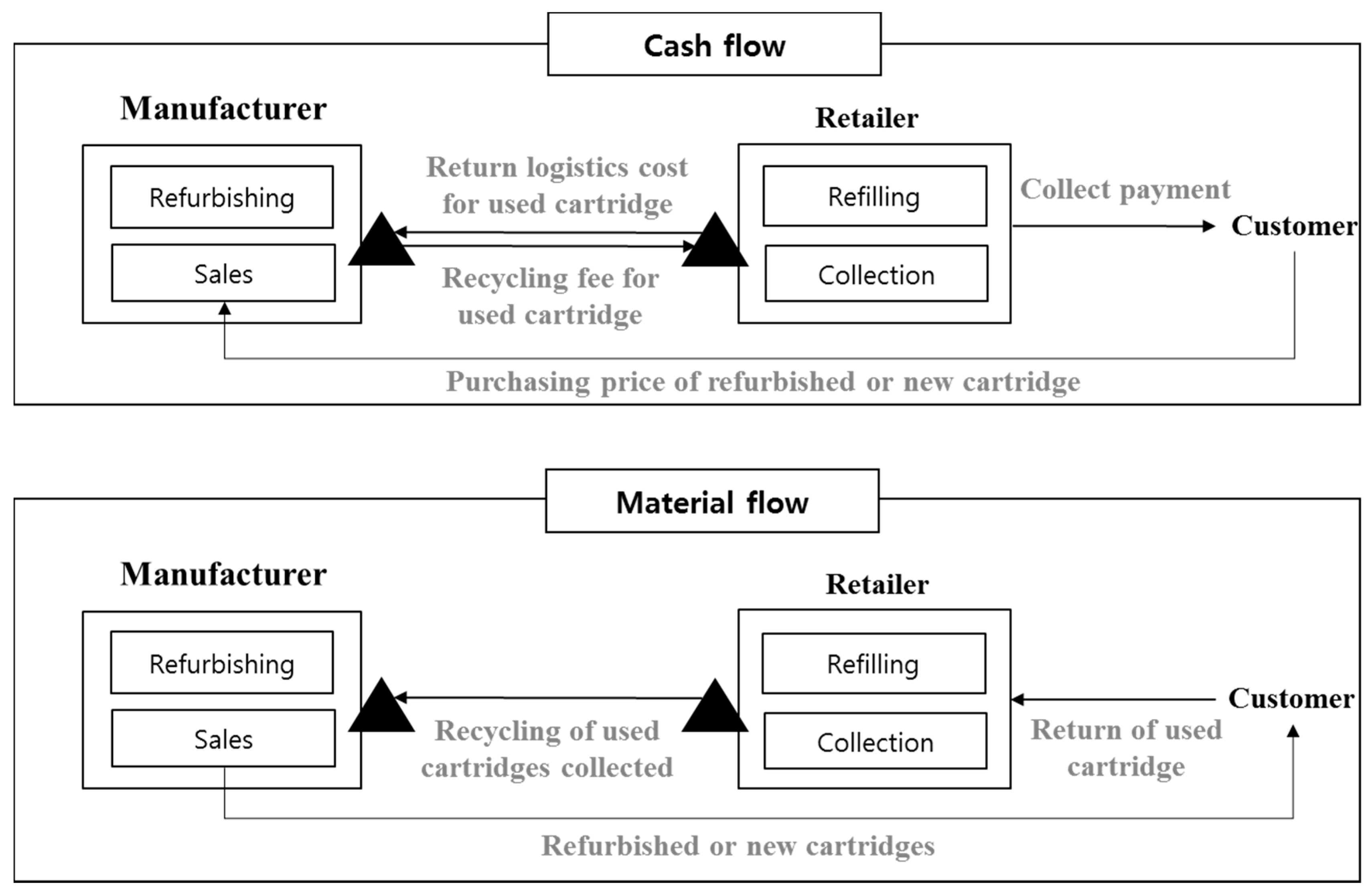
This study considered the reverse supply chain model in the print cartridge industry.
Figure 2 illustrates the model structure and the flow of cash and products between manufacturer and retailer.
We assumed that consumers who have used cartridges decide whether to return their used cartridges to the retailer or refill them. Refilling is usually less expensive than buying a new cartridge. If a consumer returns a used cartridge to the retailer, the retailer would offer a payment to the customer. When the number of used cartridges collected by the retailer reaches a certain quantity, they are transported to the manufacturer. The retailer pays the transportation cost for the collected cartridges. When the used cartridges are delivered to the manufacturer, a unit recycling fee is paid to the retailer. Kanda and Deshmukh [
21] stated that all used cartridges that have arrived at the manufacturer will go through a sorting process and then will be remanufactured based on their condition. In this paper, for simplicity, we assume that the retailer is not responsible for reselling the remanufactured cartridges.
The model includes two types of customers: those who prefer to refill their cartridges, because this is less expensive than buying new ones, and those who prefer to purchase new cartridges, because this guarantees high quality. We assume that both types of customer visit the retailer with used cartridges. The number of used cartridges returned to the retailer is calculated based on the number of customers who visit the retailer over a one-month period. The retailer then distributes the used cartridges to the manufacturer over the next month, and the remanufacturing of used cartridge for resale takes a further month. Accordingly, our model assumes that the lead time from the return of a cartridge to its remanufacture for resale is approximately three months.
We did not consider a detailed logistical network. Instead, we focus on the procedure of the contract between the retailer and manufacturer, rather than the specific supply chain network. Thus, we only consider the transportation cost of the retailer returning used cartridges to the manufacturer.
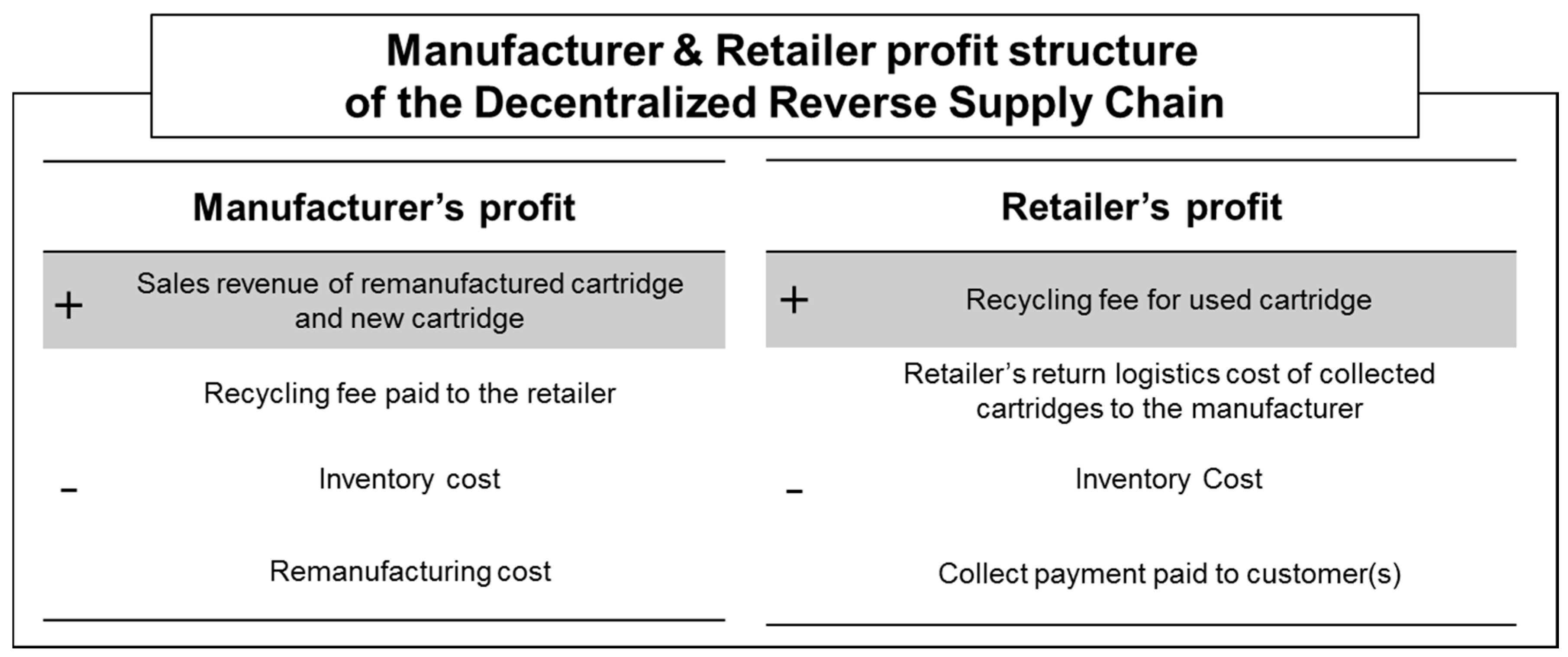
Figure 3 illustrates the profit structure of the retailer and the manufacturer under the decentralized model. The retailer’s costs are comprised of inventory costs, the reward paid to customers for used cartridges, and the transportation cost. Retailer’s revenue is the recycling fee paid by the manufacturer. The manufacturer’s burden includes inventory costs, remanufacturing process costs, and the recycling fee paid to the retailer. Manufacturer creates revenue through sales of remanufactured and new cartridges.
The manufacturer would like to collect more used cartridges, because more remanufactured products reduce the manufacturing cost of raw materials. Therefore, the manufacturer will propose contracts offering financial support to the retailer for increasing the manufacturer’s profit.
5. System Dynamics Modeling Approach
5.1. Causal Relationships
A causal loop diagram (CLD) depicts the relationships between the major variables within a feedback cycle. In a CLD, system variables are linked by arrows that show interdependencies and feedback processes between variables, and polarity markers associated with the arrows depict direct effects (positive) or inverse effects (negative).
Figure 4 depicts the CLD of the reverse supply chain model considered here. This diagram shows the relationships between the variables in our model, which include three negative feedback loops and two reinforcement loops.
Each coordination contract (manufacturer’s support strategy) influences the feedback loops. For example, if the manufacturer supports the collection payment paid by the retailer to the customer, this will influence the loops to modify the profit of the retailer and manufacturer.
The goal of the model is to construct the scenarios that occur under the various contracts used by the manufacturer to improve the collection rate of used products. This allows us to analyze the changes in the revenue and profit enjoyed by the manufacturer.
Figure 4 also indicates the causal relationship between the manufacturer’s contracts and the retailer. First, the manufacturer shares part of its profit to encourage the retailer to collect used products from customers. The retailer, in turn, uses the investment from the manufacturer to provide incentives to customers to return used cartridges and buy new ones. As such, the retailer’s activity benefits the manufacturer by encouraging the sale of more new products and providing used cartridges for the remanufacturing process, thereby reducing manufacturing costs. Second, by supporting the retailer’s transportation and collection payment costs, the manufacturer can expect to achieve higher profits. Reducing costs eventually increases profit, as the retailer can reward customers with higher collection payments.
5.2. Simulation Model
We conducted simulations to analyze the decision-making process of the manufacturer and retailer in the reverse supply chain model for used ink cartridges.
A system dynamics model was built using Vensim Pro 5.9e software (Ventana Systems: Salisbury, UK) (
Table 1). The detailed equations used in the model are described in
Appendix A.
(1) Manufacturer terms
The manufacturer makes a profit when new products are sold via forward supply channels. Customers who purchase new products through the forward channel are classified as new customers or previous customers who have returned their used products to the retailer. The total revenue of the manufacturer in the previous period can be defined as:
The manufacturer’s cost includes the cost of remanufacturing used cartridges, inventory cost, and the recycling fee paid to the retailer for used cartridges. The manufacturer’s inventory is calculated by subtracting the previous inventory and the quantity of used cartridges returned from the quantity of remanufactured used cartridges available for purchase. The quantity of used cartridges sent for remanufacturing cannot exceed the manufacturing capacity. The manufacturer pays a recycling fee to the retailer for each used cartridge. Therefore, the manufacturer’s costs in each period can be defined as:
As such, the manufacturer’s profit in each period can be defined as:
(2) Retailer terms
As customers who return their used cartridges to the retailer are assumed to buy new ones through the same retailer, a larger volume of used ink cartridges returned to the retailer corresponds to increased sales of new cartridges. While the retailer seeks to collect used ink cartridges to gain more of the manufacturer’s recycling fee, it is more significant that this gives the retailer more opportunities to sell new products to the customers returning used cartridges. The incentives offered by the retailer to the customers originate from the retailer’s profit in the previous period. New product sales are generated from new customers and customers who return used cartridges and buy new ones. Equation (7) shows that the retailer’s revenue is composed of sales profit from new cartridges and the recycling fee from the manufacturer:
We defined the probability of collecting cartridges from customers in terms of the customer willingness to return rather than refill. As shown in Equation (8), the probability of collecting used cartridges is determined by the difference between the cost of refilling and the cost of purchasing new products at the discounted price offered for returning the cartridges. A customer’s willingness to return rather than refill will increase as the discounted price of the new product approaches the cost of the refill; if there is no difference between the former and the latter, we assume that all refill-preferring customers will choose to return their used ink cartridges [
9].
Finally, Equation (9) indicates the number of customers who return used ink cartridges:
The costs incurred by the retailer, as shown in Equations (10)–(14), are determined by the size of the collection payment and the inventory cost. The retailer’s inventory is calculated by subtracting the previous inventory and the quantity of used cartridges returned from the quantity of used cartridges delivered to the manufacturer. The delivery quantity of used cartridges is smaller than the truck’s batch size.
As such, the retailer’s profit in each period can be defined as:
6. Experimental Design and Results
Table 2 shows simulation data used in this model [
4,
24].
Table 3 presents the results of Step 1, in which we calculated the individual profits of the manufacturer and retailer in a decentralized reverse supply chain model.
In Step 2, the profits are calculated under each of three contracts. In the case of incentive sharing (
Table 4), the acceptable range for the manufacturer was set to 15%. This means that even if the manufacturer shares 15% of the incentive paid by the retailer to the customer, the manufacturer can expect higher profits than in the decentralized reverse supply chain (equivalent to 0% incentive sharing).
Experiments for the two remaining contracts were also conducted. In the case of revenue sharing (
Table 5), the maximum allowance of the manufacturer was set to 30%. This means that, although the manufacturer shares up to 30% of its own profit with the retailer, the manufacturer is able to achieve profits above the $1,126,350 in the decentralized reverse supply chain.
When the manufacturer supports the transportation costs paid by the retailer, the maximum allowance level was the total cost. Even if the manufacturer supports all of the transportation costs incurred by the retailer, he can expect an additional profit of $71,850 (1,198,200 − 1,126,350) over the decentralized case (
Table 6).
In Step 3, the retailer selects the contract that maximizes their own profits under the maximum allowance level proposed by the manufacturer (see
Table 7). From the experimental results for Step 3, the best contract was found to be where the manufacturer shared 15% of his revenue with the retailer (
Table 8). In this case, the individual profits of the manufacturer and retailer were $1,145,250 and $137,348, respectively, and the return rate was 227,300 cartridges.
Table 9 presents the results of Step 4. In Step 4, the 15% revenue sharing is adjusted under the agreement of the two participants. As mentioned in our description of the research model, we considered the basic return fee as the adjustable factor. By gradually decreasing the return fee paid by the manufacturer to the retailer, we observed the change in the total profit (manufacturer profit plus retailer profit). From the results of this experiment, we found that total profits were maximized by retaining the existing return fee.
7. Conclusions
In this paper, we described a detailed contracting procedure between manufacturer and retailer under a cooperative reverse supply chain model. We first reviewed three contracting methods: (1) manufacturer revenue sharing; (2) manufacturer support of the collection fee paid to customers; and (3) manufacturer support of transportation costs paid by the retailer.
We first tested whether cooperation has a positive performance over the decentralized environment by comparing the relative profits. The results indicated that a contract between two partners is superior in terms of total profits. In the process of developing a contract between two partners, we showed how to identify the best contract and its maximum allowance level. We demonstrated that the best contract in terms of maximizing total profits is a revenue-sharing agreement in which the manufacturer shares 15% of his profit with the retailer.
This study also employs a system dynamics approach to model and analyze the detailed implementation of optimal contracts through an agreement between the manufacturer and retailer in the reverse supply chain. In a dynamic setting, the coordination can be considered as a Stackelberg game. We describe the reverse process of used print cartridges from consumers to manufacturer. We provide the conceptual, analytical, and computational tools for the modeling and analysis of the interrelationships among decision-makers in reverse supply chains, ranging from the manufacturer and retailer through to consumers. The models handle competition and cooperation, and yield the resulting returned product and profits in the chain. Game theory and the theories of variational inequalities and dynamical systems are synthesized and applied to describe the dynamics of the returned product’s price and flows, and the resulting profits. Our approach is rigorous and of sufficient generality and detail to provide an insight into the consumer behavior and structure of the complex return process of used products, which includes multiple decision-makers and their individualized and cooperative behavior.
Our results provide a practical decision-making framework for manufacturers and retailers/collectors in reverse supply chain management. We focused on how manufacturers and retailers develop and evaluate contracts so as to maximize their own profit with uncertain information. Expanding the contract procedure described in this study, will provide a useful and efficient decision methodology that can be applied to similar research areas such as the movie industry.
To summarize, our main contribution is first to describe how to design and implement the contracting process using system dynamic simulation technique and to demonstrate the detailed sequential decision making and mutual agreement progresses between two parties for maximizing coordinated profits. In future research, we intend to expand the current model to consider penalty costs imposed on the retailer. In the current study, we assumed that the retailer could always meet the manufacturer’s expected level of returned cartridges. However, the sharing of revenue or cost support from the manufacturer may depend on the number of used cartridges returned by the retailer. Thus, if the retailer does not adhere to the terms of the contract, the manufacturer may impose some penalty costs on the retailer.