Experimental Study of a Small Scale Hydraulic System for Mechanical Wind Energy Conversion into Heat
Abstract
:1. Introduction
2. Materials and Methods
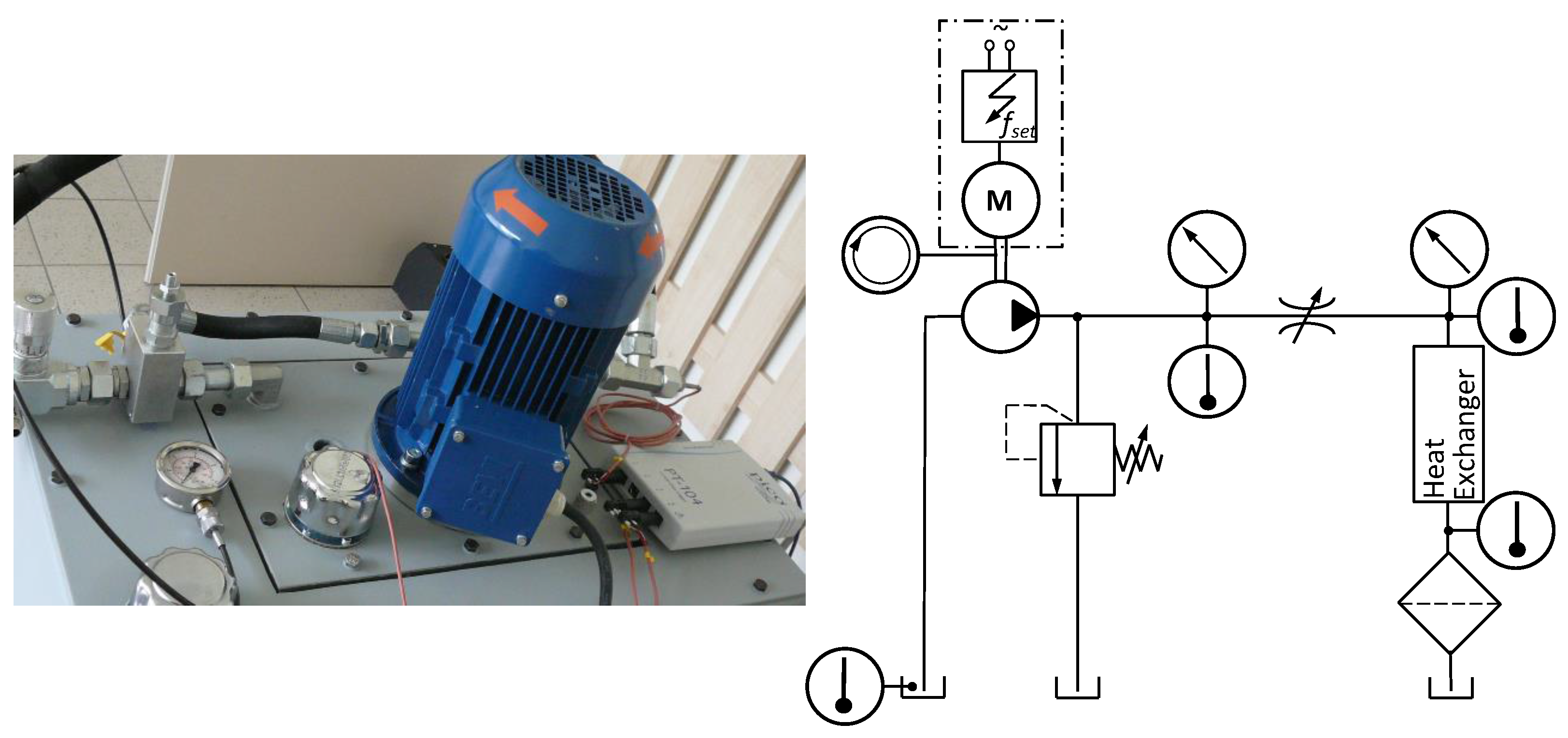
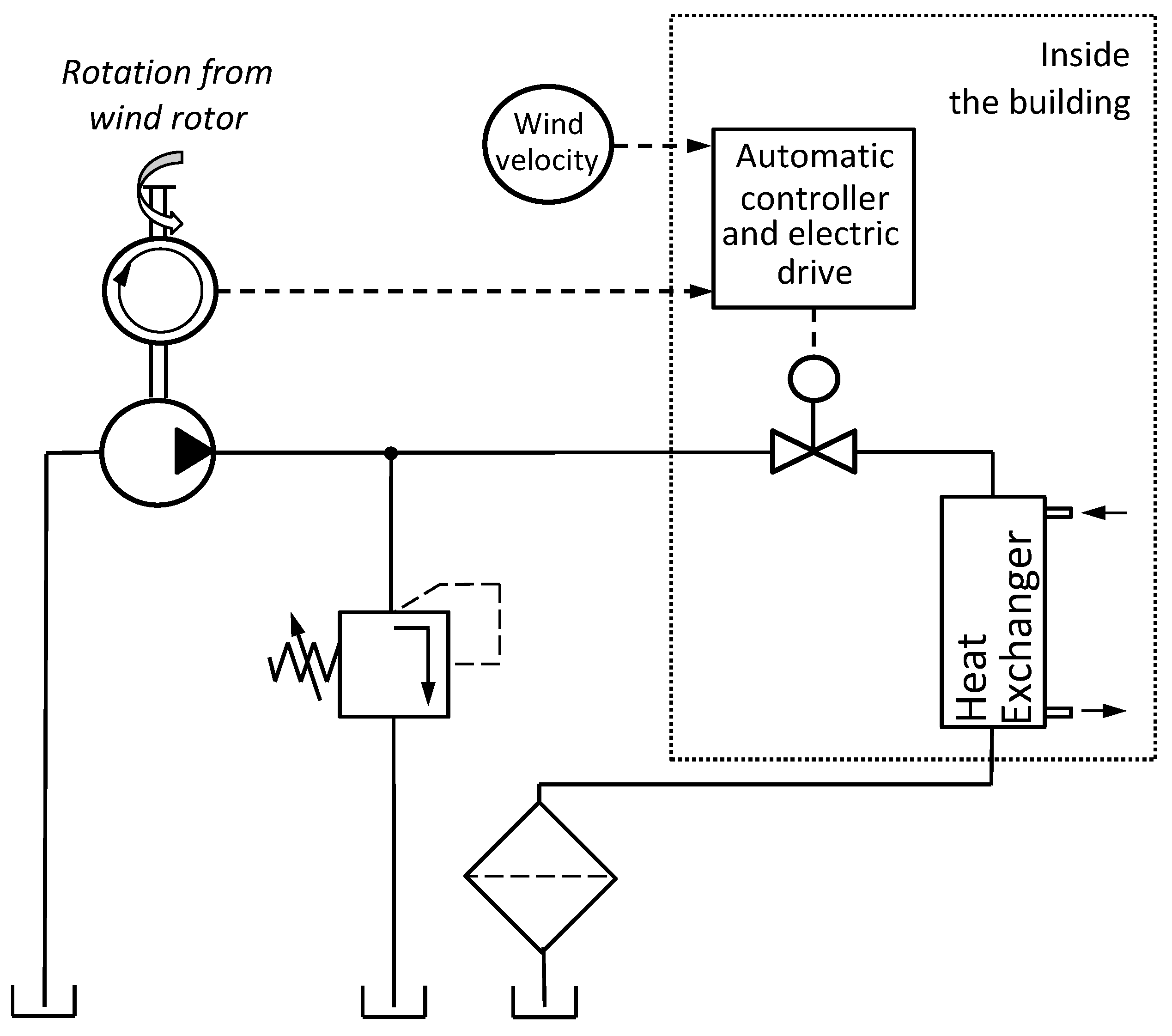
2.1. Experimental Setup
2.2. Experimental Methodology
3. Results
3.1. Mechanical Energy Simulation
3.2. Thermal Energy Generation
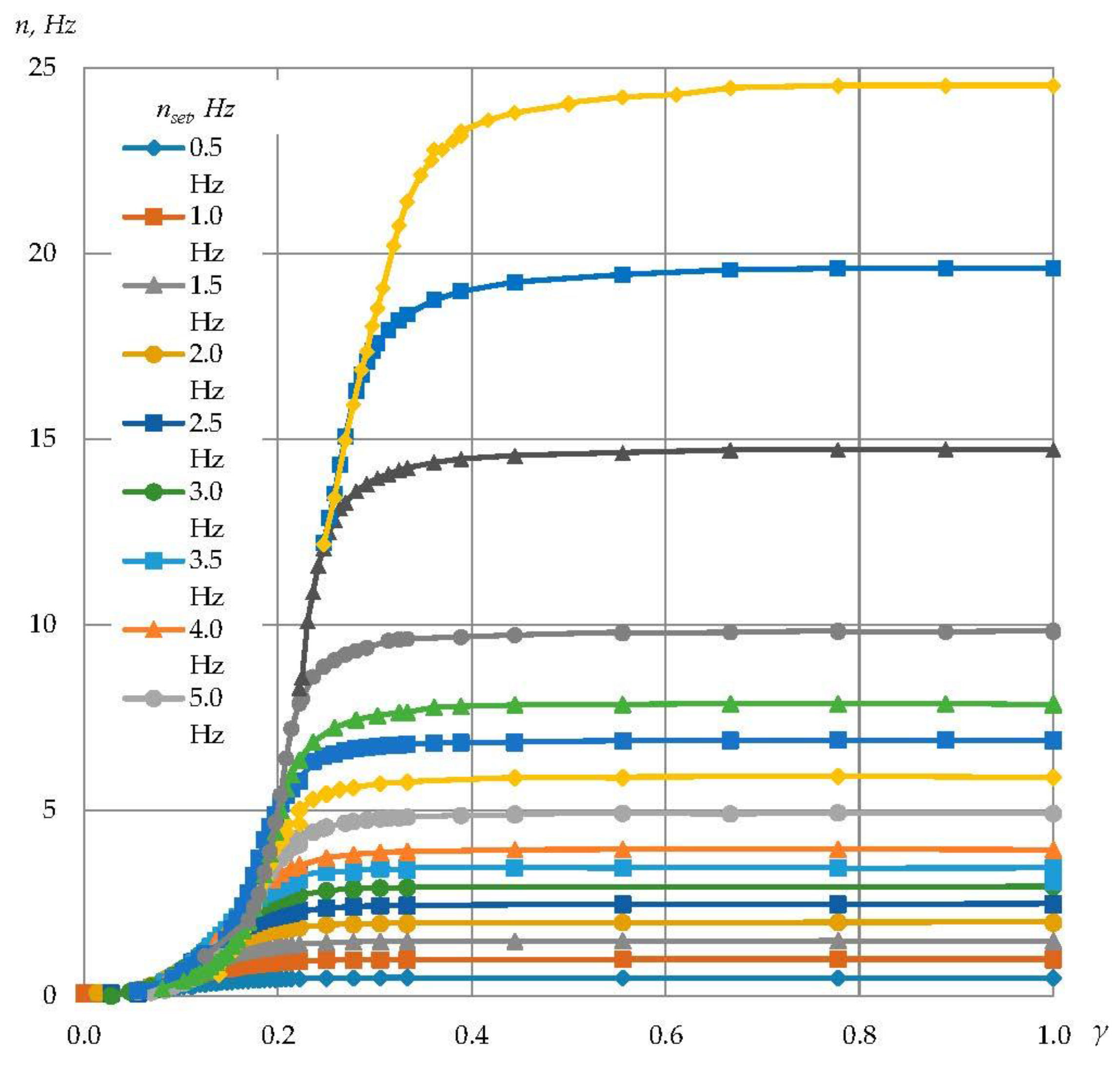
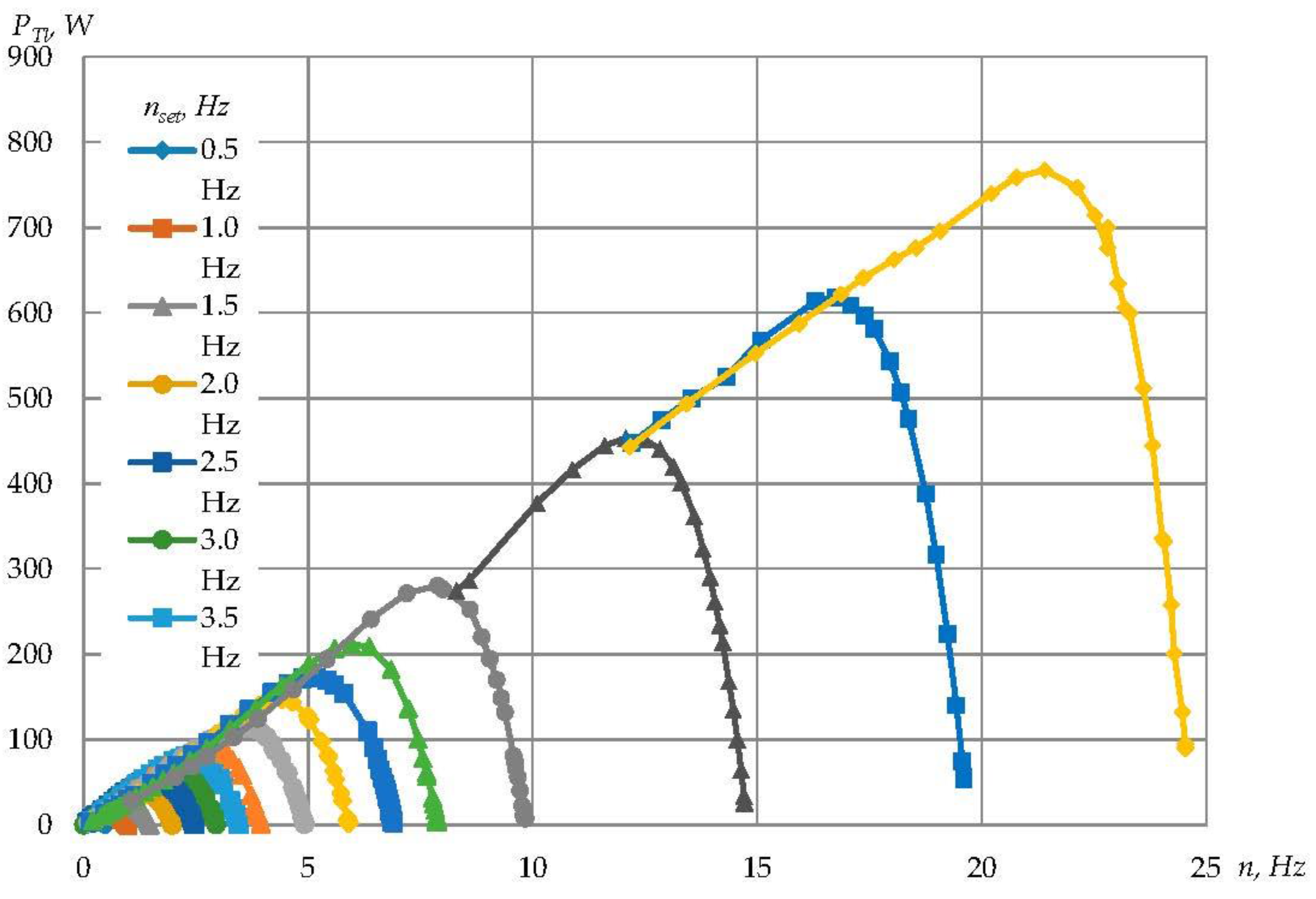
3.3. Analysis of the Automatic Control of the System
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| A | wind rotor swept area, m2 |
| c | specific heat capacity of oil, J/(kg·K) |
| cp | wind power conversion efficiency |
| d | internal diameter, m |
| fset | electric frequency, Hz |
| M | torque, N·m |
| mr | oil mass in the reservoir, kg |
| n | pump shaft rotation frequency, Hz |
| nr | wind rotor rotation frequency, Hz |
| nset | electromotor shaft rotation frequency, Hz |
| Phs_in | hydraulic pump shaft mechanical power, W |
| Phs_out | output thermal power of hydraulic system, W |
| Pm_out | electromotor shaft mechanical power, W |
| Pp_in | hydraulic pump’s input power, W |
| PT | thermal power, W |
| PT_loss | thermal power losses, W |
| PTf | thermal power from hydraulic losses in pipes and heat exchanger, W |
| PTl | thermal power generated in load regulation valve, W |
| PTp | thermal power generated in the pump, W |
| Pw | wind turbine’s output power, W |
| Q | volumetric flow rate, m3/s |
| t | time interval, s |
| Tr0 | initial temperature of the oil in the tank, K |
| Tout | oil temperature in the return pipe, K |
| Tr | oil temperature in the oil tank, K |
| v | wind velocity, m/s |
| Vp | nominal displacement of hydraulic pump, cm3/rot |
| w | average oil flow velocity, m/s |
| γ | opening degree of the load regulation valve, dimensionless |
| Δp | pressure drop, Pa |
| ζ | local loss coefficient |
| ηhs | hydraulic system efficiency for thermal energy conversion |
| ηpV | pump volumetric efficiency coefficient |
| ρ | oil density, kg/m3 |
| ρair | air density, kg/m3 |
References
- European Wind Energy Association (EWEA). Wind in Power: 2015 European Statistics. Available online: http://www.ewea.org/fileadmin/files/library/publications/statistics/EWEA-Annual-Statistics-2015.pdf (accessed on 15 April 2016).
- United Nations Conference on Climate Change. Available online: http://www.cop21.gouv.fr/en/ (accessed on 15 December 2015).
- United Nations. Framework Convention on Climate Change 1992. Available online: https://unfccc.int (accessed on 15 April 2016).
- Cheng, M.; Zhu, Y. The state of the art of wind energy conversion systems and technologies: A review. Energy Convers. Manag. 2014, 88, 332–347. [Google Scholar] [CrossRef]
- Tummala, A.; Velamati, R.K.; Sinha, D.K.; Indraja, V.; Krishna, V.H. A review on small scale wind turbines. Renew. Sustain. Energy Rev. 2016, 56, 1351–1371. [Google Scholar] [CrossRef]
- Ishugah, T.F.; Li, Y.; Wang, R.Z.; Kiplagat, J.K. Advances in wind energy resource exploitation in urban environment: A review. Renew. Sustain. Energy Rev. 2014, 37, 613–626. [Google Scholar] [CrossRef]
- Miškinis, V. Lietuvos energetika / Energy in Lithuania 2013; Lithuanian Energy Institute: Kaunas, Lithuania, 2014. [Google Scholar]
- International Energy Data and Analysis—Lithuania. Available online: http://www.eia.gov/ (accessed on 10 January 2016).
- European Parliament, Council of the European Union. EU Directive 2010/31/EU of the European Parliament and of the Council of 19 May 2010 on the energy performance of buildings (recast). Off. J. Eur. Union 2010, 153, 13–35. [Google Scholar]
- Olatomiwa, L.; Mekhilef, S.; Ismail, M.S.; Moghavvemi, M. Energy management strategies in hybrid renewable energy systems: A review. Renew. Sustain. Energy Rev. 2016, 62, 821–835. [Google Scholar] [CrossRef]
- Del Granado, P.C.; Pang, Z.; Wallace, S.W. Synergy of smart grids and hybrid distributed generation on the value of energy storage. Appl. Energy 2016, 170, 476–488. [Google Scholar] [CrossRef]
- Lott, M.C.; Kim, S.-I. Technology Roadmap: Energy Storage; International Energy Agency: Paris, France, 2014. [Google Scholar]
- Fazlollahi, S.; Schüler, N.; Maréchal, F. A solid thermal storage model for the optimization of buildings operation strategy. Energy 2015, 88, 209–222. [Google Scholar] [CrossRef]
- Okazaki, T.; Shirai, Y.; Nakamura, T. Concept study of wind power utilizing direct thermal energy conversion and thermal energy storage. Renew. Energy 2015, 83, 332–338. [Google Scholar] [CrossRef]
- Černeckienė, J. Usage of the Wind Energy for Heating of the Energy-Efficient Buildings: Analysis of Possibilities. J. Sustain. Archit. Civ. Eng. 2015, 10, 58–65. [Google Scholar] [CrossRef]
- Knecht, J.E. Wind Driven Heating System. 1983, p. 8. Available online: https://www.google.ch/patents/US4366779 (accessed on 15 May 2016).
- Ashiklan, B. Wind Motor Operated Heating System. 1973, p. 5. Available online: https://www.google.ch/patents/US3752395 (accessed on 15 May 2016).
- Ashiklan, B. Wind Operated Heating System. 1974, p. 6. Available online: https://www.google.com/patents/US3783858 (accessed on 15 May 2016).
- RISØ. The UNDP/GEF Baltic Wind Atlas; Risø National Laboratory: Roskilde, Denmark, 2003; Volume 1402. [Google Scholar]
- Troen, I.; Petersen, E.L. European Wind Atlas; Risø National Laboratory: Roskilde, Denmark, 1989. [Google Scholar]
- Žiedelis, S. Hydraulic and Pneumatic Systems; Technologija: Kaunas, Lithuania, 2009. [Google Scholar]
- Johnson, R.W. The Handbook of Fluid Dynamics; Springer-Verlag GmbH & Co: Berlin, Germany, 2000. [Google Scholar]
- Street, R.L.; Watters, G.Z.; Vennard, J.K. Elementary Fluid Mechanics; John Wiley & Sons: Toronto, ON, Canada, 1996. [Google Scholar]
- Huang, S.-C.; Lo, S.-L.; Lin, Y.-C. To Re-Explore the Causality between Barriers to Renewable Energy Development: A Case Study of Wind Energy. Energies 2013, 6, 4465–4488. [Google Scholar] [CrossRef]
- Jianu, O.; Rosen, M.A.; Naterer, G. Noise pollution prevention in wind turbines: Status and recent advances. Sustainability 2012, 4, 1104–1117. [Google Scholar] [CrossRef]
- Mathew, S. Wind Energy: Fundamentals, Resources Analysis and Economics; Springer: Berlin, Germany, 2006. [Google Scholar]
- Climatology Division at Lithuanian Hydrometeorological Service under the Ministry of Environment. Climate averages for Lithuania 1981–2010. 2013. Available online: http://www.meteo.lt/documents/20181/103901/Lietuvos_klimatas_09_25.pdf/e307f875-d20b-4a4d-aa90-c66a4dd57885 (accessed on 15 May 2016).
- Jacobs, P. Thermodynamics; Imperial College Press: London, UK, 2013. [Google Scholar]
- Commission of the European Communities. Action Plan for Energy Efficiency: Realising the Potential. 2006. Available online: http://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52006DC0545&from=EN (accessed on 15 May 2016).
- Rosso-Cerón, A.M.; Kafarov, V. Barriers to social acceptance of renewable energy systems in Colombia. Curr. Opin. Chem. Eng. 2015, 10, 103–110. [Google Scholar] [CrossRef]
- Painuly, J.P. Barriers to renewable energy penetration: A framework for analysis. Renew. Energy 2001, 24, 73–89. [Google Scholar] [CrossRef]
- Tokimatsu, K.; Konishi, S.; Ishihara, K.; Tezuka, T. Global zero emission scenario: Role of innovative technologies. Energy Procedia 2014, 61, 164–167. [Google Scholar] [CrossRef]
- Tokimatsu, K.; Konishi, S.; Ishihara, K.; Tezuka, T.; Yasuoka, R.; Nishio, M. Role of innovative technologies under the global zero emissions scenarios. Appl. Energy 2014, 162, 1483–1493. [Google Scholar] [CrossRef]
- Yuan, H.; Zhou, P.; Zhou, D. What is low-carbon development? A conceptual analysis. Energy Procedia 2011, 5, 1706–1712. [Google Scholar] [CrossRef]
- Brauers, W.K.M.; Kracka, M.; Zavadskas, E.K. Lithuanian case study of masonry buildings from the Soviet period. J. Civ. Eng. Manag. 2012, 18, 444–456. [Google Scholar] [CrossRef]
- Denafas, G.; Sitnikovas, D.; Galinis, A.; Kudrenickis, I.; Klavs, G.; Kuusik, R. Predicting CO2 and SO2 emissions in the Baltic States through reorganization of energy infrastructure. Environ. Int. 2004, 30, 1045–1053. [Google Scholar] [CrossRef] [PubMed]
- Roos, I.; Soosaar, S.; Volkova, A.; Streimikene, D. Greenhouse gas emission reduction perspectives in the Baltic States in frames of EU energy and climate policy. Renew. Sustain. Energy Rev. 2012, 16, 2133–2146. [Google Scholar] [CrossRef]
- Streimikiene, D.; Balezentis, T. Kaya identity for analysis of the main drivers of GHG emissions and feasibility to implement EU “20-20-20” targets in the Baltic States. Renew. Sustain. Energy Rev. 2016, 58, 1108–1113. [Google Scholar] [CrossRef]
- Blumberga, A.; Lauka, D.; Barisa, A.; Blumberga, D. Modelling the Baltic power system till 2050. Energy Convers. Manag. 2016, 107, 67–75. [Google Scholar] [CrossRef]
- Streimikienė, D. Review of financial support from EU Structural Funds to sustainable energy in Baltic States. Renew. Sustain. Energy Rev. 2016, 58, 1027–1038. [Google Scholar] [CrossRef]
- Lithuanian Ministry of Environment. STR 2.01.09:2012 The energy efficiency in buildings, The energy certification of buildings, Lithuanian building regulations. 2012. Available online: http://www3.lrs.lt/pls/inter3/dokpaieska.showdoc_l?p_id=431646&p_query=&p_tr2=2 (accessed on 15 May 2016).
- Thompson, J.W.; Freeman, P.A. Wind-Powered Impeller-Mixer. Patents US 4292540 A, 29 September 1980. [Google Scholar]
- Kavolynas, A. Application of solar and wind energy. Ph.D. Thesis, Aleksandras Stulginskis University, Akademija, Lithuania, 2011. [Google Scholar]


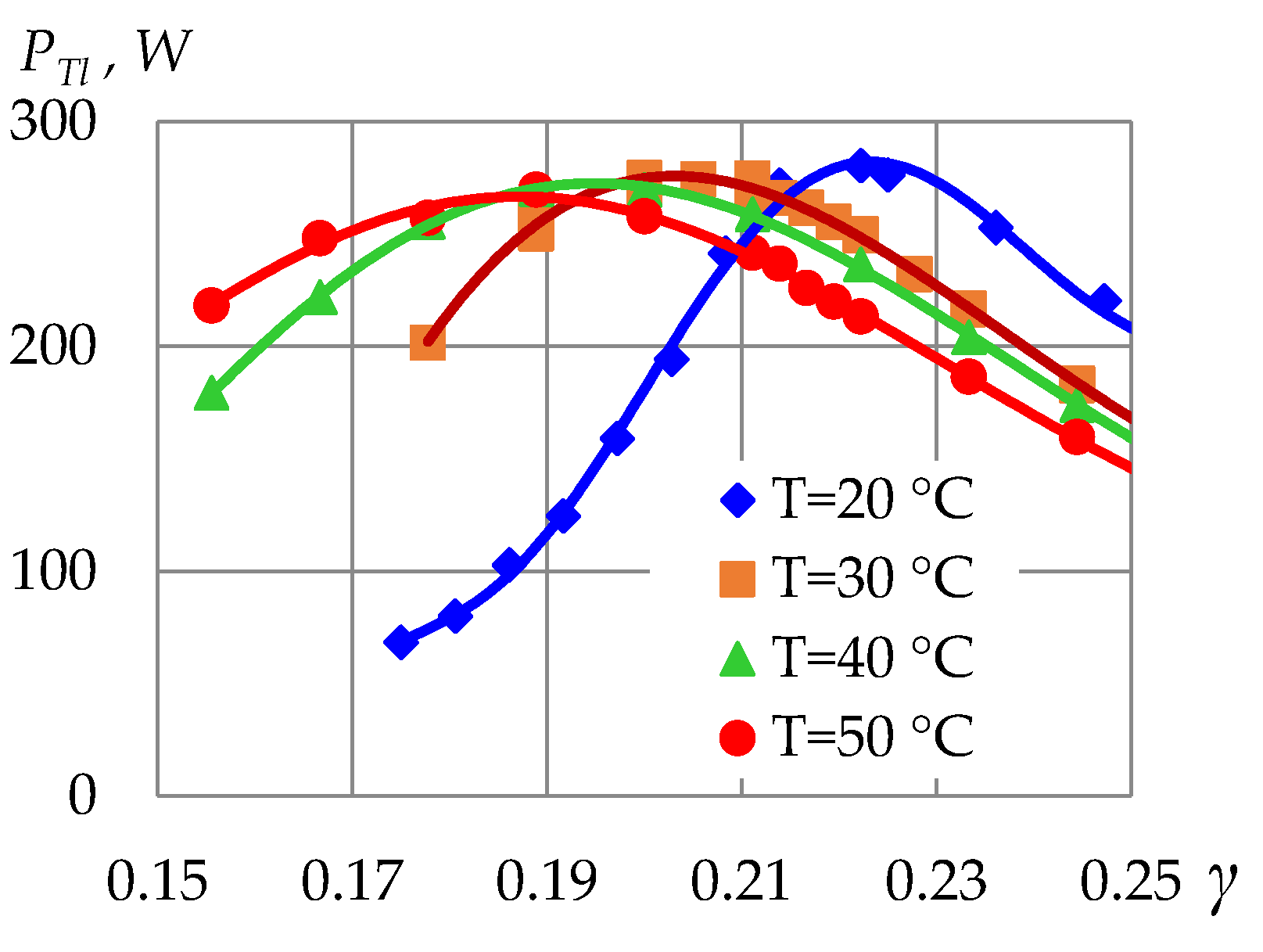
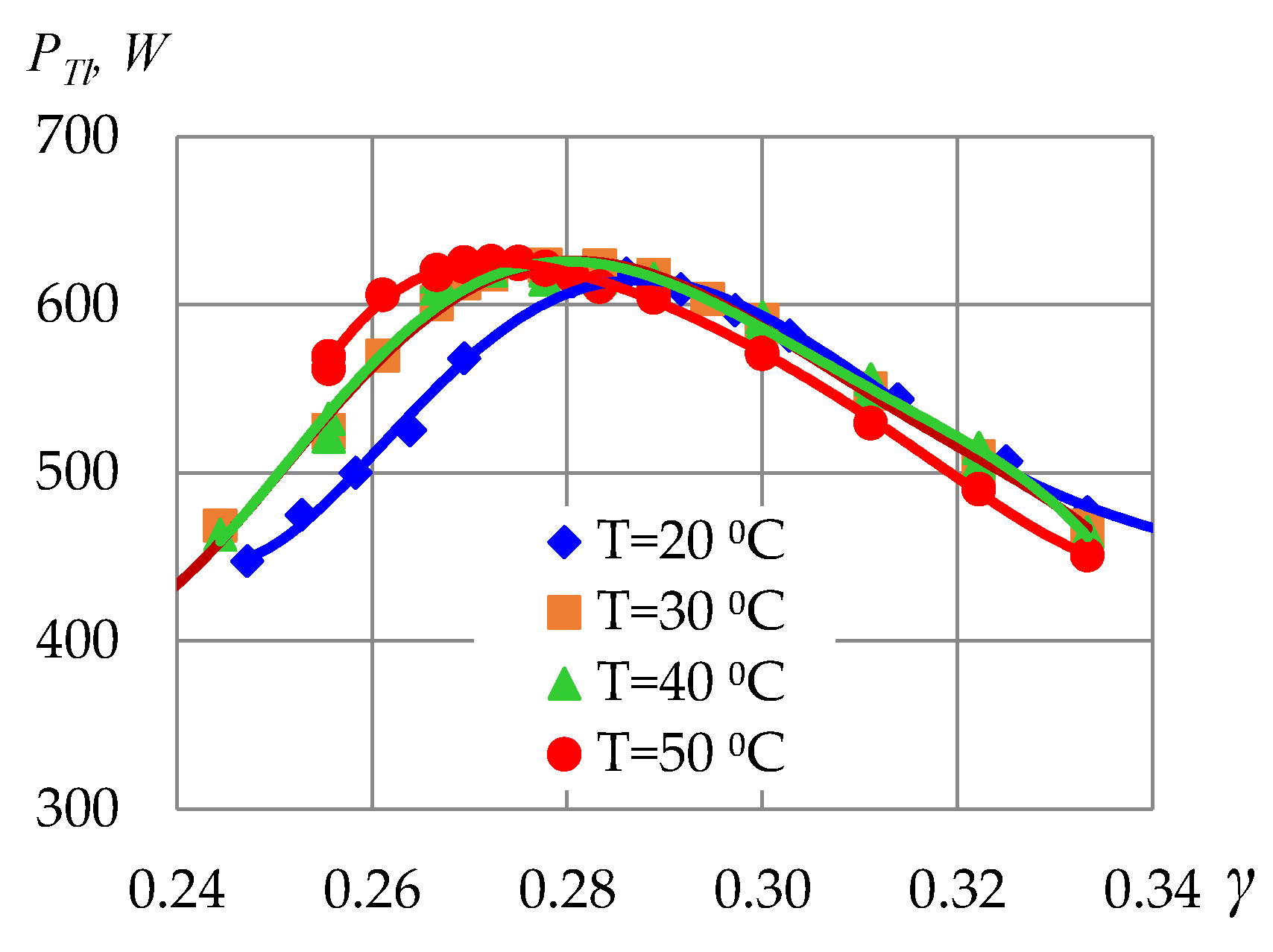
| nset, Hz | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
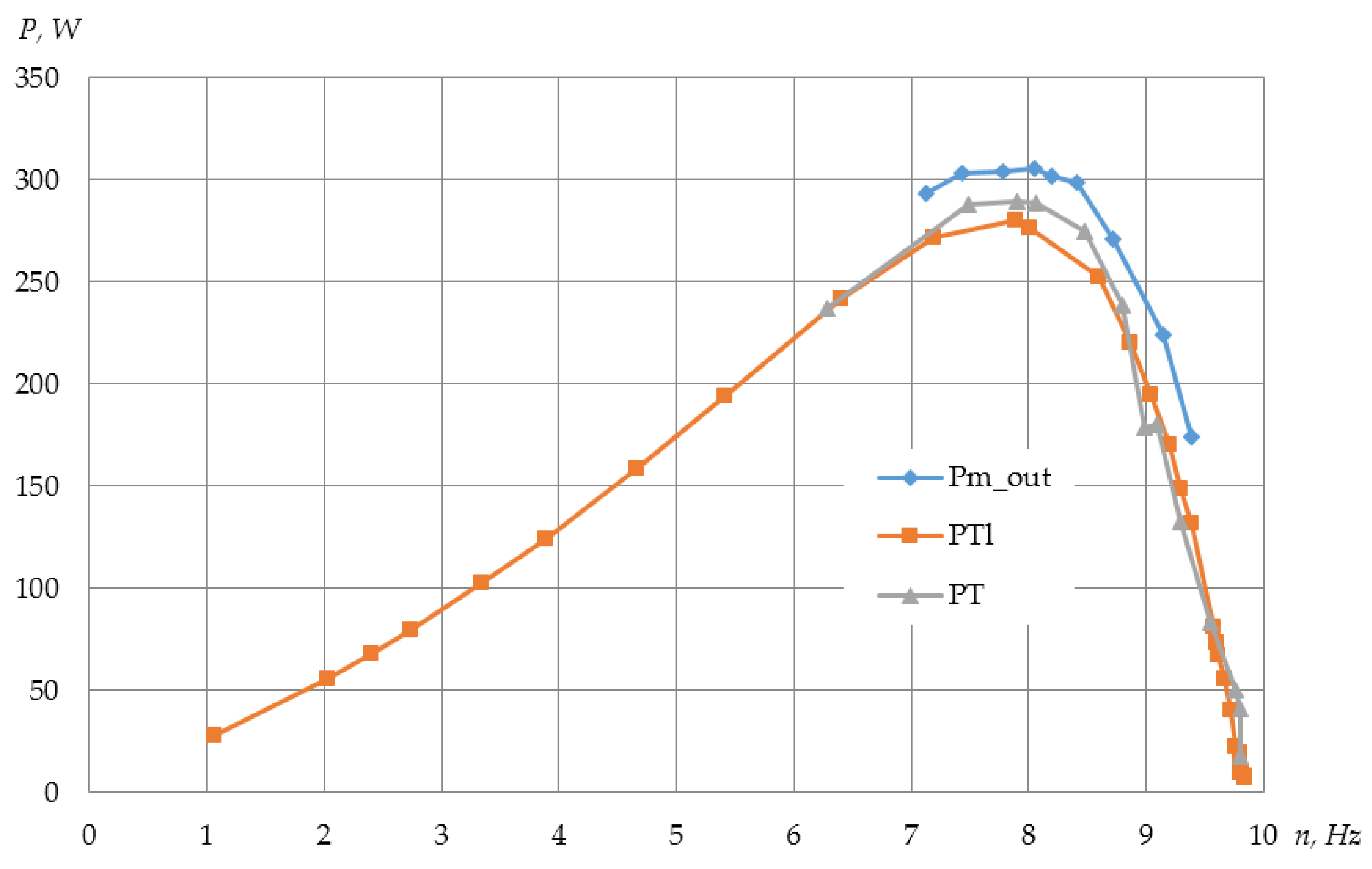
| Pm_out, W | 4.7 | 16.3 | 28.4 | 44.5 | 59.4 | 74.2 | 84.6 | 100.7 |
| nset, Hz | 5 | 6 | 7 | 8 | 10 | 15 | 20 | 25 |
| Pm_out, W | 122.5 | 159.9 | 193.8 | 233.0 | 305.9 | 518.1 | 728.7 | 959.8 |
| nset, Hz | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| v *, m/s | 1.18 | 1.79 | 2.16 | 2.50 | 2.76 | 2.97 | 3.10 | 3.29 |
| Lithuania/average v, m/s | 2.52 ÷ 4.55 | |||||||
| Latvia/average v, m/s | 2.68 ÷ 4.22 | |||||||
| Estonia/average v, m/s | 3.95 ÷ 6.86 | |||||||
| nset, Hz | 5 | 6 | 7 | 8 | 10 | 15 | 20 | 25 |
| v *, m/s | 3.51 | 3.83 | 4.09 | 4.35 | 4.76 | 5.67 | 6.36 | 6.97 |
| Lithuania/average v, m/s | 2.52 ÷ 4.55 | |||||||
| Latvia/average v, m/s | 2.68 ÷ 4.22 | |||||||
| Estonia/average v, m/s | 3.95 ÷ 6.86 | |||||||
| No. | Working Regime of the System | Opening Degree of the Valve, γ | Rotation Frequency, n and Torque, M | Pressure Drop, Δp | Flow Rate, Q |
|---|---|---|---|---|---|
| 1 | Unloaded system | γ = 1 | n = nmax M ≈ 0 | Δp ≈ 0 | Q = Qmax |
| 2 | System loading | γ ⟶ γopt (0 < γ < 1) | n ⟶ nopt M ⟶ Mopt | Δp ⟶ Δpopt | Q ⟶ Qopt |
| 3 | Rated regime(optimal performance) | γ = γopt | n = nopt M = Mopt | Δp = Δpopt | Q = Qopt |
| 4 | System overloading | γ ⟶ 0 (0 < γ < 1) | n ⟶ 0 M ⟶ Mmax | Δp ⟶ Δpmax | Q ⟶ 0 |
| 5 | Overloaded system | γ ≈ 0 | n ≈ 0 M = Mmax | Δp↓ | Q ≈ 0 |
| nset, Hz | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| v*, m/s | 1.18 | 1.79 | 2.16 | 2.50 | 2.76 | 2.97 | 3.10 | 3.29 |
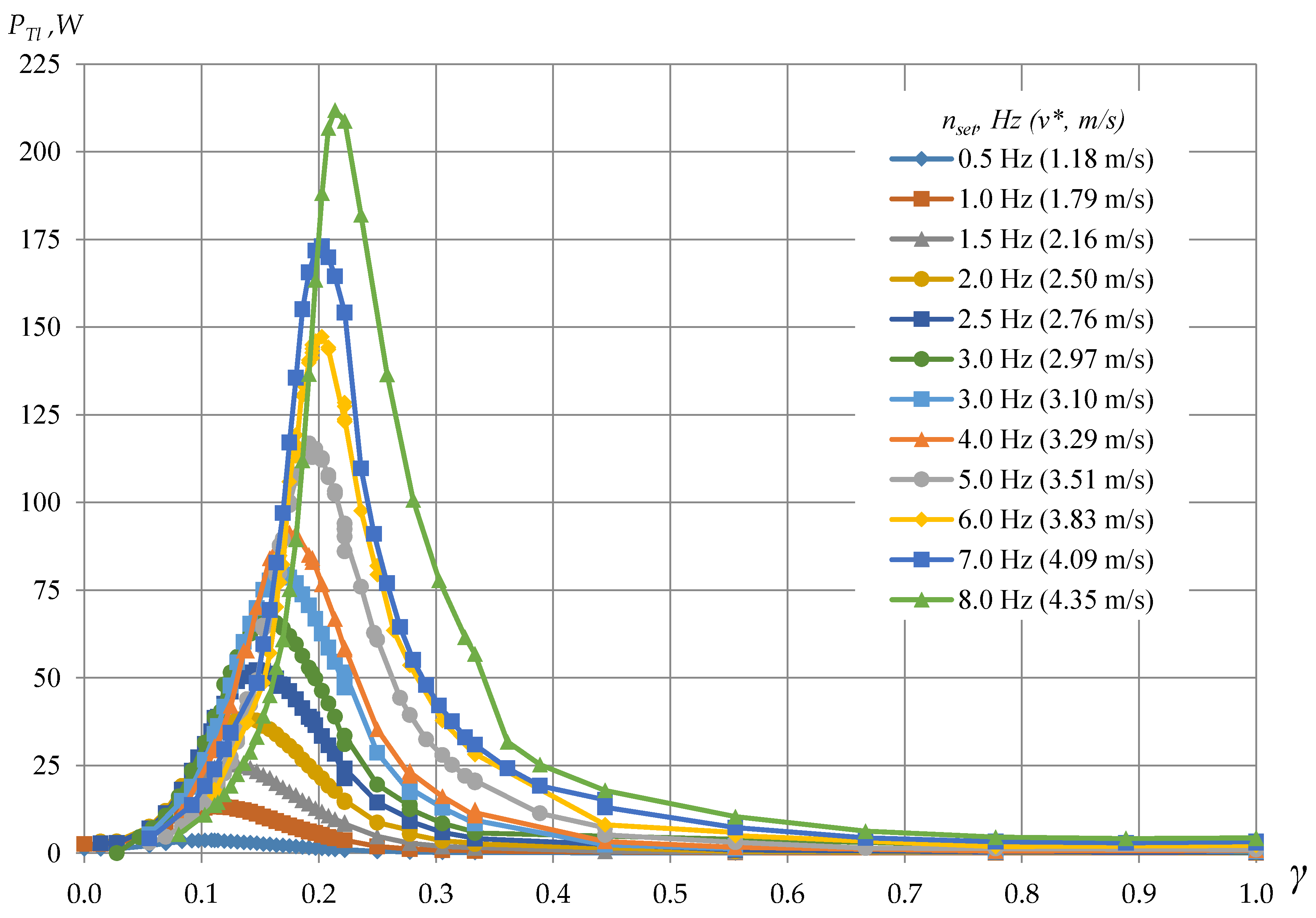
| γopt_20 °C | 0.108 | 0.114 | 0.125 | 0.136 | 0.147 | 0.158 | 0.167 | 0.181 |
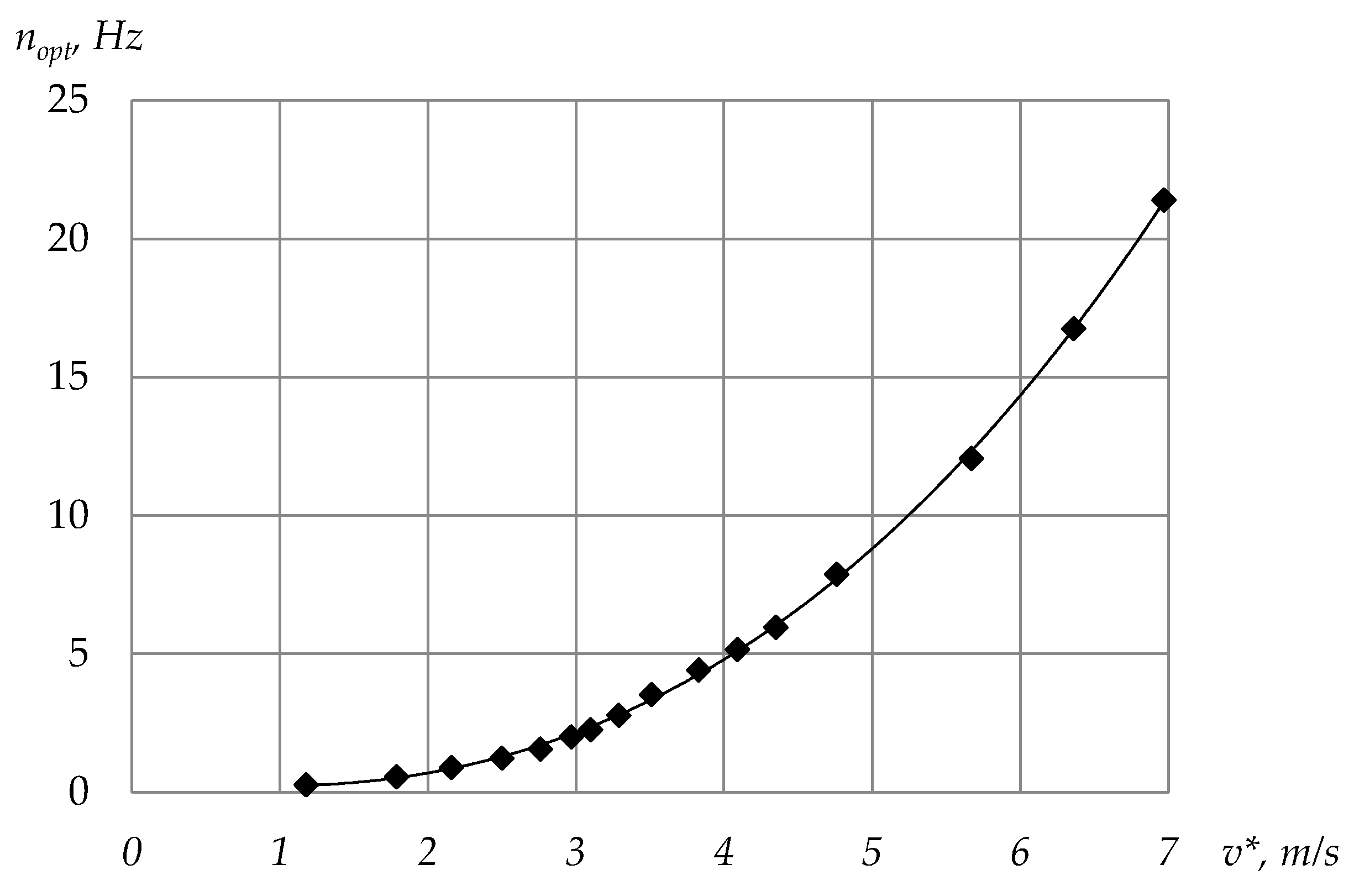
| nopt, Hz | 0.28 | 0.57 | 0.90 | 1.23 | 1.56 | 2.01 | 2.27 | 2.79 |
| PTl_max, W | 3.7 | 13.3 | 25.4 | 38.5 | 52.2 | 66.3 | 80.8 | 91.2 |
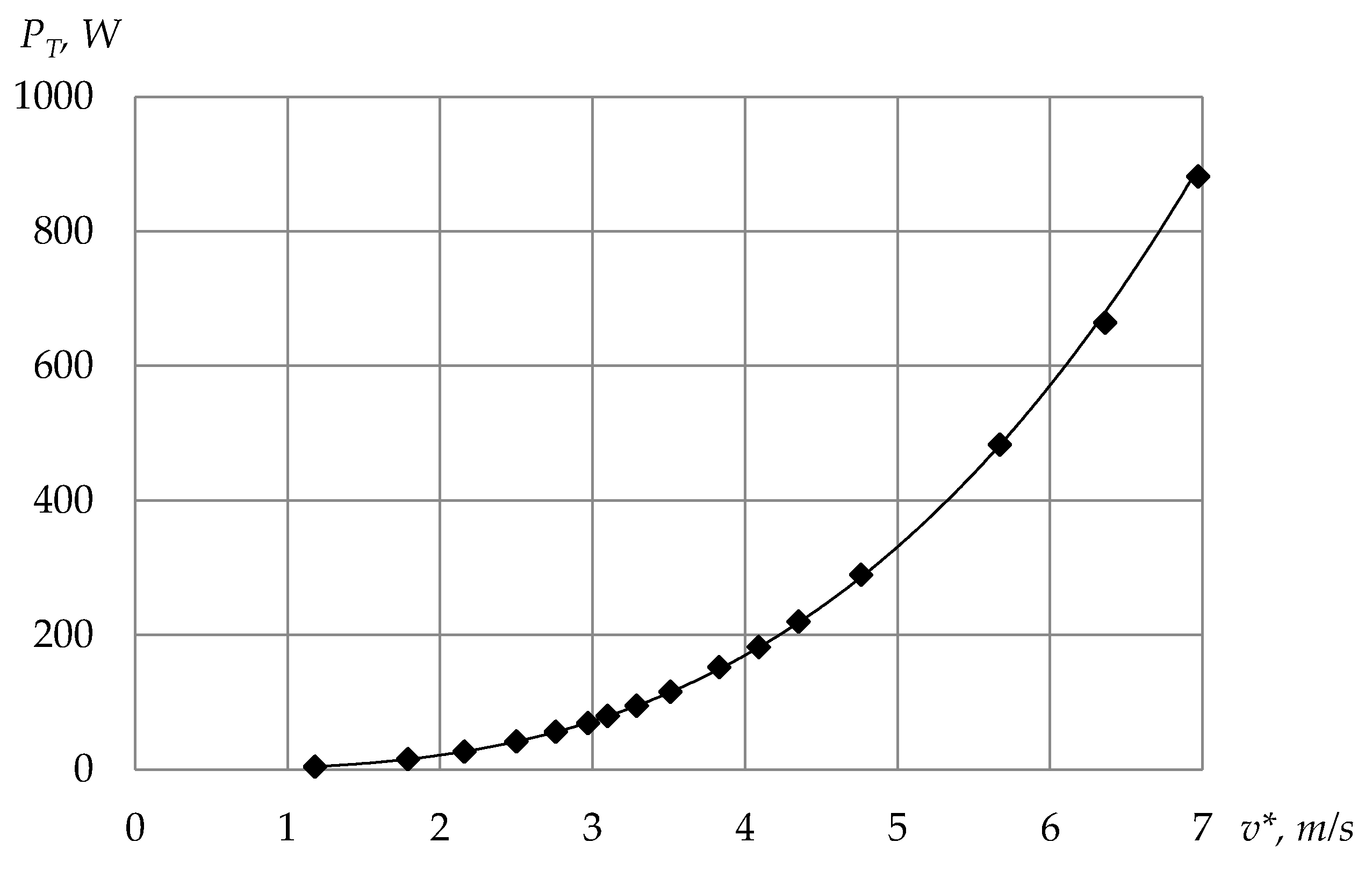
| PT_max, W | 4.4 | 15.4 | 26.5 | 41.9 | 56.1 | 69.1 | 79.8 | 95.1 |
| ηhs | 0.94 | 0.95 | 0.93 | 0.94 | 0.94 | 0.93 | 0.94 | 0.94 |
| nset, Hz | 5 | 6 | 7 | 8 | 10 | 15 | 20 | 25 |
| v*, m/s | 3.51 | 3.83 | 4.09 | 4.35 | 4.76 | 5.67 | 6.36 | 6.97 |
| γopt_20 °C | 0.192 | 0.203 | 0.203 | 0.214 | 0.222 | 0.247 | 0.286 | 0.333 |
| nopt, Hz | 3.54 | 4.42 | 5.17 | 5.96 | 7.88 | 12.07 | 16.75 | 21.40 |
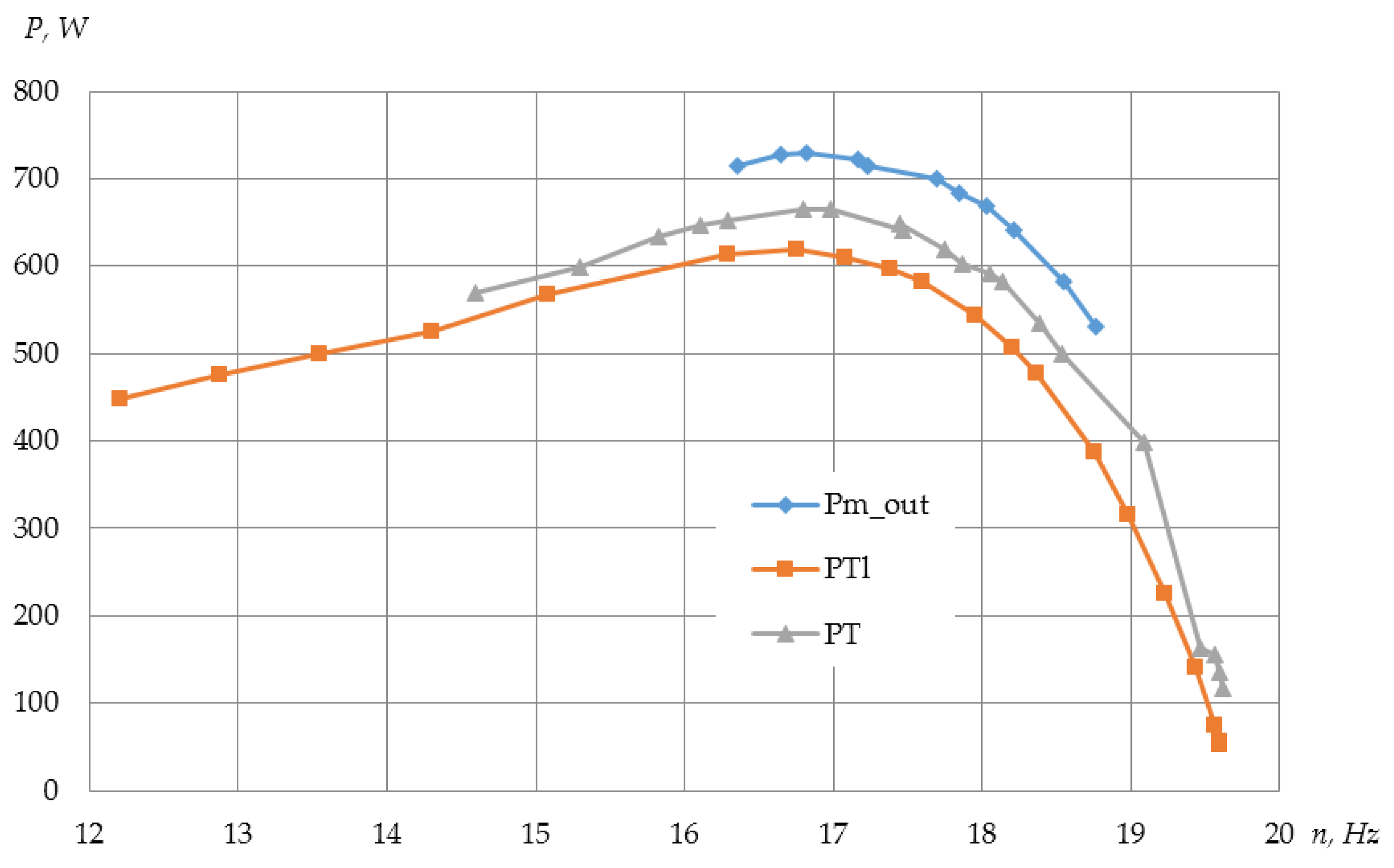
| PTl_max, W | 116.9 | 147.3 | 173.0 | 211.9 | 280.3 | 453.3 | 618.5 | 767.6 |
| PT_max, W | 115.8 | 151.9 | 181.9 | 220.0 | 289.5 | 483.1 | 664.2 | 881.9 |
| ηhs | 0.95 | 0.95 | 0.94 | 0.94 | 0.95 | 0.93 | 0.91 | 0.92 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zdankus, T.; Cerneckiene, J.; Jurelionis, A.; Vaiciunas, J. Experimental Study of a Small Scale Hydraulic System for Mechanical Wind Energy Conversion into Heat. Sustainability 2016, 8, 637. https://doi.org/10.3390/su8070637
Zdankus T, Cerneckiene J, Jurelionis A, Vaiciunas J. Experimental Study of a Small Scale Hydraulic System for Mechanical Wind Energy Conversion into Heat. Sustainability. 2016; 8(7):637. https://doi.org/10.3390/su8070637
Chicago/Turabian StyleZdankus, Tadas, Jurgita Cerneckiene, Andrius Jurelionis, and Juozas Vaiciunas. 2016. "Experimental Study of a Small Scale Hydraulic System for Mechanical Wind Energy Conversion into Heat" Sustainability 8, no. 7: 637. https://doi.org/10.3390/su8070637
APA StyleZdankus, T., Cerneckiene, J., Jurelionis, A., & Vaiciunas, J. (2016). Experimental Study of a Small Scale Hydraulic System for Mechanical Wind Energy Conversion into Heat. Sustainability, 8(7), 637. https://doi.org/10.3390/su8070637







