Issues of Application of Machine Learning Models for Virtual and Real-Life Buildings
Abstract
:1. Introduction
2. Three Machine Learning Algorithms
2.1. Artificial Neural Network
2.2. Support Vector Machine
2.3. Gaussian Process
3. First Case Study: A Virtual Building
3.1. Issue #1: Reproducibility
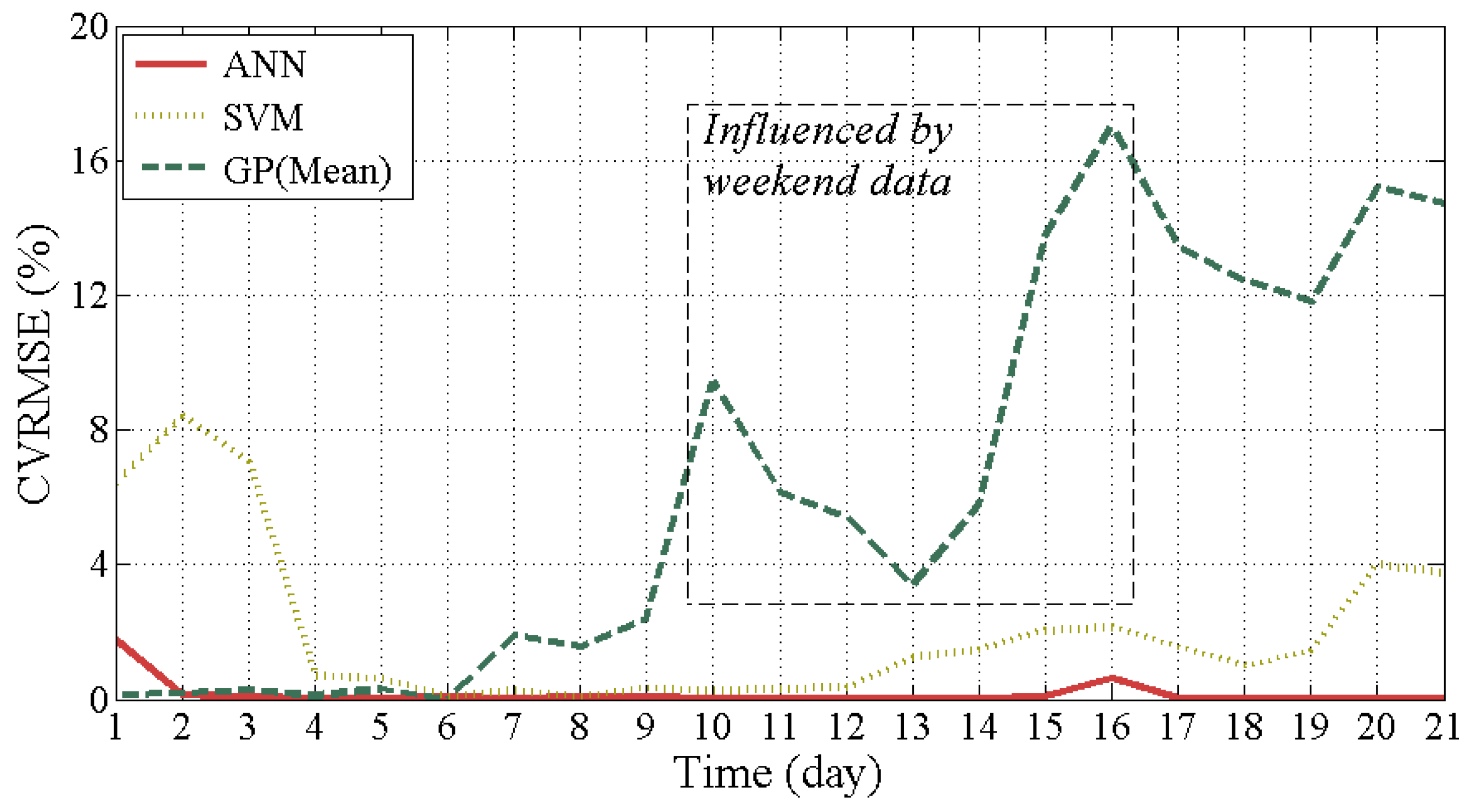
3.2. Issue #2: Training Period
3.3. Issue #3–1: Selection of Inputs (Virtual Building)
4. Second Case Study: A Real-Life Building
4.1. Issue #3–2: Selection of Inputs (Real-Life Building)
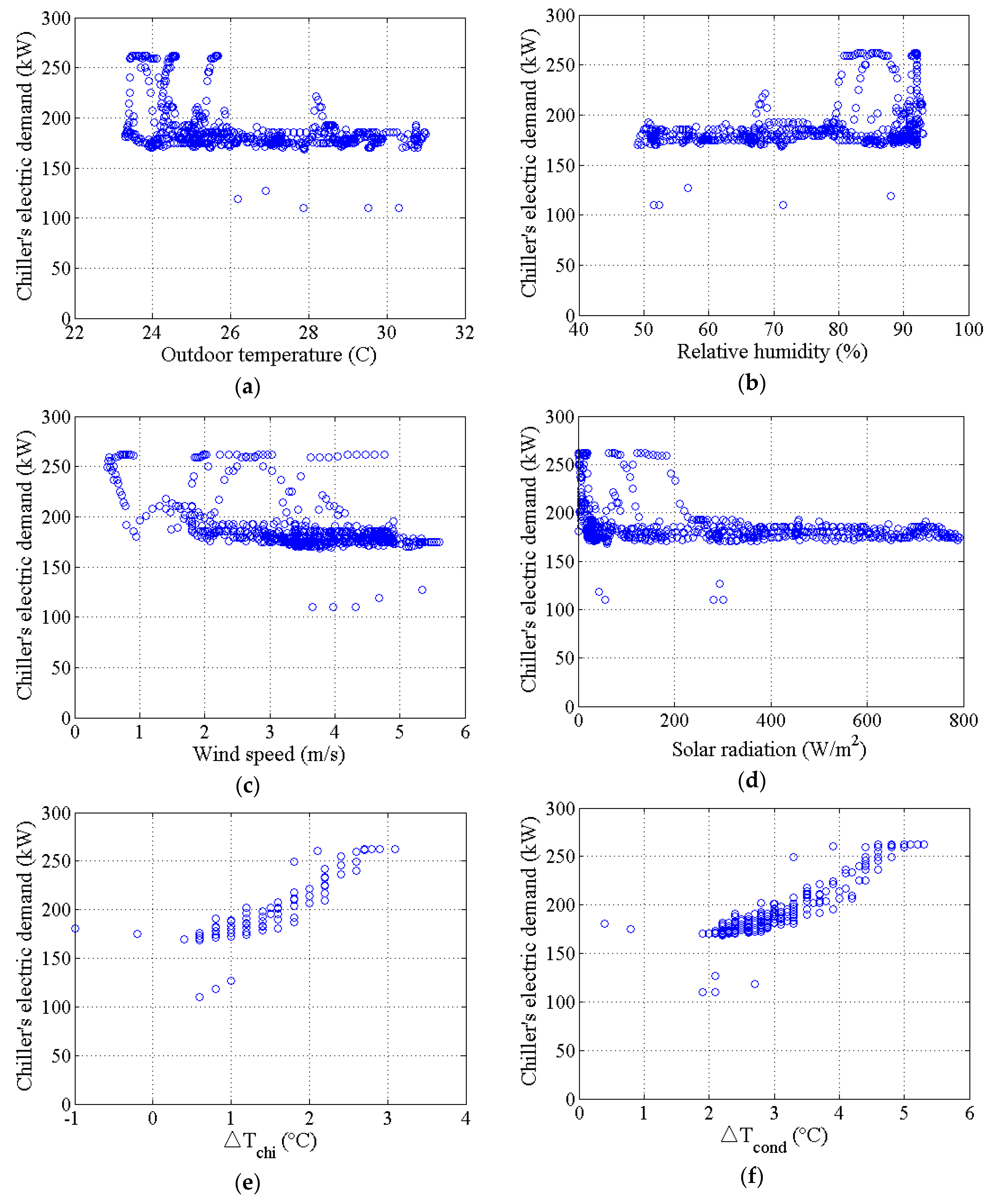
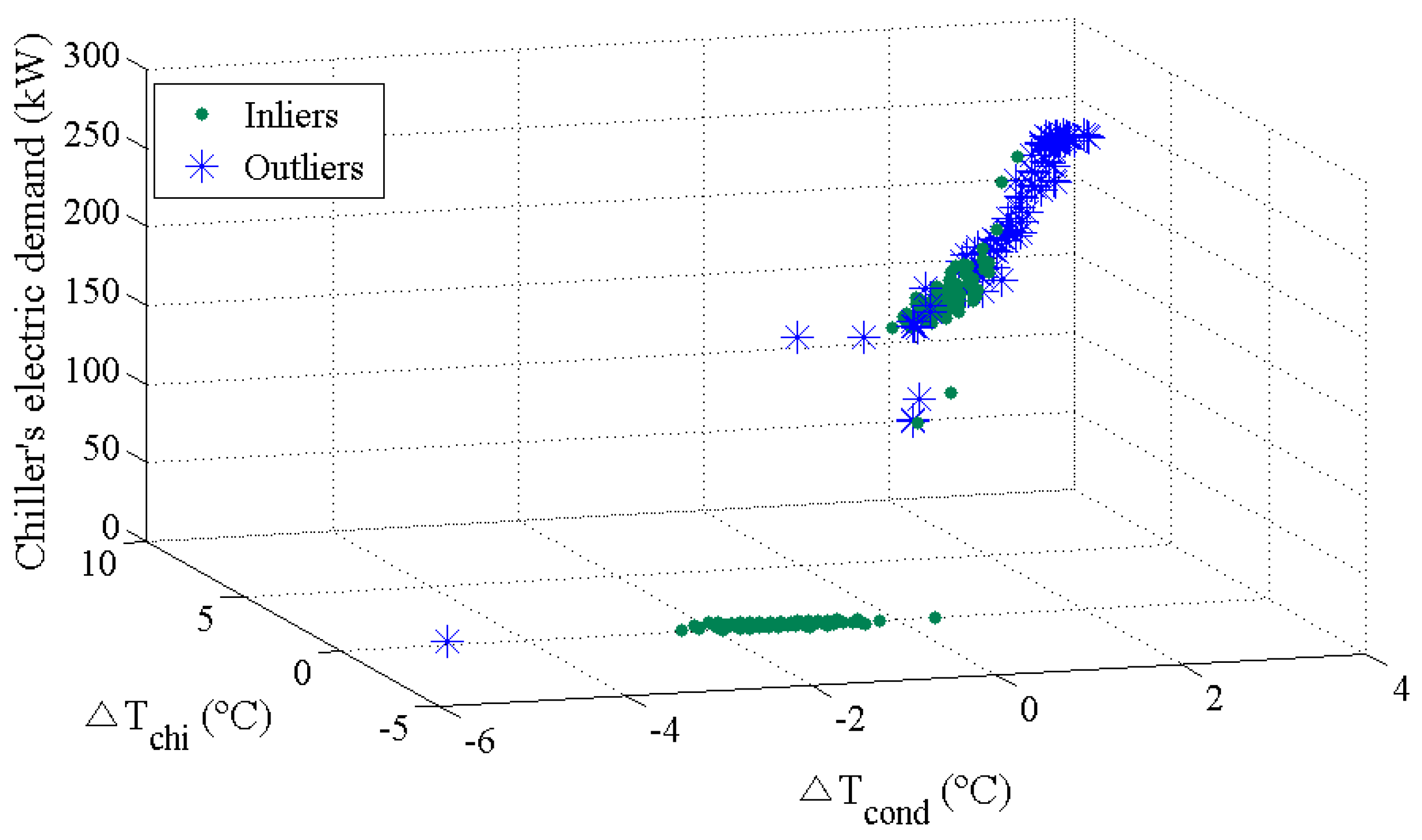
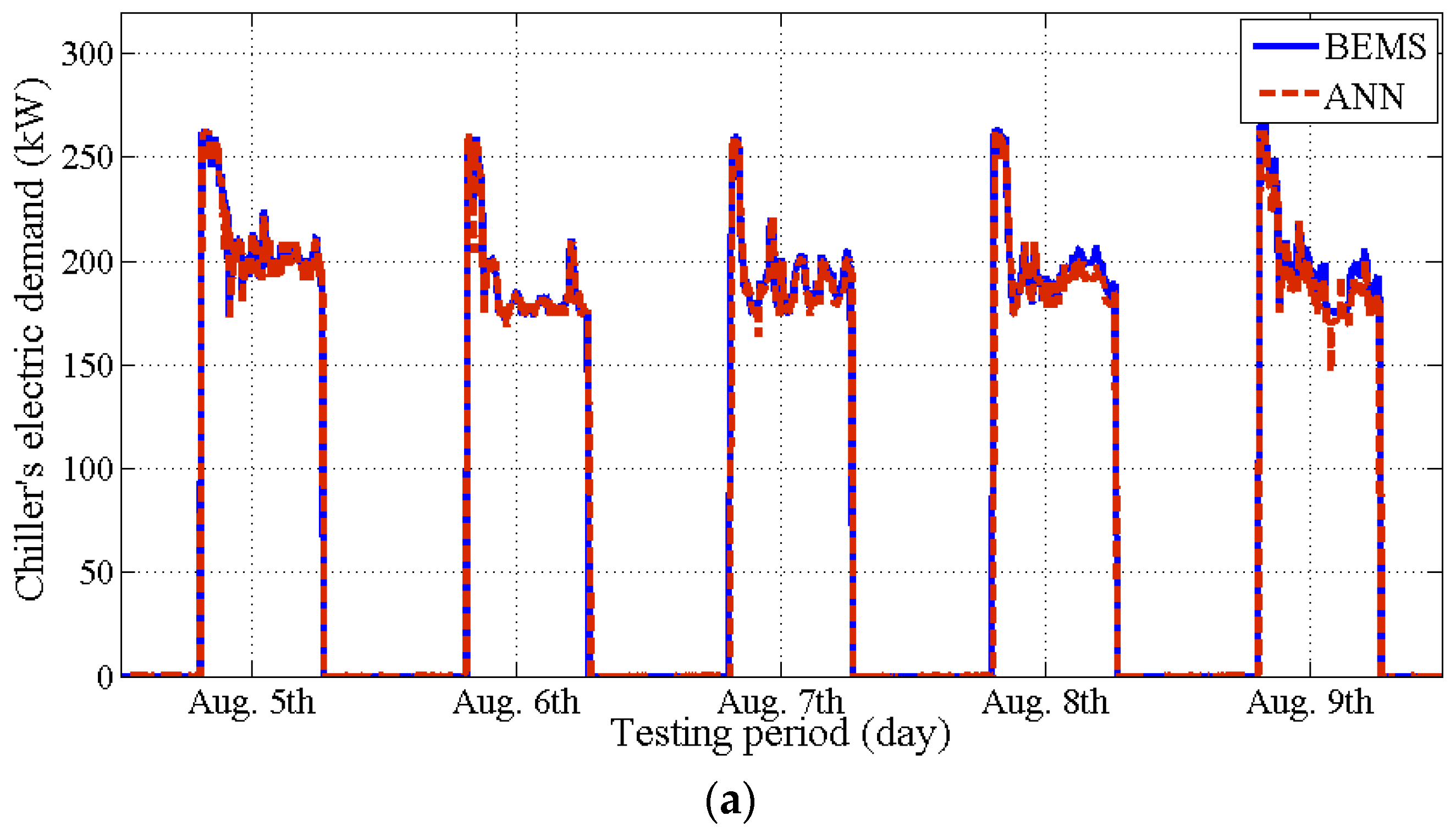
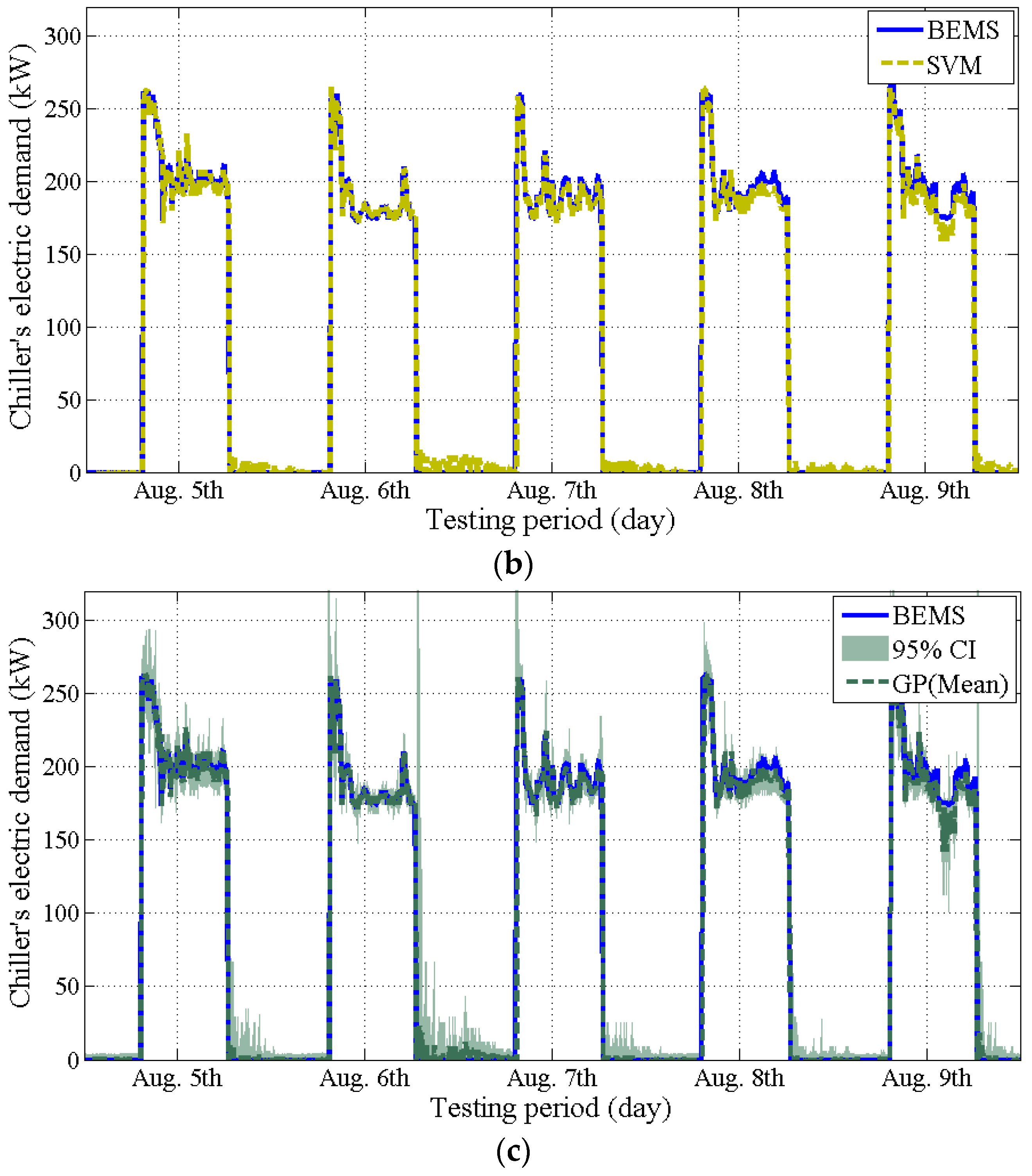
4.2. Issue #4: Missing or Outlying Data Obtained from BEMS
- Hypothesize: Minimal Sample Sets (MSSs) are randomly selected from the input dataset and parameters of the RANSAC algorithm are computed using the elements of the MSS.
- Test: RANSAC checks the elements (also called “Consensus Set”, CS) of the entire dataset that are consistent. If the probability of finding a better ranked CS drops below a certain threshold, the RANSAC terminates.
4.3. Issue#5: Validation of the Models
- The SVM model is the least effective in terms of computation time. The training took about 1 h with over 2160 data points. The computer used was an Intel(R) Core(TM) i5 CPU 2.8 GHz, RAM 6 GB, Windows 7, 64 bit.
- The ANN model shows better performance than the two other models, regardless of the training period (issues #2 and #3). However, the ANN model requires heuristic (trial and error) judgment to determine the number of hidden layers and nodes.
- The GP model could provide stochastic prediction with a confidence interval. However, the accuracy of the GP model significantly decreases when an irregular pattern of the data is included (issue #2).
5. Conclusions
- Remember that the data-driven model generated from a machine learning algorithm is not reproducible (issue #1).
- Determine the training period carefully. The GP model is strongly influenced by the training period. The ANN is least influenced by the training period (issue #2).
- Check the correlation between inputs and outputs (e.g., the Pearson’s correlation coefficient greater than 0.8) (issue #3).
- Be aware that the BEMS data from the real-life building include missing or outlying data. Such missing or outlying data could influence the prediction performance of the machine learning model (issue #4).
- Apply constraints during the training when needed (e.g., CVRMSE less than 15%, MBE less than 5%) (issue #5).
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AHU | Air Handling Unit |
| ANN | Artificial Neural Network |
| BEPS | Building Energy Performance Simulation |
| CI | Confidence Interval |
| CPU | Central Processing Unit |
| CS | Consensus Set |
| CVRMSE | Coefficient of Variation of the Root Mean Squared Error |
| FCU | Fan Coil Unit |
| GP | Gaussian Process |
| LSSVM | Least Square Support Vector Machine |
| MBE | Mean Biased Error |
| MSS | Minimal Sample Set |
| RAM | Random Access Memory |
| RANSAC | RANdom SAmple Consensus |
| RBF | Radial Basis Function |
| RMSE | Root Mean Squared Error |
| RQ | Rational Quadratic |
| SE | Squared Exponential |
| SVM | Support Vector Machine |
| VAV | Variable Air Volume |
References
- Ahn, K.U.; Kim, Y.J.; Kim, D.W.; Yoon, S.H.; Park, C.S. Difficulties and Issues in Simulation of a High-rise Office Building. In Proceedings of the 13th Conference of International Building Performance Simulation Association, Chambery, France, 26–28 August 2013; pp. 671–678.
- Yang, J.; Rivard, H.; Zmeureanu, R. On-line Building Energy Prediction using Adaptive Artificial Neural Networks. Energy Build. 2005, 37, 1250–1259. [Google Scholar] [CrossRef]
- Cam, L.M.; Zmeureanu, R.; Daoud, A. Comparison of Inverse Models used or the Forecast of the Electric Demand of Chillers. In Proceedings of the 13th International Building Performance Simulation Association, Chambery, France, 26–28 August 2013; pp. 2044–2051.
- Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
- Kim, Y.J.; Park, C.S. Nonlinear Predictive Control of Chiller System using Gaussian Process Model. In Proceedings of the 2nd Asia Conference of International Building Performance Simulation Association, Nagoya, Japan, 28–29 November 2014; pp. 594–601.
- Heo, Y.S.; Zavala, V.M. Gaussian Process Modeling for Measurement and Verification of Building Energy Savings. Energy Build. 2012, 53, 7–18. [Google Scholar] [CrossRef]
- Neto, A.H.; Fiorelli, F.A.S. Comparison between Detailed Model Simulation and Artificial Neural Network or Forecasting Building Energy Consumption. Energy Build. 2008, 40, 2169–2176. [Google Scholar] [CrossRef]
- Ben-Nakhi, A.E.; Mahmoud, M.A. Cooling load prediction for buildings using general regression neural networks. Energy Convers. Manag. 2004, 45, 2127–2141. [Google Scholar] [CrossRef]
- Amjady, N. Short-term hourly load forecasting using time-series modeling with peak load estimation capability. IEEE Trans. Power Syst. 2001, 16, 498–555. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Bojic, M. Artificial neural networks for the prediction of the energy consumption of a passive solar building. Energy 2000, 25, 479–491. [Google Scholar] [CrossRef]
- Wiliamowski, B.M.; Yu, H. Improved Computation for Levenberg–Marquardt Training, Neural Networks. IEEE Trans. Neural Netw. 2010, 21, 930–937. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Kamber, M. Data Mining: Concepts and Techniques; Morgan Kaufmann: San Francisco, CA, USA, 2001. [Google Scholar]
- Smola, A.J.; Scholkopf, B. A Tutorial on support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Wang, H.; Hu, D. Comparison of SVM and LS-SVM for Regression. In Proceedings of the International Conference on Neural Networks and Brain, Beijing, China, 13–15 October 2005; pp. 279–283.
- Suykens, J.A.K. Nonlinear Modelling and Support Vector Machines. In Proceedings of the 18th IEEE Instrumentation and Measurement Technology Conference, Budapest, Hungary, 21–23 May 2001; pp. 287–294.
- Roberts, S.; Osborne, M.; Ebden, M.; Reece, S.; Gibson, N.; Algrain, V. Gaussian Process for Time-series Modelling. Philos. Trans. R. Soc. A 1984, 371. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Process for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Zhang, Y.; O’Neil, Z.; Wagner, T.; Augenbroe, G. An Inverse Model with Uncertainty Quantification to Estimate the Energy Performance of an Office Building. In Proceedings of the 13th International Building Performance Simulation Association, Chambery, France, 26–28 August 2013; pp. 614–621.
- ASHRAE. ASHRE Handbook-Fundamentals; American Society of Heating, Refrigerating, and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2013. [Google Scholar]
- ASHRAE. ASHRAE Guideline 14: Measurement of Energy and Demand Savings; American Society of Heating, Refrigerating, and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2002. [Google Scholar]
- Zuliani, M. RANSAC for Dummies; Vision Research Lab, University of California: Santa Barbara, CA, USA, 2009. [Google Scholar]




| ANN | SVM | GP | |
|---|---|---|---|
| Structure |  | 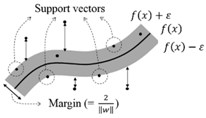 |  |
| Summary | Learning correlation between inputs and outputs adjusting the weight between nodes | Maximizing the margin () within an acceptable error bound () | Joint distribution of random variables assigned on a given data |
| Learning Algorithm | where = Output = Target | where | |
| Model Parameter | Learning rate (l) Momentum of gradient (η) | Trade-off parameter (C) Covariance of RBF kernel (σ2) | Covariance of SE kernel (λ) Hyper parameter (h) |
| Optimization Technique | Levenberg–Marquardt, Gradient descent, Bayesian Regularization | Quadratic Programming (Convex optimization) Coupled Simulated Annealing | Maximum Likelihood Estimation (MLE), Maximum A Posterior (MAP) |
| Advantages | Requires less computational demand | Advantageous to avoid an overfitting problem | Able to provide stochastic prediction |
| Model | Parameters and Search Algorithm | |
|---|---|---|
| ANN | Parameters | Learning rate (l) |
| Momentum of gradient (η) | ||
| Search | Levenberg–Marquardt method | |
| SVM | Parameters | Trade-off parameter (C) |
| Covariance of kernel function (σ2) | ||
| Search | Coupled Simulated Annealing | |
| GP | Parameters | Covariance of kernel (λ) |
| Hyper-parameter (h) | ||
| Search | Maximum Likelihood Estimation (MLE) | |
| RMSE (kW) | CVRMSE (%) | MBE (%) | ||
|---|---|---|---|---|
| ANN | Trial #1 | 0.001 | 0.012 | 0.005 |
| Trial #2 | 0.001 | 0.012 | 0.005 | |
| Trial #3 | 0.001 | 0.011 | 0.005 | |
| SVM | Trial #1 | 0.001 | 0.010 | 0.004 |
| Trial #2 | 0.001 | 0.010 | 0.005 | |
| Trial #3 | 0.001 | 0.015 | 0.005 | |
| GP | Trial #1 | 0.000 | 0.005 | 0.003 |
| Trial #2 | 0.001 | 0.013 | 0.005 | |
| Trial #3 | 0.002 | 0.026 | 0.008 |
| Input (X) | ||||
|---|---|---|---|---|
| Tout | O | ∆Tchi | ∆Tcond | |
| γXY 1 | 0.51 | 0.59 | 0.99 | 0.99 |
| Inputs | RMSE (kW) | CVRMSE (%) | MBE (%) | Remark | |
|---|---|---|---|---|---|
| ANN | Tout, O | 71.9 | 74.2 | −33.1 | Exogenous inputs only |
| ∆Tchi, ∆Tcond | 0.0008 | 0.0008 | 0.003 | Endogenous inputs only | |
| Tout, O, ∆Tchi, ∆Tcond | 0.103 | 0.105 | 0.054 | ||
| SVM | Tout, O | 65.3 | 67.4 | −13.0 | Exogenous inputs only |
| ∆Tchi, ∆Tcond | 0.0007 | 0.0007 | 0.0003 | Endogenous inputs only | |
| Tout, O, ∆Tchi, ∆Tcond | 0.544 | 0.559 | 0.173 | ||
| GP | Tout, O | 115.1 | 118.9 | 100 | Exogenous inputs only |
| ∆Tchi, ∆Tcond | 0.0004 | 0.0004 | 0.0002 | Endogenous inputs only | |
| Tout, O, ∆Tchi, ∆Tcond | 0.943 | 0.922 | 0.337 |
| Input (X) | ||||
|---|---|---|---|---|
| Tout | Hrel | Vwind | ϕ | |
| γXY 1 | −0.38 | −0.36 | −0.52 | −0.35 |
| RMSE (kW) | CVRMSE (%) | MBE (%) | |
|---|---|---|---|
| ANN | 50.45 | 25.51 | 6.17 |
| SVM | 90.96 | 46.00 | 2.29 |
| GP | 152.66 | 77.19 | 10.74 |
| RMSE (kW) | CVRMSE (%) | MBE (%) | |
|---|---|---|---|
| ANN | 9.6 | 10.5 | 2.2 |
| SVM | 10.2 | 11.2 | 0.8 |
| GP | 10.0 | 11.0 | 1.4 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.M.; Ahn, K.U.; Park, C.S. Issues of Application of Machine Learning Models for Virtual and Real-Life Buildings. Sustainability 2016, 8, 543. https://doi.org/10.3390/su8060543
Kim YM, Ahn KU, Park CS. Issues of Application of Machine Learning Models for Virtual and Real-Life Buildings. Sustainability. 2016; 8(6):543. https://doi.org/10.3390/su8060543
Chicago/Turabian StyleKim, Young Min, Ki Uhn Ahn, and Cheol Soo Park. 2016. "Issues of Application of Machine Learning Models for Virtual and Real-Life Buildings" Sustainability 8, no. 6: 543. https://doi.org/10.3390/su8060543
APA StyleKim, Y. M., Ahn, K. U., & Park, C. S. (2016). Issues of Application of Machine Learning Models for Virtual and Real-Life Buildings. Sustainability, 8(6), 543. https://doi.org/10.3390/su8060543





