1. Introduction
China’s industrial economy has achieved remarkable progress since its reform and opening up in the late 1970s. According to the
China Statistical Yearbook 2013, in the past 30 years, the average annual growth rate of the industrial gross domestic product (GDP) was approximately 16%, which is an amazing number compared to the industrial GDPs of most other countries [
1]. However, the rapid industrial economic growth has been accompanied by an increased consumption of fossil energy. The amount of fossil energy consumption for production was as high as 3.62 billion tons of standard coal in 2012, and a large part of the coal consumption was used for industrial production [
2]. In addition, coal consumption accounts for the main part of the fossil energy consumption in China and releases more harmful gases (e.g., carbon dioxide and sulfur dioxide) compared to some types of clean energy (e.g., nuclear and wind power) for the same given amount [
3]. In fact, China became the largest energy consumer and carbon emitter in the world prior to 2010 [
4], which indicate that China must face considerable pressure to promote energy-saving and low carbon industrial production. Although the famous
Kyoto Protocol does not give China a mandatory carbon emissions reduction task, as a responsible country that has been trying to achieve sustainable development for a long time, China should pay more attention to optimizing its energy structure and effectively reducing its carbon emissions [
5].
Fortunately, the central government of China has already started to pay attention to this problem and has tried to solve it. Many policies aimed at addressing excessive carbon emissions have been launched in recent years, such as the
Special Action of Response to Climate Change Science and Technology issued in 2007, which sought to speed up the development of cleaner production technologies and reduce carbon emissions in China [
6]. In addition, the
National Program on Addressing Climate Change was released in the same year and sought to limit the total amount of greenhouse gas emissions and punish enterprises and local governments that did not comply with those policies [
7]. Two years later, the central government of China promised a reduction of 45% in carbon emission intensity by 2020 compared to that in 2005, which was included in the long-term planning of national economic and social development in China [
8]. This promise has undoubtedly been conducive to the sustainable development of China’s industries. However, whether those policies have achieved remarkable effects remains unknown.
According to the
China Urban Construction Statistical Yearbook, industrial land refers to land for industrial production in built-up urban areas including factories and workshops [
5,
6,
7,
8,
9]. As an important input in the industrial production process, the amount of industrial land consumption has shown an obvious increasing trend in recent years. In 2012, industrial land accounted for approximately 20% of the total area of urban built-up zone in China [
10]. However, the proportion of industrial land in most developed countries is less than 10% (e.g., France and Japan). This implies excessive industrial land use in China. In fact, the vigorous land expansion of recent years across China has led to a seriously inefficient use of industrial land, and a large amount of industrial lands have not been used for many years in some cities. The poor economic performance of industrial land is common in China [
11]. In addition, industrial land is the main carrier of industrial production activities and suffers most from industrial pollutants. That is to say, industrial land is constantly used to create industrial products, but it also suffers serious problems of ecological environmental pollution. As the famous
Outline of the 12th Five-Year Plan for Economic and Social Development noted, improving land use efficiency was a key problem of urban development [
12]. Therefore, how to quantify and improve the economic and environmental performance of industrial land use in China is a key issue to realize the sustainable development of Chinese industry.
Regarding the research method, many previous studies of land efficiency preferred using single factor indexes such as the economic output per km
2 of land [
13]. However, as noted in some previous studies, land cannot produce products unless accompanied by other inputs such as labor and capital, and land efficiency computed under the total factor framework is more reasonable [
14]. Therefore, the data envelopment analysis (DEA) model is widely adopted by current studies because the input and output variables are incorporated into the model. Chen
et al. [
15] have analyzed industrial land use efficiency in China using a DEA model at the provincial level and found that China’s eastern region enjoys a higher industrial land use efficiency than in the central and western regions. Xiong
et al. [
16] have reached a similar conclusion and suggested that excessive inputs of industrial land were the main reasons for the inefficient use of industrial land. However, these studies consider only the economic efficiency of industrial land use, and negative outputs were not included in the models. Therefore, they can be considered as partial analyses because they ignored the negative impacts on the environment caused by industrial production. Guo
et al. [
17] have incorporated three main negative outputs (
i.e., the amounts of industrial sulfur dioxide, industrial wastewater, and industrial dust emissions) into a DEA model to measure the combined efficiency of economy and environment for 33 typical cities in China. They found that the values of efficiency computed from models that incorporated negative outputs were always lower than those from models that ignored negative outputs. Xie
et al. [
18] have applied a similar model to explore industrial land use efficiency at the city level in China, and they found that cities located in economically-developed regions performed much better than those in economically undeveloped regions. However, these results were based on contemporaneous production technology, and they were in fact static analyses, which can be referred to as cross-sectional rather than time series analysis. Therefore, the efficiencies in different years could not be compared. Zhang
et al. [
19] have applied an advanced directional distance function (DDF) approach based on global benchmark technology. Global technology enveloped all of the contemporaneous technologies, which indicated that the model actually provides a dynamic analysis, and the results for different periods therefore could be compared to one another. Moreover, Zhang
et al. [
20] noted that the traditional radial DDF model had a limitation that reduced inputs and expanded outputs at the same rate. This is clearly not consistent with reality, and they proposed a non-radial DDF to reduce inputs and expand outputs at different rates. Therefore, their model was capable of providing a more reasonable assessment.
To obtain more insights into the dynamic changes in land use efficiency, two popular approaches, the Malmquist and Luenberger indices, have been widely used in recent related studies. Both indices can decompose productivity changes into efficiency and technological changes to explore the main contributors to changes in productivity. Chung
et al. [
21] have proposed a relatively advanced approach, the Malmquist-Luenberger (ML) index, to incorporate negative outputs. Many later studies adopted this method to model environmentally sensitive productivity growth at the national level [
22], regional level [
23] and industry level [
24]. However, as Boussemart
et al. [
25] have noted, the Malmquist index tends to overestimate productivity changes because it calculates the growth in productivity as a ratio. The results measured by the Luenberger index seem more reasonable because they are calculated in an additive way and are only half of those computed using the Malmquist index approach. The difference in the two methods arises because the former adopts the geometric means of the distance functions, whereas the latter uses the arithmetic means of the distances in two periods. Many recent studies have noted that the results based on the Luenberger index are more robust than those based on the Malmquist index [
26], and Chang
et al. [
27] have made a further improvement by applying a non-radial Luenberger index. This approach was widely applied in later studies to model environmentally sensitive productivity [
28].
Unfortunately, there are no studies on the dynamic changes in the total-factor carbon emission performance of industrial land use (TCPIL) in China. You
et al. [
29] have measured the carbon emission efficiencies in China’s 30 regions by employing a traditional DEA model. However, they treated the amount of carbon emissions as an input in the production process, which was inconsistent with the actual production. Cui
et al. [
30] have modeled the carbon emission performance of urban non-agricultural land for China using a Malmquist index. However, the study was actually a static analysis because it was based on contemporaneous production technology, and it could not depict dynamic changes in the carbon emission performance of land use. In addition, many previous studies ignored carbon emission performance when exploring the negative impacts of pollutants on the environment in the process of industrial production. However, considering the serious threat to human health and socioeconomic development caused by greenhouse gases, which are mainly composed of carbon dioxide, it is obviously meaningful to consider carbon emissions.
This paper aims to apply a global DDF and non-radial Luenberger productivity index to analyze the dynamic changes in TCPIL for China. This total factor index can be referred to as the non-radial Luenberger carbon emission performance of industrial land use (NLCPIL). We then explore the main contributors to the growth in NLCPIL by decomposing the NLCPIL into two indices, i.e., efficiency change (EC) and technological change (TC), and we further find which provinces have made innovations in carbon performance. Lastly, we explore the impacts on the NLCPIL of energy utilization, production technology and environmental policy factors in Chinese industry to present some policy implications.
Therefore, this paper makes three main contributions to the relevant studies. Firstly, we compute the TCPIL for each province in China under a global environmental technology framework. Secondly, we compute the NLCPIL to measure the dynamic changes in the TCPIL and determine which NLCPIL component index, i.e., EC and TC, is the main contributor to the growth of NLCPIL. Lastly, we learn which provinces have provided innovation and leadership in environmentally friendly production technologies as examples of provinces that have poor TCPILs.
The remainder of this paper is organized as follows:
Section 2 introduces the methods and data,
Section 3 shows the results of the empirical analysis, and
Section 4 concludes the paper with some policy implications.
4. Conclusions
China has become the world’s largest energy consumer and carbon emitter, and industrial production is the primary contributor to carbon emissions. Industrial lands bear most of the industrial production activities and industrial pollutants, and the serious problems of environmental pollution in areas surrounding industrial land caused by industrial production therefore deserve more attention. Fortunately, the central government of China has already accepted the importance of improving the environmental and economic performance of industrial land use. However, the above polices cannot achieve the desired effects unless accompanied by an overall understanding of the actual situation. Therefore, modeling the dynamic changes in carbon emission performance of industrial land use in recent years and forwarding constructive policy implications are urgently needed.
In this study, we employed a global DDF approach to compute the TCPIL, and we then used a NLCPIL index to model the dynamic changes in the TCPIL. The results are as follows:
Firstly, the TCPILs for China and its three regions showed rising trends over the study period, and the eastern region performed much better in TCPIL than the central and western regions. However, all three regions have a large potential for improving their TCPILs. Most of the provinces in the eastern region (e.g., Hainan, Zhejiang and Guangdong) enjoyed better TCPILs, whereas those from the central and western regions (e.g., Gansu and Ningxia) suffered worse TCPILs.
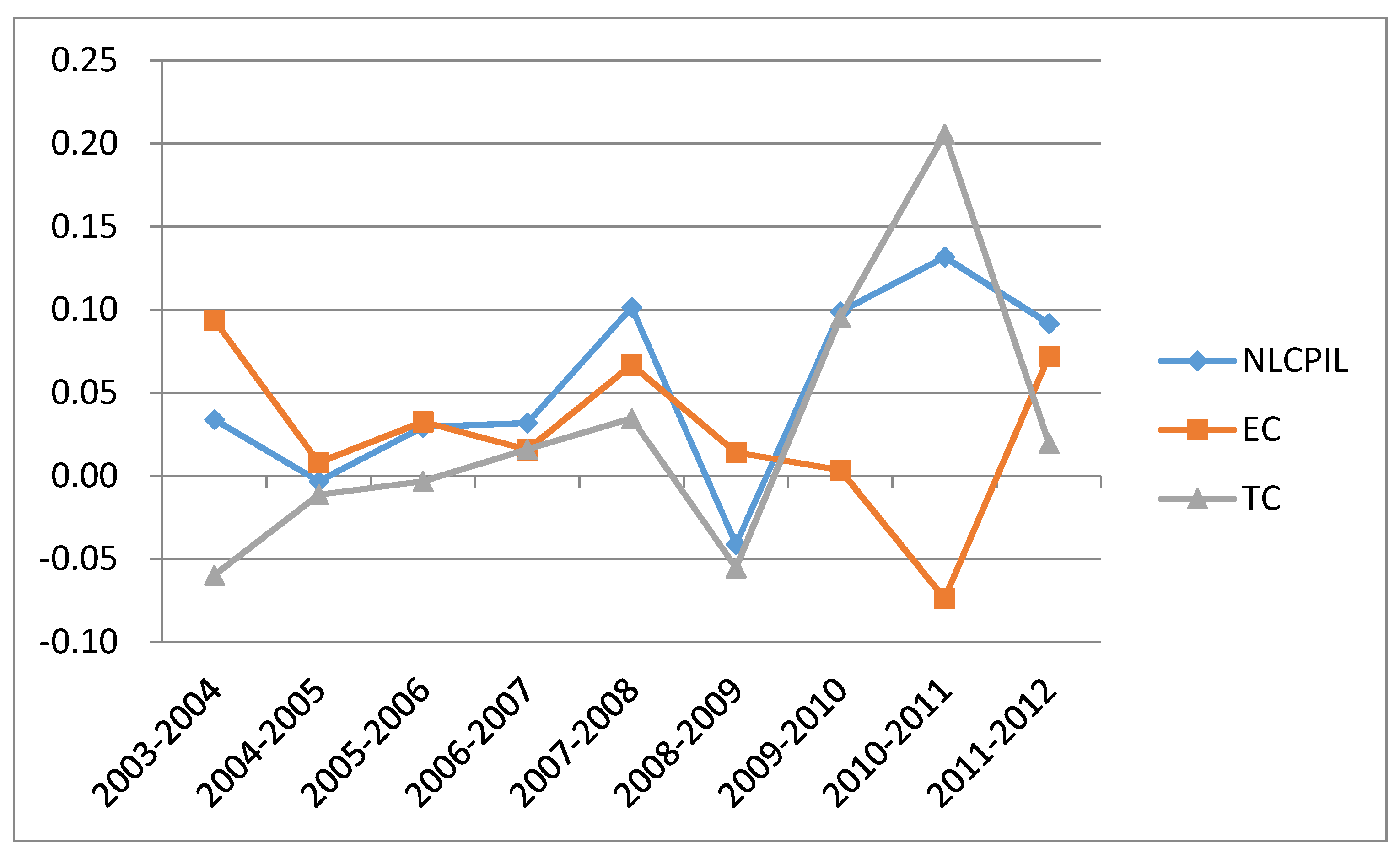
Secondly, the NLCPILs for China were greater than zero in most years of the study period, and their growth was mainly driven by ECs before 2009 and by TC subsequently. The eastern and central regions showed higher TCs, whereas the western region had a better EC performance. Many provinces with poor TCPILs had higher NLCPILs, which indicates that the regional gaps in TCPIL clearly showed a narrowing trend. In addition, most of the provinces that were identified as innovators of environmentally friendly industrial production technologies were in the eastern region (e.g., Beijing, Guangdong and Shandong).
Lastly, the results of the influencing factor analysis showed that the carbon emission reduction policies since 2009 have performed as expected, and they are helpful to improve the NLCPIL, which recommends the environmental protection policies. The EI, ES and LS indicators had expected significantly negative impacts on the NLCPIL, which means that the NLCPIL could be improved by saving more fossil energy, optimizing the energy structure by reducing the use of coal and properly solving the problem of surplus labor in the industrial sectors. The RI had an expected significantly positive impact on the NLCPIL, which implies that more investment in industrial R&D is needed. However, the FI and IS indices influenced the NLCPIL opposite the expected impacts, which had negative and positive signs, respectively. This may due to incomplete learning of foreign advanced production technologies and the fact that China has not yet fully entered into the stage of middle and late industrialization.
Based on the empirical analysis, we put forward some policy implications. Firstly, the central government of China should issue more policies on low-carbon and energy-saving industrial production to effectively protect the environment given rapid industrial economic development. In addition, the central government should strictly regulate local governments to fully implement those policies. Therefore, severe punishments for local government officials such as removing administrative duties or cutting their powers are necessary. Secondly, industrial enterprises should further optimize energy structures by reducing the use of coal and increasing the use of clean energy such as nuclear and wind power. The government should spend more money on the R&D of clean energy, subsidize enterprises that use clean energy, and promote cooperation between enterprises and research institutes. Third, we should carefully study advanced industrial production and management technologies by introducing foreign investment and industrial enterprises and by trying to develop our own technologies, especially for the regions with underdeveloped environmentally friendly industrial production technology. Lastly, the regional gaps in industrial production technology and environmental protection deserve more attention, and the central government of China should create more opportunities for underdeveloped provinces to communicate with developed provinces and introduce necessary technologies and talent. This study also has some limitations. Firstly, we only adopted a ten-year sample period because of the unavailability of data. We will try to obtain more data to extend the study period to produce more convincing and meaningful results. Secondly, some factors that play important roles in determining the efficiency of industrial land use were not considered in this paper for the same reason, such as the price of industrial land, carbon emissions trading costs and human capital. We will make these improvements in future studies.