Estimating the Contribution of Industry Structure Adjustment to the Carbon Intensity Target: A Case of Guangdong
Abstract
:1. Introduction
2. Methods and Data
2.1. GDP Forecasting
2.2. Industry Structure Prediction with the Markov Chain Model
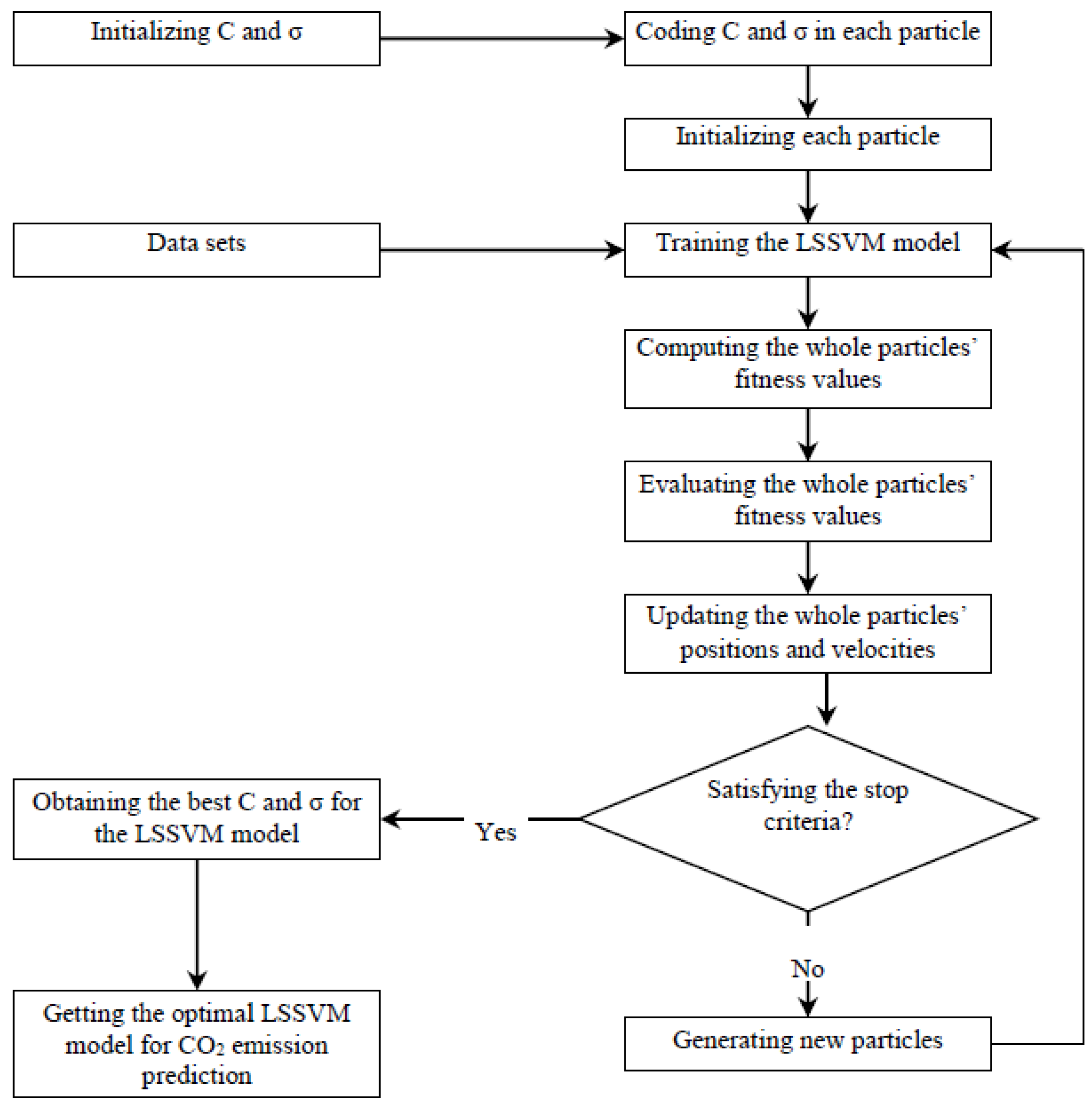
2.3. Estimating CO2 Emissions
2.4. Forecasting CO2 Emissions
2.5. Evaluating the Contribution of the Carbon Intensity Target
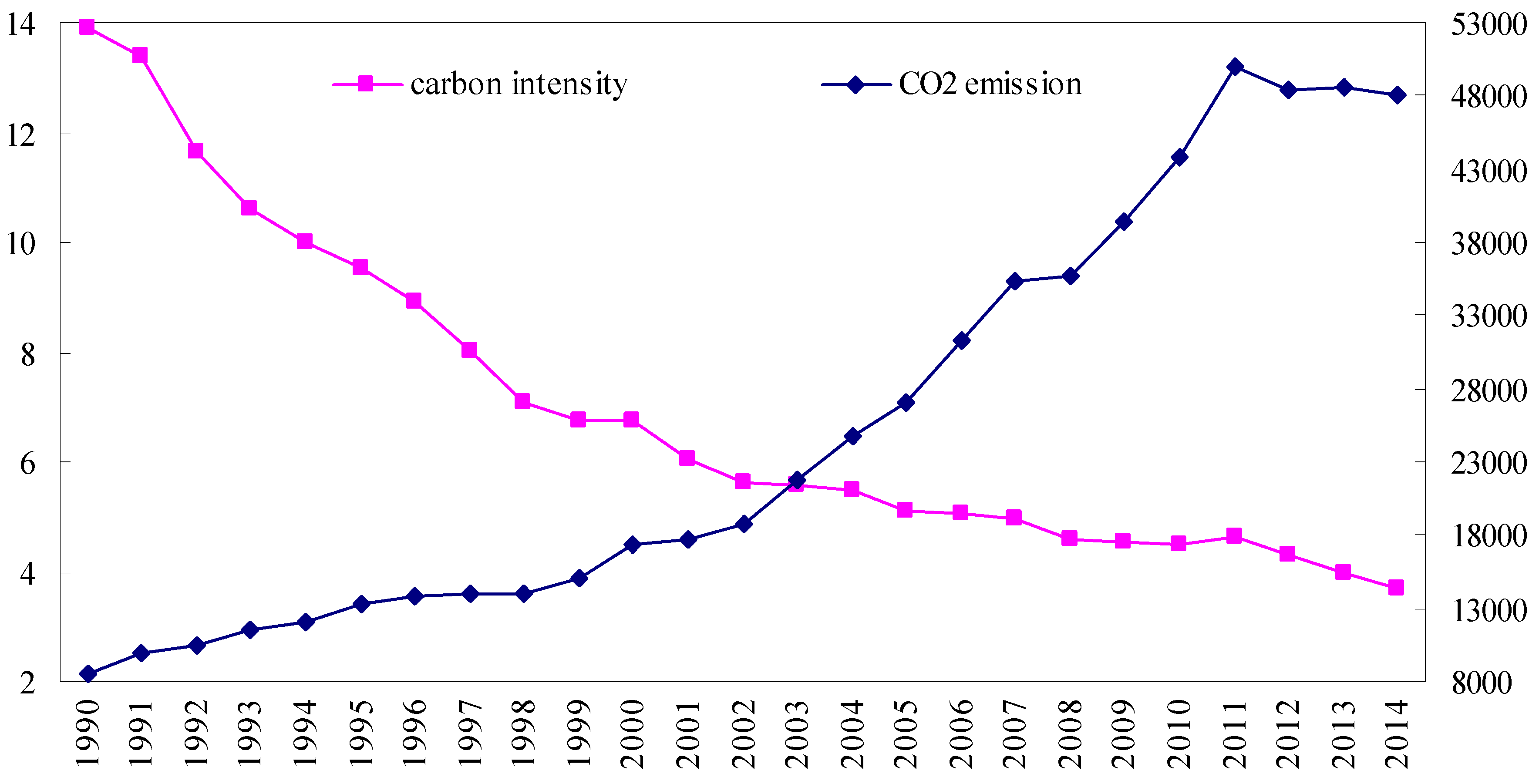
2.6. Data
3. Results and Discussion
3.1. Prediction on GDP of Guangdong in 2015
3.2. Prediction on Industry Structure of Guangdong in 2015
3.3. Prediction on CO2 Emissions of Guangdong in 2015
3.4. Prediction on Carbon Intensity of Guangdong in 2015
3.5. Prediction on CO2 Emissions of Guangdong in 2015
4. Conclusions
- (i)
- Industry structure adjustment is an effective measure for driving the reduction of carbon intensity. For a given level of economic growth, the larger the industry structure adjustment, the larger the “reduction amplitude” of the carbon intensity. For a given industry structure adjustment, the higher the economic growth, the larger the “reduction amplitude” of the carbon intensity.
- (ii)
- Under the ideal scenario (i.e., “high-speed economic growth” and “substantial industry structure adjustment”), industry structure adjustment contributes most to the realization of the carbon intensity goal, with a contribution of 130.94%. Carbon intensity would be reduced by 25.53% in 2015 as compared to 2010. Under the conservative scenario (i.e., “low-speed economic growth” and “minor industry structure adjustment”), the contribution of industry structure adjustment to meeting the carbon intensity goal will reach 122.50%. At the same time, the carbon intensity in 2015 will decrease by 23.89% as compared to 2010.
- (iii)
- The reduction by 19.5% of the carbon intensity goal can be achieved under all the combined scenarios through industry structure adjustment. Thus, it can be concluded that the set target appears scientific and reasonable for Guangdong’s government to reach its carbon intensity goal by 2015.
- (iv)
- Although the obtained results show that the goal of reducing 19.5% of Guangdong’s carbon intensity can be achieved, there are some limitations and uncertainties. In this paper, we have not taken into account the adoption and use of novel low carbon policies, which will change over time. How to capture them is the focus of one of our next works.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xiang, N.; Xu, F.; Sha, J.H. Simulation Analysis of China’s Energy and Industrial Structure Adjustment Potential to Achieve a Low-carbon Economy by 2020. Sustainability 2013, 5, 5081–5099. [Google Scholar] [CrossRef]
- Uwasu, M.; Jiang, Y.; Saijo, T. On the Chinese Carbon Reduction Target. Sustainability 2010, 2, 1553–1557. [Google Scholar] [CrossRef]
- Yi, W.J.; Zou, L.L.; Guo, J.; Wang, K.; Wei, Y.M. How can China reach its CO2 intensity reduction targets by 2020? A regional allocation based on equity and development. Energy Policy 2011, 39, 2407–2415. [Google Scholar] [CrossRef]
- Li, H.Q.; Wang, L.M.; Shen, L.; Chen, F.N. Study of the potential of low carbon energy development and its contribution to realize the reduction target of carbon intensity in China. Energy Policy 2012, 41, 393–401. [Google Scholar] [CrossRef]
- Yuan, J.H.; Hou, Y.; Xu, M. China’s 2020 carbon intensity target: Consisteney, implementations, and policy imp1ications. Renew. Sustain. Energy Rev. 2012, 16, 4970–4981. [Google Scholar] [CrossRef]
- Liu, L.W.; Zong, H.J.; Zhao, E.D.; Chen, C.X.; Wang, J.Z. Can China realize its carbon emission reduction goal in 2020: From the perspective of thermal power development. Appl. Energy 2014, 124, 199–212. [Google Scholar] [CrossRef]
- Jiao, J.L.; Qi, Y.Y.; Qun, C.; Liu, L.C.; Liang, Q.M. China’s targets for reducing the intensity of CO2 emissions by 2020. Energy Strateg. Rev. 2013, 2, 176–181. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, X.L.; Qi, T.Y.; He, J.K.; Luo, X.H. Regional disaggregation of China’s national carbon intensity reduction target by reduction pathway analysis. Energy Sustain. Dev. 2014, 23, 25–31. [Google Scholar] [CrossRef]
- Cui, L.B.; Fan, Y.; Zhu, L.; Bi, Q.H. How will the emissions trading scheme save cost for achieving China’s 2020 carbon intensity reduction target? Appl. Energy 2014, 136, 1043–1052. [Google Scholar] [CrossRef]
- Wang, X.W.; Cai, Y.P.; Xu, Y.; Zhao, H.Z.; Chen, J.J. Optimal strategies for carbon reduction at dual levels in China based on a hybrid nonlinear grey-prediction and quota-allocation model. J. Clean. Prod. 2014, 83, 185–193. [Google Scholar] [CrossRef]
- Yu, H.; Hua, L.; Wei, Y.M. Is China’s carbon reduction target allocation reasonable? An analysis based on carbon intensity convergence. Appl. Energy 2015, 142, 229–239. [Google Scholar]
- Zhu, B.Z.; Wang, K.F.; Chevallier, J.; Wang, P.; Wei, Y.M. Can China achieve its carbon intensity target by 2020 while sustaining economic growth? Ecol. Econ. 2015, 119, 209–216. [Google Scholar] [CrossRef]
- Jiusto, S. The differences that methods make: Cross-border power flows and accounting for carbon emissions from electricity use. Energy Policy 2006, 34, 2915–2928. [Google Scholar] [CrossRef]
- Yi, H. Clean Energy Policies and Electricity Sector Carbon Emissions in the U.S. States. Util. Policy 2015, 34, 19–29. [Google Scholar] [CrossRef]
- Cai, W.; Wang, C.; Chen, J.; Wang, S. Green economy and green jobs: Myth or reality? The case of China’s power generation sector. Energy 2011, 36, 5994–6003. [Google Scholar] [CrossRef]
- Yi, H.; Liu, Y. Green economy in China: Policy drivers and regional variations. Glob. Environ. Change 2015, 31, 11–19. [Google Scholar] [CrossRef]
- Huang, Y.F.; Wang, C.N.; Dang, H.S.; Lai, S.T. Predicting the Trend of Taiwan’s Electronic Paper Industry by an Effective Combined Grey Model. Sustainability 2015, 7, 10664–10683. [Google Scholar] [CrossRef]
- IPCC. Greenhouse Gas Inventory: IPCC Guidelines for National Greenhouse Gas Inventories; United Kingdom Meteorological Office: Bracknell, UK, 2006. [Google Scholar]
- Zhang, L.; Li, Y.M.; Huan, Y.X.; Wuan, Y.M. Analysis on character and potential of energy saving and carbon reducing by structure evolution in China. Chin. Soft Sci. 2011, 2, 42–51. [Google Scholar]
- Suykenns, J.A.K.; Vandewalle, J. Least squares support vector machine. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Smola, A.J. Learing with Kernels. Ph.D. Thesis, Department of Computer Science, Technical University, Berlin, Germany, 1998. [Google Scholar]
- Silva, D.A.; Silva, J.P.; Neto, A.R.R. Novel approaches using evolutionary computation for sparse least square support vector machines. Neurocomputing 2015, 168, 908–916. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE Conference on Neural Network, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948.
- Zhu, B.Z.; Wei, Y.M. Carbon price prediction with a hybrid ARIMA and least squares support vector machines methodology. Omega 2013, 41, 517–524. [Google Scholar] [CrossRef]
- Statistics Bureau of Guangdong Province. Guangdong Statistical Yearbook (2015); China Statistics Press: Beijing, China, 2015.
| High-Speed | Medium-Speed | Low-Speed | |
|---|---|---|---|
| Minor adjustment | 3.4061 | 3.4124 | 3.4188 |
| Medium adjustment | 3.3708 | 3.3771 | 3.3834 |
| Substantial adjustment | 3.3448 | 3.3510 | 3.3573 |
| High-Speed | Medium-Speed | Low-Speed | |
|---|---|---|---|
| Minor adjustment | −24.17 (123.95) | −24.03 (123.22) | −23.89 (122.50) |
| Medium adjustment | −24.95 (127.97) | −24.82 (127.26) | −24.68 (126.54) |
| Substantial adjustment | −25.53 (130.94) | −25.39 (130.23) | −25.26 (129.51) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Zhu, B. Estimating the Contribution of Industry Structure Adjustment to the Carbon Intensity Target: A Case of Guangdong. Sustainability 2016, 8, 355. https://doi.org/10.3390/su8040355
Wang P, Zhu B. Estimating the Contribution of Industry Structure Adjustment to the Carbon Intensity Target: A Case of Guangdong. Sustainability. 2016; 8(4):355. https://doi.org/10.3390/su8040355
Chicago/Turabian StyleWang, Ping, and Bangzhu Zhu. 2016. "Estimating the Contribution of Industry Structure Adjustment to the Carbon Intensity Target: A Case of Guangdong" Sustainability 8, no. 4: 355. https://doi.org/10.3390/su8040355
APA StyleWang, P., & Zhu, B. (2016). Estimating the Contribution of Industry Structure Adjustment to the Carbon Intensity Target: A Case of Guangdong. Sustainability, 8(4), 355. https://doi.org/10.3390/su8040355





