A Sustainable Outsourcing Strategy Regarding Cost, Capacity Flexibility, and Risk in a Textile Supply Chain

Abstract

The textile industry achieves economic benefits through outsourcing to low cost markets. Today, reshoring is an emerging trend due to rising cost and unemployment concerns. This problem is primarily due to an industry-wide focus on economic benefits only. Cost saving is a basic reason for international outsourcing while domestic outsourcing provides capacity flexibility. Moreover, outsourcing risk has a major impact on strategic location of the production destinations. Therefore, the merging of capacity flexibility and outsourcing risk comprises a sustainable outsourcing strategy. This paper suggests a sustainable outsourcing strategy in which a textile manufacturer outsources to international markets for cost savings and outsources to the domestic market for capacity flexibility. The manufacturer reserves some capacity with domestic suppliers, and pays a unit penalty cost if this capacity flexibility is not utilized. The manufacturer seeks minimum risk in international markets. Operational cost, penalty cost, and outsourcing risk are considered to be objective functions. Decisions include the assignment of contracts to suitable facilities, the quantity of each contract, and allocation of reserved capacity flexibility among domestic suppliers. Multi-objective problem of this research was solved using three variants of goal programming. Several insights are proposed for outsourcing decision making in the current global environment.

1. Introduction

The textile industry is a key manufacturing industry in the world. In the textile industry, supply chain globalization has brought numerous economic benefits. Today, reshoring is an emerging trend due to factors such as rising cost, quality issues, unemployment concerns, late deliveries, and quick response. In the textile industry, production and transportation decisions are directly related to environmental emissions [1]. Current sustainability issues, such as carbon footprint taxes, further complicate the issue. There are significant opportunities within the textile industry to reduce carbon emissions. Several textile companies have imposed a formal program to measure and reduce their carbon footprints [2]. The textile supply chain involves several environmental issues, including hazardous pollutants and waste management practices. The textile industry is an environmentally unfriendly industry due to hazardous pollutants such as dyeing chemicals and carbon dioxide emissions. Today, these issues are being addressed by compulsory carbon footprint taxes on textile products, sustainability rules and guidelines, International Organization for Standardization (ISO) certification, and emerging trends for corporate social responsibility [3]. International outsourcing causes more carbon emissions and environmental issues due to factors such as greater transportation distances and unsustainable practices at low-cost destinations. The utilization of a carbon footprint tax supports domestic outsourcing [4]. Furthermore, scattered consumer markets across the globe increase the difficulties associated with relocation decisions. In the textile industry, fashion business operations should consider more than just economic development [5]. Accordingly, a sustainable outsourcing strategy should include economic benefits as well as other associated factors. To increase sustainability in textile supply chains, production planning decisions that are based only on cost savings may not provide strategic benefits to the companies. Therefore, this paper suggests a sustainable outsourcing strategy based on operational cost, capacity flexibility, and outsourcing risk using three variants of goal programming.

Existing research uses various tools and methods to address the problems in the textile supply chain. The work of Vezzetti et al. [6] uses a set of different procedures to address the problems in the textile and apparel industry. The work of Jia et al. [5] employs a multi-criteria decision-making tool known as the technique for order of preference by similarity to ideal solution (TOPSIS) for ranking potential suppliers among the pool of textile suppliers. The study uses twelve criteria from economic, environmental, and social perspectives for evaluating suppliers. The work of Chen [7] proposes a two-phase supplier selection and evaluation model that takes into account the specifics of the textile industry. In the first phase, an enterprise competitive strategy is identified using a type of analysis known as strengths-weaknesses-opportunities-threats (SWOT) analysis. In the second phase, data envelopment analysis (DEA) and TOPSIS methods are used to select and evaluate suppliers. The work of Moon et al. [8] develops a multifaceted scale for supply chain flexibility through an empirical investigation. The research uses four dimensions, namely, sourcing flexibility, operating system flexibility, distribution flexibility, and information system flexibility. The work of Wang et al. [9] proposes a two-stage fuzzy analytic hierarchy process (AHP) model for the assessment of risk in implementing green initiatives in fashion industry supply chains. In the first stage, the research incorporates uncertain parameters into decision-making processes. In the second stage, the research uses analytic hierarchy processes to form a decision-making model for different green initiatives in the fashion industry. Likewise, several other existing papers use different tools and methods to deal with problems in textile supply chains [10,11,12,13,14]. One gap in the current literature, however, is a study that provides a sustainable outsourcing strategy to deal with emerging challenges, such as offshoring and reshoring practices. In the textile industry, sustainability has been addressed through various lenses of differing perspectives, methods, and approaches [15]. One way to achieve sustainability is to develop flexibility in the supply chain network. This paper uses the concept of reserved capacity flexibility. Capacity flexibility allows companies to adapt to the demands of uncertainty and global dynamics. In the example analysis herein, a textile manufacturer reserves some capacity flexibility with domestic suppliers at the tactical planning stage. In uncertain situations, this capacity flexibility helps to sustain the business. Another way to achieve sustainability in the supply chain network is to manage outsourcing risks at international destinations. Outsourcing risks affect the relocation of production processes. Therefore, this paper offers a sustainable outsourcing strategy based on the simultaneous consideration of cost savings, capacity flexibility, and outsourcing risks.

Production planning decisions are classified as strategic, tactical, and operational decisions. Strategic decisions include long-term decisions, such as capacity expansion at an in-house facility in a manufacturer’s home country or at an international subsidiary. Operational decisions include short-term decisions, such as day-to-day capacity management. Tactical decisions include medium-term decisions, such as capacity allocation decisions.

This paper concentrates on tactical planning decisions. Capacity expansion decisions are challenging at the tactical level. Tactical decisions require flexibility to deal with uncertain situations, and what is more, product demand is likely to fluctuate at the tactical level. Furthermore, making the right decisions at the tactical level allows greater flexibility for manufacturers to think about capacity allocation at production destinations across the globe. This paper evaluates outsourcing strategies based on operational costs, capacity flexibility, and outsourcing risks.

In the textile industry, international outsourcing provides significant cost savings. Current trends of reshoring are emerging due to increasing costs and risks [16,17]. However, the reshoring process involves many challenges, such as worldwide variations in labor costs, capital investment decisions, environmental issues, and availability of raw materials [16,18,19]. Labor costs are a basic motive for international outsourcing.

Table 1. Labor cost/hourly compensation—U.S. $.

Developed Markets				Emerging Markets		Developing Markets
Norway	64.50	France	42.12	Brazil	11.65	Vietnam	0.60
Belgium	54.77	Ireland	39.38	Russia	2.99	Myanmar	0.20
Denmark	51.67	Canada	36.56	India	1.17	Pakistan	0.58
Sweden	49.12	Italy	36.17	China	2.10	Sri Lanka	0.81
Germany	47.38	USA	35.53	Indonesia	1.08	Bangladesh	0.40
Australia	46.29	UK	30.77	Mexico	6.48	Colombia	2.97
Finland	44.14	Spain	28.44	Turkey	4.50
Austria	43.16	Greece	21.78
The Netherlands	42.26	Portugal	12.91

Source: Sardar and Lee [20].

highlights labor cost differences in different markets across the globe [20]. In developed markets, the unit cost of a garment includes nearly 50 percent of the labor cost. To decrease unit production cost, textile manufacturers have moved production processes to low cost markets [21]. Greater differences in unit production costs offset the transportation and transaction costs associated with low cost markets.

Companies that outsource internationally focus on achieving cost benefits, while companies that outsource domestically focus on achieving capacity flexibility [22]. Manufacturers reduce capital investments and meet inconsistent demand requirements through domestic outsourcing. Outsourcing utilizes the chase strategy of capacity planning. In the chase strategy, production capacity can be adopted to respond to uncertainty. Domestic outsourcing provides better capacity flexibility than compensating for overtime or the hiring and firing of labor at in-house facilities. However, domestic suppliers have limited capacity due to their own production planning. Therefore, domestic suppliers cannot always be available to respond to demand fluctuations. In this case, some capacity flexibility may be reserved at domestic suppliers.

This paper defines capacity flexibility as “capacity reserved with domestic suppliers to deal with uncertainty”. Uncertainty is understood as deviation from demand estimated as a proportion of demand. A manufacturer allocates capacity flexibility to different domestic suppliers, and pays unit penalty costs for any capacity flexibility that is not acquired. If the uncertainty of a market is low, then the manufacturer will likely outsource internationally for cost savings. The textile supply chain has significantly distinct divisions with complex processes [16,23]. Placement of upstream divisions in low-cost markets increases the risks of outsourcing. Subsequently, upstream divisions (e.g., fiber production, yarn production, fabric production, fabric processing, and garment manufacturing) in the textile supply chain become comparatively more ineffective and inefficient than downstream divisions (e.g., distribution and retailing) due to non-optimal inventories, lead times, transportation costs and complications, and service levels [24].

International outsourcing has a higher probability of risk due to factors such as late deliveries, cross-border bottlenecks, quality failures, and unfavorable management practices. Outsourcing risks may have a serious impact on supply chain processes and customer satisfaction. Accordingly, this paper includes outsourcing risks at international destinations. Outsourcing risks are incorporated as “the product of probability of risk at a destination and the production quantity assigned to that destination”. The probability of risk can be estimated based on several risk factors. Some risk factors from the literature are described as follows [16].

• Border crossing complexity, including the Number of crossings and level of difficulty.
• Late and unreliable deliveries due to distance, transportation modes, and complexities.
• Exchange rate and currency fluctuations at destination country.
• Communication and cultural barriers due to language and culture.
• Natural disaster including frequency of events (e.g., fire or flooding) and recovery plans.
• Loss due to terrorist attacks, terrorist activities, and the security of resources.
• Political instability/corruption (i.e., declining economies and unfair governments).

If the risks of outsourcing come to pass at a destination, then the quantities assigned at that destination are considered the resultant loss. Maximum loss is assumed to be the loss of an entire production quantity assigned to a production facility at a destination. Product loss due to outsourcing risks creates several unsustainable patterns, such as customer dissatisfaction, economic loss, and solid waste management issues.

2. Contribution to Existing Literature

The existing literature lacks practical tools for outsourcing decision making. The existing literature addresses outsourcing strategies in several ways. The work of Abdel-Malek et al. [25] compares two outsourcing strategies for outsourcing vendor selection (i.e., competitive bidding and long-term partnerships). The framework of that study is based on required safety stock in comparing annual costs of outsourcing strategies. The work of Liu and Zhang [26] presents a capacitated production planning problem with outsourcing. The objective is to minimize total costs, including production costs, setup costs, inventory holding costs, lost sales costs, and costs related to outsourcing activities. The work of Tsai and Lai [27] applies an activity-based costing model to the production of joint products when market demand exceeds the available capacity. The research examines the costs of internal capacity expansion or the decision to outsource.

The work of Wu et al. [28] looks at a bi-objective strategic outsourcing order allocation problem for semiconductor assembly with a nonlinear cost structure to minimize the total alignment gap and total allocation costs. The work of Zhen [29] proposes an integrated three-stage decision model for outsourcing and production decisions from a global perspective with export-oriented tax policies. The decisions therein include “which components should be imported and what production quantities should be assigned to domestic and international markets”.

The work of Wang et al. [30] proposes a model to integrate capacity planning and vendor selection regarding factors such as a finite number of time periods, order allocation, and costs associated with capacity additions, holding, and rework. The research claims that few studies of vendor selection have systematically considered capacity in outsourcing decisions. A study by Morlok and Chang [31] offers approaches for the measurement of capacity flexibility in transportation systems. The study defines system capacity flexibility as the “capability of a transportation system to accommodate fluctuations in traffic demand while maintaining a reasonable level of performance.” Chen and Kasikitwiwat [32] propose network models to quantify capacity flexibility for transportation networks. They use a concept of limited capacity flexibility in which additional demand deviates from fixed demand patterns. The work of Boulaksil et al. [33] studies a problem in which a supplier (i.e., a contract manufacturer) serves several manufacturers (i.e., outsourcers). Each outsourcer reserves capacity flexibility to the supplier and charges unit penalty costs to the supplier if the required quantity is not produced.

In this paper, a hypothetical manufacturer has four production options across the globe. More specifically, the options are an in-house firm in the home country, domestic suppliers in the home country, an international subsidiary, and international suppliers. The manufacturer outsources to international markets for cost savings and outsources to domestic suppliers for capacity flexibility. This paper defines capacity flexibility as “capacity reserved with domestic suppliers to deal with uncertainty.” Uncertainty is assumed to be deviation from demand estimated as a proportion of demand. The manufacturer allocates capacity flexibility to the domestic suppliers and pays a unit penalty cost if it does not acquire reserved capacity.

Domestic production can be differentiated from international production in aspects such as lead time uncertainty, quality issues, and cross-border bottlenecks, which are some of the potential problems of working on an international scale. Thus, a manufacturer deals with greater outsourcing risks at international destinations. This paper evaluates outsourcing strategies based on operational costs, penalty costs (as a function of capacity flexibility), and outsourcing risks. Three variants of goal programming are used to solve the outsourcing problem, and different solutions are compared. Based on the results, useful insights are proposed.

Table 2. Contribution to existing literature.

	Cost	Capacity Flexibility	Outsourcing Risk	Description
Abdel-Malek et al. [25]	✓	✕	✕	Costs of outsourcing strategies
Liu and Zhang [26]	✓	✕	✕	Total cost
Tsai and Lai [27]	✓	✕	✕	Total cost
Wu et al. [28]	✓	✕	✕	Total cost + alignment gap
Zhen [29]	✓	✕	✕	Profit
Wang et al. [30]	✓	✕	✕	Total cost + holding cost + rework cost
Morlok and Chang [31]	✓	✓	✕	Capacity flexibility measurement
Chen and Kasikitwiwat [32]	✓	✓	✕	Limited capacity flexibility
Boulaksil et al. [33]	✓	✓	✕	Capacity reserved
This paper	✓	✓	✓	Operational cost + capacity flexibility + outsourcing risk

summarizes the contributions of the multi-objective model herein to the existing literature, as well as demonstrates the relative contributions of existing studies to the topic of outsourcing strategies in textile supply chains.

3. Model Development

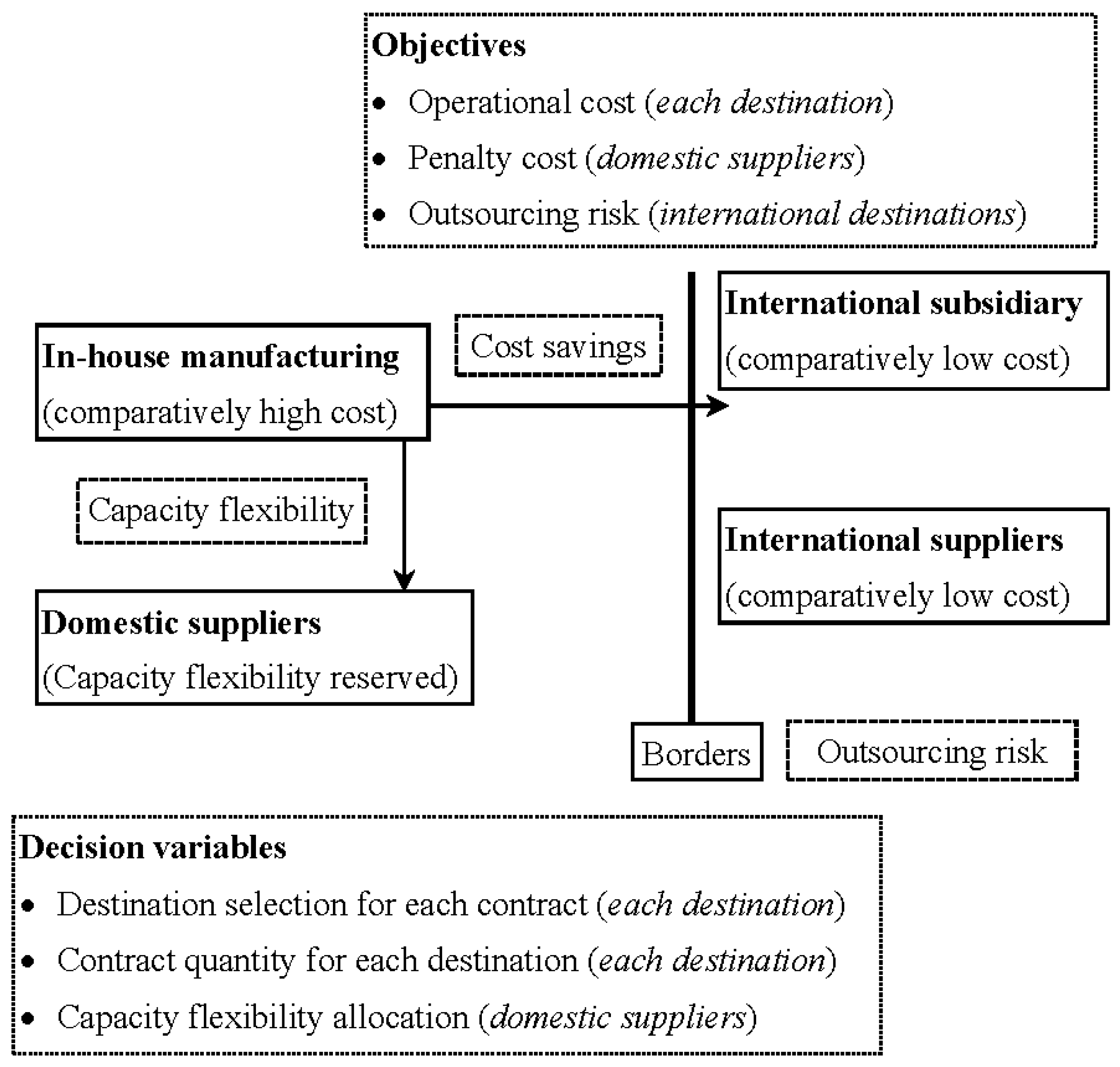
Consider a supply chain across the world (Figure 1) wherein a manufacturer decides to outsource internationally for cost savings, and domestically for capacity flexibility. There are four manufacturing options, including an in-house facility in the home country, domestic suppliers in the home country (i.e., i = 1,2,...,I), an international subsidiary, and international suppliers (i.e., $j=1,2,...,J$). The set of production contracts received from customers is $a=1,2,...,A$. It is supposed that an in-house manufacturing firm is situated in a high-cost country, which outsources domestically in the same country, and which outsources internationally to low-cost countries. Moreover, it is assumed that when the manufacturer outsources to domestic/international destinations, each product is shipped back to the in-house manufacturing firm. Hence, transportation cost is not included at the in-house firm.

The decisions for the manufacturer are to select production destinations for each contract, to determine the quantity of each contract at each selected facility, and decide the allocation of reserved capacity flexibility at the domestic suppliers. The manufacturer wants cost savings from international destinations, and capacity flexibility from domestic suppliers.

Some capacity flexibility is reserved at the domestic suppliers to deal with market uncertainty. The reserved capacity flexibility at all selected domestic suppliers should be equal to the capacity flexibility required as a proportion of demand for a contract. The reserved capacity flexibility for a contract at a domestic supplier should be greater than or equal to the quantity assigned to that domestic supplier. Each facility at each destination has a fixed capacity. Moreover, the manufacturer wants to minimize outsourcing risks at the international subsidiary and international suppliers. Selected facilities should fulfill demand for each contract. The manufacturer sets minimum production quantities with each domestic/international supplier. Each minimum production quantity at the international suppliers is assumed to be greater than the minimum production quantity at domestic suppliers. The minimum production quantities at the international suppliers should be greater due to factors such as transportation costs and environmental emissions during transportation.

The multi-objective outsourcing problem can be formulated as follows.

Minimize operational cost

$$Z_1={\displaystyle \sum _a\left\{C_a^{in}Qi{n}_a{z}_a+(C_a^{sb}+T_a^{sb})Qs{b}_a{y}_a+{\displaystyle \sum _i(C_{ai}^{ds}+T_{ai}^{ds})Qd{s}_{ai}{w}_{ai}+{\displaystyle \sum _j(C_{aj}^{is}+T_{aj}^{is})Qi{s}_{aj}{x}_{aj}}}\right\}}$$

(1)

Minimize penalty cost

$$Z_2=P{c}_{ai}^{ds}\times \left({\displaystyle {\sum }_i{F}_{ai}}-{\displaystyle {\sum }_{i}Qd{s}_{ai}}\right),\forall a$$

(2)

Minimize outsourcing risk

$$Z_3={\displaystyle \sum _{a}P{r}_a^{sb}Qs{b}_a{y}_a}+{\displaystyle \sum _a{\displaystyle \sum _{j}P{r}_{aj}^{is}Qi{s}_{aj}{x}_{aj}}}$$

(3)

subject to

$$Qi{n}_a\le z_{a}c{p}_a^{in},\forall a$$

(4)

$$Qs{b}_a\le y_{a}c{p}_a^{sb},\forall a$$

(5)

$$Qd{s}_{ai}\le w_{ai}c{p}_{ai}^{ds},\forall a,i$$

(6)

$$Qi{s}_{aj}\le x_{aj}c{p}_{aj}^{is},\forall a,j$$

(7)

$$Qi{n}_a+{\displaystyle \sum _{i}Qd{s}_{ai}}+Qs{b}_a+{\displaystyle \sum _{j}Qi{s}_{aj}}=D_a,\forall a$$

(8)

$${\displaystyle \sum _i{F}_{ai}}=P{F}_a{D}_a,\forall a$$

(9)

$$F_{ai}\ge Qd{s}_{ai},\forall a,i$$

(10)

$$Qd{s}_{ai}\ge w_{ai}m{q}_{ai}^{ds},\forall a,i$$

(11)

$$Qi{s}_{aj}\ge x_{aj}m{q}_{aj}^{is},\forall a,j$$

(12)

$$Qi{n}_a,Qd{s}_{ai},Qs{b}_a,Qi{s}_{aj},F_{ai}\ge 0$$

(13)

$$d_{OC}^{\pm },d_{PC}^{\pm },d_{OR}^{\pm }\ge 0$$

(14)

$$z_a,y_a,w_{ai},x_{aj}\in [0,1]$$

(15)

Equation (1) shows the minimization of operational costs for each contract at each production destination. Equation (2) shows the minimization of penalty costs for each contract at each domestic supplier. Please note that penalty costs will be charged only for reserved capacity that is not acquired. Equation (3) shows minimization of outsourcing risks at the international subsidiary and international suppliers. Equations (4)–(7) show that the total quantity produced at a specific facility should be less than or equal to its capacity. Equation (8) shows that the total quantity of a contract assigned at all destinations should be equal to demand. Equation (9) shows that total capacity flexibility reserved at all domestic suppliers should be equal to capacity flexibility required as a proportion of demand for a contract. Equation (10) shows that capacity flexibility reserved for a contract at a domestic supplier should be greater than or equal to the quantity assigned to that domestic supplier. Equations (11) and (12) show that the quantity of a contract outsourced to a domestic or an international supplier should be greater than or equal to the minimum quantity to be produced at that specific supplier. Equations (13) and (14) show positivity on decision variables and deviational variables. Equation (15) represents binary variables for the assignment of contracts.

4. Goal Programming Formulations

In this paper, three variants of goal programming (GP) are used to evaluate alternative cases. These variants are lexicographic GP, weighted GP, and Chebyshev GP. These variants are evaluated in the optimization package LINGO 15.0. There are three goals in the outsourcing problem, including the optimization of operational costs, penalty costs, and outsourcing risks. Target values are set for each goal. Then, deviation from the target values is minimized. The objective function is

$$MinZ=d_{OC}^{+}+d_{PC}^{+}+d_{OR}^{+}$$

(16)

In order to compare deviations in the same units, normalization is performed. This paper utilizes percentage normalization. Each deviation is converted into a percentage value away from the target value [34,35]. In normalization, each objective is divided by a constant related to each objective [35]. In this paper, the target value for each objective is used as the normalization constant. Target values are achieved through optimization of each objective separately. Thus, Equation (16) becomes

$$MinZ=\frac{d_{OC}^{+}}{T_{OC}}+\frac{d_{PC}^{+}}{T_{PC}}+\frac{d_{OR}^{+}}{T_{OR}}$$

(17)

where, $T_{OC},T_{PC},$ and $T_{OR}$ are the target values for operational cost, penalty cost, and outsourcing risk, respectively.

4.1. Lexicographic GP Formulation

Lexicographic GP is used when different objectives are clearly prioritized. This type of goal programming cannot be used to make direct comparisons between goals. The objective function involves a sequence of priority levels. Unwanted deviation for higher priority levels is minimized first (subject to constraints in the model). Then, the minimum deviation from the first priority level is used as an additional constraint for the minimization of the second priority level, and so on. This phenomenon is implemented as follows.

In lexicographic GP, the first step is to set the priority level for each goal. Deviation in a higher priority should be minimized first. A series of sequential optimizations is performed, and the minimum value of the higher priority level must be maintained [34]. Suppose priority for the three goals in the outsourcing problem is given as follows: priority 1 (P1) = operational costs, priority 2 (P2) = penalty costs, and priority 3 (P3) = outsourcing risks. Priority levels can be presented as

$$Mina=\left[P_1,P_2,P_3\right]$$

(18)

This vector restricts the preference to the satisfaction of a higher priority level to the lower priority levels. Therefore, the first priority level should be minimized first [34]. Minimization of positive deviation for the first priority level leads to the following formulation.

$$Minz=d_{OC}^{+}$$

(19)

subject to

$$\begin{array}{l}{\displaystyle \sum _a\left\{C_a^{in}Qi{n}_a{z}_a+(C_a^{sb}+T_a^{sb})Qs{b}_a{y}_a+{\displaystyle \sum _i(C_{ai}^{ds}+T_{ai}^{ds})Qd{s}_{ai}{w}_{ai}+{\displaystyle \sum _j(C_{aj}^{is}+T_{aj}^{is})Qi{s}_{aj}{x}_{aj}}}\right\}}\\ +d_{OC}^{-}-d_{OC}^{+}=T_{OC}\end{array}$$

(20)

$$P{c}_{ai}^{ds}\times \left({\displaystyle {\sum }_i{F}_{ai}}-{\displaystyle {\sum }_{i}Qd{s}_{ai}}\right)+d_{PC}^{-}-d_{PC}^{+}=T_{PC},\forall a$$

(21)

$${\displaystyle \sum _{a}P{r}_a^{sb}Qs{b}_a{y}_a}+{\displaystyle \sum _a{\displaystyle \sum _{j}P{r}_{aj}^{is}Qi{s}_{aj}{x}_{aj}}}+d_{OR}^{-}-d_{OR}^{+}=T_{OR}$$

(22)

Equations (4)–(15) are included. From optimization of the first priority level goal, the optimal value of $d_{OC}^{+}$ becomes the constraint in the second priority level. Minimization of unwanted (i.e., positive) deviation for the second priority level objective is

$$Minz=d_{PC}^{+}$$

(23)

subject to

The optimal value of $d_{OC}^{+}$ from Equation (19) is included as a constraint. Equations (4)–(15) and Equations (20)–(22) are also included. From optimization of the first and second priority level goals, the optimal values of deviations $d_{OC}^{+}$ and $d_{PC}^{+}$ become the constraints in the third priority level. Now, the third priority level objective is optimized as follows.

$$Minz=d_{OR}^{+}$$

(24)

subject to

The optimal values of $d_{OC}^{+}$ and $d_{PC}^{+}$from Equations (19) and (23) are included as constraints. Equations (4)–(15) and Equations (20)–(22) are also included. This formulation is the optimal solution for lexicographic GP. In Lexicographic GP, goals with top priority levels perform relatively well. If priority levels are changed for designated goals, then there may be different solution to the problem. Lexicographic GP is the best alternative if clear preferences for goals are available. This variant is used to avoid direct comparisons between sensitive criteria [34].

4.2. Weighted GP Formulation

Weighted GP is used when direct comparisons between different objectives are sought. The unwanted deviation of each objective is normalized. Preferential weights are used to determine the comparative importance of objectives. The objective function is the weighted sum of normalized deviations. The objective function is minimized subject to all constraints in the model. In weighted GP, percentage normalization is used. Unwanted deviation for each objective is normalized by dividing each objective by the target level for each objective. The optimal value achieved through the separate optimization of each objective is set as the target level for each associated objective. Comprehensive application of weighted GP is performed as follows.

In weighted GP, direct trade-offs between deviations are performed using weights. The achievement function is normalized [34]. Weights represent the relative importance of objectives. Weighted GP formulation is presented as follows.

$$MinZ={\omega }_1\frac{d_{OC}^{+}}{T_{OC}}+{\omega }_2\frac{d_{PC}^{+}}{T_{PC}}+{\omega }_3\frac{d_{OR}^{+}}{T_{OR}}$$

(25)

where ${\omega }_1,{\omega }_2,$ and ${\omega }_3$ represent the relative weights for three objectives, subject to

$${\displaystyle \sum _{q=1}^3{\omega }_q=1}$$

(26)

Equations (4)–(15) and Equations (20)–(22) are also included.

4.3. Chebyshev GP Formulation

In weighted GP and lexicographic GP, some goals perform well and other goals remain very far from the target. This imbalance can be minimized using Chebyshev GP. This method aims for a balanced achievement of all objectives. Chebyshev GP is based on minimization of the maximal (i.e., worst) unwanted deviation from any single objective. In this method, each objective is normalized as in weighted GP. The objective function minimizes the worst deviation from any single goal. In addition to all the constraints in the problem, additional constraints are identified when “normalized deviation for individual goals is less than or equal to maximal deviation from among the set of three goals”. The implementation of Chebyshev GP is performed as follows.

In Chebyshev GP, the maximum deviation from a single goal is minimized, as opposed to the sum of all deviations [34]. If $\lambda$ is the maximal deviation from among the set of goals, then Chebyshev GP formulation is presented as follows [34]

$$Minz=\lambda$$

(27)

subject to

$$\frac{d_{OC}^{+}}{T_{OC}}\le \lambda$$

(28)

$$\frac{d_{PC}^{+}}{T_{PC}}\le \lambda$$

(29)

$$\frac{d_{OR}^{+}}{T_{OR}}\le \lambda$$

(30)

Equations (4)–(15) and Equations (20)–(22) are also included.

5. Numerical Example

The usefulness of the multi-objective model can be clarified using a numerical example that was designed according to the model parameters and assumptions. There are three contracts scheduled for production. Example data is presented in

Table 3. Input data for outsourcing problem.

Contract No.	In-House	Domestic Suppliers		Subsidiary	International Suppliers
		1	2		1	2
Unit production cost ($)
1	177	186	189	89	93	95
2	272	286	291	136	143	146
3	70	74	75	35	37	37
Demand (units/contract)
1	3636
2	5547
3	4960
Capacity flexibility required at domestic suppliers as a proportion of demand (percent/contract)
1		0.09
2		0.13
3		0.09
Production capacity at each destination (units/contract)
1	2402	2522	2618	2357	2475	2569
2	3980	4179	4338	4276	4490	4661
3	4656	4898	5085	4636	4868	5053
Unit penalty cost ($)
1		09	21
2		14	32
3		04	08
Probability of outsourcing risk
1				0.07	0.15	0.05
2				0.06	0.15	0.16
3				0.04	0.05	0.17
Transportation cost per unit ($)
Contract 1 to 3		0.33	0.35	1.38	1.46	2.48
Minimum production quantity committed with suppliers (units/contract)
Contract 1 to 3		100	100		200	200

. The numerical example is designed based on general numbers, but it represents a realistic scenario.

In developing the model, it was assumed that the in-house manufacturing firm is situated in a high-cost country (e.g., China), which outsources domestically in the same country and which outsources internationally to low-cost countries (e.g., Vietnam). Therefore, unit production costs were considered to be relatively low at the international destinations. Production capacities were different at different destinations. Transportation costs were not included at the in-house firm.

Transportation costs per unit were considered to be greater at international destinations in comparison to transportation costs per unit at domestic suppliers. The minimum production quantity at international suppliers was assumed to be greater at international destinations than at domestic suppliers due to factors such as transportation costs and environmental emissions during transportation.

The best achieved values for operational costs, penalty costs, and outsourcing risks are $1,286,004.00, $5.30, and 96.11 units, respectively. These optimal values are set as target values for corresponding objectives.

If only the operational cost is minimized, then the result is $1,286,004.00. In this case, the observed penalty cost is $33,519.00 and the observed outsourcing risk is 1006 units. The majority of production is allocated to low-cost international destinations. If only the penalty cost is minimized, then the result is $5.30. In this case, the observed operational cost is $1,575,844.00 and the observed outsourcing risk is 1070 units. The reserved capacity flexibility is fully utilized. If only the outsourcing risk is minimized, then the result is 96.11 units. In this case, the observed operational cost is $2,333,131.00 and the observed penalty cost is $11.76. Also in this case, maximum production is assigned to domestic destinations.

Six cases are presented based on changing priority levels in lexicographic GP and preferential weights in weighted GP. In each case, the preferential weights for the first, second, and third preferences are set as 0.65, 0.25, and 0.10, respectively. Chebyshev GP shows the same results in all six cases. Abbreviations are used as follows: operational cost = OC, penalty cost = PC, and outsourcing risk = OR.

Cost and risk objectives are measured in different units. To compare the results on the same scale, each objective was normalized using the value path approach (VPA). The VPA is the most efficient way to graphically represent the trade-offs among different objectives. In this approach, the achieved value for an objective is divided by the best solution for this objective. Some papers apply the VPA to compare different objectives [36,37].

The process of normalizing values results in values that are greater than or equal to one $\left(\ge 1\right)$. Therefore, the minimum value for each objective is one. As the value increases from one, the performance of an objective decreases.

Table 4. GP solution and normalized comparison for alternative cases.

	Operational Cost ($)	Penalty Cost ($)	Outsourcing Risk (Loss Units)
Minimum value for each objective	1,286,004	5.30	96.11
Case 1. OC—PC—OR sequence
Lexicographic GP	1,286,004	14,826	1006
Weighted or non-preemptive GP	1,867,110	5.30	301.91
Chebyshev or Minmax GP	2,179,152	8.98	162.85
Normalized comparison (case 1)
Lexicographic GP	1.00	2797.42	10.46
Weighted or non-preemptive GP	1.45	1.00	3.14
Chebyshev or Minmax GP	1.69	1.69	1.69
Case 2. OC—OR—PC sequence
Lexicographic GP	1,286,004	14,826	1006
Weighted or non-preemptive GP	2,328,857	5.30	96.11
Chebyshev or Minmax GP	2,179,152	8.98	162.85
Normalized comparison (case 2)
Lexicographic GP	1.00	2797.42	10.46
Weighted or non-preemptive GP	1.81	1.00	1.00
Chebyshev or Minmax GP	1.69	1.69	1.69
Case 3. PC—OC—OR sequence
Lexicographic GP	1,434,586	5.30	827.41
Weighted or non-preemptive GP	2,328,857	5.30	96.11
Chebyshev or Minmax GP	2,179,152	8.98	162.85
Normalized comparison (case 3)
Lexicographic GP	1.12	1.00	8.61
Weighted or non-preemptive GP	1.81	1.00	1.00
Chebyshev or Minmax GP	1.69	1.69	1.69
Case 4. PC—OR—OC sequence; Case 6. OR—PC—OC sequence
Lexicographic GP	2,328,857	5.30	96.11
Weighted or non-preemptive GP	2,328,857	5.30	96.11
Chebyshev or Minmax GP	2,179,152	8.98	162.85
Normalized comparison (case 4 and case 6)
Lexicographic GP	1.81	1.00	1.00
Weighted or non-preemptive GP	1.81	1.00	1.00
Chebyshev or Minmax GP	1.69	1.69	1.69
Case 5. OR—OC—PC sequence
Lexicographic GP	2,328,242	573.30	96.11
Weighted or non-preemptive GP	2,328,857	5.30	96.11
Chebyshev or Minmax GP	2,179,152	8.98	162.85
Normalized comparison (case 5)
Lexicographic GP	1.81	108.17	1.00
Weighted or non-preemptive GP	1.81	1.00	1.00
Chebyshev or Minmax GP	1.69	1.69	1.69

presents a summary of results and normalized values.

6. Results and Discussion

Three variants of GP can be compared for the six cases using normalized values from Table 4. For example, consider case 1. In terms of operational costs, weighted GP performs 0.17 times better than Chebyshev GP. This is obtained with the following formula.

$$\frac{Highervalue-Lowervalue}{Lowervalue}=\frac{1.69-1.45}{1.45}=0.17timesbetter=17\%better$$

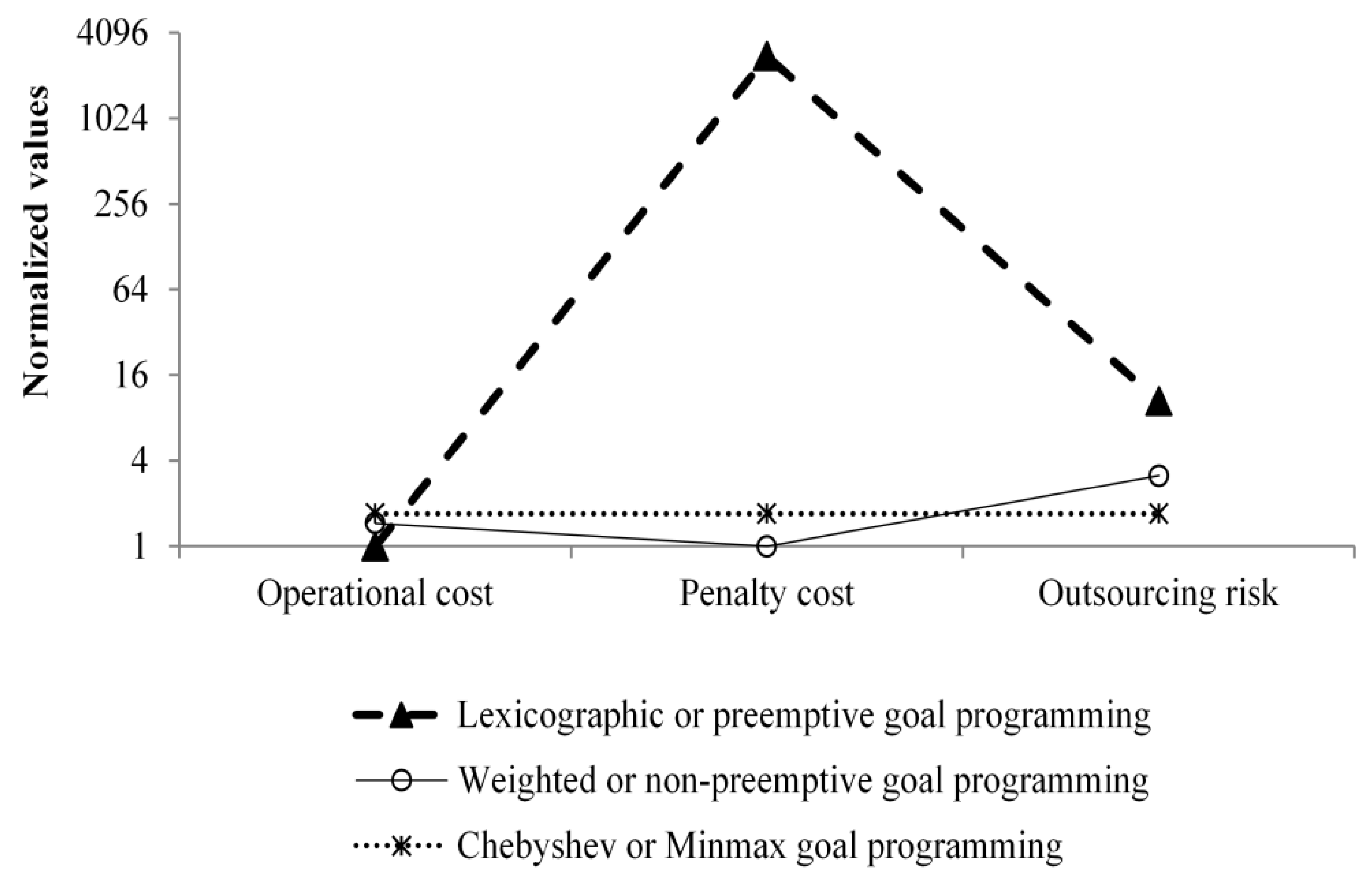
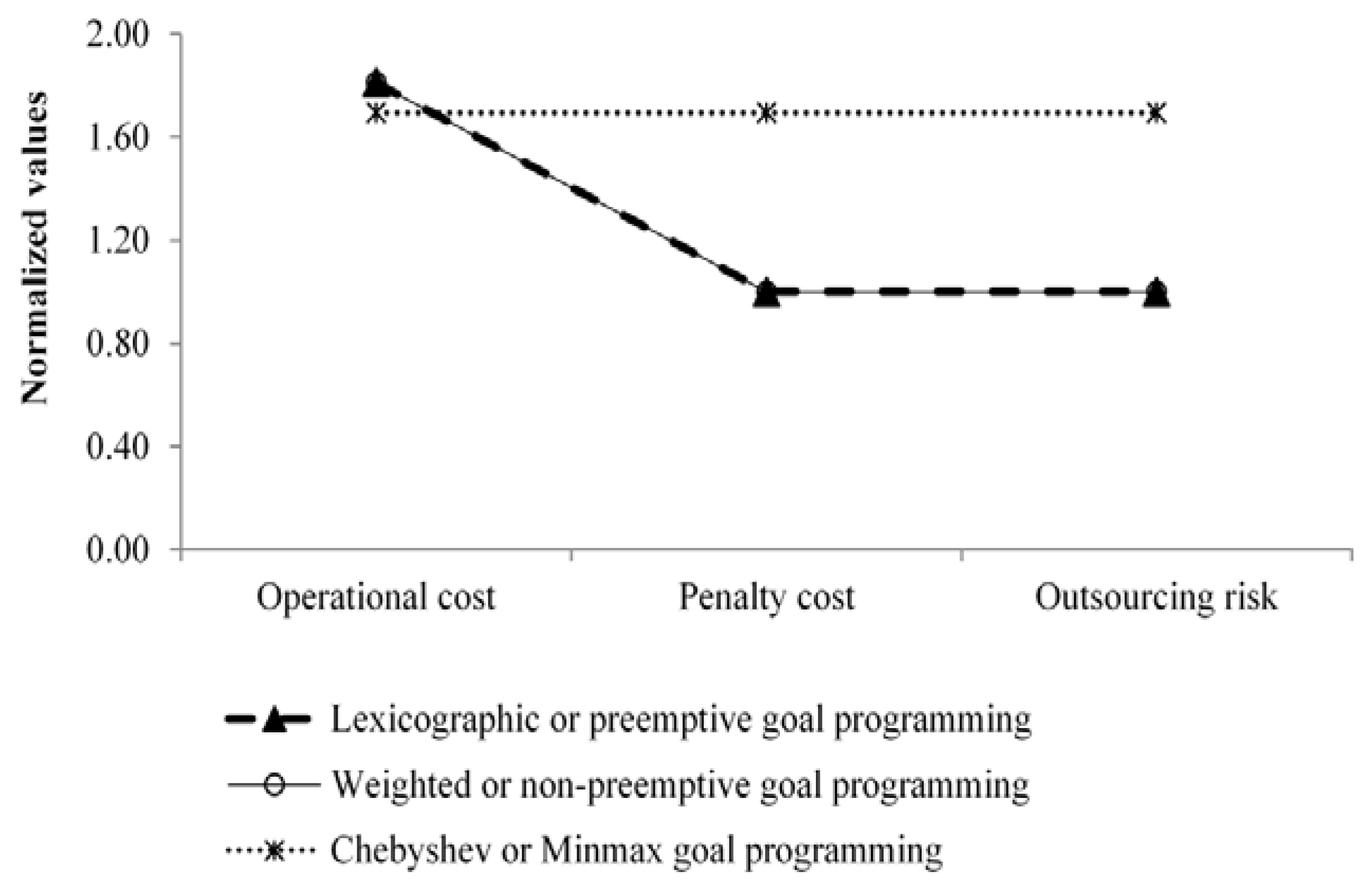
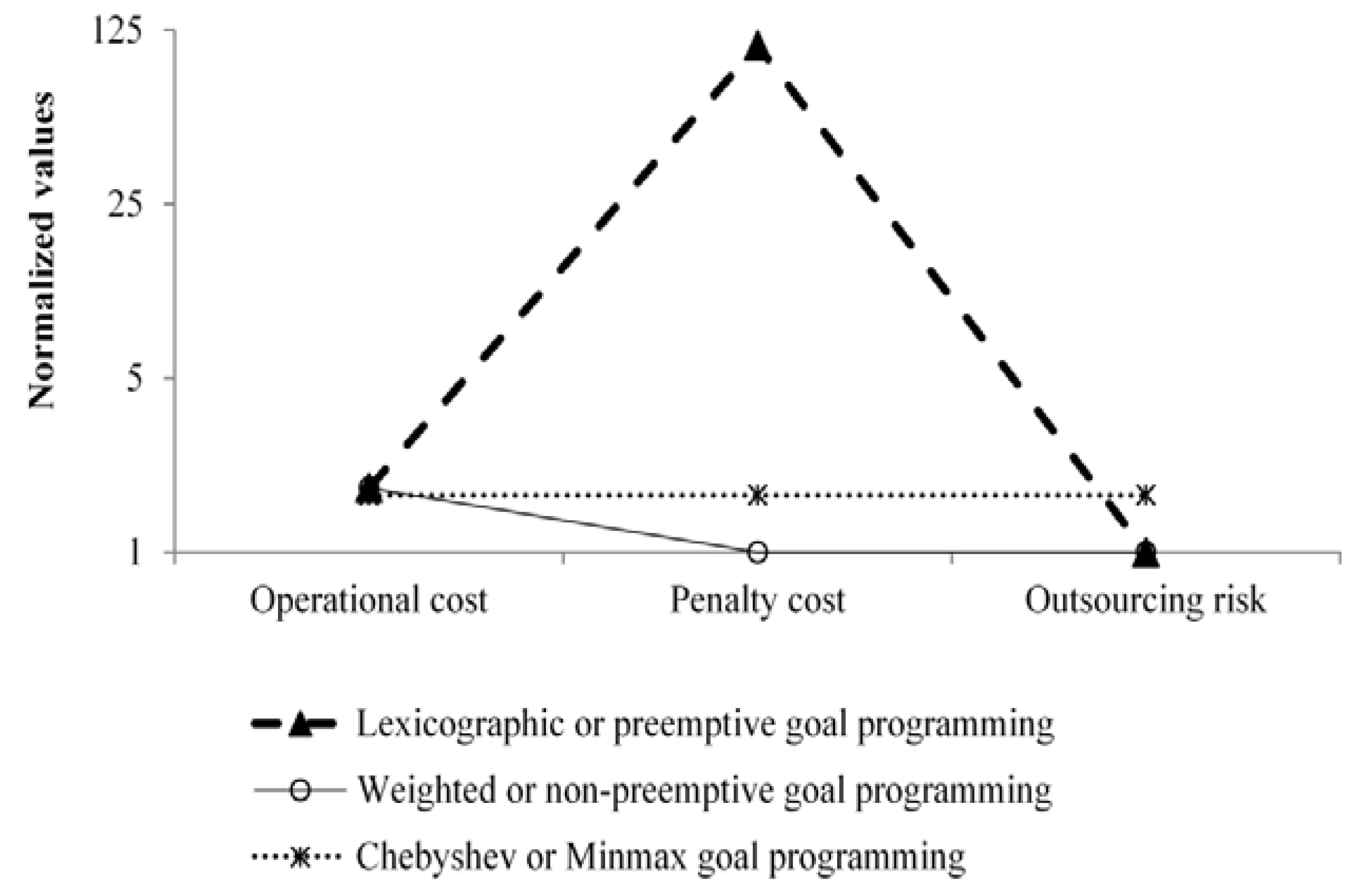
Only key observations are summarized below. Graphical representations are shown in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6. In case 1 and case 2, for penalty costs and outsourcing risks, lexicographic GP performs worse than the other two variants (Figure 2 and Figure 3).

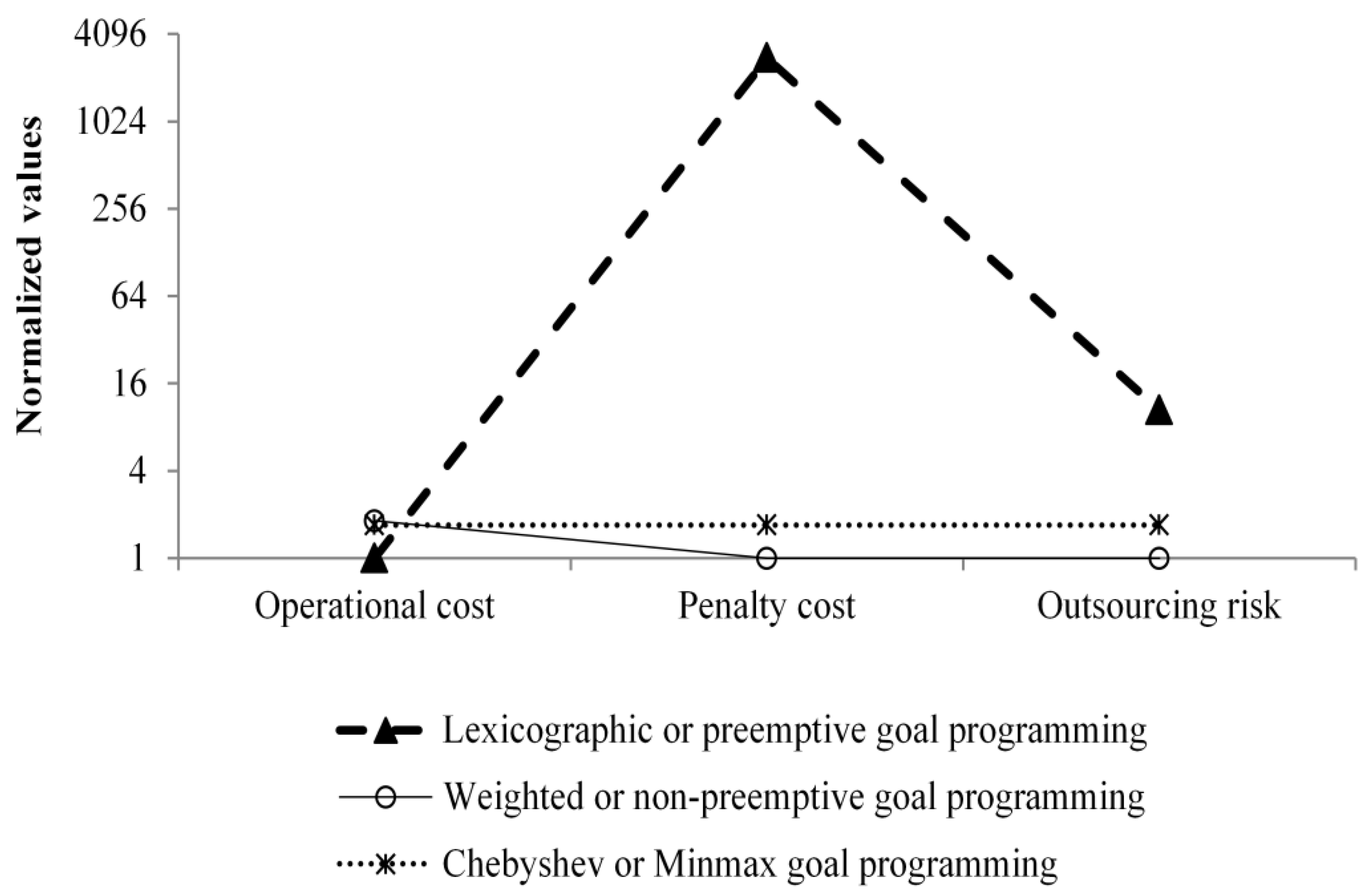
In case 3, for operational costs, lexicographic GP performs better than the other two variants. For penalty costs, Chebyshev GP performs worse than the other two variants. For outsourcing risks, weighted GP performs better than the other two variants. In case 3, Chebyshev GP performs better than lexicographic GP (Figure 4).

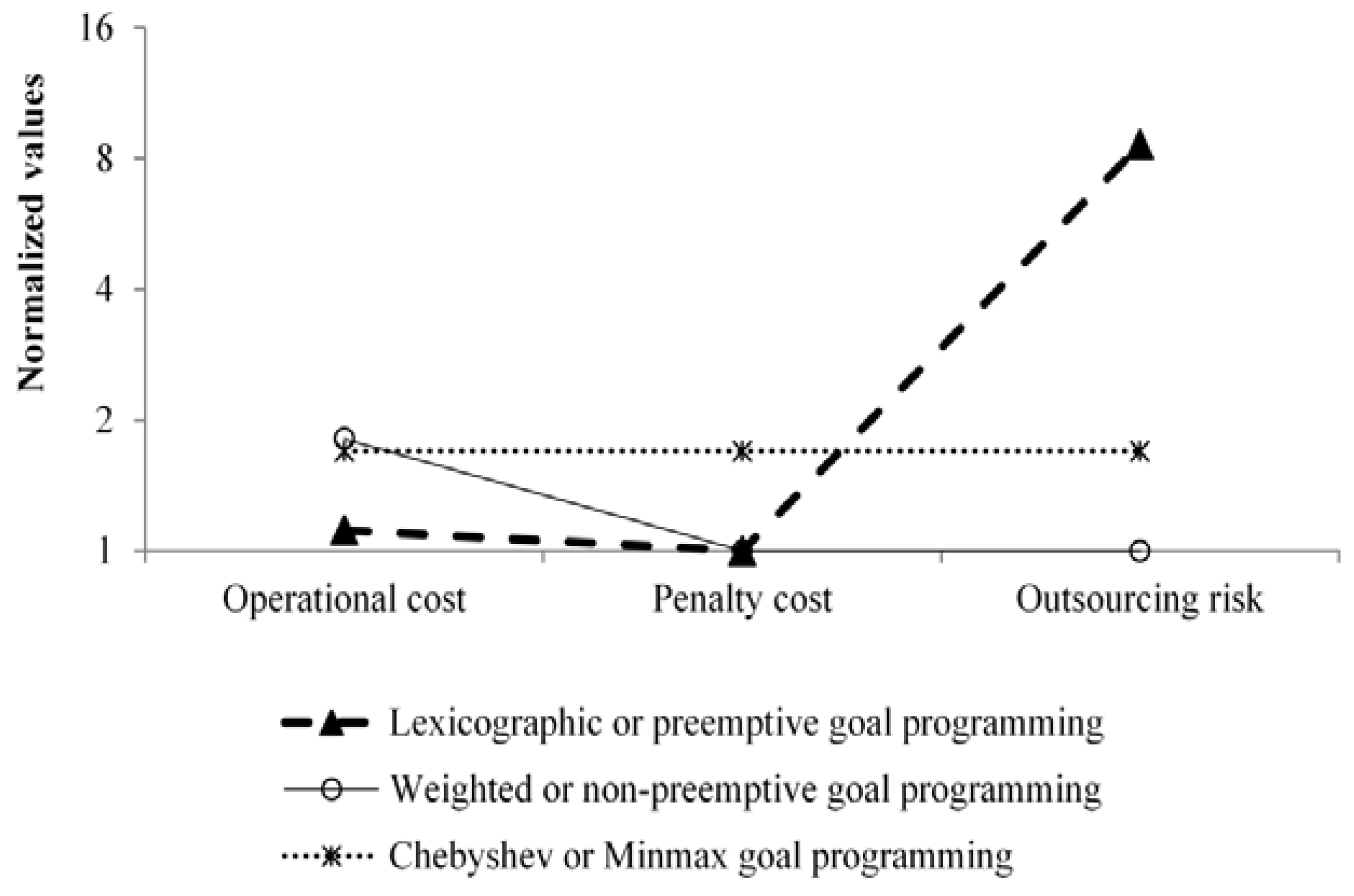
In case 4, lexicographic GP and weighted GP perform similarly for each of the three objectives (Figure 5). For penalty costs and outsourcing risks in case 4, Chebyshev GP performs worse than the other two variants. Case 6 behaves identically to case 4. In case 5, for penalty costs, lexicographic GP performs worse than the other two variants. In case 5, weighted GP performs better than Chebyshev GP. For outsourcing risks, Chebyshev GP performs worse than the other two variants (Figure 6).

In the lexicographic GP variant of goal programming, if high preference is given to operational costs, then the majority of production is assigned to low-cost international destinations. In this scenario, penalty costs and outsourcing risks become higher. In the lexicographic GP variant, if high preference is given to capacity flexibility, then most of the capacity flexibility is utilized, resulting in lesser penalty costs. In this scenario, if operational costs are the second option, then the contracts move toward low-cost destinations due to the low preference for outsourcing risks. Hence, outsourcing risks become higher and operational costs tend to decrease. However, if penalty costs are the first option and operational costs are the third option, then the magnitude of risk tends to decrease, resulting in higher operational costs due to lesser production at international destinations.

In the lexicographic GP variant, if high preference is given to risks, then most of the production moves toward local facilities, resulting in moderate penalty costs. In this scenario, if operational costs are the second preference, then operational costs are higher due to the high preference for outsourcing risks. Almost the entirety of production moves toward domestic destinations, which triggers cost-based competition in domestic markets. Hence, penalty costs depend on the total costs at individual domestic destinations. The least penalty costs are achieved in scenarios wherein capacity flexibility is the second option for the manufacturer.

In the lexicographic GP variant of goal programming, as the priority of an objective decreases, the value of an objective tends to become worse. In case 1 (OC—PC—OR sequence), penalty costs are given second preference. Thus the values of penalty costs and outsourcing risks are worse. In contrast, in case 5 (OR—OC—PC sequence), penalty costs are given third preference, but the penalty costs in case 5 are less than the penalty costs in case 1. Therefore, case 5 performs better than case 1 in terms of penalty costs, but the operational costs are comparatively higher in case 5 than in case 1. In case 5, the higher preference for outsourcing risks has already moved the production toward domestic destinations, resulting in lower penalty costs. Thus if a decision maker has clear priorities in mind in terms of the objectives, the lexicographic GP variant seems best.

In the weighted GP variant of goal programming, if approximately equal weight is given to each objective, operational costs tend to become higher because capacity flexibility and outsourcing risks move production contracts toward domestic destinations. In this scenario, if the saving of operational costs is the goal, then high weight should be assigned to operational costs. In the weighted or non-preemptive GP variant for each of the six cases, some objectives are satisfied while others have worse values. This shows that the weighted GP variant achieves target levels for some objectives at the expense of achieving worse value for other objectives. If a decision maker wants to determine direct trade-offs between objectives for the sake of comparison, the weighted or non-preemptive GP variant seems beneficial.

The Chebyshev or min-max GP variant of goal programming provides balanced achievement of the three objectives. In this scenario, operational costs remain higher due to the opposite effects of both capacity flexibility and outsourcing risks. Solution times were compared for each GP variant, using the weights and priorities from case 1 (i.e., OC—PC—OR sequence). The following four problem sizes were used to compare solution times.

• Problem size A: Contracts = 1, domestic suppliers = 2, international suppliers = 1
• Problem size B: Contracts = 1, domestic suppliers = 2, international suppliers = 2
• Problem size C: Contracts = 2, domestic suppliers = 2, international suppliers = 2
• Problem size D: Contracts = 3, domestic suppliers = 2, international suppliers = 2

For each GP variant, a slight increase in the problem size caused a considerable increase in the solution time (Figure 7). In addition to these four problem sizes, the problem size was further increased to test solution times. It was consistently observed that a slight increase in problem size causes a significant increase in solution time. Therefore, future work may develop an efficient algorithm to solve large-size problems.

7. Insights for Practitioners

The multi-objective GP model provides a tool for outsourcing decisions, including which contract should be produced at which facility across the globe, what proportion of a contract must be assigned to each selected facility, and how much capacity flexibility should be allocated at domestic suppliers in such a way that operational costs, penalty costs (as a function of capacity flexibility), and outsourcing risks remain under control. Our evaluation of GP variants provides several insights for outsourcing decision making.

International outsourcing provides greater cost savings. If operational costs are given first priority, then domestic suppliers (i.e., suppliers located in the home country of a manufacturer with similar labor costs) receive negligible production orders because they expend some extra resources, such as capital utilization, transportation costs, transaction costs, and any penalty costs for reserved capacity flexibility.

In the case of uncertainty, domestic suppliers offer capacity benefits that are similar to capacity expansion at an in-house facility in the home country of a manufacturer. In this scenario, capacity flexibility should be given first priority. Capacity expansion/contraction is a strategic decision. At the strategic level, management has already made decisions about capacity expansion/contraction. If demand uncertainty still exists after a stage of potential capacity expansion/contraction has passed, then domestic outsourcing provides similar benefits to in-house capacity expansion in the home country. Moreover, if an international subsidiary outsources to domestic suppliers in the same country that the subsidiary is located in, then the domestic suppliers provide the same capacity flexibility as the capacity expansion of the subsidiary.

If operational costs increase at an international market, then switching to a lower cost market will restore cost saving benefits. However, moving from existing textile markets to lower cost destinations is a strategic decision. For example, operational costs are increasing in emerging markets (e.g., China). In this case, moving to developing markets (e.g., Vietnam) may restore cost savings. It must be taken into account, however, that outsourcing risks decrease the benefits associated with low cost markets. In this case, if a manufacturer wants cost savings, then the same priority may be given to both operational costs and outsourcing risks (i.e., first priority). In this case, the sum of two deviations (i.e., operational costs and outsourcing risks) should be simultaneously minimized first (in the lexicographic GP variant). Capacity flexibility may be given second priority.

If the priorities for operational costs, capacity flexibility, and outsourcing risks are not clear in the minds of decision makers, then the decision makers may use the weighted GP variant to compare the direct trade-offs between the three objectives using weights. On the other hand, the Chebyshev GP variant may be used for balanced achievement of each objective.

Companies outsource domestically for capacity flexibility and they outsource internationally for cost savings. Outsourcing risks have major effects on outsourcing strategies. Therefore, this paper captures the realistic aspects of outsourcing decision-making in the global environment. Outsourcing decision-making based on realistic situations is becoming much more important due to recent challenges, such as the emergence of reshoring, increasing costs, supply chain network complexity, and environmental concerns. Comprehensive decision-making based on operational costs, capacity flexibility, and outsourcing risks is more practical. A suitable combination of domestic and international facilities provides a sustainable strategy in such a way that manufacturers have the flexibility to design their supply chain networks according to both economic and environmental factors.

8. Conclusions and Future Work

In this paper, a sustainable outsourcing strategy is proposed based on operational costs, penalty costs (as a function of capacity flexibility), and outsourcing risks. The multi-objective outsourcing problem deals with comprehensive decision making for the assignment of contracts to production destinations, the division of contracts among different facilities at different destinations, and allocation decisions for reserved capacity flexibility at domestic suppliers.

Our multi-objective model captures the realistic aspects of outsourcing decision-making in the global environment. Domestic outsourcing provides more capacity flexibility in comparison to international destinations. International outsourcing to low cost markets brings comparatively more cost savings. In the case of continuous increases in operational costs at international markets, shifting toward comparatively low cost markets tends to restore cost benefits. However, outsourcing risks should be managed in outsourcing and offshoring decision making. A suitable combination of domestic and international destinations is a sustainable, risk sharing-based strategy.

Goal programming variants provide flexible techniques for outsourcing and offshoring decision making. Decision makers are able to evaluate several possible alternatives based on existing circumstances. When goals are clearly prioritized, decision makers may rely on lexicographic GP. In contrast, weighted GP may be used to compare direct trade-offs between goals or Chebyshev GP may be used for the balanced achievement of goals.

Our proposed GP model was solved using Lingo 15. As problem size increases, solution time increases. To solve a large-size problem, future work may develop an improved algorithm. Future work may consider several uncertain situations in which capacity flexibility cannot be estimated exactly as a proportion of fixed demand patterns. How to maintain capacity flexibility in specific circumstances that differ in various contexts is a practical research area in the outsourcing problem. The risks associated with globalization and environmental issues may be incorporated in different ways. Capacity expansion/contraction decisions may be included to study the emerging phenomena of offshoring and reshoring. This paper considers tactical-level decisions. Future work may evaluate outsourcing strategies with comprehensive production planning based on strategic, tactical, and operational-level decisions.