A Study on Estimation of Land Value Using Spatial Statistics: Focusing on Real Transaction Land Prices in Korea
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Method
2.2.1. Spatial Autocorrelation
2.2.2. Spatial Regression Model
3. Analysis
3.1. Analysis of Spatial Autocorrelation and Heteroscedasticity, Non-Normality
3.2. Result of Spatial Regression Analysis
4. Performance Verification of Model
4.1. Horizontal Equity
4.2. Vertical Equity
5. Conclusions and Future Research
Author Contributions
Conflicts of Interest
Appendix
| Classification | Description |
|---|---|
| More than 25 m wide road | Land one side of which is adjacent to a street of 25 m wide or over |
| More than 25 m wide road (corner lot) | Land one side of which is adjacent to a wide street, and one or more sides of which are adjacent to a small-sized street (8–12 m wide) or a bigger one |
| More than 25 m wide road (corner lot) | Land one side of which is adjacent to a wide street, and one or more sides of which are adjacent to a narrow street (ga) where car can pass |
| 12~25 m wide road | Land one side of which is adjacent to a street of 12–25 m wide |
| 12~25 m wide road (corner lot) | Land one side of which is adjacent to a mid-sized street, and one or more sides of which are adjacent to mid-sized, small-sized, or narrow street (ga) where car can pass |
| 8~12 m wide road | Land one side of which is adjacent to a street of 8–12 m wide |
| 8~12 m wide road (corner lot) | Land one side of which is adjacent to a small-sized street, and one or more sides of which are adjacent to small-sized, or narrow street (ga) where car can pass |
| Less than 8 m wide road | Land one side of which is adjacent to a street whose width is narrower than 8 m, but where car can pass |
| Less than 8 m wide road (corner lot) | Land more than two sides of which are adjacent to a narrow street where car can pass |
| Less than 8 m wide road (vehicle inaccessible) | Land one side of which is adjacent to a narrow road where can cannot pass, but two-wheeled vehicle can pass |
| Less than 8 m wide road (vehicle inaccessible & corner lot) | Land two or more sides of which are adjacent to a narrow road where can cannot pass, but two-wheeled vehicle can pass |
| Landlocked lot | Land adjacent to a narrow road where two-wheeled vehicle cannot pass, or land which is not adjacent to road |
References
- Malpezzi, S. Hedonic Pricing Models: A Selective and Applied Review. In Housing Economics: Essays in Honor of Duncan Maclennan; O’Sullivan, A., Gibb, K., Eds.; Blackwell: Oxford, UK, 2003; pp. 67–89. [Google Scholar]
- Rosen, S. Hedonic Prices and Implicit Market: Product Differentiation in Pure Competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Kumar, P.; Pardhan, B.K.; Subramanian, A. Farmland Prices in a Developing Economy: Some Stylised Facts and Determinants. J. Int. Area Stud. 2005, 12, 93–113. [Google Scholar]
- Plantinga, A.J.; Lubowski, R.N.; Stavins, R.N. The Effects of Potential Land Development on Agricultural Land Prices. J. Urban Econo. 2002, 52, 561–581. [Google Scholar] [CrossRef]
- Basu, S.; Thibodeau, T. Analysis of Spatial Autocorrelation in House Prices. J. Real Estate Financ. Econ. 1998, 17, 61–85. [Google Scholar] [CrossRef]
- Patton, M.; McErlean, S. Spatial Effects within the Agricultural Land Market in Northern Ireland. J. Agric. Econ. 2003, 1, 35–54. [Google Scholar] [CrossRef]
- Pace, R.; Barry, J.; Rodriques, M. Spatiotemporal Autoregressive Models of Neighborhood Effects. J. Real Estate Financ. Econ. 1998, 17, 15–33. [Google Scholar] [CrossRef]
- Can, A. Specification and Estimation of Hedonic Price Model. Reg. Sci. Urban Econo. 1992, 22, 453–473. [Google Scholar] [CrossRef]
- Gillen, K.; Thibodeau, T.; Wachter, S. Anisotropic Autocorrelation in Housing Prices. J. Real Estate Financ. Econ. 2001, 23, 5–30. [Google Scholar] [CrossRef]
- Dubin, R. Estimation of Regression Coefficients in the Presence of Spatially Autocorrelated Error Terms. Rev. Econ. Stat. 1988, 70, 466–474. [Google Scholar] [CrossRef]
- Dubin, R. Spatial Autocorrelation and Neighborhood Quality. Reg. Sci. Urban Econ. 1992, 22, 433–452. [Google Scholar] [CrossRef]
- Olmo, J.C. Spatial Estimation of Housing Price and Locational Rents. Urban Stud. 1995, 32, 1331–1344. [Google Scholar] [CrossRef]
- Pace, R.K.; Barry, R.; Sirmans, C.F. Spatial Statistics and Real Estates. J. Real Estate Financ. Econ. 1999, 17, 5–13. [Google Scholar] [CrossRef]
- Park, H.S. A Study on Estimation of Farmland Price Using Spatial Econometrics Approach: Focus on Urban Fringe in Seoul Metropolitan Area. Korea Spat. Plan. Rev. 2012, 72, 121–140. [Google Scholar]
- Ministry of Land, Infrastructure and Transport (MOLIT). Annual Report on Real-Estate Price System in 2015; Korea Government: Sejong, Korea, 2011. (in Korea)
- Ministry of Land Infrastructure and Transport (MOLIT). A Study on Land Price Comparison Table for 2015; Korea Government: Sejong, Korea, 2014. (in Korea)
- Hur, Y.K. A Study on the Estimation of House Price in Regard of Spatial Effects. Hous. Stud. Rev. 2007, 15, 5–23. [Google Scholar]
- Choi, Y.; Lee, B.H. A Study on the Estimation of Land Price Considering Characteristic of the Adjacent Land Use and Spatial Autocorrelation in residential Zone. J. Korea Plan. Assoc. 2006, 41, 45–60. [Google Scholar]
- Park, H.S. The Estimation of Seoul Apartment Prices Using Spatiotemporal Autoregressive Models. Korea Spat. Plan. Rev. 2003, 38, 95–106. [Google Scholar]
- Kim, S.W.; Chung, K.S. The Robust Estimation with Spatial Econometrics Models using 3-Dimension Weight Matrix considering the Height of the House. Hous. Stud. Rev. 2010, 18, 73–92. [Google Scholar]
- Park, H.M. An Analysis of the Factors Affecting on the Prices of the Urban-life Housing Type of the Structure of the Urban Spaces in Seoul: Focused on the System of Structured Spaces in the basic city planning of Seoul 2030. J. Korea Plan. Assoc. 2013, 48, 419–435. [Google Scholar]
- Lee, C.R.; Park, K.H. The Effects of Neighborhood Segmentation on the Adequacy of a Spatial Regression Model. J. Korean Geogr. Soc. 2013, 48, 978–993. [Google Scholar]
- Cho, M.J.; Lee, M.H. Effects of regional and neighborhood living environment to the prices of aged apartments. J. Korea Plan. Assoc. 2015, 50, 23–47. [Google Scholar] [CrossRef]
- Seoul Statistics of Seoul Metropolitan Government. Available online: http://stat.seoul.go.kr/jsp3/index.jsp (accessed on 18 February 2016).
- Rawlings, J.O.; Pantul, S.G.; Dickey, D.A. Applied Regression Analysis: A Research Tool, 2nd ed.; Springer: Berlin, Germany, 2001; pp. 213–214. [Google Scholar]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Moran, P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Kissling, W.D.; Carl, G. Spatial Autocorrelation and the Selection of Simultaneous Autoregressive Models. Glob. Ecol. Biogeogr. 2008, 17, 59–71. [Google Scholar] [CrossRef]
- Stakhoych, S.; Bijmolt, T. Specification of Spatial Models: A Simulation Study on Weights Matrices. Pap. Reg. Sci. 2008, 88, 389–408. [Google Scholar] [CrossRef]
- Anselin, L. Local Indicators of Spatial Association-LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Aselin, L. Exploring Spatial Data with GeoDaTM: A Workbook; Center for Spatially Integrated Social Science: Santa Barbara, CA, USA, 2005. [Google Scholar]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24, 189–207. [Google Scholar] [CrossRef]
- European Central Bank. Spatial Dependence in Commercial Property prices Micro Evidence from the Netherlands. Work. Pap. Ser. 2014, 1627, 1–32. [Google Scholar]
- International Association of Assessing Officers (IAAO). Standard on Ratio Study; IAAO: Kansas City, MO, USA, 2010. [Google Scholar]
- International Association of Assessing Officers (IAAO). Improving Real Property Assessment: A Reference Manual; IAAO: Chicago, IL, USA, 1978. [Google Scholar]
- Sirmans, S.G.; Diskin, B.S.; Friday, S.H. Vertical Inequity in the Taxation of Real Property. Natl. Tax J. 1995, 48, 71–84. [Google Scholar]
- Oldman, O.; Aaron, H. Assessment-Sale Ratios under the Boston Property Tax. Natl. Tax J. 1965, 18, 36–49. [Google Scholar]
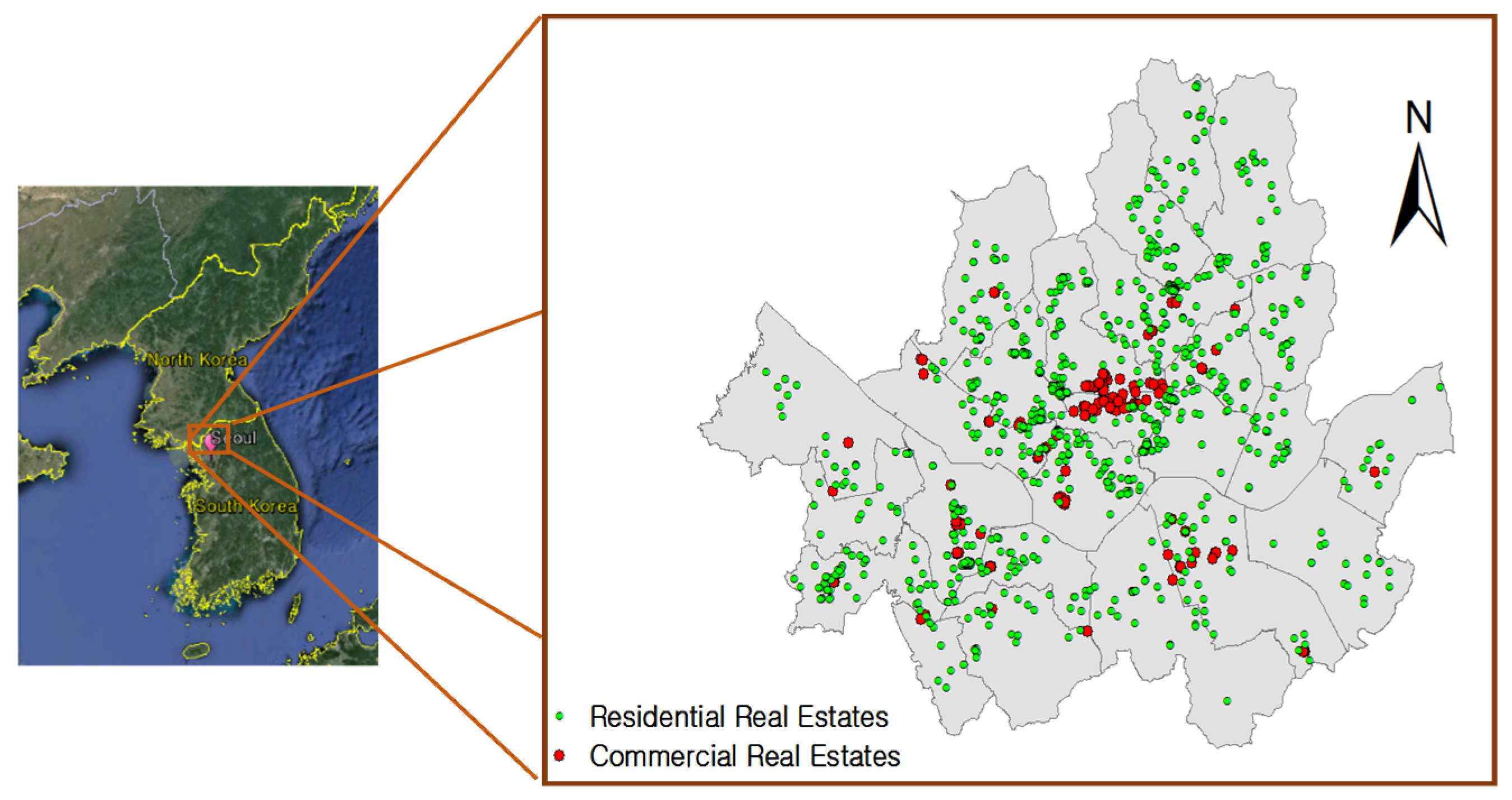

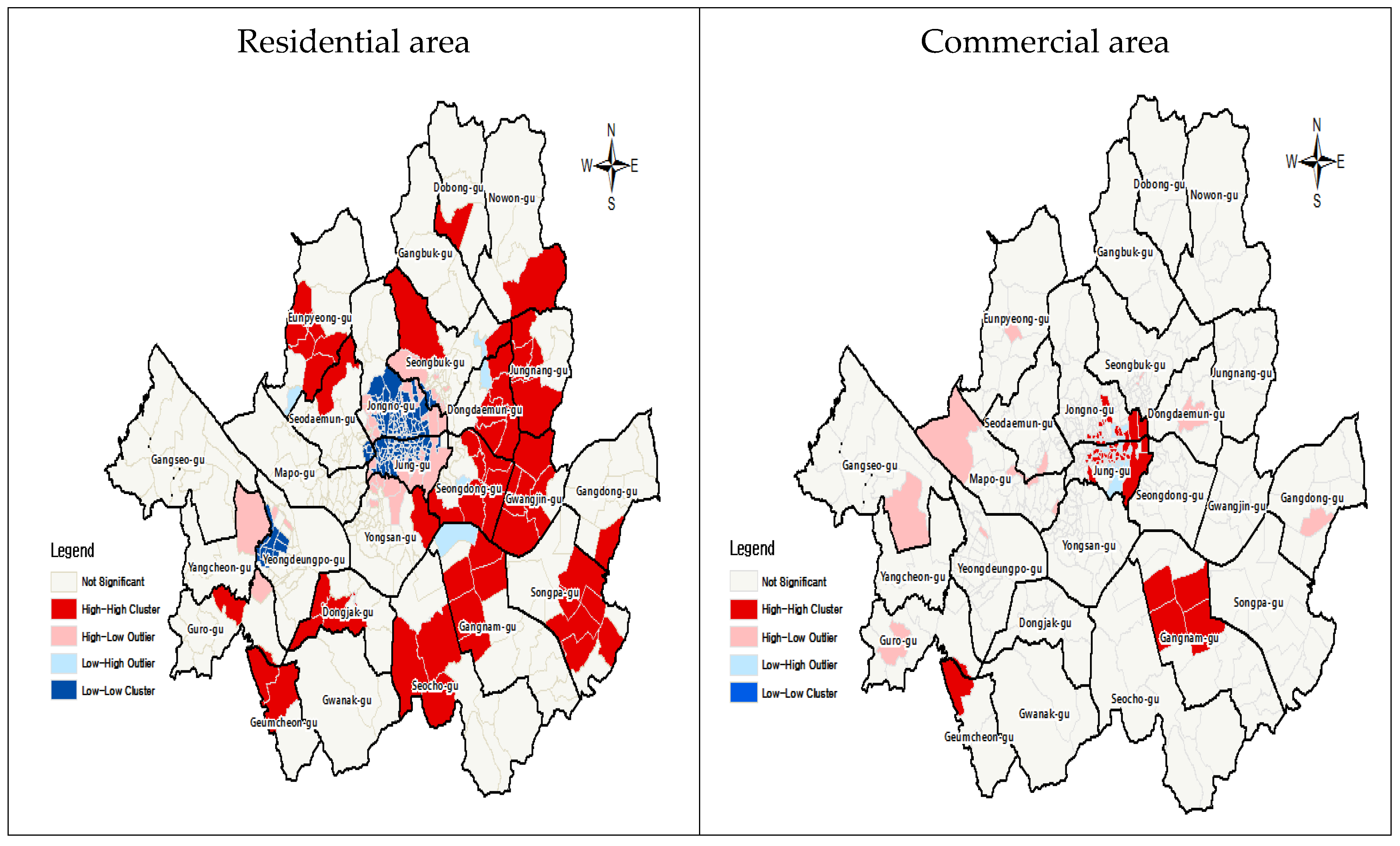
| Classification | Total Number of Parcel | Residential Area | Commercial Area | Industrial Area | Green Zone | Green Belt Area |
|---|---|---|---|---|---|---|
| Number of Parcel (%) | 937,355 (100.00%) | 796,281 (84.95%) | 62,733 (6.69%) | 25,808 (2.75%) | 18,938 (2.02%) | 33,595 (3.58%) |
| Classification | Residential | Commercial | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Sd | Min | Max | Median | Mean | Sd | Min | Max | Median | ||
| Real transaction price | 4.1 | 2.1 | 0.1 | 10.3 | 3.7 | 13.3 | 7.7 | 1.8 | 35.3 | 12.0 | |
| Land use | Residential | 3.5 | 1.7 | 0.3 | 10.0 | 3.2 | 5.8 | 2.5 | 2.1 | 10.8 | 5.5 |
| commercial | 6.3 | 2.0 | 0.1 | 10.3 | 6.4 | 14.4 | 7.8 | 1.8 | 35.3 | 14.6 | |
| residential and commercial | 5.3 | 2.1 | 1.1 | 10.1 | 5.0 | 11.0 | 5.3 | 4.9 | 21.9 | 8.5 | |
| Industrial | 3.4 | 1.3 | 1.0 | 5.4 | 3.2 | - | - | - | - | - | |
| Farmland | 1.1 | 0.8 | 0.3 | 2.2 | 0.5 | - | - | - | - | - | |
| Designated use district | not designated | 4.0 | 2.0 | 0.1 | 10.1 | 3.5 | 11.3 | 6.4 | 1.8 | 35.3 | 9.1 |
| Designated | 4.5 | 2.3 | 0.3 | 10.3 | 4.2 | 15.9 | 8.5 | 2.1 | 35.0 | 15.0 | |
| Altitude | Lowland | 3.6 | - | 3.6 | 3.6 | 3.6 | - | - | - | - | - |
| Flatland | 4.3 | 2.2 | 0.1 | 10.3 | 3.9 | 13.4 | 7.7 | 1.8 | 35.3 | 12.2 | |
| mild slope | 4.0 | 1.9 | 0.5 | 9.1 | 3.5 | 3.7 | 1.7 | 2.5 | 4.9 | 3.7 | |
| steep slope | 2.2 | 1.1 | 0.3 | 5.1 | 2.1 | - | - | - | - | - | |
| high land | 1.1 | 0.6 | 0.3 | 2.2 | 0.9 | - | - | - | - | - | |
| Land form | square type | 4.1 | 1.6 | 1.3 | 8.7 | 3.9 | 19.1 | 10.9 | 5.6 | 35.0 | 19.0 |
| horizontally rectangle | 4.6 | 2.0 | 0.1 | 10.1 | 4.2 | 13.8 | 7.4 | 1.8 | 31.5 | 12.3 | |
| vertically rectangle | 4.7 | 2.4 | 0.5 | 10.0 | 4.5 | 12.5 | 7.4 | 3.5 | 28.3 | 9.3 | |
| Ladder | 4.1 | 2.1 | 0.3 | 10.3 | 3.6 | 13.8 | 7.9 | 1.9 | 32.9 | 14.0 | |
| Triangle | 3.2 | 2.1 | 0.4 | 8.6 | 2.6 | 14.9 | 3.8 | 8.9 | 20.4 | 15.9 | |
| inverse triangle | 1.1 | - | 1.1 | 1.1 | 1.1 | 5.8 | - | 5.8 | 5.8 | 5.8 | |
| un-formed | 3.7 | 1.9 | 0.3 | 10.0 | 3.4 | 10.6 | 7.2 | 1.9 | 35.3 | 7.6 | |
| bag-typed | 3.5 | 1.5 | 0.6 | 8.2 | 3.4 | 8.2 | 8.9 | 2.1 | 18.4 | 4.0 | |
| Contact with road | More than 25 m wide road | 4.7 | 2.0 | 1.0 | 10.0 | 4.2 | 11.9 | 6.5 | 4.0 | 28.3 | 9.2 |
| More than 25 m wide road (corner lot) | 5.0 | 1.8 | 1.1 | 10.3 | 4.6 | 15.6 | 7.9 | 6.8 | 35.0 | 16.2 | |
| 12–25 m wide road | 4.8 | 1.6 | 2.5 | 8.3 | 4.3 | 13.6 | 10.7 | 7.5 | 34.7 | 8.6 | |
| 12–25 m wide road (corner lot) | 5.8 | 1.9 | 1.9 | 9.2 | 5.5 | 19.1 | 9.1 | 5.7 | 32.9 | 19.7 | |
| 12–25 m wide road (corner lot) | 5.7 | 2.1 | 1.8 | 10.0 | 5.1 | 16.4 | 7.6 | 6.5 | 30.7 | 16.8 | |
| 8–12 m wide road | 4.6 | 2.3 | 0.6 | 10.1 | 4.1 | 14.1 | 5.3 | 1.9 | 21.3 | 15.2 | |
| 8–12 m wide road (corner lot) | 4.4 | 2.3 | 0.1 | 9.2 | 3.8 | 12.2 | 8.2 | 6.6 | 31.5 | 8.7 | |
| Less than 8 m wide road | 3.6 | 1.8 | 0.3 | 10.0 | 3.2 | 12.1 | 7.2 | 2.1 | 35.3 | 9.9 | |
| Less than 8 m wide road (corner lot) | 4.2 | 2.1 | 0.5 | 9.8 | 3.7 | 10.1 | 3.3 | 5.8 | 16.8 | 9.5 | |
| Less than 8 m wide road (vehicle inaccessible) | 3.4 | 1.7 | 0.4 | 8.7 | 3.0 | 11.4 | 7.5 | 1.8 | 29.3 | 9.1 | |
| Less than 8 m wide road (vehicle inaccessible & corner lot) | 4.0 | 2.2 | 1.0 | 8.2 | 4.0 | 4.0 | 1.6 | 2.5 | 5.6 | 3.7 | |
| Landlocked lot | 2.0 | 1.3 | 0.3 | 5.8 | 1.8 | 21.4 | 8.6 | 11.6 | 32.9 | 17.7 | |
| Distance from railroad | related area | 2.8 | - | 2.8 | 2.8 | 2.8 | 5.7 | 5.7 | 5.7 | 5.7 | |
| within 50 m | 4.6 | 1.8 | 1.9 | 9.0 | 4.2 | 7.1 | 1.5 | 4.0 | 9.8 | 7.1 | |
| within 100 m | 4.7 | 2.1 | 0.9 | 10.0 | 4.6 | 9.6 | 1.3 | 8.5 | 11.0 | 9.3 | |
| within 500 m | 3.8 | 1.9 | 0.5 | 10.0 | 3.3 | 11.5 | 6.2 | 4.4 | 25.0 | 9.5 | |
| farther than 500 m | 4.2 | 2.1 | 0.1 | 10.3 | 3.9 | 14.5 | 8.1 | 1.8 | 35.3 | 14.8 | |
| Distance from waste treatment facilities | within 50 m | 4.1 | 0.1 | 4.0 | 4.3 | 4.0 | - | - | - | - | - |
| within 100 m | 5.4 | - | 5.4 | 5.4 | 5.4 | - | - | - | - | - | |
| within 500 m | 3.2 | 1.6 | 0.5 | 5.2 | 3.4 | - | - | - | - | - | |
| within 1 km | 2.9 | 1.2 | 0.7 | 4.1 | 3.4 | 7.6 | 2.8 | 5.8 | 10.8 | 6.2 | |
| farther than 1 km | 4.1 | 2.1 | 0.1 | 10.3 | 3.7 | 13.6 | 7.8 | 1.8 | 35.3 | 12.5 | |
| Big projects | not designated | 3.9 | 2.1 | 0.1 | 10.1 | 3.6 | 12.2 | 7.3 | 1.9 | 35.0 | 9.6 |
| designated | 4.4 | 2.0 | 0.3 | 10.3 | 4.0 | 14.9 | 8.0 | 1.8 | 35.3 | 15.3 | |
| Classification | DF | Value | Prob | |
|---|---|---|---|---|
| Breusch-Pagan | Residential | 64 | 124.891 | 0.0000 |
| Commercial | 28 | 72.0873 | 0.0000 | |
| Jarque-Bera | Residential | 2 | 68.5969 | 0.0000 |
| Commercial | 2 | 34.2445 | 0.0000 | |
| Classification | OLS (Semi-log) | Spatial Lag Model (SLM) | Spatial Error Model (SEM) | |
|---|---|---|---|---|
| Coefficient | Coefficient | Coefficient | ||
| CONSTANT | 14.83472 | 14.82524 | 14.85509 | |
| Land use | residential@ | |||
| commercial | 0.5469259 *** | 0.5416114 *** | 0.5093336 *** | |
| residential and commercial | 0.3771436 *** | 0.3748667 *** | 0.3227859 *** | |
| industrial | 0.1832284 | 0.1722477 | 0.03741222 | |
| farmland | −1.196621 *** | −1.20475 *** | −1.214586 *** | |
| Designated use district | not designated@ | |||
| designated | −0.0120364 | −0.01184117 | −0.01881827 | |
| Altitude | lowland | 0.2841206 | 0.2896764 | 0.258335 |
| flatland@ | ||||
| mild slope | 0.04743765 | 0.0447668 | 0.04567435 | |
| steep slope | −0.3338102 *** | −0.3374818 *** | −0.3875679 *** | |
| high land | −1.044598 *** | −1.043713 *** | −0.986019 *** | |
| Land form | Square type | 0.1110292 * | 0.1145919 * | 0.1094205 * |
| horizontally rectangle | 0.06804747 | 0.06577143 | 0.07135691 | |
| vertically rectangle | 0.07785566 * | 0.07764363 * | 0.09032908 ** | |
| ladder@ | ||||
| triangle | −0.2830486 *** | −0.2826095 *** | −0.2563851 *** | |
| inverse triangle | −0.8766148 * | −0.8711198 * | −0.9126258 ** | |
| un-formed | −0.07472117 * | −0.07319313 * | −0.06475986 * | |
| bag-typed | 0.08350172 | 0.08218725 | 0.03499114 | |
| Contact with road | More than 25 m wide road | 0.1753543 ** | 0.173421 ** | 0.1407968 |
| More than 25 m wide road (corner lot) | 0.2648574 *** | 0.2695362 *** | 0.2834018 *** | |
| More than 25 m wide road (corner lot) | 0.04102786 | 0.0453212 | 0.08430525 | |
| 12~25 m wide road | 0.2121089 *** | 0.2099386 *** | 0.1959752 *** | |
| 12~25 m wide road (corner lot) | 0.2035506 *** | 0.2020034 *** | 0.2030704 *** | |
| 8~12 m wide road | 0.1143958 * | 0.1180087 * | 0.1441317 ** | |
| 8~12 m wide road (corner lot) | −0.05901025 | −0.05664801 | −0.05843944 | |
| Less than 8 m wide road@ | ||||
| Less than 8 m wide road (corner lot) | 0.07113948 | 0.07390742 | 0.04711873 | |
| Less than 8 m wide road (vehicle inaccessible) | −0.02160676 | −0.01787072 | −0.00940768 | |
| Less than 8 m wide road (vehicle inaccessible & corner lot) | 0.04261649 | 0.04581873 | 0.09876319 | |
| Landlocked lot | −0.2218566 ** | −0.2260322 ** | −0.1948716 * | |
| Distance from railroad | related area | −0.3568872 | −0.3745543 | −0.2599451 |
| within 50 m | 0.1215657 | 0.1115059 | 0.05919571 | |
| within 100 m | 0.2486583 *** | 0.2464752 *** | 0.1716129 ** | |
| within 500 m | −0.04780102 | −0.04754497 | −0.04435743 | |
| farther than 500 m@ | ||||
| Distance from waste treatment facilities | within 50 m | −0.06168175 | −0.07671985 | −0.05218356 |
| within 100 m | 0.03166474 | 0.04685257 | 0.05161758 | |
| within 500 m | −0.1276944 | −0.1279039 | −0.07557862 | |
| within 1 km | −0.3795877 *** | −0.3707301 ** | −0.3885153 *** | |
| farther than 1 km@ | ||||
| Big projects | not designated@ | |||
| designated | 0.19963 *** | 0.19671 *** | 0.16678 *** | |
| Model Summary | ρ | 0.00214987 | ||
| λ | 0.45051 | |||
| R2 | 0.37974 | 0.38037 | 0.49083 | |
| F | 19.60830 | |||
| log likelihood | −790.14000 | −789.53400 | −712.32676 | |
| AIC | 1654.28000 | 1655.07000 | 1498.65000 | |
| SC | 1842.30000 | 1848.17000 | 1686.68000 | |
| Classification | OLS (Semi-log) | Spatial Lag Model (SLM) | Spatial Error Model (SEM) | |
|---|---|---|---|---|
| Coefficient | Coefficient | Coefficient | ||
| CONSTANT | 16.26555 | 16.19756 | 16.10117 | |
| Land use | residential | −0.56734 *** | −0.56362 *** | −0.34863 ** |
| commercial@ | ||||
| residential and commercial | −0.20084 | −0.19289 | −0.16179 | |
| Designated use district | not designated@ | |||
| designated | 0.18447 | 0.196912 * | 0.071741 | |
| Altitude | flatland@ | |||
| mild slope | −0.43857 | −0.39566 | −0.45656 | |
| Land form | square type | 0.433742 ** | 0.462156 ** | 0.40724 *** |
| horizontally rectangle | 0.050793 | 0.049254 | 0.115032 | |
| vertically rectangle | −0.10283 | −0.07975 | 0.013715 | |
| ladder@ | ||||
| triangle | 0.140089 | 0.141495 | 0.137457 | |
| inverse triangle | −0.54266 | −0.50821 | −0.44029 | |
| un-formed | −0.17522 | −0.16085 | −0.02921 | |
| bag-typed | −0.40088 | −0.36687 | −0.52933* | |
| Contact with road | More than 25 m wide road | −0.12782 | −0.13167 | 0.091888 |
| More than 25 m wide road (corner lot) | 0.035283 | 0.069685 | 0.266705 | |
| More than 25 m wide road (corner lot) | −0.2753 | −0.25662 | 0.127429 | |
| 12~25 m wide road | 0.161914 | 0.157438 | 0.377807 * | |
| 12~25 m wide road (corner lot) | 0.176606 | 0.17941 | 0.518848 *** | |
| 8~12 m wide road | −0.12536 | −0.12843 | −0.02952 | |
| 8~12 m wide road (corner lot) | −0.04683 | −0.0401 | 0.201648 | |
| Less than 8 m wide road@ | ||||
| Less than 8 m wide road (corner lot) | −0.13176 | −0.08926 | −0.07459 | |
| Less than 8 m wide road (vehicle inaccessible) | −0.12973 | −0.11657 | 0.005967 | |
| Less than 8 m wide road (vehicle inaccessible & corner lot) | −0.8066 ** | −0.77331 ** | −0.79625 ** | |
| Landlocked lot | 0.402993 * | 0.42369 * | 0.489134 ** | |
| Distance from railroad | related area | −0.54084 | −0.57193 | −0.72667 |
| within 50 m | −0.25601 | −0.27963 | −0.20975 | |
| within 100 m | −0.27167 | −0.2132 | −0.41978 | |
| within 500 m | −0.0019 | 0.025664 | −0.16044 | |
| farther than 500 m@ | ||||
| Distance from waste treatment facilities | within 1 km | −0.43448 | −0.43116 | −0.16796 |
| farther than 1 km@ | ||||
| Big projects | not designated@ | |||
| designated | 0.08727 | 0.09995 | 0.12187 | |
| Model Summary | ρ | 0.00526 | ||
| λ | 0.58232 | |||
| R2 | 0.34169 | 0.34489 | 0.55069 | |
| F | 2.89183 | |||
| log likelihood | −141.34500 | −140.89500 | −117.77049 | |
| AIC | 340.69100 | 341.79100 | 293.54100 | |
| SC | 434.08100 | 438.40200 | 386.93100 | |
| Division | Formula | Interpretation | ||
|---|---|---|---|---|
| Verification of horizontal equity | COD | Independent house and apartment house | 5.0–15.0 (5.0–20.0 only in case of many new house and residential area of same quality) | |
| Other real estate for resident | 5.0–20.0 | |||
| Real estate for commercial use | 5.0–20.0 (but 5.0–15.0 only for areas of big cities) | |||
| Vacant land | 5.0–20.0 | |||
| Other real estate | Different depending on local condition | |||
| COV | Assessing the better the lower the value | |||
| Verification of vertical PRD | PRD | arithmetic mean of actualization ratio of taxation weighted mean of actualization ratio of taxation | Formation of regressive inequity | Prd > 1.03 |
| Formation of progressive inequity | PRD < 0.98 | |||
| Division | OLS | SLM | SEM | |||
|---|---|---|---|---|---|---|
| COD | COV | COD | COV | COD | COV | |
| residential area | 19.1762 | 35.02 | 19.68803 | 35.11 | 18.96052 | 32.65 |
| commercial area | 15.0438 | 35.12 | 15.66974 | 35.44 | 14.8889 | 33.00 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, B.; Kim, T. A Study on Estimation of Land Value Using Spatial Statistics: Focusing on Real Transaction Land Prices in Korea. Sustainability 2016, 8, 203. https://doi.org/10.3390/su8030203
Kim B, Kim T. A Study on Estimation of Land Value Using Spatial Statistics: Focusing on Real Transaction Land Prices in Korea. Sustainability. 2016; 8(3):203. https://doi.org/10.3390/su8030203
Chicago/Turabian StyleKim, Bongjoon, and Taeyoung Kim. 2016. "A Study on Estimation of Land Value Using Spatial Statistics: Focusing on Real Transaction Land Prices in Korea" Sustainability 8, no. 3: 203. https://doi.org/10.3390/su8030203
APA StyleKim, B., & Kim, T. (2016). A Study on Estimation of Land Value Using Spatial Statistics: Focusing on Real Transaction Land Prices in Korea. Sustainability, 8(3), 203. https://doi.org/10.3390/su8030203





