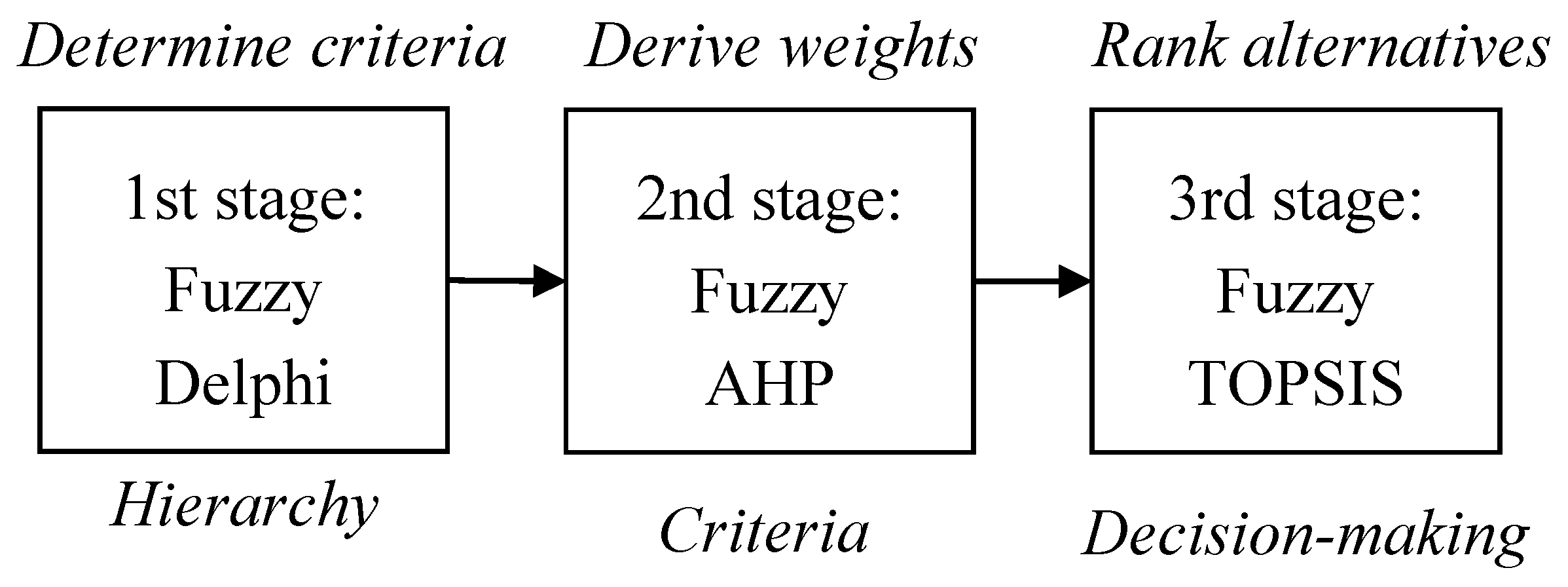
Compared to traditional binary sets, fuzzy logic variables may have a membership value that ranges in degree between 0 and 1 [
15]. Thus, fuzzy logic offers a more realistic mode for human reasoning than the traditional two-valued logic. In view of the applicability of fuzzy prioritized operators [
16,
17], this study integrated the fuzzy set theory with three MCDM methods to establish a three-stage technology selection process. This section, therefore, presents the three fuzzy MCDM methods (fuzzy Delphi, fuzzy AHP, and fuzzy TOPSIS) to be applied later to the empirical example.
3.1. Fuzzy Delphi Method
Noorderhaven [
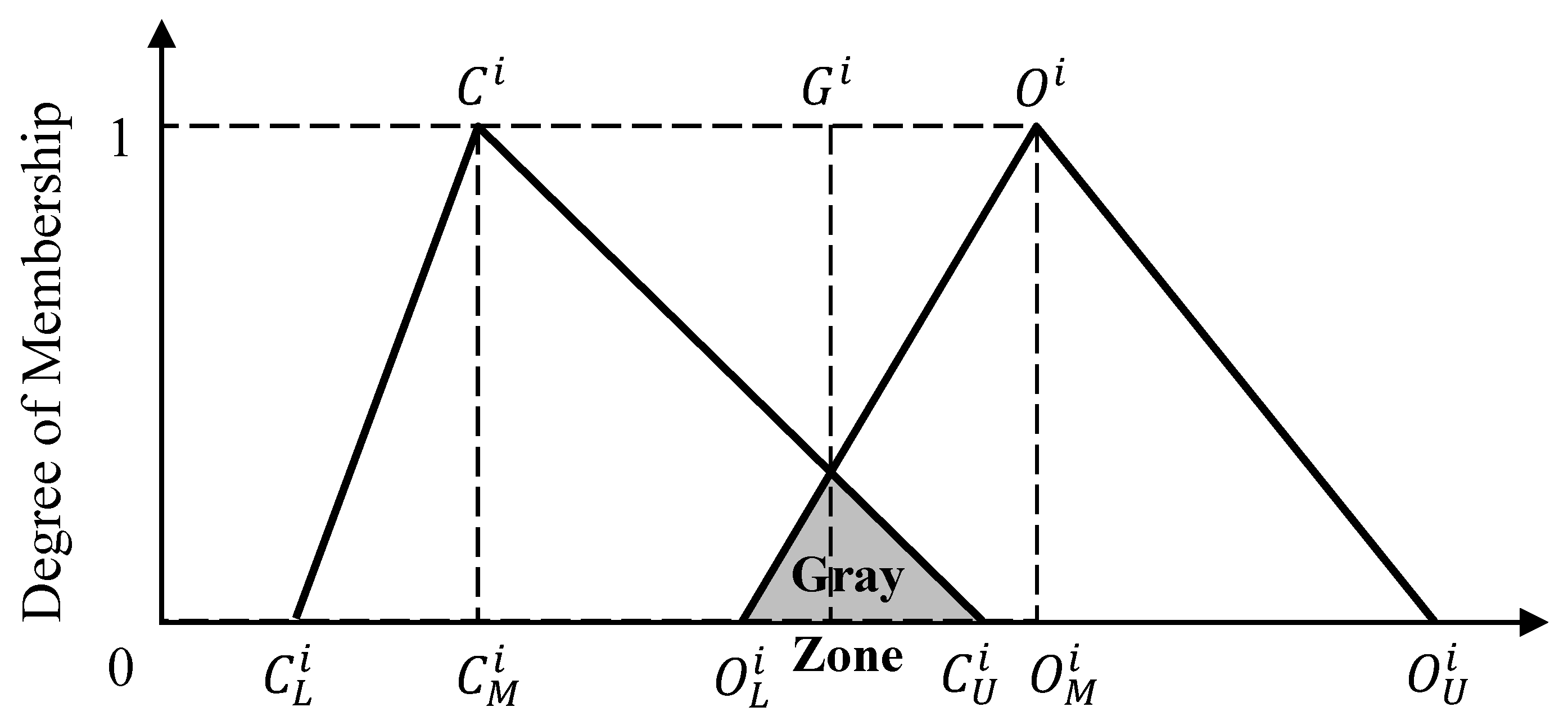
18] indicated that applying the fuzzy Delphi method to a group decision can solve the fuzziness of the common understanding of expert opinions. This study applied the double triangular membership function to solve the group decision, as shown in
Figure 2, since it could well testify whether the experts’ judgments would reach unanimity by using a gray zone test through the overlapping situation of two triangular fuzzy numbers [
19]. One of the two triangular fuzzy numbers, denoted as
, represents all of the experts’ most optimistic cognitions for each criterion; the other triangular fuzzy number, denoted as
, signifies all of the experts’ most conservative cognitions for each criterion. A gray zone test may reveal three situational types:
- (1)
No overlap exists between the two triangular fuzzy numbers (). The arithmetic mean is acquired through the geometric mean and .
- (2)
If , the values of and are first acquired. If the crosspoint of the two triangular fuzzy numbers is equal to the value of the experts’ consensus in the gray zone , the level of membership in the gray zone is , where .
- (3)
If and , the value of the experts’ consensus cannot be converged, and the tests should be refined again, with the reference value attached.
Figure 2.
Double triangular fuzzy numbers.
Figure 2.
Double triangular fuzzy numbers.
Finally, the important criteria can be selected if the consensus values are greater than a given threshold value and, hence, can be used for building a structural hierarchy.
3.2. Fuzzy AHP
The AHP is one of the MCDM methods based on an additive weighting process, in which the multi-attribute weight measurements are calculated through pairwise comparisons of the relative importance of every pair of criteria [
20]. However, the fuzzy AHP can reflect the human thinking style by converting experts’ crisp values to fuzzy numbers in the paired comparison of matrices; thus, it can solve the hierarchical fuzzy problems. The procedures of the fuzzy AHP were described as follows:
- (1)
Establish a hierarchical structure.
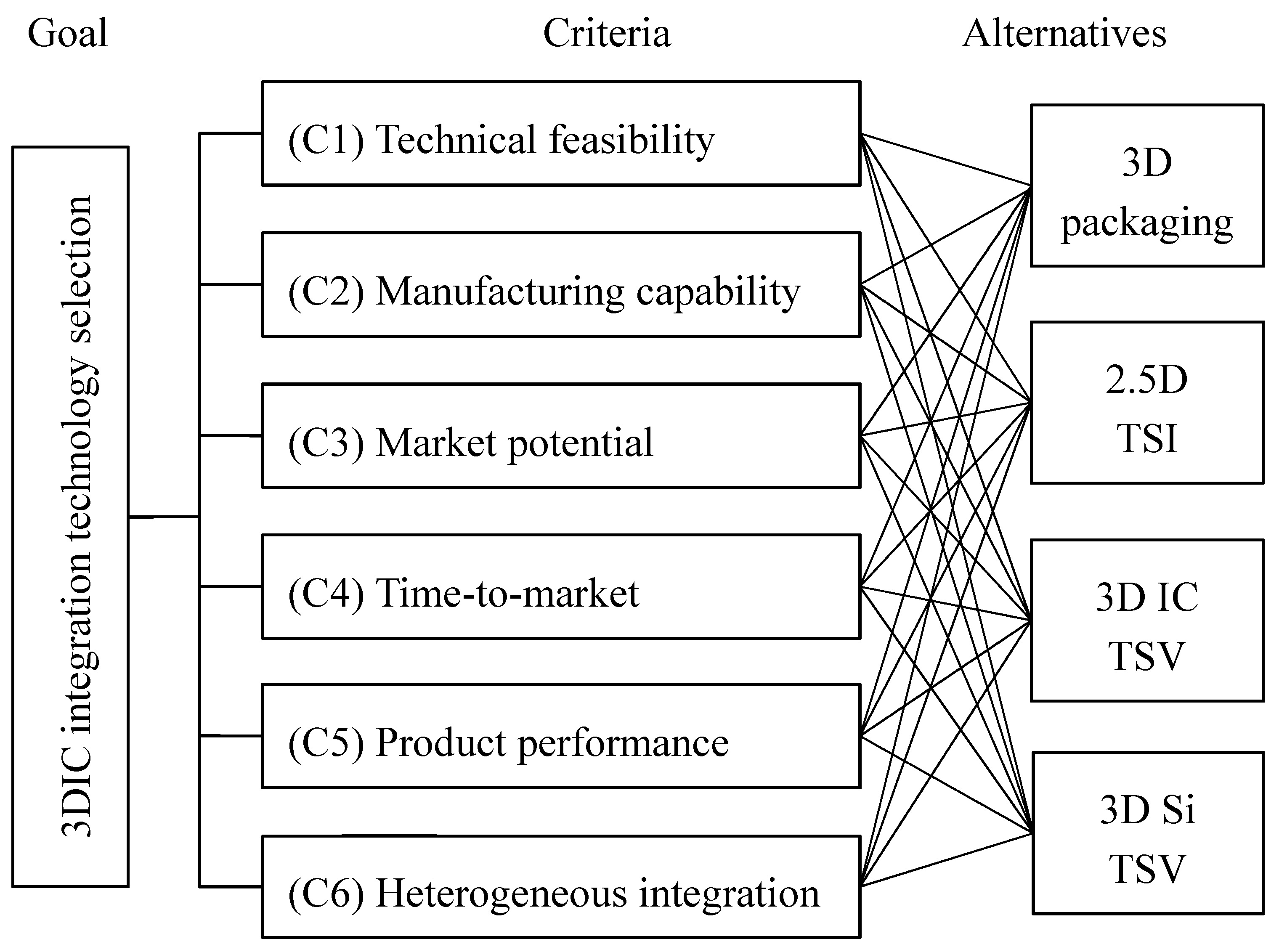
Determine the important criteria screened by fuzzy Delphi investigations to establish the hierarchical structure.
- (2)
Construct fuzzy decision matrices.
Compare the relative importance of the criteria in pairs, and convert crisp values to fuzzy numbers for constructing fuzzy decision matrices based on a defined membership function of linguistic variables.
A fuzzy decision matrix can be defined as:
where
is the fuzzy decision matrix of evaluator
k,
is the fuzzy assessments between criterion
i and criterion
j of evaluator
k, and
n is the number of criteria at the same level:
To verify whether a pairwise comparison matrix is sufficiently consistent, the maximum eigenvalue
can be computed as:
where
A is a pairwise comparison matrix, and
W is a weight matrix.
Saaty [
21] defined a consistency index (
CI) to test the consistency within the pairwise comparison matrices, as well as that of entire hierarchy. The
CI is formulated as follows:
where
is the maximum eigenvalue, and
n is the dimension of the matrix.
The consistency ratio (
CR) is accordingly defined as follows:
where
RI is the random consistency index.
The matrix will be considered consistent if the resulting ratio is less than 0.1. Csutora and Buckley [
22] further demonstrated that if a crisp decision matrix
R was consistent, then the corresponding fuzzy decision matrix
would, accordingly, be consistent.
- (4)
Perform defuzzification.
Adopt the method of converting fuzzy data to crisp scores (CFCS), developed by Opricovic and Tzeng [
23] for performing defuzzification. Let
indicate the fuzzy assessments between criterion
i and criterion
j of evaluator
k. The steps of CFCS method were described as follows:
Step 1. Perform normalization:
where
Step 2. Compute the lower (
ls) and upper (
us) normalized value:
and
Step 3. Compute the total normalized crisp value:
Step 4. Compute the crisp value:
where
are the crisp assessments between criterion
i and criterion
j of evaluator
k.
Step 5. Integrate the crisp values:
where
is the integrated crisp assessment of criterion
i and criterion
j of total
K evaluators.
- (5)
Establish an aggregate crisp decision matrix.
where
is the aggregate crisp decision matrix of k evaluators.
- (6)
Calculate criteria weights.
Obtain eigenvector value
of the aggregate crisp decision matrix
by using a row vector geometric mean technique:
Following the above-mentioned procedures of the fuzzy AHP, the weights of the criteria can be effectively obtained.
3.3. Fuzzy TOPSIS
Hwang and Yoon [
24] first proposed the TOPSIS to solve multiple-attribute decision-making (MADM) problems by using the concept of the optimal compromise solution. The algorithm of TOPSIS considers both the positive ideal solution (PIS) and the negative ideal solution (NIS) to determine the optimal solution to a multiple-objective decision-making (MODM) problem [
25]. The TOPSIS was then extended to the fuzzy environment, namely the fuzzy TOPSIS, to suit the real world. The procedures of the fuzzy TOPSIS were described as follows:
- (1)
Obtain the fuzzy weights of the criteria.
This study employs the fuzzy AHP to obtain the fuzzy preference weights of the criteria.
- (2)
Construct the fuzzy decision matrix and determine the appropriate linguistic variables for the alternatives, with respect to criteria:
where
is the performance rating of alternative
, with respect to criterion
, evaluated by the
kth expert, and
K is the total number of experts.
- (3)
Normalize the fuzzy decision matrix.
The normalized fuzzy decision matrix
can be expressed as:
Then the weighted fuzzy normalized decision matrix
can be expressed as:
- (4)
Determine the fuzzy positive ideal solution (FPIS) and the fuzzy negative ideal solution (FNIS).
The FPIS
(aspiration levels) and FNIS
(worst levels) can be defined as [
26,
27]:
and
- (5)
Calculate the distance of each alternative from the FPIS and the FNIS.
The distances (
and
) of each alternative from
and
can be obtained through the following calculations:
and
- (6)
Obtain the closeness coefficients and improve the gap degrees for achieving the aspiration levels:
where
is defined as the fuzzy satisfaction degree and
is defined as the fuzzy gap degree.
Following the above-mentioned procedures of fuzzy TOPSIS, the alternative 3DIC integration technologies can be effectively prioritized and selected.