1. Introduction
Regional disparity has attracted a considerable amount of attention in China. This country has been struggling to follow a balanced growth path and is still confronted with unprecedented pressures and challenges. There is indeed a vast literature devoted to regional disparity in China, and various contributions have identified the existence of strong geographical patterns in inequality. Among the numerous works on inequality in China, here we recall Kanbur and Zhang [
1]; Knight and Song [
2]; Démurger et al. [
3]; Wei [
4]; Kanbur and Zhang [
5]; Wan and Zhou [
6]; Pedroni and Yao [
7]; Sicular et al. [
8]; Wan et al. [
9]; Wan and Zhang [
10]; Wei et al. [
11]; Hao and Wei [
12]; Li and Wei [
13]; Wei et al. [
14]; Candelaria et al. [
15]; Cheong and Wu [
16]; Cheong and Wu [
17]; Knight [
18].
To estimate very uneven processes of regional development, Quah [
19,
20,
21] develops a new framework of intra-distribution dynamics: the stochastic kernel estimation. The application of this approach has revealed the presence of an empirical regularity in the evolution of most cross-country income distributions over time, which is the emergence of “twin peaks”. This approach has been further developed in the empirical studies. For instance, Cheong and Wu [
22,
23] calculated the net probabilities of moving upwards and downwards in the distribution for different states while they performed traditional Markov transition matrix analyses. The distribution dynamics approach has been gaining popularity in the examination of the transitional dynamics in China. Cheong and Wu [
23] have listed a series of studies employing the distribution dynamics approach in analyzing the convergence and evolution of various economic terms in China. Among these, a certain number of works have come to the conclusion that the distribution dynamics of GDP or income per capita in China presents a bi-modal (or twin-peak) pattern. For instance, Barone et al. [
24], Cheong and Wu [
16,
17,
23], Herrerias and Ordonez [
25], Sakamoto and Fan [
26], Villaverde et al. [
27], Wei and Ye [
28], and Zhou and Zou [
29] provide some evidence of a pattern of growth club convergence. Contrary to these studies, Li [
30] finds little real GDP per capita convergence among the Chinese provinces during the period 1978–1998, a result supported also by Sakamoto and Islam [
31]. The latter studied the period of 1952–2003 and concluded that the possibility of a long-run convergence remains as an open issue.
Some studies also investigate the dynamic distributions of other economic-related items such as productivity (see Zhu et al. [
32], Wang [
33], Herrerías [
34] for instance) and some value-added components. Sakamoto and Fan [
35] investigates the dynamic distribution of four factors, namely, the compensation of employees, operating surplus, depreciation of fixed assets, and net tax on production. In contrast, relatively fewer works have gone “beyond GDP” and focused on other social issues. For instance, Wu et al. [
36] investigated the convergence of carbon dioxide emissions in Chinese cities; Wang and Zhu [
37] examined the city-size distribution by urban or nonagricultural population in each city. This work challenges that distribution dynamics approach can be applied to the more multifaceted concept of development and provides evidence of the existence of a three-peak distribution in the distribution dynamics of regional socioeconomic convergence in China.
Most of the very many works on income distribution focus analysis on the provincial level and have long-term coverage (for instance, consider Barone et al. [
24], Cheong and Wu [
12], Li [
30], Herrerias and Ordonez [
25], Sakamoto and Islam [
31], Villaverde et al. [
27]). Other contributions in the literature focus on lower level administrative units, particularly those located in special zones. Wei and Ye [
11], for instance, use prefectures within the Zhejiang province and find a polarization between the coastal and the interior areas of Zhejiang. Sakamoto and Fan [
26] investigate 75 cities and counties in the Yangtze River Delta and show a bimodal distribution dynamics of per capita income from 1990 to 2005. Zhou and Zou [
29], by focusing on prefectural cities during the period 1995–2004, conclude the existence of twin peaks in the dynamic distribution of urban income. Cheong and Wu [
17,
23].employ county-level data to explore the distributions of income during 1997–2007 and industrial output during 1997–2010, respectively.
One common limitation of these studies is that they mainly rely on GDP or income per capita as the sole indicator to assess economic and social convergence. Given the political importance of a coordinated development strategy proposed by the central government and considering the high levels of regional disparity in China, this scope of the analysis might seem too narrow. It seems instead important to construct and use a multidimensional index that may better inform the choices of Chinese authorities. As a matter of fact, the Chinese policy-makers have recently acknowledged the limitations of using GDP per capita as a single measure to evaluate the performance of local leaders, and they started attaching greater attention to the reduction of inequality, as well as to the promotion of widespread social development and the protection of the environment. In the national conference on organizational work of 2013 in China, President Xi Jinping underlined that “we should no longer evaluate the performance of leaders simply by GDP growth. Instead, we should look at welfare improvement, social development and environmental indicators to evaluate leaders”. Until now, more than 70 Chinese prefectures have abandoned the GDP as the sole indicator to assess the leaders’ performances and local government records. Therefore, developing and investigating new synthetic measures that capture the multifaceted dimensions of socioeconomic development is of utmost importance for both researchers and policy-makers. Studying the distribution dynamics over the recent period may also provide further knowledge of the development process in China.
A vast literature has attempted to measure regional development conditions through composite indexes (Farley and Farmer [
38] list a series of relevant works that use composite index;
Appendix A also gives a brief illustration of several indexes). One of the most popular indexes is the
Human Development Index (HDI), produced and reported by the United Nations Development Programme (UNDP). Less known but equally interesting are the indexes developed by individual researchers and institutions to map the various dimensions of regional development in, for example, the
Basic Capabilities Index (BCI, previously
Quality of Life Index), the
Capital Access Index (CAI), the
Commitment to Development Index (CDI), the
Country Performance Assessment (CPA), the
Economic Freedom of the Word Index (EFW), the
Education for all Development Index (EDI), and
the Global Competitiveness Index (GCI). Composite indexes of environmental sustainability have been employed increasingly frequently, as is the case for the OECD environmental performance review, the
Environmental Sustainability Index (ESI), and the
Environmental Vulnerability Index (EVI). Environmental sustainability has recently gained importance in China and has been integrated into the
China Urban Sustainability Index (see Xiao et al. [
39] and Li et al. [
40] for instance). Meanwhile, how to guarantee the quality of a composite index has also been well-discussed (see Decancq and Lugo [
41], OECD [
42], Farley and Farmer [
38], for instance). This study aims to produce empirical evidence on the distribution dynamics of regional socioeconomic convergence in China, thereby filling a gap in the literature. This contributes to the literature in several ways. First, it develops a new Composite Index of Regional Development (CIRD), going beyond GDP and involving five different sub-dimensions of the concept of development: macroeconomic conditions, science and innovation, human capital, environmental sustainability, and public facilities. As regional socioeconomic development regards multiple realms, both scholars and policy-makers have shown to be interested in the various aspects of regional inequality in China. Some studies have constructed indexes focusing on economic activities (see Luo [
43]; Curran and Funke [
44]; Liu et al. [
45]; Balcioglu and Vural [
46]; Adams et al. [
47]; Schminke and Van Biesebroe [
48]; Yue et al. [
49]; Fernald et al. [
50] for instance). The concerns about sustainable development have led to a series of studies employing multidimensional indexes. Some studies link economic development to indicators of technology and innovation (see Chen et al. [
51]; Fleisher et al. [
52]; Dan [
53]; Wright [
54] for instance) as well as social development (see Démurger et al. [
3]; Basu [
55]; Li et al. [
56]; Lin [
57]; Zimmer et al. [
58]; Fan et al [
59]; Yang et al. [
60] for instance), while some others have focused on environment and resources (see Xiao et al. [
39]; Wang [
37]; Bouton et al. [
61]; Li et al. [
40]; Yang et al. [
62]; Zhang et al. [
63] for instance). Despite the increasing number of academic studies on synthetic indexes, little research has been done to create a multidimensional index covering all the various aspects of socioeconomic development. Building up such an index for China is a complicated undertaking due to the scarce availability of data and various technical aspects. This work tackles such problems and constructs the CIRD. The development of the CIRD at a relatively highly disaggregated geographical level and its calculation over a considerable time span (i.e., 1998–2010) are among the major contributions of this study to the literature on regional inequality in China.
Second, this work is the first to adopt a composite index of socioeconomic development to evaluate its dynamic distribution across 30 (of 31) regions over time, in an attempt to overcome the limitations of using a single measure of economic activity (either GDP or income per capita) as done in previous studies. This work applies the Quah [
19,
20,
21,
64,
65] method to the CIRD index and to some of its sub-pillar indexes: this allows for the observation of the dynamics of the multidimensional process of development across the Chinese regions over the interval 1998–2010, a period embracing three “Five-Year Plans”. This approach also allows for a more comprehensive understanding of the diversified regional development levels and of the evolution of regional disparities in China over time. Although this approach cannot capture all the very many socioeconomic dimensions of development, it represents a step forward, whose amelioration may produce progress in the understanding of this important aspect.
The rest of the paper is as follows:
Section 2 presents the methodology following Quah’s stochastic kernel estimation in this study;
Section 3 introduces the multidimensional index (CIRD);
Section 4 is dedicated to estimate the regional disparity and dynamics of distribution according to the CIRD in China;
Section 5 draws closing remarks.
2. Methodology: Stochastic Kernel Estimation
Following Quah [
19,
20,
21,
64,
65], this study adopts the approach of distribution dynamics to model the transitional dynamics of regional socioeconomic development in China. The cores of this approach are stochastic kernel estimation and the Markov transition matrix. Based on the Markov Chain theory, this allows for the formation of convergence clubs, polarization or persistence inequality, as well as other patterns. The stochastic kernel estimation can circumvent the “arbitrary” selection of boundary values in the demarcation required by the traditional Markov transition matrix method (see Cheong and Wu [
16] for detailed technical derivation of the traditional Markov transition matrix). Hence, it is regarded as an expansion of the Markov transition matrix method with a constant infinity of states (Cheong and Wu [
23]). As this non-parametric approach requires a panel data over several years, a large panel dataset is built up involving 30 Chinese provinces and municipalities from 1998 to 2010 (Tibet is excluded because of missing data—it is removed in two sub-pillars (SII and ESI), and thus also in the CIRD).
To explore the intra-distribution mobility within Quah’s framework of distribution dynamics, it is assumed that the distribution of the CIRD scores (denoted with
) at time
(e.g., 1998 or another year) can be described by the density function
. Given that the distribution evolution is time stationary and first-order Markov, the distribution at time
(for
) depends only on the distribution at time
but not on the distribution prior to
. Let
denote the
-period-ahead distribution density function of CIRD conditional on
. Then, the relationship between the two distributions at time
to
can be expressed as
where
is the transition probability kernel, indicating the probability that one region shifts to a certain state of the CIRD at time
to another state at time
. If
is the total number of states, then
can be viewed as a
transition probability matrix, with its (
i,
j)th element symbolized by
. To examine the transition probability of one region shifting from state
to state
,
can be calculated as follows:
where
is the value of the kernel estimator with the transitions from state
to state
.
If we extend the analysis to the continuous distribution dynamics in the long run, it is required to introduce the ergodic distribution. The ergodic density shows a long-term equilibrium emerges when
approaches infinity. The law of motion for such a process can be shown as
where
is the ergodic density function. The stochastic kernel
is multiplied
times by itself until the density has converged (in the higher-order Markov with a higher dimensional state space, which is computationally much more difficult to handle,
can indicate the probability that one region shifts to a certain state of the CIRD given that it is in a certain state at the starting year.). Here it can be used to connect any two different distributions. The technical derivation above is abridged for the sake of brevity, and more detailed elaborations can be found in Quah [
20,
21], Johnson [
66], and Juessen [
67]. Since this analysis aims to explore the distribution dynamics across Chinese provinces, the ergodic distribution is based on the administrative units on the provincial level.
To better illustrate the transitional dynamics of regional socioeconomic development in China, this study presents the estimation results based on the stochastic kernel density and discrete transition probability matrix approach. The discrete transition probability matrix approach was pioneered by Quah [
64], which roughly divided the observations equally into five groups between the grid cells, corresponding to approximately one quintile in the distribution of income per capita. One major issue in the discrete transition probability matrix approach is the selection of the boundary values to demarcate the states. As suggested by Cheong and Wu [
16], when the sample size is small, the grid values can be set by uniform proportion to keep an equal proportion in each state at the initial time, hence to guarantee the sufficiency of transition episodes for the analysis. This demarcation method is applied in this study considering that only 30 provinces are observed. The stochastic kernel estimation can be presented by the contour plot and the three-dimensional plot. It is helpful to briefly illustrate how to interpret the plots derived by applying this approach. When the distribution tends to move over time towards one point mass, this can be considered a sign of convergence. On the contrary, a process of polarization or stratification is associated with a tendency of distribution in a pattern of bimodality or multimodality.
This approach identifies the distribution dynamics by applying the main concepts of the stochastic kernel. To operationalize these concepts, the kernel density estimation is a key step. The estimator
calculating the percentage of regions close to the point
can be defined as [
68]:
where
is the bandwidth to measure the smoothness of the distribution curve at a given moment in time;
is one random point to gauge the density distribution by its distance to
x;
is the kernel function with symmetry as
. The joint natural kernel estimator of
can be demonstrated as follows:
where
and
are the relative CIRD levels at time
t and
t + s. The kernel density estimation is significantly determined by the appropriate selections of the kernel function and the bandwidth. There are several kernel functions one can employ: Biweight, Cosine, Epanechnikov (alternative: Epan2), Gaussian, Parzen, Rectangular, and Triangular. The Epanechnikov function is the default function with high efficiency in minimizing the mean integrated squared error. Considering this study covers just 30 geographical units, the choice falls on the alternative Epan2 function, which can be expressed as follows (see Hardle [
69] and Cameron and Trivedi [
70] for instance):
The bandwidth
, as another key factor to drive the number of values that are included in the density estimation at every single point, can be determined as:
where
is the CIRD values to estimate the kernel, and
is the number of regions, which is 30 in this study.
3. The Construction of the CIRD
This work embraces the Principal Component Analysis (PCA) approach to develop an innovative composite index able to capture a comprehensive measure of regional development in China. The CIRD index, to the best of our knowledge, qualifies as the first composite index able to capture five main dimensions of the regional socioeconomic development in China. It is worth noticing that, given the existing problems in matching Chinese datasets, the construction of such large a dataset at the provincial level represents in itself a contribution to the literature on Chinese regional development.
3.1. The Principal Component Analysis
The aggregation of various indicators covering diverse socioeconomic realms into a single index has been identified as a very promising solution. Parametric approaches to aggregate the indicator have been widely accepted as the most suitable ways to define the weights for the indicators entering a composite index. One of the most common methodologies is the
Principal Component Analysis (PCA). It is a data reduction method introduced by Hotelling [
71] that allows us to identify a few unobservable factors that account for most of the variability in an underlying large set of indicators. This method is frequently applied to integrate different indicators, or sub-indexes, since it permits a relatively easier selection of the sub-set of the components of interest [
72] and serves a simpler application without assumptions attached to the original data [
73]. The list of contributions using PCA to aggregate a composite index or to create a multidimensional measure would be extremely long. Dreher [
74] and Heshmati [
75], for example, apply PCA to estimate the weights of sub-indexes of a composite globalization index. Chen and Woo [
73] use PCA to obtain a composite index of economic integration in the Asia-Pacific region.
The premise to run a PCA is to use the original variables that are highly correlated, and to identify a reduced number of uncorrelated linear combinations from these variables. It also requires the normalization of the data in terms of mean and standard deviation, the formula is:
where
represents the values of
observations (regions) for each indicator (see Shlens [
76] and Smith [
77]). As is suggested by Decancq and Lugo [
41] and Chen and Woo [
73], the single indicators
also need to be standardized from the raw data to avoid heterogeneous measurement scales before aggregation. The goal of the PCA method is to find those
principal components (PC) that describe most of the variability in the data. Each PC can be seen as a linear combination of all the included indicators. All these PCs are orthogonal to each other. The first PC contains the most information of the original indicators as it accounts for the highest value of the total variation, the second PC explains the second largest variation, and so on. The loadings in a PC are the weights of the corresponding indicators in the dimension represented by that PC.
This study builds a multidimensional dataset
for the 30 observations (regions) in each year, where
represents the multiple dimensions (indicators) to constitute the composite index (CIRD). Then, the principal components can be expressed as
where
represents the
principal components as a series of linear combinations of the indicators
;
is the eigenvector matrix where
represents the
ith eigenvector of the indicator correlation matrix. Suppose that
is the correlation matrix of the
indicator series, and
is the
ith eigenvalue of the correlation matrix (this denotes the variance of the
ith
principal component. The eigenvalue corresponding to a component represents the share of variance it explains; the sum of eigenvalues equals the original number of variables; therefore, a lower level of eigenvalues explains less than the standardized variance, which should be equal to 1). Given the concepts of eigenvalue and eigenvector, they should satisfy
where
is the
identity matrix. To keep the variances of PC to be determined by the different weight of the original variables, the coefficient sizes across components must be constrained with the following equation:
The subsequent step of the analysis consists in the aggregation of the
principal components by attaching given weights to each component. Assigning appropriate weights concerns very important issues such as whether the index would be misrepresented or overstated, or, further up, whether the result would mislead policy and practice. Decancq and Lugo [
41] proposed three schemes to determine the weights. In this study, a parametric method with assigned weights is adopted to determine the individual contributions to the CIRD. These weights are calculated according to the following equation:
In order to overcome the bias weights that might be caused by the highly-correlated indicators [
78], this study uses a two-stage PCA recommended by Chen and Woo [
73]. Considering the property of the data and index, this study makes some adjustments in running the two-stage PCA. Instead of “grouping the highly inter-correlated indicators together and construct a composite sub-index first”, it runs the first-stage PCA for the five sub-indexes since the indicators for the sub-indexes are not very highly-correlated. First, the PCA is run for the 25 indicators in every year of the sample and plural
principal component(s) are obtained (there are 6 PCs in the years of 1998, 2006, 2007, 2009, and 2010, respectively, and 5 PCs in the years of 1999–2005 and 2008, respectively). The weight assigned to each indicator should be its loading in each of the selected PCs weighted by the relative significance of that component, accounting for the total variation of the original data. In the second stage, the PCA is run again with these plural
principal component(s) in every year (to better understand the logic in this stage, we can view the PCs here as new single “indicators”). Using the weights calculated with Equation (12), the final composite index (CIRD) is constructed as follows:
where
denotes the
jth column of the indicator matrix in the index. This two-stage PCA is also applied in each of the five sub-dimensional indexes to calculate the sub-index scores. Following the Kaiser rule, this study always selects the PCs with eigenvalues higher than 1.
3.2. The Composition of the CIRD
The inclusion of variables capturing the various aspects of socioeconomic development is a key contribution of this work. Hence, the selection of appropriate indicators that underpin the aggregate index must reflect a comprehensive understanding of the various issues at stake. Moreover, the selection follows a number of criteria that any composite index should conform to.
The first criterion regards the ability of the index to take a full-size snapshot of the socioeconomic development of the regions; it must cover various aspects of development. The second criterion is that the index must be capable to track down the evolving regional disparity, hence it must be based on the individual indicators that are consistent and comparable both horizontally (among regions) and vertically (across years). A number of other conditions must be equally satisfied: the selection must be underpinned by a solid theoretical framework; the indicators must be available for data reduction and it must be transparent in order to be applied by other studies (see Saisana and Tarantola [
79] and OECD [
42] for instance).
Endowed with a good composite index, one can then determine, for example, what regions are leading and lagging behind in terms of socioeconomic development and what indicators contribute more to determining the level of local development. This makes the index a powerful tool both for comparative purposes and for policy goals.
Taking stock of the authoritative studies about the construction of a composite index (for instance, OECD [
42]; Annoni and Kozovska [
80,
81]; Michalek and Zarnekow [
82]), this study selects a large set of available indicators at the Chinese provincial level over the time period 1998–2010 in an attempt to cover multiple domains of the regional socioeconomic development in China (such as production, investment, trade, employment, human resources, infrastructures, environment protection, science and technology). These indicators, which are described in
Table 1, are grouped into five sub-indexes that represent what can be identified as the main pillars regional development in China: a
Macroeconomic Index (MEI), a
Science and Innovation Index (SII), an
Environmental Sustainability Index (ESI), a
Human Capital Index (HCI) and a
Public Facility Index (PFI). It is worth noticing that, to identify the 25 indicators constituting the CIRD, a larger dataset containing 68 potential indicators has been initially built and analyzed, which cover the majority of the available data to describe socioeconomic development in the sample period. The 25 indicators (5 in each sub pillar) have been subsequently selected after the following three steps: the first step is the collection of all available data related to the pillars; insignificant indicators are then removed according to their poor correlation with the GDP per capita and the growth rate; the five baseline indicators for each pillar are selected on the basis of what variables with the highest significance among the candidate indicators. Meanwhile, this selection uses previous studies that focused on different dimensions of socioeconomic development for reference (such as Mishra [
78]; OECD [
42]; Balcioglu and Vural [
46]; Chen et al. [
51]; Adams et al. [
47]; Annoni and Kozovska [
80,
81]; Dan [
53]; Fleisher et al. [
52]) and considers the feasibility of conducting the following research. Though some imperfections could exist in this CIRD, it is an experiment endeavoring to construct a multidimensional index proxy to reflect the full picture of regional socioeconomic development.
The MEI pillar goes beyond the conventional GDP per capita and it covers: FDI and international trade to benchmark the level of openness, final consumption rate, and labor remuneration to scale the wealth of local inhabitants and market revitalization in different regions. However, the shares of consumption and labor remuneration in GDP have kept shrinking in recent decades and are hence negatively correlated with GDP per capita (reasons such as capital expansion and industry restructure are well discussed for the decreasing tendency, but this is beyond the scope of this study). Special attention must be paid to the change of statistical standards that has caused a sharp decrease of labor remuneration in 2004. The self-employment income has been removed from labor remuneration and reclassified into operating surplus since 2004. This study removes self-employment income from labor remuneration before 2004 to keep the consistency of the indicator, and reverses the two indicators negatively correlated with GDP per capita to obtain a valid PCA result.
The SII pillar employs the following indicators: the share of government expenditure in science and technology to estimate the importance of government investment to science and technology, the labor productivity and income per capita in high-tech enterprises to investigate the vitality of individual enterprises and firms, the R&D expenditure proportion to assess its the sustainability , and the trading value in the science and technology markets to evaluate the activity of the new market in science and technology.
The ESI pillar uses Columbia’s Environmental Sustainability Index, the Environmental Vulnerability Index, and the China Urban Sustainability Index for references and is based on the proportion of industry waste water discharged under the qualified standards to evaluate the capacity of facilities to clean industry waste water, the utilization ratio and output value of industry waste to assess the waste recycling, the discharge of living waste per capita to assess the pollutant from local inhabitants (which has to be reversed to keep a positive relation with GDP growth rate), and the investment in anti-pollution projects in industry firms to estimate how the industry pollution is controlled by their producers.
Stemmed from the well-known HDI, which has three dimensions: longevity (life expectancy), education (knowledge), and resource (standard of living), the HCI employs the proportion of the literate population as an indicator of education and the estimated life expectancy as a proxy of longevity. Since the standard of living is already included in the MEI pillar, the HCI mainly concerns the other two dimensions. The life expectancy is calculated by the national population census reports of 1990, 2000, and 2010. The additional indicators replenish this dimension with the employee ratio between the third and the first sector to sketch the local employment structure, the share of the working-age population to assess the available labor force, and the share of urban population to estimate the population who can obtain greater access to better living standards such as health care, education, and transportation.
The PFI uses the China Urban Sustainability Index for reference, and assesses the public facilities possessed by the local inhabitants from basic aspects such as transportation, education, and medical health. It also selects the share of financial expenditure in public service to explore the local government investment in public facilities.
The 25 indicators in these five pillars constitute the final CIRD with the weights calculated by the methodology of PCA presented in
Section 2. The average weights assigned for the 25 indicators are reported in
Appendix B. Higher weights are assigned to the GRP per capita (0.141), consumption (0.157), and government expenditure in science (0.152), whereas trade balance (0.034) and medical health (0.037) have low weights. As is suggested by Chen and Woo (2010), a good composite index should not be biased towards any indicators. In this CIRD, even though the weights are not evenly distributed, none of the indicators is dominant, thus guaranteeing the rationality of the design.
4. Results
Based on the concepts of stochastic kernel density discussed in
Section 2, this section focuses on the estimation of transitional dynamics of CIRD and its five sub-indexes. A comparison between the CIRD and GDP per capita is also conducted to demonstrate how the CIRD draws a different picture of transitional dynamics and distribution of 30 Chinese regions.
4.1. The Transitional Dynamics Based on Stochastic Kernel Estimation
4.1.1. The Transition Dynamics of CIRD
This study estimates a persistent stratification on a socioeconomic level across 30 Chinese regions during 1998 to 2010.
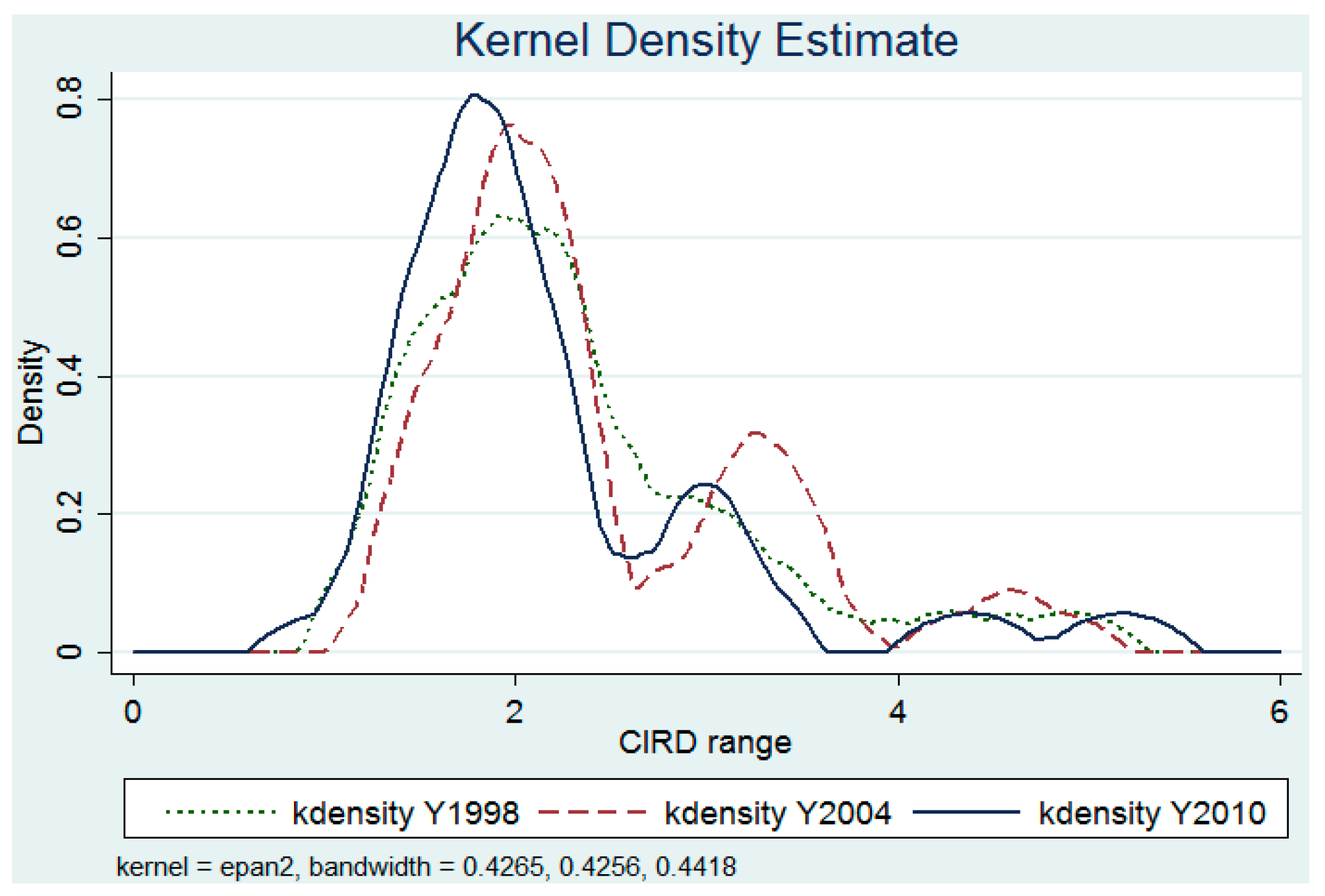
Figure 1 reports three kernel density curves of the CIRD for the years 1998, 2004, and 2010 (for the CIRD values see
Appendix C). One can observe that the marginal distribution remains a pattern of multimodality over the three years, and this multimodality of the distribution becomes clearer over time.
At the first year (1998), the multimodality is not evident. The kernel density curve is characterized by a main mode indicating that around 60% of Chinese regions fell between 1.75 and 2.25 times of the average CIRD, and by a long right tail indicating that the rest was distributed over levels higher than 2.25 times the average CIRD. At the second year (2004), the kernel curve shows a clear pattern of triple modality. There is a small but clear increasing tendency in the main mode of the distribution compared to 1998’s main mode. The previous uniform distribution in the higher levels breaks down into two modes: one gathers around 3.25 times the average and one gathers around 4.5 times the average. At the last year (2010), the multimodality pattern remains and moves slightly leftward as a result of a slight mobility to the lower level clubs. These three kernel curves suggest that a stratification remains across Chinese regions in their distribution based on socioeconomic development, and that the Chinese regions tend to converge (eventually) towards several different values of the CIRD, in line with a sort of club-convergence.
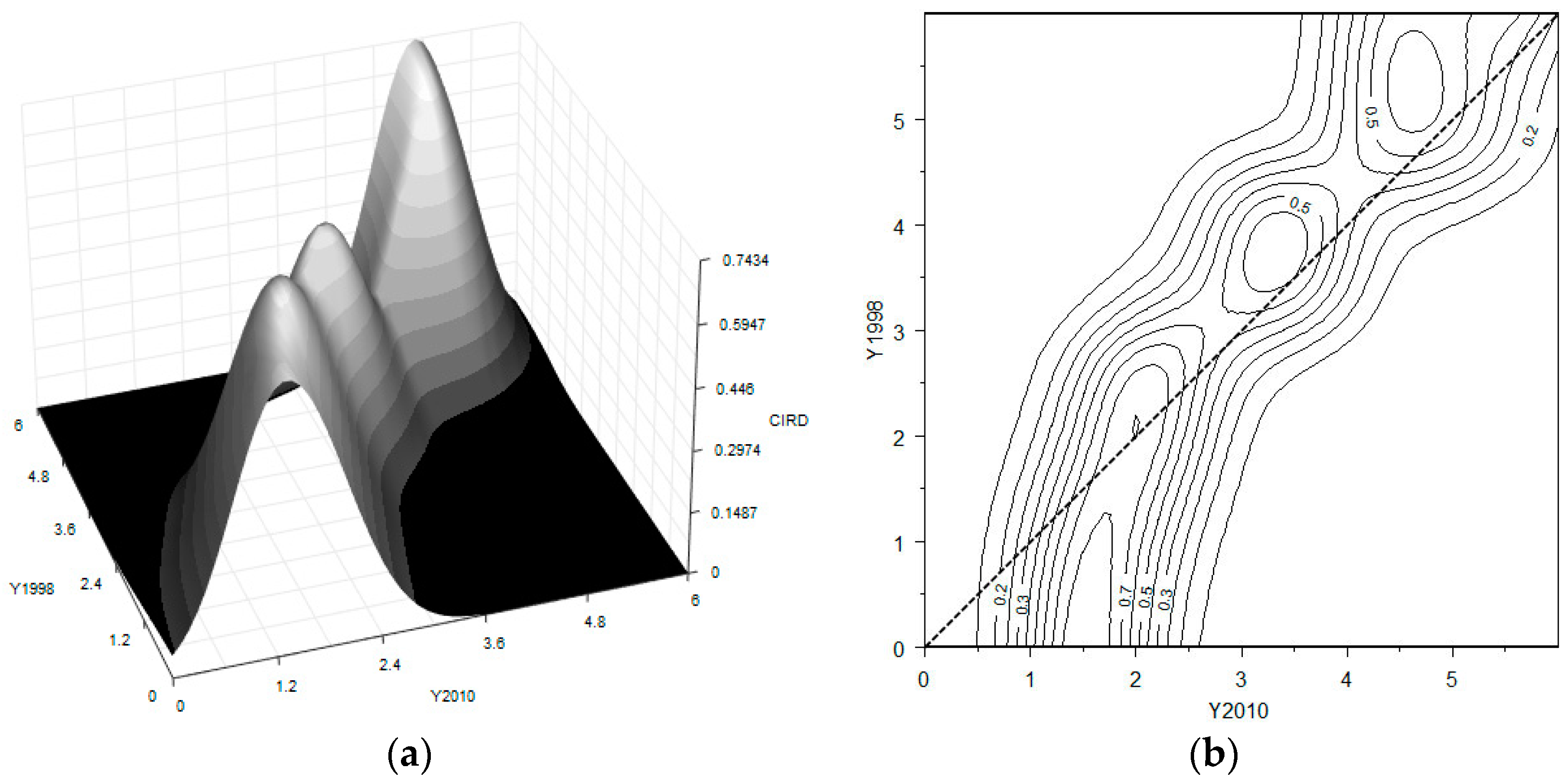
In order to investigate the dynamic distribution of socioeconomic development across Chinese regions, a three-dimensional plot and a contour plot of the stochastic kernel for the 30 Chinese regions are reproduced in
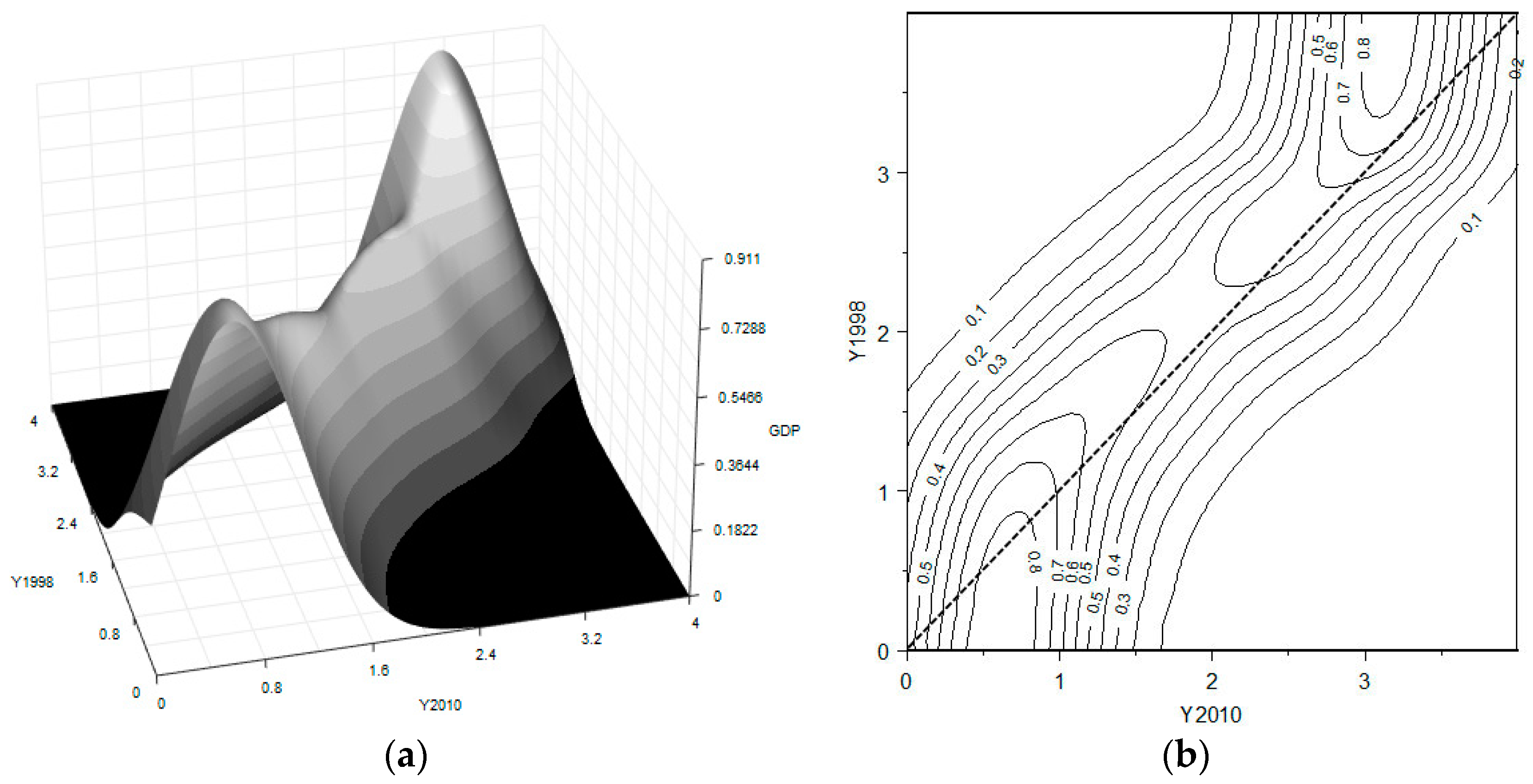
Figure 2.
Both plots reveal a triple-peak distribution of socioeconomic development in China. In the 3D plot, the x-axis represents the relative distribution of the CIRD for the last year (2010), while the y-axis represents the same for the first year (1998); the z-axis reports the value of the stochastic kernel (i.e., how the conditional density of distribution in 1998 changes to the one in 2010). The heights of the peaks indicate the mobility of the transitions over the 13 years: the higher the peaks, the more active the transitions of the distributions in the corresponding parts. The contour plot is the corresponding projection of the 3D kernel surface in the two dimensions, where each line connects all the points on the stochastic kernel with the same height.
One can clearly observe that there are three clubs gathering around the 1.5, 3.5, and 5 values on the x-axis. A strong constancy of these values is also revealed by the fact that all three modes (or peaks) lie on the diagonal. This implies that there is a high probability that a region stays in the same as or a similar position to the distribution of regional socioeconomic development over the 13-year period. To be precise, however, there is also a moderate tendency of a counter-clockwise movement with respect to the diagonal, especially if one inspects the first club. Such a pattern indicates that the transitions in this club are more active. Hence, the stochastic kernel plot provides evidence of stratification and of convergence club formation in the socioeconomic development of China during 1998–2010, stemming from the formation of a middle level club. Moreover, in light of the literature discussed in the Introduction, this is one of the more significant findings of this work.
4.1.2. The Dynamic Distributions of the Five Dimensions of CIRD
This section further explores the five sub-indexes (MEI, SII, ESI, HCI, and PFI) included in the CIRD, so as to shed light on specific regional policies.
Figure 3,
Figure 4,
Figure 5,
Figure 6 and
Figure 7 contain several panels reporting the graphical representation of the Kernel surfaces and the contour plots of the sub-indexes.
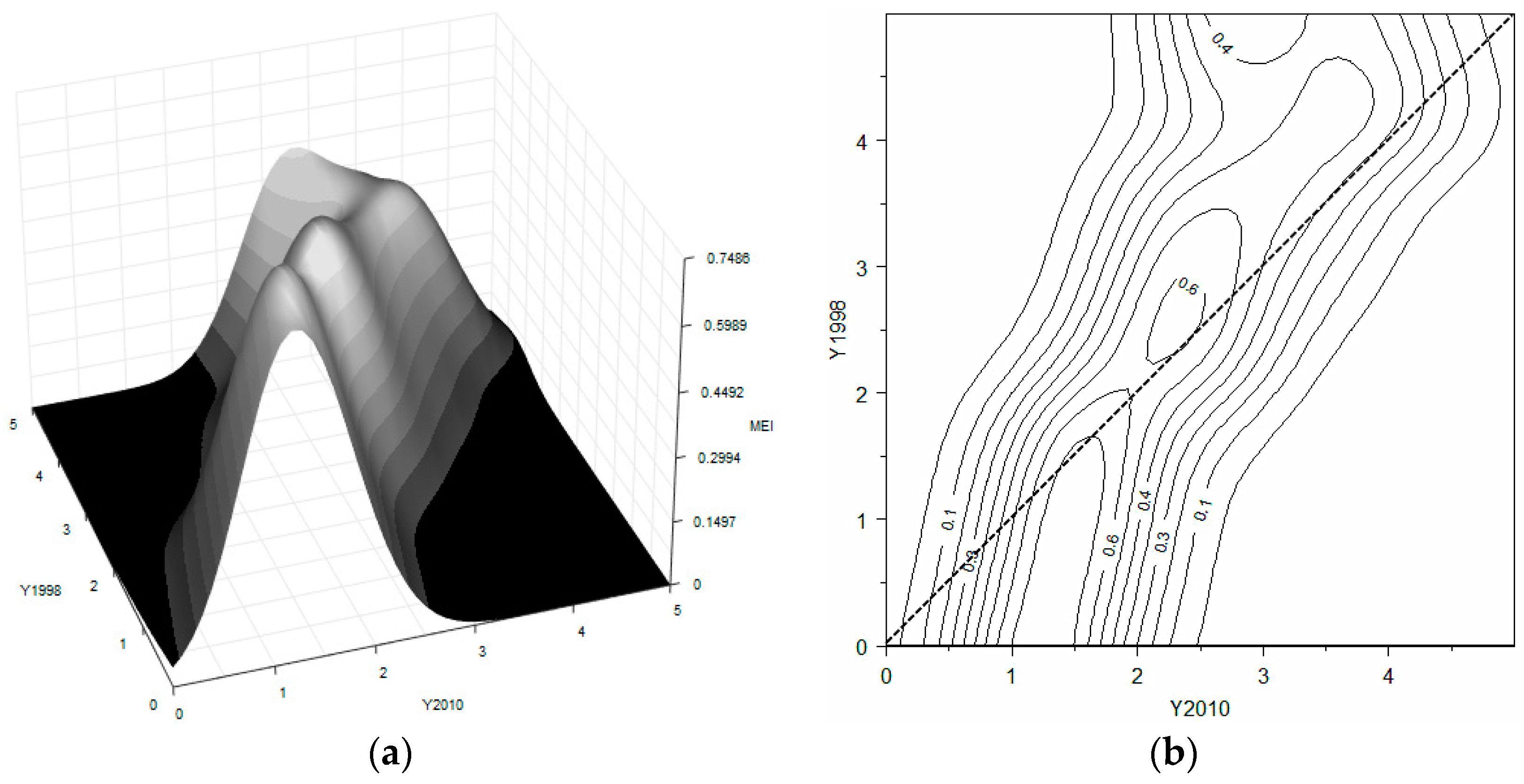
In terms of the macroeconomic conditions,
Figure 3 indicates a multi-peak distribution of the MEI across the 30 Chinese regions. The contour plot reveals three clubs gathering around the values of 1.5, 2.5, and 3 of the national average. However, unlike the triple-peak distribution of CIRD, the three clubs identified by the macroeconomic index show a convergence tendency given that the mass tends to move counter-clockwise with respect to the diagonal. This movement is more apparent when observing the middle-level and high-level clubs. The 3D Kernel surface confirms this movement by the active transitions of distributions of all the clubs in terms of their macroeconomic situations. The lower clubs grow fast and tend to catch up with the upper one. The middle-level club shows a more drastic transition, as some of its members are likely to break the club and form a new sub-club.
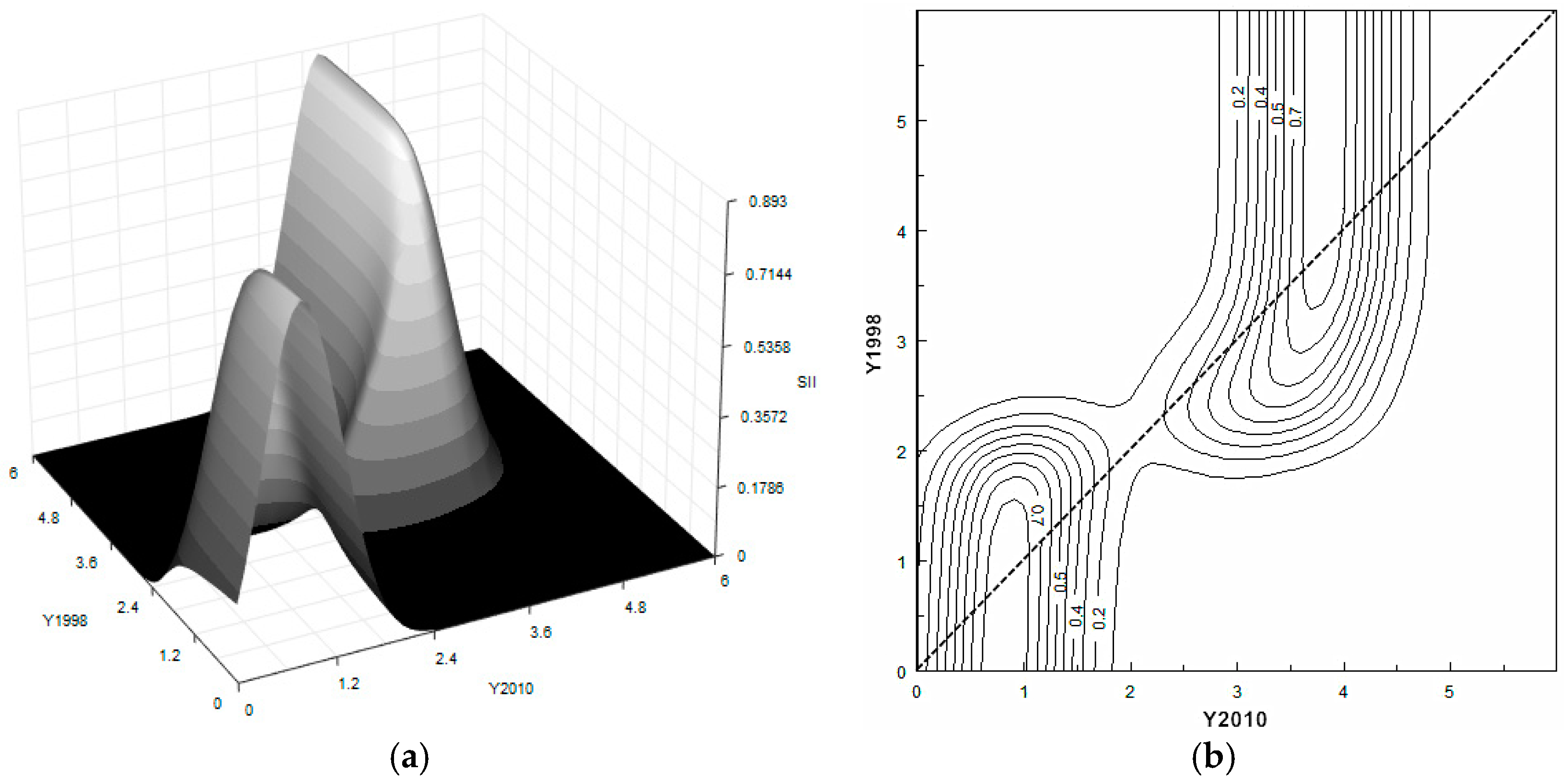
A bimodal distribution is easy to spot in terms of the science and innovation index (see
Figure 4). The two clubs gather around the values of 0.8 and 3.6 of the national average. However, in contrast with the conventional concept of persistence, whereby the elements in the distribution remain where they are at the beginning of the period, there is an evident counter-clockwise movement with respect to the diagonal inside each single club. This drives the two blocks parallel to the vertical axis, which can be easily observed in the contour plot. Such movement indicates the existence of an internal convergence in terms of science and innovation. The 3D kernel surface additionally reveals a more active transition in the high-level club of science and innovation.
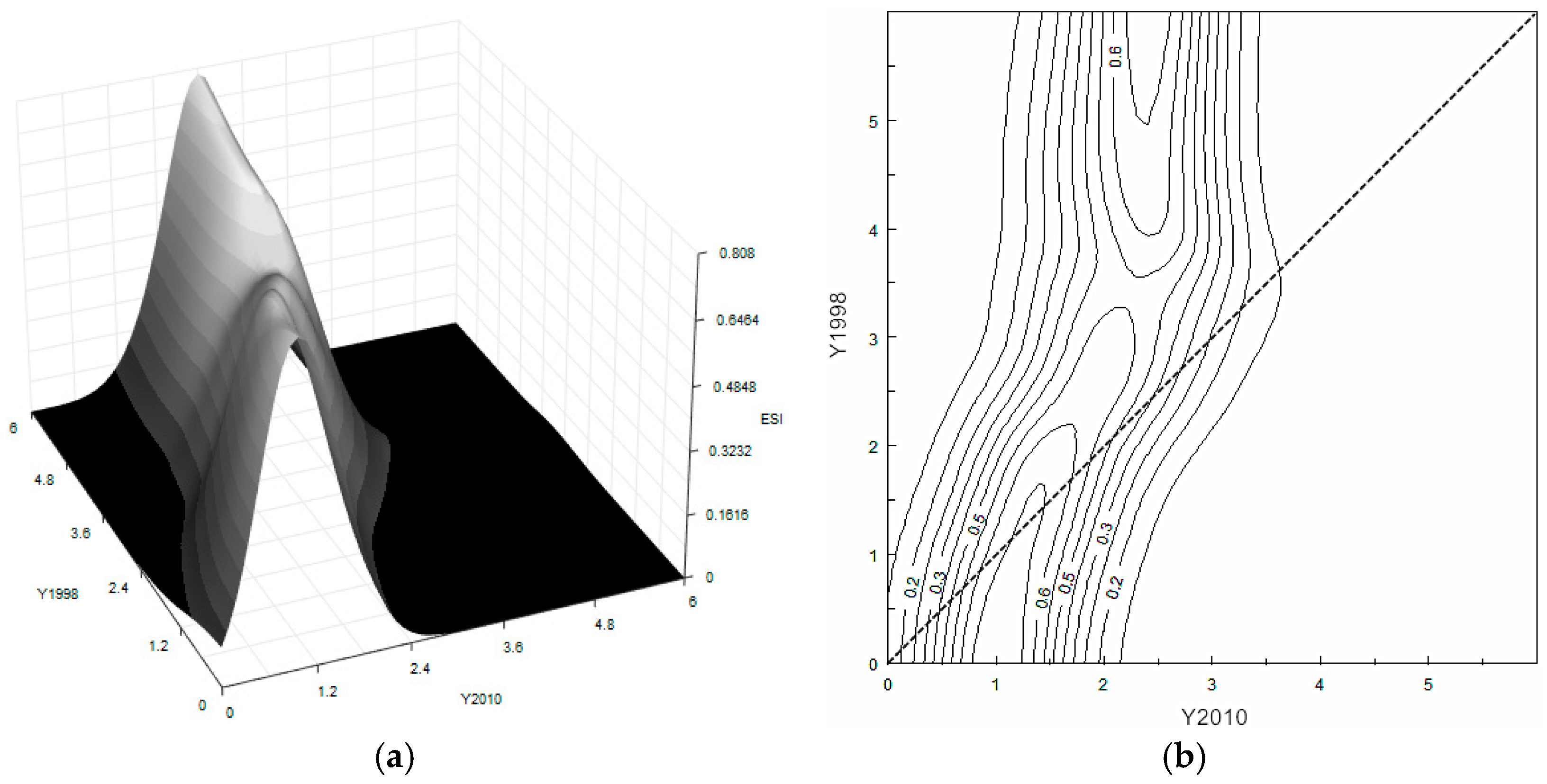
The dynamic transition of the environmental sustainability index exhibits a catching-up progress (see
Figure 5). Two clubs gather around the values of 1.3 and 2.5 of the national average. Some members in the low-level club grow faster, and this drives the mass to move counter-clockwise with respect to the diagonal. The block of the high-level club is approximately parallel to the vertical axis. This indicates that the two clubs are getting closer to each other in terms of environmental sustainability, but still have a gap that cannot be ignored.
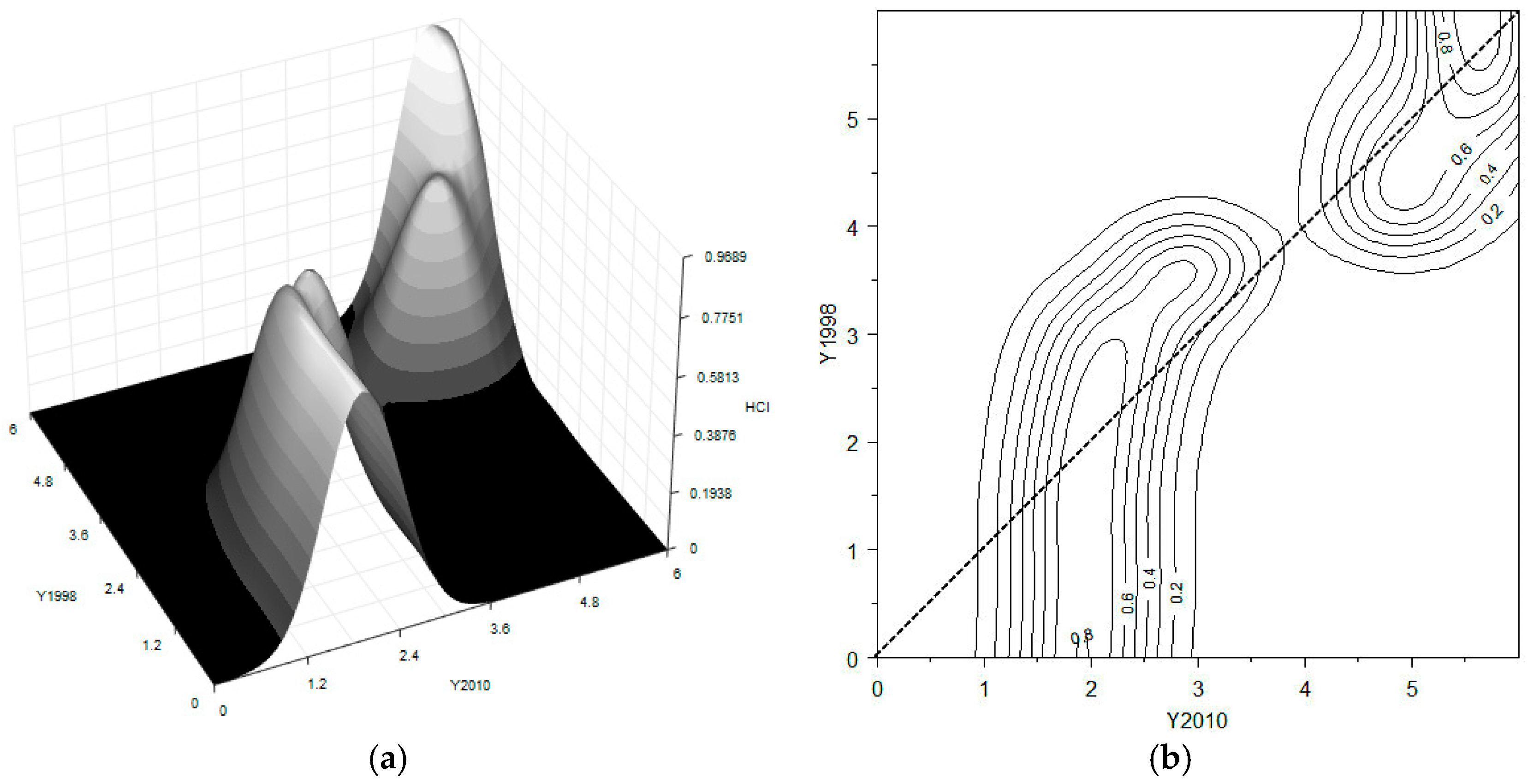
In terms of human capital,
Figure 6 clearly displays a bimodal distribution of the sub-index. The regions diverge into two clubs: one club gathers around the value of 2 of the national average, and the other around 5. The middle class vanishes in terms of human capital. The club with the low level of human capital moves counter-clockwise with respect to the diagonal, driving this part parallel to the vertical axis. This reveals that the members inside this low-level club tend to converge towards internal equality. However, some of the members of this club continue to exhibit a relatively higher level of human capital. This tendency is more evident in the 3D surface.
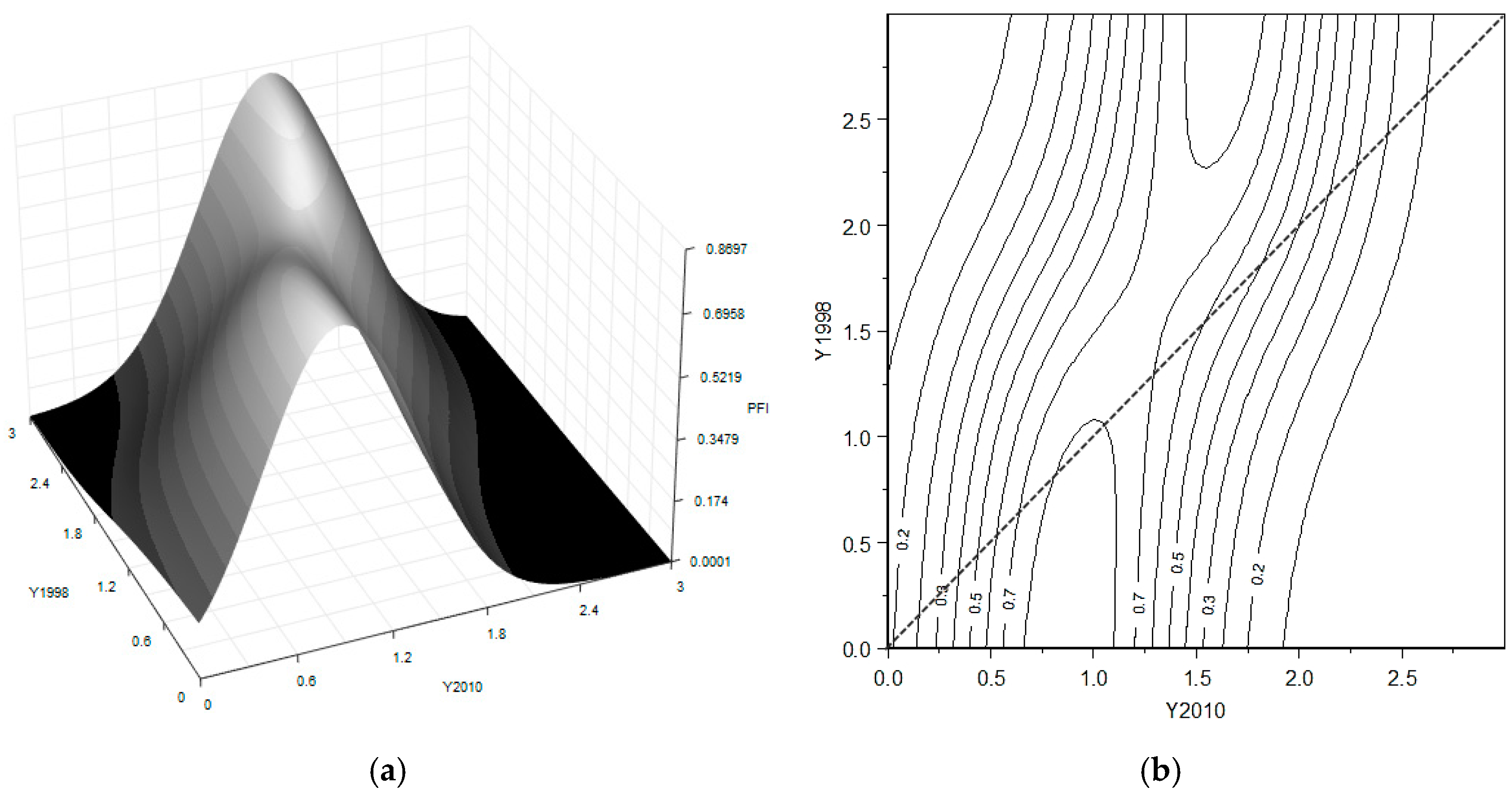
The “twin-peaks” pattern identified for the CIRD is less apparent in terms of public facilities (see
Figure 7). The two clubs are closer to each other with respect to the other dimensions analyzed before. One club gathers around the value of 0.9, and the other gathers around 1.5 of the national average. The mass moves counter-clockwise with respect to the diagonal, which indicates that the cross-section distribution tends to converge towards the equality.
4.2. The Transition Matrix and Ergodic Distribution of CIRD
To better explore the mobility and evolution of the CIRD during 1998–2010, this study employs the discrete transition probability matrix approach described in
Section 2. Following Quah [
64,
65], each provincial-level region is categorized into one of the five states according to its ratio of CIRD to the average CIRD of the sample considered (see
Table 2 for the demarcation of states).
Table 3 reports the Markov transition matrix of CIRD. Corresponding to findings in
Section 4.1, the transition matrix indicates a low interclass mobility among clubs, since there are high probabilities for the majority to stay in their original states over the 13 years (1998–2010). Even though the selection of grid values in the transition matrix is questioned to be somewhat arbitrary, it still gives a conventional perspective to examine the mobility among different states. The significantly high values lying at the two ends of the diagonal, which are 0.91 and 0.99 respectively, signify that the regions belonging to the lowest CIRD group, and the highest CIRD group, have an extremely high probability of remaining in their CIRD states. In particular, the high probability of remaining in State 1 implies the insurmountable transition barriers for the underdeveloped regions to migrate to higher CIRD states. This finding is consistent with the works of Villaverde et al. [
27] and Cheong and Wu [
17], both of which presented a considerable persistence in the distribution of income especially with high-value diagonal elements in State 1 and State 5.
The ergodic distribution, which can be used to examine the evolution of the distribution of CIRD in the future, shows a relatively even distribution among the five states over the 13 years. The ergodic distribution has the highest proportion in State 2. This indicates that more Chinese regions will migrate to the low level of CIRD in the long run. Specifically, the future distribution of socioeconomic levels will cluster to the level below the average. Other relatively higher proportions can also be observed in State 1 and State 5. The high probabilities at the two ends signify the congregations at the lowest and highest levels of CIRD in the future respectively.
A further look at the probabilities of moving upwards and downwards can contribute to a better understanding of the transition dynamics. The probabilities of moving upwards and downwards for State 2 are 0.17 and 0.04 respectively (take 0.17 for instance, it is calculated by the sum of the transition probabilities from State 2 to the superior states, which are 0.16 to State 3 and 0.01 to State 4 respectively). The entities in State 2 are most likely to upgrade to State 3 when they move away from State 2 (with a probability of 0.16). The largest transition can be observed in State 3, where the entities have the highest probability (0.31) of degrading to State 2 and a relatively higher probability (0.12) of upgrading to State 4 in their transitions. State 4 also presents a higher probability of moving downwards (0.19 to State 3 and 0.05 to State 2). Special attention should be paid to the predominance of the downward transitions. This finding is also in accordance with Cheong and Wu [
17], who raised this issue by a deeper examination of transitions of GDP per capita in China.
This empirical study is extended to the five sub-dimensions to provide a comprehensive understanding of the transition dynamics and convergence patterns.
Table 4 shows the Markov transition matrices for the five sub-indices. The relatively high values of the diagonal elements in every matrix indicate high persistence in all sub-dimensions. However, the persistence levels are different among indices. For instance, MEI shows a relatively higher probability of moving up among different states. This upward tendency is more evident in ESI and PFI. Higher values can be observed in State 5 in all the sub pillars. Thus, the persistence in the highest state of each sub-index is more pronounced than that in other states. The ergodic distribution of each dimension shows a scattered distribution among different states. However, the ergodic distribution of ESI and PFI show that the peaks of distributions are in State 3. Thus, a tendency of convergence to the middle level can be detected in these two pillars. In contrast, the ergodic distribution of MEI, SII, and HCI show less evidence of convergence as the distribution peaks are either in State 4 or State 1.
4.3. Grouping and Mapping
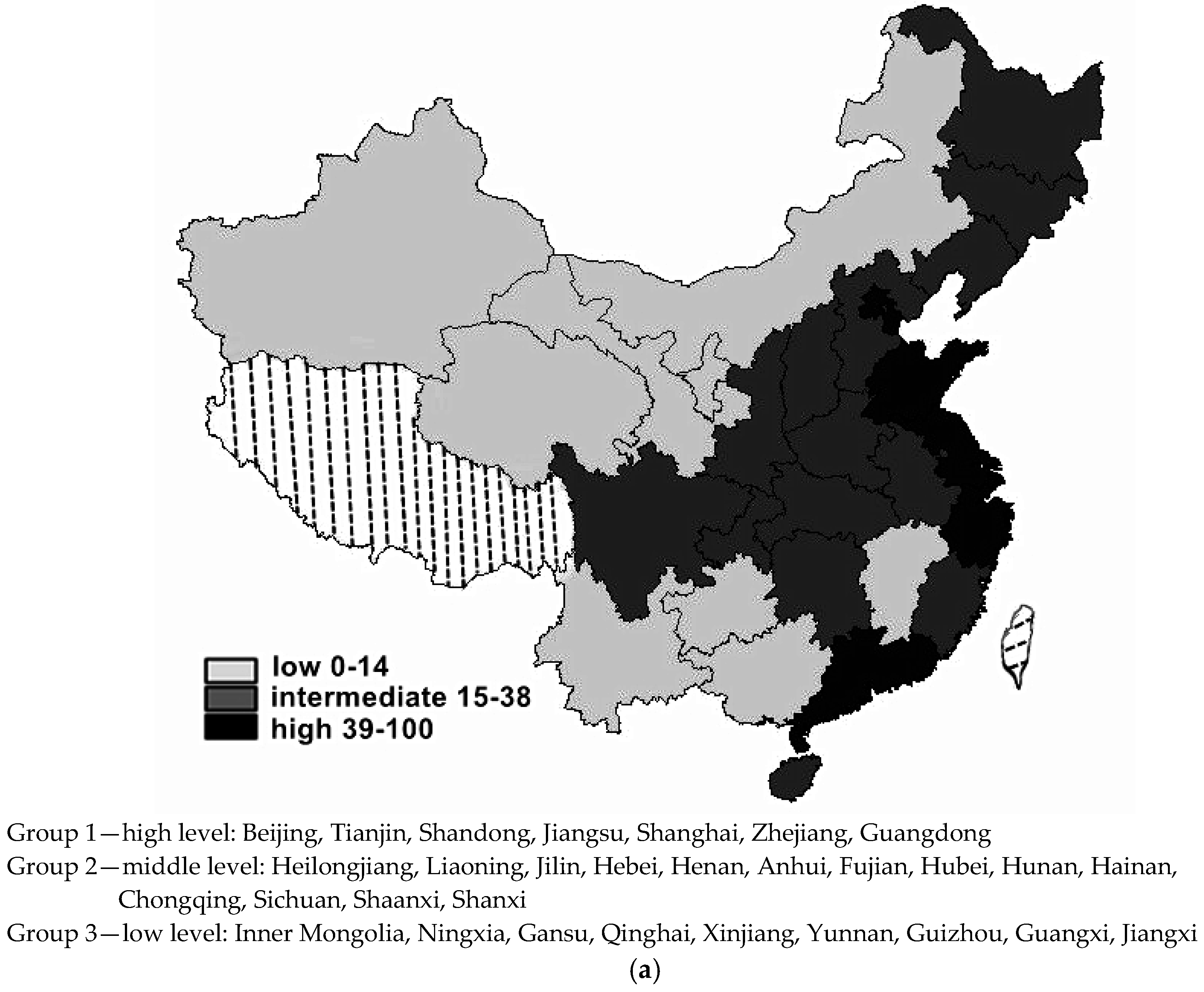
To visualize the three peaks of the stochastic kernel better, in
Figure 8, the Chinese regions are clustered into three groups according to their average scores and average changing levels of the CIRD. Here, the regions are grouped by the default algorithm of
Natural Breaks in terms of their grades of average CIRD values and average changes. Quoted from the GIS dictionary, the algorithm of
Natural Breaks classifies data on the basis of “natural groups in the data distribution”, which are presented as “the low points of valleys” in the histogram—for example, the first group by
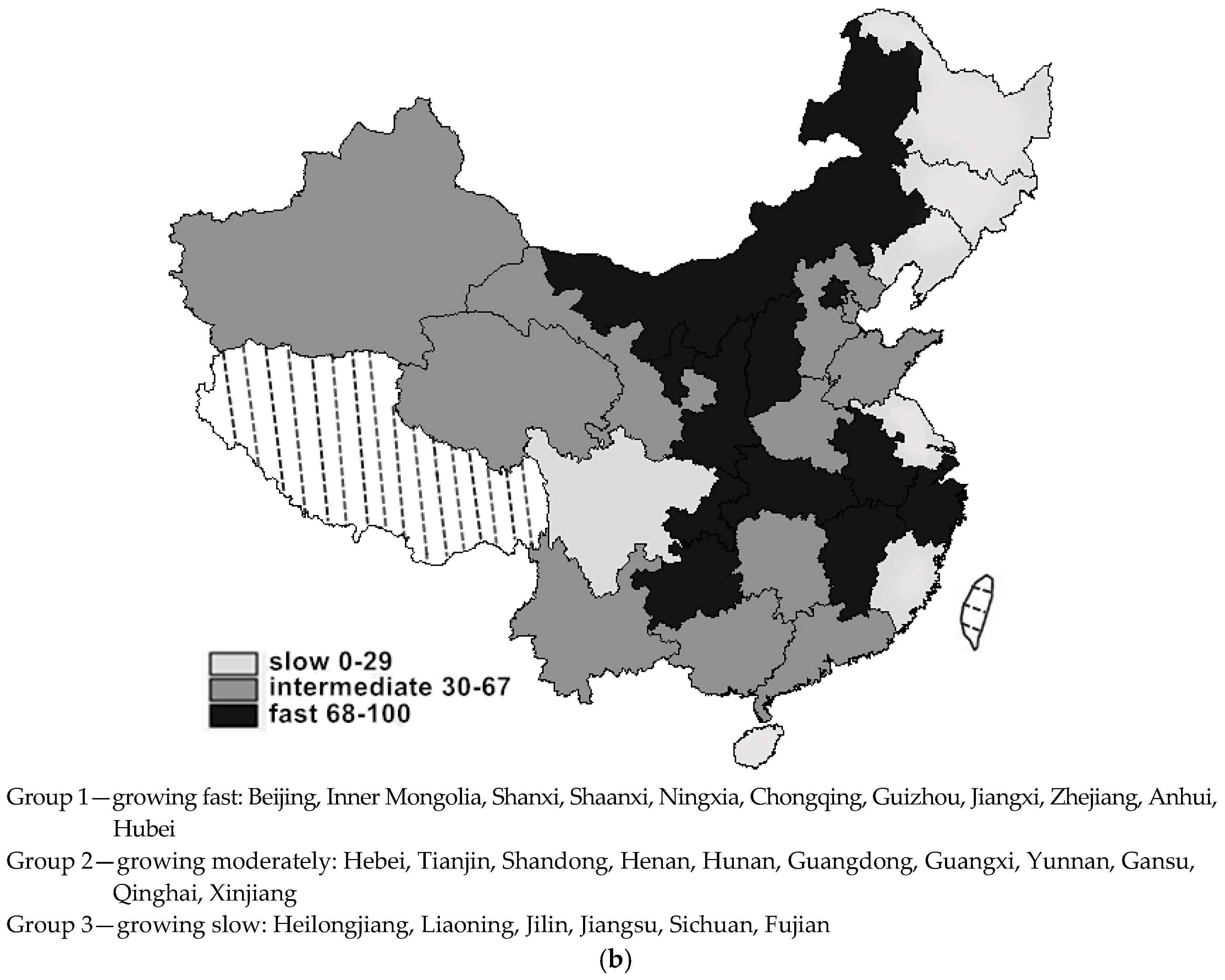
Natural Breaks is allocated at “the largest valley”. The three groups benchmarked by the regional CIRD levels are as follows: one in the low socioeconomic status, ranging from 0 to 14 of the average CIRD grades; one in the middle level of socioeconomic status, ranging from 15 to 38 of the grades; and one in the high socioeconomic status, ranging from 39 to 100 of the grades. The three groups benchmarked by the regional CIRD changes are as follows: one grows slowly in the regional socioeconomic development, scored from 0 to 29 in the average changes of CIRD; one grows in an average rate, scored from 30 to 69 in the average changes; and one grows fast in the regional socioeconomic development, scored from 70 to 100 in the average changes.
The clustering tendency largely corresponds to the geographic locations in the map based on the average CIRD scores: the highly developed group includes most of the east coast regions, while the underdeveloped group mainly contains western inland and peripheral regions, and the remaining central and northeastern regions constitute the middle level group.
Interestingly, the groups benchmarked by average changes of CIRD show a different picture: the fast-developing group mainly comprises the inland and peripheral regions belonging to the middle or low level groups in the previous classification according to the average CIRD scores, while the slow-developing group contains only five members and shows a scattered distribution, i.e., the northeast, southwest (Sichuan) and the east coast (Jiangsu); the majority of Chinese regions develops at an average rate. This corroborates the regional transition progress to a certain extent. This implies the existence of a club-convergence pattern where the catch-up process is far from been completed.
4.4. The Performance of the Three Groups in the Individual Indicators
This section provides a specific examination of the three groups based on the single indicators.
Table 5 quantifies how the three groups perform in terms of each indicator and dimension of CIRD. It is clear that Group 1 has pre-eminence than the other two, especially in GRP per capita, labor remuneration, government expenditure in science, R&D expenditure, waste utilization, employment in the third sector, urban population share, and transportation, where Group 1 has doubled and redoubled compared with the other two. Group 2 performs better than Group 3 in most of the indicators. However, the differences between Group 2 and 3 are not all very significant, and this is the case, for instance, for GRP per capita, R&D expenditure, trade in science and technology market, discharged living waste, and employment in the third sector.
In terms of changes, although Group 1 still shows a better performance in the majority of the indicators, it is not extraordinarily more advanced than the other two. Group 2 even changes faster than Group 1 in some aspects, such as FDI, trade balance, share of educated population, public medical services, and government expenditure in public facilities. Group 3 is not anymore the one with the majority of the lowest values. Its changing speed exceeds Group 2 in terms of GRP per capita, labor productivity in science and technology firms, and employment in the third sector.
The largest gap exists in the dimension of science and innovation (SII), where the upper group is more than twice of the lower. This scale-up gap can be found also between Groups 2 and 3 in the dimension of environment sustainability. Large group gaps, though less sharp, can be found for macroeconomic levels and human capital, too. This can be corroborated by the scores of the CIRD change, as Groups 2 and 3 have lower values in those dimensions. Group 3 overtakes Group 2 in the average level of public facilities, where we can also observe the smallest gap among three groups. A similar turn-back can be found in the change of macroeconomic conditions, where Group 3 grows nearly 13% faster than Group 2. This indicates a rapid catch-up process of the lower groups.
The wide group gaps in the average and change indicate that, in terms of macroeconomic conditions, science and innovation, environment sustainability, and human capital, the Chinese regions not only stand in very different states but also develop in various velocities. Meanwhile, the superiority of Group 1 cannot be simply taken by the other groups due to its faster changes. The levels of public facilities tend to stay flat among different regions, given the relatively small gaps of group average and faster change of the low-level group.
4.5. A Comparison between the GDP per Capita and CIRD
This section provides a comparison study by employing the conventional indicator—GDP per capita. The GDP per capita of the 30 Chinese regions follows a different path of transitional dynamics and distribution in the same time period.
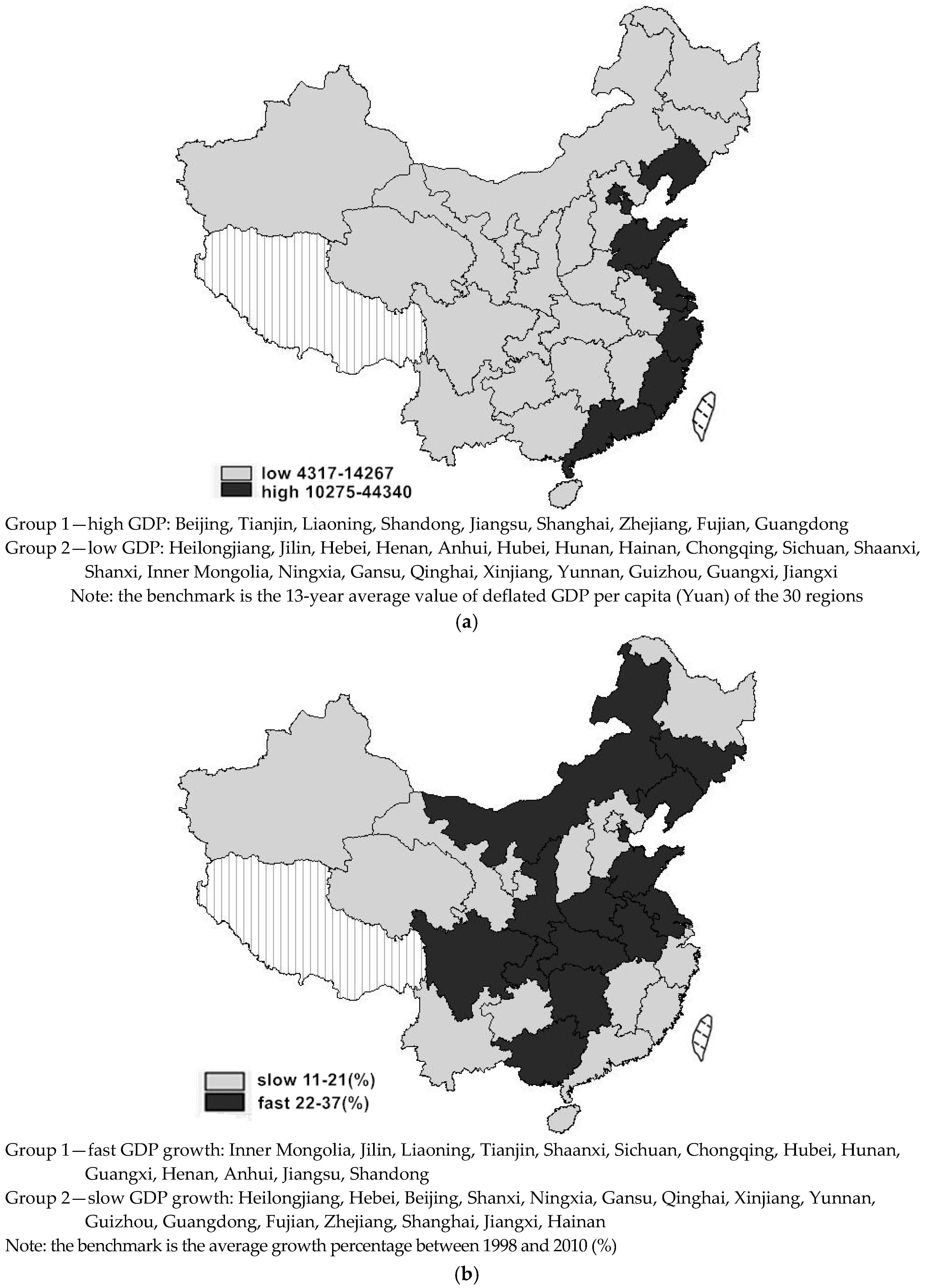
Figure 9 shows the presence of a bimodal distribution with two converging groups.
The contour plot indicates that the GDP per capita of one group converges to the value around 0.9 of the national average, while the other locates around three times the national average. The dynamic distribution of GDP per capita, similar to the CIRD, reveals a constancy of distribution among 30 Chinese regions during 1998 to 2010, since the main modes lie on the diagonal. This implies a high probability of a region staying in the same or a similar position in the dynamic distribution over the 13 years, either of its socioeconomic development levels or GDP per capita.
However, the middle-level group existing in the distribution of regional socioeconomic development disappeared in the transitional dynamics and distribution of GDP per capita. Instead of the triple-peak pattern pictured by the CIRD, the GDP per capita highlights a more heterogeneous country, where the regions are polarized into two groups far from each other.
Figure 10 groups the 30 regions by the 13-year average value of GDP per capita (Yuan) and GDP change rate between 1998 and 2010 (%). A coastal–inland divide can be observed by the GDP per capita levels. If we compare this coastal–inland divide with the CIRD classification, some central regions (for instance, Henan, Hubei, Hunan, and Anhui) and western regions (for instance, Sichuan, Chongqing, and Shaanxi) are separated from the low-GDP group, and constitute a middle-level group of CIRD (see the first maps in
Figure 8 and
Figure 10). Moreover, the northeast demonstrates convergence in terms of their CIRD levels, whereas a diverging tendency is observed in the three Northeastern regions at the levels of GDP per capita. There is one thing in common when observing the two maps of rates of change (see the second maps in
Figure 8 and
Figure 10): the majority of the central and some peripheral regions develop faster than the coast. However, some central regions (such as Henan, Hubei, and Hunan) are separated from the group of faster GDP growth, and classified into the middle group of CIRD change rates. However, two northeast regions (Jilin and Liaoning), which grow fast in GDP per capita, fall into the slow group of the CIRD change.
5. Discussion and Conclusions
It is hard to understand the complexity of regional disparity in China without linking socioeconomic conditions to the policy background. This closing section aims to offer some insights to interpret the results presented above while taking into account the evolution of national and regional policies in China.
The east coast has certainly enjoyed a head start from the decentralization of Chinese regional policies in the early stage of its pro-market reforms from 1978 onwards. In the framework of Deng Xiaoping’s guideline for prioritizing the development of certain regions in China, Special Economic Zones (SEZ), where freer economic activities were facilitated, were established, and 14 coastal cities were open to foreign investors in 1984 (Deng Xiaoping delivered a speech stating that it should be allowable for some people and some regions to obtain wealth before others for the very first time in 1985, and he recurred to this subject twice in 1986). This approach had a twofold result. On the one hand, it facilitated market liberalization and boosted its exporting sectors by attracting Foreign Direct Investments (FDI) (see Bonatti and Fracasso [
83] for reference). On the other hand, it fostered the Chinese pattern of growth clubs (see Andersson et.al [
84] for reference) with an uneven path of regional development as a side effect.
The Chinese central government realized the unintended consequences of its geographically biased policies and started to emphasize the need of restructuring and coordinating regional development since the 1996’s “Ninth Five-Year Plan”. Accordingly, a series of preferential policies to support rural and inland regions were developed to balance the previous disproportional benefits reserved to the coastal regions. In the “Tenth Five-Year Plan” started in 2001, the well-known program of “Western Development (Go-West)” was initiated. This was followed by several other regional programs implemented in 2003 and 2004, respectively targeted at the revitalization of the traditional northeast industry and at the promotion of central China (“Go-Central”). The “Eleventh Five-Year Plan” followed the guideline of a coordinated and balanced growth, aiming to improve the mechanism of regional coordination, so as to support regional programs and promote the common prosperity of the eastern, central, and western areas. During the “Twelfth Five-Year Plan”, a new program called “One Belt One Road” was proposed by the new Chinese leadership to deepen regional cooperation. In general, the development strategy followed by the central government exhibited a gradual shift of the attention from the eastern regions to the central and western areas of the country. This implies a pattern of growth characterized by the emergence of the growth clubs, where the development of the coastal regions was the first priority, and inland regions had to catch up later.
Contrary to conventional wisdom, this study shows that the dynamic distribution of the socioeconomic development levels across Chinese regions follows a pattern of multi-peak stratification. This finding is based on a new multidimensional index (CIRD) that captures all the main pillars of socioeconomic development. More importantly, the result challenges the common opinion that the east coast regions or their adjacent areas developed more rapidly in all socioeconomic aspects. The analysis shows that a few inland and peripheral regions with the lowest levels of development have grown relatively faster. Specifically, some regions adjacent to the coast, such as Hebei, were overcome by Shanxi and other central inland and peripheral regions (such as Inner Mongolia). However, there is a high level of persistence in the transition process, given that a certain number of regions stay in the same group during the period. The analysis of the transition matrix also reveals this low interclass mobility among clubs during 1998–2010, as the majority has high probabilities of staying in their initial states. This suggests that the regional agglomeration has been increasingly evident. Therefore, more importance needs to be attached to the “clubs” in their strategic formulation of regional development. Such regional strategies and policies should allow the clubs to fully exploit the advantages of their peculiar advantages in resources and markets, and benefit from industrial agglomeration and scale production.
Moreover, the transition matrix of CIRD shows that the regions are more likely to migrate downwards in the transition process. This implies, to a certain extent, that regional inequality in China may be exacerbated further, and will bedevil China in the years ahead. Notwithstanding the improvement recorded for some areas, catching up on most of the undeveloped regions still has a long way to go.
The examination of individual dimensions of the CIRD leads to a better understanding of it, especially for what concerns its non-GDP-related dimensions. A bimodal distribution is displayed for each non-GDP-related index, yet with a certain difference across the various dimensions. The macroeconomic index closely relates to the GDP and exhibits a trimodal distribution during the observation period. In terms of dynamics, the indexes for the macroeconomic condition, environmental sustainability, and public facilities exhibited several intergroup transitions, showing a non-negligible dynamism. On the contrary, the indexes for science and innovation, and human capital are characterized by relatively high levels of persistence. In the attempt to qualify the geographic dimension of the process of convergence, the analysis revealed that a certain number of central and western regions have upgraded to the higher level groups in the non-GDP-related dimensions, whereas the majority of the northeast has done the opposite (especially in environmental sustainability, human capital, and public facilities).
The strategy of balancing the uneven growth process in China has not been completed yet: in spite of the remarkable achievements in poverty reduction (it is reported that the proportion of population living in poverty reduced from 81.6% to 10.4%), regional disparity among the various areas of the country has not been eliminated. The central and western regions are still far behind the east and coastal areas in various socioeconomic aspects. Yet progress has been made, due in part to geographically differentiated actions. However, it is worth noticing that a certain extent of resemblance exists in a variety of different local strategies. For instance, many local governments are keen to develop high-tech industries and construct high-tech development zones, whereas the sound progress of such industry requires a fairly high level of local economic and social development that can guarantee the adequate financial investments and high-standard supporting facilities. Hence, it is very likely to be counterproductive if the underdeveloped regions blindly invest in the high-tech industry regardless of their own socioeconomic conditions. As shown by this analysis, it seems particularly important that specific policies and programs target different aspects across the different regions and are designed differently so as to fit the specific characteristics. Regions do not necessarily lead or lag behind in all dimensions of development, and policy interventions need thus to be targeted so as to reflect their underlying conditions.
Besides such findings, this study raises a number of issues for possible further research. First, it shows that it could be interesting to tackle the potential interactions across the five sub-dimensions of the CIRD with a view to seeing whether certain dimensions are positively or negatively correlated with each other. Second, it would be valuable to assess the effects of different policies on regional disparity in China so as to provide more concrete instructions for an assessment of the impact of local policies on different domains. The main challenges in pursuing these types of studies lie in the availability of reliable and consistent disaggregated data and in the small size of the sample under observation. Possible improvements in this direction could be the introduction of a sub-dimensional division of urban–rural disparity or the expansion of the sample to an inferior administrative level of prefectural regions. They both fall beyond the scope of this analysis and, accordingly, remain objects for future research.