Abstract
Distributed generators (DG) using renewable energy sources (RESs) have been attracting special attention within distribution systems. However, a large amount of DG penetration causes voltage deviation and reverse power flow in the smart grid. Therefore, the smart grid needs a solution for voltage control, power flow control and power outage prevention. This paper proposes a decision technique of optimal reference scheduling for a battery energy storage system (BESS), inverters interfacing with a DG and voltage control devices for optimal operation. Moreover, the reconfiguration of the distribution system is made possible by the installation of a loop power flow controller (LPC). Two separate simulations are provided to maintain the reliability in the stable power supply and economical aspects. First, the effectiveness of the smart grid with installed BESS or LPC devices is demonstrated in fault situations. Second, the active smart grid using LCPs is proposed. Real-time techniques of the dual scheduling algorithm are applied to the system. The aforementioned control objective is formulated and solved using the particle swarm optimization (PSO) algorithm with an adaptive inertia weight (AIW) function. The effectiveness of the optimal operation in ordinal and fault situations is verified by numerical simulations.
1. Introduction
Recently, renewable energy sources (RES) are catching much attention with the aim of being a low carbon society [1,2,3,4,5]. However, RES, such as photovoltaics (PV) and wind generators (WG), have a power output that has the direct influence of the weather [6,7]. The fluctuation can cause voltage deviations and reverse power flow in the distribution system. Generally, with the deep penetration of distributed generators (DGs) of RESs [8,9], the DG output must be restricted within the proper range. However, this leads to wasted power, because customers have the likelihood of not fully utilizing the surplus power of the RESs in limited situations. In order to solve unstable power quality issues from the voltage and frequency fluctuation problems by the high penetration of RESs, the battery energy storage system (BESS) is proposed, and BESS management has also been verified in [10,11,12,13]. The reverse power flow problem is solved by the BESS installed at the interconnection point, because the system can absorb surplus DG output power. Moreover, effective power management considering the customer side and system operator is made possible. James et al. [14] proposed an optimal reactive power control using a stochastic optimization technique for the voltage deviation problem. An effective utilization of electric vehicle (EV) batteries also has been studied [12,15]. Those forms of power storage can compensate for the fluctuating power outputs of RES generators; moreover, these are also valid for fluctuations with higher frequencies.
Recent technology has been developing regarding BESS performance, such as enabling a longer life time and a huge capacity, a reduction of the cost, loss reduction and improvement of the power conversion efficiency. The BESS is expected as a method for the continuation of the power supply even when a fault has occurred in the distribution line [16]. Moreover, Karan et al. [17] presented a method of islanding utilizing different types of DGs. On the other hand, a loop power flow controller (LPC) is expected as a method to avoid outages occurring during disconnection accidents [18]. Most distribution networks comprise a radial network configuration [11,19,20,21]. Once any line in the distribution system is broken, the area after the fault point will not be supplied with power. However, this network can be viewed as a mesh distribution system by installing an LPC device. For this reason, the installation of an LPC achieves an augmented voltage stability. The problems of voltage deviation, reverse power flow and frequency fluctuations are solved by using smart grid technology and optimization or management techniques; however, a detailed simulation, such as that of a whole day operation, and fault analysis have not been captured simultaneously in the above-mentioned literature.
In this paper, three simulation cases are provided for the assessment of the performance of BESSs and LPCs as follows:
- Case 1: BESS management is provided; the simulation can be divided into two operation modes. One operation is the normal operation, which is optimized from the loss reduction aspects. The second mode provides continuous power supply in a disconnected fault situation.
- Case 2: An LPC reconfiguration system is proven to supply energy in an outage. In terms of a fault, electrical power is supplied from the installed DGs, and an optimized reconfiguration is demonstrated in some configurations.
- Case 3: The smart grid with the adopted LPC can be seen as an active smart grid system; the active smart grid is reconstituted in order to minimize distribution losses in real time.
The optimization method of adaptive inertia weight particle swarm optimization (AIWPSO) is applied to all cases. The meta-heuristics method is able to simply extend a model and variables. In the simulation Cases 2 and 3, it is a conclusive combinatorial problem (i.e., -hard problem) for LPC configurations. The AIWPSO is a powerful method for complex problems, such as -hard problems. Furthermore, the dual scheme optimization algorithm is included for the decision making of the reconfiguration of the active smart grid.
Hence, the main contributions of this work are as follows: BESS management is advanced by two mode simulation. Furthermore, case studies are provided as the choices of the system design for BESS or LPC in fault situations. The active smart grid with a real-time reconfiguration is enabled to make a mesh distribution system from a radial system. It achieves a high reliability and stable power supply. In the optimization method, a modified meta-heuristics optimization method and dual scheduling method are used to solve complex problems and can also determine an optimal schedule for the system operator.
The remainder of this paper is structured as follows: Section 2 explains the control objective, and the control devices and methodology are described in Section 3. Section 4 provides the optimization method for optimal scheduling of the distribution network. In the simulation results of Section 5, the effectiveness of BESSs and LPCs is provided by detailed case studies. Finally, this paper is concluded in Section 6.
2. Reliability and Stable Power Supply
The system operator must maintain the power quality for a reliable and stable power supply. In this paper, the three main points of focus are a continuous power supply, voltage control and the prevention of reverse power flow towards the high voltage system.
According to the electricity laws in Japan, the acceptable range of voltage at the residential consumer side must be within 101 ± 6 V. Generally, the distribution voltage is 6.6 kV for high-voltage distribution systems. When the load is heavy, up to a 6.5 V voltage drop can occur instantaneously. When the power flows from DGs to the system, a voltage rise up to 2 V may also occur. However, it is difficult to simulate a system for the entirety of a whole day using a very short time step (e.g., a few ms). Therefore, in order to consider steep voltage fluctuation, a strict voltage range is applied to the system. Therefore, the low voltage range is determined from 101.5 V (0.967 pu) to 105 V (1.0 pu) in this paper. Similarly, the voltage range of the upper distribution line from pole transformers should be maintained within 6380 V (0.968 pu) to 6600 V (1.0 pu), as well as the low voltage area [11,22]. This range can compensate for short-term voltage changes in spite of the one hour simulation time step.
On the other hand, it is also necessary to set the interconnection power flow to an acceptable range. Moreover, it is known that a large active power flow causes an increase of distribution losses. Therefore, the active power flow must be kept low [12,23,24,25] in order to reduce distribution losses.
3. Control Devices and Configuration
3.1. LRT and SVRs
Generally, in order to prevent power system problems, many control devices are installed. As a conventional method, voltage deviation has been handled by using LRT and SVR devices. These devices can control the node voltage by changing the tap positions. It is important to note that tap positions are discrete variables [22]. The allocations of SVRs are optimized in this paper. In order to treat the optimal placement problem, the placement value is coded as a binary string. The optimization problem includes combinatorial problems (CP); therefore, PSO is used for optimization, because the method makes it possible to extend the variables and configuration in the distribution system.
3.2. BESS
It is desirable for BESS installation to suppress a large variation of active and reactive power flow at the interconnection point. Furthermore, a large BESS is installed at the end of the distribution line as a back up source. Active and reactive power from the BESS are used to increase system reliability, especially when a disconnection fault occurs. In the ordinal situation, these BESSs are managed to reduce distribution losses. The active and reactive power output control system for the BESSs is shown in Figure 1. In this paper, the BESS is assumed to have NAS batteries.
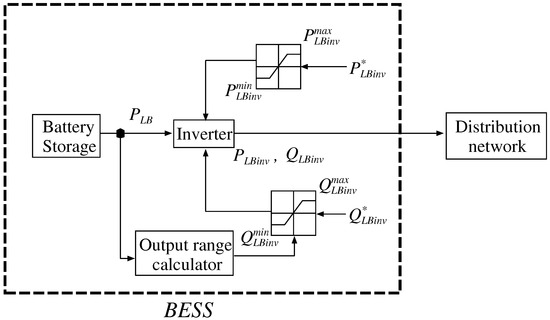
Figure 1.
BESS control system.
3.3. PV System
In this paper, the DGs considered are based on PV generators, which are the most popular in smart houses. PV output is controlled using the MPPT algorithm because the PV output may be changed by the weather conditions. It is also known that the maximum power output point characteristic fluctuates from moment to moment. Otherwise, the reactive power outputs from the inverters interfacing with the DGs are used to control the distribution system voltage as a cooperative operation. It is unnecessary to install additional control devices when using the PV inverter margin. Thus, the limit of the reactive power supply depends on the PV active power output [11]. The reactive power control scheme is shown in Figure 2.
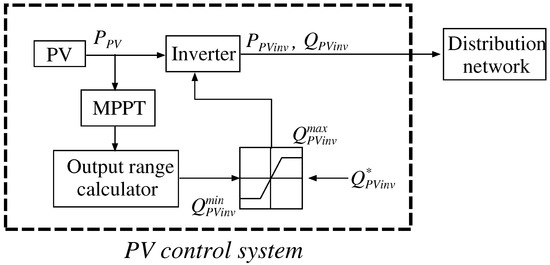
Figure 2.
Reactive power control system for PV.
3.4. LPC
The LPC can restructure the distribution system to a mesh or loop configuration by using an opened switch, which can connect one node to other node. In this paper, the LPC modeling method is achieved with the admittance matrix, which is also the overall distribution system. The effectiveness of LPC is first demonstrated in fault simulation. On the other hand, it can also be expected to enable loss reduction via the active smart grid system. The active smart grid system is reconstructed using multiple LPCs [18].
3.5. Home BESS
It is assumed that the house BESSs are installed in all customer homes for Cases 2 and 3 of the simulation. This installation is applied for demand response (DR). Generally, with DR, megawatt (saved energy) trading is provided in the day-ahead electricity market [26]. However, it is only considered as power consumption. It is desirable to use reactive power control to maintain the node voltage. In addition to the cooperative operation of PV inverters, reactive power DR by home BESS is proposed in this paper.
4. Formulation of the Modeling and Optimization Method
The following section describes the decision technique for the LRT, the reactive power control values using inverters interfaced with the DGs and the large capacity and house BESSs; the objective function and constraints are described in this section [11].
4.1. Modeling of the Distribution System
In this paper, the Newton–Raphson method is used for power flow calculations. The power balance equations are described in Equations (1)–(4).
Active power loss can be determined as Equation (5).
4.1.1. The Objective Function and Constraints
The objective function of this optimization problem is aimed at minimizing distribution losses and guaranteeing distribution quality. It can be formulated as follows:
Objective Function
Equation (6) represents the minimization of distribution losses as a function of BESS active and reactive powers, photovoltaic reactive power, home BESS reactive power and LRT and SVR tap positions, respectively. This objective function is used for all cases and all operation modes.
Constraints
Equations (7)–(9) represent technical constraints; these are the voltage constraints of the distribution system, the active power flow constraints and the reactive power constraints, respectively. The bandwidth of the voltage and active power flow have already been mentioned in Section 2.
These are the constraints of the large capacity BESS inverter, considering the charging and discharging losses of the BESS for each power constraint and the SOC constraints to suppress rapid degradation of the BESS, as shown in Equations (10)–(12), respectively.
The PV inverter capacity used for cooperative operations can be described as Equation (13). The constraints of the cooperative operation of reactive power from the home BESSs is determined as shown in Equation (14). In this paper, the active power of the home BESSs is not injected into the smart grid in order to secure usage for the homes.
This constraint of Equation (15) relates to the LRT’s and the SVR’s tap position constraints.
5. Adaptive Inertia Weight PSO Method for the Decision Making of the Optimal Operation Schedule
There are many methods to solve optimization problems. Among these, the PSO method was selected to solve the power system optimization problem [27,28]. This meta-heuristics method is known for its feature of having a simple algorithm and high extendibility. For this reason, this method is applied to many problems. Moreover, it is applied to nonlinear problems, such as the complex power system optimization problem. In this paper, a modified PSO method is demonstrated for finding a solution of the mentioned problem, including CP. The conventional PSO and adaptive inertia weight (AIW) function are provided in the following section.
5.1. Particle Swarm Optimization
The PSO is modeled after the actions that flocks of birds perform to find the path to food through cooperation. By these actions, the search space becomes very wide, and it becomes easy to find a global optimization value. The PSO algorithm is as follows:
- Step 1:
- Generate an initial searching point for each swarm.
- Step 2:
- Evaluate the objective function using each swarm’s searching point.
- Step 3:
- Finish searching if the stopping conditions are satisfied. If not, go to Step 4.
- Step 4:
- Search the next point considering the best of the current swarm’s searching points, as well as each swarm’s best searching point. Go to Step 2.
The searching algorithm communicates information about the best positions to all swarms, and each continues updating its own positions and velocities until searching is finished. The action is given by the following equations:
5.2. Flexible Inertia Strategy of PSO
Generally, the PSO weight is determined at the first step in the initialization. The searching area and accuracy of solutions depend on the best local solutions and the weight function. In order to improve and expand the searching area and increase the accuracy of the solution, an AIW function is applied to the PSO algorithm as a flexible inertia strategy. The AIW function is given by Equations (18) and (19):
Swarm acceleration is adjusted by the adaptive inertia function. As the objective function value improves, the AIW value becomes smaller. This way, the AIW function helps to find a more accurate solution than the conventional PSO method.
5.3. Scheduling Method for Reconfiguration
An optimized schedule will help the system operator maintain system security. In order to evaluate the system and make an optimal schedule, the one day-ahead scheduling method is applied from previous studies [11]. It is more desirable that the optimized operation schedule for a 24-h period is calculated in one optimization iteration. However, considering a realistic model and a multitude of variables, the 24-h calculation becomes a heavy load for the computer. Furthermore, the aforementioned problem includes a CP (i.e., the LPC reconfiguration). In order to solve this difficulty, much of the literature applies a scheduling method for one hour-ahead scheduling. This algorithm makes an optimal schedule at a given time period; usually, this time period is one hour. After making the one period scheduling, this algorithm will run at the next period to optimize and update the schedule. Thus, the solution is optimal for the chosen target period. This system might not optimize the schedule for a full day term. The scheduling method is dependent on a previous step in time, if the algorithm holds two candidate solutions, only one is the best solution in the target period. The other solution is often compromised only by a small amount in comparison to the best solution. Naturally, the conventional scheduling method choice is often the best solution; however, a compromise solution may lead to a better solution for the full day in the long run. This is because the conventional process uses only target period information.
Therefore, this paper proposes a new method, which is a form of dual scheduling. A conceptual diagram of the method is shown in Figure 3. This method uses two schemes, the conventional one hour scheduling method (SC1) and a once-every-two-hour scheduling method (SC2), simultaneously. It is difficult to achieve convergence using only SC1, because the previous values of the variables for the target period might not be good even if the solution has been optimized at a previous period. Moreover, the SC1 method often leads to over control and unnecessary operations. A dual scheduling method can compensate these problems. It can increase the likelihood of convergence, and it will avoid over control.
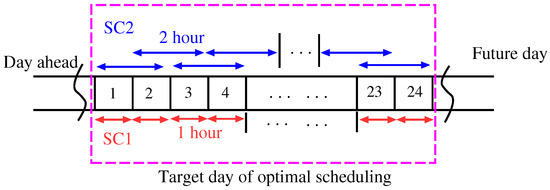
Figure 3.
Scheduling method for optimal scheduling.
6. Simulation Results
6.1. Simulation Model
In this research, a common type of radial distribution system is used, as shown in Figure 4, in order to verify the effects of the BESS and the active smart grid system. Each system model is represented as shown in the section of the case studies. PV generation systems are installed for more than half of the customers: the simulated output of one of these is shown in Figure 5a. In order to simplify the analysis, the forecast error of PV output and load demand is not assumed. The customers comprise two areas. One of these areas is a residential area; the other is an office area. Their load usage is completely different, as shown in Figure 5b. A high penetration of DGs is assumed in this research. From these loads and the amount of PV output, voltage deviation and reverse power flow are caused without control. The BESS capacity standard is shown in Table 1.
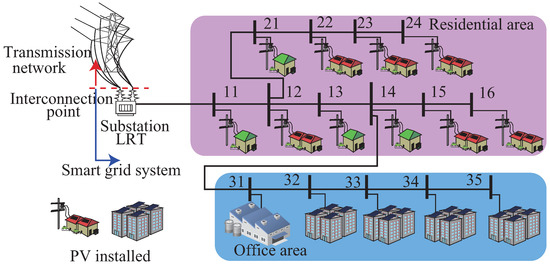
Figure 4.
Model of the distribution system.
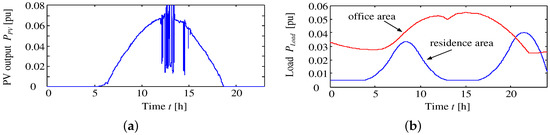
Figure 5.
PV output and load demand. (a) PV output and (b) load demand of each area.

Table 1.
Parameters of the distribution system.
Three cases are demonstrated to confirm the effectiveness of the BESS and the active smart grid system using an LPC as a case study. The simulation conditions of the case study are summarized in Table 2 and as follows:

Table 2.
Case study contents.
- Case 1:
- BESS 1 is installed at the interconnection point to protect the upper high voltage system from reverse power flow. BESS 2 is installed in a branched office area as an emergency energy storage. In this case, BESS management is simulated in two modes of operation: operation Mode 1 is normal operation without a fault. On the other hand, when a disconnection fault occurs in the office area of Figure 6, islanding is applied by using BESS 2 as a power supply. As control devices for active and reactive power supply, BESS 1, BESS 2, LRT, SVR, SVC and inverters interfacing with the PVs are used. The results of each mode in Case 1 are provided in Figure 7 and Figure 8.
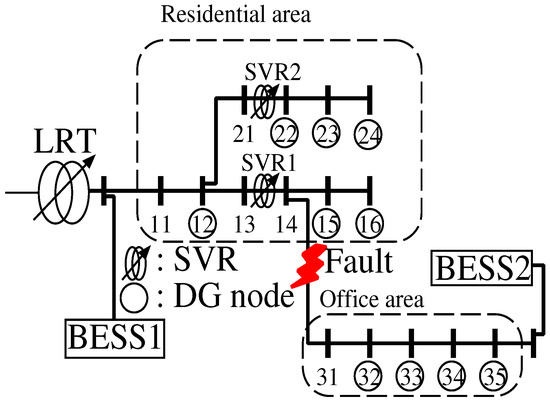 Figure 6. Model of the distribution system for Case 1.
Figure 6. Model of the distribution system for Case 1.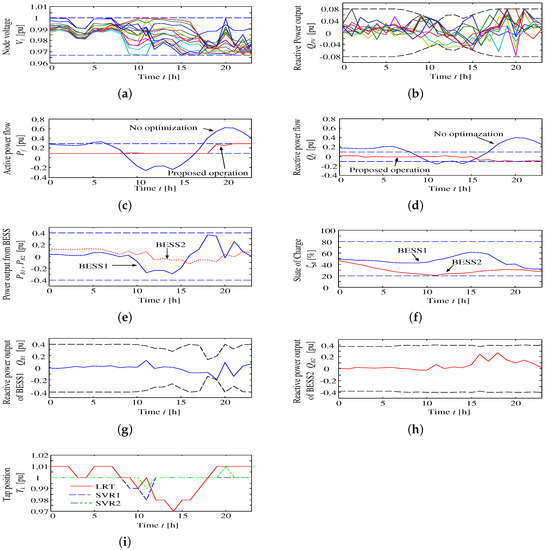 Figure 7. Simulation results of Case 1 without fault (operation Mode 1); all control devices’ operations are listed as: (a) node voltage; (b) reactive power output by inverters interfacing the PV; (c) active power flow at the interconnection point; (d) reactive power flow at the interconnection point; (e) active power output of each large BESS; (f) states of charge of each large BESS; (g) reactive power output of BESS 1; (h) reactive power output of BESS 2; and (i) tap positions of the LRTs and SVRs.
Figure 7. Simulation results of Case 1 without fault (operation Mode 1); all control devices’ operations are listed as: (a) node voltage; (b) reactive power output by inverters interfacing the PV; (c) active power flow at the interconnection point; (d) reactive power flow at the interconnection point; (e) active power output of each large BESS; (f) states of charge of each large BESS; (g) reactive power output of BESS 1; (h) reactive power output of BESS 2; and (i) tap positions of the LRTs and SVRs.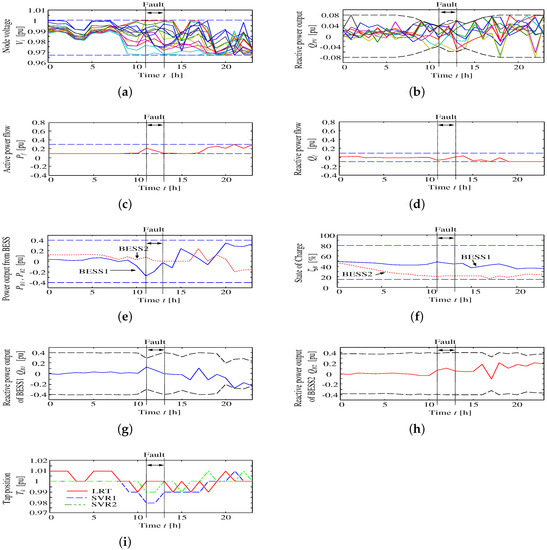 Figure 8. Simulation results during fault in Case 1: (a) node voltage; (b) reactive power output of inverters interfacing the PVs; (c) active power flow at the interconnection point; (d) reactive power flow at the interconnection point; (e) active power output of each large BESS; (f) states of charge of each large BESS; (g) reactive power output of BESS1; (h) reactive power output of BESS2; and (i) tap positions of LRT and SVRs.
Figure 8. Simulation results during fault in Case 1: (a) node voltage; (b) reactive power output of inverters interfacing the PVs; (c) active power flow at the interconnection point; (d) reactive power flow at the interconnection point; (e) active power output of each large BESS; (f) states of charge of each large BESS; (g) reactive power output of BESS1; (h) reactive power output of BESS2; and (i) tap positions of LRT and SVRs. - Case 2:
- In this case, LPCs are installed instead of BESSs in a fault situation. Moreover, the home BESS is introduced in DG nodes to supply reactive power. A three line disconnection fault will be considered. The fault locations and some examples of active smart grid configurations are shown in Figure 9 and Figure 10, respectively. The comparison of active smart grid is presented as Figure 11, Figure 12, and Table 3. To note this case, LPCs run only in fault conditions.
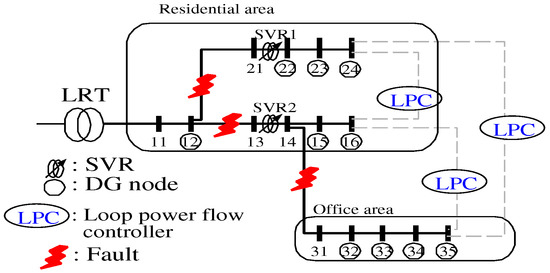 Figure 9. Model of the distribution system for Case 2.
Figure 9. Model of the distribution system for Case 2.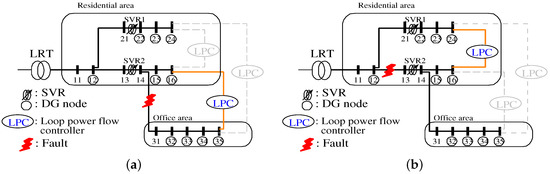 Figure 10. Examples of the active smart grid system: (a) end Node 16 is connected to end Node 35 in Case 2 (i); and (b) end Node 16 is connected to end Node 24 of the office area in Case 2 (v).
Figure 10. Examples of the active smart grid system: (a) end Node 16 is connected to end Node 35 in Case 2 (i); and (b) end Node 16 is connected to end Node 24 of the office area in Case 2 (v).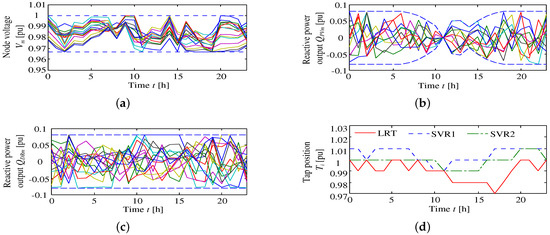 Figure 11. Simulation results of Case 2 (0): (a) node voltages; (b) reactive power outputs from interfacing inverter of the PV; (c) reactive power output by demand response; and (d) tap positions of LRT and SVRs.
Figure 11. Simulation results of Case 2 (0): (a) node voltages; (b) reactive power outputs from interfacing inverter of the PV; (c) reactive power output by demand response; and (d) tap positions of LRT and SVRs.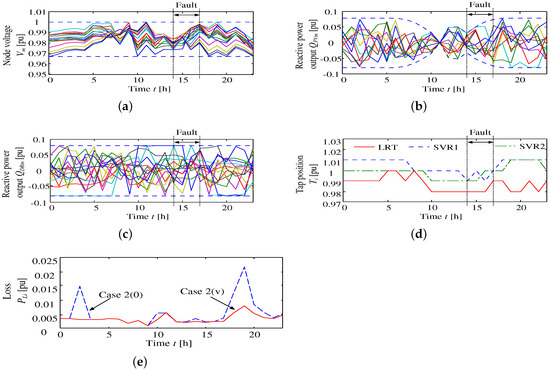 Figure 12. Simulation results considering a line fault in Case 2 (v): (a) node voltages; (b) reactive power output from the inverter interfacing the PV; (c) reactive power output by demand response; (d) tap position of LRT and SVRs; and (e) comparison of distribution losses.
Figure 12. Simulation results considering a line fault in Case 2 (v): (a) node voltages; (b) reactive power output from the inverter interfacing the PV; (c) reactive power output by demand response; (d) tap position of LRT and SVRs; and (e) comparison of distribution losses. Table 3. Simulation pattern of Case 2.
Table 3. Simulation pattern of Case 2. - Case 3:
- The six LPCs are installed in the smart grid system as shown in Figure 13. Case 3 is different from Case 2 in that the system configuration will be changed in real time as a one-hour step. A reconfiguration operation of the active smart grid is optimized to minimize distribution losses. In order to solve the complex optimization including CP, a dual scheduling method is applied to the system.
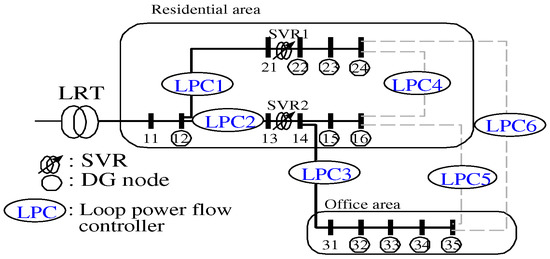 Figure 13. Model of the distribution system for Case 3.
Figure 13. Model of the distribution system for Case 3.
The optimal operations of all case studies are solved with the AIWPSO method.
6.2. Case Studies
6.2.1. Case 1: BESSs Management
In Case 1, first, the optimal schedule is made using the optimization method without a fault occurrence. The result is shown in Figure 7. From Figure 7c,d, these values represent active and reactive power flow at the interconnection point, respectively. It can be confirmed that there is a violation of the upper and lower bounds. However, in the optimized operation of normal mode without a fault, all node voltages, active power flow and reactive power flow are suppressed and kept within the proper ranges. From the voltage results of Figure 7a, the voltage is maintained in order to compensate instant DG output changes. The results prove an effective operation schedule in the normal operation mode.
The second operation is shown in Figure 8. The result of operation Mode 1 shows the minimum SOC of the BESS at 11 o’clock in Figure 7f. In order to consider strict conditions, a disconnection accident of the distribution line occurs at 11 o’clock, and the fault continues for 3 h. The disconnection accident occurs between Nodes 14 and 31. During the fault, the office area is disconnected from the main distribution line, and power is supplied by BESS 2 as an emergency source assuming isolated operation. The fault simulation result of Case 1 is shown in Figure 8. From the results, it can be confirmed that all values and constraints are maintained within the proper range. Especially, node voltages are representative of the prevention of local outages in the office area. Moreover, it has been made possible to supply energy by using BESS 2 and PV output without changes in load demand consumption for the isolated operation term. The reactive power of BESSs 1 and 2 and the PV inverter output are used for voltage control. Tap control of LRT and SVR is also provided for voltage control. It was possible to avoid reverse power flow, as seen in Figure 8d.
However, the disadvantage of the BESS is that if a disconnected area does not contain a BESS, it is impossible to respond to a disconnection fault. Thus, in order to consider this, the next case simulation will be considered as a mesh smart grid configuration by using LPCs instead of the installation of BESSs.
6.2.2. Case 2: Prevention of Local Outage by LPC Operation
In this case, in order to verify an active smart grid system, LPCs are installed at each end-node as, shown in Figure 9. These are placed between Nodes 16 and 24, 24 and 35 and 35 and 16. A disconnection fault occurs at either 11 or 14 o’clock and may happen between Nodes 12 and 21, 12 and 13 or 14 and 31. A total of 12 patterns for the active smart grid system is tested in the case study. Distribution losses of each case are written in Table 3. One configuration example of the active smart grid system of Case 2 (i) is shown in Figure 10a from Table 3. The described configuration pattern is demonstrated by the AIWPSO method; the optimized distribution losses are listed in Table 3. From the results, it can be confirmed that Case 2 (v) and Case 2 (xi) represent the minimum distribution losses of 438.5 (kWh) and 450.8 (kW) in active system fault, respectively. Moreover, each optimal operation of Case 2 (0) and Case 2 (v) are shown in Figure 11 and Figure 12, respectively. The conditions of Case 2 (0) are such that there is no fault, and the reconfiguration operation is not executed for comparison with other operations. Case 2 (0) operation can maintain all constraints. Furthermore, when a disconnection fault occurs between Hours 14–17 in Case 2 (v), it can be confirmed from the voltage values that power is safely supplied. In order to suppress the voltage deviation, reactive power output from the home BESS is used for demand response. Therefore, in the case of fault, continued operation without an outage can be achieved when the demand side is disconnected from the main distribution line connected using LPCs as an active smart grid system.
On the other hand, from Table 3, it can be seen that Case 2 (v) has smaller losses than those of Case 2 (0). Intuitively, regardless of the absence or occurrence of a fault, reconfiguration seems to be beneficial. This is further demonstrated in Case 3.
6.2.3. Case 3: Optimal Active Smart Grid System Design Using LPCs
The prevention of power outage by using LPCs is discussed in Case 2. In this case, in order to search for an optimal operation schedule for the active smart grid system and to demonstrate effectiveness, the active smart grid shape will be changed each time step (e.g., 1, 2, ⋯, 24) in real time. The active smart grid patterns are considered heptagonal shown in Figure 13, and these distribution system operations are optimized through a period of 24 h. Some examples of active smart grid configurations and the result of fixed system configurations are shown in Figure 14 and Table 4, and Case 3 (vi) represents the optimal operation in a fixed configuration of the smart grid for which the optimal scheduling is shown in Figure 15. However, the optimal active smart grid shape is different for each hour, when the distribution system changed, as shown in Table 5; optimal operation is shown in Figure 16, which achieves more than that of a fixed distribution line through one day of operation from a power loss reduction point of view.
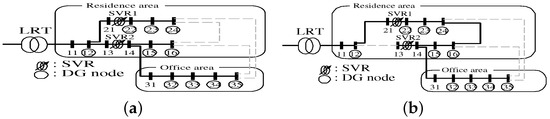
Figure 14.
Examples of the distribution system configuration in Case 3 illustrated as: (a) the reconstructed distribution model of Case 3 (i); and (b) the reconstructed distribution model of Case 3 (vi) listed in Table 4.

Table 4.
Minimum distribution losses of the fixed connecting point of LPCs.
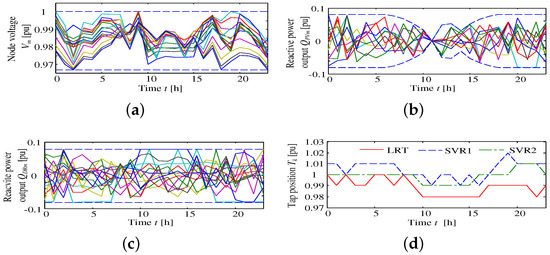
Figure 15.
Simulation results of Case 3 (vi): (a) node voltages; (b) reactive power output from the inverter interfacing the PV; (c) reactive power output by demand response; and (d) tap positions of LRT and SVRs. Note that the reconstruction distribution system of Case 3 (vi) represents the most reduced distribution losses.

Table 5.
Proposed active smart grid network.
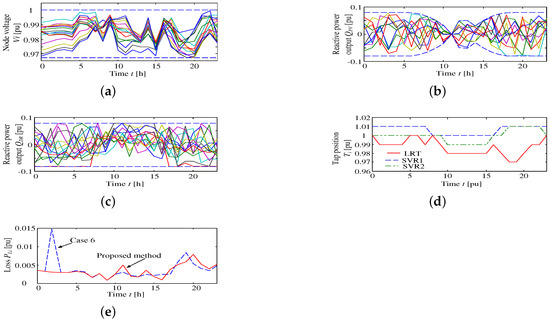
Figure 16.
Simulation results of the proposed method of Case 3: (a) node voltages; (b) reactive power output from inverter interfacing the PV; (c) reactive power output by demand response; (d) tap positions of LRT and SVRs; and (e) comparison of distribution losses.
The dual scheduling algorithm is applied to the Case 3 reconfiguration operation; when the algorithm is not applied to the optimization, convergence to a solution was not possible. Furthermore, the comparison of the results of the proposed optimization method is provided in Figure 17. It can be seen that AIEPSO has a faster convergence and better objective function value than the convectional PSO method. Moreover, the computational calculation time of AIWPSO and PSO takes 21,322 (s) and 38,467 (s), respectively. The proposed method achieves a time savings of 44.6%. This leads to the reduction of both the calculation time and heavy loads.
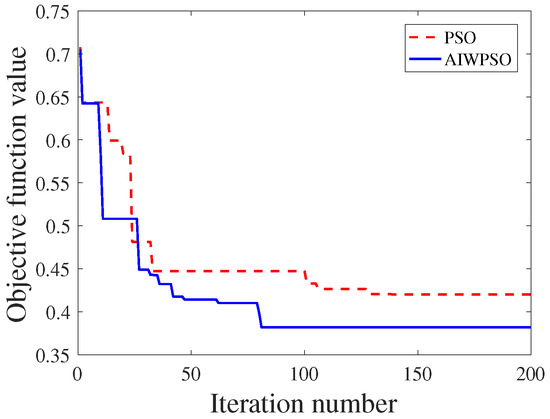
Figure 17.
Comparison of the convergence performance.
7. Conclusions
In this paper, the effectiveness of a BESS, an LPC and the reactive power control of DR with a home BESS is verified through case studies with high penetrations of DGs using PV and heavy loads. Reactive power control using a BESS and customer side cooperative operation increases the power quality and prevents voltage deviation. Moreover, the simulation of the fault conditions proves that it is possible to continue supplying energy during fault occurrences using emergency BESS or temporarily rebuilding the smart grid system with LPCs. From the results, the best smart grid design options of the BESS and LPCs are provided. Otherwise, the simulation of an active smart grid system using LPCs in ordinal conditions represents an optimal reconstruction of the system and the optimal operation of control devices. Minimum distribution losses are demonstrated by an active smart grid system in the case studies. The effectiveness of the dual scheduling algorithm and proposed AIWPSO are proven by numerical simulation data.
Author Contributions
Ryuto Shigenobu (R.S.): Has done the major work of the paper, from the conception of the problem, topology and systems configuration including writing the article. Ahmad Samim Noorzad (A.S.N.): Has suggested the control devices (LRT and SVR) to be used to prevent the power system outages and its allocation problem by mean of PSO algorithm. Cirio Muarapaz (C.M.): Has suggested the Modeling and optimization Method for the reactive power control by mean of inverters interfaced with distributed generators and the house battery energy storage system. Atsushi Yona (A.Y.): Has contributed on the optimal operation schedule using the Adaptive Inertia Weight Particle Swarm Optimization Tomonobu Senjyu (T.S.): Helped in analyzing the data used and judging the simulation results from the different proposed methodologies.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| AIW | Adaptive inertia weight |
| BESS | Battery energy storage system |
| CP | Combinatorial problem |
| DG | Distributed generator |
| DisCo | Distribution company |
| EV | Electric vehicle |
| LRT | Load ratio transformer |
| MPPT | Maximum power point tracking |
| NAS | Liquid sodium (Na) and sulfur (S) |
| PSO | Particle swarm optimization |
| PV | Photovoltaic |
| RES | Renewable energy source |
| SOC | State of charge |
| SVC | Static var compensator |
| SVR | Step voltage regulator |
| WG | Wind turbine generator |
| η | Charging and discharging efficiency of large BESS. |
| LPCs connection set. | |
| ζ | SOC of house BESSs, BESS and EVs. |
| Imaginary part of admittance . | |
| Weight for the position of the current best particle. | |
| Weight for the best position of the particle swarm. | |
| Capacity of large BESS. | |
| Real part of admittance . | |
| Best position of the particle swarm. | |
| Adjustment value of the inertia weight at generation h. | |
| Particle number n at generation h. | |
| Node number of the distribution system. | |
| Active power flow at the interconnection point. | |
| Lower and upper limit of the active power flow at the interconnection point. | |
| Active power from the k node generator. | |
| Load demand at the k node. | |
| Order value of the active power output of BESS from DisCo. | |
| Lower and upper limit of the active power of large BESS inverter. | |
| Active power output of large BESS. | |
| Distribution loss at node i. | |
| Active power loss of node i. | |
| Active power output from the PV generator system. | |
| Active power output from the PV panel. | |
| Position of the current best particle. | |
| Reactive power output of inverters interfaced with home BESS. | |
| Lower and upper limit of the home battery inverter regarding reactive power output. | |
| Reactive power flow at the interconnection point. | |
| Lower and upper limit of the reactive power flow at the interconnection point. | |
| Reactive power from the k node generator. | |
| Load demand at the k node. | |
| Reactive power output of large BESS. | |
| Order value of the reactive power output of BESS from DisCo. | |
| Lower and upper limit of the reactive power output of large BESS inverter. | |
| Reactive power output of inverters interfaced with PV. | |
| Order value of reactive power. | |
| Lower and upper limit of the PV inverter regarding reactive power output. | |
| Resistance between node k and i. | |
| Uniform random numbers from 0–1. | |
| Search position of the i-th particle in the h-th search. | |
| Inverter capacity of large BESS. | |
| Inverter capacity of the PV inverter. | |
| t | Time step at optimization. |
| Tap positions of LRT and SVR. | |
| Lower and upper tap limit of LRT and SVRs. | |
| i-th particle velocity in the -th search. | |
| Minimum and maximum of the voltage constraints. | |
| Node voltage at node m. | |
| w | Weight of inertia. |
| Updated inertia weight value. |
References
- Han, J.; Sic Choi, C.; Park, W.-K.; Lee, I.; Kim, S.-H. Smart home energy management system including renewable energy based on zigbee and plc. IEEE Trans. Consum. Electron. 2014, 60, 198–202. [Google Scholar] [CrossRef]
- Smith, J.; Sunderman, W.; Dugan, R.; Seal, B. Smart inverter volt/var control functions for high penetration of pv on distribution systems. In Proceedings of the 2011 IEEE/PES Power Systems Conference and Exposition (PSCE), Phoenix, AZ, USA, 20–23 March 2011; pp. 1–6.
- Tsubasa, S.; Hayato, T.; Hidehito, M.; Atsushi, Y.; Tomonobu, S. Comparison and Validation of Operational Cost in Smart Houses with the Introduction of a Heat Pump or a Gas Engine. Int. J. Emerg. Electr. Power Syst. 2015, 16, 59–74. [Google Scholar]
- Shimoji, T.; Tahara, H.; Matayoshi, H.; Yona, A.; Senjyu, T. Optimal Scheduling Method of Controllable Loads in DC Smart Apartment Building. Int. J. Emerg. Electr. Power Syst. 2015, 16, 579–589. [Google Scholar] [CrossRef]
- Howlader, H.O.R.; Matayoshi, H.; Senjyu, T. Thermal Units Commitment Integrated with Reactive Power Scheduling for the Smart Grid Considering Voltage Constraints. Int. J. Emerg. Electr. Power Syst. 2015, 16, 323–330. [Google Scholar] [CrossRef]
- Woyte, A.; van Thong, V.; Belmans, R.; Nijs, J. Voltage fluctuations on distribution level introduced by photovoltaic systems. IEEE Trans. Energy Convers. 2006, 21, 202–209. [Google Scholar] [CrossRef]
- Iyer, S.V.; Wu, B.; Li, Y.; Singh, B. A Mathematical Model to Predict Voltage Fluctuations in a Distribution System with Renewable Energy Sources. Int. J. Emerg. Electr. Power Syst. 2015, 16, 549–557. [Google Scholar] [CrossRef]
- Rao, B.N.; Abhyankar, A.R.; Nilanjan, S. DG Planning with Amalgamation of Operational and Reliability Considerations. Int. J. Emerg. Electr. Power Syst. 2016, 17, 131–141. [Google Scholar]
- Hojo, M.; Hatano, H.; Fuwa, Y. Voltage rise suppression by reactive power control with cooperating photovoltaic generation systems. In Proceedings of the 20th International Conference and Exhibition on Electricity Distribution—Part 2, CIRED 2009, Prague, Czech, 8–11 June 2009; p. 1.
- Hatta, H.; Uemura, S.; Kobayashi, H. Cooperative control of distribution system with customer equipments to reduce reverse power flow from distributed generation. In Proceedings of the 2010 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2010; pp. 1–6.
- Ziadi, Z.; Taira, S.; Oshiro, M.; Funabashi, T. Optimal power scheduling for smart grids considering controllable loads and high penetration of photovoltaic generation. IEEE Trans. Smart Grid 2014, 5, 2350–2359. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, J. The energy management and optimized operation of electric vehicles based on microgrid. IEEE Trans. Power Deliv. 2014, 29, 1427–1435. [Google Scholar] [CrossRef]
- Choudar, A.; Boukhetala, D.; Barkat, S.; Brucker, J.-M. A local energy management of a hybrid pv-storage based distributed generation for microgrids. Energy Convers. Manag. 2015, 90, 21–33. [Google Scholar] [CrossRef]
- Momoh, J.A.; Reddy, S.S. Feasibility of Stochastic Voltage/VAr Optimization Considering Renewable Energy Resources for Smart Grid. Int. J. Emerg. Electr. Power Syst. 2016, 17, 287–300. [Google Scholar] [CrossRef]
- Khederzadeh, M.; Khalili, M. High Penetration of Electrical Vehicles in Microgrids: Threats and Opportunities. Int. J. Emerg. Electr. Power Syst. 2014, 15, 457–469. [Google Scholar] [CrossRef]
- Minh, B.D.; Shi-Lin, C.; Keng-Yu, L.; Jheng-Lun, J. A Generalised Fault Protection Structure Proposed for Uni-grounded Low-Voltage AC Microgrids. Int. J. Emerg. Electr. Power Syst. 2016, 17, 69–89. [Google Scholar]
- Karan, S.; Bhalja, B.R.; Prakash, M.R. Evaluation of Superimposed Sequence Components of Currents based Islanding Detection Scheme during DG Interconnections. Int. J. Emerg. Electr. Power Syst. 2016, 17, 1–14. [Google Scholar]
- Okada, N.; Kobayashi, H.; Takigawa, K.; Ichikawa, M.; Kurokawa, K. Loop power flow control and voltage characteristics of distribution system for distributed generation including pv system. In Proceedings of 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; Volume 3, pp. 2284–2287.
- Thatte, A.; Ilic, M. An assessment of reactive power/voltage control devices in distribution networks. In Proceedings of 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 8.
- Han, X.; Sandels, C.; Zhu, K.; Nordström, L. Modelling framework and the quantitative analysis of distributed energy resources in future distribution networks. Int. J. Emerg. Electr. Power Syst. 2013, 14, 421–431. [Google Scholar] [CrossRef]
- Reddy, S.S.; Hwan, L.Y. Optimum Location of Voltage Regulators in the Radial Distribution Systems. Int. J. Emerg. Electr. Power Syst. 2016, 17, 351–361. [Google Scholar]
- Ryuto, S.; Samim, N.A.; Cirio, M.; Atsushi, Y.; Tomonobu, S. Optimal Operation and Management for Smart Grid Subsumed High Penetration of Renewable Energy, Electric Vehicle, and Battery Energy Storage System. Int. J. Emerg. Electr. Power Syst. 2016, 17, 173–189. [Google Scholar]
- Wang, J.-C.; Chiang, H.-D.; Miu, K.; Darling, G. Capacitor placement and real time control in large-scale unbalanced distribution systems: loss reduction formula, problem formulation, solution methodology and mathematical justification. In Proceedings of the 1996 IEEE Transmission and Distribution Conference, Los Angeles, CA, USA, 15–20 September 1996; pp. 236–241.
- Roy, P.; Ghoshal, S.; Thakur, S. Optimal var control for improvements in voltage profiles and for real power loss minimization using biogeography based optimization. Int. J. Electr. Power Energy Syst. 2012, 43, 830–838. [Google Scholar] [CrossRef]
- Song, I.-K.; Jung, W.-W.; Kim, J.-Y.; Yun, S.-Y.; Choi, J.-H.; Ahn, S.-J. Operation schemes of smart distribution networks with distributed energy resources for loss reduction and service restoration. IEEE Trans. Smart Grid 2013, 4, 367–374. [Google Scholar] [CrossRef]
- Tomic, S. Economic effects of trading watts and negawatts by agile customers in hierarchic energy markets. In Proceedings of the 2012 9th International Conference on the European Energy Market (EEM), Florence, Italy, 10–12 May 2012; pp. 1–6.
- Mostafa, H.E.; El-Sharkawy, M.A.; Emary, A.A.; Yassin, K. Design and allocation of power system stabilizers using the particle swarm optimization technique for an interconnected power system. Int. J. Electr. Power Energy Syst. 2012, 34, 57–65. [Google Scholar] [CrossRef]
- Al-Saedi, W.; Lachowicz, S.W.; Habibi, D.; Bass, O. Power quality enhancement in autonomous microgrid operation using particle swarm optimization. Int. J. Electr. Power Energy Syst. 2012, 42, 139–149. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).