Impacts on CO2 Emission Allowance Prices in China: A Quantile Regression Analysis of the Shanghai Emission Trading Scheme
Abstract
:1. Introduction
2. Materials and Methods
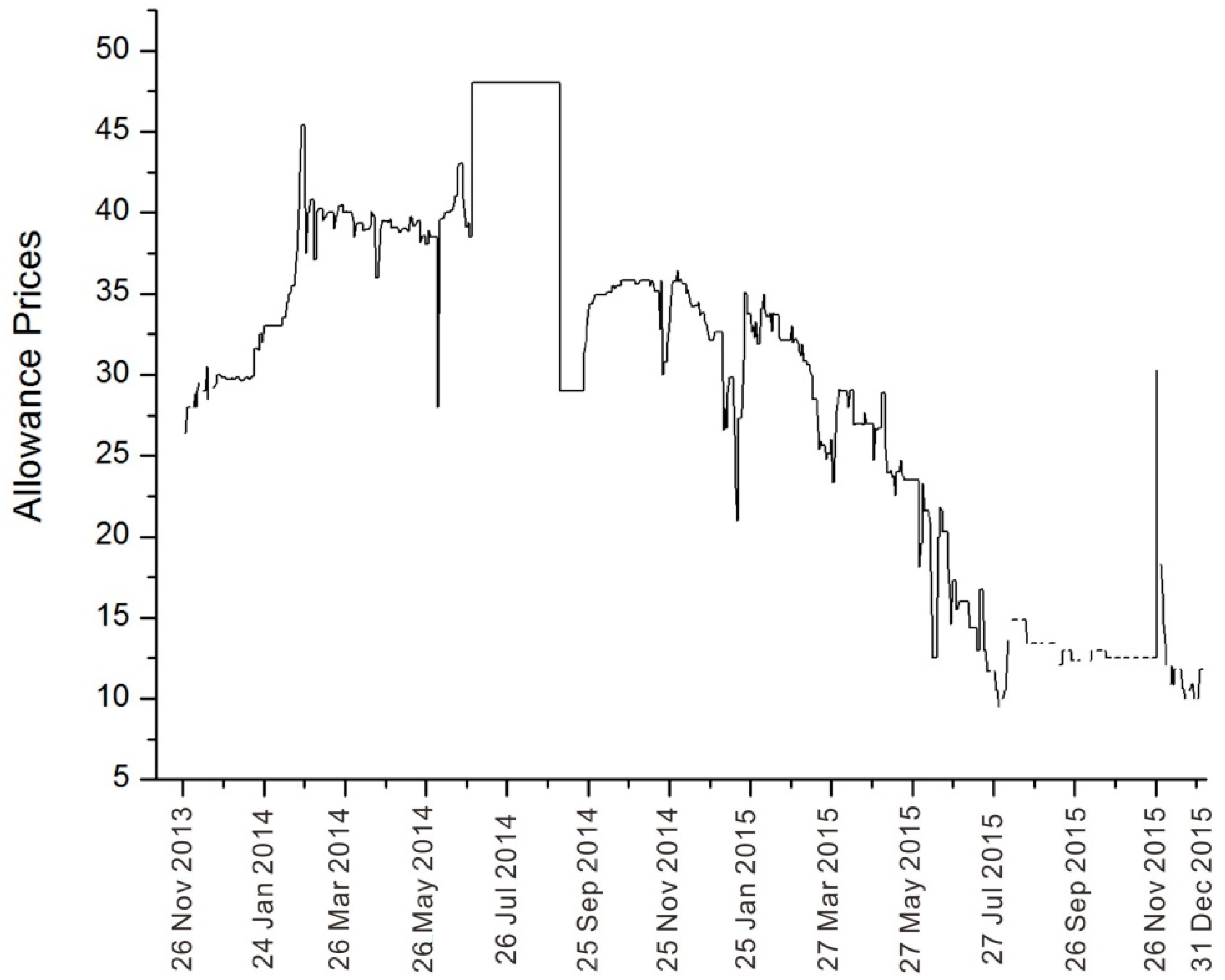
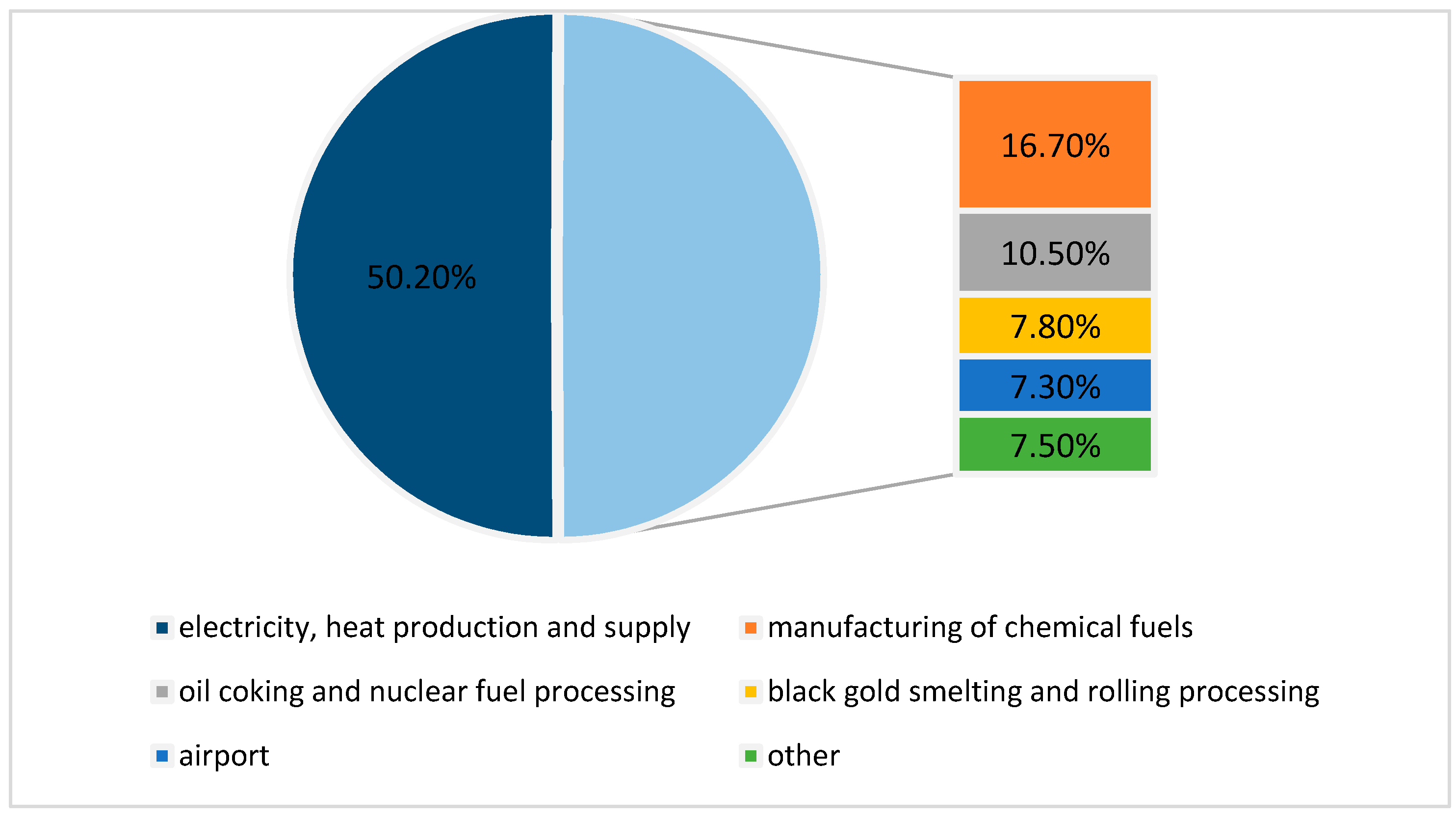
2.1. Data
2.2. Methodology
3. Results and Discussion
4. Conclusions and Policy Implications
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SH-ETS | Shanghai Emission Trading Scheme |
| SHEA | Shanghai Emission Allowances |
| CDS | Clean Dark Spreads |
| CSS | Clean Spark Spreads |
| VAR | Vectorial Autoregression |
References
- Du, L.; Hanley, A.; Wei, C. Estimating the marginal abatement cost curve of CO2 emissions in China: Provincial Panel Data Analysis. Energy Econ. 2015, 48, 217–229. [Google Scholar] [CrossRef]
- Du, L.; Mao, J. Estimating the environmental efficiency and marginal CO2 abatement cost of coal-fired power plants in China. Energy Policy 2015, 85, 347–356. [Google Scholar] [CrossRef]
- Zhou, X.; Fan, L.W.; Zhou, P. Marginal CO2 abatement costs: Findings from alternative shadow price estimates for Shanghai industrial sectors. Energy Policy 2015, 77, 109–117. [Google Scholar] [CrossRef]
- Mansanet-Bataller, M.; Pardo, Á. What you should know about carbon markets. Energies 2008, 1, 120–153. [Google Scholar] [CrossRef]
- Hintermann, B. Allowance price drivers in the first phase of the EU ETS. J. Environ. Econ. Manag. 2010, 59, 43–56. [Google Scholar] [CrossRef]
- China’s Carbon Emission Website. Available online: http://www.tanpaifang.com/ (accessed on 28 September 2016). (In Chinese)
- Shanghai Bureau of Statistical. Shanghai Statistical Yearbook, 2015; China Statistics Press: Beijing, China, 2015. (In Chinese)
- Fezzi, C.; Bunn, D.W. Structural interactions of European carbon trading and energy prices. J. Energy Markets 2009, 2, 53. [Google Scholar] [CrossRef]
- Kim, H.S.; Koo, W.W. Factors affecting the carbon allowance market in the US. Energy Policy 2010, 38, 1879–1884. [Google Scholar] [CrossRef]
- Chevallier, J. Time-varying correlations in oil, gas and CO2 prices: An application using BEKK, CCC and DCC-MGARCH models. Appl. Econ. 2012, 44, 4257–4274. [Google Scholar] [CrossRef]
- Hammoudeh, S.; Lahiani, A.; Nguyen, D.K.; Sousa, R.M. Asymmetric and Nonlinear Pass-Through of Energy Prices to CO2 Emission Allowance Prices. Available online: http://repositorium.sdum.uminho.pt/handle/1822/28105 (assessed on 2 November 2016).
- Hammoudeh, S.; Nguyen, D.K.; Sousa, R.M. What explain the short-term dynamics of the prices of CO2 emissions? Energy Econ. 2014, 46, 122–135. [Google Scholar] [CrossRef]
- Keppler, J.H.; Mansanet-Bataller, M. Causalities between CO2, electricity, and other energy variables during phase I and phase II of the EU ETS. Energy Policy 2010, 38, 3329–3341. [Google Scholar] [CrossRef]
- Bredin, D.; Muckley, C. An emerging equilibrium in the EU emissions trading scheme. Energy Econ. 2011, 33, 353–362. [Google Scholar] [CrossRef]
- Wang, W.; Bai, L. A study of the impacting factors related to EUCA price. J. Yunnan Normal Univ. 2013, 45, 135–143. [Google Scholar]
- Delarue, E.D.; D’haeseleer, W.D. Price determination of ETS allowances through the switching level of coal and gas in the power sector. Int. J. Energy Res. 2007, 31, 1001–1015. [Google Scholar] [CrossRef]
- Creti, A.; Jouvet, P.A.; Mignon, V. Carbon price drivers: Phase I versus Phase II equilibrium? Energy Econ. 2012, 34, 327–334. [Google Scholar] [CrossRef]
- Rickels, W.; Duscha, V.; Keller, A.; Peterson, S. The determinants of allowance prices in the European emissions trading scheme: Can we expect an efficient allowance market 2008? Kiel Inst. World Econ. Work. Pap. 2007, 1387, 28. [Google Scholar]
- Mansanet-Bataller, M.; Pardo, A.; Valor, E. CO2 Prices, Energy and Weather. Energy J. 2007, 28, 73–92. [Google Scholar] [CrossRef]
- Alberola, E.; Chevallier, J.; Chèze, B. Price drivers and structural breaks in European carbon prices 2005–2007. Energy Policy 2008, 36, 787–797. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Z. The empirical research on price impact factors of Carbon Emission Exchange: Evidence from EU ETS. Syst. Eng. 2012, 2, 009. (In Chinese) [Google Scholar]
- Chen, X.; Hu, W.; Wang, Z. The empirical research on price impact factors of Carbon Exchange of Voluntary Market: Evidence from CCX of USA. Chin. J. Manag. Sci. 2013, 21, 74–81. (In Chinese) [Google Scholar]
- Christiansen, A.C.; Arvanitakis, A.; Tangen, K.; Hasselknippe, H. Price determinants in the EU emissions trading scheme. Clim. Policy 2005, 5, 15–30. [Google Scholar] [CrossRef]
- Chevallier, J. Evaluating the carbon-macroeconomy relationship: Evidence from threshold vector error-correction and Markov-switching VAR models. Econ. Model. 2011, 28, 2634–2656. [Google Scholar] [CrossRef]
- Chevallier, J. A model of carbon price interactions with macroeconomic and energy dynamics. Energy Econ. 2011, 33, 1295–1312. [Google Scholar] [CrossRef]
- Sousa, R.; Conraria, L.A. Dynamics of CO2 Price Drivers. Available online: http://repositorium.sdum.uminho.pt/handle/1822/27956 (assessed on 2 November 2016).
- Hammoudeh, S.; Nguyen, D.K.; Sousa, R.M. Energy prices and CO2 emission allowance prices: A quantile regression approach. Energy Policy 2014, 70, 201–206. [Google Scholar] [CrossRef]
- Tansel, A.; Bodur, F.B. Wage inequality and returns to education in Turkey: A quantile regression analysis. Rev. Dev. Econ. 2012, 16, 107–121. [Google Scholar] [CrossRef]
- Azam, M. Changes in wage structure in urban India, 1983–2004: A quantile regression decomposition. World Dev. 2012, 40, 1135–1150. [Google Scholar] [CrossRef]
- Xia, Q.; Song, L.; Li, S.; Appleton, S. The effect of the state sector on wage inequality in urban China: 1988–2007. J. Chin. Econ. Bus. Stud. 2014, 12, 29–45. [Google Scholar] [CrossRef]
- Zhao, H. Dynamic relationship between exchange rate and stock price: Evidence from China. Res. Int. Bus. Financ. 2010, 24, 103–112. [Google Scholar] [CrossRef]
- Lin, C.H. The comovement between exchange rates and stock prices in the Asian emerging markets. Int. Rev. Econ. Financ. 2012, 22, 161–172. [Google Scholar] [CrossRef]
- Tsagkanos, A.; Siriopoulos, C. A long-run relationship between stock price index and exchange rate: A structural nonparametric cointegrating regression approach. J. Int. Financ. Markets Inst. Money 2013, 25, 106–118. [Google Scholar] [CrossRef]
- Zhu, H.; Guo, Y.; You, W.; Xu, Y. The heterogeneity dependence between crude oil price changes and industry stock market returns in China: Evidence from a quantile regression approach. Energy Econ. 2016, 55, 30–41. [Google Scholar] [CrossRef]
- Chen, W.; Lei, Y.; Jiang, Y. Influencing factors analysis of China’s iron import price: Based on quantile regression model. Resour. Policy 2016, 48, 68–76. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Uddin, G.S. Do financial stress and policy uncertainty have an impact on the energy and metals markets? A quantile regression approach. Int. Rev. Econ. Financ. 2016, 43, 284–298. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Jin, Y.L.; Chevallier, J.; Shen, B. The effect of corruption on carbon dioxide emissions in APEC countries: A panel quantile regression analysis. Technol. Forecast. Soc. Chang. 2016, 112, 220–227. [Google Scholar] [CrossRef]
- Xu, B.; Lin, B. A quantile regression analysis of China’s provincial CO2 emissions: Where does the difference lie? Energy Policy 2016, 98, 328–342. [Google Scholar] [CrossRef]
- National Bureau of Statistical of China. China Statistical Yearbook, 2015; China Statistics Press: Beijing, China, 2015. (In Chinese)
- China Weather Website. Available online: http://www.weather.com.cn/weather/101190101.shtml (accessed on 28 September 2016). (In Chinese)
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Koenker, R.; Hallock, K. Quantile regression: An introduction. J. Econ. Perspect. 2001, 15, 43–56. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Johansen, S. Statistical analysis of cointegration vectors. J. Econ. Dyn. Control 1988, 12, 231–254. [Google Scholar] [CrossRef]
- Durbin, J.; Watson, G.S. Testing for serial correlation in least squares regression: I. Biometrika 1950, 37, 409–428. [Google Scholar] [PubMed]
- Cochrane, D.; Orcutt, G.H. Application of least squares regression to relationships containing auto-correlated error terms. J. Am. Stat. Assoc. 1949, 44, 32–61. [Google Scholar]
- Das, J.K.; Chakraborty, G. The Hedging Performance of Commodity Futures in India: An Empirical Study on Some Agricultural Commodities. Int. J. Inf. Bus. Manag. 2015, 7, 162. [Google Scholar]
- Corcoran, P.; Griffin, E.; Arensman, E.; Fitzgerald, A.P.; Perry, I.J. Impact of the economic recession and subsequent austerity on suicide and self-harm in Ireland: An interrupted time series analysis. Int. J. Epidemiol. 2015. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.D.; Olson, D.L. Pricing of Carbon Emission Exchange in the EU ETS. Enterprise Risk Management in Finance; Palgrave Macmillan: London, UK, 2015; pp. 183–198. [Google Scholar]
- Hao, Y.; Liao, H.; Wei, Y.M. Is China’s carbon reduction target allocation reasonable? An analysis based on carbon intensity convergence. Appl. Energy 2015, 142, 229–239. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, B.; Liu, T. Empirical analysis on the factors influencing national and regional carbon intensity in China. Renew. Sustain. Energy Rev. 2016, 55, 34–42. [Google Scholar] [CrossRef]
- Shanghai Environment and Energy Exchange. Shanghai’s Carbon Market Report. 2015. Available online: http://www.cneeex.com/sub.jsp?main_colid=240&top_id=238 (accessed on 28 September 2016). (In Chinese)
| Variable | Unit | |
|---|---|---|
| Dependent variable | SHEA | Yuan |
| Explanatory variable | SZZS | Percent |
| Fuel oil | yuan/ton | |
| Steam coal | yuan/ton | |
| Temperature | degree Centigrade | |
| Variable | Obs. | Mean | Max | Min | Std. Dev. | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| SHEA | 341 | 30.35 | 48.00 | 9.50 | 8.38 | −0.86 | 0.11 |
| SZZS | 341 | 2936.52 | 5166.35 | 1991.25 | 907.99 | 0.68 | −0.71 |
| Fuel oil | 341 | 3480.07 | 4809.29 | 2007.00 | 604.31 | −0.06 | −0.59 |
| Steam coal | 341 | 477.56 | 595.60 | 290.04 | 68.46 | −0.83 | 0.48 |
| Temperature | 341 | 14.78 | 34.00 | 1.50 | 7.84 | 0.22 | −1.08 |
| Variable | ADF Value | 1st Difference of ADF |
|---|---|---|
| lnSHEA | −1.064833 | −22.58128 *** |
| lnSZZS | 1.211579 | −14.48983 *** |
| lnoil | −1.217713 | −17.76263 *** |
| lncoal | −2.305738 ** | −27.39583 *** |
| lntemp | −0.603371 | −13.30092 *** |
| Hypothesized No. of CE(s) | Eigenvalue | Trace Statistic | 0.05 Critical Value | Prob.** |
|---|---|---|---|---|
| None * | 0.124383 | 70.73127 | 69.81889 | 0.0422 |
| At most 1 | 0.037331 | 25.83582 | 47.85613 | 0.0945 |
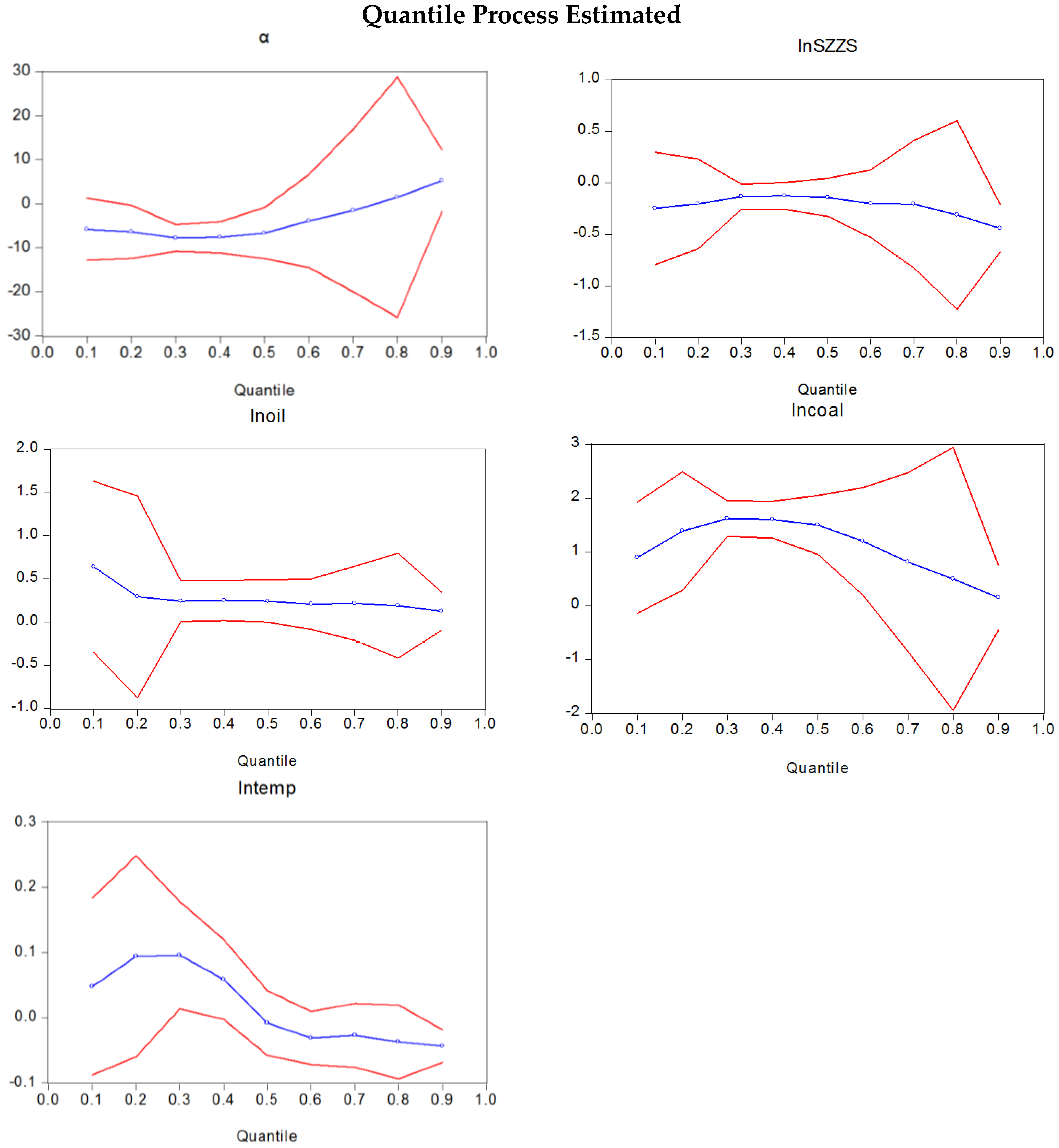
| Variable | Ols | 10% | 25% | 50% | 75% | 90% |
|---|---|---|---|---|---|---|
| α | 9.21008 *** | −5.825944 | −6.110953 *** | −6.664879 ** | 0.034741 | 5.215025 |
| lnSZZS | −0.221336 | −0.248885 | −0.222590 *** | −0.141646 | −0.256483 | −0.442152 *** |
| lnoil | 0.112685 | 0.639462 | 0.205251 | 0.244556 * | 0.173301 | 0.127672 |
| lncoal | −0.830799 *** | 0.893984 * | 1.481077 *** | 1.501282 *** | 0.679181 | 0.148548 |
| lntemp | −0.074253 *** | 0.047651 | 0.143950 *** | −0.008275 | −0.029189 | −0.043573 *** |
| AR(1) | 0.990766 *** | - | - | - | - | - |
| D.W | 2.309793 | - | - | - | - | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, L. Impacts on CO2 Emission Allowance Prices in China: A Quantile Regression Analysis of the Shanghai Emission Trading Scheme. Sustainability 2016, 8, 1195. https://doi.org/10.3390/su8111195
Zhang J, Zhang L. Impacts on CO2 Emission Allowance Prices in China: A Quantile Regression Analysis of the Shanghai Emission Trading Scheme. Sustainability. 2016; 8(11):1195. https://doi.org/10.3390/su8111195
Chicago/Turabian StyleZhang, Jie, and Lu Zhang. 2016. "Impacts on CO2 Emission Allowance Prices in China: A Quantile Regression Analysis of the Shanghai Emission Trading Scheme" Sustainability 8, no. 11: 1195. https://doi.org/10.3390/su8111195
APA StyleZhang, J., & Zhang, L. (2016). Impacts on CO2 Emission Allowance Prices in China: A Quantile Regression Analysis of the Shanghai Emission Trading Scheme. Sustainability, 8(11), 1195. https://doi.org/10.3390/su8111195





