1. Introduction
Agriculture and forestry play essential roles in a country, contributing to the creation of food, conservation of forest resources, and improvement of soil fertility. Agroforestry is a land-use system and technology [
1]. Agroforestry systems can be advantageous over conventional agricultural and forest production methods. Typically, it increases productivity, economic benefits, and diversity in ecological goods and services. An agroforestry system includes the following features: (1) two or more species (possibly both trees and animals), which must be perennial; (2) at least two or more products in the system; (3) a production cycle of more than one year; (4) ecological and economical diversity; and (5) the need for perennials and other compatible component relationships [
2]. Every country has unique natural and ecological conditions that lead it to create different ways for developing an agroforestry industry to satisfy societal needs. For example, Thailand developed methods for holding water agroforestry, retaining moisture, and improving the ecological environment and people’s living standards [
3]. India implemented a famous “green revolution” [
4] to produce enough food not only to overcome hunger but also to support and increase extra rice exports.
Agroforestry studies in Vietnam began about three decades ago. To sustain the use of land and secure food sources, many programs have been initiated. One of them involved cooperation with Finland, which introduced various agroforestry systems into the areas around the Ban Kan province for the sustainable development of vast uplands [
5]. All relevant programs have adapted to the local climate conditions, capacity of local peoples, and market availability. In 2003, Vietnam implemented a project called “Capacity Building of Agriculture and Forestry in Vietnam”, which aimed to establish projects in Vietnam and Southeast Asia to support the development of alternatives to slash and burn, and to strengthening research capacity and agricultural and forestry education. In this project, for example, Vietnam developed an amplification system to replace the slash and burn system.
In short, agroforestry in Vietnam is a traditional industry, and its importance has been steadily increasing. However, according to statistical data, the export value of agroforestry products in the first quarter in 2014 declined by approximately 13.2%. Coffee exports dropped sharply during the first quarter of this year. Data showed that around 350,000 tons of coffee were exported in the period, worth $734 million, decreasing by 41.4% in volume and 37.3% in value compared with last year. Rice exports slipped by 28.1% and 32% in export volume and value, respectively. In March, 517,000 tons of rice were exported, taking the total rice export volume in the first quarter to 1.01 million tons, with a total value of $440 million [
6]. However, some products happened to increase in export value despite a drop in export volume, such as with tea, cashews, and pepper. The agricultural and forestry sectors needed to enhance the quality of products and build brands to become more competitive in the world market. Vietnam has the benefit of exporting agricultural and forestry products, which reached $30.8 billion last year. The Vietnamese annual growth rate is dedicated to accelerating the growth momentum in the coming years [
7]. Therefore, new discoveries and a more efficient system need to be emphasized. Agroforestry has had a wide impact on the Vietnamese community in the past centuries, and has been adopted in Vietnamese mainstream forestry and agricultural development.
The sustainable development of the agroforestry industry in Vietnam, and other countries, requires an effective approach to change productivity performance. Moreover, from the views of decision-makers and stakeholders in agroforestry, good productivity is an important issue for them to deploy their operational strategy and to judge their investment. The performance index is not just counted for a single time period; they should be combined with several time periods for catching development tends. Moreover, people not only want to know the historical performance but want to find potential good candidates for the future [
8]. Therefore, this research proposes a hybrid approach, which combines a grey model (GM) with a Malmquist productivity index (MPI), is used to assess and foresee “past-current-future” performances of the agroforestry enterprises in Vietnam. Specifically, based on the historical data collected from the stock market from 2011 to 2014, the GM was first used to forecast the values of selected input and output variables for Vietnam agroforestry enterprises in 2015 and 2016. Then, the MPI was used to measure efficiency changes and productivity changes for these selected enterprises from 2011 to 2016. The proposed method provides insight for decision-makers to adjust their strategies. For government, the proposed method also guides policy directions toward sustainable development of the agroforestry industry in Vietnam. For global investors or stakeholders, the proposed method provides a channel to obtain performance information about an enterprise, as well [
9]. Moreover, the proposed method may be applicable to other industries for performance evaluation.
The remainder of this paper is organized as follows:
Section 2 is a literature review;
Section 3 presents the research procedure; the methodology introduction is depicted in
Section 4;
Section 5 conducts an empirical study and results analysis; and conclusions and suggestions for future directions are presented in
Section 6.
2. Literature Review
Data envelopment analysis (DEA) is a useful method for estimating production frontiers [
10]. It has been applied to various application domains, including operations research, management science, economics, etc. In essence, DEA is a non-parametric data analytical technique whose domain of inquiry is a set of decision-making units (DMUs), which can receive multiple inputs and express multiple outputs. Given a set of DMUs, the DEA can establish the relative efficiencies of each DMU within this set. When applying DEA, only limited data is required to measure performance. The selection of input and output variables is important for DEA as they can affect decision-making. One prerequisite for applying DEA is that the selected input and output variables should keep an isotonic relationship, which can be validated by correlation analysis [
11]. If the correlation between input and output variables are positive, this means the variables maintain an isotonic relationship and can be used by the DEA model. Otherwise, it needs to re-examine these variables. In past studies, Liu [
12] used the number of employees, assets, and purchased funds as input variables, and demand deposits, short-term loans, and long-term loans as output variables. Romano and Guirrini [
13] used the cost of labor, cost of material, cost of service, and cost of lease as inputs, and the population served and water delivered as outputs. The input and output variables used in these studies are referred to in this present research. In addition to comparing the relative performance of DMUs at a specific period, DEA can also be used to calculate the productivity changes of a DMU over time to examine the relative progress among competitors. In the past two decades, increasing publications have adopted MPI as the evaluation techniques to assess the efficiency of an enterprise. For example, Briec et al. [
14] employed MPI to analyze the productivity growth and technological change of a Portuguese hydroelectric plant in 2001–2008. Yang et al. [
15] thought forestry enterprises were important elements of the forestry economy in China. The increasing investment of the government in science and technology accelerates the development of the forestry economy in China. Qazi and Yulin [
16] had to use MPI to measure changes in China’s high-tech industry’s productivity in 2000 with fifteen high-tech industries. It concluded that the electronic component and office equipment industries are considered to be valid.
Grey system theory was introduced by Deng [
17]. It has become popular due to the advantage of managing a system with unknown parameters. Compared with traditional statistical methods, grey system theory requires little data for forecasting. Under the missing information or partially unknown parameters or uncertainty problems, this theory has become a popular method. Superior to conventional statistical models, grey forecasting can only use a limited amount of data to evaluate the unknown systems [
18]. The GM (1,1) is one of the most popular grey forecasting models. Ren proved that using GM (1,N) to predict the yield of bio-hydrogen under scanty data conditions could give a better predictability result than the use of an artificial neural network [
19]. There are some studies to have employed grey system theory. Kuo et al. [
20] applied grey relational analysis for multiple attributes decision making. These studies indicate that grey system theory as been employed in various application areas. Lin et al. [
21] proposed a gray forecast model to deal with the factor analysis of multivariate series forecasting problems. The results show that the model is better than other existing models.
Chen and Chen [
22] used DEA and MPI to explore Taiwanese chip manufacturing company operating performance. The results show that if the wafer manufacturing company in Taiwan wished to improve their operating performance, they should improve their efficiency of constant returns to scale (CRS) and variable returns to scale (VRS), as there is no economy of scale. Wang et al. evaluated the performance of the Indian energy industry under multiple different input and output criteria. The DEA and grey theory are used to conduct this study [
23].
Referring to the operational characteristics of Vietnamese agroforestry companies and summarizing the DEA literature mentioned in
Section 2 [
11,
12,
13,
14,
15,
16,
22,
23], this research selects total assets, liabilities, and equity as three input factors because they are key financial indicators contributing to the performance of DMUs in the agroforestry industry. On the other hand, net revenue and gross profit are selected as output factors, as they are important indices for measuring the performance of DMUs in the agroforestry industry.
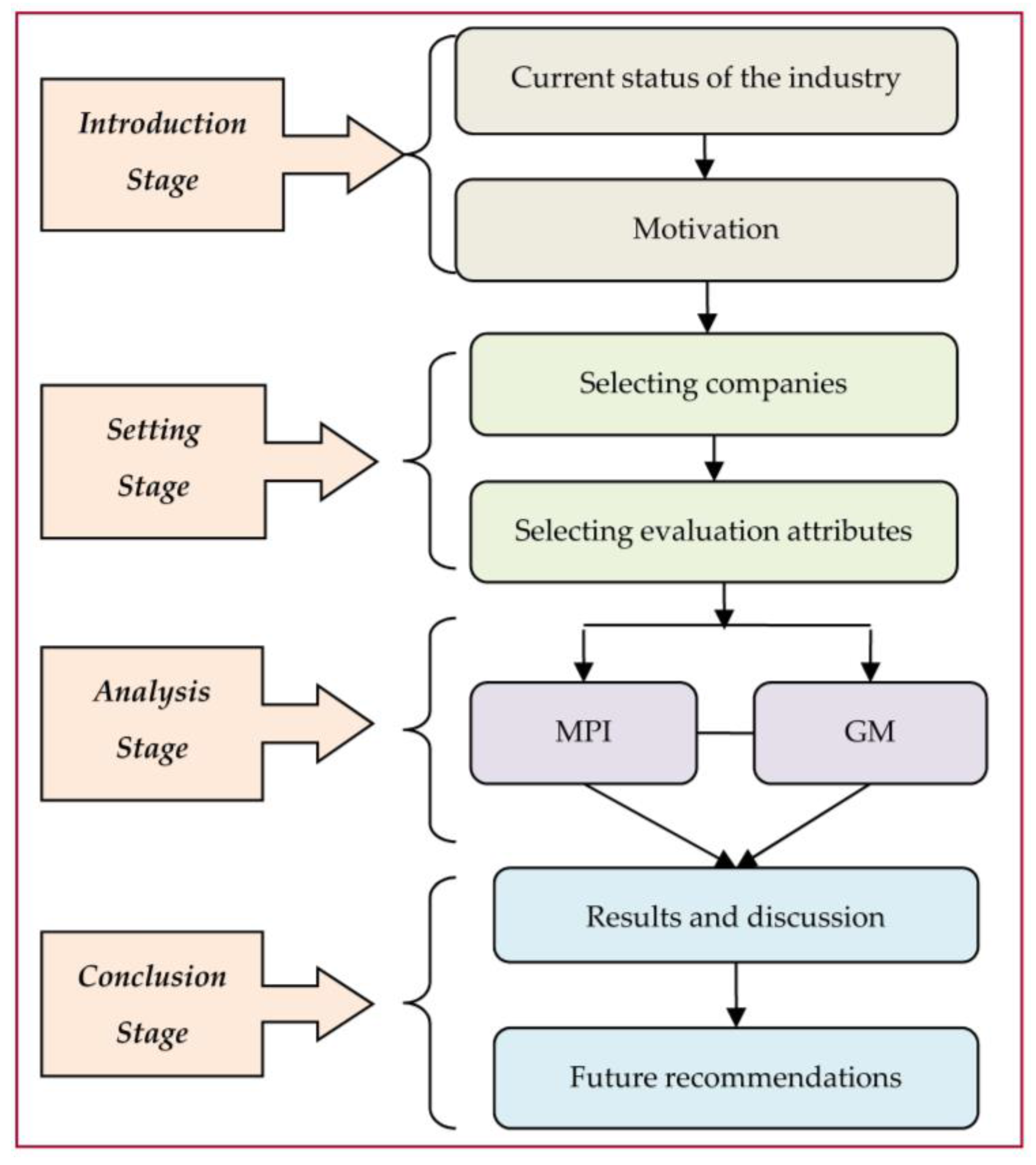
3. Research Procedure
In this research, a seven-step procedure is used, and the details of each step are described below and in
Figure 1.
Step 1: Choose DMUs and collect their data: This step focuses on choosing DMUs in the Vietnam agroforestry industry and collecting their relevant information. The study investigates the relevant enterprises to find all potential candidates’ DMU lists. A total of 10 Vietnamese agroforestry companies with financial reports on the stock market during the period 2011–2014 are selected.
Step 2: Choose input/output variables: This step focuses on selecting the input and output variables. The selected input and output variables are critical, as they can affect the results. In this research, we refer to previous studies in order to make an appropriate choice. The Pearson correlation test will be used in Step 6 to check the suitability of these selected variables. However, according to the rule of thumb from Golany and Roll [
11], the total DMUs need to be more or equal than double the number of inputs plus outputs.
Step 3: Grey prediction: In this step, the GM is used to predict the future data in 2015 and 2016. Since the prediction always exists with errors, the mean absolute percent error (MAPE) is used in the next step to check the prediction accuracy of the GM. Even though there are several prediction methodologies, almost all of them need to prepare lots of historical data. The GM is the only one that uses a minimum of four historical data types for prediction. The historical data are difficult to be collected in the Vietnamese agroforestry industry. Therefore, this study uses GM as a prediction method for overcoming a shortage of data.
Step 4: Check forecasting accuracy: As stated in the previous step, the MAPE is employed to check the prediction accuracy of the GM (1,1). Lewis [
24] gave MAPE an assessment standard: a MAPE value < 10% is considered “good”; a MAPE value between 10%–20% is considered “qualified”; a MAPE value between 20%–50% is considered “just”; and a MAPE value > 50% is considered “unqualified”. If the forecasting error is too high, we have to go back to the Step 2 to reselect the input and output variables.
Step 5: Pearson correlation test: DEA requires the selected input and output variables to have an isotonic relationship. Therefore, to test that the data matches this isotonic prerequisite, the variable correlation analysis is calculated to verify a positive correlation between the selected inputs and outputs. If there are negative coefficient variables, the input and output variables need to be changed. Thus, we have to revert to the Step 2, until this prerequisite is met. In this research, we will employ the Pearson correlation test for this purpose.
Step 6: Choose the DEA model: This step includes many DEA models. Most of them can only analyze a single time period. However, only MPI can combine several time periods for integrated analysis and can separately discuss the changes of efficiency and technology. These characteristics match our data of several time periods and match our requirement of integrated analysis. Therefore, this study chooses a MPI model to assess and rank the efficiencies of DMUs for our analysis.
Step 7: Performance analysis: In this step, the forecasting performances of DMUs will be thoroughly analyzed.
5. Empirical Results
Following the research procedure proposed in
Section 3,
Table 1 shows 10 Vietnamese agroforestry companies selected for this research. These companies are the top companies in the agroforestry industry in Vietnam, and their data are posted publicly and prestigiously. These companies are qualified with transparent financial data. Information about these DMUs was collected from the market observation posting system of Vietstock.vn, which is a premier site for business and financial market news in Vietnam.
Referring to the literature review, this research selects total assets, liabilities, and equity as the three inputs factors, and net revenue and gross profit as the output factors. The total has 10 DMUs with three inputs and two outputs. Matching the rule of thumb from Golany and Roll [
11], which states that the total number of DMUs need to be more or equal than double the number of inputs plus outputs. The correlation of these selected input and output variables will be validated by the Pearson correlation test.
Having determined these input and output variables, we collect the historical data of these DMUs from 2011 to 2014 [
6,
29]. However, due to space limitations, only the data of the year 2014 are listed in
Table 2.
Following the research procedure, the GM (1,1) is used in this section to predict the future data from 2015 and 2016 for the selected DMUs.
Table 3 shows the DMU
1’s historical data (2011–2014) used by the GM (1,1).
Below, we use the “total asset data” of DMU
1 in
Table 3 to illustrate the generation of the forecasting data of DMU
1 step-by-step.
- (1)
Create the primitive series
- (2)
Generate the accumulated series
- (3)
Create mean series dataset
To find the mean series dataset
, Equation (6) is used and we derive the following data.
Then,
- (4)
Find the values for coefficients a and b
Let , , .
Then, using the Equation (8), we can derived the values of
a and
b as below.
- (5)
Generate the accumulated data series
Substitute the two coefficients
a and
b, as well as the
k values (
k = 0, …, 7), into the Equation (9); then we can derive the accumulated data series in the third column in
Table 4.
- (6)
Generate the series values of prediction
Substitute the two coefficients
a and
b, as well as the
k values (
k = 0, …, 7) into the Equation (11); then we can the derive the fifth column in
Table 4.
With the same computational process, the study could obtain the forecasting data of all DMUs in 2015 and 2016, as shown in
Table 5.
In this step we check the prediction accuracy of the GM (1,1) based on the MAPE values. When a MAPE value is small it means the predicted value is close to the actual value. The MAPE values obtained are shown in
Table 6.
As the MAPE values obtained are, mostly, smaller than 10%, especially as the average MAPE of the 10 DMUs reaches 5.111% (below 10%, as well), it confirms that the GM (1,1) provides a good prediction accuracy in this research.
However, before using this DEA model, we have to ensure that input and output variables have isotonic relationships. This means that if the input quantity increases, then the output quantity could not decrease under the same condition. Thus, a Pearson correlation test is first used to ensure this prerequisite. A higher correlation coefficient refers to a closer relationship between two variables, and a low correlation coefficient means a low relationship. The interpretation of the correlation coefficient is explained in more detail as follows: The correlation coefficient is always between −1 and +1. When the correlation coefficient is closer to ± 1, this means two groups are closer to a perfect linear relationship. When a correlation value is less than 0.2 then the degree of correlation is considered “very low”; a value between 0.4–0.6 is considered “average high”; a value between 0.6–0.8 is considered “efficient high”; a value between 0.8–1 is considered “upper high”. Our empirical results (
Table 7) indicate that these variables have strong positive correlations, indicating that these selected input and output factors are qualified.
Though some DEA models are available for assessing DMUs, the efficiencies of DMUs of several time periods cannot be compared for most of the DEA models [
30]. In this research, the Malmquist model is used to evaluate the performances of DMUs.
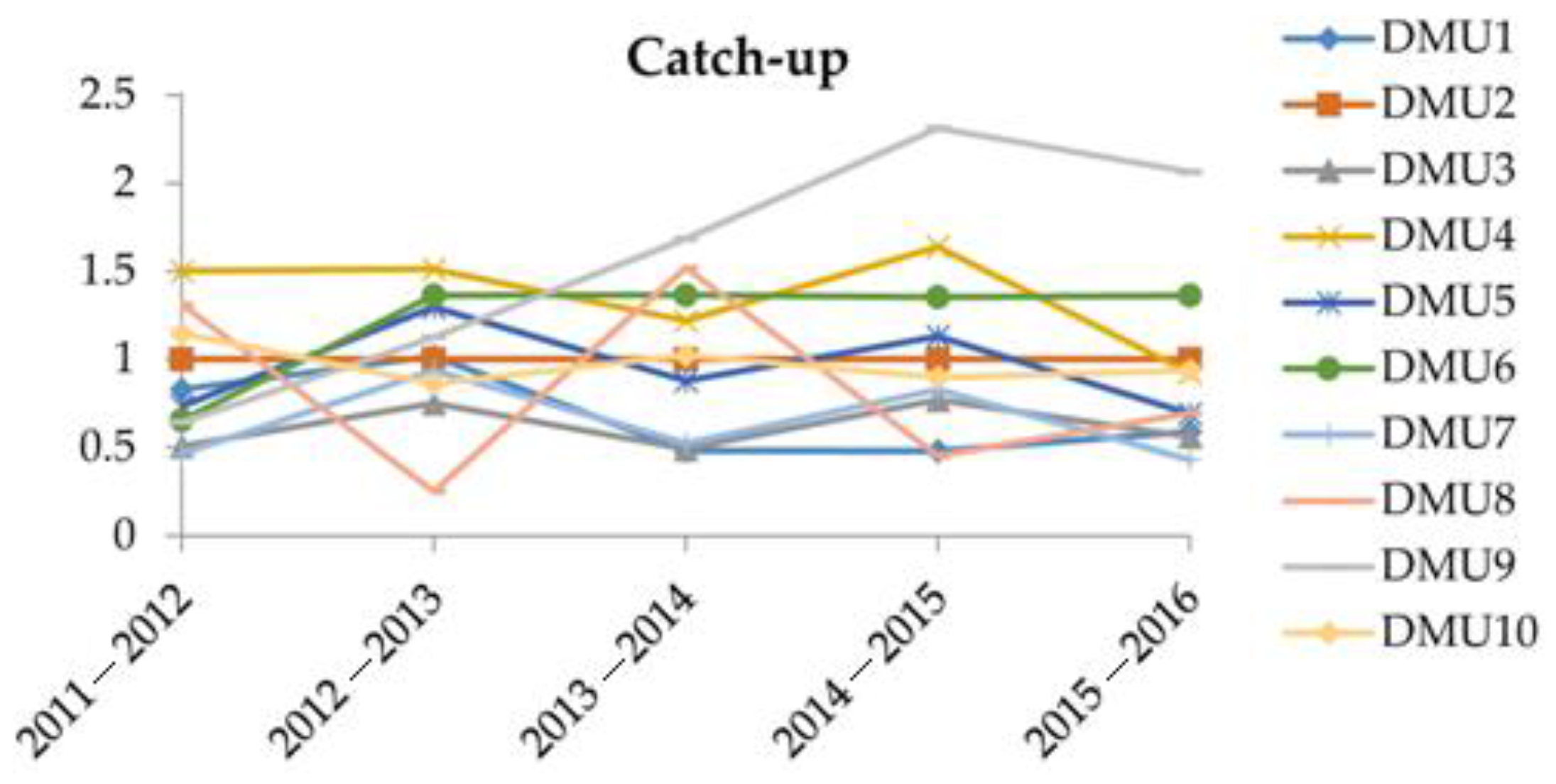
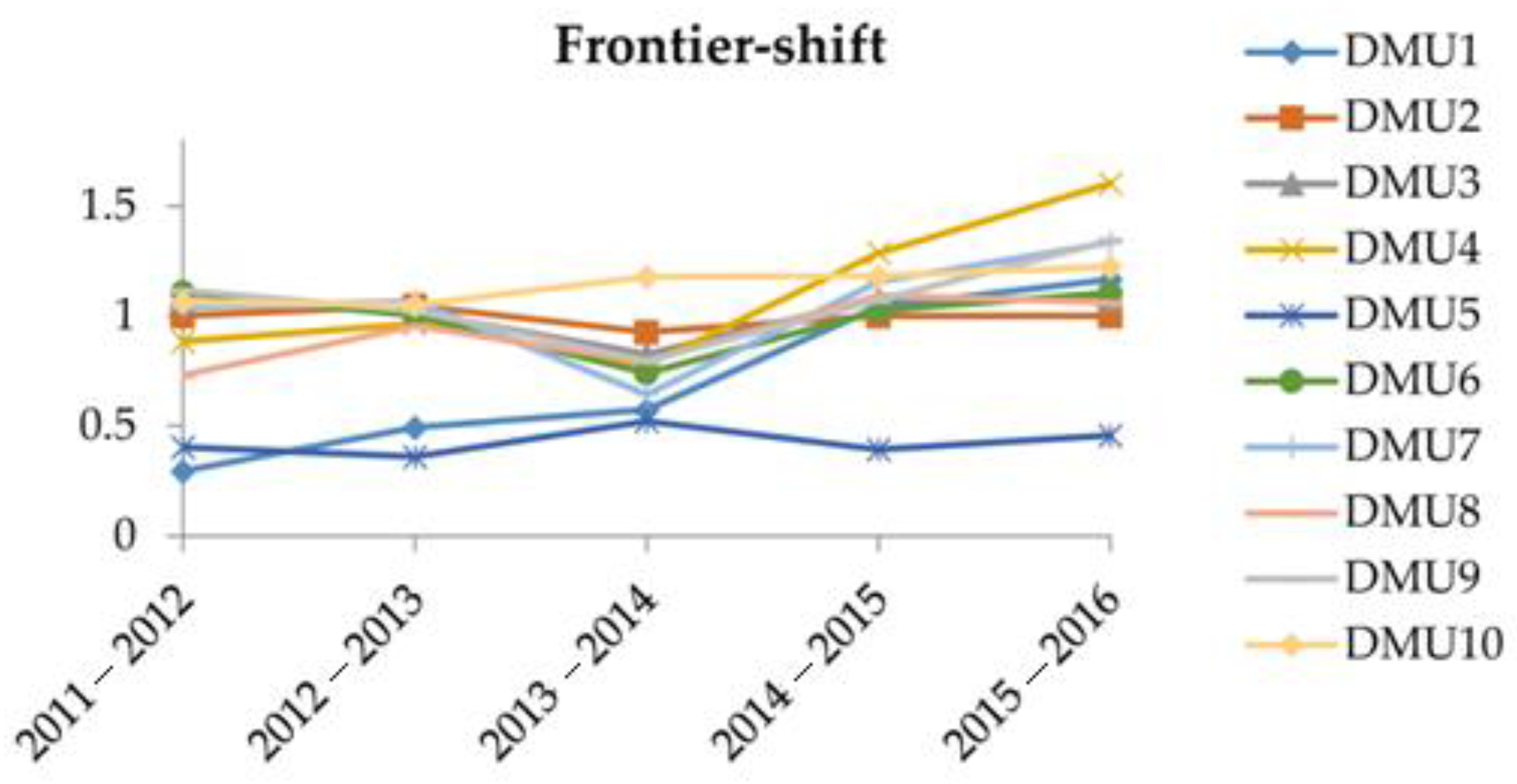
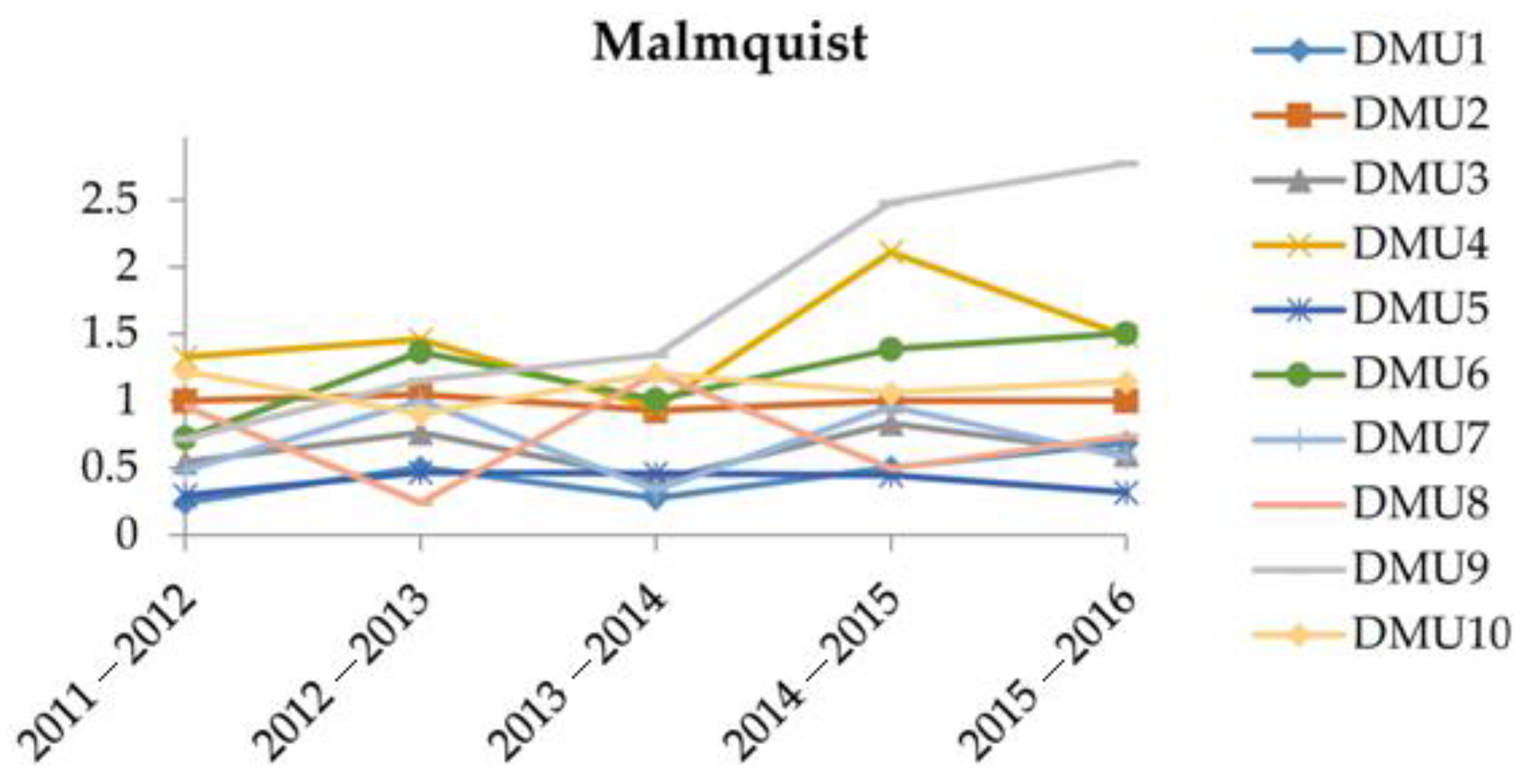
Table 8 shows the results derived from the Malmquist O-V model. To facilitate the analysis, the values of efficiency change, technological change, and MPI are depicted in
Figure 2,
Figure 3 and
Figure 4, respectively.
Figure 2 shows the “efficiency changes” (catch-up effects) of the 10 DMUs over the time period 2011–2016. It is found that the efficiency changes of these DMUs fluctuated over these years, especially DMU
3, DMU
4, and DMU
8. DMU
3 had experienced a dramatic efficiency rise during the time period 2011–2015, and DMU
4 experienced a dramatic efficiency drop during the time period 2015–2016, while the DMU
8 had experienced a dramatic drop during the time period 2014–2015. Except for DMU
2 and DMU
6, which had experienced slight efficiency changes, the other DMUs all had experienced some degree of efficiency fluctuations. In terms of “efficiency change”, DMU
9, DMU
4, and DMU
6 are the top three best companies, while the top three worst companies are DMU
3, DMU
7, and DMU
1. DMU
2 is found with a stable efficiency, but it also had not improved its efficiency in the current and near future. From
Figure 2, we can determine and predict the efficiency changes, or the “catch-up” effects, of each DMU.
Figure 3 show the “technological changes” (frontier-shift) of the 10 DMUs from 2011–2016. It is found that, except for DMU
5, other DMUs had experienced an upward technological change, though most of them had experienced an efficiency drop during 2013–2014. This implies most of these DMUs had continued to improve their technological capabilities. DMU
5 always keeps a lower “technological changes” score, indicating that it has not actively improved its technology. Thus, DMU
5 requires further investigation into the causes that lead to its tardiness on technology development. In terms of “technological change”, DMU
10, DMU
4, and DMU
9 are the top three best companies, while the top three worst companies are DMU
5, DMU
1, and DMU
8.
Figure 4 shows the MPI, the total productivity of the 10 DMUs from 2011–2016. It is noted that DMU
6 and DMU
9 had a long-term upward trend during 2011–2016, though DMU
6 had experienced a drop during 2013–2014. In terms of MPI, DMU
9, DMU
4, and DMU
10 are the top three best companies, while the top three worst companies are DMU
5, DMU
1, and DMU
7. DMU
8 appears unstable due to having the largest fluctuation; thus, it requires intense care for its development. In summary, to sustain the development of the agroforestry industry, the Vietnamese government needs to especially focus on DMU
5, DMU
1, DMU
7, and DMU
8.
6. Conclusions
For sustainable development of the Vietnamese agroforestry industry, this research has proposed a hybrid approach combining GM and DEA to assess the current, and predict the future, performance of agroforestry companies. This study first selects total assets, liabilities, and equity as input variables, and net revenue and gross profit as output variables. After collecting the historical data (2011–2014) from the Vietnam stock market, the GM (1,1) model is used to forecast the future data in 2015–2016 for selected agroforestry enterprises. The MAPE value of 5.11% confirms the desired accuracy of the GM (1,1). Based on the historical and predicted data, the Malmquist model is used to assess the performance of these DMUs. The derived results provide insight views into the agroforestry companies in terms of “efficiency changes”, “technological changes”, and MPI (total productivity). These results can also provide insight into the “past-current-future” performances of these DMUs. In summary, to sustain the development of Vietnamese agroforestry industry, the government should take more care in the developments of these companies, which are DMU5, DMU1, DMU7, and DMU8.
This research also demonstrates that the proposed approach can help decision-makers. Policy-makers can use the approach to develop strategies to sustain the development of the Vietnamese agroforestry industry. Investors can use of this approach to discover the good companies for investments. This mathematical approach reduces the errors and risks in decision-making. In addition, the approach can be used in other industries to extend its contributions. This study provides many significant and noticeable results. This numerical study gives us better “past-present-future” insights through the integration method, and this work could be used as a better model for performance analysis among the decision-makers of varied industries.
The proposed approach has been applied to the Vietnamese agroforestry industry; however, it only includes 10 companies listed on the stock market. Including more companies can provide further focus. In addition, some other input and output variables (such as the number of staff, number of branches, revenue, research and development, etc.) can be taken to measure the performance of these companies. Moreover, different DEA models can be further investigated for comparisons. Furthermore, this approach can be applied to other industries.