Abstract
When designing “multi-MW arrays” of Wave Energy Converters (WECs), having a low number of converters with high individual power ratings can be beneficial as the Operation and Maintenance (O&M) costs may be reduced. However, having converters of small dimensions or small power ratings could also be beneficial, as suggested by previous works, due to a reduction in material costs as compared to power production, and the use of small, inexpensive vessels. In this work, a case study investigating the optimum size of WEC for a 20 MW array is performed. Analysis is carried out based on the CorPower Ocean technology. In this case study, firstly a Levelized Cost of Energy (LCOE) model is created. This model incorporates the latest Capital Expenditure (CAPEX) estimates for CorPower Ocean’s 250 kW prototype. Using this techno-economic model, several sizes/ratings of WEC are tested for use in a 20 MW array. Operational Expenditure (OPEX) is calculated using two different calculation approaches in order to check its influence on final indicators. OPEX is firstly calculated as a percentage of CAPEX, as shown in previous works, and secondly using a failure-repair model, taking into account individual failures of WECs in the array. Size/rating analysis is carried out for several European locations in order to establish any dependence between site location and optimal WEC size/rating. Several metrics for techno-economic assessment of marine energy converters, other than LCOE, are compared in this work. A comparison of several devices with each these metrics is performed within this study.
1. Introduction
The marine energy sector is an emerging industry that is still in the early stages of development. Two sources of marine energy that have been identified as having significant potential to contribute to the European energy system are tidal streams and ocean waves [1,2].
The problem that marine energy faces is that it is not yet cost competitive with offshore wind, which currently delivers a lower LCOE [3]. Whilst marine and offshore wind are not competing for the same resource, they do compete for investment from utility companies that want to deliver clean energy for the lowest possible cost [4]. It is therefore important that the LCOE of marine energy is driven down to levels comparable with offshore wind, thus allowing marine energy to secure a foothold as part of the future world energy mix. Moreover, some authors were found to account for risk in an LCOE analysis by considering the probability of a return on the investment for different sized wave farms through calculation of the Value at Risk (VaR) and Conditional Value at Risk (CVaR) [5]. Also, O’Connor et al. [6] studied the OPEX costs for wave energy projects, and Guanche et al. [7] analysed the uncertainty of financial indicators for wave energy farms, giving a good overview of the economic situation of the sector.
The marine energy sector is not yet considered mature, with prototypes being deployed as proof of concept devices [1]. Offshore wind technology, on the other hand, builds to a large extent on established solutions from on-shore technology, and has thus been able to mature more rapidly and attract capital investment. Commercial-size offshore windfarms have already been deployed at several locations around the North Sea and the rest of the world [8]. In order for marine energy to compete with offshore wind, a significant investment is required to increase the learning rate and drive down costs to competitive levels [9]. The IEA provides a LCOE value for offshore wind of around 120 £/MWh [10], significantly lower than current estimates for ocean energy. However, the offshore wind sector has seen a significant cost reduction in recent years, providing an insight into the level of cost reduction that can be achieved by the marine energy sector.
When designing “multi-MW arrays” of Wave Energy Converters (WECs), having a low number of converters with high individual power ratings can be beneficial as the Operation and Maintenance (O&M) costs may be reduced. However, having converters of small dimensions or small power ratings could also be beneficial as suggested by De Andres et al. [11] due to a reduction in material costs as compared to power production, the use of small, inexpensive vessels, and a lower learning process cost. This paper, however, only took into account the hull costs (cost of the external structure) for its comparison and did not carry out a full LCOE study for the comparison.
Regarding techno-economic assessment, a detailed study was recently published that presents a methodology for the design and economic analysis of four Marine Energy Conversion (MEC) technology point designs. The O&M Strategy Module includes a failure matrix (measure of reliability) for device and infrastructure (BOS) components, which accounts for the likelihood of failure of each component along with the requirements for the repair as well as the number and unit cost of service trips. Many techno-economic analyses have been carried out to assess the feasibility of marine energy. De Andres et al. [12] conducted a study investigating the effect of differing development strategies on LCOE. Furthermore, consulting engineer Julia Fernandez Chozas has developed a tool to standardise the process for calculation the LCOE of wave energy developments, allowing input variables to be changed in order to investigate the effect of design changes on the final LCOE [13]. While these examples show that large amounts of work have been done to investigate the effect of device and deployment parameters on the LCOE, the studies do not directly address the assessment of full-scale rating for WECs.
The aim of this paper is to determine the optimal size, in terms of economic performance, of a given wave energy converter. This problem can be split into two parts: static; and dynamic. Looking firstly at the static problem, the aim is to determine an optimal device size once the marine energy sector has fully matured to deliver the lowest possible cost of electricity. With the dynamic problem, the aim is to determine the best strategy for upscaling marine energy devices to an optimal size within a fully matured market, in such a way as to minimise the cost of learning and the amount of investment required to make marine energy competitive with other renewable technologies. In this paper, for the sake of simplicity, the static problem will be analysed based on a specific wave energy converter.
This topic has been investigated by a number of authors in the past. For instance, O’Connor et al. [14] give an investigation of several differently rated versions of the Wavestar and Pelamis devices. One conclusion was that multiple smaller rated devices produced higher energy outputs and capacity factors at all locations and for both device types. From an economic perspective, however, the most attractive returns occurred when using larger rated devices. Several power ratings for a Wavestar inspired device have also been investigated [12]. Although it was concluded that having converters of small dimensions or small power ratings could be beneficial, in terms of the efficiency of the conversion devices, tuning to the specific location is recommended. This paper, however, only takes into account OPEX as a percentage of the CAPEX. Furthermore, the scaling of CAPEX was not performed following a scaling law.
This paper will present a case study of the techno-economic performance of an inherently resonant point absorber wave energy converter with several ratings. Performance will be tested at various locations in order to check the location dependency of the rating decision. Furthermore, two approaches to OPEX calculation will be followed in order to check the dependency of device rating on OPEX assumptions. All assumptions and the techno-economic model will be explained in greater detail in the Methodology (Section 2), while the Results (Section 4) is split into three subsections: results for a 20 MW wave farm; a sensitivity analysis based on CAPEX and OPEX; and a device comparison with various metrics.
2. Methodology
In this section the tools and assumptions that have been used to perform a device rating analysis are explained. Firstly, an explanation of the device and the rating adaptation for the power matrices is given. Secondly, the economic tool used for this analysis is presented following O’Connor et al. [6] and, finally, the sites examined in this study are described.
2.1. Device Specifications
CorPower Ocean’s Wave Energy Converter (WEC) technology belongs to the point-absorber category, with a heaving buoy on the surface absorbing energy from ocean waves while being connected to the seabed using a taut mooring line. It provides pneumatic pre-tension between the mooring and the buoy to enable a lightweight system. A novel phase control technology called WaveSpring widens the buoy’s response bandwidth, and thereby also increases the power capture [15]. The absorbed wave energy is converted into electricity using a new type of mechanical direct drive PTO, located inside the buoy (see Figure 1).
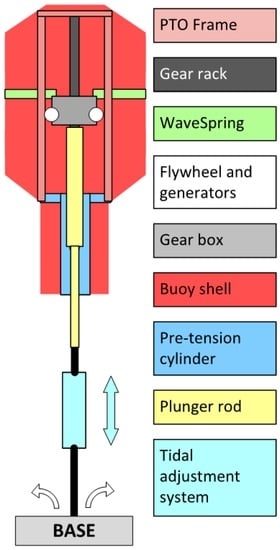
Figure 1.
Schema of the Corpower device.
A key component is a cascade gear box, capable of efficient conversion of linear-to-rotating motion with high durability. The cascade gear has a design principle similar to a planetary gear box, dividing a large load into a multiple of small gears, arranged to allow conversion of linear-to-rotation motion in combination with a gear rack. A dual set of flywheels/generators provides power conversion and temporary energy storage for power smoothing. Generators and power electronics are standard components known from the wind industry, enabling well-known grid connection architecture. The units are designed to operate autonomously by a Programmable Logic Controller (PLC) located on the PTO, with an interface for remote control and data acquisition to shore over fibre and a radio link.
This WEC incorporates a pneumatic pre-tensioning system that reduces the mass of the oscillating body, thereby giving a high natural frequency of oscillation. Advantages of this technology stem from an increase of annual energy capture by +300% for a given point absorber size, and a reduction of required materials/mass by 40% for the absorber (primary structure) as compared to the chosen benchmark derived in Babarit [16].
Due to the commercial sensitivity of the data, the power matrix cannot be included within this paper. However, it should be noticed that the power matrix is smooth (not peaky) with the rated power within sea states corresponding to high wave periods (12–17 s) and high wave height (4.5–7.5 m). However, the scatter plots obtained from Chozas et al. [13] of the five selected sites have been included in Figure 2 in order to help the understanding of the scaling operation, as well as the differences between sites.
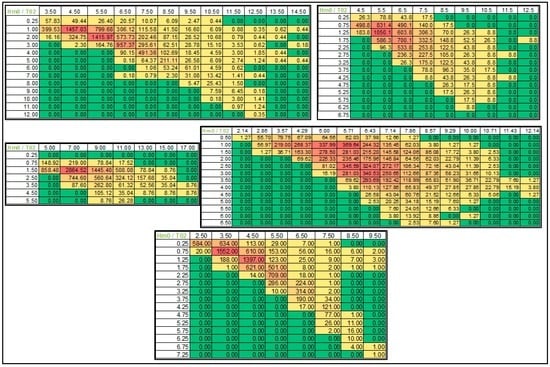
Figure 2.
Wave climate scatter plots for the five selected sites (number of occurrences per year). EMEC (top left), WaveHub (top right), Bimep (mid left), Yeu (mid right), and DK North Sea Point 2 (bottom) [12].
2.2. Techno-Economic Model
The underlying goal of this paper is to ascertain the optimal size for a marine energy converter in terms of economic performance. The first step that must be taken then is to select an adequate indicator that represents the economic performance of a device. Various reports by leading bodies in marine energy development were found to frequently refer to LCOE when detailing the cost of production [3,17].
LCOE is defined as the total capital, operational, and maintenance costs associated with the generation, discounted to present day value, divided by the electricity generated to the grid throughout the technology’s operational life [11]. Equation (1) shows this, where LCOE is the levelised cost of electricity, CAPEX is the capital expenditures, OPEX is the operational expenditures, WEC production (often named Annual Energy Production—AEP) is the annual electricity production, n is the lifespan of the system, and r is the discount rate:
It is clear that LCOE is a widely used concept throughout the energy generation industry and so, in order to stay consistent with the industry and allow comparison of the performance of marine energy devices with alternative forms of electricity production, LCOE should be used.
In this case, the COE calculation tool from Chozas et al. [13] was used as the reference modelling tool. This tool was used mainly as a basis for met-ocean conditions (scatter plots) and scaling of the power matrix.
2.3. Assumptions
As previously mentioned, LCOE will be the main parameter used in this techno-economic study. However, for “low to medium TRL technologies”, some assumptions need to be made due to a lack of data and in order to simplify the sizing study:
- Power matrices are scaled with the Froude scale (further explained below).
- For all ratings, the device is in survival mode in sea states where Hs > 10 m.
- No interaction effects are considered among devices (q factor = 1).
- CAPEX is scaled based on the following equation:where CAPEX1 corresponds to the CAPEX of the 25 kW device, Scale corresponds to the scale of the device calculated through the rated power conversion, and Scale parameter corresponds to the CAPEX Scale parameter that is further explained below.
- 1st OPEX calculation approach:For the sake of simplicity, and due to the absence of adequate O&M data for wave energy converters, OPEX is calculated as a percentage of the CAPEX. O’Connor et al. [6] showed different figures of OPEX calculated as a percentage of CAPEX. In this case, following Guanche et al. [7], it was assumed that the initial OPEX was 8% of CAPEX.
- 2nd OPEX calculation approach:As a second approach, OPEX is calculated based on the real cost of the repair actions through the life-cycle of the device. The assumption of one major repair being performed every two years is used. Costs are based on consultations with a vessel company in Orkney. It is assumed that the same type of vessel is used for the repair action, independently of the rating of the device.
- For both OPEX approaches it is assumed that OPEX is the same for all locations.
- The same level of availability is assumed for all locations, and is taken to be 95% based on Guanche et al. [17].
- It is assumed that the wave energy farm is designed for a 20-year life-cycle.
- A discount rate of 8% has been chosen following Guanche et al. [7].
- A feed in tariff of 375 Eur/MWh has been selected, as this is the current feed in tariff in the United Kingdom for wave and tidal projects.
- It is assumed that this will be the first 20 MW farm developed and so the selection of interest rate, availability, and OPEX has been made with this in mind.
- A learning rate is applied to CAPEX due to bulk production. In this case, as the first units produced, a factor of 0.82 is selected as suggested as an optimistic scenario in Guanche et al. [7]. For OPEX, a learning rate of 0.92 is applied (normally OPEX shows slower learning than CAPEX).
2.4. Power Matrix Scaling Methodology
In order to produce the power matrices for different ratings, the procedure explained in De Andres et al. [11] has been used.
In order to assess the different ratings of the device at different sites, the original power matrix was scaled. Froude similitude was utilised, in which the Froude number (Fr) was kept the same for different sizes of device. The Froude number is one of the important fluid flow dimensionless numbers (DN) and is defined by Equation (3):
where ν is the fluid velocity, g is the gravitational constant and l is the length. The dynamic system is assumed to be linear with the Froude number being equal for both the model and the prototype: i.e., Fr1 = Fr2 as represented in Equation (4):
The Scale Factor is λ = l1/l2 based on Froude similitude. Force is defined in Equation (5) and velocity is defined in Equation (6). This results in the power being expressed in terms of λ in Equation (7). The wave heights scale linearly with the scale ratio (Equation (8)) and the wave period scales as a square root to the scale ratio (Equation (9)).
Wave height scale = λ
This allows the calculation of the scale ratio λ when scaling from one power matrix to another.
The scaled matrices chosen for the case study are 25, 50, 100, 250, 500, 750, 1000, and 2000 kW. Scaling was based on the original 250 kW power matrix. With this method the device response remains the same, with the spread over the frequency range similar.
Step 1. Scaling of power outputs
The values of power output in each cell were initially scaled in proportion to the original power matrix.
Step 2. Scaling of the wave height and wave period axis
For each of the power matrices that were scaled, the scale factor was determined using Equation (7), taking into account the power rating of the device at 250 kW (as it is considered the base for the power matrix). The values of wave height on the y-axis were scaled linearly based on Equation (8). The values of wave period on the x-axis were scaled based on Equation (9).
Step 3. Removal of excess rows and columns when downscaling
A correct power matrix must have only one column or row value for each bin. When downscaling (e.g., 0.75 MW to 0.25 MW), some columns or rows will have two or more values. This excess must be removed so that only one remains. This is performed through an interpolation.
Step 4. Insertion of extra rows and columns when upscaling
As a result of upscaling, there will be fewer rows and columns than in the original power matrix. This requires extra rows and columns to be inserted via interpolation so that there is one column representing the values for each column bin and one row representing the values for each row bin.
Step 5. Interpolation of power output values
The individual power output values in each cell were proportionally scaled by interpolating the y-axis and x-axis using the old and new values of the wave height and period axis, respectively, and the power output values from Step 1.
It should be underlined that the study presented in this paper represents just the first step in the sizing decision for the full-scale prototype. Because the original power matrix was optimized for 250 kW, the subsequent matrices obtained by applying the Froude law will be penalized. Taking this into account, the power matrices of the different ratings will be obtained numerically for future studies.
2.5. CAPEX Scaling
As previously mentioned, a scaling factor was assumed for CAPEX. In order to compute this parameter, an individual Scale parameter was computed for each of the modules, which are subsystems within the CorPower Ocean WEC. This subdivision of modules has been done depending on the functionality of each of the systems (see Table 1). The scale parameters of each module have been calculated depending on the nature of the module. For the modules related to force, a scale parameter of 3 was applied, while for the modules related to power, 3.5 was applied following Froude’s law. On the other hand, for the modules related to surface, a parameter of 2 was used, while for the modules related to longitudinal quantities a factor of 1 was applied.

Table 1.
Scale parameter for each of the modules.
It should be noted that, for instance, in the case of the Tidal module, a scale parameter of 0.5 has been applied. This is because the tidal module is required for the small-scale prototype. However, for the larger scale prototypes, due to the longer stroke of the PTO, the need for the tidal module will be diminished.
Table 1 shows the Scale parameter used for each of the modules. In the end a weighted scale parameter was calculated depending on the budget for the individual modules.
3. Sites
For this study five sites have been chosen in order to determine the techno-economic performance of the device in different locations (Figure 3). The met-ocean data (scatter plots) for these sites have been obtained from the techno-economic tool [12]. Table 2 shows the characteristics of the sites in terms of resource, water depth, and distance to shore. These locations were selected due to the availability of data and to give a good spread of characteristics (especially with regards to resource at 12 kW/m to 28.5 kW/m). Figure 2 shows the scatter plots for the different sites chosen [12].
Figure 3.
Sites.

Table 2.
Site characteristics.
4. Results
The results of this study will be given in three subsections. Firstly the analysis of indicators for a 20 MW wave farm with several device ratings is presented. In this case, OPEX is calculated following the first approach previously mentioned.
Secondly, the influence of the two OPEX calculation approaches as well as the CAPEX scale parameter is investigated. In this case, the lowest LCOE rating option is shown with the objective of checking the impact of these assumptions on the final sizing decision. Finally, in a third subsection, indicators are calculated for several devices taken from Babarit [15].
4.1. The 20 MW Farm Analysis
For this case study a 20 MW wave energy farm was analysed with different power ratings of the CorPower Ocean device. In order to make it to the 20 MW rating, different numbers of devices were used for each rating (800, 400, 200, 80, 40, 27, 20, 14, and 10 devices respectively).
Figure 4 shows the annual power production for each of the 20 MW arrays. It is shown that the annual Energy production is higher for devices with smaller ratings. This is due to the Froude scaling of the power matrices.
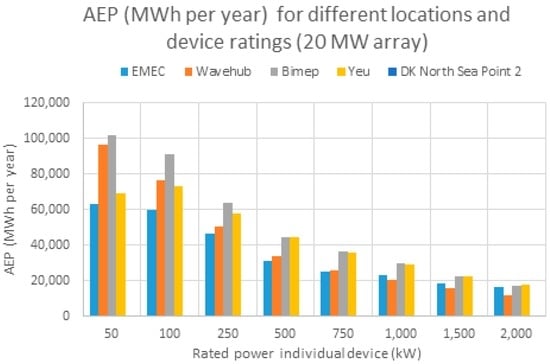
Figure 4.
Annual energy production of the 20 MW arrays for each rating.
When dealing with smaller ratings the devices work at rated power a larger proportion of the time, and thereby the capacity factor and the total energy capture are larger. On the other hand, when dealing with large buoys that have high power ratings, the devices work most of the time at only a fraction of their rated power and thereby give a lower total energy capture. As can be seen, the CorPower Ocean device has a similar performance in Wavehub and Bimep for the low ratings (25 to 100 kW), despite the different average resource. Wavehub met-ocean characteristics are a good match for this device, as the occurrences are concentrated on the low Hs–low Te area. It is noticeable how, in Wavehub, the smaller rating versions perform much better than the high ratings. In contrast, for instance in Yeu, the medium rating version performs as well as the small rating version
It is noticeable that EMEC is the location with the highest resource, although for some ratings (especially low ones) the energy delivery is poor compared to other sites. This can be explained by observing the characteristics of the scatter plot, as explained by [18]. The occurrence distribution and the energy distribution at EMEC are disjointed, which means that a large part of the annual available energy will be brought by a reduced number of sea states. Sea states with an energy period Te between 5.5 and 6.5 s make up nearly 50% of the annual occurrences, while they only represent 16% of the annual available energy. Most of the energy comes from high-energy, low-probability sea states that are not captured by the CorPower Ocean device. It should be noted that the specific device model being studied had been equipped with a PTO optimized for the lower end of the wave period range. A PTO optimized for longer waves would likely perform better at EMEC. It should be emphasized that the reference power matrix is optimized for Yeu and this penalizes the other locations. For future studies the power matrices will be calculated numerically and will be optimized for each location.
The comparison between Wavehub and DK North sea Point 2 should also be emphasized. Both locations have a similar resource level (16 and 12 kW/m), although the performance is completely different for some of the device ratings. For instance, the 25 kW device gives a farm AEP that is 1.5 times higher at Wavehub than in DK North Sea (while the resource is only 1.3 higher). This is due to the favourable distribution of the sea states in Wavehub, matching with the CorPower Ocean device performance.
As an alternative way to compare performance, Figure 5 presents the capture width ratio of the different converters (in this case for a single device). Capture Width Ratio (CWR) is a measure of the effectiveness of conversion with respect to the incident wave resource and the size of the device (see Babarit [15] for definition). It is calculated from the dimensions of the device, the available resource, and the annual energy production. The lower the CWR, the worse the conversion effectiveness and vice versa. In this figure some tendencies are clearly shown. For instance, all curves initially increase before holding steady.
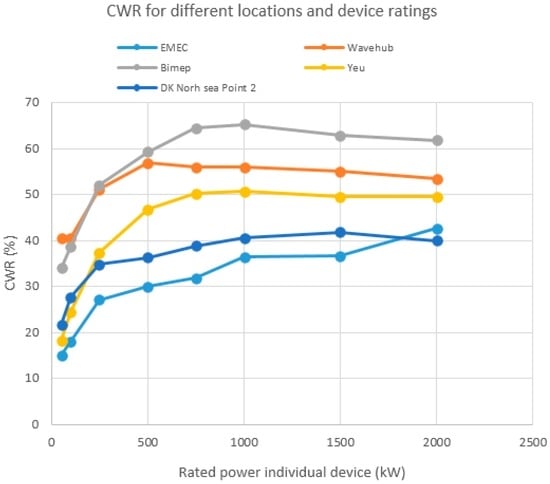
Figure 5.
Annual average capture width ratio (CWR) for different locations.
This means that the effectiveness of conversion is higher with higher ratings until they reach a threshold. In general, for most locations, higher CWR corresponds to ratings between 500 and 1000 kW. If the optimum CWR is computed for each of the locations it can be seen that they are different within a considerable range. This leads to the same idea previously mentioned about the site dependence of the rating decision, specifically that the CWR value for different ratings is site-related.
On the one hand, and checking the differences among locations, Bimep is the location with the highest CWR for all ratings except for 25 kW. On the other hand, EMEC is the location with the lowest CWR for most ratings (except 2000 kW).
In this analysis the LCOE as well as the financial indicators were calculated for the 20 MW wave farms. It should be noted that CAPEX was calculated using the procedure previously mentioned with the Scale factor. Also, OPEX was calculated following the first approach previously mentioned, taking OPEX as a percentage of CAPEX.
Figure 6 shows the LCOE of the analysed device for each of the ratings at each location. It is noticeable how the location DK, North Sea point 2 is the one with the highest LCOE for all ratings and shows a high difference compared with all other locations. This difference comes from the difference in the resource (12 kW/m as compared to other locations that have a resource of around 20 kW/m). Furthermore, it should be highlighted that for all locations the LCOE is higher for higher ratings. This contrasts with the results previously presented in the CWR figure. In the last comparisons all the locations had optimum ratings in terms of CWR at around 1000 to 2000 kW. In the LCOE case the minimum LCOE corresponds to the lowest rating option for all the locations.
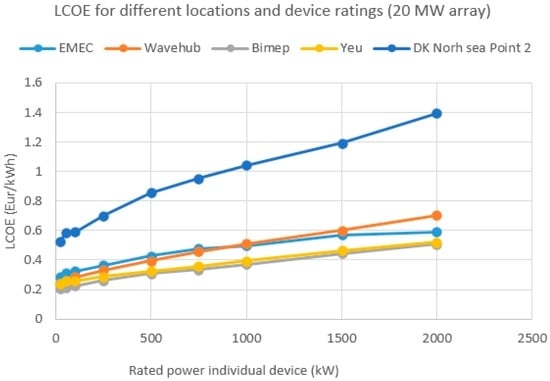
Figure 6.
LCOE for a 20 MW array.
This is due to the CAPEX and OPEX calculation. CAPEX is scaled with a scale factor of 2.39 as previously explained and OPEX is calculated as 8% of CAPEX. If these costs are compared to the AEP for all locations (Figure 4), it can be seen how the decrease in power production for the higher ratings is not balanced by a decrease in costs.
Also, the fact that OPEX is related to CAPEX in this approach means that the higher the rating the higher the OPEX, and so the benefit of maintaining a lower number of units to achieve 20 MW is not shown.
It is also noticeable that most locations have a fairly constant slope except for EMEC. As explained before, EMEC’s met-ocean conditions have a mismatch between energy and occurrences. The scatter plot in Figure 6 does not fit very well with the low ratings versions as the high power area of the power matrix is centred on the high Hs, high Te area.
In Figure 7 the Net Present Value of the 20 MW array is shown for all considered ratings. This figure shows similar results to the previous LCOE analysis. The differences between locations shown in the previous graph are highlighted here. The NPV is negative for DK North Sea Point 2 for all ratings considered in this study. It is also noticeable that rating options from 500 kW to 2000 kW have both positive and negative NPV depending on the location.
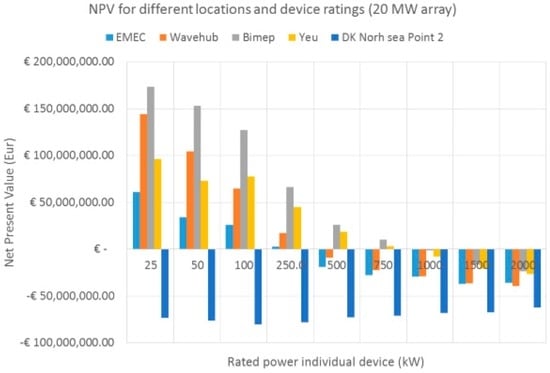
Figure 7.
Net present value for the 20 MW array.
4.2. Sensitivity Analysis: CAPEX and OPEX
The analysis performed in the last section is based on some assumptions regarding CAPEX and OPEX scaling. This section intends to perform a sensitivity analysis in order to check the dependency of the results on the assumptions.
Firstly, the CAPEX scaling function is going to be validated. The CAPEX scaling factor was calculated before based on some expert feedback for each of the modules (see Table 1). However, this factor is uncertain as the only way to calculate it properly is to have a budget for each of the rating options (which is unrealistic at this stage of development of the prototype). Due to this uncertainty, it was decided to perform a sensitivity analysis of the results with different CAPEX scaling factors.
Secondly, the OPEX was calculated as a percentage of the CAPEX following [6,7]. However, this approach is inaccurate as it relies on the CAPEX calculation and does not take into account the number of devices per MW, which is a key parameter for the sizing study.
In the second OPEX calculation approach it is assumed that every WEC has an inspection every two years, for all ratings tested in this case study. These inspections consist of a WEC retrieval, WEC inspection/repair on shore, and a WEC redeployment. Apart from this inspection, two other secondary inspections are budgeted: a general corrosion and biofouling inspection every two years and a diver mooring cleaning inspection every five years.
This OPEX calculation has been performed based on consultations with local maintenance companies in the Orkney Islands but was set as standard for all locations.
Table 3 shows the rating associated with the lowest LCOE for each of the sites and scaling factors, while Table 4 shows the same but with OPEX calculated with the second approach.

Table 3.
Rating option (kW) associated with minimum LCOE with OPEX calculated with the first approach.

Table 4.
Rating option (kW) associated with minimum LC with OPEX calculated with the second approach.
Table 4 shows how, in general, the ratings chosen with this OPEX calculation are much higher than under the first option. The second approach to calculate the OPEX benefits the higher ratings, as a low number of units (10 units for the 2000 kW case) makes it to 20 MW. This benefits a lower OPEX, as a lower number of vessels/transits are needed during the whole lifetime of the project. On the other hand, the low rating versions are decremented by the fact that a large number of devices (and then a large number of operations) are required to make it to 20 MW.
Notably, it has been assumed that the same type of vessel is used for all ratings. This assumption is partially inaccurate as, due to device size, different vessels are likely required for the 25 kW and the 2000 kW options, for example. However, due to the absence of data and in order to maintain simplicity, it was decided to proceed in this manner. If different vessels were considered this would probably disadvantage the high rating options as their OPEX would be higher.
With respect to the CAPEX scale factor, Table 3 shows that the rating choice depends on the scale factor but only for factors from 0.5 to 1.5, as for the higher factors the lowest rating (25 kW) is chosen. In this case, as OPEX and CAPEX are directly linked, the low rating versions are favourable.
In both tables it can be seen that the higher the Scale parameter, the lower the lowest LCOE rating version. This is due to the fact that AEP is higher for the low rating versions and if CAPEX scaling increases then the low-rated versions are benefited. In general, both tables show that the results are very dependent on initial assumptions and for a detailed study, an accurate CAPEX and OPEX calculation are required in order to avoid large uncertainties in the results.
4.3. Metrics Comparison among Devices
In the previous sections, LCOE was chosen as the metric to perform the sizing study. However, as noted in the previous section, many assumptions are required in order to compute the LCOE, mostly due to a lack of data.
Depending on the Technology Readiness Level (TRL being a method of estimating technology maturity of Critical Technology Elements (CTE) of a program during the acquisition process) of the prototypes, these LCOE assumptions can be more valid or closer to reality. However, for low to medium TRL prototypes it is sometimes difficult to use sensible assumptions due to the lack of data. Some authors such as Pascal et al. [19] suggest the use of other indicators (e.g., TPL (Technology Performance Level), or TRL-TPL-matrix) in order to demonstrate the commercial readiness of a prototype. Other authors such as Babarit [15] used indicators related to mass, surface, and energy in order to measure the performance of a particular device.
Within the latest attempts to find alternative metrics to LCOE, the Wave Energy Prize developed Average Climate Capture Width per Characteristic Capital Expenditure (ACE) as a way to measure the commercial performance of a prototype for low TRLs, Weber [18]. RST represents the Representative Structural Thickness, US Department of Energy [20].
Under this approach it has been determined that the total surface area adjusted for material cost tracks most closely to capital cost, which is the most important LCOE driver for WEC devices today, along with annual energy production (AEP). The two components that comprise the ACE ratio are the Average Climate Capture Width that measures the conversion capacity of the device, and the Characteristic Capital Expenditure that represents an indicative CAPEX cost based on some material estimations (see Weber [18] for a complete definition).
In this section a comparison of several devices is shown with different indicators. The devices have been taken from Babarit [15] and they have been compared with the CorPower Ocean 250 kW device. The metrics selected for this comparison are the Capture Width Ratio that measures the effectiveness of the conversion with respect to the incident resource (similar to the capacity factor in wind energy), the kWh per kg that represents the absorbed energy per unit mass, the MWh per m2 that represents the absorbed energy per surface unit, and the ACE that is a proxy for LCOE.
The capture width ratio, the kWh per kg, and the MWh per square meter for the first eight devices were taken from Babarit [16], while the ACE was calculated for all devices based on a thickness assumption, a steel density, and a cost of steel per kg. For the CorPower Ocean device all the indicators have been calculated according to the device specifications and the material (glass fibre) characteristics.
Table 5 shows indicators for each of the converters presented in Babarit [16], and the CorPower Ocean device, for the Yeu location. This location was selected because the CorPower 250 kW device is optimized for this location. If attention is fixed on the Capture Width Ratio, it can be seen that the bottom fixed oscillating flap is the one with the highest CWR, followed by the floating OWC and the floating two-body heaving converter.

Table 5.
Metrics comparison for the Yeu location.
This contrasts with the kWh per kg indicator. In this case the highest figure corresponds to the CorPower Ocean 250 kW device (by approximately an order of magnitude), followed by the bottom-fixed heave-buoy array.
With respect to the MWh per surface area, the highest figure corresponds to the CorPower Ocean device followed by the bottom fixed oscillating flap and the floating OWC (those devices are the only ones that are above 1 MWh/m2).
As can be seen from the comparison of these indicators, depending on the nature of the metrics, the results change completely. An efficient conversion (with a high CWR) does not necessarily mean efficiency in economic terms. This concurs with the conclusion by MacGillivray et al. [9]. The new indicator ACE (as a LCOE proxy for low TRL prototypes) pretends to collate performance and costs together when the scarcity of data is still very important.
As Table 5 shows, the CorPower 250 kW device is the one with the highest ACE (25.92 m/M€) followed by the floating OWC (11.26 m/M€) and the bottom-fixed oscillating flap (7.99 m/M€). These results are similar to the MWh per surface area indicator. Unfortunately, there are no LCOE values for these converters in order to compare ACE with LCOE.
5. Relation of LCOE to Other Indicators
In the previous section, several indicators were chosen as proxies for LCOE. It was concluded that the different indicators give different answers/scores depending on what they measure. Therefore, when making decisions based on these indicators, it is important to understand what they measure and how they relate to LCOE.
As these indicators are normally used for early TRL technologies when LCOE is difficult to calculate, the relation of LCOE to these metrics is still unknown. This section tries to identify the relation between these metrics and LCOE in order to identify which indicators are more closely linked and so can be used for optimization purposes.
All Corpower device rating options studied in Section 3 in each location have been plotted here. In the following figures, LCOE (calculated with the first approach; OPEX as a percentage of CAPEX) is plotted against other indicators. This comparison is carried out for several ratings of the Corpower device, intending to find relations between various metrics and LCOE, although the findings are specific to this device. Moreover, it should be highlighted that the purpose of this work is to find the parametric relations (linear, power, or logarithmic) between the metrics, not specific numeric relations. Taking that into account, similar relations would be expected for other devices, although future studies will need to prove this.
Figure 8 shows LCOE versus CAPEX in Euros (€). This plot will be of use when taking device sizing decisions. It should be noted that, in general, the curves have a decreasing tendency and a lower LCOE generally means a higher investment.
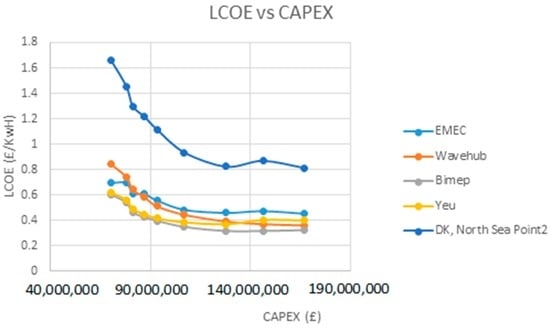
Figure 8.
CAPEX (€) vs. LCOE (€/kWh).
However, this tendency does not mean that the option with highest CAPEX needs to be chosen. When financing a marine renewables project, different financing products might be available depending on the size of the project and sometimes a higher initial investment can mean worse financing rates.
It should be noticed that for the last part of the curve (CAPEX ranging from 140 M€ to 160 M€) the decrease in LCOE is very mild and so a slightly higher LCOE could mean a big decrease in the initial investment.
From this figure it can be concluded that, although LCOE is the main indicator for techno-economic decision making, it is also useful to take into account the amount of investment required.
The remaining figures in this section show a variety of alternative indicators plotted against LCOE.
Figure 9 show energy per square area versus LCOE. All curves for the various sites have a similar behaviour, although it cannot be said that a clear relationship can be established between this indicator and LCOE. The curves have a descending tendency until a certain point but a clear parametric relationship between these two parameters cannot be identified.
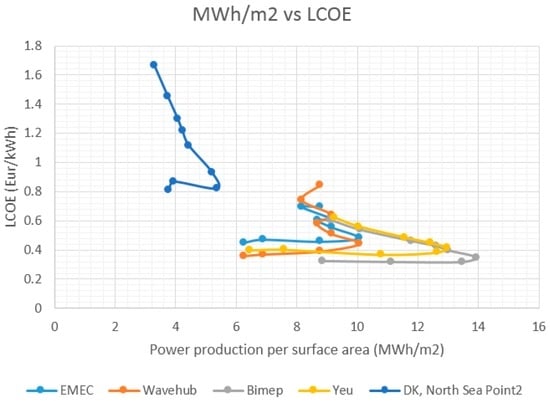
Figure 9.
Energy per surface area vs. LCOE.
It should be noticed that these relationships are specific for the device studied within this paper and that other, more clear relationships might exist for other devices.
Figure 10 shows the energy absorbed per mass coefficient against LCOE. As can be seen, all lines follow a similar distribution. Different regression types have been tested for the dots and a power distribution was found to have the highest correlation coefficient for all sites.
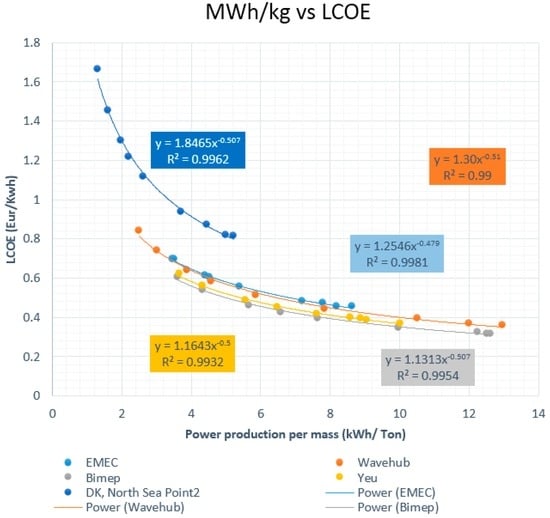
Figure 10.
Energy per mass vs. LCOE.
It should be highlighted that for all sites the regression has a similar format, a location dependent coefficient and a number close to −0.5 on the exponent. This relation is detailed in Equation (10):
where RDC is a resource/location dependent coefficient.
Figure 11 shows ACE plotted against LCOE for the various locations and ratings. As in previous figures, all curves show similar behaviour with a power relation between ACE and LCOE. In this case, again, the relation is constant and is represented by Equation (11):
where RDC is a resource/location-dependent coefficient.
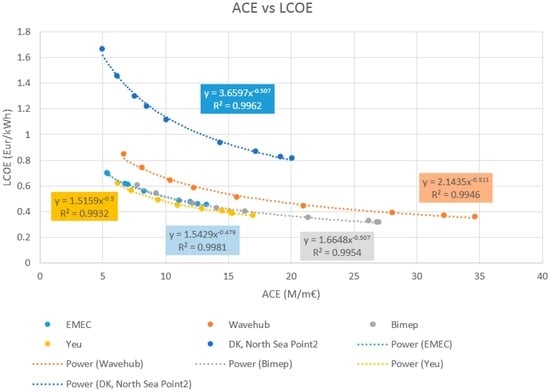
Figure 11.
ACE vs. LCOE for the different locations.
It should be noted that these relations are found for a specific device. The main use of these relations between LCOE and the other indicators should be for optimization purposes within the early stages of design of a device. Both the energy per mass indicator and ACE are easily calculated and can be the objective function for any kind of optimization performed within the device. Evidently these relations should not be used for comparison amongst devices as the different devices might have different numerical coefficients.
6. Conclusions
In this paper a techno-economic study of a real prototype has been developed for several sizes/ratings of wave energy converter. The aim of this study was to define the optimum scale/rating for a full-scale prototype in a 20 MW wave farm.
The results, in general, show a tendency for low to medium ratings (100 kW to 250 kW) to be optimum. However, it should be highlighted that the base assumptions were found to be key in the sizing decision. For this kind of study, a methodology to calculate CAPEX and OPEX is always required.
CAPEX and OPEX calculations are very important and, depending on the methodology used, the sizing results might be completely different. For instance, if OPEX is calculated as a percentage of CAPEX, this benefits the lower rating options, while if OPEX is based on a fixed repair scheme then the high rating options are benefited (due to the lower number of devices/repairs needed to make it to the total rated power of the farm).
It can be concluded that the sizing decision is relatively independent of the location (within similar resource levels). In this case study, most of the locations showed similar behaviour and had the same optimum ratings. It should be noticed that, when locations have a low resource, then the location becomes important for the sizing decision (this is clear from the results of DK, North Sea Point 2).
A comparison of several devices has been carried out, using different metrics taken from Babarit [14] as a basis. These indicators are useful for low TRL technologies when LCOE requires many assumptions to be made. The results show completely different behaviours depending on the indicators taken into account. It was, for instance, concluded that capture width ratio is an indicator that shows hydrodynamic effectiveness although it does not necessarily match with techno-economic performance.
Finally, a comparison of the different metrics and LCOE was performed within this work. It was found that while energy per surface area does not have any clear relation with LCOE, both energy per mass and ACE do. Both indicators have a power relation with LCOE with an exponent of −0.5 and a resource/location-dependent coefficient. These relations are useful for optimization purposes as objective functions when LCOE cannot be calculated properly.
It should be noted that the results of this study depend heavily on all the assumptions, for instance the scaling of the power matrices by the Froude law. Future research will validate this power matrix scaling through numerical modelling. Furthermore, many assumptions have been performed in terms of the OPEX calculation; for instance, it should be taken into account that the same level of availability/accessibility was taken for all locations. This assumption is partially inaccurate and future studies will consider different levels for different locations. Due to all these uncertainties related to the assumptions, a Monte Carlo analysis will be carried out in future research to analyse the effect of each of the variables on the techno-economic results.
Acknowledgments
The authors gratefully acknowledge the financial support from Wave Energy Scotland to the HiDrive project, and from KIC InnoEnergy and the Swedish Energy Agency for the HiWave project. Also, the authors would like to thank EPSRC for covering the fees for open source publication of this paper.
Author Contributions
Adrian de Andres led the work on this paper. He set up the techno-economic model and analyzed the results. Jéromine Maillet assisted with the CAPEX and OPEX calculation for the Corpower device. David Bould, Henry Jeffrey, Jørgen Hals Todalshaug and Patrik Möller provided very useful feedback on the results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- SI Ocean (Strategic Initiative for Ocean Energy). Ocean Energy: State of the Art; SI Ocean: Brussels, Belgium, 2012. [Google Scholar]
- Azzellino, A.; Conley, D.; Vicinanza, D.; Kofoed, J.P. Marine renewable energies: Perspectives and implications for marine ecosystems. Sci. World J. 2013. [Google Scholar] [CrossRef] [PubMed]
- Gunn, K.; Stock-Williams, C. Quantifying the global wave power resource. Renew. Energy 2012, 44, 296–304. [Google Scholar] [CrossRef]
- MacGillivray, A.; Jeffrey, H.; Hanmer, C.; Magagna, D.; Raventos, A.; Badcock-Broe, A. Ocean Energy Technology: Gaps and Barriers; SI Ocean: Brussels, Belgium, 2013. [Google Scholar]
- Farrell, N.; O’Donoghue, C.; Morrissey, K. Quantifying the uncertainty of wave energy conversion device cost for policy appraisal: An Irish case study. Energy Policy 2015, 1, 62–77. [Google Scholar] [CrossRef]
- O’Connor, M.; Lewis, T.; Dalton, G. Operational expenditure costs for wave energy projects and impacts on financial returns. Renew. Energy 2013, 50, 1119–1131. [Google Scholar] [CrossRef]
- Guanche, R.; de Andrés, A.D.; Simal, P.D.; Vidal, C.; Losada, I.J. Uncertainty analysis of wave energy farms financial indicators. Renew. Energy 2014, 68, 570–580. [Google Scholar] [CrossRef]
- The European Offshore Wind Industry. Key Trends and Statistics 1st Half 2015; European Wind Energy Association: Brussels, Belgium, 2015. [Google Scholar]
- MacGillivray, A.; Jeffrey, H.; Winskel, M.; Bryden, I. Innovation and cost reduction for marine renewable energy: A learning investment sensitivity analysis. Technol. Forecast. Soc. Chang. 2014, 87, 108–124. [Google Scholar] [CrossRef]
- IEA (International Energy Agency). Projected Costs of Generating Electricity; IEA: Paris, France, 2015. [Google Scholar]
- De Andres, A.; Guanche, R.; Vidal, C.; Losada, I.J. Adaptability of a generic wave energy converter to different climate conditions. Renew. Energy 2015, 78, 322–333. [Google Scholar] [CrossRef]
- De Andres, A.; MacGillivray, A.; Cuanche, R.; Jeffrey, H. Factors Affecting LCOE of Ocean Energy Technologies: A Study of Technology and Deployment Attractiveness. In Proceedings of the International Conference on Ocean Energy, Halifax, NS, Canada, 4–6 November 2014.
- Chozas, J.F.; Kofoed, J.P.; Jensen, N.E.H. User Guide—COE Calculation Tool for Wave Energy Converters: Ver. 1.6—April 2014 1st; DCE Technical Reports; No. 161; Department of Civil Engineering, Aalborg University: Aalborg, Denmark, 2014. [Google Scholar]
- O’Connor, M.; Lewis, T.; Dalton, G. Techno-economic performance of the Pelamis P1 and Wavestar at different ratings and various locations in Europe. Renew. Energy 2013, 50, 889–900. [Google Scholar] [CrossRef]
- Babarit, A. A database of capture width ratio of wave energy converters. Renew. Energy 2015, 80, 610–680. [Google Scholar] [CrossRef]
- Babarit, A.; Hals, J.; Muliawan, M.J.; Kurniawan, A.; Moan, T.; Krokstad, J. Numerical benchmarking study of a selection of wave energy converters. Renew. Energy 2012, 41, 44–63. [Google Scholar] [CrossRef]
- Guanche, R.; de Andrés, A.; Losada, I.J.; Vidal, C. A global analysis of the operation and maintenance role on the placing of wave energy farms. Energy Convers. Manag. 2015, 106, 440–456. [Google Scholar] [CrossRef]
- Weber, J. WEC Technology Readiness and Performance Matrix—Finding the best research technology development trajectory. In Proceedings of the International Conference on Ocean and Energy, Dublin, Ireland, 17–19 October 2012.
- Pascal, R.; Torres, A.; Gonzalez, A. Going Further Than the Scatter Diagram: Tools for Analysing the Wave Resource and Classifying Sites. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015.
- US Department of Energy. Wave Energy Prize Rules; US Department of Energy: Washington, DC, USA, 2012.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).