1. Introduction
Since the beginning of the 21st Century, the structure of the world energy market appeared to have obvious change trends, mainly reflected in the consumption structure change and consumption center transfer. After oil and coal dominated the world energy consumption market, the oil crisis, soaring prices and environmental pollution appeared. Some nations and politicians emphasized the necessity of diversified energy consumption and clean energies, and the proportion of oil and coal in primary energy consumption are falling relatively. Moreover, nuclear energy development will still be constrained to some extent, and natural gas and renewable energy will play an important role in the future energy market. Natural gas with low-pollution and high heat value tends to grow continuously due to the breakthrough of nonconventional natural gas, and natural gas is promising to gradually substitute oil, coal and other energy resources and become the main energy product in the future—the global gas consumption has increased nearly 50% in 2015, and is becoming the fastest growing product in the fossil fuel sector. In recent years in developing countries, especially emerging markets, the energy industry and energy demand have been expanding rapidly, International Energy Agency (IEA) forecasts that India and China will become major energy consumers by 2040, and two countries may account for 50% of the increase in world energy demand. Ten developing countries such as Brazil, Mexico account for 30% (IEA, 2015). As the government support of emerging economies increases and energy consumption of developed economies is relatively weak, the influence of emerging economies on the future world energy consumption gradually intensifies. The emerging economies at the stage of industrialization and urbanization grow rapidly, and their energy demand increases rigidly; however, they are also constrained by resources and environment, so natural gas as a cleaner fossil energy is very suitable for a low-carbon energy system and likely to be transferred to emerging economies and make them become the main consuming subjects of natural gas.
As a clean energy, natural gas is widely studied in academics, and most analysis and forecasts tend to focus on studying the influential factors. The most common studies research the causal relationship between gas consumption and economic growth. For example, Kum et al. [
1] examined the relationship between natural gas consumption and economic growth of the G7 countries using a bootstrap-corrected causality test. Apergis et al. [
2] found the existence of bidirectional causality between natural gas consumption and economic growth in the long run using a panel vector error correction model. However, we also find that the results of the relationship between the two variables exist considerable differences. While there is a positive relationship between two variables, the policy of protecting natural gas would hinder the economy [
3], but the result found in Işik [
4] is that natural gas consumption and economic growth are negatively correlated in the long term. The urbanization process leads to a downward trend for energy consumption [
5], although many studies demonstrate that there was positive causality running from urbanization to energy consumption, and higher urbanization rate might lead to higher energy use [
6,
7,
8], a strongly negative correlation between urbanization and energy consumption also exists in many studies [
9,
10]. Industrialization as an influencing factor is also examined by a number of studies. Zamani [
11] investigated a long-term bidirectional relationship between natural gas consumption and industrial added value using the parsimonious vector error-correction (PVEC) model. Jiang et al. [
12] estimated the relationships between energy consumption, industrialization and urbanization by comparing China with America and Japan, and the results indicated that the shorter transition industrialization phase is, the faster energy demand grows. According to the above research results, we obtain that economic growth, urbanization and industrialization as determinants of energy and natural gas consumption have been widely studied, and in fact, natural gas consumption of China and other emerging economies is growing rapidly in the stimulation of economic growth, urbanization and industrialization [
13]. Therefore, this paper specified GDP per capita, industrialization and urbanization to further examine the relationships between natural gas consumption and those economic variables.
All the above-mentioned studies investigated natural gas consumption based on the linear regression model, however, since the relationship between variables follows an asymmetric and nonlinear model in economic phenomenon, the estimated results obtained from a linear model may not reliable, and it is most likely that natural gas consumption follows a certain nonlinear model [
14]. As shown in a study conducted in Aslan [
15], natural gas consumption in approximately over 60% of 50 states follows a nonlinear behavior. In fact, research in energy consumption’s nonlinearity involves a mechanism transition model’s application with representativeness and universality, including Markov regime switching (MRS) model, threshold regression (TR) model and smooth transition regression (STR) model. In a study obtained in Fallahi [
16], the result showed that the causality between GDP and energy consumption differs in different regimes, by adopting a Markov-switching vector autoregressive (MS-VAR) model. However, Moral-Carcedo et al. [
17] concluded that the STR model is superior to the other two models when examining Spain’s electricity consumption using STR model, TR model and RS model respectively. Likewise, Zhao et al. [
18] also adopted nonlinear STR model and found that the effect of China’s economic growth in energy consumption has nonlinear, asymmetric and periodic characteristics. Kani et al. [
14] applied the same STR model and obtained a result that there exist nonlinear relationships between natural gas demand and GDP, and natural gas price and temperature, by taking the actual natural gas price as transition variable. Following the STR model, which applies to time series, the PSTR application on panel data has also been widely used in the field of energy. He et al. [
19] studied the nonlinear relationship between China’s energy consumption and economic growth using PSTR model. Lee et al. [
20] also used the PSTR model to study the nonlinear relationships between electricity consumption and actual income, electricity price and temperature by using 24 OECD countries data, and Bessec et al. [
21] analyzed European electricity consumption using the same method.
Through the analysis of existing literature, we find that, in terms of the research methods, the relationship analyses among variables mostly adopt co-integration tests and causality tests, which are for linear relationships. Even where some papers found nonlinear characteristics, less practical models are established. And regarding the research object, most of the existing published studies of nonlinear behaviour have focused on the electricity consumption and total energy consumption; nonlinear researches of natural gas consumption are relatively few. In addition, regarding the selected data, the most used data in the existing research is the time series, and the established model based on this cannot analyze regional differences. For the studies using the panel data, most use a linear model or selected single country or OECD as panel. In recent years, the rapid development of emerging economies has caused scholars to give more attention to the emerging markets’ energy consumption. For example, Sadorsky [
22,
23] studied the relationship among energy consumption, income and financial development in emerging economies. Asif et al. [
24] made a comparative study on developed economies and emerging economies about energy supply, energy consumption and energy security. But most of these studies are based on linear models and take the total energy consumption as the research object. As is known, as the pattern of energy consumption center transfers and consumption structure transformation is gradually formed, the study of natural gas consumption of emerging economies plays a particularly important role in grasping the development trend of the world’s energy. Thus, this paper chose emerging economies as panel, including those countries with rapid economic growth, since their industrialization and urbanization continue to make progress and have great potential in the future. We select three variables—GDP per capita, industrialization and urbanization rate—as explanatory variables to study the nonlinear relationships between natural gas consumption and three economic variables by employing a nonlinear PSTR model, and utilize this to learn about the trend of natural gas consumption of emerging economies and recognize the optimization potential of energy consumption structure. Moreover, this paper provides a reference for these emerging countries to make optimization policies about industrial structure and population structure during economic development in consideration of energy saving, energy consumption structure optimization and other sustainable development strategies.
The remainder of this study is organized as follows:
Section 2 introduces the variables, data and model specification in this paper, including variables’ definitions, data sources and data processing, and PSTR model introduction;
Section 3 is empirical results, including stability test of variables, nonlinear test of model and estimation of PSTR model;
Section 4 concludes the discussion.
2. Variables, Data and Model Specification
2.1. Definition of Variables and Data
According to the existing research, we choose per capital GDP, industrialization and urbanization as the transition variables.
Per capital GDP: The rapid development of economy tends to be accompanied by strong energy demand [
2], and Kani et al. [
14] in the study pointed out that there exists a nonlinear relationship between gas demand and GDP. Many other studies also examined the nonlinear relationship by investigating whether a “Kuznets curve” for energy use exists [
25,
26,
27]. Therefore, as one of the decisive factors, the relationship between economic growth and natural gas consumption may show nonlinear and complicated characteristics and is taken into the research scope of this paper by specifying per capital GDP as transition variable.
Industrialization: Industrial development could increase energy consumption and the cost of energy [
11,
12], and in regard to the gas consumption structure of industry, the industrial consumption proportion of natural gas is about 60%–85% in most emerging markets. This means that there may be a great stimulus impact of industrialization on natural gas consumption in emerging markets. On the other hand, industrial development also can promote the progress of various technologies; technological progress can improve energy utilization rate in turn, thereby saving energy. This uncertain effect of the industrial level on energy consumption may be due to the nonlinear relationship among them in different stages of industrialization and requires that we use it as transition variable in this article to further analysis.
Urbanization: Jones [
28] estimated the energy consumption of urban residents generally was about 3.5–4 times that of rural residents and was given priority to the high quality energy such as natural gas, electricity. Therefore, with the movement of rural residents to towns, the demand of natural gas will rise. Moreover, in terms of urbanization development law, Northa [
29] pointed out that the process of urbanization has a periodic trend, and its whole process of development can be depicted by an “inverted S” curve. Whether gas consumption also shows this kind of nonlinearity because of urbanization’s development law should not be ignored in our study.
Since first proposed in 1979, the definition of emerging economies is continuously enriched along with the progress of economic globalization and the improvement of marketization reform in developing countries. English weekly magazine, The Economist, advanced the “BRICS” (i.e., the five major emerging economies including Brazil, Russia, India, China and South Africa) and the “Next-11” (i.e., the next 11 emerging economies including Bangladesh, Egypt, Indonesia, Iran, South Korea, Mexico, Nigeria, Pakistan, the Philippines, Turkey and Vietnam) in 2006, and classified emerging economies into two gradients. The International Monetary Fund (IMF), in its 2009 World Economic Outlook, listed 26 emerging economies. Boao Forum for Asia 2010 defined 11 developing countries in G20 as “E11” emerging economies. In combination with the definitions of emerging economies above, this paper selects 16 major natural gas consuming countries in emerging economies as research objects in respect that the proportion of natural gas consumption in global natural gas consumption exceeded one percent in 2014, and the panel data is annual and its period is from 1995 to 2014, the related database sources including World Bank Database and 2015 BP Statistical Reviews of World Energy. Variables in this paper include an explained variable: natural gas consumption (counted as billion cubic meters); and explanatory variables: GDP per capita (counted as USD), industrialization (weight of industrial value added in GDP, %) and urbanization rate (weight of urban population in gross population, %).
2.2. Model Specifications
This paper studies the nonlinear relationships among natural gas consumption, GDP per capita, industrialization and urbanization rates of emerging economies by the panel smooth transition regression (PSTR) model followed by González et al. [
30] and Fouquau et al. [
31]. The two-regime PSTR model is defined as follows:
Here,
,
,
and
represent the log-transformed natural gas consumption, log-transformed GDP per capita, log-transformed industrialization and urbanization rate, respectively;
is the error term;
,
,
and
denote the time dimension and cross-section of the panel, respectively; Coefficient
represents the fixed individual effect. Normally, the transition variable
may be an exogenous variable or a combination of the lagged endogenous one, as noted by Dijk et al. [
32]. In this study we employ lagged endogenous variables as transition variables, including
,
and
, and select which one is the optimal variable.
The transition function
is a continuous function of the observable transition variable
and is normalized to be bounded between 0 and 1. More generally, the value of
determines the value of the transition function
, so the effective regression coefficient of individual
at time
is
,
and
. We follow Granger and Teräsvirta [
33,
34] by using the logistic transition function specification:
where
is a m-dimensional vector of location parameters, and the smooth parameter
determines the smoothness of the transition. In the empirical study, it is usually sufficient to consider
or
, as these values allow for commonly encountered types of variation in the parameters [
32]. For
, note that a logistic PSTR model with two regimes are associated with low and high value of
, and effective coefficient changes around
monotonously, e.g., from
to
. When
, the transition function
becomes an indicator function,
if
, and
if
. In this case, the PSTR model is reduce to the two-regime panel threshold model followed by Hansen [
35]. For
, transition function falls to its minimum at
, and attains the value 1 both at low and high value of transition variable
, when
, the model is a three-regime threshold model whose low regime and high regime are identical and different from the middle regime. Normally, when
and
, the model still is obviously two regimes, and the value of transition function between 0 and 1. For any value of
the transition function
becomes constant when
, in this case, the model collapses into a homogeneous or linear panel regression model with fixed effects.
To improve the potential endogeneity bias, we follow Fouquau et al. [
31] and Lee et al. [
20] and adopt the instrumental variable (IV) estimators in this context. The estimation of the parameters is carried out in two steps. Firstly, the individual effects
are eliminated by removing individual-specific means. The individual means in Equation (1) are as follows:
Here,
,
,
,
,
,
,
and
are individual means. Subtracting Equation (3) from Equation (1) yields:
Let
and
, Equation (4) can be written as:
The matrix of the instrumental variables is . Let , where , .
The matrix of transformed explanatory variables
and the matrix of instrumental variables
depend on the parameters of the transition function. Thus we need a recalculation at each iteration, and, given a couple
, the estimate can be yielded by using the instrumental variables as follows:
4. Conclusions and Policy Implications
With the speeding up of economic growth and the advancement of industrialization and urbanization, energy demand also increases quickly. Compared to the developed economies, energy consumption is rising the fastest in emerging economies. Upon the dual stimulation of low-carbon development strategies and energy consumption structure optimization, natural gas as a kind of clean energy plays an important role in reducing the greenhouse effect and diversified energy products. Thus, it is important to accurately examine the influence factors and characteristics of natural gas consumption, for understanding expectations of supply and demand and formulating appropriate development policy. After the overview of many references about nonlinear studies on energy consumption, this paper attempts to study natural gas consumption using the PSTR model and data from 16 emerging economies, and draws the following conclusions.
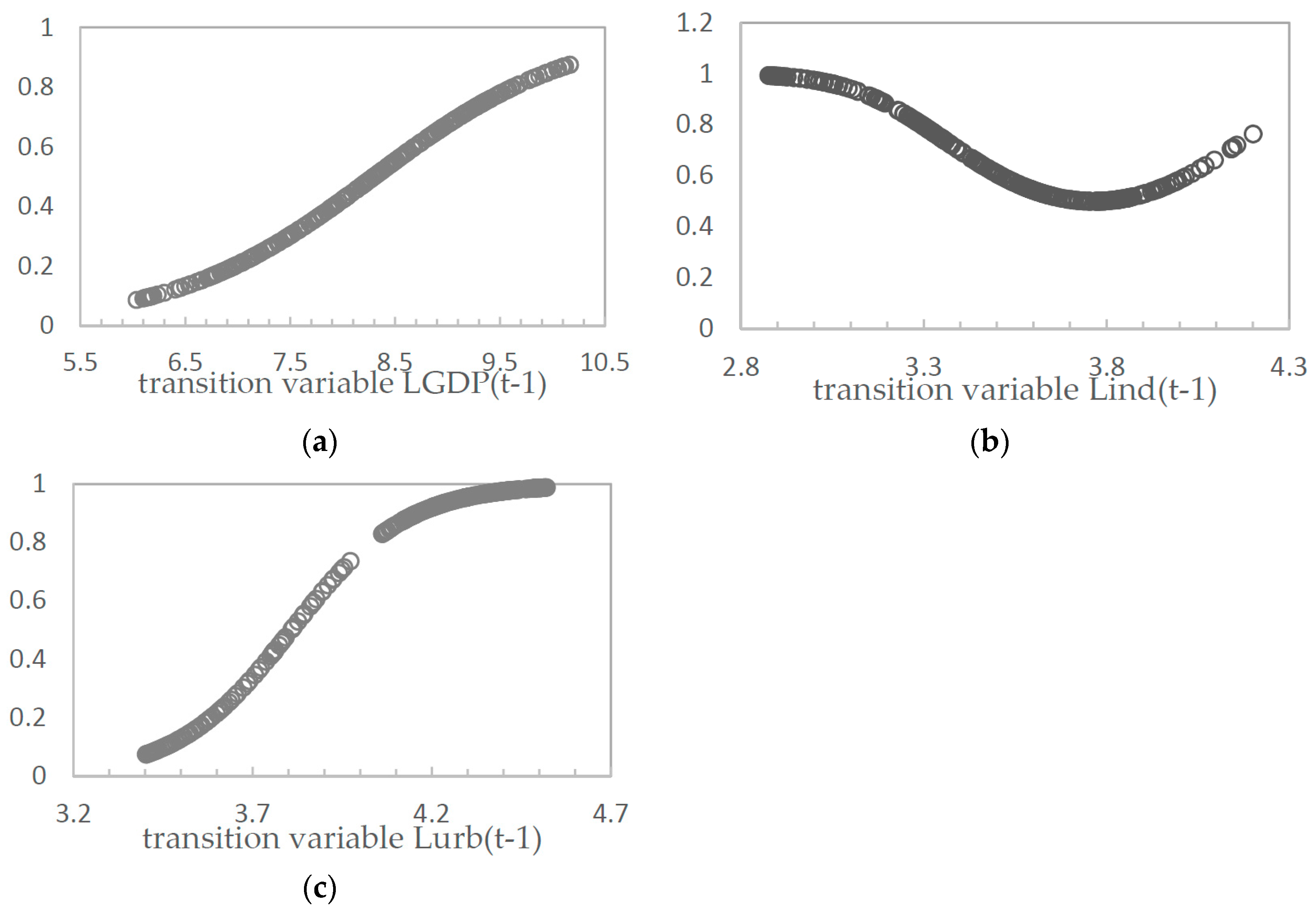
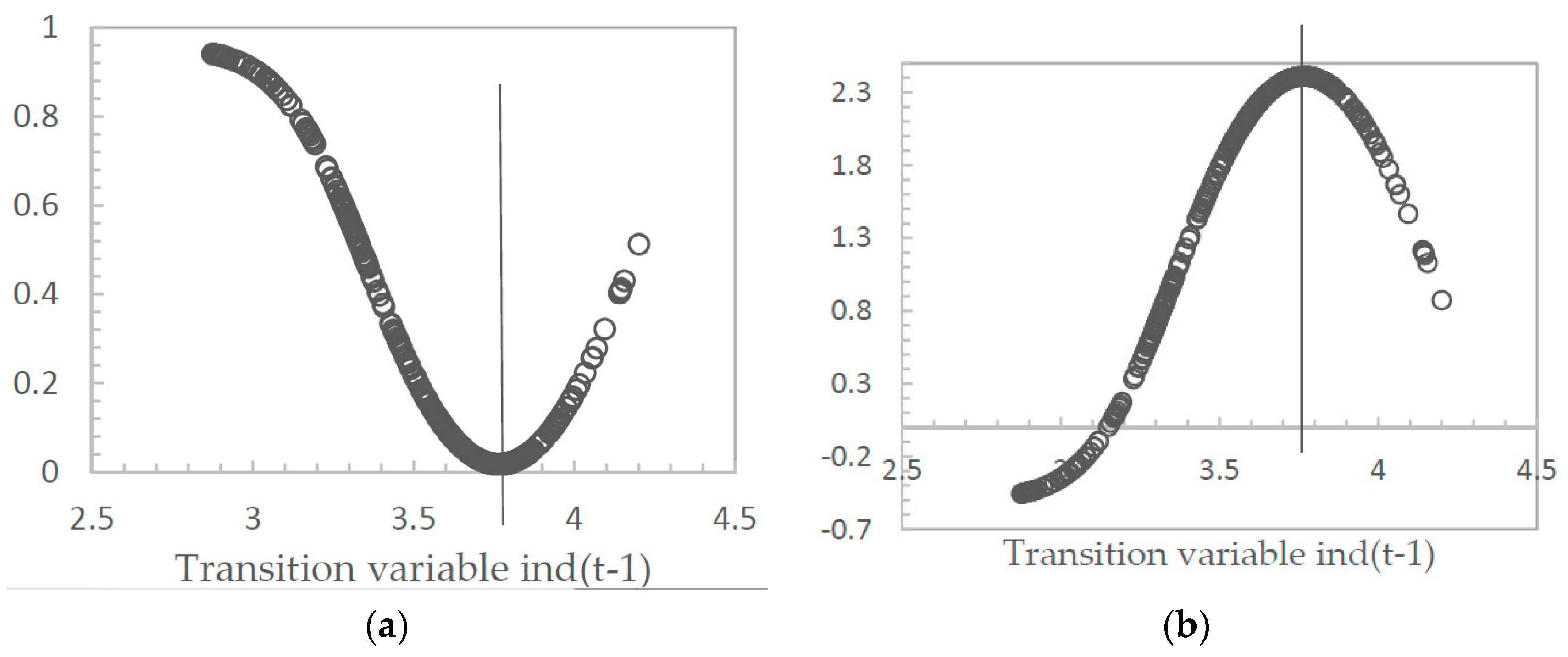
First, the empirical results show that evidence reported for a nonlinear relationship among natural gas consumption, GDP per capita, industrialization and urbanization. Such a nonlinear result may be the reason why existing studies on natural gas consumption, economic growth and industrial development appear to give diverse results. Results from three nonlinear models where the optimal model uses industrialization as transition variable, implying that the influence of industrialization on natural gas consumption of current emerging economies is non-negligible.
Second, specifying GDP per capita, industrialization and urbanization as transition variables, the threshold level of system transformation is US $4,023.8, 43.2% and 45.1%, respectively. Before and after the turning point, the effect of per capita GDP on natural gas consumption is relatively complex. When the transition variable is itself, the effect on natural gas consumption is promoting in the two regimes; when industrialization is adopted as the transition variable, influence effects range from inhibition to promotion, and the effects are relatively small comparing with another influential factors generally. When the transition variable is urbanization, influence effects range from promotion to suppression. The impacts of industrialization on natural gas consumption are from promotion to suppression in three PSTR models, which means that industrial transformation and upgrading can save energy, and that industrialization is also a major factor impacting natural gas consumption from estimated coefficients. The influence of urbanization on natural gas consumption is always to promote, which suggests that urbanization will bring huge gas consumption and its growth is rigid.
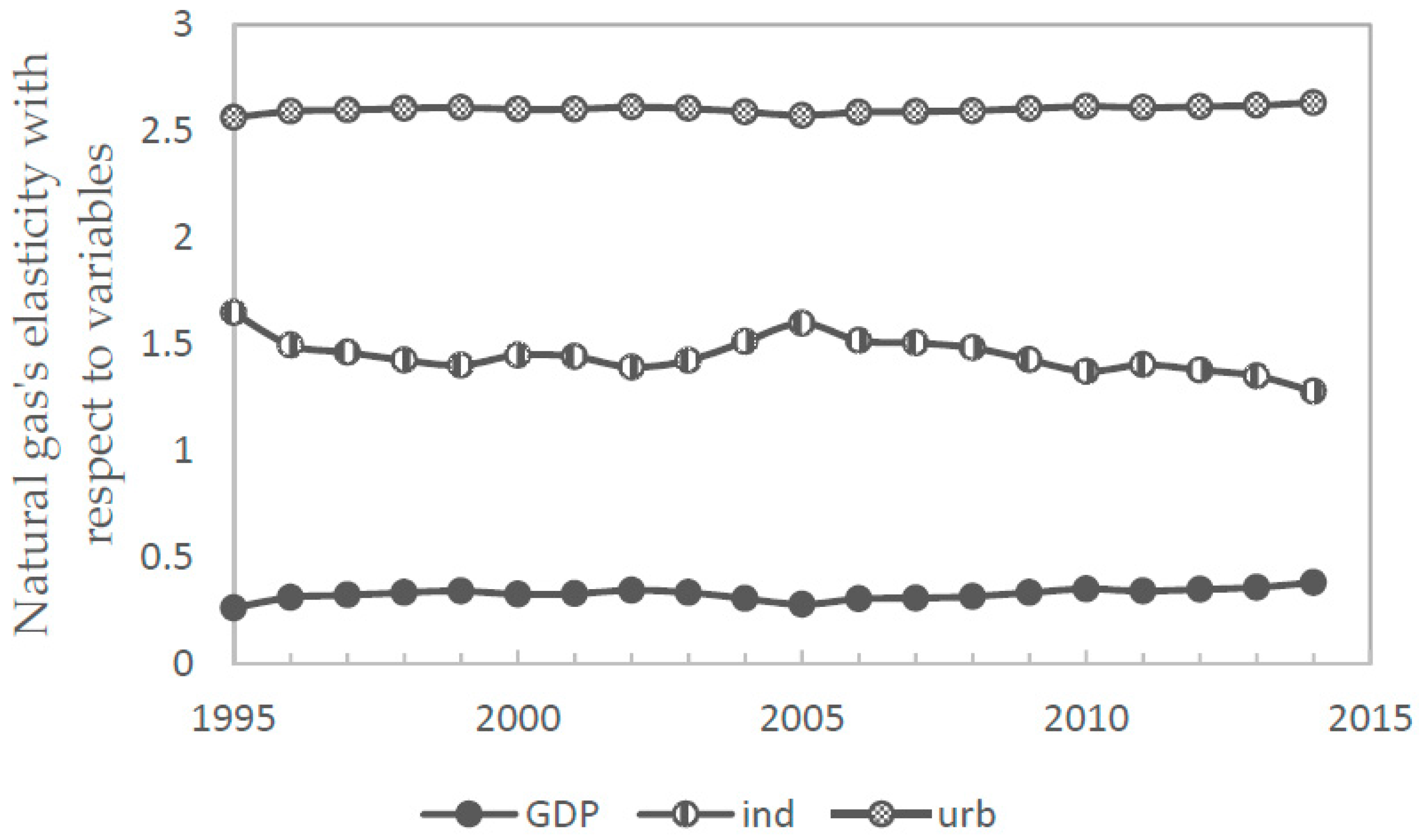
Third, the estimated elasticities of the time dynamic suggest that natural gas consumption has inelastic GDP per capita, elastic industrialization, and elastic urbanization. Moreover, the elasticity of GDP per capita fluctate and rise generally as time goes by, which may be because emerging economies are still in economic transformation and upgrade stages, and economic development promotes not natural gas consumption specifically but gross energy consumption, implying that economic development costs energy consumption, but this study obtains that natural gas consumption is insensitive to the change of GDP per capita. The elasticity of industrialization tends to fall with fluctuations, which is because both the dual pressure from industrial transformation and upgrade, energy saving and emissions reduction and technological advancement inhibit energy consumption, inclusive of natural gas consumption, when industrial development reaches a certain level. The elasticity of urbanization shows linear and stability features at a high level over time, because natural gas consumption is mainly for civil use, and the consumption of household energy is normally rigid, and its contribution to natural gas consumption is large under the pull of urbanization.
Forth and finally, according to the regional difference analysis for 16 emerging economies, the results show that an influential effect on natural gas consumption exists with significant regional difference during economic development. Most of these countries are in the first regime of the industrialization level, and in this regime the promotion effect of GDP per capita on natural gas consumption gradually weakens. The influence of industrialization on natural gas consumption turns from negative to positive, and then this promotion becomes further strengthened with the progress of industrialization.
The findings suggest that any factor of natural gas consumption changes cause structural change of the relationships among natural gas consumption, GDP per capita, industrialization and urbanization rate. According to the above research, we can provide the following beneficial conclusions for the sustainable development of emerging economies. Firstly, under the environment of global economic downturn and coexisting energy shortage problem, the industry upgrading and transformation strategy for emerging economies is the engine of economic development and also plays an important role in saving energy. Secondly, regardless of which stage the countries are in, the development of urbanization may make natural gas consumption under pressure of accelerated growth in the future. While the increase of natural gas consumption is the embodiment of the energy consumption structure optimization, on the other hand, countries should be prepared for changes to the natural gas supply in the development of urbanization. Thirdly, countries should focus on the complex relation between natural gas consumption and per capita GDP in different transition variables, and develop relevant strategies according to their own development policy and development stage properly. Lastly, the most important is that each country should not ignore the “threshold effect” between industrialization and natural gas consumption, and the structural change caused by the transition variable of industrialization should be taken into full account when analyzing and forecasting the natural gas consumption of emerging economies. Moreover, policy-makers should not neglect such nonlinear relationships of natural gas consumption before taking any measurements about economic development and sustainable development.