Identifying Potential Area and Financial Prospects of Rooftop Solar Photovoltaics (PV)
Abstract
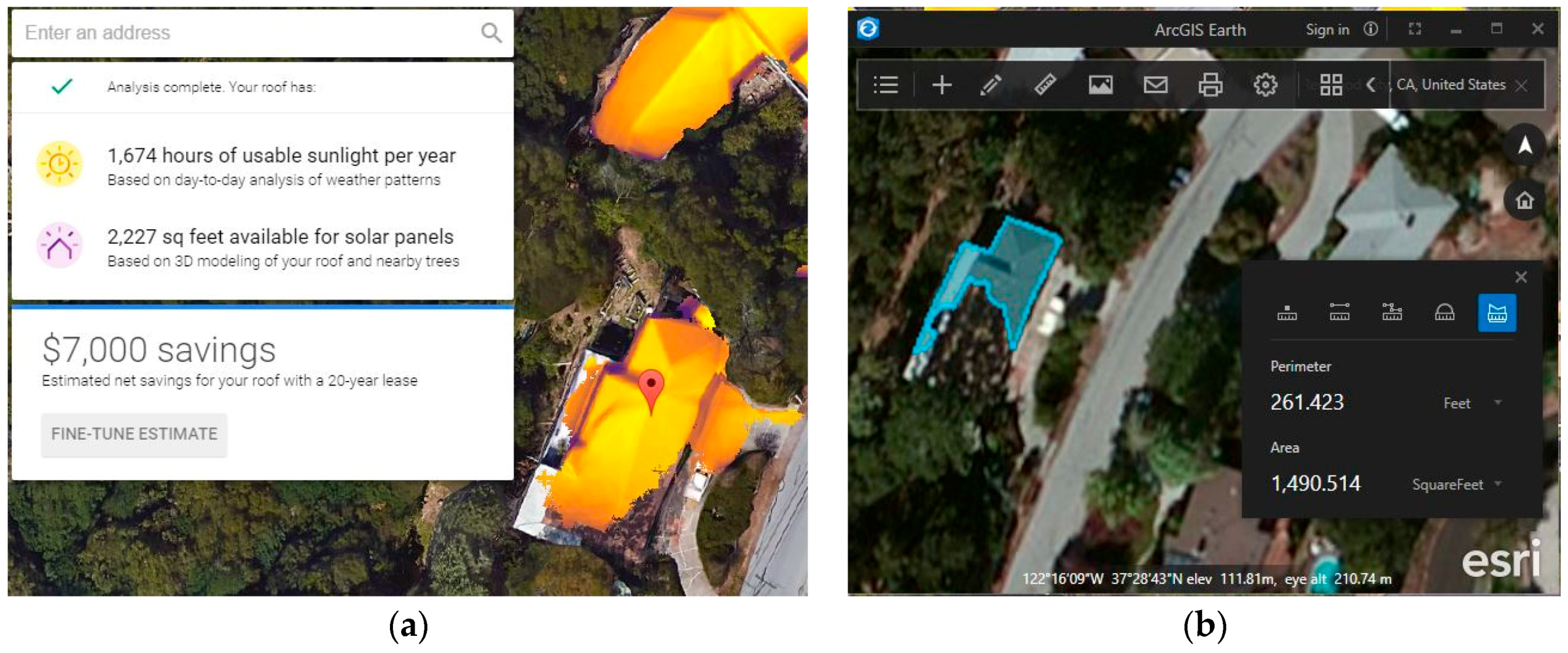
:1. Introduction
2. Materials and Methods
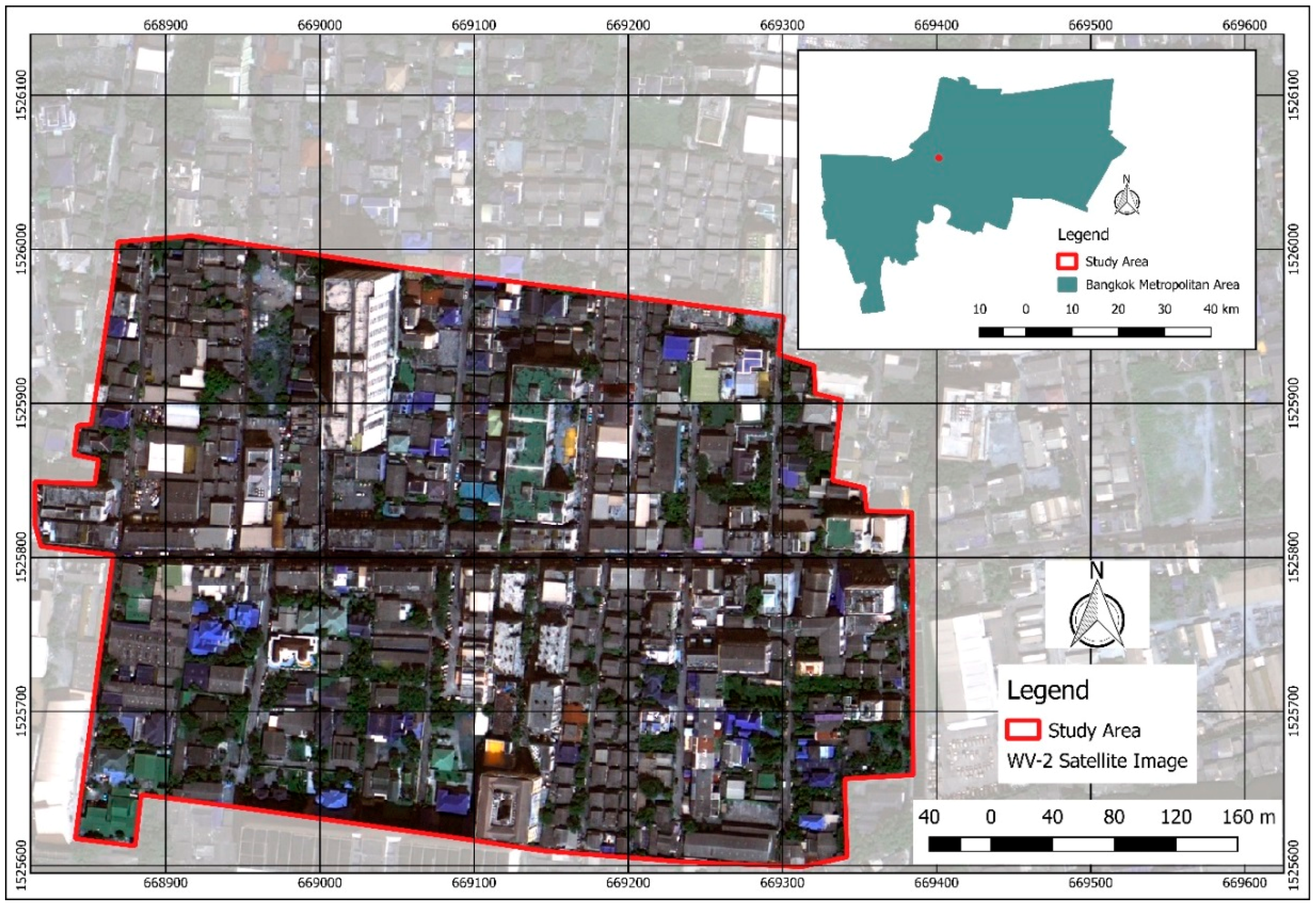
2.1. Study Site
2.2. Dataset
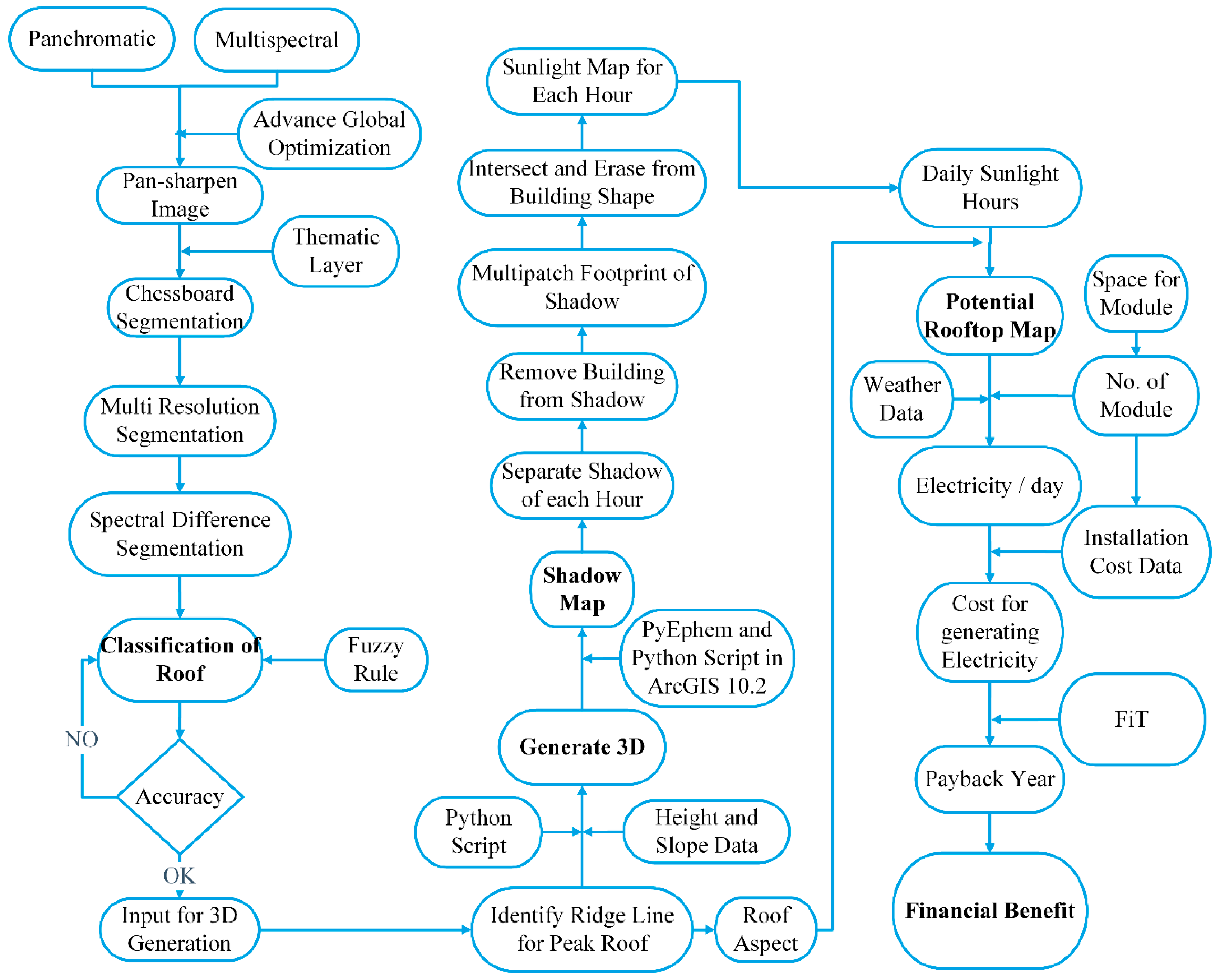
2.3. Data Preparation
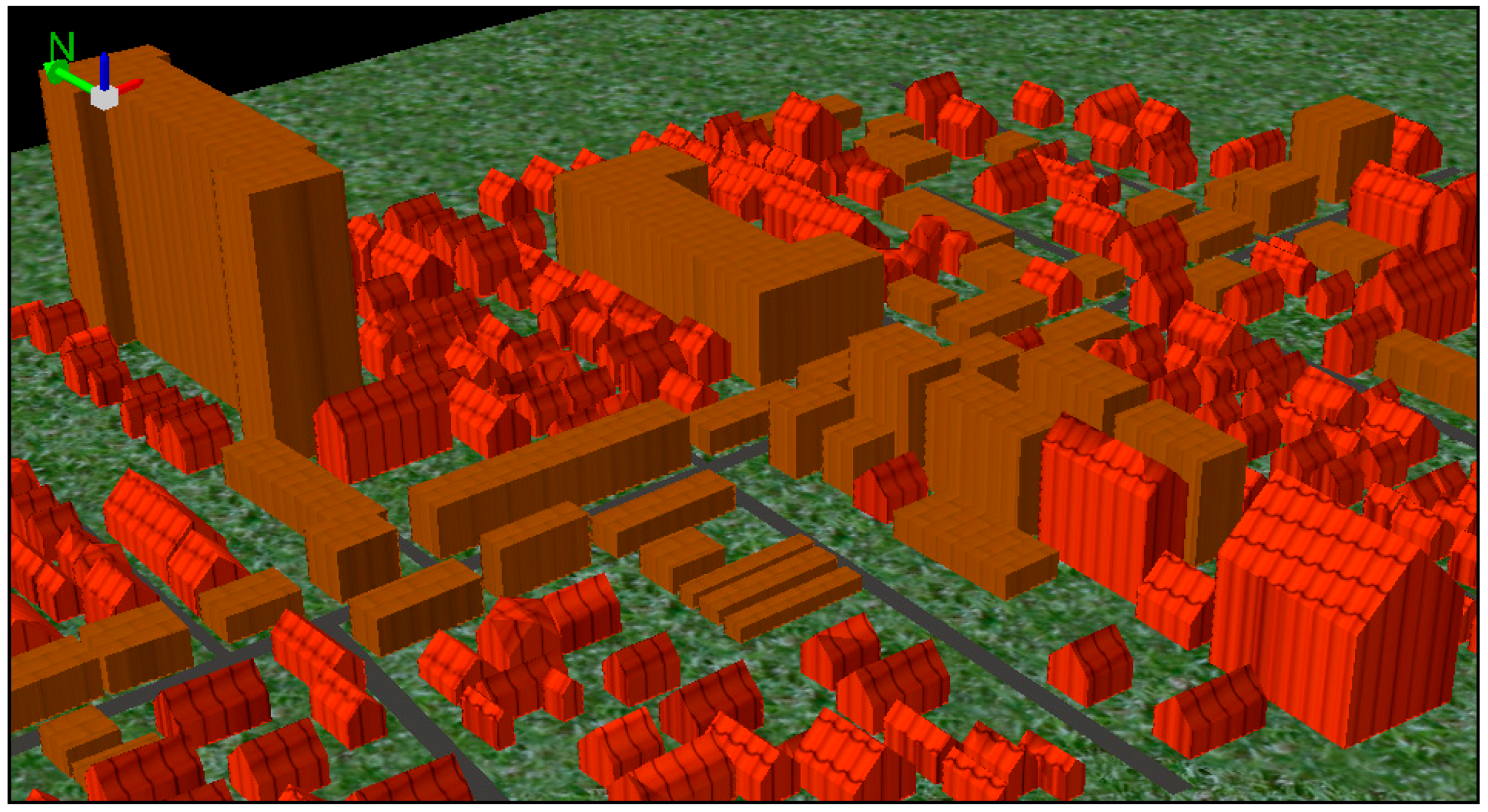
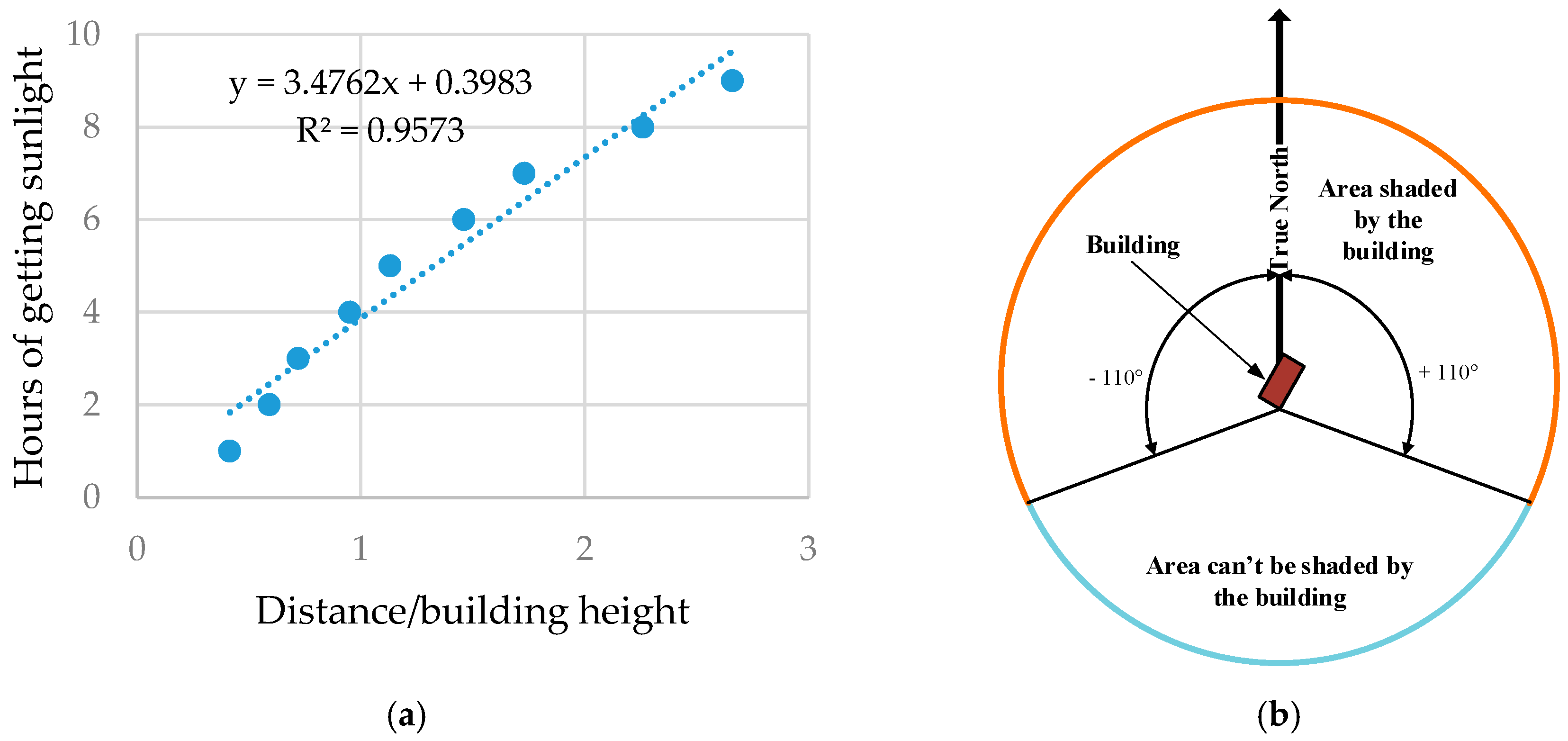
2.4. Analysis
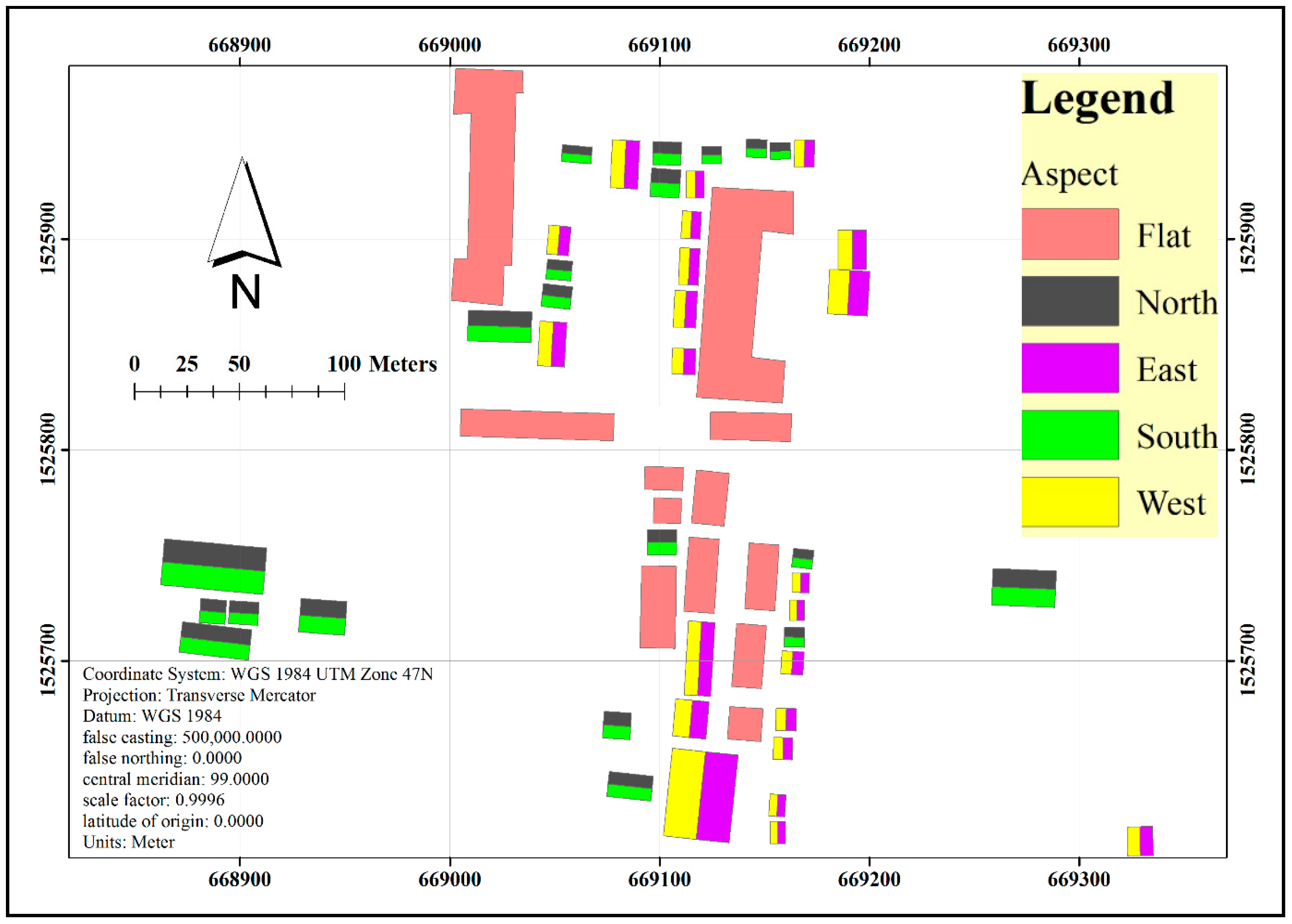
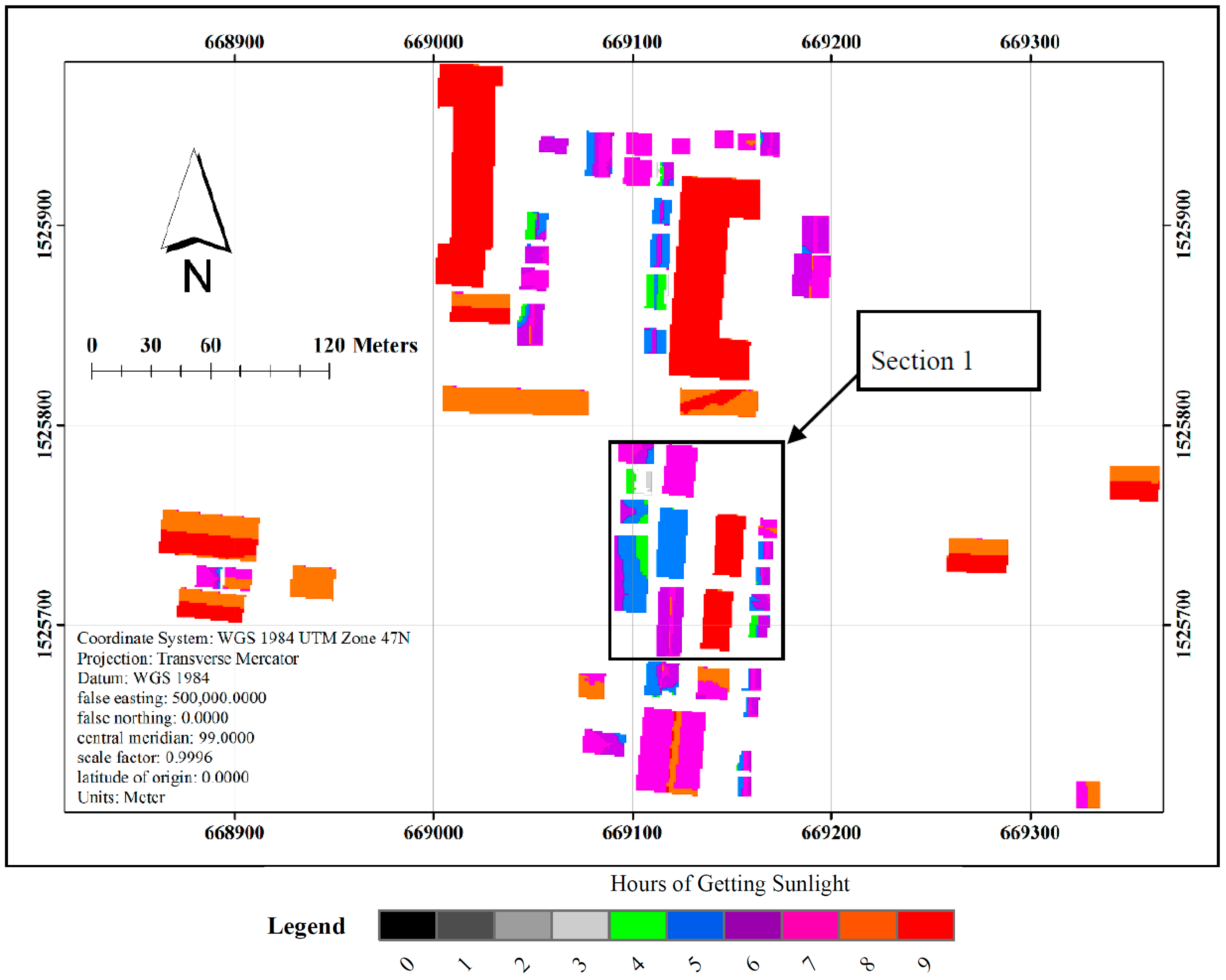
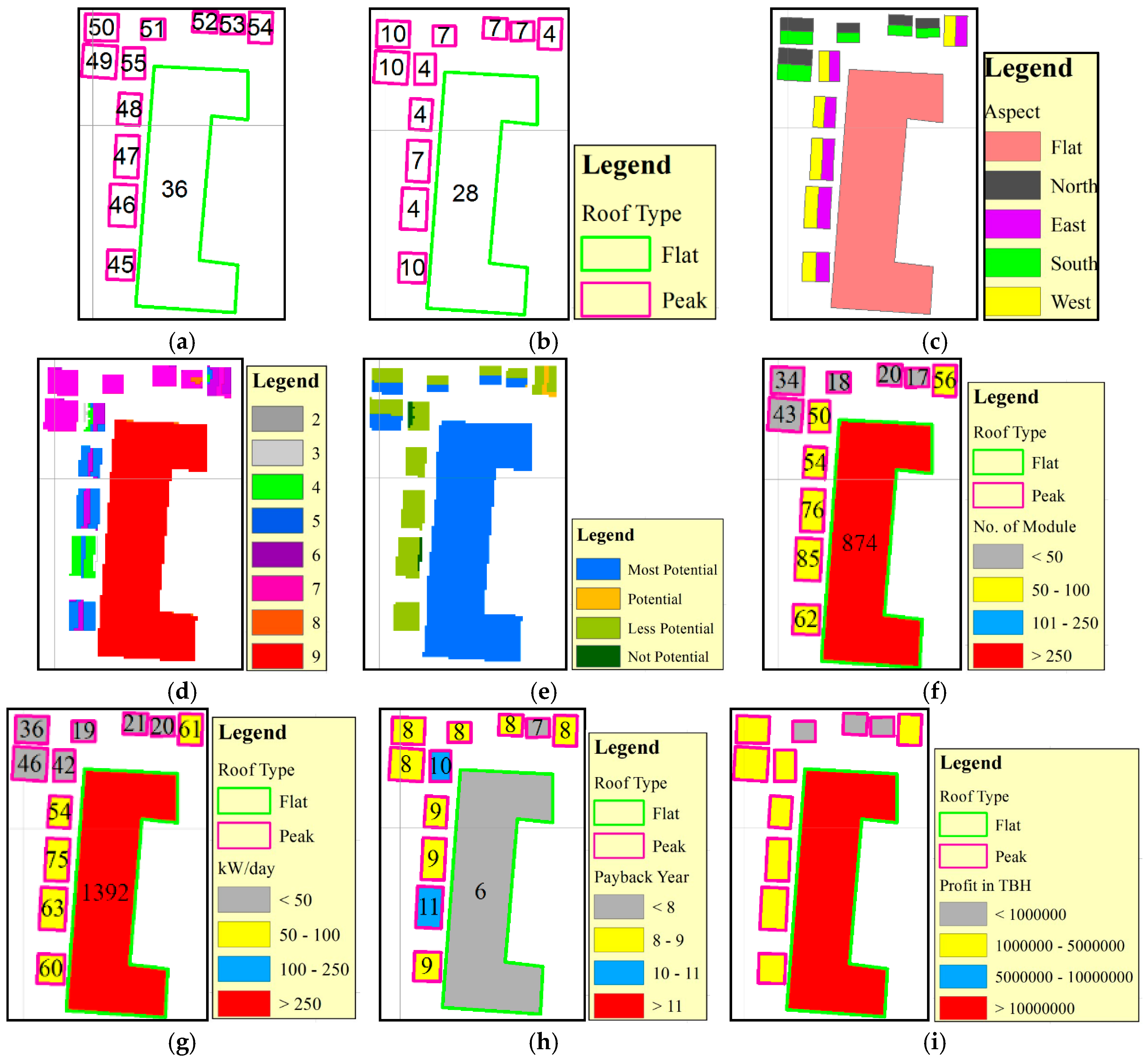
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shafiullah, G.M.; Amanullah, M.T.O.; Ali, A.S.; Jarvis, D.; Wolfs, P. Prospects of renewable energy—A feasibility study in the Australian context. Renew. Energy 2012, 39, 183–197. [Google Scholar] [CrossRef]
- Joshi, A. Estimating per Unit Area Energy Output from Solar PV Modules. 2011. Available online: http://www.ncpre.iitb.ac.in/page.php?pageid=51 (accessed on 5 September 2013).
- Kruangam, D. Pre-Feasibility Study on the Production of Solar Cells and Related Materials in Thailand; Department of Development of Alternative Energy and Energy Efficiency: Bangkok, Thailand, 2007.
- Bangkok Post, Roof Rental Is Solar Power for All. Available online: http://www.bangkokpost.com/print/432272/ (accessed on 16 September 2014).
- Castro, M.; Delgado, A.; Argul, F.J.; Colmenar, A.; Yeves, F.; Peire, J. Grid-connected PV buildings: Analysis of future scenarios with an example of Southern Spain. Sol. Energy 2005, 79, 86–95. [Google Scholar] [CrossRef]
- Bhaskaran, S.; Paramananda, S.; Ramnarayan, M. Per-pixel and object-oriented classification methods for mapping urban features using Ikonos satellite data. Appl. Geogr. 2010, 30, 650–65. [Google Scholar] [CrossRef]
- Sebari, I.; He, D.C. Automatic fuzzy object-based analysis of VHSR images for urban objects extraction. ISPRS J. Photogramm. Remote Sens. 2013, 79, 171–184. [Google Scholar] [CrossRef]
- Aldred, D.A.; Wang, J. A method for obtaining and applying classification parameters in object-based urban rooftop extraction from VHR multispectral images. Int. J. Remote Sens. 2011, 32, 2811–2823. [Google Scholar] [CrossRef]
- Kupková, L.; Potůčková, M.; Kopalová, I.; Kolář, J. Object Based Image Analysis for Urbanized Areas. In Imagin [e, g] Europe: Proceedings of the 29th Symposium of the European Association of Remote Sensing Laboratories, Chania, Greece; IOS Press: Amsterdam, The Netherlands, 2010; p. 231. [Google Scholar]
- Huang, Y.; Yu, B.; Hu, Z.; Wu, J.; Wu, B. Locating suitable roofs for utilization of solar energy in downtown area using airborne LiDAR data and object-based method: A case study of the Lujiazui region, Shanghai. In Proceedings of the 2012 Second International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Shanghai, China, 8–11 June 2012; pp. 322–326.
- Huang, X.; Kwoh, L.K. Monoplotting—A semiautomated approach for 3D reconstruction from single satellite images. Int. Arch. Photogramm. Rem. Sens. Spat. Inf. Sci. 2008, 37, 735–740. [Google Scholar]
- Vosselman, G.; Dijkman, S. 3D building model reconstruction from point clouds and ground plans. Int. Arch. Photogramm. Rem. Sens. Spat. Inf. Sci. 2001, 34, 37–44. [Google Scholar]
- López-Fernández, L.; Lagüela, S.; Picón, I.; González-Aguilera, D. Large Scale Automatic Analysis and Classification of Roof Surfaces for the Installation of Solar Panels Using a Multi-Sensor Aerial Platform. Remote Sens. 2015, 7, 11226–11248. [Google Scholar] [CrossRef]
- Fu, P.; Rich, P.M. Design and implementation of the Solar Analyst: An ArcView extension for modeling solar radiation at landscape scales. In Proceedings of the Nineteenth Annual ESRI User Conference, San Diego, CA, USA, 26–30 July 1999; pp. 1–31.
- Wilson, J.P. Secondary topographic attributes. In Terrain Analysis: Principles and Applications; Wilson, J.P., Gallant, J.C., Eds.; John Wiley & Sons: New York, NY, USA, 2000; pp. 87–131. [Google Scholar]
- Šúri, M.; Hofierka, J. A new GIS-based solar radiation model and its application to photovoltaic assessments. Trans. GIS 2004, 8, 175–90. [Google Scholar] [CrossRef]
- Hofierka, J.; Kaňuk, J. Assessment of photovoltaic potential in urban areas using open-source solar radiation tools. Renew. Energy 2009, 34, 2206–2214. [Google Scholar] [CrossRef]
- Šúri, M.; Huld, T.; Dunlop, E.D.; Hofierka, J. Solar resource modelling for energy applications. In Digital Terrain Modelling; Springer: Berlin/Heidelberg, Germany, 2007; pp. 259–273. [Google Scholar]
- Šúri, M.; Huld, T.A.; Dunlop, E.D. PV-GIS: A web-based solar radiation database for the calculation of PV potential in Europe. Int. J. Sustain. Energy 2005, 24, 55–67. [Google Scholar] [CrossRef]
- Neteler, M.; Mitasova, H. Open Source GIS: A GRASS GIS Approach; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Gadsden, S.; Rylatt, M.; Lomas, K. Putting solar energy on the urban map: A new GIS-based approach for dwellings. Sol. Energy 2003, 74, 397–407. [Google Scholar] [CrossRef]
- Hammer, A.; Heinemann, D.; Hoyer, C.; Kuhlemann, R.; Lorenz, E.; Müller, R.; Beyer, H.G. Solar energy assessment using remote sensing technologies. Remote Sens. Environ. 2003, 86, 423–432. [Google Scholar] [CrossRef]
- Biljecki, F.; Stoter, J.; Ledoux, H.; Zlatanova, S.; Çöltekin, A. Applications of 3D city models: State of the art review. ISPRS Int. J. Geo-Inf. 2015, 4, 2842–2889. [Google Scholar] [CrossRef]
- Izquierdo, S.; Rodrigues, M.; Fueyo, N. A method for estimating the geographical distribution of the available roof surface area for large-scale photovoltaic energy-potential evaluations. Sol. Energy 2008, 82, 929–939. [Google Scholar] [CrossRef]
- Jo, J.H.; Otanicar, T.P. A hierarchical methodology for the mesoscale assessment of building integrated roof solar energy systems. Renew. Energy 2011, 36, 2992–3000. [Google Scholar] [CrossRef]
- Ordóñez, J.; Jadraque, E.; Alegre, J.; Martínez, G. Analysis of the photovoltaic solar energy capacity of residential rooftops in Andalusia (Spain). Renew. Sustain. Energy Rev. 2010, 14, 2122–2130. [Google Scholar] [CrossRef]
- Yu, B.; Liu, H.; Wu, J.; Hu, Y.; Zhang, L. Automated derivation of urban building density information using airborne LiDAR data and object-based method. Landsc. Urban Plann. 2010, 98, 210–219. [Google Scholar] [CrossRef]
- Alexander, C.; Smith-Voysey, S.; Jarvis, C.; Tansey, K. Integrating building footprints and LiDAR elevation data to classify roof structures and visualise buildings. Comput. Environ. Urban Syst. 2009, 33, 285–292. [Google Scholar] [CrossRef]
- Lukač, N.; Žlaus, D.; Seme, S.; Žalik, B.; Štumberger, G. Rating of roofs’ surfaces regarding their solar potential and suitability for PV systems, based on LiDAR data. Appl. Energy 2013, 102, 803–812. [Google Scholar] [CrossRef]
- Le, T.B.; Kholdi, D.; Xie, H.; Dong, B.; Vega, R.E. LiDAR-Based Solar Mapping for Distributed Solar Plant Design and Grid Integration in San Antonio, Texas. Remote Sens. 2016, 8, 247. [Google Scholar] [CrossRef]
- Szabó, S.; Enyedi, P.; Horváth, M.; Kovács, Z.; Burai, P.; Csoknyai, T.; Szabó, G. Automated registration of potential locations for solar energy production with Light Detection And Ranging (LiDAR) and small format photogrammetry. J. Clean. Prod. 2016, 112, 3820–3829. [Google Scholar] [CrossRef]
- Catani, A.; Gómez, F.; Pesch, R.; Schumacher, J.; Pietruschka, D.; Eicker, U. Shading losses of building integrated photovoltaic systems. In Proceedings of the 23th European Photovoltaic Solar Energy Conference and Exhibition, Valencia, Spain, 1–5 September 2008.
- Stevanović, S. Optimization of passive solar design strategies: A review. Renew. Sustain. Energy Rev. 2013, 25, 177–196. [Google Scholar] [CrossRef]
- BBC, Weather Bangkok. Available online: http://www.bbc.co.uk/weather/1609350 (accessed on 14 August 2013).
- Geosage. Available online: http://www.geosage.com/highview/imagefusion.html (accessed on 1 September 2013).
- Braga, F.; Tosi, L.; Prati, C.; Alberotanza, L. Shoreline detection: Capability of COSMO-SkyMed and high-resolution multispectral images. Eur. J. Remote Sens. 2013, 46, 837–853. [Google Scholar] [CrossRef]
- Zhang, Y.; Mishra, R.K. A review and comparison of commercially available pan-sharpening techniques for high resolution satellite image fusion. In Proceedings of the 2012 IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012.
- Definiens. Definiens, Developer 7, User Guide; Definiens AG: München, Germany, 2007. [Google Scholar]
- Baatz, M.; Schäpe, A. Multiresolution segmentation: An optimization approach for high quality multi-scale image segmentation. Angew. Geogr. Informationsverarbeitung XII 2000, 58, 12–23. [Google Scholar]
- Im, J.; Jensen, J.R.; Tullis, J.A. Object-based change detection using correlation image analysis and image segmentation. Int. J. Remote Sens. 2008, 29, 399–423. [Google Scholar] [CrossRef]
- Nobrega, R.A.A.; O’hara, C.G.; Quintanilha, J.A. Detecting roads in informal settlements surrounding Sao Paulo city by using object-based classification. In Proceedings of the 1st International Conference on Object-based Image Analysis (OBIA 2006), Salzburg, Austria, 4–5 July 2006.
- CTBUH. Council on Tall Buildings and Urban Habitat. Available online: http://www.ctbuh.org/TallBuildings/HeightStatistics/HeightCalculator/tabid/1007/language/en-US/Default.asp (accessed on 10 September 2013).
- Boonjub, W. The Study of Thai Traditional Architecture as a Resource for Contemporary Building Design in Thailand. Ph.D. Thesis, Silpakorn University, Bangkok, Thailand, 2009. [Google Scholar]
- North American Board of Certified Energy Practitioners (NABCEP). NABCEP, Photovoltaic (PV) Installation Professional Resource Guide; Brooks, W., Dunlop, J., Eds.; NABCEP: Clifton Park, NY, USA, 2013. [Google Scholar]
- Li, D.H.; Lam, T.N. Determining the optimum tilt angle and orientation for solar energy collection based on measured solar radiance data. Int. J. Photoenergy 2007. [Google Scholar] [CrossRef]
- Techathawiekul, S. Calculations of fixed optimum tilt angle for flat-plate solar collectos for Songkhala, Bangkok, Khon Kaen and Chiang Mai. Sci. Soc. Thail. 1984, 10, 119–122. [Google Scholar] [CrossRef]
- Katartzis, A.; Sahli, H. A stochastic framework for the identification of building rooftops using a single remote sensing image. IEEE Trans. Geosci. Remote Sens. 2008, 46, 259–271. [Google Scholar] [CrossRef]
- Liow, Y.T.; Pavlidis, T. Use of shadows for extracting buildings in aerial images. Comput. Vis. Graph. Image Process. 1990, 49, 242–277. [Google Scholar] [CrossRef]
- Tseng, Y.H.; Wang, S. Semiautomated building extraction based on CSG model-image fitting. Photogramm. Eng. Remote Sens. 2003, 69, 171–180. [Google Scholar] [CrossRef]
- Croitoru, A.; Doytsher, Y. Monocular right-angle building hypothesis generation in regularized urban areas by pose clustering. Photogramm. Eng. Remote Sens. 2003, 69, 151–169. [Google Scholar] [CrossRef]
- Muhammad-Sukki, F.; Ramirez-Iniguez, R.; Munir, A.B.; Yasin, S.H.M.; Abu-Bakar, S.H.; McMeekin, S.G.; Stewart, B.G. Revised feed-in tariff for solar photovoltaic in the United Kingdom: A cloudy future ahead? Energy Policy 2013, 52, 832–838. [Google Scholar] [CrossRef]



| Data Type | Source and Specification |
|---|---|
| WorldView2 | Geo-Informatics and Space Technology Development Agency (GISTDA), Thailand Resolution: Panchromatic—0.46 m; Multispectral—1.85 m; Acquisition date: 8 January 2013 |
| Solar Insolation for the year 2013 | Thai Meteorological Department |
| Solar PV components and installation cost | Two local companies providing and installing solar PV |
| Number of floors | Field survey (visual inspection) |
| FiT Data | Department of Alternative Energy Development and Efficiency (DEDE) |
| Rule No. | Rule Description |
|---|---|
| 1 | For each spectral difference image object: |
| IF compactness membership is high | |
| AND rectangular fit membership is high | |
| THEN P1 membership is high | |
| ELSE F1 membership is high | |
| 2 | IF length/width ratio membership is high |
| AND number of segments membership is high | |
| OR roundness membership is high | |
| THEN P2 membership is high | |
| ELSE F2 membership is high | |
| 3 | IF P2 membership is high |
| THEN Object label = Peaked | |
| ELSE Object label = Flat |
| Aspect | Footprint Area (Sq. Meter) | Available Area (Sq. Meter) | Space for Each Module | Panel | Installation Cost (Million Baht) | Hour | Earning/Year (Thousand Baht) | Payback | Earnings per Sq. Meter Footprint |
|---|---|---|---|---|---|---|---|---|---|
| Flat | 250 | 225 | 3.2 | 70 | 1.4 | 9 | 270 | 5 | 21,653 |
| N–S | 250 | 177 | 2.2 | 80 | 1.6 | 9 | 309 | 5 | 24,746 |
| E–W | 250 | 354 | 2.2 | 160 | 3.2 | 7 | 409 | 8 | 27,812 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ninsawat, S.; Hossain, M.D. Identifying Potential Area and Financial Prospects of Rooftop Solar Photovoltaics (PV). Sustainability 2016, 8, 1068. https://doi.org/10.3390/su8101068
Ninsawat S, Hossain MD. Identifying Potential Area and Financial Prospects of Rooftop Solar Photovoltaics (PV). Sustainability. 2016; 8(10):1068. https://doi.org/10.3390/su8101068
Chicago/Turabian StyleNinsawat, Sarawut, and Mohammad Dalower Hossain. 2016. "Identifying Potential Area and Financial Prospects of Rooftop Solar Photovoltaics (PV)" Sustainability 8, no. 10: 1068. https://doi.org/10.3390/su8101068
APA StyleNinsawat, S., & Hossain, M. D. (2016). Identifying Potential Area and Financial Prospects of Rooftop Solar Photovoltaics (PV). Sustainability, 8(10), 1068. https://doi.org/10.3390/su8101068






