An Application of the Short-Term Forecasting with Limited Data in the Healthcare Traveling Industry
Abstract
:1. Introduction
2. Theoretical Foundation
2.1. The Time Series Forecasting Using Exponential Smoothing
2.2. The Grey Forecasting
2.3. The Lotka-Vottera System
3. Methodology
3.1. The Exponential Smoothing Model
- : Predicted value for the time period i + 1
- : Predicted value for the time period i
- α: Smoothing constant
3.2. Traditional Grey Forecasting Model GM(1,1)
3.3. The Lotka-Votterra Forecasting Model
- is the variation in the random process,
- is the time steps
- is the dynamic change of .
3.4. Assessing Forecast Performance
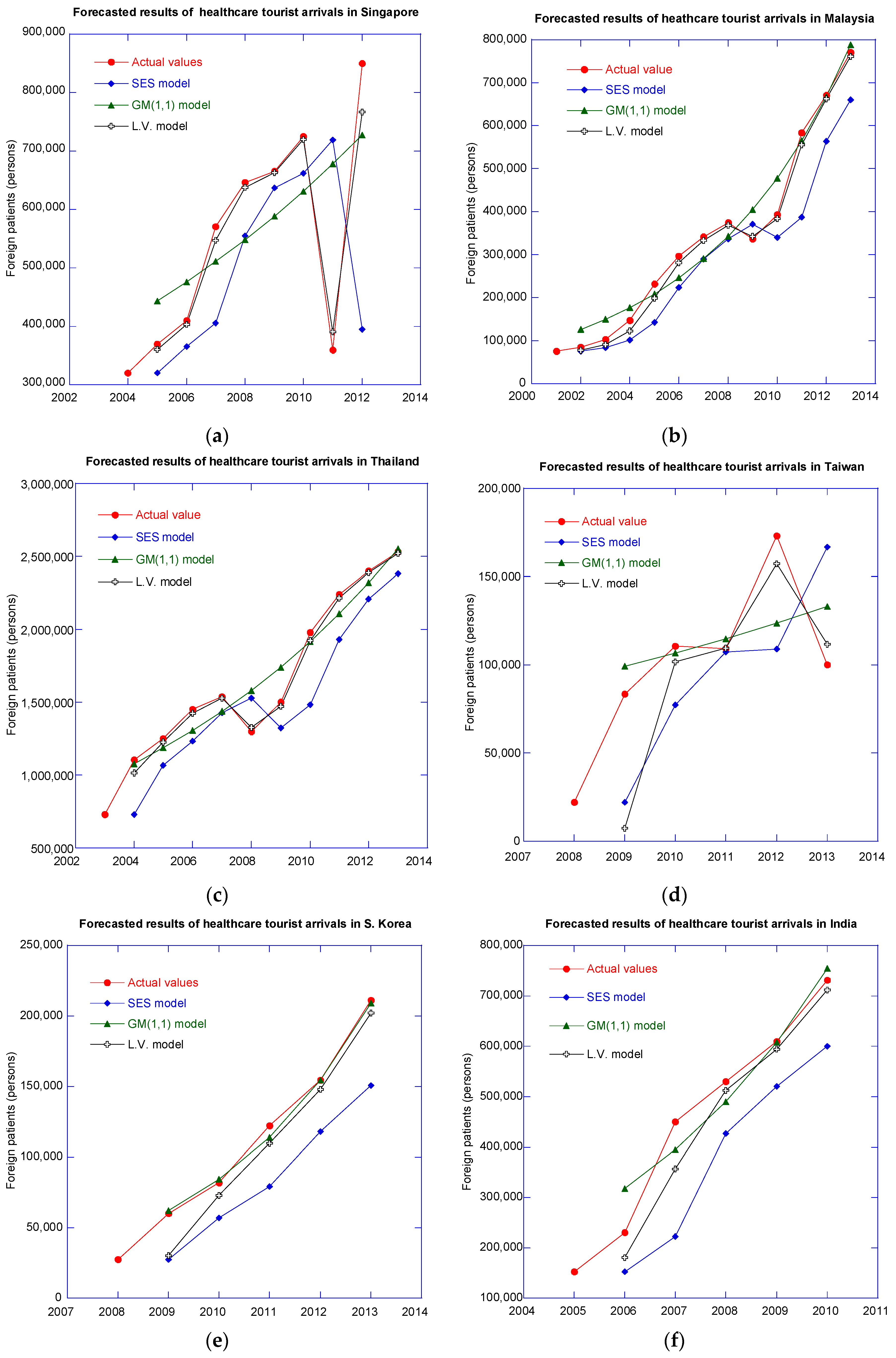
4. Results and Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Burkett, L. Medical Tourism. J. Leg. Med. 2007, 28, 223–245. [Google Scholar] [CrossRef] [PubMed]
- Mudur, G. Hospitals in India woo foreign patients. Br. Med. J. 2004, 328, 1338. [Google Scholar] [CrossRef] [PubMed]
- Lunt, N.; Mannion, R. Patient mobility in the global marketplace: A multidisciplinary perspective. Int. J. Health Pol. Manag. 2014, 2, 155–157. [Google Scholar] [CrossRef] [PubMed]
- Transparency Market Research. Medical Tourism Market (India, Thailand, Singapore, Malaysia, Mexico, Brazil, Taiwan, Turkey, Korea, Costa Rica, Poland, Dubai and Philippines)—Global Industry Analysis, Size, Share, Growth, Trends and Forecast, 2013–2019. Available online: http://www.transparencymarketresearch.com/medical-tourism.html (accessed on 31 May 2016).
- NaRanong, A.; NaRanong, V. The effects of medical tourism: Thailand’s experience. Bull. World Health Organ. 2011, 89, 336–344. [Google Scholar] [CrossRef] [PubMed]
- Chee, H.L. Medical tourism and the state in Malaysia and Singapore. Glob. Soc. Pol. 2010, 10, 336–357. [Google Scholar] [CrossRef]
- Penang Institute. Available online: http://penanginstitute.org/v3/resources/articles/statistics/611-an-appendix-on-nurses (accessed on 13 October 2016).
- International Medical Travel Journal. Available online: https://www.imtj.com/news/new-plans-boost-korean-medical-tourism/ (accessed on 13 October 2016).
- Report of Taiwan Ministry of Health and Welfare. Available online: http://issue.thrf.org.tw/Uploads/%7B00BD37F7-036B-496C-BBD4-FC57AE9A8D28%7D_%E8%A1%9B%E7%A6%8F%E9%83%A8%E5%A0%B1%E5%91%8A%E4%B8%80.pdf (accessed on 13 October 2016).
- Tourism Bureau of Taiwan. Available online: http://admin.taiwan.net.tw/statistics/release_en.aspx?no=7 (accessed on 13 October 2016).
- KaisiKon Research Center. Available online: https://www.kasikornresearch.com/EN/K-EconAnalysis/Pages/ViewSummary.aspx?docid=9504 (accessed on 13 October 2016).
- International Medical Travel Journal. Available online: https://www.imtj.com/news/latest-figures-medical-tourism-thailand/ (accessed on 13 October 2016).
- Khan, M.J.; Chelliah, S.; Haron, M.S. Medical tourism destination image formation process: A conceptual model. Int. J. Healthc. Manag. 2016, 9, 134–143. [Google Scholar] [CrossRef]
- Darwazeh, D. Medical Tourism: Establishing a Sustainable Medical Facility. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, August 2011. [Google Scholar]
- Archer, B.; Ritchie, J.R.B.; Goeldner, C.R. Demand Forecasting and Estimation. Travel, Tourism, and Hospitality Research. A Handbook for Managers and Researchers; John Wiley & Sons, Inc.: New York, NY, USA, 1987. [Google Scholar]
- Van Doorn, J.W.M. Tourism forecasting and the policymaker. Tour. Manag. 1984, 5, 24–39. [Google Scholar] [CrossRef]
- Song, H.; Li, G. Tourism demand modelling and forecasting—A review of recent research. Tour. Manag. 2008, 29, 203–220. [Google Scholar] [CrossRef]
- Li, G. Recent developments in econometric modelling and forecasting. J. Trav. Res. 2005, 44, 82–99. [Google Scholar] [CrossRef]
- Huang, Y.L. Forecasting the demand for health tourism in Asian countries using a GM(1,1)-alpha model. Tour. Hospit. Manag. 2012, 18, 171–181. [Google Scholar]
- Rai, A.; Chakrabarty, P.; Sarkar, A. Forecasting the demand for medical tourism in India. IOSR Int. J. Humanit. Soc. Sci. 2014, 19, 22–30. [Google Scholar] [CrossRef]
- Teng, H.; Huang, Y. The use for the competition theory of the industrial investment decisions—A case study of the Taiwan IC assembly industry. Int. J. Prod. Econ. 2013, 141, 335–338. [Google Scholar] [CrossRef]
- Stevenson, W.J. Operations Management-9/E.: International Student Edition with Global Readings; McGraw-Hill Education (Asia): Singapore, 2007. [Google Scholar]
- Lin, C.S. Forecasting and analyzing the competitive diffusion of mobile cellular broadband and fixed broad-band in Taiwan with limited historical data. Econ. Model. 2013, 35, 207–213. [Google Scholar] [CrossRef]
- Wilson, J.H.; Allison-Koerber, D. Combining subjective and objective forecasts improve results. J. Bus. Forecast. 1992, 11, 3–8. [Google Scholar]
- Brown, R.G. Smoothing, Forecasting and Prediction of Discrete Time Series; Dover Publications: Mineola, NY, USA, 2004. [Google Scholar]
- Gardner, E.S. Exponential smoothing: The state of the art. J. Forecast. 1985, 4, 1–28. [Google Scholar] [CrossRef]
- Harrison, P.J. Exponential smoothing and short-term sales forecasting. Manag. Sci. 1967, 13, 821–842. [Google Scholar] [CrossRef]
- Snyder, R.D.; Koehler, A.B.; Ord, J.K. Forecasting for inventory control with exponential smoothing. Int. J. Forecast. 2002, 18, 5–18. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Wen, K.L.; Huang, Y.F. The development of grey Verhulst toolbox and the analysis of population saturation state in Taiwan-Fukien. In Proceeding of the IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No.04CH37583), The Hague, The Netherlands, 10–13 October 2004.
- Huang, Y.-F.; Wang, C.-N.; Dang, H.-S.; Lai, S.-T. Predicting the trend of Taiwan’s electronic paper industry by an effective combined grey model. Sustainability 2015, 7, 10664–10683. [Google Scholar] [CrossRef]
- Hsu, L.-C. Applying the Grey prediction model to the global integrated circuit industry. Technol. Forecast. Soc. Chang. 2003, 70, 563–574. [Google Scholar] [CrossRef]
- Huang, Y.-F.; Wang, C.-N.; Dang, H.-S.; Lai, S.-T. Evaluating performance of the DGM(2,1) model and its modified models. Appl. Sci. 2016. [Google Scholar] [CrossRef]
- Lotka, A.J. Elements of Physical Biology, 1924; Republished as Elements of mathematical biology; Dover Publications: New York, NY, USA, 1956. [Google Scholar]
- Lee, S.J.; Lee, D.J.; Oh, H.S. Technological forecasting at the Korean stock market: A dynamic competition analysis using Lotka–Volterra model. Technol. Forecast. Soc. Chang. 2005, 72, 1044–1057. [Google Scholar] [CrossRef]
- Wijeratne, A.W.; Karunaratne, J.A.; Wang, C.; Wei, J. An empirical Lotka-Volterra system for competition dynamics in the telecommunication sector of Sri Lanka. Int. J. Bus. Inform. Syst. 2008, 3, 482–497. [Google Scholar] [CrossRef]
- Wijeratne, A.W.; Yi, F.; Wei, J. Bifurcation analysis in the diffusive Lotka–Volterra system: An application to market economy. Chaos Solitons Fractals 2009, 40, 902–911. [Google Scholar] [CrossRef]
- Marasco, A.; Picucci, A.; Romano, A. Market share dynamics using Lotka–Volterra models. Technol. Forecast. Soc. Chang. 2016, 105, 49–62. [Google Scholar] [CrossRef]
- Hung, H.-C.; Tsai, Y.-S.; Wu, M.-C. A modified Lotka–Volterra model for competition forecasting in Taiwan’s retail industry. Comput. Ind. Eng. 2014, 77, 70–79. [Google Scholar] [CrossRef]
- Makridakis, S.; Wheelwright, S.C.; McGee, V.E. Forecasting: Methods and Applications; John Wiley & Son, Inc.: New York, NY, USA, 1983. [Google Scholar]
- Ravinder, H.V. Determining the optimal values of exponential smoothing constants-does solver really work? Am. J. Bus. Educ. 2013. [Google Scholar] [CrossRef]
- Chopra, S.; Meindl, P. Supply Chain Management: Strategy, Planning, and Operation, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Lewis, C.D. Industrial and Business Forecasting Methods: A Practical Guide to Exponential Smoothing and Curve Fitting; Butterworth-Heinemann: Oxford, UK, 1982. [Google Scholar]
- Ma, H.; Zhang, Z. Grey Prediction with Markov-Chain for crude oil production and consumption in China. Adv. Intell. Soft Comput. 2009, 56, 551–561. [Google Scholar]
| Years | Destinations | |||||
|---|---|---|---|---|---|---|
| Malaysia | Singapore | Thailand | Korea | Taiwan | India | |
| 2001 | 75,210 | |||||
| 2002 | 84,585 | |||||
| 2003 | 102,946 | 730,000 | ||||
| 2004 | 147,189 | 320,000 | 1,103,905 | |||
| 2005 | 232,161 | 370,000 | 1,249,984 | 153,000 | ||
| 2006 | 296,689 | 410,000 | 1,450,000 | 230,000 | ||
| 2007 | 341,228 | 571,000 | 1,540,000 | 450,000 | ||
| 2008 | 374,063 | 646,000 | 1,300,000 | 27,480 | 21,974 | 530,000 |
| 2009 | 336,225 | 665,000 | 1,500,000 | 60,201 | 83,496 | 609,000 |
| 2010 | 392,956 | 725,000 | 1,980,000 | 81,789 | 110,664 | 731,000 |
| 2011 | 583,296 | 359,590 | 2,240,000 | 122,297 | 109,133 | |
| 2012 | 671,227 | 850,000 | 2,400,000 | 159,464 | 173,081 | |
| 2013 | 770,134 | 2,530,000 | 211,218 | 100,083 | ||
| Forecast Models | Data Requirement | Time Horizon for Forecasting |
|---|---|---|
| Moving average | 2 to 30 | Short |
| Simple exponential smoothing | 5 to 10 | Short |
| Trend models | 10 to 20 | Short, medium |
| Casual regression models | 10 observations per independent variable | Short, medium, or long |
| Box–Jenkins | 50 | Long |
| Neural network | Large number | Short |
| Grey models | 4 | Short, medium, or long |
| Evaluative items | Maylaysia | Singapore | Thailand | Korea | Taiwan | India | |
|---|---|---|---|---|---|---|---|
| Exponential Smoothing | MAD | 191,682.06 | 157,220.89 | 669,091.67 | 32,907.03 | 45,471.7 | 125,534.9 |
| RMSE | 293,201.8 | 218,369.8 | 1,058,751 | 37,672.3 | 51,854.5 | 136,711.7 | |
| MAPE (%) | 39.73 | 29.28 | 31.9 | 34.42 | 41.8 | 27.21 | |
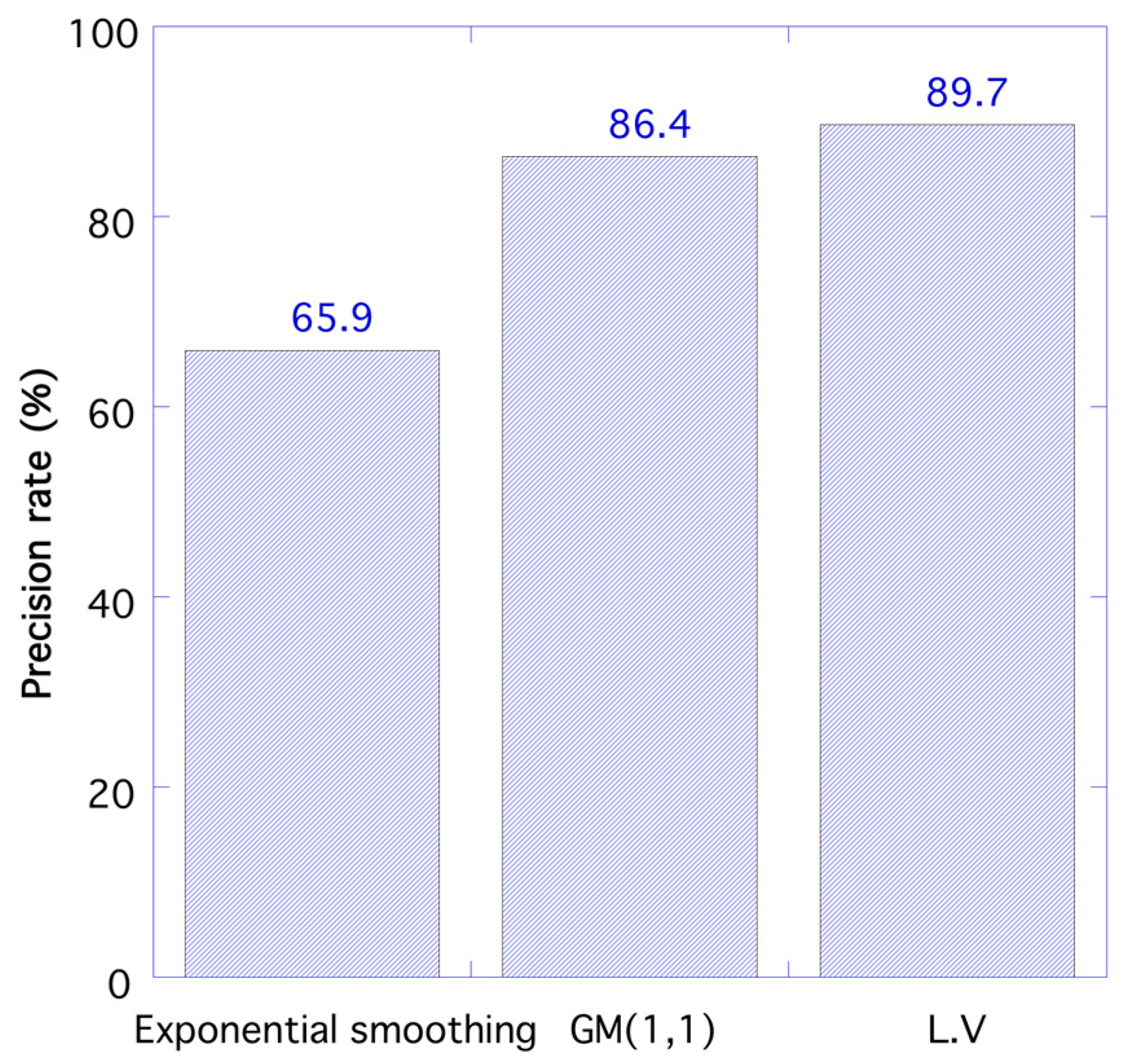
| Precision rate (%) | 60.27 | 70.72 | 68.1 | 65.58 | 58.2 | 72.79 | |
| Forecasting grade | Unqualified | Unqualified | Unqualified | Unqualified | Unqualified | Unqualified | |
| GM(1,1) Model | MAD | 39,040.55 | 113,545.53 | 115,834.49 | 2993.99 | 21,540.44 | 41,644.10 |
| RMSE | 44,825.44 | 138,653.14 | 142,023.39 | 4068.66 | 27,664.76 | 50,930.88 | |
| MAPE (%) | 17.74 | 23.62 | 7.51 | 2.84 | 17.80 | 12.31 | |
| Precision rate (%) | 82.26 | 76.38 | 92.49 | 97.16 | 82.20 | 87.69 | |
| Forecasting grade | Unqualified | Unqualified | Good | Excellent | Unqualified | Qualified | |
| Lotka-Votterra Model | MAD | 13,995.98 | 21,074.99 | 30,303.99 | 13,415.29 | 22,615.54 | 38,838.85 |
| RMSE | 16,634.61 | 32,782.83 | 38,064.03 | 15,842.45 | 35,483.61 | 49,104.61 | |
| MAPE (%) | 6.03 | 3.61 | 2.10 | 15.87 | 24.10 | 10.10 | |
| Precision rate (%) | 93.97 | 96.39 | 97.90 | 84.13 | 75.90 | 89.90 | |
| Forecasting grade | Good | Excellent | Excellent | Unqualified | Unqualified | Qualified |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, H.-S.; Huang, Y.-F.; Wang, C.-N.; Nguyen, T.-M.-T. An Application of the Short-Term Forecasting with Limited Data in the Healthcare Traveling Industry. Sustainability 2016, 8, 1037. https://doi.org/10.3390/su8101037
Dang H-S, Huang Y-F, Wang C-N, Nguyen T-M-T. An Application of the Short-Term Forecasting with Limited Data in the Healthcare Traveling Industry. Sustainability. 2016; 8(10):1037. https://doi.org/10.3390/su8101037
Chicago/Turabian StyleDang, Hoang-Sa, Ying-Fang Huang, Chia-Nan Wang, and Thuy-Mai-Trinh Nguyen. 2016. "An Application of the Short-Term Forecasting with Limited Data in the Healthcare Traveling Industry" Sustainability 8, no. 10: 1037. https://doi.org/10.3390/su8101037
APA StyleDang, H.-S., Huang, Y.-F., Wang, C.-N., & Nguyen, T.-M.-T. (2016). An Application of the Short-Term Forecasting with Limited Data in the Healthcare Traveling Industry. Sustainability, 8(10), 1037. https://doi.org/10.3390/su8101037







